1 Introduction

Epidemic models take a variety of mathematical forms (Anderson and May 1992; Keeling and Rohani 2008), and are are now routinely used to inform policy on disease control and contribute towards public health plans (Baguelin et al. 2010; Ferguson et al. 2003; Riley et al. 2003; Tildesley et al. 2006). One of the most commonly investigated forms of models are susceptible-infectious-removed (SIR), in which everyone is either susceptible to the disease, infectious with it, or removed from the future disease dynamics. This model is a simplification of reality, but provides a useful starting point for modelling diseases where previous infection confers long-lasting immunity, for example outbreaks of childhood diseases like measles, some respiratory illnesses like pandemic influenza, and historical pathogens such as smallpox (Keeling and Rohani 2008).

Simple models of epidemics have assumed that all members of a population interact at a homogeneous rate and therefore that at a given time every susceptible has an equal probability of contracting the disease from any infectious individual. A more realistic way to think of the spread of diseases can be that they spread through contacts between people, with these contacts describing a network of interactions. In the case of homogeneous mixing this network is under some conditions an Erdös-Rényi (ER) random graph. There have been many examples of using networks to study the spread of disease and two review papers (Bansal et al. 2007; Danon et al. 2011) compare several different approaches to network modelling.

Longstanding generalisations of homogeneous mixing epidemic dynamics include heterogeneous network models (Eames and Keeling 2002) and regular clustered networks (Keeling 1999). Regularity (each individual having exactly \(n\) links) is appropriate for some populations (and was originally motivated by spatially embedded ecological and veterinary applications) but for human respiratory transmission (Mossong et al. 2008) and sexually transmitted infections (Kamp 2010; Schneeberger et al. 2004), this is almost definitely inaccurate and the contact network is highly degree-heterogeneous. In this work, we represent heterogeneity in degree using what has become a de facto standard: the configuration model (Molloy and Reed 1995).

As relevant theory has developed, through moment-closure approximations and other methods (Bansal et al. 2007; Danon et al. 2011; Lindquist et al. 2011; Rand 1999), the use of heterogeneous networks has become more and more common in the literature. Several areas of interest for epidemics have been studied. The invasion threshold of the infection has been calculated (Diekmann and Heesterbeek 2000), and involves the mean and variance of the degree distribution. The final size of an epidemic with a given degree distribution along with the mean degree of the individuals infected has been derived (Newman 2002). In particular we note the use of a probability generating function (Miller 2010; Volz 2008) to derive a small number of nonlinear ODEs that describe the dynamics of a SIR infection on a random heterogeneous network. In most cases where networks are used they are static, i.e. decided at one point in time and fixed that way rather than changing over time, though there are several examples where this assumption is not made (Kamp 2010; Miller et al. 2012; Volz and Myers 2007). There are also examples of networks on which the individuals have heterogeneous degree and are always changing contacts (May and Lloyd 2001; Pastor-Satorras and Vespignani 2001), although there is some precedence for this modelling framework before the widespread use of networks as a conceptual tool (May and Anderson 1988). Though the extremes of static or extremely dynamic networks are obviously unrealistic, they are useful to enable some analytic traction and also increase the ease with which we can simulate. More recently though there have been attempts to include some additional way of passing on the disease rather than just through the defined links of the network in an attempt to describe the fact that diseases can be passed between members of the population that do not have more than one interaction, i.e. a ‘global’ infection term (Kiss et al. 2006).

Observed epidemics are noisy and unpredictable, which motivates the use of stochastic epidemic models (Andersson and Britton 2000). While some asymptotic results for invasion and final size of stochastic epidemics on networks can be derived in a discrete-time branching process framework, if one is interested in transient dynamics then the natural model is an appropriate continuous time Markov chain. For an SIR-type epidemic model on an arbitrary graph with \(N\) nodes, such a Markov chain would involve \(3^N\) ODEs, which quickly becomes computationally intractable. The method proposed by Ball and Neal (2008) involves creating a configuration model network at the same time as the epidemic tree, and this stochastic process manifestly asymptotically converges on \(2M\) ODEs in the deterministic large \(N\) limit, where \(M\) is the maximum number of contacts that the most well connected individual on a network has. Unfortunately, this can still be very large depending on the exact degree distribution and any attempt to cut down the number of equations by ignoring individuals who have more than a given number of neighbours, will inevitably ignore some of the most important individuals for the dynamics. Fortunately, recent work (Decreusefond et al. 2012) has shown that a more sophisticated convergence proof leads to the smaller equation set of Volz (2008).

The desire to model stochasticity without a massive increase in dimensionality has led researchers to consider the diffusion limit. This general approach to stochastic processes is typically either attributed to van Kampen (1992) or Kurtz (1970; 1971), but the basic idea is that provided that our population is sufficiently large, we can approximate the Markov process that describes the epidemic by a deterministic model together with appropriately scaled white noise processes that are defined by the transition rates between the states of the Markov chain. Such methods have been used to derive a low dimensional model in which properties of the noise in a stochastic epidemic model can be investigated analytically (Alonso et al. 2007; Black et al. 2009), by Ross (2006) to obtain expressions for the mean and variance of a metapopulation model, and by Colizza et al. (2006) to model the effect of air travel on the spread of epidemics in a large-scale network. These models are attractive since they have the same dimensionality as the deterministic limit, but are actually stochastic, and corrections to the approximation are \(O(N^{-1})\).

In this paper we will apply the results of Kurtz to SIR-type epidemic dynamics on a configuration model network, as was done for SIS dynamics on a regular graph by Dangerfield et al. (2009). Using this we obtain a four-dimensional set of stochastic ODEs, from which we derive an analytical expression for the variance of the asymptotic early growth of an epidemic on a network given its degree distribution. We provide an argument that our approach is asymptotically exact, and simulate epidemics on various networks to confirm the utility of our analytical results.

2 Network model

The use of networks as a generalisation from homogeneous mixing is becoming one of the most widely used in epidemiological modelling. Contact between two individuals of the population we are considering forms a link between them. Once a link is established, the infection can be passed along it in either direction. Specifically what contact is represented depends on the disease, i.e. it is different for a respiratory infection compared to a sexually transmitted infection. These differences will affect how the contact network is constructed, but we use a common modelling framework once the network is known.

The network can be described by a symmetric \(N\times N\) matrix \(\mathbf A \), which has binary entries, \(A_{i,j}\in \{0,1\}\), where the entry \(A_{i,j}\) will be 1 if nodes \(i\) and \(j\) have a link between them and 0 otherwise. We do not allow self links in the network or multiple links between nodes. We make the simplifying assumptions that all links are of equal strength and that once a link is made it will be there throughout the spread of the epidemic.

The degree distribution of a network, \(P(k)\), specifies what the probability is that a node selected uniformly at random will have \(k\) neighbours. To construct an uncorrelated network with a given degree distribution, \(P(k)\), the configuration model is used (Molloy and Reed 1995). The method for this is as follows:

  • Each member of the population \(i\) is given a number of “half-links” or “stubs”, \(k_i\), which is drawn from the degree distribution \(P(k)\). Once this is done we can define \(d_k\) to be the proportion of nodes in the network that have \(k\) neighbours.

  • Pairs of stubs are then picked uniformly at random and are then joined up forming an undirected edge between the two corresponding vertices.

Later in the paper, when we simulate an epidemic on a network, this is the method that is used to create a network with the degree distribution that we require. Asymptotically, the differences due to different ways of dealing with repeated- and self-edges will be \(O(N^{-1})\). Our choice for how to deal with these in a finite system is to obtain a list of all the nodes which have multiple connections between them and self-edges. One by one, the extra links between nodes will be broken, say between node \(i\) and \(j\), and then a randomly selected and connected pair of nodes will also be selected, say nodes \(\imath ^{\prime }\) and \(\jmath ^{\prime }\). We then connect \(i\) and \(\imath ^{\prime }\) together and \(j\) and \(\jmath ^{\prime }\) together, which leaves the degree distribution unaltered. This is then repeated until there are no repeated- and self-edges.

3 Diffusion model

3.1 Model definition

We assume a population of \(N\) individuals on a configuration model network. Individuals are stratified by their disease state \(S, I\), or \(R\), and their degree on the network \(k\). Individuals of type \(S_k\) become \(I_k\) at a rate equal to the product of the transmission rate \(\tau \) and their number of infectious neighbours. Individuals of type \(I_k\) become \(R_k\) at a rate \(\gamma \). We are interested in the large \(N\) regime, in which we write \([S_k]\) for the expected number of susceptibles of degree \(k, [I_k]\) for the expected number of infectious individuals of degree \(k\), and \([AB]\) for the number of connected pairs of individuals on the network where one is type \(A\) and the other is type \(B\). Omission of a subscript denotes implicit summation, e.g. \([S] = \sum _k [S_k]\).

To derive pairwise equations, we require knowledge of the neighbourhood of each node. This is due to the fact that when an infection or recovery takes place the number of pairs of type \([AB]\) will be changed in a way which is dependent on the neighbours that the node has. This is why it is not straightforward to write down a low-dimensional form for this process as the population size becomes large, since this requires the distribution of neighbours of each node. We therefore make the following assumption, that we will justify below: The distribution of neighbourhoods with \(x\) susceptibles and \(y\) infectious individuals around a susceptible individual of degree \(k\), is a multinomial with probabilities that do not depend on \(k\), i.e.

$$\begin{aligned} D^S_{x,y,k}=\left( {\begin{array}{c}k\\ x,y\end{array}}\right) (1-p_S-q_S)^{k-x-y}p_S^xq_S^y \text{, } \end{aligned}$$
(1)

where,

$$\begin{aligned} p_S = \frac{[S S]}{\sum _k k [S_k]}, q_S = \frac{[S I]}{\sum _k k [S_k]}\text{. } \end{aligned}$$
(2)

Here the term \(\left( {\begin{array}{c}k\\ x,y\end{array}}\right) = k!/x!y! \), is the multinomial coefficient. We have not detailed an assumption for the neighbourhoods of infected nodes here, as this requires more care to be taken. This will be detailed later, and will be denoted by \(D_{x,k}^I\). With these assumptions, it is possible to reduce the state space of the Markov chain dramatically. In fact, a closed system is obtained that is of dimension four. The insight that allows this dimensional reduction is from Volz (2008), although our model uses pairwise notation and is derived explicitly from applying the results of Kurtz to an underlying stochastic process. We note that \(g(x) = \sum _k d_k x^k\) (where \(d_k\), as defined above, is the proportion of nodes with degree \(k\)) is the probability generating function (pgf) of the degree distribution. We also define and keep track of the variable \(\theta \) in our dynamical system. \(\theta \) is defined to be the proportion of degree one nodes that are still susceptible at time \(t\). Infection down each link is assumed to be independent, which implies that the probability that a node of degree \(k\) being susceptible at time \(t\) will be \(\theta ^k\). We can then write the number of degree \(k\) nodes that are still susceptible at time \(t\) as \([S_k] = N d_k \theta (t)^k\). If there are no degree one nodes in the population, then we can think of \(\theta \) in terms of its relationship with degree \(k\) nodes. It is the \(1/k\)-th power of the probability that a randomly chosen degree \(k\) node is susceptible.

We also note that many important features of the network can be written simply using the pgf. In particular: \(N g(\theta ) = N \sum _{k} d_k \theta ^k = \sum _k [S_k] = [S] \), and \(g^{\prime }(1) = \sum _k k d_k = \bar{n}\), where \(\bar{n}\) is the mean number of links per node.

To construct the deterministic limit of the epidemic on the large network (called the fluid limit by some), we must consider the change in the variables of our system due to an event. For the SIR model our events are infections of susceptibles and recoveries of infecteds. As we are considering the epidemic on a network, to fully describe the events, we are interested in how many neighbours someone has who are infectious and susceptible. Keeping this in mind we therefore consider two types of events. The first type of event is a susceptible of degree \(k\), who has \(x\) susceptible neighbours and \(y\) infected neighbours, becoming infected, i.e. going from \(S\) to \(I\). The second is an infected individual of degree \(k\), who has \(x\) susceptible neighbours, recovering from the infection, i.e. going from \(I\) to \(R\). We denote these two events as \(e_\tau (k,x,y)\) and \(e_\gamma (k,x)\) respectively, where \(\tau \) and \(\gamma \) are the rates of infection and recovery, and write \(\mathcal E \) for the set of such events.

We then denote the rates of these events as \(f_\tau (k,x,y)\) and \(f_\gamma (k,x)\). The rates are given by:

$$\begin{aligned} f_\tau (k,x,y)&= y \tau [S_k] D_{x,y,k}^S \text{, }\nonumber \\ f_\gamma (k,x)&= \gamma [I_k] D_{x,k}^I\text{. } \end{aligned}$$
(3)

We then sum the changes in our variables due to an event, multiplied by the rate of that event, over all events to get the set of equations that we require. With this in mind, we have a state space \(\mathbf p = (\theta ,[I],[SS],[SI])^\top \) obeying

$$\begin{aligned} \dot{\mathbf{p }} = \tau \sum _{k,x,y} \Delta \mathbf p _{\tau } y [S_k] D^S_{x,y,k} + \gamma \sum _{k,x} \Delta \mathbf p _{\gamma } [I_k] D^I_{x,k} \text{, } \end{aligned}$$
(4)

where \(\Delta \mathbf p _{\tau }\) and \(\Delta \mathbf p _{\gamma }\) are the changes to our variable under transmission and recovery respectively. We also note that as we are not keeping track of the variable \([II]\), we will not be concerned with the number of infected neighbours of an infective central node. Therefore when we are concerned with making an assumption about the neighbourhood of an infective, we will only be interested in the number of susceptible neighbours that it has. To work out the change in \([SI]\) say due to an infection, we have to consider the neighbourhood of the infected node. The node in question was susceptible, becomes infected, meaning that the pairs which were \([SS]\) pairs before infection, become \([SI]\) pairs and the \([SI]\) pairs will become \([II]\) pairs. If our node had \(x\) susceptible neighbours and \(y\) infected neighbours, i.e. it formed \(x\) \([SS]\) pairs and \(y\) \([SI]\) pairs, then the change in \([SI]\) will be \(x-y\). We can do similar calculations for the other variables. We note that there is a subtlety in the calculations for \(\theta \) as we require the node which becomes infected to be of degree 1, and it also depends on the number of nodes which are degree 1, given by \(N d_1\).

Doing this we obtain the following expressions for \(\Delta \mathbf p _{\tau }\) and \(\Delta \mathbf p _{\gamma }\),

$$\begin{aligned} \Delta \mathbf p _{\tau } = (-\delta _{k,1}/N d_1, 1, -2x,x-y)^\top \text{, } \Delta \mathbf p _{\gamma } = (0,-1,0,-x)^\top \text{, } \end{aligned}$$
(5)

which are the changes in the variables \(\mathbf p \) from an infection and a recovery respectively. If we write down the exact but unclosed pairwise equation for our system \(\mathbf p \), then we get the following set of equations:

$$\begin{aligned} \dot{\theta }&= - \tau \frac{[SI]}{Ng^{\prime }(\theta )}\nonumber \\ \dot{[I]}&= \tau [SI] - \gamma [I] \nonumber \\ \dot{[SS]}&= - 2 \tau [SSI] \nonumber \\ \dot{[SI]}&= \tau ( [SSI] -[ISI] -[SI]) - \gamma [SI]\text{. } \end{aligned}$$
(6)

We note that the expressions that we obtain for the recovery terms (terms multiplied by \(\gamma \)) are the ones that we would require our assumption about the neighbours of infecteds to calculate from (4). Due to the fact that the equations concerning the recovery terms in (6) are exact and closed, we have two conditions that we require \(D_{x,k}^I\), to satisfy, viz.

$$\begin{aligned} \sum _{k,x} [I_k] D_{x,k}^I = [I] \text{, } \qquad \sum _{k,x} x [I_k] D_{x,k}^I =[SI] \text{. } \end{aligned}$$
(7)

Now when we evaluate (4) using our main assumption (1) we get the model of Volz (2008) in pairwise notation. We note that the assumption of multinomially distributed neighbours allows us to get a relatively simple set of equations, as the summation over all events is equivalent to taking various moments of the distribution. We get

$$\begin{aligned} N \dot{\theta }&= - \tau \frac{[SI]}{g^{\prime }(\theta )}\nonumber \\ \dot{[I]}&= \tau [SI] - \gamma [I] \nonumber \\ \dot{[SS]}&= - 2 \tau [SS][SI] \frac{g^{\prime \prime }(\theta )}{N g^{\prime }(\theta )^2}\nonumber \\ \dot{[SI]}&= \tau [SI] \left( \frac{g^{\prime \prime }(\theta )}{Ng^{\prime }(\theta )^2} \left( [SS]-[SI] \right) - 1 \right) - \gamma [SI]\text{. } \end{aligned}$$
(8)

This can be thought of as a deterministic approximation to the underlying stochastic evolution of the epidemic and is the exact limit of the stochastic process, which we describe in the next section, when \(N \rightarrow \infty \) and (1) holds. It is important to note that one cannot simply start with (8) and ‘add noise’. Defining appropriate events and rates, together with the explicit statement of (1), is essential.

3.2 Diffusion limit

The work of Kurtz (1970; 1971) also tells us that the noise around the deterministic limit given above should be a Gaussian centred around this limit with an appropriate density. These results require certain technical conditions to be satisfied in order to apply. In particular, they require a family of right-continuous, temporally homogeneous jump Markov processes with elements \(\mathbf X _N\) indexed by an integer \(N\). In our case, \(N\) is the number of nodes and the state of the Markov chain is \((X^S_{x,y,k}, X^I_{x,k})\) where \(X^S_{x,y,k}\) is the number of degree-\(k\) susceptible nodes with \(x\) susceptible and \(y\) infectious neighbours, and \(X^I_{x,k}\) is the number of degree-\(k\) infectious nodes with \(x\) susceptible neighbours. We seek a limit

$$\begin{aligned} N\rightarrow \infty \text{, } \qquad X^S_{x,y,k} \rightarrow [S_k] D^S_{x,y,k} \text{, } \qquad X^I_{x,k} \rightarrow [I_k] D^I_{x,k} \text{, } \end{aligned}$$
(9)

and then lump the equations derived to reduce the system dimensionality. The infinitesimal parameters for the rate of going from state \(\mathbf x \) to state \(\mathbf x ^{\prime }\) also need to obey

$$\begin{aligned} Q^N_\mathbf{x ,\mathbf x ^{\prime }} = N F(N^{-1} \mathbf x ,\mathbf x ^{\prime }) \text{, } \end{aligned}$$
(10)

for some function \(F\). If we can write the rates in this form, the general results give us the exact formula to work out what these noise terms should be and the full stochastic equations in the diffusion limit are

$$\begin{aligned} \dot{\mathbf{p }}&= \tau \sum _{k,x,y} \Delta \mathbf p _{\tau } y [S_k] D^S_{x,y,k} + \sum _{k,x,y} \Delta \mathbf p _{\tau } \sqrt{\tau y [S_k] D^S_{x,y,k}} \xi _\tau (t)\nonumber \\&+ \gamma \sum _{k,x} \Delta \mathbf p _{\gamma } [I_k] D^I_{x,k} + \sum _{k,x}\Delta \mathbf p _{\gamma }\sqrt{\gamma [I_k] D^I_{x,k}} \xi _\gamma (t) \text{, } \end{aligned}$$
(11)

where \(\xi _\tau (t)\) and \(\xi _\gamma (t)\) are independent standard Gaussian noise processes associated with transmission and recovery respectively. We note that there is no simple expression for the amplitudes of the noise processes, as the square root prevents us from taking the moments of the multinomial distribution and then expressing these in terms of the variables of our system, as we do for the non-stochastic terms. Therefore we do not explicitly write the full stochastic system, as the equations would be in a similar (but more complicated looking) form to (11).

We use methodology that is derived from Kurtz (1970; 1971) and set out conveniently in Dangerfield et al. (2009), to analyse the variance in the infection levels during the early growth of the epidemic. We define the early growth period to be the time before there has been depletion to the pool of susceptibles which is significant enough to affect the rate of growth in the number of infecteds. Our starting point is assuming that the early growth of the infection is exponential, with rate \(r\). That is,

$$\begin{aligned} \left[ I\right] = \tilde{I} \text{ exp }(rt) \text{, } \end{aligned}$$
(12)

where \(\tilde{I}\) is a constant related to the prevalence of the infection as the early asymptomatic behaviour commences. Note that an additional assumption in taking the diffusion limit is that this quantity should be significantly larger than 1 but also significantly smaller than the total population size \(N\). We then use this to work out the early behaviour of the other variables,

$$\begin{aligned} \theta&= 1 - K_{\theta } \left[ I\right] /N \text{, }\nonumber \\ \left[ SS\right]&= N g^{\prime }(1) - K_{SS} \left[ I\right] \text{, }\nonumber \\ \left[ SI\right]&= K_{SI} \left[ I\right] \text{. } \end{aligned}$$
(13)

We now define the local covariance matrix associated with an event i.e. when a susceptible node becomes infected, or an infected node recovers. This is calculated as follows,

$$\begin{aligned} \mathbf G _{ij} = \sum _{e\in \mathcal E } f_e \Delta \mathbf p _{i,e} \Delta \mathbf p _{j,e} \text{, } \end{aligned}$$
(14)

where \(e \in \mathcal E \) means that \(e\) is either an infection or recovery event associated with a particular neighbourhood. Using the early growth Ansatz, specifically ignoring terms \(O([I]^2)\), we find that this can be written as \(\hat{\mathbf{G }}[I](t)\), where \( \hat{\mathbf{G }}\) is constant. We can now use the following equation from Dangerfield et al. (2009), which is again derived from the theoretical work of Kurtz (1970; 1971),

$$\begin{aligned} r \varvec{\sigma }^2 -\mathbf B \varvec{\sigma }^2 - \varvec{\sigma }^2 \mathbf B ^{T} = \left[ \hat{\mathbf{G }} \text{ exp }(r t) - \text{ exp }(\mathbf B t)\hat{\mathbf{G }}\text{ exp }(\mathbf B t)^T \right] \tilde{I}\text{, } \end{aligned}$$
(15)

where \(\varvec{\sigma }^2\) is the time dependent covariance matrix of our state variables \(\mathbf p , r\) is the early exponential growth rate, \(\mathbf B \) is the Jacobian of the fluid limit of our system (8), evaluated using the early growth Ansatz (12) and (13), and \(\hat{\mathbf{G }}\) is given above. The aim is to find an expression for \(\varvec{\sigma }^2\), as this will give us the variance of the epidemic during the early growth phase.

We now give specific details of how the various matrices in the above equation can be calculated. To calculate \(\hat{\mathbf{G }}\), we calculate the matrix \(\mathbf G \) and then divide by \([I](t)\). To do this we substitute in the changes in variables \(\Delta \mathbf p \), which are given above by (5). This means that we can write \(\mathbf G \) as follows,

$$\begin{aligned} \mathbf G = \tau \sum _{k,x,y} y [S_k] D^S_{x,y,k} \mathbf F _{\tau } +\gamma \sum _{k,x} [I_k] D^I_{x,k} \mathbf F _{\gamma } \text{, } \end{aligned}$$
(16)

where

$$\begin{aligned} \mathbf F _{\tau } \!=\!\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \frac{\delta _{1,k}}{N^2 d_1^2} &{} -\frac{\delta _{1,k}}{N d_1} &{} \frac{2 x \delta _{1,k}}{N d_1} &{} \frac{(y-x) \delta _{1,k}}{N d_1}\\ -\frac{\delta _{1,k}}{N d_1} &{} 1 &{} -2 x &{} x-y \\ \frac{2 x \delta _{1,k}}{N d_1} &{} -2 x &{} 4 x^2 &{} 2 x (y-x) \\ \frac{(y-x) \delta _{1,k}}{N d_1} &{} x-y &{} 2 x (y-x) &{} (x-y)^2 \end{array}\right) \text{, } \quad \mathbf F _{\gamma }\!=\!\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} x \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} x &{} 0 &{} x^2 \end{array}\right) \text{, }\nonumber \\ \end{aligned}$$
(17)

are the outer products of the change in each variable vectors \(\Delta \mathbf p _\tau \) and \(\Delta \mathbf p _\gamma \).

Let us consider how this calculation is done in practice by working out the entry \(\mathbf G _{[I],[SS]}\). We use the (2,3) entry of \(\mathbf F _{\tau } = -2x \) and \(\mathbf F _{\gamma } = 0\), which gives us that \(\mathbf G _{[I],[SS]} = - 2 \tau \sum _{k,x,y} [S_k] xy D_{x,y,k}^S\). We can separate the sum over \(k\) from the sum over \(x\) and \(y\), and we can use the fact that the (1,1) moment of a multinomial distribution with variables \(k,p\) and \(q\) is given by \(k(k-1) p q\). Therefore \(\mathbf G _{[I],[SS]} = - 2 \tau \sum _{k,x,y} [S_k] k (k-1) p_S q_S\). We can then use our assumption about the probabilities of connecting to susceptibles or infecteds from (2) and sum over the indices. We get:

$$\begin{aligned} \mathbf G _{[I],[SS]} = - 2 \tau [SS][SI]\frac{g^{\prime \prime }(\theta )}{N g^{\prime }(\theta )^2} \text{. } \end{aligned}$$
(18)

When we have calculated all the terms for the \( \mathbf G \) matrix we will input (12) and (13) to obtain the correct matrix for the early growth period. We evaluate this for \(\mathbf G _{[I],[SS]}\) linearising it with respect to \([I]/N\), i.e. any term which is \(O(([I]/N)^2)\) will be ignored. We then obtain the following expression for \(\mathbf G _{[I],[SS]}\):

$$\begin{aligned} \mathbf G _{[I],[SS]} = -2 \tau [I] \frac{g^{\prime \prime } \left( g^{\prime \prime } - g^{\prime }\right) }{(g^{\prime })^2} +O([I]/N)^2 \text{, } \end{aligned}$$
(19)

where we have used the fact that \(g^{\prime }(\theta )\) and \(g^{\prime \prime }(\theta )\) will become \(g^{\prime }(1)\) and \(g^{\prime \prime }(1)\) with the use of the early growth Ansatz, and then writing this in terms of \(g\), where we define \(g^{(n)} \equiv g^{(n)}(1)\). This now gives us that,

$$\begin{aligned} \hat{\mathbf{G }}_{[I],[SS]} = -2 \tau \frac{g^{\prime \prime } \left( g^{\prime \prime } - g^{\prime }\right) }{(g^{\prime })^2} \text{. } \end{aligned}$$
(20)

We show all the entries of \(\hat{\mathbf{G }}\) in Appendix B.

The \(\mathbf B \) matrix from (15) as stated above is the Jacobian matrix of the deterministic limit of the system, evaluated using (12) and (13) and is therefore given by

$$\begin{aligned} \mathbf B =\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} -\frac{\tau }{Ng^{\prime }(1)} \\ 0 &{} -\gamma &{} 0 &{} \tau \\ 0 &{} 0 &{} 0 &{} -\frac{\tau g^{\prime \prime }(1) }{g^{\prime }(1)} \\ 0 &{} 0 &{} 0 &{} r \end{array} \right) \text{. } \end{aligned}$$
(21)

Now we have calculated \(\hat{\mathbf{G }}\) and \(\mathbf B \) we can solve (15) for \(\varvec{\sigma }^2\).

3.3 Neighbourhoods around an infected node

The discussion above has so far not dealt with the neighbourhood of an infective. This only becomes an important consideration for the bottom right term in \(\mathbf F _{\gamma }\), where we have to work out the square of the change in \([SI]\) pairs due to recovery of an infectious node; in particular we are interested in calculation of the quantity

$$\begin{aligned} \chi := \sum _{k,x} x^2 [I_k] D_{x,k}^I \text{, } \end{aligned}$$
(22)

and so the task is to determine the number of infectives of degree \(k\), and the second moment of the distribution of the number of susceptibles around such infectives. Now, the rate at which infectives of degree \(k\) are produced is given by

$$\begin{aligned} -\frac{\mathrm{d}}{\mathrm{d}t}[S_k] = -N d_k \frac{\mathrm{d}}{\mathrm{d}t} \theta ^k = -N d_k k \dot{\theta } \theta ^{k-1} \text{. } \end{aligned}$$
(23)

We also know that the probability that an infective of age \(a\) (a node which was infected length of time \(a\) ago) is still infective is given by \(e^{-\gamma a}\). We can therefore work out \([I_k]\) at a given time \(t\) by evaluating the following integral:

$$\begin{aligned}{}[I_k] = -N d_k k \int _0^t \dot{\theta }(t-a) (\theta (t-a))^{k-1} e^{-\gamma a}\; \mathrm{d}a \text{. } \end{aligned}$$
(24)

Now consider the neighbourhood around such an infective. Ignoring the very first cases, every infectious individual must have been infected by someone, leaving \(k-1\) individuals who are potentially susceptible. If the infection of the central node happened a time \(a\) ago, then each of the \(k-1\) potentially susceptible neighbours has an independent probability \(e^{-\tau a}\) of avoiding infection from that central node, and in the event that central infection is avoided and the neighbouring node is of degree \(l\) a probability of \(\theta ^{l-1}\) of avoiding infection from any other source. Summing over \(l\) then gives the general expression

$$\begin{aligned}{}[I_k] D_{x,k}^I \!=\! -N d_k k \int _0^t \dot{\theta }(t\!-\!a) (\theta (t\!-\!a))^{k-1} e^{-\gamma a}\; \mathrm{Bin}\left( \!x\; \bigg |\; k\!-\!1,\; \frac{g^{\prime }(\theta (t))}{g^{\prime }(1)} e^{-\tau a}\!\right) \mathrm{d}a \text{, }\nonumber \\ \end{aligned}$$
(25)

where \(\mathrm{Bin}(x|k,\pi )\) is the binomial probability mass function, representing the probability that \(x\) of \(k\) trials with independent probability of success \(\pi \) will be successful. Since we are interested in early asymptotic behaviour, we then linearise this expression making use of the expressions

$$\begin{aligned} \theta \rightarrow 1 \text{, }\qquad \dot{\theta } = -r \frac{K_{\theta }}{N} [I] \text{. } \end{aligned}$$
(26)

This gives asymptotic results

$$\begin{aligned} \begin{aligned} \left[ I_k\right] D_{x,k}^I&\rightarrow [I] \frac{r+\gamma }{g^{\prime }(1)} \int _0^t e^{-(r+\gamma )a}\; \mathrm{Bin}(x|k-1,e^{-\tau a})\; \mathrm{d}a \\ \Rightarrow \chi&\rightarrow [I] \frac{r+\gamma }{g^{\prime }}\left( \frac{g^{\prime \prime }}{\tau +r + \gamma } + \frac{g^{\prime \prime \prime }}{2 \tau +r + \gamma } \right) \text{. } \end{aligned} \end{aligned}$$
(27)

We have now calculated the entirety of the \(\mathbf G \) matrix and can express it in the form \(\hat{\mathbf{G }}[I]\), where \(\hat{\mathbf{G }}\) is constant, as is required to use the results of Kurtz.

3.4 Rate of convergence

We now consider the rate at which convergence to our model will happen. Our approach here is heuristic rather than formal, and is based on the fundamental contributions by Ball and Neal (2008), and more recently Decreusefond et al. (2012) We start by redefining the network and epidemic processes in ways that are less useful for practical calculation than our initial definitions, but which make the rate of convergence more clear. In each case, we start with \(N\) individuals indexed \(i,j,\ldots \)

In a configuration model process, we let individual \(i\) have \(K_i\) stubs, and start the network ajacency matrix \(A_{i,j}(t=0)=0, \forall i,j\). Then the process is defined to take

$$\begin{aligned} (K_i, K_j, A_{i,j}, A_{j,i}) \rightarrow (K_i-1, K_j-1, A_{i,j}+1, A_{j,i}+1) \text{ at } \text{ rate } \propto K_i K_j \text{. }\qquad \end{aligned}$$
(28)

Running this process until the absorbing state \(K_i = 0, \forall i\) gives the adjacency matrix of a configuration model network, although depending on what one decides about repeated- or self-edges, different corrections of \(O(N^{-1})\) may arise (Durrett 2007).

In the epidemic process, individuals have non-independent random variables for their state \(X_i\), that can take values \(S, I\) or \(R\). Then

$$\begin{aligned} (S_i,I_j) \rightarrow (I_i,I_j)\quad \text{ at } \text{ rate } \tau A_{ij} \text{, } \end{aligned}$$
(29)

and infectious nodes recover at rate \(\gamma \). The fundamental insight from Ball and Neal (2008) is that these two processes can be combined. In this construction, every node in the network is given a number of half-links, which are then paired up as the epidemic progresses to form contacts between individuals in the following two ways:

  • An infected with \(l\) remaining half-links makes contacts at rate \(\tau l\); if it links to a susceptible then the infection will be transmitted with probability 1.

  • When an infected recovers (which happens at rate \(\gamma \)) all of its remaining half-links will be independently paired off with remaining half-links in the population.

The question of what a susceptible neighbourhood looks like at a given time in this picture is answered by halting the epidemic process, and running the configuration model process to completion, then counting the neighbours of each susceptible. As noted by Decreusefond et al. (2012) (who use a slightly different construction but the same basic idea) at finite \(N\) this gives each susceptible a multivariate hypergeometric neighbourhood, as they sample without replacement from the population. As \(N\) becomes large, this tends to a multinomial distribution with corrections \(O(N^{-1})\).

A similar argument can be made for the neighbourhood around an infectious individual, in terms of its links that remain unpaired. In the absence of susceptible depletion, it is then possible to make a stochastic version of the deterministic argument about the neighbourhood around an infective in Sect. 3.3 above.

Since the diffusion limit deals with terms of \(O(N^{-1/2})\) and ignores terms of \(O(N^{-1})\), we are therefore justified in making the multinomial assumption for the neighourhood around a susceptible. We note that it therefore implies the exactness of several other deterministic approaches in the absence of clustering, such as the pairwise closure techniques from Keeling (1999) and the maximum entropy moment closure method of Rogers (2011).

3.5 Early growth variance

As described above we can solve (15) for \(\varvec{\sigma }^2\). We did this through computer algebra, due to the complexity of expressions involved. The variance of the number of infecteds during early growth is shown in full in Appendix A. This can be simplified in the certain regimes. If we define the time at which the epidemic grows at the rate predicted in Diekmann and Heesterbeek (2000) as \(t_\mathrm{early}\), and the time at which the depletion of susceptibles affects the growth rate and we leave the early growth phase at \(t_\mathrm{depleted}\), then when the current time satisfies \(t_\mathrm{early} \ll t \ll t_\mathrm{depleted}\), we can simplify the expression in Appendix A. We note that this regime will exist in an infinite size network if the initial amount of infection in the network \(\tilde{I}\) is sufficiently small. It is dominated by a single term which involves the mean, variance and skew of the networks degree distribution along with the recovery and transmission rates of the infection. In this limit, the mean and variance of prevalence obey

$$\begin{aligned} \text{ Mean }(I)&\rightarrow \tilde{I}e^{rt} \text{, } \text{ for } \quad r = \tau \left( \frac{g^{\prime \prime }}{g^{\prime }} -1\right) - \gamma \text{, }\nonumber \\ \frac{\text{ Var }(I)}{\text{ Mean }(I)^2}&\rightarrow \frac{ g^{\prime 2} (g^{\prime \prime \prime }+(\tau +1) (g^{\prime \prime }+g^{\prime }))}{(g^{\prime 2}-g^{\prime \prime 2}) ((\gamma +\tau ) g^{\prime }-\tau g^{\prime \prime })} \text{. } \end{aligned}$$
(30)

where \(\tilde{I}\) is a constant related to the prevalence of infection as the early asymptotic behaviour commences at \(t_\mathrm{early}\), and \(g^{(n)} \equiv g^{(n)}(1)\).

Figure 1 shows how the variance in prevalence changes as skew in degree increases. Seeing that as the skew increases we get an increase in the variance of the epidemic during early growth, we would therefore see that if we had a network whose degree distribution is a power law, would show greater variation than a negative binomially distributed network with the same mean and variance would show. We think of this increase in variation being caused by the members of the population who are very well connected in the network. These people have been called super-spreaders in the past. If the disease reaches these people in the early growth phase of the epidemic then we can expect a rapid increase in disease prevalence, as there will be many \([SI]\) pairs through which the disease can be passed, whilst if they do not get it in this early phase, there will not be this rapid increase, which generates the large variance in this stage of the epidemic. We note that for the \(\tilde{I}\) term in (30) we have no analytical traction on what this should be for a given epidemic. If we wish to compare this result to simulation, we will fit the value of \(\tilde{I}\) so that the analytical prediction and the simulated results agree at a given point. As this is simply multiplied by the other terms, fitting it simply scales the prediction up or down rather than fine tuning the prediction itself.

Fig. 1
figure 1

Early asymptotic dependence of the standard deviation of infection prevalence, divided by infection prevalence, on the skew \(\Gamma \) of the network degree distribution. The curve is plotted from equation (30) in the main text. Parameter values are: mean degree \(\approx 5.4\); variance in degree \(\approx 67.2\); transmission rate \(\tau = 0.0308\); recovery rate \(\gamma = 0.1\). Skewness of degree is varied between realistic values (0 and 100) to see how the variance of the asymptotic early prevalence of infection is affected. We see that as the skewness is increased we get a higher variability of prevalence. This is as expected, since the higher the skew, the more neighbours the most connected individuals of the population have, reducing the predictability of the epidemic due to chance events amongst this small but epidemiologically important group

Full size image

4 Comparison with simulation

We have also used simulation to test our conclusion that if we fix the mean and variance of the degree distribution, but have different skew values, then the network which has the higher value of skew will also exhibit a higher variance of infecteds during the early growth period. We wish to see whether we get a match between the analytical result that we have obtained and the simulated result. There are several difficulties to achieving this that we wish to note. First, the networks are extremely large in the case of the analytical results and we do not know how exactly fast the convergence to the answer should be (although the corrections are \(O(N^{-1})\) we do not know what prefactors multiply this term). We have run our simulations on networks of size \(10^5\), representing a small city, which in the end seemed sufficient.

Secondly, the analytical results only work for the early growth phase of the infection, which can be defined as the time when the pool of susceptibles is not significantly depleted. Whilst in an arbitrarily large network this can last for an arbitrarily long time, in a finite network, this is not true and will vary depending on the degree distribution of the network. This means that if we want to compare the early growth variance of two networks, we may have a very brief window in which we can actually do it. This is exacerbated by the fact that we will have to allow for a period at the very beginning of the epidemic to be discounted, as we want the system to approach some sort of early asymptotic behaviour unaffected by the random selection of initial infected.

Finally, there were also several assumptions made for the analytical system such as how the number of triples in the network can be approximated by doubles and the pgf \(g(x)\). With the finite network that we construct there is no guarantee that this will be accurate; again, convergence is \(O(N^{-1})\) but we do not have knowledge of the prefactors.

We implemented the Gillespie algorithm (Gillespie 1977) to simulate the time evolution of the epidemic, on networks of size \(10^5\). To obtain the correct mean early growth behaviour, we allow each simulation to achieve a certain number of infections (\(10^2\)) and then we set the simulation time to zero and let the epidemic progress from there. By allowing this initial amount of infection we will be able to absorb the initial conditions that we choose and get to the average behaviour of the system. In the system of size \(10^5\), allowing \(10^2\) infections is also small enough that the susceptibles will not be depleted significantly enough to affect the rate of growth of the epidemic. We ran \(10^3\) simulations on two networks with the same mean and variance but with different skewness. We note that the same networks were used for each of the \(10^3\) simulations.

Figure 2 shows the result of these simulations compared with the prediction given by (31) in Appendix A. We can see that as predicted the network with the higher skew exhibits more variance in number of infecteds in the early growth stage and also we see that the analytical prediction for what the variance should be, is a good fit for what the simulations show. The early time disagreement is as we would expect, since this is when the \(O(N^{-1})\) corrections should be most significant (Fig. 3).

Fig. 2
figure 2

Comparison of simulated results to analytical predictions. Dashed lines are simulations and full lines are analytical predictions. Simulations are on two different networks, which have the same mean and variance for their degree distribution (mean \(\approx 5.4\) and variance \(\approx 67.2\)) but different skewness: 24.3 for red/black lines and 6.7 for the pink/grey lines. Transmission and recovery rates are \(\tau = 0.0308\) and \(\gamma = 0.1\) respectively. a shows a period of time at which we have agreement in the growth of the number of infecteds between the two networks that is strongly in agreement with the theoretical prediction from Diekmann and Heesterbeek (2000). b is also taken for this time and we can see that the theoretical prediction that we have described previously in this paper deviates slightly from simulation, with this most pronounced early on when \(O(N^{-1})\) corrections should be most significant (color figure online)

Full size image
Fig. 3
figure 3

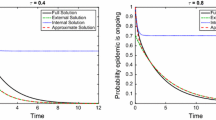
Test of the binomial assumption. 100 Monte Carlo realisations were run for parameters \(N=10^5, P(4) = 2/3, P(8) = 1/3, \tau = 0.8, \gamma = 1\). a shows a typical epidemic curve and four time points sampled. b shows the empirical histograms for \(I\) around an \(S_k\) node and \(S\) around an \(I_k\) node at each time point, and the equivalent binomial for susceptible central nodes, together with 95 % prediction intervals across simulations (where each simulation is time-shifted to agree on the first time at which \([I]=100\)) to give an indication of finite-size effects. This shows the accuracy of the asymptotic results even at finite size.

Full size image

5 Discussion

We have considered the spread of SIR-type infections on networks of heterogenous degree. Using the assumption that the neighbourhood around a node will have a distribution of susceptibles and infecteds which is multinomial (1), we have derived a low dimension deterministic approximation (8) to the stochastic dynamics of the infection which we can write down precisely in the form given by equation (11). A heuristic argument has been given to justify this assumption in the large \(N\) regime.

Computer algebra was then used to calculate the covariance matrix of our model using an equation derived by Kurtz. This was then used to give us the variance of the early growth of the epidemic on the network and we extracted the dominant term in the \(t_\mathrm{early} \ll t \ll t_\mathrm{depleted}\) regime which is given by (30). These analytic results were derived for networks of extremely large size.

By comparing the solution that was derived analytically with simulations, we have been able to demonstrate that with a network of size \(10^5\) we can get a strong agreement between the two as can be seen in Fig. 2.

We have shown that as the degree skewness of the network increases, so does the variance of the number of infecteds during the early growth. An implication of this result is that in the situation of an outbreak of a disease, if we are able to target the very well connected people in the network, then we can (as well as has been previously established) decrease the impact of the disease efficiently—but such an intervention would also mitigate the ‘reasonable worst case scenario’ in how many people will become infected by reducing the variability of the epidemic.

Another potential application of our results is to improve the estimation of epidemiological parameters during early growth of an epidemic. The possibility of estimating the variability in prevalence, together with a relationship between such variability and underlying model parameters, could enhance statistical work on epidemic prevalence curves.

In conclusion, we have shown how a low-dimensional system of stochastic differential equations can be used to describe the diffusion limit of a stochastic epidemic on a heterogeneous network, and have drawn out epidemiological conclusions from this model.