A bond-topological approach to theoretical mineralogy: crystal structure, chemical composition and chemical reactions

Abstract

Here, I describe a theoretical approach to the structure and chemical composition of minerals based on their bond topology. This approach allows consideration of many aspects of minerals and mineral behaviour that cannot be addressed by current theoretical methods. It consists of combining the bond topology of the structure with aspects of graph theory and bond-valence theory (both long range and short range), and using the moments approach to the electronic energy density-of-states to interpret topological aspects of crystal structures. The structure hierarchy hypothesis states that higher bond-valence polyhedra polymerize to form the (usually anionic) structural unit, the excess charge of which is balanced by the interstitial complex (usually consisting of large low-valence cations and (H₂O) groups). This hypothesis may be justified within the framework of bond topology and bond-valence theory, and may be used to hierarchically classify oxysalt minerals. It is the weak interaction between the structural unit and the interstitial complex that controls the stability of the structural arrangement. The principle of correspondence of Lewis acidity–basicity states that stable structures will form when the Lewis-acid strength of the interstitial complex closely matches the Lewis-base strength of the structural unit, and allows us to examine the factors that control the chemical composition and aspects of the structural arrangements of minerals. It also provides a connection between a structure, the speciation of its constituents in aqueous solution and its mechanism of crystallization. The moments approach to the electronic energy density-of-states provides a link between the bond topology of a structure and its thermodynamic properties, as indicated by correlations between average anion coordination number and reduced enthalpy of formation from the oxides for ^[6]Mg ^[4] _m Si _n O_(m+2n) and MgSO₄(H₂O) _n .

Introduction

The last 50 years have seen an explosion in analytical mineralogy as experimental techniques have allowed more and more detailed characterization of smaller and smaller samples. As a result of these capabilities, our factual knowledge of chemical and structural variations in common minerals is now fairly comprehensive, and apart from a few residual problems, it seems difficult to justify working extensively on most groups of rock-forming minerals at ambient conditions. We already know what they are like, and we understand them at an empirical level. What kind of theoretical framework have we been using to interpret the data that we have accumulated over the past 50 years? We have been using crystal chemistry to systematize mineral properties and behaviour, classical thermodynamics to examine processes involving minerals, and more recently, computational mineralogy to derive properties of minerals the stabilities of which are beyond the reach of current experimental techniques. The strength of thermodynamics is that we can do calculations and understand things about minerals and mineral reactions while having a high degree of ignorance about where the atoms are and what the atoms are doing. However, the question arises as to why we have been deriving the atomic arrangements in minerals if we are not using the results to try and understand why minerals are the way they are and why they behave the way they do. Crystal chemistry, thermodynamics and computational mineralogy are very powerful, but they have tended to dictate the questions that we ask about minerals. We ask questions to which standard theory can give us an answer. What about other questions of scientific interest which are opaque to our current theoretical approaches? These are neglected because they are seen as intractable or even irrelevant to current issues of applied science. Why do minerals have the chemical formulae that they do? Why do they have their specific structural arrangements? Why are minerals stable over specific ranges of pH, Eh, temperature, pressure and activities of their various constituents? What are the relations between crystal structure and both enthalpy and Gibbs free energy of formation? Many of these questions are fundamental to Mineralogy itself and yet have tended to be ignored in the past. Here, I will examine how we can address such questions from a theoretical perspective, and how we can incorporate process (e.g., crystallization, dissolution) into these considerations, as distinct from using purely descriptive vehicles. My intent is to try and understand the atomic-scale factors that control the chemical compositions and structural arrangements of (oxygen-based) minerals, and to relate those atomic-scale factors to processes that affect minerals (e.g., crystallization, dissolution). Although I speak of “prediction” in the following text, it is not the principal aim of this approach to predict things. I wish this approach to impart some intuitive understanding to the stability of minerals and their participation in geochemical processes. Background material is given in Hawthorne (2006). Much of the material discussed here has been given elsewhere, but in a rather fragmentary fashion; here, I attempt to integrate it into a more coherent scheme.

Mineral chemistry and structure

Why do minerals have the chemical and structural features that they do? In considering the crystallization or stability of a structure, I will presume that all the constituent elements are available to form that structure. Of course, the geochemical evolution of various environments will often prevent the association of specific elements in sufficient concentration to form a mineral, but this is not the case for synthesized materials.

First, consider simple minerals, such as halite and quartz, in which the constituents have significant differences in their electropositive character. The electroneutrality principle fixes the chemical formulae of such minerals, and the handshaking lemma of graph theory (Wilson 1979) requires certain relations between the (average) coordination numbers of their different constituents. Thus, in NaCl, Na and Cl must have the same coordination number, and in SiO₂, the coordination number of Si must be twice that of O, irrespective of the bond topologies of the longer-range structures. The latter will be affected by the conditions of crystallization, and NaCl and SiO₂ adopt various different atomic arrangements as a function of these conditions. The empirical rules of crystal chemistry tell us that Na and Cl may have coordination numbers of [6], and then the principle of maximum symmetry allows mapping of [^[6]Na^[6]Cl]_∞ onto the vertices of the F-centred cubic lattice to produce the crystal structure of halite. The crystal structures of SiO₂ are more difficult to deal with, but are still susceptible to such an analysis. There are other types of approach to the issue of structural arrangements of simple compounds. These often involve proposing a chemical composition and then deriving a structural arrangement by using a variational approach to minimize or optimize some function of the structural arrangement. However, there is no way to reliably assess the stability of such arrangements, or even the stability of such a compound versus that of an assemblage of its constituents. Moreover, all of these approaches rapidly become intractable with increasing chemical complexity of the system of interest.

Second, consider slightly more complicated minerals, for example, the hydrated magnesium sulphate compounds, Mg(SO₄)(H₂O) _n where n = 0–7, 11: synthetic Mg(SO₄); kieserite, Mg(SO₄)(H₂O); sanderite, Mg(SO₄)(H₂O)₂; synthetic Mg(SO₄)(H₂O)₃; starkeyite, Mg(SO₄)(H₂O)₄; cranswickite, Mg(SO₄)(H₂O)₄; pentahydrite, Mg(SO₄)(H₂O)₅; hexahydrite, Mg(SO₄)(H₂O)₆; epsomite, Mg(SO₄)(H₂O)₇; and meridianiite, Mg(SO₄)(H₂O)₁₁. The electroneutrality principle fixes the Mg(SO₄) part of the chemical formulae, but some other factor controls the degree of hydration of each mineral. With regard to the structures of these minerals, there is a gradual depolymerization of the (MgΦ₆) and (SO₄) polyhedra (Φ = O, H₂O) with increasing (H₂O) content as the valence sum rule (Brown 2002) prevents linkage of polyhedra through (H₂O) ligands (Hawthorne 1992; Hawthorne and Sokolova 2012). Although we are aware that (H₂O) has this effect on the structures of minerals (and synthetic inorganic solids), we have little idea of how such depolymerization generally proceeds with increasing (H₂O) content, what is the effect of other (interstitial) cations in the structures, and what are the bond topologies of the resulting structures.

Third, consider complicated minerals such as botryogen, Mg₂(H₂O)₁₄ [Fe₂ ³⁺(SO₄)₄]₂, or metavoltine, K₂Na₆Fe²⁺(H₂O)₆[Fe₃ ³⁺O(SO₄)₆(H₂O)₃]₂(H₂O)₆. First, we know that their chemical formulae are constrained by the electroneutrality principle. However, what dictates the rest of the details of their chemical formulae? These minerals are not rare; they are found at many locations around the world with the same chemical formulae. Why does botryogen have Mg₂ and not Ca₂ or Na₄ in its structure? Both Ca₂ and Na₄ also satisfy electroneutrality requirements and are common constituents in environments in which botryogen occurs, but something does not allow them to be incorporated into the structure. It is not obviously the coordination around Mg in the structure as Mg is coordinated by six (H₂O) groups in a very open structure. Why does botryogen have 14 (H₂O) groups in its formula? Why does not it have (for example) 8 (H₂O) groups? Why does botryogen have any (H₂O) groups at all and what are the roles of these (H₂O) groups in the structure? How do these aspects of structure and chemistry relate to the stability of botryogen as a function of Eh and pH?

Many of these questions cannot currently be addressed by the usual methods of theoretical investigation, and for those that can, we often must be satisfied with an explanation that has little to do with any atomic-scale mechanism.

Mineral reactions

Why do minerals react with one another and with their coexisting fluids? What are the atomic-scale driving mechanisms that induce chemical reactions to occur? Consider the following reaction:

$$ {\text{Forsterite}} = {\text{Periclase}} + {\text{Quartz}}. $$

What are the structural characteristics of forsterite that make it more stable than a mixture of periclase and quartz under certain conditions? Consider the following trend in amphibole composition with increasing temperature of metamorphism:

$$ {\text{Tremolite}} \to {\text{Pargasite}} - {\text{Sadanagaite}} $$

What are the structural characteristics of amphibole that drive this continuous reaction with increasing temperature?

We need to seek answers to these questions in the bond topologies and bond lengths of the constituent minerals. How do we do this? We need to relate bond topology and bond geometry to energetics to see what drives these processes at the most basic level. We need to put a different framework in place, a framework where our knowledge of the energetics of minerals is related at an intuitive level to the topology of chemical bonding. Here, I will outline an approach by which this may be done.

Crystal structures as graphs

Crystal structures are commonly illustrated by drawings, showing which atoms are bonded to which. Using this type of representation, we can make qualitative arguments as to the basic architecture of a structure, and qualitatively relate different structure types to each other, but we do not have a quantitative expression of the important features of the structure. On the other hand, description of a structure via its unit cell, symmetry and a table of atom coordinates provides us with a quantitative description of a structure (and allows us to do various structure–property calculations), but offers little intuitive insight into relations between structures. Graph theory offers a potential solution to this problem.

We may define a graph as a nonempty set of elements, V(G), called vertices, and a nonempty set of unordered pairs of these vertices, E(G), called edges (Wilson 1979). We may colour the vertices, we may label the vertices, we may assign a direction to the edges, and we may assign weights to the edges. The result is a weighted labelled polychromatic digraph, illustrated pictorially in Fig. 1a. This graph may be represented numerically as a matrix (Fig. 2). Each column and row of the matrix is associated with a specific (coloured labelled) vertex, and the corresponding matrix entries denote whether (positive) or not (zero) two vertices are adjacent, that is joined by an edge. If the matrix elements are the weight functions of the edge set, then this matrix is called the adjacency matrix. The adjacency matrix is thus a numerical representation of the graph.

Fig. 1

a A weighted polychromatic digraph with the coloured vertex set {1, 2, 3, 4} and the directed weighted edge set {12, 32, 34, 14}; b a simple idealized square molecule consisting of four atoms labelled 1–4

Fig. 2

The adjacency matrix corresponding to the graph in Fig. 1a

The degree of a vertex is the number of edges involving that vertex, and the sum of the degrees of all vertices is even as each edge contributes two degrees to that sum. This relation is known as the handshaking lemma for obvious reasons. In a digraph, the indegree of a vertex is the number of edges incident at that vertex, and the outdegree of a vertex is the number of edges exident at that vertex. These relations are very useful in dealing with problems involving coordination number and connectivity in structures.

Figure 1b shows a simple idealized molecule consisting four atoms labelled 1–4, linked by chemical bonds that are represented by lines between the atoms 1–4. This representation, a set of points joined by lines, resembles the pictorial representation of a graph. We may colour Fig. 1b to denote the different types of atoms, we may label the atoms, and we may assign a direction to the edges by denoting the direction from the more electropositive atom to the more electronegative atom. Note that I use the words ‘cation’ and ‘anion’ here to denote atoms of low and high electronegativity, respectively; these terms are not intended to denote ionic bonding. We may assign weights to the edges, weights that correspond to the relative strengths of the chemical bonds. Comparison of Fig. 1a, b shows that there is a one-to-one mapping of the molecule in Fig. 1b onto the graph of Fig. 1a. The graph in Fig. 1a and the adjacency matrix in Fig. 2 are thus analogue and digital representations of the structure, respectively. The graph and the adjacency matrix do not preserve the geometrical features of a structure: bond lengths and bond angles are lost. However, it does preserve the topological features of the bond network, and may carry additional information concerning the strengths (or orders) of the chemical bonds. Thus, graph theory provides us with a way of quantifying the topological aspects of the bond network of a group of atoms.

Topological aspects of molecular orbital theory

I will now briefly describe some of the relations between topological (or graphical) aspects of structure and chemical bonding, focusing on the similarity between energetics of bonding and topological aspects of structure. The interested reader is referred to Burdett (1980), Albright et al. (1985), Hoffman (1988), Rohrer (2001) and Balaban (2002) for more details.

Molecules

The electronic structure of a molecule may be considered as the sum of the electronic properties of its constituent atoms, as modified by the interactions between these atoms. This may be done at various degrees of comprehensiveness (e.g., using all orbitals, or using just valence orbitals), depending on the intent of the approach. Here, I am looking for maximum transparency and hence will construct the molecular orbital wavefunction as a linear combination of atomic orbitals. These wavefunctions are eigenstates of an effective one-electron Hamiltonian, H ^eff, that may be written as H ^effψ = Eψ where E is the energy associated with ψ, and the molecular orbital wavefunction is written as ψ = Σ _i c _i φ _i where {φ _i } are the valence orbitals of the atoms and c _i is the contribution of a specific atomic orbital to a specific molecular orbital (e.g., Gibbs 1980). The total electron energy of the state described by this wave function may be written as

$$ E = {{\left( {\int {\psi^{*} H^{\text{eff}} \psi {\text{d}}\tau } } \right)} \mathord{\left/ {\vphantom {{\left( {\int {\psi^{*} H^{\text{eff}} \psi {\text{d}}\tau } } \right)} {\left( {\int {\psi^{*} \psi {\text{d}}\tau } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\int {\psi^{*} \psi {\text{d}}\tau } } \right)}} = {{\left( {\left\langle {\psi^{*} H^{\text{eff}} \psi {\text{d}}\tau } \right\rangle } \right)} \mathord{\left/ {\vphantom {{\left( {\left\langle {\psi^{*} H^{\text{eff}} \psi {\text{d}}\tau } \right\rangle } \right)} {\left( {\left\langle {\psi^{*} \psi } \right\rangle } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\left\langle {\psi^{*} \psi } \right\rangle } \right)}} $$

(1)

in which the integration is over all space. Substituting for ψ(=Σc _i φ _i ) gives

$$ E = {{\left( {\Upsigma_{i} \Upsigma_{j} c_{i} c_{j} \left\langle {\varphi_{i} \left| {H^{\text{eff}} } \right|\varphi_{j} } \right\rangle } \right)} \mathord{\left/ {\vphantom {{\left( {\Upsigma_{i} \Upsigma_{j} c_{i} c_{j} \left\langle {\varphi_{i} \left| {H^{\text{eff}} } \right|\varphi_{j} } \right\rangle } \right)} {\left( {\Upsigma_{i} \Upsigma_{j} c_{i} c_{j} \left\langle {\varphi_{i} |\varphi_{j} } \right\rangle } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\Upsigma_{i} \Upsigma_{j} c_{i} c_{j} \left\langle {\varphi_{i} |\varphi_{j} } \right\rangle } \right)}}. $$

(2)

This equation may be simplified as follows: (a) $\left\langle {\varphi_{i} |\varphi_{j} } \right\rangle$ is the overlap integral between atomic orbitals on different atoms, denoted as S _ij ; it is always ≤1; where i = j, $\left\langle {\varphi_{i} |\varphi_{j} } \right\rangle = 1$ for a normalized (atomic) basis set of orbitals. (b) $\left\langle {\varphi_{i} \left| {H^{\text{eff}} } \right|\varphi_{j} } \right\rangle = H_{ii}$; this represents the energy of an electron in orbital φ _i and can be approximated by the orbital ionization potential. (c) $\left\langle {\varphi_{i} \left| {H^{\text{eff}} } \right|\varphi_{j} } \right\rangle = H_{ij}$; this is the resonance integral. The molecular orbital energies may be calculated from Eq. (2) by minimizing the energy with respect to the coefficients c _i . The eigenvalues (roots) of the following secular determinant equation give the molecular orbital energy levels:

$$ \left| {H_{ij} -S_{ij} E} \right| = 0. $$

(3)

The topological content of this approach is best shown by the Hückel approximation (Trinajstic 1983). For the pπ orbitals, all H _ii values are set equal to α, all nonzero H _ij are set equal to β, and all S _ij (i ≠ j) are set equal to zero. Consider the idealized square molecule shown in Fig. 1b; the expanded secular determinant equation is as follows:

$$ \left| {\begin{array}{*{20}c} {\alpha - E} & \beta & 0 & \beta \\ \beta & {\alpha - E} & \beta & 0 \\ 0 & \beta & {\alpha - E} & \beta \\ \beta & 0 & \beta & {\alpha - E} \\ \end{array} } \right| = 0 $$

(4)

Compare the matrix entries in Eq. (4) with the structure of Fig. 1b. In the absence of any off-diagonal β terms, there are no chemical bonds present and the energies of the electrons in the atomic orbitals are the roots of the equation. Where the atoms are bonded together, the energies are modified by the off-diagonal β terms. Where two atoms are bonded together (i.e., atoms 1 and 2 in Fig. 1b), there is a nonzero value at this particular (1, 2) entry in the secular determinant; when two atoms are not bonded together (i.e., atoms 1 and 3 in Fig. 1b), then the corresponding determinant entry (1, 3) is zero.

The roots of the secular determinant equation may be shown as energy levels as in Fig. 3. In the H matrix, the diagonal entries scale the absolute values of the energy levels and the off-diagonal entries produce the splitting of the energy levels. The description of the energetics of the molecule via the H matrix is similar to the adjacency matrix of the graph of the molecule (Fig. 2). In normalized Hückel theory (Trinajstic 1983), β is the energy unit and α is the zero-energy reference point, and the determinant of the H matrix of Eq. (4) is identical to the analogous adjacency matrix of the graph of the molecule (Fig. 2). Hence, it is the topological characteristics of a molecule, rather than its geometrical details, that determine the form of the Hückel molecular orbitals (Trinajstic 1983).

Fig. 3

The energy levels derived from solving the secular determinant Eq. (4) for the molecule shown in Fig. 1b

Crystals

If we were to solve Eq. (3) for a large number of atoms (e.g., a crystal), we would obtain a large number of molecular-orbital energies. Their representation solely as a function of energy (Fig. 4a) is not useful; it is more informative to express the electron occupancy of a specific energy interval (band) as a function of orbital energy: a density-of-states diagram (Fig. 4b).

Fig. 4

Representations of the energy levels of a crystal: a sketch of a conventional energy-level diagram; b energy density-of-states diagram

So how do we deal with a crystal containing approximately Avogadro’s number of atoms? We cannot use the same sort of calculation, as this is way beyond any foreseeable computational capability. We use translational symmetry to reduce the problem to a reasonable size by using Bloch orbitals (Ziman 1965), which constrain the orbital content of the unit cell to the translational periodicity of the crystal. This may be done using the special points method, whereby the secular determinant is solved at a representative set of points within the Brillouin zone. This gives a representative sampling of the orbital energy levels that may be smoothed to give a density-of-states representation. Integrating the electronic energy density-of-states up to the Fermi level gives the total orbital energy.

The differences between a molecule and a crystal may be stated as follows: in a molecule, there is a set of discrete orbital energy levels; in a crystal, these levels broaden into bands, and the occupancies of these bands as a function of energy are the electronic energy density-of-states.

The method of moments

There is little intuitive connection between the essential features of a crystal structure, the relative positions of the atoms and the disposition of the chemical bonds, and the usual methods for deriving the electronic energy density-of-states. Burdett et al. (1984) changed this situation by developing a novel way of deriving the electronic energy density-of-states using the method of moments. Here, I will give only a brief outline of their method; the interested reader should consult the original paper for mathematical details, and also Burdett (1986, 1988) and Burdett and Lee (1985) for further applications.

To solve the secular determinant in Eq. (4), we diagonalize the Hamiltonian matrix. The trace of this matrix may be written as follows:

$$ {\text{Tr}}(H^{n} ) = \sum\limits_{i} {\sum\limits_{j,k, \ldots ,n} {H_{ij} H_{jk} \ldots H_{ni} } } $$

(5)

Figure 5 shows a topological interpretation of one term in this sum. Each H _ij term is the interaction integral between orbitals i and j; H _ij  = β (if the atoms are bonded), H _ij  = 0 (if the atoms are not bonded, or if i = j when α = 0). Thus, in Eq. (5), a single term {H _ij H _ik … H _ln } is nonzero only if all individual H _ij terms are nonzero, for example, {H ₁₂ H ₂₃ H ₃₄ H ₄₁}. The last H _ij term is the interaction between the nth orbital and the first orbital, and hence the {H _ij H _jk … H _ni } term represents a closed path in the graph of the orbitals (molecule). If one of the terms in the closed path is zero (e.g., H ₃₁ in Fig. 5), the complete term in the sum is zero, that is, {H ₁₂ H ₂₃ H ₃₁} = 0, and this term does not contribute to the trace of the Hamiltonian matrix. Thus, the sum in Eq. (5) represents all closed paths through the graph of (the orbital structure of) the molecule. Under diagonalization, the trace of the matrix remains invariant, and thus

$$ {\text{Tr}}(H^{n} ) = {\text{ Tr}}(E^{n} ) = \mu_{n} $$

(6)

where E is the diagonal matrix of eigenvalues (energy levels) and μ _n is the nth moment of E, formally denoted by

$$ \mu_{n} = \sum\limits_{i} {E_{i}^{n} } $$

(7)

The density-of-states may be obtained by inverting the collection of moments {μ _n } [see Burdett et al. (1984) for details]. The result is that we can evaluate Tr(H ⁿ) directly from the topology of the orbital interactions (bond topology), and hence can derive the electronic energy density-of-states directly from the bond topology. We have already seen that this is the case by showing the correspondence of the secular determinant and the adjacency matrix of the molecule.

Fig. 5

Interpretation of paths through the molecule shown in Fig. 1b; the path 1 → 2 → 3 → 4 contains only nonzero H _ij terms and contributes to the trace of the matrix, whereas the path 1 → 2 → 4 contains a zero H _ij term (H ₃₁) and does not contribute to the trace of the matrix

The method of moments generalizes to infinite systems (i.e., crystals). If ρ(E) is the density-of-states of a crystal, we may define the nth moment of E as

$$ \mu_{n} = \int {E^{n} \rho (E){\text{d}}E} $$

(8)

In principle, the moments may be evaluated as above and inverted to give the electronic energy density-of-states, demonstrating the topological content of the electronic energy density-of-states of a crystal.

The energy difference between two structures can be expressed in terms of the first few disparate moments of their electronic energy density-of-states (Burdett 1986). Thus, the most important energetic differences between two structures involve the most local topological differences between those structures. Moreover, in structures with bonds of different strengths, each edge of each closed path that contributes to each moment will be weighted according to the strength of the bond analogous to that edge. Thus, strongly bonded closed paths through the structure will contribute more to the electronic energy density-of-states than weakly bonded closed paths.

Low-order moments and crystal chemistry

The number of steps in a closed path through the bonded atoms in a structure is the moment of that path. Let us examine the structural features corresponding to the lower-order moments, those that are the more energetically important in the structure. A zero-moment path has no steps and corresponds to remaining still (a walk in place). Such a path specifies the identity of the atom at that vertex of the graph of the structure, and hence the complete set of zero-moment paths defines the chemical composition of the structure. A second-moment closed path has two edges and is a walk from one vertex to an adjacent vertex and back. The collection of second-moment closed paths from a single vertex defines the coordination number of the atom corresponding to that vertex. A fourth-moment closed path has four edges and is a walk from an atom (e.g., a cation) to an anion to another cation and back again, and hence specifies the linkage of two coordination polyhedra. Higher-moment closed paths will specify more complicated polyhedron linkages, but these will be less energetically important than the low-moment linkages. What this immediately tells us is that traditional crystal chemistry is correct in focusing on coordination number and local linkage between coordination polyhedra as the most important differences between structures (apart from chemical composition), as the moments approach tell us that these are the most energetically important of the linkages in a structure.

The most important energetic features of a structure are thus chemical composition, coordination number and nearest-neighbour polyhedron linkage. Furthermore, the local connectivity of the strongly bonded coordination polyhedra in the structure is more energetically important than the connectivity of the weakly bonded coordination polyhedra as they have larger H _ij terms in Eq. (5). This provides energetic justification for a hypothesis that we will introduce later, the Structure Hierarchy Hypothesis, that structures may be ordered according to the polymerization of the more strongly bonded coordination polyhedra (Hawthorne 1983).

Bond topology and bond-valence theory

Brown (1981, 2002, 2009) has developed a simple but quantitative approach to chemical bonding in inorganic structures. Here, I shall briefly review these ideas and later develop them further to deal with aspects of complex inorganic structures that are intractable by other methods.

Network solids, electroneutrality and the valence-sum rule

In dealing with oxide and oxysalt minerals, we are interested primarily in materials which have significant differences between the electronegativities of the bonded atoms; I will refer to these atoms as cations and anions, with no implication as to the character of their chemical bonding. We may define a crystal, liquid or cluster as a network of atoms connected by heteronuclear chemical bonds. Cations and anions alternate along any path through this network, and the network must conform to the law of electroneutrality: the total valence of the cations is equal to the total valence of the anions. Bond valence is defined as the strength of a chemical bond, and for any pair of bonded atoms, the bond valence is inversely proportional to the distance between those atoms: high bond valences are associated with short bonds, and vice versa. Thus, the ratios of the bond valences are a function of the ratios of the associated bond lengths. In order to obtain numerical values for the bond valences, each bond is assigned a bond valence such that the valence-sum rule is satisfied (Brown 2002):

The sum of the bond valences at each atom is equal to the magnitude of the atomic valence. [1]

Bond valences are scaled to the formal valences of the cations and anions of the chemical bonds. Bond valences can be calculated from the curves of Brown (2002) if the relevant interatomic distances are known. If the interatomic distances are not known, bond valences can be (1) approximated by Pauling bond strengths (Pauling 1960) or (2) calculated by the method described by Brown (2002, Appendix 3).

Characteristic bond valences

An a priori approach to structure stability is needed if we are to develop any predictive capability for crystal structures and chemical compositions. Brown (1981) introduced a very important idea with regard to such a priori prediction. The bond valences around a specific cation in all crystal structures lie within ~20 % of their mean value, a value that is characteristic of that particular cation. If the cation occurs only in one coordination, then the mean bond valence for that cation will be equal to the Pauling bond strength; thus, S⁶⁺ always occurs in tetrahedral coordination to O in minerals, and hence will have a mean bond valence of 6/4 = 1.5 v.u. (valence units). Where a cation has two or more coordination numbers, then the mean bond valence will be the weighted mean of the bond valences in all observed structures. Thus, B³⁺ occurs in various coordinations from [2] to [5]; the tendency is for [3]- and [4]-coordinations to be more common than [2]- and [5]-coordinations, and the mean bond valence is 0.88 v.u. Table 1 shows typical values for cations of major geochemical significance.

Table 1 Lewis acid strengths (v.u.) for cations

Lewis acid and base strengths

Electronegativity is a measure of the electrophilic strength (electron-accepting capacity) of a cation, and a Lewis acid is a species that can accept electron density from another species. The characteristic bond valence of a cation correlates strongly with its electronegativity (Fig. 6), and hence the characteristic bond valence of a cation is a measure of the Lewis acid strength of that cation. This gives rise to the following definition (Brown 1981):

The Lewis acid strength of a cation may be defined as the characteristic (bond) valence = atomic (formal) valence/mean coordination-number.

The Lewis base strength of an anion can be defined as the characteristic valence of the bonds formed by the anion. However, this is often not a very useful definition, as variations in bond valence around anions are much greater than variations in bond valence around cations. Consider the valences of bonds to O²⁻; these may vary between nearly zero and 2.0 v.u.; thus, in dravite, Na is [9]-coordinated and the O atoms to which it is bonded receive on average 0.11 v.u. from each Na–O bond. In CrO₃ (Stephens and Cruickshank 1970), which consists of pyroxene-like chains of ^[4]CrO₃, one O is bonded only to Cr⁶⁺ and receives 2.00 v.u. from the Cr–O bond. With this amount of variation, that is, 0.11–2.00 v.u., it is not useful to define a Lewis base strength for O²⁻. However, the situation changes when we consider heteronuclear oxyanions such as (SO₄)²⁻ (Fig. 7). Each O atom of the (SO₄)²⁻ group receives 1.5 v.u. from S⁶⁺ and requires an additional 0.5 v.u. from other neighbouring cations. If [n] is the coordination number of O²⁻, the average valence of the bonds to O²⁻ (exclusive of the S–O bond) is 0.5/(n − 1) v.u.; if n = 2, 3, 4 or 5, the mean bond valences to O are 0.50, 0.25, 0.17 or 0.11 v.u., respectively. The average bond-valence received by the oxyanion is the same as the average bond valence received by each individual O atom, defining the Lewis basicity of the oxyanion. Note that for the (SO₄)²⁻ oxyanion, the range of possible average bond valences is quite tightly constrained (0.50–0.11 v.u.) and we may calculate a useful Lewis basicity. Table 2 lists Lewis basicities for geochemically common oxyanions.

Fig. 6

The variation in electronegativity as a function of Lewis acid strength various cations [from Brown (1981)]

Fig. 7

The bond-valence structure of the (SO₄) oxyanion in thenardite, with the individual bond valences shown in valence units [after Hawthorne (1994)]

Table 2 Lewis basicities (v.u.) for selected oxyanions

The valence-matching principle

A criterion for chemical bonding results from the definitions of Lewis acid and Lewis base strengths given above, the valence-matching principle (Brown 2002, 2009):

Stable structures will form when the Lewis-acid strength of the cation closely matches the Lewis-base strength of the anion. [2]

The valence-matching principle is the most important and powerful idea in bond-valence theory: instead of merely interpreting known structures or compounds, we can test the probability that stable compounds will form; thus, we have moved from a posteriore to a priori analysis. I will give three simple examples (taken from Hawthorne 1994) to illustrate the operation of this principle.

Consider the chemical formula Na₂SO₄. The Lewis basicity of the (SO₄) group is 0.17 v.u. (Table 2) and the Lewis acidity of Na is 0.17 v.u. (Table 1). The Lewis acidity of the cation matches the Lewis basicity of the anion, and the valence-matching principle is satisfied. Thus, Na₂SO₄ is a stable structure, thenardite.

Consider the chemical formula Na₄SiO₄. The Lewis basicity of the (SiO₄) group is 0.33 v.u. (Table 2) and the Lewis acidity of Na is 0.17 v.u. The Lewis acidity of the cation is not equal to the Lewis basicity of the anion, and the valence-matching principle is not satisfied. Hence, there is no stable structure that corresponds to the composition Na₄SiO₄.

Consider the chemical formula Na[AlSiO₄]. The Lewis basicity of the [AlSiO₄] group is 0.13 v.u. and the Lewis acidity of Na is 0.17 v.u. The Lewis acidity of the cation is approximately equal to the Lewis basicity of the anion, and the valence-matching principle is satisfied. Nepheline, Na AlSiO₄, is a stable structure. However, nepheline shows incommensurate behaviour (e.g., Angel et al. 2008), perhaps reflecting the slight mismatch between the Lewis basicity and acidity of its constituents.

The valence-matching principle is a simple way in which we can evaluate the possible stability of specific cation–anion interactions of interest. This is an a priori analysis; it is important to recognize that we need no crystal-structure information to evaluate the stability of the putative compound.

Bond-valence theory as an ionic theory

Preiser et al. (1999) presented a justification of bond-valence theory in terms of an ionic model of chemical bonding. They wrote the energy, W, of an inorganic solid as the sum of the classical electrostatic energy, W _{electrostatic}, and the quantum–mechanical repulsion, W _Fermi:

$$ W = W_{\text{electrostatic}} + W_{\text{Fermi}} $$

(9)

The term W _{electrostatic} can be derived, in principle, from the sum of the electrostatic fields of each atom, E _atom, where

$$ E_{\text{atom}} = E_{\text{mono}} + E_{\text{mult}} + E_{\text{local}} $$

(10)

The following points are important (Preiser et al. 1999): (1) E _local represents the field inside the atom and is zero outside the atom; (2) E _mult represents point-multipole terms for atoms with non-spherically symmetric electron density. These multipole terms are commonly small and decrease rapidly with distance from the atom, and Preiser et al. (1999) combined E _mult and E _local into a short-range term, leaving only E _mono to contribute to long-range effects. The energy can thus be written as

$$ W = W_{\text{Madelung}} + W_{{{\text{short}}\,{\text{range}}}} $$

(11)

where W _Madelung is the Madelung energy resulting from E _mono.

The Coulomb field

Preiser et al. (1999) note that the set of “all lines joining two charges defines a region in space that represents the electrostatic link between them” and that “every point in space…must belong to one of these link regions. Thus E _Madelung directly partitions space into a collection of localized link regions separated by zero-flux boundaries” (compare Bragg 1930, pp. 296–297). This situation is shown for rutile in Fig. 8.

Fig. 8

The Madelung field for rutile in the (1 1 0) plane. The light lines represent the field lines, and the heavy lines show the zero-flux boundary that partitions space into link (bond) regions [from Preiser et al. (1999)]

Where two atoms i and j are connected by a link region with an electrostatic flux, Φ _ij , we may write

$$ \Upphi_{ij} = \int {E_{\text{Madelung}} } {\text{d}}A $$

(12)

where the integration is over the cross-section of the link region. In Eq. (12), the terms Φ _ij obey Gauss’s law, which relates the flux of the electric-field intensity through a closed surface to the total net charge within that surface:

$$ \sum\limits_{j} {\Upphi_{ij} } = \oint {E_{\text{Madelung}} } {\text{d}}A = Q_{i} $$

(13)

where the sum is over all links connected to Q _i and the integration is over any closed surface surrounding Q _i . The fluxes can be calculated for any crystal structure (e.g., rutile as in Fig. 8). The partition of the electrostatic field into link regions implies that these link regions are synonymous with chemical bonds, and Preiser et al. (1999) propose that “The fluxes linking atoms in the electrostatic model are the same as the bond valences assigned using the bond valence method”.

Preiser et al. (1999) calculated the fluxes for many structures and compared them with the analogous bond valences (Fig. 9). The agreement is very close, supporting the relation between electrostatic flux and bond valence. Preiser et al. (1999) emphasize that the long-range Coulombic interactions are transmitted inductively through a crystal by the operation of Gauss’s law on the Coulomb field at each atom.

Fig. 9

Flux versus experimental bond valence for unstrained structures [from Preiser et al. (1999)]

Bond-valence theory as a molecular-orbital theory

Burdett and Hawthorne (1993) used the one-electron model to examine the interaction of two orbitals on directly bonded atoms using the secular-determinant method (Burdett 1980). This method focuses on the interaction of atomic orbitals to produce molecular orbitals. The secular determinant for such systems (e.g., the AB system of Fig. 10a) has diagonal elements of the form H _ii  − E, where H _ii is the energy of an electron in orbital i, and off-diagonal elements of the form H _ij , where H _ij is the interaction between orbitals i and j; note that φ _i is an orbital of a cation and φ _j is an orbital of an O atom. The energy of an electron in orbital j is labelled H _jj . The secular determinant for the system in Fig. 10a is

$$ \left| {\begin{array}{*{20}c} {H_{jj} - E} & {H_{ij} } \\ {H_{ij} } & {H_{ii} - E} \\ \end{array} } \right| = 0 $$

(14)

The determinant of Eq. (14) may be expanded to give the molecular orbital energies: E _b is the energy of the bonding orbital (ψ _b in Fig. 10a) and E _a is the energy of the antibonding orbital (ψ _a in Fig. 10a). In a system with two electrons in ψ _b , the stabilization energy is 2ε_stab (Fig. 10a) (i.e., the anion-centred orbitals are full and the cation-centred orbitals are empty). Expansion of Eq. (14) gives the following:

$$ \varepsilon_{\text{stab}} = \frac{{H_{ij}^{2} }}{\Updelta E} + \frac{{H_{ij}^{4} }}{{(\Updelta E)^{3} }} + \cdots $$

(15)

There needs to be a nonzero energy gap between interacting orbitals on anion and cation, and this is generally the case for oxide and oxysalt minerals.

Fig. 10

a Interaction of two atomic orbitals φ _i and φ _j on A and B to give two molecular orbitals ψ _a and ψ _b ; the stabilization energy of the lower (filled) orbital is ε_stab. b Interaction of three atomic orbitals for the AB ₂ case to give three molecular orbitals; ψ _b , ψ _a and ψ _n are bonding, antibonding and nonbonding orbitals, respectively [from Burdett and Hawthorne 1993]

In the system AB ₂ (Fig. 10b), the secular determinant equation is as follows:

$$ \left| {\begin{array}{*{20}c} {H_{ii} - E} & {H_{ij} } & {H_{ij} } \\ {H_{ij} } & {H_{jj} - E} & 0 \\ {H_{ij} } & 0 & {H_{jj} - E} \\ \end{array} } \right| = 0 $$

(16)

This equation has three roots, corresponding to the bonding, non-bonding and antibonding orbitals, respectively. The root for the bonding orbital gives the following stabilization energy:

$$ \varepsilon_{\text{stab}} = \frac{{2H_{ij}^{2} }}{\Updelta E} - \frac{{4H_{ij}^{4} }}{{(\Updelta E)^{3} }} + \cdots $$

(17)

Second-moment scaling

In Eqs. (15) and (17), H _ii and H _jj are first-moment terms and define the energies of the electrons in the ith and jth orbitals (here, they set the zero of the energy scale). H _ij are second-moment terms, and the second moment is the sum of the squares of the interaction integrals linking one orbital to its neighbour. Variation in interatomic distances may be well described by simple one-electron models if the second moment of the electron-energy density-of-states is kept constant (e.g., Pettifor and Podlucky 1984; Hoistad and Lee 1991; Lee 1991). Consider an atom with C bonded atoms at equal distances from the central atom; we may write the second moment as Cβ² which we may set equal to a constant Q. The overlap integral β may be written as β = A/r ^m, where A is a constant (Harrison 1983). We may incorporate the constant second moment into this expression to give the equilibrium separation, r _e , as

$$ r_{e}^{2m} = C\frac{{A^{2} }}{Q} $$

(18)

Equation (18) may be rewritten as:

$$ \left( {\frac{{r_{e} }}{{r_{o} }}} \right)^{ - 2m} = \left( \frac{1}{C} \right)\left( {\frac{Q}{{A^{2} }}} \right)\left( {\frac{1}{{r_{o}^{ - 2m} }}} \right) $$

(19)

For a specific atomic arrangement, (Q/A ²)(1/r ^−2m _o ) is fixed, and we set it equal to some constant V:

$$ \left( {\frac{{r_{e} }}{{r_{o} }}} \right)^{ - 2m} = \left( \frac{1}{C} \right)V $$

(20)

Summing over all bonds in the coordination polyhedron gives

$$ \sum {\left( {\frac{{r_{e} }}{{r_{o} }}} \right)}^{ - 2m} = V $$

(21)

Brown and Shannon (1973) and Brown and Altermatt (1985) define bond valence, s, with several different expressions. However, the following form is the most useful in the present circumstances:

$$ s = \left( {\frac{{r_{e} }}{{r_{o} }}} \right)^{ - N} $$

(22)

where r _o and N are dependent on which cations and anions are involved in the bond. Summing over all bonds in the coordination polyhedron gives

$$ \sum {s = \sum {\left( {\frac{{r_{e} }}{{r_{o} }}} \right)^{ - N} } } = V $$

(23)

if 2m in Eq. (21) is associated with N in Eq. (23), with the result that these simple orbital and bond-valence descriptions are algebraically identical.

Bond-valence theory, ionicity and covalence

Brown and Shannon (1973) stressed the difference between the ionic model and bond-valence theory. In bond-valence theory, a series of atomic cores are held together by valence electrons that are associated with chemical bonds between atoms. The valence electrons may be associated with chemical bonds in a symmetric (covalent) or asymmetric (ionic) manner. Moreover, the electron distribution is quantitatively derived from application of the bond-valence curves to the observed structure. Preiser et al. (1999) gave an ionic justification of the bond-valence model (see above), and Burdett and Hawthorne (1993) showed that the bond-valence bond-length relation may be derived algebraically from a molecular orbital description of a solid (see above). One may conclude that bond-valence theory is not a theory of “ionic” bonds or “covalent” bonds; it is not a theory of types of chemical bond at all. So what is bond-valence theory? I will address this issue in the following section.

Bond topology and bond-valence theory

There are two important theorems in bond-valence theory: (1) the valence-sum rule (statement [1] above), and (2) the valence-matching principle (statement [2] above). Let us examine each of these theorems in terms of the above discussion of bond-valence theory.

The valence-sum rule

Bragg (1930) noted that the lines representing the electric field will emanate from an atom and then converge at the closest point (i.e., atom) of opposite charge. Preiser et al. (1999) note that E _Madelung partitions space into a set of link regions separated by zero-flux boundaries, suggesting that these link regions can be identified as chemical bonds. The electrostatic flux, Φ _ij , is between atoms i and j within a link region; Preiser et al. (1999) proposed that the fluxes linking atoms in the electrostatic model are the same as the bond valences assigned in the bond-valence method, and provide numerous correlations to illustrate this point. As noted above, the terms Φ _ij are constrained to obey Gauss’s law, which relates the flux of the electric field intensity through a closed surface to the total net charge enclosed within that surface [(Eq. (12)]. This being the case, the valence-sum rule is a corollary of Gauss’s theorem. Preiser et al. (1999) also emphasize that long-range Coulombic interactions are transmitted inductively through a crystal by the operation of Gauss’s law on the Coulombic field at each atom: $\sum\nolimits_{j} {\Upphi_{ij} } = \oint {E_{\text{Madelung}} } {\text{d}}A = Q_{i}$. Thus, there are i equations corresponding to the vertex set of the graph of the structure, and the summation at each atom (vertex) is over the bonds (edges) incident at that atom (vertex). Thus, the magnitudes of the fluxes (bond valences) are functions of the formal charges of each atom (at each vertex) and the numbers of chemical bonds (edges) incident at each atom (vertex). The valence-sum rule derives from the operation of Gauss’s law on the pattern of flux associated with the graph representing the bond topology of the structure.

The valence-matching principle

Stable structures will form when the Lewis acid strength of the cation closely matches the Lewis base strength of the anion (Brown 2002). Lewis acidity is a measure of the electron-attracting capacity of the cation, and Lewis basicity is a measure of the electron-donating capacity of the anion. As a chemical bond involves both a cation and an anion, then the electron-attracting capacity of the cation must match the electron-donating capacity of the anion for a chemical bond to form (Fig. 11). The valence-matching principle is the chemical analogue of the handshaking lemma in graph theory (see above).

Fig. 11

The valence-matching principle

Bond topology as an approach to the chemical composition, structure and stability of minerals

It is apparent from the above discussion that the quantitative aspects of bond-valence theory arise from the topological (or graphical) characteristics of structures as arrangements of atoms and chemical bonds. We also saw that the moments approach to the energetics of crystal structures allows us to associate the most important energetic differences between different structural arrangements with the lowest-moment differences in their bond topologies. Thus, the bond-topological approach can provide us with a quantitative method of dealing with questions of chemical composition and structure that have hitherto been intractable. Below, I will give several examples, but emphasize that these are by no means exhaustive.

The structure hierarchy hypothesis

A structural hierarchy is a classification of atomic arrangements ranked according to their constituent cation coordination polyhedra and the connectivity of those polyhedra. An adequate structural hierarchy of minerals should provide an epistemological basis for the interpretation of the role of minerals in Earth processes (Hawthorne 1985). In principle, the physical, chemical and paragenetic characteristics of a mineral should arise as natural consequences of its crystal structure and the interaction of that structure with the environment in which it occurs. We have not yet reached this stage for any major class of minerals, but significant advances have been made.

As knowledge of the crystal structures of silicate minerals developed in the early part of the twentieth century, Matchatski (1928) proposed that aluminosilicate minerals be classified according to the linkage of the aluminosilicate groups, and Bragg (1930) produced the neso (ortho-), soro- (pyro-), cyclo- (ring-), ino- (chain-), phyllo- (sheet-), tecto- (framework) silicate classification that we still teach today. Bowen (1928) developed his reaction series, which describes the sequence in which silicate minerals crystallize from a parent basaltic magma: olivine → pyroxene → amphibole → mica → feldspar → quartz. The parallels between the Matchatski–Bragg–Liebau classification of silicates (i.e., the bond topology of the structures) and Bowen’s reaction series cannot be accidental. There is a gradual condensation of the aluminosilicate tetrahedra in the crystallizing minerals with progressive crystallization, indicating that the bond topology of the resultant minerals is closely related to the crystallization process in basaltic magmas. In borate minerals, B may occur as (Bφ₃) and (Bφ₄) groups (φ = O²⁻, OH), and classifications by Edwards and Ross (1960), Ross and Edwards (1967), Christ (1960), Tennyson (1963) and Heller (1970) took into account the polymerization of these two different types of polyhedra. In structures such as sulphates, phosphates, arsenates and vanadates, systematic classifications were slower to arise. Moore (1973) proposed classifying phosphate minerals according to the polymerization of their constituent divalent metal octahedra, and showed a relation between structural arrangement and paragenesis in pegmatite phosphate minerals. However, the infrequency or complete absence of polymerization of the principal oxyanion group has been a major factor in inhibiting the development of hierarchical classifications of other mineral groups.

Hawthorne (1983, 1994) introduced the Structure Hierarchy Hypothesis: structures may be ordered hierarchically according to the polymerization of coordination polyhedra of higher bond valence. The absence of self-polymerization of the principal oxyanion in many mineral groups is avoided by considering the polymerization of different coordination polyhedra (e.g., tetrahedra and octahedra) that comprise higher mean bond-valences (usually ≥ 0.33 v.u.) in these structures. Higher bond-valence polyhedra polymerize to form homo- or heteropolyhedron clusters; these may be considered as the fundamental building block (FBB) of the structure. The FBB is repeated (often polymerized) by symmetry to form the structural unit, a complex (usually anionic) polyhedron array (not necessarily connected), the excess charge of which is balanced by the presence of interstitial species, usually large low-valence cations (Hawthorne 1985). The clusters may polymerize in the following ways: (1) unconnected polyhedra; (2) finite clusters; (3) infinite chains; (4) infinite sheets; (5) infinite frameworks. This approach has been used extensively to develop hierarchical classifications for a range of oxysalt minerals, for example, phosphates, arsenates and vanadates (Kostov and Breskovska 1989), phosphates (Huminicki and Hawthorne 2002), sulphates (Sabelli and Trosti-Ferroni 1985; Hawthorne et al. 2000a), borates (Burns et al. 1995; Hawthorne et al. 1996a; Grice et al. 1999). In addition, other approaches have attempted to span several traditional chemical groups of minerals (e.g., Lima-de-Faria 1978, 1983, 1994; Hawthorne 1985, 1986, 1990, 1997a; Burns 1999, 2005; Burns et al. 1996; Filatov et al. 1992; Krivovichev 2008; Krivovichev et al. 1998). I will illustrate this procedure below on a subset of the hydroxy-hydrated borate minerals, and the ensuing hierarchy will provide a basis for further exegesis.

Structural hierarchy of borate minerals

B³⁺ is small (^[3] r = 0.01, ^[4] r = 0.11 Å; Shannon 1976), and both triangular and tetrahedral coordination by oxygen, (Bφ₃) and (Bφ₄) (φ = O²⁻, OH), are common in borate minerals. In a (Bφ₃) group, the mean bond-valence is 3/3 = 1.00 v.u., and in a (Bφ₄) group, the mean bond-valence is 3/4 = 0.75 v.u. Polymerization of borate polyhedra results in incident bond-valence sums ≤2.0 v.u. at the linking anion; as interstitial cations in the structure can provide additional bond-valence to the linking anions, the valence-sum rule (Brown 2002) may be satisfied, and such polymerization is common in borate minerals. Early classifications were reviewed by Christ and Clark (1977) who produced a scheme in general use for 20 years, until superseded by the scheme of Burns et al. (1995), Hawthorne et al. (1996a) and Grice et al. (1999).

B–B graphs and algebraic descriptors

When considering topological aspects of complicated crystal structures, particularly in the form of nets, it is common practice to omit the anions from the graphical representation of structure (e.g., Smith 1977, 1978, 1988; Hawthorne 1983, 1990; Burns et al. 1995). We may represent the FBBs of the borate structures as graphs, with the vertices corresponding to B atoms (which are denoted as Δ or □, depending on their coordination number; where the coordination number is not specified, B is used) and the edges corresponding to B–φ–B linkages (with φ, the linking anion, omitted). We may write an algebraic descriptor of the cluster (Burns et al. 1995) that contains information on (1) the number of borate polyhedra; (2) the number of (Bφ₃) triangles and the number of (Bφ₄) tetrahedra; (3) the connectivity of the polyhedra; (4) the presence of rings of polyhedra in the cluster; (5) the connectivity of those rings within the cluster. The descriptor has the general form A:B, where A is the number of (Bφ₃) triangles and (Bφ₄) tetrahedra in the cluster, and B is a character string that contains the connectivity information of those polyhedra. I will now consider the types of polyhedron linkage that can occur and show how we may represent them as both graphs and algebraic descriptors.

Linkage of polyhedra

The simplest clusters consist of a (Bφ₃) triangle (A:B = 1Δ:Δ) or a (Bφ₄) tetrahedron (1□:□) (Fig. 12a, b). Borate polyhedra self-polymerize by sharing corners, and hence more than one polyhedron in the descriptor indicates that the polyhedra polymerize by sharing corners. Thus, the cluster 1Δ1□:Δ□ contains one (Bφ₃) triangle and one (Bφ₄) tetrahedron, and these link by sharing a corner (Fig. 12c). In the B string of the descriptor, adjacent polyhedra are linked; hence graphical isomers (Hawthorne 1983) can be distinguished, for example, for the clusters 1Δ2□:□Δ□ and 1Δ2□:Δ□□ (Fig. 12d, e). Rings of polyhedra are very common in borate structures. Such rings are denoted by enclosing the polyhedra of the ring by $\left\langle {} \right\rangle$ in the B string of the descriptor; thus a three-membered ring of one (Bφ₃) triangle and two (Bφ₄) tetrahedra (Fig. 12f) is denoted by $1\Updelta 2\square :\left\langle {\Updelta 2\square } \right\rangle$. We can thus distinguish between the decorated three-membered ring $2\Updelta 2\square :\left\langle {\Updelta 2\square } \right\rangle \Updelta$ (Fig. 12g) and the four-membered ring $2\Updelta 2\square :\left\langle {\Updelta \square \Updelta \square } \right\rangle$ (Fig. 12h). Where rings of polyhedra polymerize, the number of polyhedra common to both rings is denoted by the symbols −, = and ≡ for one, two and three polyhedra, respectively. Thus, the cluster $2\Updelta 2\square :\left\langle {\Updelta 2\square } \right\rangle = \left\langle {\Updelta 2\square } \right\rangle$ consists of two $\left\langle {\Updelta 2\square } \right\rangle$ rings with two borate polyhedra in common (Fig. 12i).

Fig. 12

Common borate clusters, their corresponding B–B graphs and algebraic descriptors [after Burns et al. (1995)]

Linking anions do not bond to more than two B atoms in most borate FBBs. However, there are exceptions; in tunnellite (Burns and Hawthorne 1994), one oxygen atom is bonded to three B atoms, the local structure accommodating this linkage by lengthening the B–O bonds in accord with the valence-sum rule. To denote such a linkage, [] are used to indicate any three- or higher-connected anion (φ), polyhedron (Δ or □) or ring of polyhedra (e.g., $\left\langle {\Updelta 2\square } \right\rangle$), and the polyhedra or rings connected to the central linking unit follow the []. Discrete clusters that connect to the central linking unit are separated by the symbol |. Thus, the symbol 3□:[φ]□|□|□| denotes three (Bφ₄) polyhedra linked by a common anion φ (Fig. 12j) in which the anion φ links to three separate (Bφ₄) tetrahedra. Consider a central anion linked to three (Bφ₄) tetrahedra, all of which link to (Bφ₃) triangles to form two $\left\langle {\Updelta 2\square } \right\rangle$ rings (Fig. 12k). The descriptor for this cluster is $2\Updelta 3\square :[\varphi ]\left\langle {\Updelta 2\square } \right\rangle \left| {\left\langle {\Updelta 2\square } \right\rangle } \right|$; although the sharing of one (Bφ₄) tetrahedron between the two rings is not indicated explicitly in the descriptor, it is implicit in the A string.

Selected borate minerals and their algebraic descriptors are listed in Table 3. A complete description of structural variation in borate minerals is too long to be feasible here. However, I will briefly describe some of the structural variations in these minerals in order to give a flavour of the information contained in a structural hierarchy, and later, we will see how this information can be used to understand aspects of the behaviour of these minerals.

Table 3 Selected borate minerals and their structural descriptors

Structures based on isolated polyhedra

There are two possible FBBs here, Δ and □, and we can divide the constituent minerals into two groups on this basis. We may also divide each group into two subgroups on the basis of the anions coordinating B: O²⁻ or (OH)⁻, as the type of anion is important, both structurally and paragenetically.

FBB = Δ, φ = O²⁻

There is a dominant structural theme in the minerals of this subgroup, encapsulated in the name 3Å wallpaper structures (Moore and Araki 1974). These structures are based on infinite [Mφ₄] chains of edge-sharing octahedra, cross-linked perpendicular to their length by (Bφ₃) triangles and (Bφ₄) tetrahedra, and by sharing edges and vertices with adjacent chains. The [Mφ₄] chain has an intrinsic repeat distance of ~3 Å along its length, hence the name. If ordering along the length of the chains is ignored, the topological aspects of these structures may be idealized as colourings of the plane net 3⁶. Selected frameworks are shown in Fig. 13. The structures show intriguingly similar linkages, and some quantitative structural relations have been derived (Cooper and Hawthorne 1998), but no general quantitative algebraic description of these structures has yet been developed.

Fig. 13

Selected wallpaper borate structures; a fluoborite; b warwickite; c ludwigite; d pinakiolite; e karlite; f wightmanite; g suanite; h szaibelyite. Orange: (BO₃); green: (MgO₆); yellow: (FeO₆); turquoise circles: Cl; yellow circles: (H₂O)

FBB = □, φ = OH⁻

In this group, isolated tetrahedra are linked most commonly by alkali and alkaline-earth cations (primarily Na and Ca). The extended cohesion of the structure is provided by linkage of the larger polyhedra and by hydrogen bonding. This is the case in hexahydroborite (Table 3) where chains of edge-sharing (Caφ₈) polyhedra are decorated by [B(OH)₄] tetrahedra, and link in the other two dimensions by hydrogen bonding.

It is important to note here that the division of the isolated Δ and □ groups into two subgroups on the basis of the identity of φ is quite significant from a paragenetic viewpoint. All minerals in the φ = O²⁻ subgroups are from metamorphic or igneous (pegmatite) parageneses, whereas the minerals in the φ = (OH)⁻ subgroups are from sedimentary (usually evaporite) environments.

Structures based on finite clusters of polyhedra

These may be divided into seven sets:

(1) 2B; (2) $\left\langle {3{\text{B}}} \right\rangle$; (3) $\left\langle {3{\text{B}}} \right\rangle = \left\langle {3{\text{B}}} \right\rangle$; (4) $\left\langle {3{\text{B}}} \right\rangle {\text{B}}$; (5) $\left\langle {3{\text{B}}} \right\rangle - \left\langle {3{\text{B}}} \right\rangle$; (6) $[\varphi ]\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |$; (7) $\left\{ {\left\langle {3{\text{B}}} \right\rangle -\left\langle {3{\text{B}}} \right\rangle } \right\}$

In these minerals, there are twelve distinct clusters, ten of which involve three-membered rings of polyhedra.

FBB = 2Δ

Two of this group are 3Å wallpaper structures. Suanite (Table 3; Fig. 13g) consists of ribbons of octahedra, four octahedra wide, that are cross-linked by [B₂O₅] groups. Szaibelyite (Fig. 13h) consists of 1 × 2 ribbons of edge-sharing octahedra that link by sharing vertices to form corrugated octahedron sheets that are cross-linked into a framework by [B₂O₅] groups.

${\text{FBB}} = \left\langle {\Updelta 2\square } \right\rangle$

In kurnakovite, the $\left\langle {\Updelta 2\square } \right\rangle$ ring (Table 3) links to two symmetrically equivalent (Mgφ₆) octahedra to form chains that (Fig. 14a) have the same stoichiometry as the cluster in inderite. The chains are linked via direct hydrogen bonding and also by hydrogen bonding involving the single interstitial (H₂O) group.

Fig. 14

Selected cluster, chain, sheet and framework borate structures; a kurchatovite; b ameghinite; c hungchaoite; d colemanite; e kernite; f aristarainite; g biringuccite; h tunellite; i fabianite; j hilgardite-1A; k pringleite

${\text{FBB}} = \left\langle {2\Updelta \square } \right\rangle$

In ameghnite, $\left\langle {2\Updelta \square } \right\rangle$ clusters (Table 3; Fig. 14b) are linked by [Na₂φ₁₀] dimers to form a framework, with extensive hydrogen bonding providing further linkage.

${\text{FBB}} = \left\langle {\Updelta 2\square } \right\rangle = \left\langle {\Updelta 2\square } \right\rangle$

Hungchaoite consists of $\left\langle {\Updelta 2\square } \right\rangle = \left\langle {\Updelta 2\square } \right\rangle$ clusters (Table 3; Fig. 14c) that link by corner sharing to {Mg(OH)(H₂O)₅} octahedra, forming a Mg[B₄O₅(OH)₄](H₂O)₅ cluster. This cluster is neutral and links to other identical clusters by direct hydrogen bonding and through a hydrogen-bond network involving two interstitial (H₂O) groups.

Structures based on infinite chains of polyhedra

These may be divided into six sets:

(1) B; (2) $\left\langle {3{\text{B}}} \right\rangle$; (3) $\left\langle {3{\text{B}}} \right\rangle - \left\langle {3{\text{B}}} \right\rangle$; (4) $\left\langle {3{\text{B}}} \right\rangle - \left\langle {3{\text{B}}} \right\rangle {\text{B}}$; (5) $\left\langle {3{\text{B}}} \right\rangle - \left\langle {3{\text{B}}} \right\rangle - \left\langle {3{\text{B}}} \right\rangle$; (6) $[\varphi ]\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |$

There are seven distinct clusters, all but one of which involve three-membered rings of polyhedra.

${\text{FBB}} = \left\langle {\Updelta 2\square } \right\rangle$

In colemanite (Table 3; Fig. 14d), $\left\langle {\Updelta 2\square } \right\rangle$ rings share two vertices between triangles and tetrahedra of adjacent rings to form a chain. The Caφ₈ polyhedra share corners to form chains that cross-link the borate chains into a heteropolyhedral framework.

${\text{FBB}} = \left\langle {\Updelta 2\square } \right\rangle - \left\langle {\Updelta 2\square } \right\rangle - \left\langle {\Updelta 2\square } \right\rangle$

In kernite (Table 3; Fig. 14e), $\left\langle {\Updelta 2\square } \right\rangle$ rings polymerize to form chains via sharing of common tetrahedra between adjacent rings. These chains are linked by Na atoms and a complex network of hydrogen bonds.

${\text{FBB}} = [\varphi ]\left\langle {\Updelta 2\square } \right\rangle |\left\langle {\Updelta 2\square } \right\rangle |\left\langle {\Updelta 2\square } \right\rangle$

In aristarainite (Table 3; Fig. 14f), three $\left\langle {\Updelta 2\square } \right\rangle$ rings link to a central anion ([φ] in the FBB descriptor). This cluster links to other clusters through (Bφ₃) and (Bφ₄) groups to form chains. These chains are cross-linked into sheets, and these sheets link in three dimensions through (Naφ₅) polyhedra and a network of hydrogen bonds.

Structures based on infinite sheets of polyhedra

These may be divided into seven sets:

(1) $\left\langle {3{\text{B}}} \right\rangle - \left\langle {3{\text{B}}} \right\rangle$; (2) $[\varphi ]\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |$; (3) $[\varphi]\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |2{\text{B}}$; (4) $[\varphi ]\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |-[\varphi ]\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |2{\text{B}}$; (5) $\left\langle {3{\text{B}}} \right\rangle = \left\langle {4{\text{B}}} \right\rangle = \left\langle {3{\text{B}}} \right\rangle$; (6) $\left\langle {6{\text{B}}} \right\rangle = \left\langle {4{\text{B}}} \right\rangle$; (7) ${\text{B}}\left\langle {3{\text{B}}} \right\rangle -\left\langle {3{\text{B}}} \right\rangle -\left\langle {3{\text{B}}} \right\rangle -\left\langle {3{\text{B}}} \right\rangle {\text{B}}$

There are eight distinct clusters, all but one of which involve three-membered rings of polyhedra.

${\text{FBB}} = \left\langle {2\Updelta \square } \right\rangle -\left\langle {\Updelta 2\square } \right\rangle$

In biringuccite (Table 3; Fig. 14g), the $\left\langle {2\Updelta \square } \right\rangle -\left\langle {\Updelta 2\square } \right\rangle$ FBB polymerizes to form [B₅O₈(OH)] sheets that are cross-linked by interstitial Na cations.

${\text{FBB}} = [\varphi ]\left\langle {\Updelta 2\square } \right\rangle |\left\langle {2\Updelta \square } \right\rangle |$

In tunellite, three $\left\langle {2\Updelta \square } \right\rangle$ rings link by sharing tetrahedra. Three tetrahedra link through a common vertex, denoted by [φ] in the FBB descriptor (Table 3), to form a cluster involving three triangles and three tetrahedra. Three peripheral triangle-vertices link to apical vertices of tetrahedra from adjacent clusters to form sheets (Fig. 14h) that are cross-linked by Sr and a network of hydrogen bonds.

${\text{FBB}} = \left\langle {\Updelta 2\square } \right\rangle = \left\langle {4\square } \right\rangle = \left\langle {\Updelta 2\square } \right\rangle$

In fabianite, a four-membered ring of tetrahedra, $\left\langle {4\square } \right\rangle$, shares two trans edges with two three-membered rings, $\left\langle {\Updelta 2\square } \right\rangle$; the resulting cluster consists of four tetrahedra and two triangles (Table 3). Two tetrahedra- and two triangle-vertices are shared with adjacent clusters to form sheets (Fig. 14i) that are cross-linked by chains of (Caφ₈) polyhedra.

Structures based on infinite frameworks of polyhedra

These may be divided into six sets:

(1) $\left\langle {3{\text{B}}} \right\rangle$; (2) $\left\langle {3{\text{B}}} \right\rangle = \left\langle {3{\text{B}}} \right\rangle$; (3) $\left\langle {3{\text{B}}} \right\rangle - \left\langle {3{\text{B}}} \right\rangle$; (4) $[\varphi ]\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |\left\langle {3{\text{B}}} \right\rangle |{\text{B}}$; (5) $[\varphi ]4{\text{B}}|$; (6) $\left\langle {3{\text{B}}} \right\rangle {\text{B}}$

There are six distinct types of FBB, all but one of which involves a three-membered ring of polyhedra.

${\text{FBB}} = \left\langle {\Updelta 2\square } \right\rangle -\left\langle {\Updelta 2\square } \right\rangle$

The three polymorphs of hilgardite have the FBB $\left\langle {\Updelta 2\square } \right\rangle -\left\langle {\Updelta 2\square } \right\rangle$ (Table 3). The FBBs share corners to form chains that cross-link by sharing corners between (Bφ₃) and (Bφ₄) groups (Fig. 14j). Interstitial Ca, Cl and (H₂O) groups occupy the interstices of the framework, and polymorphism results from different linkages of the two types of stereoisomer of the FBB.

${\text{FBB}} = \left\langle {\Updelta \square \bullet } \right\rangle = \left\langle {\Updelta 2\square } \right\rangle \Updelta$

This FBB is a twelve-membered ring of alternating (Bφ₃) triangles and (Bφ₄) tetrahedra (Fig. 14k) that is linked to a decorated three-membered ring of one (Bφ₃) triangle and two (Bφ₄) tetrahedra. It occurs in the structures of the dimorphs pringleite (space group P1) and ruitenbergite (space group P2₁), both of which have the composition Ca₉[B₂₀O₂₈(OH)₁₈][B₆O₆(OH)₆]Cl₄(H₂O)₁₃. In both structures, the FBBs link directly to form a mixed-borate framework of twelve- and three-membered rings (Fig. 14k), and polymorphism arises from subtle topological differences in the polymerization of the FBBs.

Justification of the structure hierarchy hypothesis

Why should we be concerned with such hierarchical classifications? First, there is the (rather trivial) reason that they give us an orderly arrangement of our knowledge of minerals, and this arrangement makes it easier to “do” mineralogy. Second, such structural classifications tend to order other characteristics of minerals that are dependent on structure. In particular, there is a strong relation between sequences of minerals in a hierarchical classification and their paragenesis. The classic example is the parallel between the Bragg classification of (alumino)silicate minerals (Bragg 1930) and Bowen’s reaction series (Bowen 1928). Other correlations have been briefly discussed in the literature (e.g., Moore 1973; Schindler and Hawthorne 2001c; Schindler et al. 2000b), but the difficulties of developing comprehensive paragenetic schemes for large assemblages of minerals in the field have hindered such work in the past.

There are several additional advantages to the structure hierarchy hypothesis. In particular, we may justify this idea within the framework of Bond Topology and Bond-Valence Theory in the following manner (Hawthorne 1983). In a structure, the bond-valence requirements of the cations give rise to the formation of coordination polyhedra of anions around the cations. As the net charge of the coordinating anions generally exceeds the charge of the central cation, we can think of the structure as an array of complex oxyanions. In order to satisfy the (simple) anion bond-valence requirements of these oxyanions according to the valence-sum rule, the oxyanions polymerize, thereby providing more bond valence to their ligands. This formulation suggests that the most important polymerizations in a structure involve those coordination polyhedra of higher bond valence, subject to the constraint that the valence-sum rule is not exceeded, as these linkages most easily satisfy the valence-sum rule. Minor bond-valence requirements and overall electroneutrality of the structure are satisfied by the incorporation of weakly bonded interstitial cations.

Polymerization of the principal coordination polyhedra in a structure is another way of expressing the topology of the bond network, and we can consider this approach via the Method of Moments introduced above. In structures with bonds of different strength, each edge of each closed path that contributes to each moment is weighted according to the value of the strength of the bond corresponding to that edge. Thus, strongly bonded closed paths through the structure will contribute more to the electronic energy density-of-states than weakly bonded closed paths. The most important energetic features of a structure are thus not only the local connectivity, but the local connectivity of the strongly bonded coordination polyhedra in the structure. Thus, we may recognize an energetic basis for the hierarchical organization of crystal structures according to the polymerization of their strongly bonded coordination polyhedra.

Physical aspects of the structure hierarchy hypothesis

Inspection of the crystal structures of the hydroxy-hydrated borate minerals shows that their structures may be constructed from the six borate clusters shown in Fig. 15. Of course, all borate structures may be constructed from the [B(OH)₃] and [B(OH)₄] clusters, but this is not a useful way to proceed. We may combine [B(OH)₃] and [B(OH)₄] to form many clusters that we do not find in borate minerals (Burns 1995). On the other hand, the small number of polynuclear clusters in Fig. 15 can be used to form all borate structures. This fact is of major significance as these six clusters are also the principal borate complexes occurring in aqueous solution (Fig. 16). This correspondence shows us that the clusters identified as principal FBBs of the hydroxy-hydrated borate minerals are real physical entities in geological processes and not just mental constructs that we have abstracted from structures in an attempt to understand the patterns of atoms in these crystals. This is a very important point; it suggests that these clusters are coherent objects that can retain their identity through geological processes such as crystallization and dissolution.

Fig. 15

The six borate clusters from which all borate minerals are constructed

Fig. 16

The distribution of B species in aqueous solution of 0.40 molar on total B(OH)₃ [after Christ et al. (1967) from the data of Ingri (1963)]

The existence of these clusters embedded both in aqueous solution and in crystal structures suggests that crystallization of these minerals proceeds by condensation of the hydrated cations and oxysalt species in solution. This seems fairly evident for borate structures containing isolated clusters of borate polyhedra, as we can identify the isolated cluster directly in the structure itself and in the chemical formula of the mineral. This situation is illustrated for inderite in Fig. 17. The structure of inderite is based on the [B₃O₃(OH)₅] cluster, illustrated in yellow [BO₃] and brown [BO₄] in Fig. 17, and which corresponds to the yellow and purple tetrahedra in the structure itself. Moreover, the cluster [B₃O₃(OH)₅] can be identified in the chemical formula of inderite, Mg[B₃O₃(OH)₅](H₂O)₅, in which it is shown in square brackets. For non-cluster structures, this process is only slightly more complicated. Consider the framework-structure borate-mineral hilgardite: Ca₂[B₅O₉]Cl(H₂O), the structure of which is illustrated in Fig. 18. The framework can be envisioned as consisting of three of the six clusters shown in Fig. 15: [B₃O₃(OH)₅], B(OH)₄ and B(OH)₃. Moreover, one can write a crystallization reaction (Fig. 18) whereby these clusters polymerize to form the [B₅O₉] framework and release (H₂O) to the aqueous solution.

Fig. 17

A sketch of the crystal structure of inderite showing the [B₃O₃(OH)₅] cluster from Fig. 15 (yellow and orange) and its presence in the crystal structure of inderite (yellow and purple) and in the chemical formula of inderite (orange)

Fig. 18

A sketch of the structure of the framework borate hilgardite, showing how the [B₅O₉] framework is built up of [B(OH)₃], {B(OH)₄] and [B₃O₃(OH)₅] clusters, and how crystallization of the framework can be envisioned as a reaction between these three aqueous species

Inspection of Fig. 16 shows that the pH at which each cluster has its maximum concentration increases from left to right in the sequence shown in Fig. 15. We may use bond-valence theory to calculate the Lewis basicity of these clusters (Hawthorne et al. 1996a). As is apparent in Fig. 19, the aggregate average basicity (a proxy for the Lewis basicity, Hawthorne and Schindler 2008) correlates with the pH of the nascent aqueous solution. Here, we see a direct connection between conditions in aqueous solution and the atomic arrangements in the minerals crystallizing from that solution, as these arrangements are formed by condensation of the clusters existing in solution. In turn, this relation suggests that the atomic arrangements of these borate minerals contain a record of the pH of the solution from which they crystallized through the aggregate Lewis basicity of the clusters from which they formed. This relation deserves to be pursued in more detail as it is the first indication of a quantitative relation between the details of chemical bonding and the physical conditions at which a mineral crystallized.

Fig. 19

Variation in aggregate average basicity as a function of pH for the borate clusters in the aqueous solution shown in Fig. 16

Bond-topological controls on the structure and chemical composition of oxysalt minerals

Above, I introduced the problem of understanding the controls on the chemical compositions of minerals, particularly complicated oxysalt minerals such as botryogen, Mg₂(H₂O)₁₄[Fe₂ ³⁺(SO₄)₄]₂, and metavoltine, K₂Na₆Fe²⁺(H₂O)₆[Fe₃ ³⁺ ₃O(SO₄)₆(H₂O)₃]₂(H₂O)₆. What controls the details of their chemical formulae? What are the reasons why botryogen has (1) Mg rather than Ca or Ba as its divalent interstitial cation; (2) divalent interstitial cations, Mg₂, rather than monovalent interstitial cations, Na₄ or K₄; (3) 14 (H₂O) groups in its formula; why does not it have (for example) 12 (H₂O) groups; (4) (H₂O) groups at all; what is the role of these (H₂O) groups in the structure? How do the chemical formula and structural arrangement of botryogen relate to its stability as a function of Eh and pH?

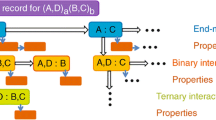
In complex oxysalt minerals, there are many different atom interactions, the topological, chemical and geometrical characteristics of which are important. The situation is somewhat analogous to that of an atom: in an atom, there is a nucleus surrounded by electrons in a series of orbitals, all interacting in a very complicated manner. Nonetheless, an atom can still be usefully considered as a discrete entity with simple properties such as size and charge; this is the basis of crystal chemistry. Let us adopt a similar approach to complicated crystal structures (Hawthorne 1983, 1985), dividing them into two components (Fig. 20). The structural unit is defined as the strongly bonded part of the structure (oxyanions and low coordination number cations), and the interstitial complex is defined as the weakly bonded part of a structure [an assemblage of (usually monovalent and divalent) cations, (H₂O) and, less commonly, (OH)] that controls the stability of the structure. In order to take full advantage of this type of structural representation, we need a quantitative way to look at the weak interactions that bind the structural unit and interstitial complex into a complete structure. The important issue is the following: it is the weak interaction between the interstitial complex and the structural unit that controls the stability of the arrangement (Fig. 21). When a structure breaks down, it generally does so by breaking the weakest bonds, which allows the structure to disaggregate into component fragments that can then recombine to produce other structural arrangements. To summarize, this binary representation of complex structure gives a simple but quantitative model of even the most complicated mineral, and provides insight into the weak interactions that control the stability of its structure.

Fig. 20

Partitioning of the complex crystal structure of botryogen, Mg₂(H₂O)₁₀ [Fe₂ ³⁺(SO₄)₄(H₂O)₂]₂, into two units, the strongly bonded structural unit (shown as coloured polyhedra) and the weakly bonded interstitial complex (shown as individual atoms and chemical bonds)

Fig. 21

A sketch showing how the interaction between the structural unit and the interstitial complex controls the stability of a mineral, particularly those minerals stable at the surface of the Earth

The principle of correspondence of Lewis acidity–basicity

How do we examine the interaction between the structural unit and the interstitial complex? In simple minerals, we have used the valence-matching principle (Brown 2002) for this purpose (see above). For complicated hydroxy-hydrated oxysalt minerals, the situation is somewhat more involved as we are not dealing with one type of interaction, but the aggregate of several different types of interaction. Let us consider botryogen, {Mg₂(H₂O)₁₀}[${\text{Fe}}^{3+}{}_{2}$(SO)₄(H₂O)₂]₂, from this perspective (Fig. 22). We have partitioned the structure into a structural unit, a cluster of Fe³⁺ octahedra and sulphate tetrahedra, and an interstitial complex, Mg cations together with their associated (H₂O) groups. We may define a Lewis basicity for the structural unit and a Lewis acidity for the interstitial complex as aggregate properties of these two units. The interaction between the structural unit and the interstitial complex may now be examined in a manner similar to the application of the valence-matching principle to simple chemical compositions using the principle of correspondence of Lewis acidity-basicity (Hawthorne and Schindler 2008):

Stable structures will form when the Lewis-acid strength of the interstitial complex closely matches the Lewis-base strength of the structural unit (Fig. 11).

The principle of correspondence of Lewis acidity–basicity is thus the mean-field equivalent of the valence-matching principle.

Fig. 22

The principle of correspondence of Lewis acidity–basicity, the mean-field equivalent of the valence-matching principle

Bond-valence controls on interstitial cations

The factors that govern the identity of interstitial cations are obscure. For most minerals, the chemical system from which they formed was often extremely large and the crystallizing structures had access to many possible constituents. However, a specific structure type can have extreme selectivity in the incorporation of interstitial cations despite its occurrence in a wide variety of chemical environments and geographical locations. Let us consider minerals with chain structural units of the form [M²⁺(T⁵⁺O₄)₂(H₂O)₂] and [M^2+,3+(T⁵⁺O₄)₂(H₂O)] (Table 4). Both structure types contain interstitial divalent cations and yet there is virtually no commonality between the types of interstitial cation in the two structure types (note that this is not a geochemical feature; both types of cation were often available to the crystallizing minerals). The [M²⁺(T⁵⁺O₄)₂(H₂O)₂] minerals are dominated by interstitial Ca, whereas the [M^2+,3+(T⁵⁺O₄)₂(H₂O)] minerals are dominated by interstitial Pb²⁺, Sr and Ba (differences in charge of the high-valence cation can result in interstitial cations of different charge, for example, Na in kröhnkite and REE in tornebohmite).

Table 4 Minerals with chain units of stoichiometry [M²⁺(T⁵⁺O₄)₂(H₂O)₂] and [M²⁺(T^5+,6+O₄)₂(H₂O,OH)]

The principle of correspondence of Lewis acidity–basicity requires that the Lewis acidity of the interstitial complex matches the Lewis basicity of the structural unit. Let us examine the identity of the interstitial cations in brandtite and arsenbrackebuschite (Table 4). I shall assign the coordination number [4] to all O anions and [3] to all (H₂O) groups (i.e., two H cations and one additional cation); this is not required for this calculation (see Hawthorne and Schindler 2008) but it does make the procedure much more transparent. Hydrogen has a coordination number of [2]; the O(donor)–H bond is part of the structural unit whereas the H···O(acceptor) bond is not part of the structural unit. Using the cation coordination numbers indicated in Table 5, there are 18 bonds within the structural unit of brandtite, leaving an additional 20 bonds needed to attain the requisite anion coordination numbers. There are four hydrogen bonds incident to the structural unit (generally from adjacent structural units), which leaves 16 bonds needed from interstitial cations. The structural unit has a residual charge of 4⁻ (per [Mn²⁺(AsO₄)₂(H₂O)₂] unit) and hence the Lewis basicity of the structural unit is the aggregate charge divided by the number of bonds required: 4/16 = 0.25 v.u. Table 1 shows that Ca has a Lewis acidity of 0.27 v.u., in close accord with the Lewis basicity of the structural unit. Hence, the principle of correspondence of Lewis acidity–basicity is satisfied, and brandtite is a stable structure.

Table 5 Calculation of structural-unit basicity for brandtite and brackebuschite

In brackebuschite (Table 5), there are 16 bonds within the structural unit, leaving an additional 19 bonds needed to attain the requisite anion coordination numbers. Two of these bonds are hydrogen bonds from adjacent structural units, and 17 bonds must come from the interstitial cations. The structural unit has a residual charge of 4⁻, and hence the basicity of the structural unit is 4/17 = 0.23 v.u. This value matches up quite well with the Lewis basicity of Pb²⁺ (0.20 v.u., see Table 1), the principle of correspondence of Lewis acidity–basicity is satisfied and brackebuschite is a stable structure. Thus, Ca can form the brandtite-type structure as its Lewis acidity (0.27 v.u.) matches the Lewis basicity of the brandtite-type structural unit, whereas Pb²⁺ (also Ba and Sr) cannot form brandtite-type structures as their Lewis acidities (~0.20 v.u.) do not match the Lewis basicity of the brandtite-type structural unit. Similarly, Pb²⁺, Ba and Sr form brackebuschite-type structures, whereas Ca does not for the same reason.

The nature of the interstitial cation(s) is controlled by the principle of correspondence of Lewis acidity–basicity: the Lewis acidity of the interstitial cation must match the Lewis basicity of the structural unit. Some very interesting questions now emerge concerning the nature of the crystallization process. Does the availability of a particular interstitial cation dictate the form of the structural unit or does the form of the structural unit dictate the identity of the interstitial cations? Does the pH of the environment have a strong effect on the form of the structural unit or the amount of (H₂O) incorporated into the structure? Are there synergetic interactions between these factors? We can begin to investigate some of these questions using binary structural representation and the principle of correspondence of Lewis acidity–basicity in conjunction with the bond-topological characteristics of the structural unit.

The role of H₂O in crystal structures

Hawthorne (1992) showed that that there are several different major roles for hydrogen (H) in structures, all of them deriving from the common asymmetry of O–H bonds. Of principal terrestrial importance are the (OH) and (H₂O) groups, primarily because of their polar nature: on one side (the O side), each group acts like an anion, whereas on the other side (the H side), the group acts as a cation that generally has a very soft interaction with its associated anions. The importance of this effect is difficult to overemphasize. It moderates a large number of biological interactions that are integral to life, and it imparts a subtlety and diversity to inorganic mineralogical interactions that would otherwise be absent.

Let us focus on (H₂O). There are two principal roles of (H₂O) in minerals (Hawthorne 1992, 1997a): (1) as a moderator of Lewis acidity and Lewis basicity; (2) as a control on the dimensional polymerization of structural units.

(H₂O) as a moderator of bond valence

Here, I examine the possible stereochemical arrangements adopted by (H₂O), and following Schindler and Hawthorne (2004) and Hawthorne and Schindler (2008), consider their effect in moderating the Lewis acidity of the interstitial complex and the Lewis basicity of the structural unit.

(H₂O) bonded to one cation

A cation, M, bonds to an anion S with a bond valence of v v.u. (Fig. 23a). A cation, M, bonds to an (H₂O) group, and the (H₂O) group bonds to an anion, S (Fig. 23b). In the first case, the anion receives one bond of bond valence v v.u. In the second case, the O atom of the (H₂O) group receives a bond strength of v v.u. from the cation M, and the valence-sum rule at the central O atom is satisfied by two short O–H bonds of strength (1 − v/2) v.u. In turn, each H forms at least one hydrogen bond with its neighbouring anions in order to satisfy its own bond-valence requirements. As a result, the S anion receives a bond valence one half of what it received where it was bonded directly to the M cation. The (H₂O) group is acting as a bond-strength transformer, splitting one bond (bond strength = v v.u.) into two bonds of (on average) half the strength (bond valence = v/2 v.u.); this type of (H₂O) is designated transformer (H₂O), and is denoted by the subscript d: (H₂O) _d .

Fig. 23

The bond-valence structure around (H₂O) as a function of local bond topology; a a cation, C (green) bonded to an anion, S (yellow) with bond valence v v.u.; b a cation bonded to an (H₂O) group (O: orange; H: black) with bond valence v v.u.; the H atoms hydrogen bond to the anion S with bond valence v/2 v.u.; (c) two cations bonded to an (H₂O) group with bond valence v v.u.; the H atoms hydrogen bond to the anion S with bond valence v v.u

(H₂O) bonded to two cations

Where two cations, M, bond to an (H₂O) group which bonds to two anions S (Fig. 23c), the O atom receives a bond valence of 2v v.u. from the two cations, and the valence-sum rule is satisfied by two short O–H bonds, each of strength (1 − v) v.u., and each H atom forms at least one hydrogen bond with its neighbouring anions. In Fig. 23c, one of these hydrogen bonds involves the S anion, which thus receives the same bond strength (v v.u.) as where it is bonded directly to one M cation (Fig. 23b). In this case, the (H₂O) group does not act as a bond-valance transformer; I refer to this type of (H₂O) group as non-transformer (H₂O) and denote it by the subscript e: (H₂O) _e .

(H₂O) not bonded to any cation

Where (H₂O) is involved only in a hydrogen-bond network, its O atom is usually [4]-coordinated, and the (H₂O) group participates in two O–H (donor-hydrogen) bonds and two H⋯O (hydrogen⋯acceptor) bonds, called hydrogen bonds. In this case, two hydrogen bonds of strength v v.u. are incident at the O atom of the (H₂O) group. The bond-valence requirements of the central O atom (i.e., the operation of the valence-sum rule at the central O atom) are satisfied by two O–H bonds of strength (1 − v) v.u. Each H atom forms a hydrogen bond of strength v v.u. to another anion, and an (H₂O) group not bonded to any cation(s) normally does not modify the strengths of its exident chemical bonds; it merely propagates them through space, similar to the case where the (H₂O) group is bonded to two cations (Fig. 23c). I refer to this type of (H₂O) group as non-transformer (H₂O) and denote it by the subscript g: (H₂O) _g .

(H₂O) as a component of the interstitial complex

There are two principal roles for interstitial (H₂O) groups in a structure: (1) to satisfy the bond-valence requirements around an interstitial cation when there are insufficient adjacent anions to do so from neighbouring structural units. We may also state this in a somewhat different way: to propagate bond valence from the interstitial cation to a distant unsatisfied anion via a hydrogen bond. (2) To act as a bond-valence transformer between interstitial cations and the structural unit. In the first case, the (H₂O) groups are merely propagating bond valence through space, and hence will be non-transformer (H₂O) groups. In the second case, the transformer (H₂O) groups will moderate the Lewis acidity of the interstitial complex and play a crucial role in affecting the stability of a chemical composition through the operation of the principle of correspondence of Lewis acidity–basicity. These are qualitative descriptions of the role of (H₂O) in crystal structures. However, we want a quantitative understanding of the role of (H₂O) in structures and this approach can give it to us. As an example, I will examine the role of interstitial (H₂O) from a bond-topological perspective and develop a quantitative understanding of its presence in complex oxysalt minerals.

(H₂O) and the principle of correspondence of Lewis acidity–basicity

Above, we saw how the valence-matching principle allows us to assess the possible stability of any simple chemical formula, and we have developed the principle of correspondence of Lewis acidity–basicity to have a similar role with regard to complex oxysalt structures: Stable structures will form when the Lewis-acid strength of the interstitial complex closely matches the Lewis-base strength of the structural unit. The Lewis basicity of the structural unit is the average bond valence of bonds to that structural unit from surrounding interstitial complexes and neighbouring structural units. The electroneutrality principle requires that the bonds to the structural unit neutralize the charge of the structural unit, and hence we can define the Lewis basicity of the structural unit as the charge on the structural unit divided by the number of bonds to the structural unit. Here, I will not discuss how to calculate the range in Lewis basicity of the structural unit; the calculation is complicated but not difficult, and full details are given by Hawthorne and Schindler (2008). Instead, I will focus on the interstitial complex and show how we can graphically represent the variation in Lewis acid strength of an interstitial complex as a function of chemical composition and structure, and then use the principle of correspondence of Lewis acidity–basicity to examine the interaction between the structural unit and interstitial complex as a function of varying chemical composition of each component of a structure.

We may write the chemical formula of a generalized interstitial complex as

$$ \lbrace { {}^{[m]} M_{a}^{ + } \,^{[n]} M_{b}^{2 + } \,^{[l]} M_{c}^{3 + } ({\text{H}}_{2} {\text{O}})_{d} ({\text{H}}_{2} {\text{O}})_{e} ( {^{[q]} {\text{OH}}} )_{f} ({\text{H}}_{2} {\text{O}})_{g} } \rbrace^{Z + } $$

where M are interstitial cations of different charge and with coordination numbers [m], [n] and [l], d = the amount of transformer (H₂O), e = the amount of non-transformer (H₂O) and g = the amount of (H₂O) not bonded to any interstitial cation (Schindler and Hawthorne 2001a). The requirement of electroneutrality determines the formal charge of the interstitial complex, Z+; we wish to understand what determines the constitution of the rest of the interstitial complex, particularly a to g, l to n, and q. The Lewis acidity of the interstitial complex may be calculated as a function of the variables a to g, l to n, q and Z in the above expression, and represented graphically as shown in Fig. 24: the curved lines show the variation in Lewis acidity (shown on the ordinate) as a function of the number of transformer (H₂O) groups per cation (shown on the abscissa) for interstitial cations of different formal charge and coordination number (shown by families of curves; the corresponding cation charges and coordination numbers are shown to the left of the curves). Hawthorne and Schindler (2008) describe how to incorporate the monovalent anions (OH, Cl) into this formalism.

Fig. 24

Variation in Lewis acidity of a general interstitial complex as a function of the number of transformer (H₂O) groups per cation. The lines shown are for interstitial cations with different formal charges and coordination numbers shown to the left of the plot [after Hawthorne and Schindler (2008)]

The operation of the principle of correspondence of Lewis acidity–basicity is shown schematically in Fig. 22. However, rather than compare two single-valued quantities as we do with the valence-matching principle, we compare two expressions that vary as a function of chemical composition and structure. How we do this is shown in Fig. 25. The range in Lewis basicity of the structural unit is plotted on the same graph as the Lewis acidity function. Where the properties of the structural unit (the yellow bands in Fig. 25) and the interstitial complexes (the family of curved lines in Fig. 25) intersect, structures of those particular compositions are in accord with the principle of correspondence of Lewis acidity–basicity, and may be stable. Where the properties of the structural unit and interstitial complexes do not intersect (i.e., outside the yellow bands in Fig. 25), structures of those compositions are in not accord with the principle of correspondence of Lewis acidity–basicity, and are not expected to be stable. Thus, the principle of correspondence of Lewis acidity–basicity allows us to examine the interaction between the structural unit and interstitial complex as a function of varying chemical composition of each component. Let us now look at what we can do with this approach for a subset of the hydroxy-hydrated borate minerals considered above.

Fig. 25

Variation in Lewis acidity as a function of the number of transformer (H₂O) groups per cation for different interstitial-cation charges and coordination numbers for a general interstitial complex; the range in Lewis basicity of the structural units of selected borate minerals is shown by the yellow fields: a [B₄O₅(OH)₄]²⁻; b [B₃O₃(OH)₅]²⁻; c [B₆O₇(OH)₆]²⁻ [from Schindler and Hawthorne (2001b)]

[B₄O₅(OH)₄]²⁻

The effective charge (Hawthorne and Schindler 2008) of this structural unit is (2 + 0.2 × 4)⁻ = 2.8⁻. To calculate the Lewis basicity of the structural unit, we need to know the number of bonds to the structural unit. Schindler and Hawthorne (2004) showed that there is a relation between the CDA (Charge Deficiency per Anion: the effective charge divided by the number of simple anions) of the structural unit and $\left\langle {\text{NB}} \right\rangle_{\text{in}}$ the number of bonds to the structural unit (per anion of the structural unit) from the interstitial complex and adjacent structural units. This relation is shown for borate minerals in Fig. 26. For [B₄O₅ (OH)₄]²⁻, the number of O atoms in the structural unit is 9; hence, the CDA of the structural unit is 2.8/9 = 0.31 v.u. and the corresponding range in $\left\langle {\text{NB}} \right\rangle_{\text{in}}$ from Fig. 26 is 1.30–1.80. As there are nine anions in the structural unit, the range in the total number of bonds to the structural unit is 9 × (1.3–1.8) = 11.7–16.2. For this structural unit, the range in Lewis basicity is equal to the effective charge divided by the range in the number of bonds to the structural unit, $\left\langle {\text{NB}} \right\rangle_{\text{in}}$: 2.8/11.7 and 2.8/16.2 = 0.17–0.24 v.u.

Fig. 26

Variation in $\left\langle {\text{NB}} \right\rangle_{\text{in}}$, the number of bonds (per anion of the structural unit) from the interstitial complex and adjacent structural units, as a function of CDA (Charge Deficiency per Anion) for structural units of borate minerals [after Hawthorne and Schindler (2008)]

The range in chemical composition for possible interstitial complexes may be predicted from Fig. 25a. For monovalent interstitial cations, only the coordination numbers [5] and [6] are possible, and these have 0–1 and 0 transformer (H₂O) groups, respectively (Table 6). Interstitial [6]- and [8]-coordinated divalent cations, ^[6] M ²⁺ and ^[8] M ²⁺, are possible with 2–5 and 0–3 transformer (H₂O) groups. For trivalent interstitial cations, there are two possibilities, depending on the presence or absence of interstitial (OH). Interstitial ^[6] M ³⁺ and ^[8] M ³⁺ are possible with 6 transformer (H₂O) and 4–8 transformer (H₂O) groups, and also with one (OH) group and 4 transformer (H₂O) groups. The structural unit [B₄O₅(OH)₄]²⁻ occurs in borax: Na₂(H₂O)₈[B₄O₅(OH)₄]; tincalconite: Na₂(H₂O)_2.67[B₄ O₅ (OH)₄]; and hungchaoite: Mg(H₂O)₅[B₄O₅(OH)₄] (H₂O)₂. In borax, the interstitial complex is {^[6]Na(H₂O)₀…}⁺ (predicted: {^[6]Na(H₂O)₀…}⁺), in hungchaoite, the interstitial complex is {^[6]Mg(H₂O)₄…}²⁺ (predicted: {^[6]Mg(H₂O)_2–6…}²⁺). In tincalconite, the interstitial complex has cations in two different coordinations {^[5] ${\text{Na}}_{1.33}^{}{}^{[6]}$Na_0.67(H₂O)₀…}; combining predictions for ^[5]M⁺ and ^[6]M⁺ results in an aggregate predicted interstitial complex of {^[5] ${\text{Na}}_{1.33}^{}{}^{[6]}$Na_0.67(H₂O)_0–1…}.

Table 6 The [B₃O₃(OH)₅]²⁻, [B₄O₄(OH)₄]²⁻ and [B₆O₇(OH)₆]²⁻ structural units: predicted and observed interstitial complexes

[B₃O₃(OH)₅]²⁻

This structural unit has an effective charge of (2 + 0.2 × 5)⁻ = 3.0⁻, the number of O atoms in the structural unit is 8, the CDA of the structural unit is 3.0/8 = 0.38 v.u., and the range in the number of bonds per anion to the structural unit $\left\langle {\text{NB}} \right\rangle_{in}$ is 1.55–2.00 (Fig. 26). The resultant range in Lewis basicity is 3/8 × 2.00 − 2/8 × 1.55 = 0.19–0.24 v.u.

Interstitial monovalent cations cannot occur for coordination numbers of [6] and above, and can occur with a coordination number of [5] only with zero transformer (H₂O) groups (Table 6). Divalent interstitial cations are possible only for [6]-coordination with 2–4 transformer (H₂O) groups, for [7]-coordination with 1–3 transformer (H₂O) groups and for [8]-coordination with 0–2 transformer (H₂O) groups. Trivalent interstitial cations are possible for coordination numbers [6], [7] and [8] with 5–6, 4–7 and 3–7 transformer (H₂O) groups, respectively. This structural unit occurs in inyoite: Ca(H₂O)₃[B₃O₃(OH)₅](H₂O); inderite: Mg(H₂O)₄[B₃O₃(OH)₅](H₂O); kurnakovite: Mg(H₂O)₄[B₃O₃(OH)₅](H₂O); meyerhofferite: Ca(H₂O)[B₃O₃(OH)₅]; and inderborite: CaMg(H₂O)₄ [B₃O₃(OH)₅]₂(H₂O)₂. The interstitial complexes in inderite and kurnakovite are {^[6]Mg(H₂O)₄…}²⁺ (predicted: {^[6]Mg(H₂O)_2–4…}²⁺), in inyoite and meyerhofferite are {^[8]Ca(H₂O)₁…}²⁺ (predicted: {^[8]Ca(H₂O)_0–2…}²⁺), and in inderborite are ^[8]Ca and ^[6]Mg: {^[6]Mg^[8]Ca(H₂O)₂…}⁴⁺ (predicted: {^[6]Mg^[8]Ca(H₂O)_2–6…}⁴⁺).

[B₆O₇(OH)₆]²⁻

This structural unit has an effective charge of (2 + 0.2 × 6)⁻ = 3.2⁻, the number of O atoms in the structural unit is 13, the CDA of the structural unit is 3.2/13 = 0.25 v.u., and the range in the number of bonds per anion to the structural unit $\left\langle {\text{NB}} \right\rangle_{in}$ is 1.0–1.5 (Fig. 26). The resultant range in Lewis basicity of the [B₆ O₇ (OH)₆]²⁻ structural unit is 0.16–0.25 v.u.

Interstitial monovalent cations can occur for [6]-coordination only with 0 transformer (H₂O) groups, and ^[7] M ⁺ (not shown in Fig. 25c) and ^[8] M ⁺ are not possible (Table 6). Divalent interstitial cations are possible for [6]-coordination with 2–5 transformer (H₂O) groups, for [7]-coordination (not shown in Fig. 25c) with 1–4 transformer (H₂O) groups and for [8]-coordination with 0–3 transformer (H₂O) groups. This structural unit occurs in mcallisterite: Mg(H₂O)₃[B₆O₇(OH)₆] (H₂O)_1.5; admontite: Mg(H₂O)₃[B₆O₇(OH)₆](H₂O); aksaite: Mg(H₂O)₂ [B₆O₇(OH)₆](H₂O); and rivadavite: Na₆Mg(H₂O)₁₀[B₆O₇(OH)₆]. Mcallisterite and admontite have interstitial complexes {^[6]Mg(H₂O)₃…}²⁺ (predicted: {^[6]Mg(H₂O)_2–5…}²⁺), and aksaite has an interstitial complex {^[6]Mg(H₂O)₁…}²⁺, (predicted: {^[6]Mg (H₂O)_2–5…}²⁺).

Prediction of interstitial complexes for Cl-free hydroxy-hydrated borate minerals

The above calculations show that we can predict aspects of the interstitial complex of a mineral reasonably well, given its structural unit. Figure 27 shows that the coordination numbers of interstitial cations (from [4] to [11]) in borate minerals are predicted quite accurately.

Fig. 27

Comparison of the observed and predicted coordination numbers of interstitial cations in borate minerals; the sizes of the circles are proportional to the number of data defining each point [from Schindler and Hawthorne (2001b)]

This approach also predicts the number of transformer (H₂O) groups in the interstitial complex reasonably well. In most (95 %) of the hydroxyl-hydrated borate minerals, the observed amount of transformer (H₂O) is within the predicted range (not considering microporous structures such as pringleite). The structural unit has a range in Lewis basicity (reflecting its stability over a range of pH), and hence there is a range in the predicted number of transformer (H₂O) groups. Factors that affect the amount of transformer (H₂O) within the predicted range are not yet understood, but presumably relate to the stereochemical details of the interaction between the interstitial complex and the structural unit.

Other oxysalt minerals

Above, I have focused on hydroxy-hydrated borate minerals, and have shown that many aspects of their structure, chemical composition and stability are susceptible to understanding using this approach based on the bond topology of the crystal structure. This approach has also been used to examine the structure, chemical composition and stability of the vanadate (Schindler et al. 2000a, b), sulphate (Schindler et al. 2006) and uranyl-oxysalt minerals (Schindler and Hawthorne 2004, 2008), and has the potential to be applied to other low-temperature oxysalt minerals. An important aspect of the approach described here is the fact that it attempts to relate bond topology and bond valence to processes involved in crystallization (e.g., Figs. 15, 16, 17, 18, 19). This does make this approach more difficult to apply to minerals that crystallized from magmas, as the structures of the latter are much less well understood than those of aqueous solutions. However, it does encourage us to learn more about the details of crystallization processes at the atomic scale in magmatic systems.

(H₂O) and (OH) as controls on dimensional polymerization of the structural unit

On the anion side of the (H₂O) and (OH) groups, the bonding interaction is commonly relatively strong [~0.40 v.u. for (H₂O); 0.80 v.u. for (OH)], and on the cation side of these groups, the bonding interaction is much weaker [~0.20 v.u. for both (H₂O) and (OH)]. Hence, the anion interaction is part of the structural unit, whereas the cation interaction is not part of the structural unit (Hawthorne 1985). The result of this is illustrated for the structure of newberyite, Mg₃(PO₃OH) (H₂O)₃, in Fig. 28. Consider first the acid phosphate group, (PO₃OH). Each tetrahedron links to three (Mgφ₆) octahedra, forming a sheet in the ac plane. The remaining vertex of the tetrahedron points in the ±b direction, forming a potential point of linkage (polymerization) in this direction. However, H is attached to the O anion occupying this vertex, and the valence-sum rule prevents further linkage to another tetrahedron or octahedron (i.e., preventing polymerization of the structural unit in the b direction through the phosphate group). Consider next the {MgO₃(H₂O)₃} octahedron. This is linked by the tetrahedron into a sheet, as noted above, by sharing three vertices with neighbouring tetrahedra. The remaining three vertices of the octahedron can potentially link in the third dimension to form a framework structure. However, the anions occupying these three vertices also link to two H atoms, satisfying their bond-valence requirements and preventing any polymerization in the b direction.

Fig. 28

The crystal structure of newberyite, Mg₃(PO₃OH)(H₂O)₃, projected onto (010), showing how the presence of H prevents polymerization of the P and Mg polyhedra; Mg octahedra: green; P tetrahedra: yellow; H atoms: red

Thus, (OH) and (H₂O) groups can limit the dimensional polymerization of a structural unit in one or more directions. It is difficult to overemphasize the importance of this role, as this capability to control the polymerization of the structural unit is a major cause of structural diversity in oxygen-based minerals. Moreover, the geochemical distribution of H throughout the Earth, together with the anharmonic nature of the hydrogen bond, is a major factor in accounting for the systematic distribution in mineral species from the core to the surface of the Earth.

Mineral reactions

Above, I emphasized that when comparing two structures, the important energetic terms are the most local topological differences between the structures. Let us consider briefly what this means in terms of mineral reactions. Here, we look at the lowest-moment changes, gradually increasing the order of the moment.

Zero-moment changes

Zero-moment changes involve changes in chemical composition; that is, a chemical reaction in which the constituents are not conserved. Such a reaction shows open-system behaviour and is a metasomatic reaction.

Second-moment changes

A second-moment change involves changes in coordination number, and hence such reactions are characterized by changes in one or more coordination numbers in the constituent phases. A change in coordination number usually involves a first-order phase transition, and such a reaction is a discontinuous reaction. For example, consider the following reaction:

$$ \begin{aligned} & {\text{Forsterite}} = {\text{Periclase}} + {\text{Quartz}} \\ &^{[6]} {\text{Mg}}_{2} {}^{[4]} {\text{Si}}^{[4]} {\text{O}}_{4} ={}^{[6]} {\text{Mg}}^{[6]} {\text{O}} +{}^{[4]}{\text{Si}}\,^{[2]} {\text{O}}_{2} \\ \end{aligned} $$

in which the coordination numbers of all the constituent atoms are noted. The coordination numbers of Mg and Si are conserved in the reaction, but the coordination numbers of O are not conserved. The moments considerations (discussed above) indicate that it is the change in coordination number of O that is the major driver of this reaction, as these are the lowest-moment differences between each side of the reaction. The driving force of this reaction may also be expressed as the enthalpy of reaction, ΔH, suggesting that there should be a correlation between the change in coordination numbers and the enthalpy of reaction. Let us consider the reactions

$$ ^{[6]} {\text{Mg}}_{m} \,^{[4]} {\text{Si}}_{n} {\text{O}}_{(m + 2n)} = m{\text{MgO}} + n{\text{SiO}}_{2} $$

for m, n = 2, 1; 3, 2; 1, 1; 1, 2; 2, 5; 1, 3. We may calculate ΔH of reaction with the model of Aja et al. (1992), using fictive enthalpies of formation from their Table 3. However, before we can relate anion coordination numbers to these enthalpies of formation, we must take into account the fact that change in coordination number is an intensive variable, whereas enthalpy of formation is an extensive variable. We must transform the enthalpies of formation into an intensive variable. We may do this by dividing the enthalpy of formation by the molecular weight of the reactant to produce the intensive variable ΔH/MW which I will call the reduced enthalpy of formation. Figure 29 shows the variation in ΔH/MW as a function of mean anion coordination number of the reactant; there is a strong correlation between these two variables, in accord with the strong influence of coordination number on the energetics of reaction indicated by the arguments given above.

Fig. 29

Variation in reduced enthalpy of formation (from the oxides) of ^[6]Mg ^[4] _m Si _n O_(m+2n) versus mean anion coordination number of the reactant

We may consider a slightly more complicated reaction involving some minerals mentioned above, the hydrated magnesium sulphate compounds, Mg(SO₄)(H₂O) _n where n = 0–7, 11: synthetic Mg(SO₄); kieserite, Mg(SO₄)(H₂O); sanderite, Mg(SO₄)(H₂O)₂; synthetic Mg(SO₄)(H₂O)₃; starkeyite, Mg(SO₄)(H₂O)₄; cranswickite, Mg(SO₄)(H₂O)₄; pentahydrite, Mg(SO₄)(H₂O)₅; hexahydrite, Mg(SO₄)(H₂O)₆; epsomite, Mg(SO₄)(H₂O)₇ and meridianiite, Mg(SO₄)(H₂O)₁₁, the bond-topological characteristics of which have been considered recently by Hawthorne and Sokolova (2012). We may write the following general reaction:

$$ {\text{MgSO}}_{4} ({\text{H}}_{2} {\text{O}})_{n} = {\text{MgO}} + {\text{SO}}_{3} + n({\text{H}}_{2} {\text{O}}) $$

Figure 30 shows the variation in the reduced enthalpy of formation as a function of the mean anion coordination number. There is a linear relation between the two variables similar to that exhibited in Fig. 29 for the Mg silicates, in accord with our contention that anion coordination number is a driving force of these reactions. However, there are two significant deviations from linearity in Fig. 30 for n = 1 and 3. These differences are far greater than the uncertainties in the enthalpies of formation and may relate to bond-topological differences within this series of minerals. Hawthorne and Sokolova (2012) showed that the anion coordination numbers for MgSO₄ and kieserite (n = 1) are significantly different from those of the rest of the series: if there are a anions of coordination [2] and b anions of coordination [3], combination of the handshaking lemma (Wilson 1979) for a digraph with the valence-sum rule of bond-valence theory shows that a + 2b = 6 for the Mg(SO₄)(H₂O) _n structures. There are four possible integer solutions to this equation and there are (4 + n − a − b) [4]-coordinated anions in these structures. For n = 0–1, a = b = 2 and there are no [4]-coordinated anions in these structures; for n = 2–11, a = 0, b = 6 and there are [4]-coordinated anions in these structures. Thus, it is not unexpected to find that kieserite (n = 1) is nonlinear with the n = 2–11 structures. The n = 3 structure also deviates somewhat from the linear relation; this structure is unknown and hence we cannot evaluate any effects of differing anion coordination number.

Fig. 30

Variation in reduced enthalpy of formation (from the oxides) of MgSO₄(H₂O) _n versus mean anion coordination number of the reactant

In summary, the general correlation between anion coordination number and reduced enthalpy of formation from the oxides is in accord with the moments approach to the electronic energy density-of-states that suggests that such reactions should be driven primarily by changes in coordination number. Moreover, this approach may allow us to evaluate the effects of differing bond topology, as expressed in differing anion coordination numbers, on changes in the (reduced) enthalpy of formation.

Fourth-moment changes

A fourth-moment change involves changes in next-nearest-neighbour atoms while maintaining chemical composition and both cation- and anion coordination numbers. Such changes involve the identities of next-nearest-neighbour cations and/or anions, and hence involve the nature of local (short-range) clusters of ions. Such changes in SRO (short-range order) are common in amphiboles (e.g., Hawthorne et al. 1996b, c, 1997, 2000b; Della Ventura et al. 1999; Hawthorne and Della Ventura 2007), and the short-range version of the valence-sum rule (Hawthorne 1997b) indicates that such short-range order–disorder should be common in all minerals with polyvalent substitutions. Major chemical variations in amphiboles in metabasic rocks involve the following change:

$$ \begin{aligned} & {\text{Tremolite}} \to {\text{Sadanagaite}} \\ & \square {\text{Ca}}_{2} {\text{Mg}}_{5} {\text{Si}}_{8} {\text{O}}_{22} ({\text{OH}})_{2} \to {\text{NaCa}}_{2} ({\text{Mg}}_{3} {\text{Al}}_{2} )({\text{Si}}_{5} {\text{Al}}_{3} ){\text{O}}_{22} ({\text{OH}})_{2} \\ \end{aligned} $$

This change involves a continuous reaction which progresses to the right with increasing grade of metamorphism. What are the structural characteristics of amphibole involved in this continuous reaction with increasing temperature and pressure? In such a reaction, the bond topology of the amphibole is conserved, and any energetic differences with regard to the amphiboles involve only atom identities and their relative locations; this is short-range order–disorder and we know that this is ubiquitous in amphiboles. End-member tremolite is completely ordered, whereas end-member sadanagaite must show extensive short-range order/disorder and the short-range order/disorder in tremolite-sadanagaite solid-solution must have a major effect on the energetics of the resulting minerals and their reactions with other phases.

The reaction principle

A mineral crystallizes from a prior assemblage of atoms, and this prior assemblage of atoms has structure, that of an aqueous fluid or a magma or a pre-existing assemblage of minerals (and commonly a coexisting fluid). The valence-sum rule (see above) has been used extensively for atoms in crystals, and to a lesser extent for atoms in glasses and aqueous fluids. It seems logical to propose that atoms in transition between these various states of matter also obey the valence-sum rule (although probably to a lesser degree than in a crystal). This leads to the Reaction Principle which we may define as follows:

The Reaction Principle: During a chemical reaction, atoms move relative to each other such that they continually minimize local deviations from the valence-sum rule.

This being the case, the initial arrangement of atoms in a system will commonly have an influence on the initial product of any reaction. Above, we have already used this idea when considering the crystallization of borate minerals as a condensation of the molecular species in aqueous solution (Figs. 16, 17, 18, 19). A similar argument can be made for minerals crystallizing from magmas. For example, Gaskell et al. (1991) showed that a glass of composition CaSiO₃ has a local structure very similar to that of wollastonite. Assuming that the structure of the glass is somewhat similar to that of CaSiO₃ melt close to the liquidus, the initial reactant in the crystallization of wollastonite (a CaSiO₃ “magma”) is already templated with much of the wollastonite structure, and many of the atoms in the system will obey the Reaction Principle, resulting in the crystallization of wollastonite.

In reactants that have weak bonds and little extended structure (e.g., NaCl in aqueous solution), one expects little in the way of influence of the reactant structure on the product structure, and direct crystallization of the product with the lowest free energy. Where the structure of the reactant is defined by strong bonds and possibly more extended structure (e.g., SiO₂ in aqueous solution), there is the potential for the structure of the reactant to influence the structure of the initial product phase via the Reaction Principle. If the structure of the reactant is far from that of the lowest-energy product phase, it is easy to see that the Reaction Principle may give rise to a product phase that is not the lowest-energy product phase but one whose structure is more strongly related to the structure of the reactant. In turn, the product phase may transform, again under the constraint of the Reaction Principle, into another product phase and work its way toward the lowest-energy product phase via a series of steps that accord with the Reaction Principle. Alternatively, the initial product phase, or one of the later “intermediate” product phases, may be sufficiently stable (although not the phase with the lowest energy) that this sequence of reactions terminates in a metastable product.

The Reaction Principle leads naturally to Ostwald’s Step Rule (Ostwald 1897). This may be stated as follows: “If a reaction can result in several products, it is not the most stable state with the least amount of free energy that is initially obtained, but the least stable one, lying nearest to the original state in free energy” (Morse and Casey 1988). This rule is not followed all the time, but sufficient systems are in accord with this rule that one must pay attention to it, and rationale has been given for the rule in terms of irreversible thermodynamics and kinetic theory (e.g., van Santen 1984; Morse and Casey 1988; Nývit 1996; ten Wolde and Frenkel 1999). From a bond-topological perspective, we may examine the operation of this rule, not in terms of the stability or metastability of the products, but in terms of the mechanism(s) of the reaction and its possible influence on the structure(s) of the product(s). The Reaction Principle accounts for the observations encompassed by Ostwald’s rule. As noted above, in reactants that have weak bonds and very local structure, one expects little in the way of influence of the reactant structure on the product structure, and direct crystallization of the product with the lowest free energy, in accord with the observation that Ostwald’s step rule “does not work all the time”. In reactants with strong bonds and more extended structures, one expects the structure of the reactant to influence that of the product via the Reaction Principle, and a series of product phases may result in accord with Ostwald’s step rule.

In regard to Ostwald’s step rule, it is interesting to further examine the example of wollastonite given above. The product of the reaction CaSiO₃ (magma) → wollastonite with the “least amount of energy” will be a single crystal of wollastonite. Of course, this will never occur; the actual product will be an assemblage of crystals of wollastonite in different orientations, presumably the result of the magma consisting of regions of wollastonite-like structure in different orientations. Thus, we can think of the product phase according to the Ostwald step rule as consisting of an assemblage of mineral grains instead of one large crystal.

Coda

I have described a theoretical approach to the structure and chemical composition of minerals based on their bond topology, aspects of graph theory and bond-valence theory, and the moments approach to the electronic energy density-of-states. The above description is rather complicated, and to give an overview, below I identify the principal features of this approach in point form, and also what has been done thus far in its application to the structure, chemical composition and stability of minerals:

• [1] An arrangement of atoms and chemical bonds may be represented by a weighted polychromatic digraph, and the handshaking lemma may be used to examine many aspects of atom coordination and the linkage of coordination polyhedra, which is an expression of the bond topology.

• [2] The method-of-moments approach to the electronic energy density-of-states provides a bond-topological interpretation of the energetics of structure.

• [3] When comparing structures, the most important structural differences involve the first few disparate moments of the electronic energy density-of-states.

• [4] We may classify chemical reactions according to the lowest-order moment of the electronic energy density-of-states that is conserved.

• [5] This allows us to identify the principal structural changes that drive chemical change: (a) coordination number for discontinuous reactions and (b) short-range order for continuous reactions.

• [6] The algebraic form of bond-valence theory may be derived from both ionic and covalent models of the chemical bond.

• [7] It may be shown that the quantitative aspects of bond-valence theory arise from the topological (or graphical) characteristics of structures as arrangements of atoms and chemical bonds.

• [8] Binary Representation: A crystal structure may be divided into two components, the structural unit, a strongly bonded part of the structure, and the interstitial complex, an assemblage of (usually monovalent and divalent) cations, anions and neutral groups that weakly bind the structural units into a continuous crystal structure. It is the weak interaction between the structural unit and the interstitial complex that controls the stability of the structural arrangement.

• [9] The Structure Hierarchy Hypothesis states that higher bond-valence polyhedra polymerize to form the (usually anionic) structural unit, the excess charge of which is balanced by the interstitial complex (usually consisting of large low-valence cations and (H₂O) groups). This hypothesis may be justified within the framework of bond topology and bond-valence theory.

• [10] The possible modes of polymerization are (1) unconnected polyhedra, (2) isolated clusters, (3) infinite chains, (4) infinite sheets and (5) infinite frameworks.

• [11] The Structure Hierarchy Hypothesis may be used to hierarchically classify oxysalt minerals, and the degree of connectedness can be used to hierarchically classify minerals within each of these major groups.

• [12] Borate minerals are made of six polyhedron clusters that are also the clusters that occur in aqueous borate solutions, and the Lewis basicity of the clusters scale with the pH of the solution at the maximum concentration of each cluster, providing a link between the conditions in the nascent aqueous solution and the minerals which crystallize from it.

• [13] The Principle of Correspondence of Lewis Acidity–Basicity states that stable structures will form when the Lewis-acid strength of the interstitial complex closely matches the Lewis-base strength of the structural unit.

• [14] The Principle of Correspondence of Lewis Acidity–Basicity provides a connection between a structure, the speciation of its constituents in aqueous solution and its mechanism of crystallization, and allows us to examine the factors that control the chemical composition and aspects of the structural arrangement of minerals.

• [15] (H₂O) groups in the structural unit limit the polymerization of the structural unit in one or more directions, controlling the dimensional polymerization of the structural unit. This is a major cause of structural diversity in oxygen-based minerals, and accounts for the systematic distribution in mineral species from the core to the surface of the Earth.

• [16] Interstitial (H₂O) groups may (1) satisfy the bond-valence requirements around an interstitial cation where there are insufficient adjacent anions to do so from neighbouring structural units, or (2) moderate the Lewis acidity of the interstitial complex and affect the stability of a chemical composition through the operation of the principle of correspondence of Lewis acidity–basicity.

• [17] Discontinuous chemical reactions are driven primarily by second-moment changes in bond topology; that is, changes in coordination numbers; in many mineral reactions, cation coordination numbers are conserved and it is the change in anion coordination numbers that are the important driver of these reactions.

• [18] In accord with [17], the variation in the reduced enthalpy of formation from the oxides for the ^[6]Mg ^[4] _m Si _n O_(m+2n) structures is a monotonic function of the mean anion coordination number in the latter.

• [19] Continuous chemical reactions are driven primarily by fourth-moment changes in bond topology; that is, changes in next-nearest-neighbour ions, indicating that the energetics of such reactions should be affected strongly by changes in short-range order/disorder.

• [20] The Reaction Principle: During a chemical reaction, atoms move relative to each other such that they continually minimize local deviations from the valence-sum rule.

• [21] The Reaction Principle leads to Ostwald’s Step Rule: If a chemical reaction can result in several products, it is not the most stable state with the least amount of free energy that is initially obtained, but the least stable one, lying nearest to the original state in free energy.

My prime motivation in developing this approach to minerals and their behaviour is to try and understand the atomic-scale factors that control the chemical compositions and structural arrangements of (oxygen-based) minerals, and to relate these factors to the behaviour of minerals in geochemical processes.