Bridgeland’s stabilities on abelian surfaces

Abstract

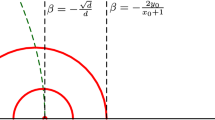
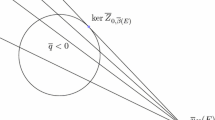
In this paper, we shall study the structure of walls for Bridgeland’s stability conditions on abelian surfaces. In particular, we shall study the structure of walls for the moduli spaces of rank 1 complexes on an abelian surface with the Picard number 1.

Appendix

1.1 The action of Fourier–Mukai transforms on $\mathbb{H }$

Assume that $\mathrm{NS }(X)=\mathbb{Z }H$. Then $\beta +\sqrt{-1}\omega =\frac{z}{ \sqrt{n}}H$ with $z \in \mathbb{H }$, where $z:=x+\sqrt{-1}y$ with $x \in \mathbb{R }$ and $y \in \mathbb{R }_{>0}$. Thus we have an identification of $\mathrm{NS }(X)_\mathbb{R } \times \mathrm{Amp }(X)_\mathbb{R }$ with $\mathbb{H }$. We set $Z_z:=Z_{(\beta ,\omega )}$.

We study the action of Fourier–Mukai transforms on our parameter space of stability conditions in Sect. 3.1. We set $\gamma :=\beta +\lambda H$ and write

$$\begin{aligned} \widetilde{\beta }+\sqrt{-1} \widetilde{\omega }= \frac{z'}{\sqrt{n}}H,\; z' \in \mathbb{H }. \end{aligned}$$

Let $\Phi _{X \rightarrow X_1}^\mathbf{E}:\mathbf{D}(X) \rightarrow \mathbf{D}(X_1)$ be a Fourier–Mukai transform such that $\mathbf{E}$ is a coherent sheaf. Then there is

$$\begin{aligned} A=\left( \begin{array}{l@{\quad }l} a &{} b \\ c &{} d \end{array}\right) \in G \end{aligned}$$

such that $\mu (\Phi _{X \rightarrow X_1}^\mathbf{E}(\mathfrak{k }_x))=\frac{a}{c} \sqrt{n}$ and $\mu (\Phi _{X \rightarrow X_1}^\mathbf{E}(\mathcal{O }_X))=\frac{b}{d}\sqrt{n}$. $X_1=M_H(c^2 e^{\frac{d}{c}\frac{H}{\sqrt{n}}})$ and $\mathbf{E}$ is unique up to the action of $X \times \mathrm{Pic }^0(X)$. Then

$$\begin{aligned} \theta (\Phi _{X \rightarrow X_1}^{\mathbf{E}})= \left( \begin{array}{l@{\quad }l} d &{} b \\ c &{} a \end{array}\right) \in G. \end{aligned}$$

Definition 8.1

For $\Phi _{X \rightarrow X_1}^\mathbf{E}$, we set

$$\begin{aligned} \varphi (\Phi _{X \rightarrow X_1}^\mathbf{E}):= \pm \left( \begin{array}{ll} a &{} b\\ c &{} d \end{array}\right) \in G/\{\pm 1\}. \end{aligned}$$

For $\Phi =\Phi _{X \rightarrow X_1}^{\mathbf{E}}$, we have

$$\begin{aligned} r_1 e^{\gamma }&= c^2-\frac{cd}{\sqrt{n}}H+d^2 \varrho _X, \\ r_1 e^{\gamma '}&= c^2+\frac{ac}{\sqrt{n}}\widehat{H}+a^2 \varrho _{X_1}. \end{aligned}$$

Hence

$$\begin{aligned} \frac{z}{\sqrt{n}}+\frac{d}{c \sqrt{n}}=-\lambda +\sqrt{-1} t,\; \frac{z'}{\sqrt{n}}-\frac{a}{c \sqrt{n}}= \frac{\lambda +\sqrt{-1} t}{(\lambda ^2+t^2)nc^2}, \end{aligned}$$

where $\omega =tH$. Thus we get

$$\begin{aligned} \frac{z'}{\sqrt{n}}&= \frac{a}{c \sqrt{n}}-\frac{1}{c^2 n \Bigg (\frac{z}{\sqrt{n}}+\frac{d}{c \sqrt{n}}\Bigg )}\\&= \frac{ac z-(1-ad)}{c(cz+d)\sqrt{n}} =\frac{a z+b}{\sqrt{n}(c z+d)}. \end{aligned}$$

Therefore the action of $A$ on $\mathbb{H }$ is the natural action of $\mathrm{SL }(2,\mathbb{R })$.

As in (3.3), we set

$$\begin{aligned} \zeta :=-c^2 \frac{\Bigg (\lambda -t \sqrt{-1}\Bigg )^2 (H^2)}{2}= -c^2 \frac{\Bigg (\frac{z}{\sqrt{n}}+\frac{d}{c\sqrt{n}}\Bigg )^2 (H^2)}{2} =-(cz+d)^2. \end{aligned}$$

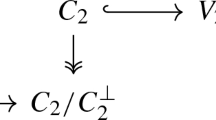
Then we can rewrite the commutative diagram (3.2) as follows.

Proposition 8.2

For $\Phi _{X \rightarrow X_1}^\mathbf{E}$ with $\varphi (\Phi _{X \rightarrow X_1}^\mathbf{E})= \left( \begin{array}{l@{\quad }l} a &{} b\\ c &{} d \end{array}\right) \in G$,

$$\begin{aligned} -(cz+d)^2 Z_{\frac{az+b}{cz+d}\frac{\widehat{H}}{\sqrt{n}}} =Z_{z \frac{H}{\sqrt{n}}} \circ (\Phi _{X \rightarrow X_1}^\mathbf{E})^{-1}. \end{aligned}$$

We also have

$$\begin{aligned} \Phi _{X \rightarrow X_1}^\mathbf{E}(\mathbb{Q }e^{\lambda \frac{H}{{\sqrt{n}}}}) =\mathbb{Q }e^{\frac{a\lambda +b}{c\lambda +d}\frac{\widehat{H}}{\sqrt{n}}}. \end{aligned}$$

We now extend the action of $G$ to $\widehat{G}$. We set

$$\begin{aligned} \Delta :=\left( \begin{array}{l@{\quad }l} 1 &{} 0\\ 0 &{} -1 \end{array}\right) . \end{aligned}$$

We note that

$$\begin{aligned} \widehat{G}=G \rtimes \left\langle \Delta \right\rangle \end{aligned}$$

with

$$\begin{aligned} \left( \begin{array}{l@{\quad }l} 1 &{} 0\\ 0 &{} -1 \end{array}\right) \left( \begin{array}{l@{\quad }l} a &{} b\\ c &{} d \end{array}\right) \left( \begin{array}{l@{\quad }l} 1 &{} 0\\ 0 &{} -1 \end{array}\right) = \left( \begin{array}{l@{\quad }l} a &{} -b\\ -c &{} d \end{array}\right) . \end{aligned}$$

We define the action of $\Delta$ on $\mathbb{H }$ as $\Delta (z):=-\overline{z}$. Then we have

$$\begin{aligned} \Delta (A(\Delta (z)))=\frac{az-b}{-cz+d},\; A=\left( \begin{array}{l@{\quad }l} a &{} b\\ c &{} d \end{array}\right) . \end{aligned}$$

Thus we have an action of $\widehat{G}$ on $\mathbb{H }$.

Proposition 8.3

We can extend the action of $G$ to the action of $\widehat{G}$ by

$$\begin{aligned} (g,\Delta ^n) \cdot z:= \left\{ \begin{array}{l@{\quad }l} g \cdot z, &{} 2|n,\\ -\overline{g \cdot z},&{} 2 \not | n, \end{array}\right. \end{aligned}$$

where $g \in G$ and $\overline{g \cdot z}$ is the complex conjugate of $g \cdot z$.

Remark 8.4

In [14], we showed that the cohomological action of $\mathrm{Eq }_0(\mathbf{D}(X),\mathbf{D}(X))$ defines a normal subgroup of $G$ which is a conjugate of $\Gamma _0(n)$ in $\mathrm{GL }(2,\mathbb{R })$. More precisely, we set $G_0:=\theta (\mathrm{Eq }_0(\mathbf{D}(X),\mathbf{D}(X)))$. Then

$$\begin{aligned} \left( \begin{array}{l@{\quad }l} \sqrt{n} &{} 0 \\ 0 &{} 1 \end{array}\right) ^{-1} G_0 \left( \begin{array}{l@{\quad }l} \sqrt{n} &{} 0 \\ 0 &{} 1 \end{array}\right) =\Gamma _0(n), \end{aligned}$$

where

$$\begin{aligned} \Gamma _0(n):= \left\{ \left. \left( \begin{array}{l@{\quad }l} a &{} b \\ c &{} d \end{array}\right) \in \mathrm{SL }(2,\mathbb{Z }) \right| c \in n \mathbb{Z } \right\} . \end{aligned}$$

We set $\beta +\sqrt{-1}\omega =w H$. Then $\mathrm{Eq }_0(\mathbf{D}(X),\mathbf{D}(X))$ acts on $w$-plane as the action of $\Gamma _0(n)$ on $w$-plane.