1 Introduction

There are vast research works dealing with the cogging torque reduction issues in the permanent magnet machines, e.g. [1–7]. Although much has been done in this area to date, newer publications show that it is still of significant concern to the designers of permanent magnet machines [7–11]. Among many approaches developed to cope with this problem, the skew of the stator stack sheet pack is the most natural and perhaps, the simplest method of preventing the machine from generating the reluctance-type torques to apply at the design stage [1, 3, 7–11]. In permanent magnet machines, the major task of skew is to get rid of the cogging torque. In all machines, the angle of skew should be selected among values of mechanical angles between 0 and \(2\pi /Q\), where \(Q\) stands for the least number of slots on either stator or rotor side. A basic role of skew should be the cancellation of the most influential slot harmonic of the magnetic field which interacts with the fundamental stator mmf harmonic to produce the reluctance-type torque. An appropriate choice for the angle of skew can be made only after detailed investigation on the magnetic field distribution in the machine air-gap, because a principle of generation of the electromagnetic torque is complex [7].

In this work, the authors show a different point of view on the application of the stack skew in the permanent magnet machines. The difference is in the value of the skew angle used. We developed a simple formula for best skew angle which is different to that used by the majority of designers [1, 3, 5, 7]. This formula results from the analysis of the distribution of the magnetic field harmonics in the motor air-gap, like the other methods, but it gives best angle of skew for the particular motor, and not the minimum one like the other approaches. In the conventional methods, the starting point of the considerations is a skew factor which is a component of winding factor [10, 11]. In the simplest manner, the influence of skew on \(j\)th harmonic of the magnetic flux density is considered the same with an averaging filter:

$$\begin{aligned} B_{{sk}j} =\frac{1}{\alpha _{sk} }\int \limits _{-0.5\alpha _{\mathrm{sk}}}^{+0.5\alpha _{sk} } {B_{nsj} \cos \left( {jp\alpha } \right){\mathrm{d}}\alpha }, \end{aligned}$$
(1)

where \(B_{ns}\) is a magnitude of magnetic flux density in the machine without skew, and \(B_{sk}\) is a magnitude of flux density in the same machine with skew. The skew factor is:

$$\begin{aligned} k_{skj} =\frac{B_{skj}}{B_{nsj}}=\frac{2\sin \frac{jp\alpha _{sk}}{2}}{jp\alpha _{sk}} \end{aligned}$$
(2)

The minimum angle of skew is determined from (2) as to provide zero value of skew factor for the most influential harmonic order. The most common choice for skew angle is \(\alpha _{sk} =\tau \). If this is the case, the most suppressed harmonic would be of order \(Q/p\), because from (2):

$$\begin{aligned} \alpha _{sk} =\frac{2k\pi }{Q},\qquad k=1,2,\ldots n \end{aligned}$$
(3)

for \(k= 1\) is understood as the minimum value, equal to \(\tau \).

In the above formula, the choice of most influential harmonic number is suggested by the mathematical formula without physical considerations on the magnetic field distribution in the motor air-gap. It can be shown that the best angle of skew can be even smaller than that suggested by (3) when the reference quantity of the considerations is the electromagnetic torque not the magnetic flux density. The skew angle given by (3) did not result in total reduction of the cogging torque. A much better value of the skew angle can be deduced in the following way.

Assume a permanent magnet machine at standstill with the number of poles \(2p\) and the number of slots \(Q\). For simplicity, also assume \(Q/p\) being integer. The order of the fundamental harmonic of the cogging torque in all permanent magnet machines (excluding the fractional-slot machines) is the least common multiple of 2 and number of slots divided by number of pole-pairs. In such a case, an obvious choice for skew angle would be angular width of one slot pitch, as it is done in (3). On the other hand, it is well known that the principle of generation of the electromagnetic torque is based on a cross product between all terms of Fourier series expansion of the distributions of radial (\(B_{\mathrm{r}}\)) and tangential (\(B_\psi \)) components of magnetic flux density. This is because an instantaneous value of the electromagnetic torque is in proportion to the product \(B_{\mathrm{r}} \cdot B_\psi \) [7]. This analytical operation results in an infinite sum of products of trigonometric functions. Each such product can be further expanded into a sum of two trigonometric functions of the sum and the difference between their arguments.

Most of the cogging torque produced in permanent magnet machines comes from an interaction of the fundamental flux density harmonic, due to magnets, with the most influential harmonic due to slotting [7]. It is well-known that in machines having integer \(Q/p\) all slot harmonic ordinals are contained in series: \(h \cdot (Q/p)+ 1\), with \(h=\pm 1, \pm 2, \ldots \) An order of the fundamental harmonic of the cogging torque is known. It is always equal to (\(Q/p\)) or, more generally, \(\text{ lcm}\left({2,Q/p} \right)\). Following this principle it can be deduced that it results from interaction between fundamental harmonic of the magnetic field and one of the harmonics having ordinals \(Q/p+1 \left( {\text{ h}=1} \right)\) or \(-Q/p+1\left( {\text{ h}=-1} \right)\). Consequently, to calculate best the angle of skew for the machine with integer-slot type winding, one can use one of the following expressions:

$$\begin{aligned} \alpha _{sk} =\frac{2\pi }{p\cdot \left({\text{ lcm}\left( {2,Q/p} \right)+1} \right)} \end{aligned}$$
(4)

For the case when harmonic \(Q/p+1\) is more influential than harmonic \(-Q/p+1\), and:

$$\begin{aligned} \alpha _{sk} =\frac{2\pi }{p\cdot \left( {\text{ lcm}\left( {2,Q/p} \right)-1} \right)} \end{aligned}$$
(5)

otherwise. It is much more advantageous to use the skew angle calculated from (4) that resulted from (5), not only due to higher skew factor involved. Such a choice is also motivated by the fact that in the surface-mounted machines besides slot harmonics having ordinal \(-Q/p+1\) there is a harmonics due to permanent magnets having the same absolute ordinal, but a reverse sign. In such a situation, the negative slot harmonic will be weakened, whilst the positive one will be strengthened by the field due to permanent magnets. Consequently, Eq. (4) becomes the most appropriate choice for machines with the surface-mounted magnets having integer \(Q/p\).

Table 1 summarizes values of skew angles given by (4) for the most commonly used arrangements of rotor pole-pairs and stator slot numbers.

Table 1 Relative skew angles calculated from (4) referred to slot-pitch width (integer-slot machines)
Full size table

From the results summarized in Table 1, it can be observed that with increasing number of slots the angle of skew approaches the angular width of one slot-pitch, which is the most commonly used by designers. Skewing as a method of cogging torque reduction is usually applied to machines with distributed windings where the unity coil-span and distribution factor can be achieved relatively easily rather than in those with concentrated windings. This is due to the fundamental coil-span factor being less than unity and to the value of fundamental skew factor which has to be significantly smaller.

The skew affects all harmonics of the magnetic flux density, not only the slot harmonics, and the adequate analysis method must be involved to assess the results after application of skew angle resulted from (4). The skew factors resulted from this formula are slightly higher than those resulted from (3), and consequently it is worth investigating how application of new skew angle values influences the overall performance of machine as it may lead to cost-effective solutions. To characterize these effects quantitatively, the authors develop a quasi-3D multi mesh-slice finite element model [12]. An investigation is presented including the model development and the analysis of machine operation under no-load and full-load conditions. Additionally, the analysis of core loss is presented. The results are partially backed by measurements carried out on the laboratory test stand for a prototype outer rotor brushless DC motor, designed for a gearless drive of an electrically powered wheelchair.

2 Laboratory machine

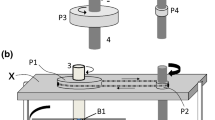
Figure 1a–c depicts the supply system, a stator, and a winding configuration for the motor. The technical specifications are summarized in Table 2. The motor is fed from 24 V batteries via the two-level voltage wave inverter and operates in 120 electrical degree mode of commutation with discrete position sensors.

Fig. 1
figure 1

Permanent magnet brushless DC motor supply system (a), skewed stator (b), relative position of magnet versus stator teeth (c)

Full size image
Table 2 Specifications of the prototype motor
Full size table

3 Motor model for performance analysis

A quasi-3D numerical model for magnetic computation assumes uniform magnetic field distribution along with single two-dimensional submodel (slice) in \(z\) direction [12]. The whole model is composed of \(n_{\mathrm{s}}\) such slices. In case of an outer-rotor configuration, the \(q\)th submodel (see Fig. 2) contains the geometry with stator geometry moved to angular position:

$$\begin{aligned} \alpha _{skq} =\left( {\frac{q-1}{n_{\mathrm{s}} -1}-\frac{1}{2}} \right)\alpha _{sk} \end{aligned}$$
(6)
Fig. 2
figure 2

Skewed stator of an outer rotor permanent magnet motor (a) represented by means of multi-slice model (b)

Full size image

A distribution of two-dimensional magnetic field over \(q\)th submodel is governed by the Ampére’s law [6, 7]:

$$\begin{aligned} \left( {v \frac{\partial ^{2}A}{\partial x^{2}}+v \frac{\partial ^{2}A}{\partial y^{2}}} \right)_q =-\sum _u {\sum _{n=1}^{pQ_s } {\frac{n_{\mathrm{t}} \eta _u \eta _n i_u }{S_n }} } +\left( {\nabla \times \mathbf{H}_c } \right)_{z_{q}} \nonumber \\ \end{aligned}$$
(7)

where subscript \(z\) denotes \(z\)th component of vector product. The equation that describes connection of electric circuits associated with coils of single phase of the motor is:

$$\begin{aligned} v_u =R_u i_u +L_{eu} \frac{{\mathrm{d}}i_u }{{\mathrm{d}}t}+\sum _{q=1}^{n_{\mathrm{s}} } {\left( {\frac{{\mathrm{d}}\lambda _u }{{\mathrm{d}}t}} \right)_q } \end{aligned}$$
(8a)

A distributed winding without parallel paths is assumed. The flux linkages in (8a) are evaluated from:

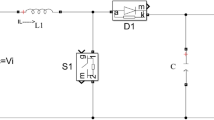
$$\begin{aligned} \lambda _u =\frac{1}{n_{\mathrm{s}} }\sum _{q=1}^{n_{\mathrm{s}} } {\left( {\ell \sum _{n=1}^{2pQ_s } {\frac{n_{\mathrm{t}} \eta _n }{S_{un} }\int \limits _{S_{un} } {A{\mathrm{d}}S} } } \right)}_q \end{aligned}$$
(8b)

The Kirchhoff’s equations of the circuit in Fig. 3 in matrix form are

$$\begin{aligned} \begin{aligned}&{{\varvec{v}}}_b ={{\varvec{Ri}}}_b +{{\varvec{L}}}\frac{\mathrm{d}{{\varvec{i}}}_b}{\mathrm{dt}}+{{\varvec{k}}}_1 \frac{\mathrm{d}}{\mathrm{dt}}\varvec{\lambda } +{{\varvec{k}}}_2 u_{cf}\\&0=C_f \frac{{\mathrm{d}u}_{Cf} }{\mathrm{dt}}+{{\varvec{k}}}_2^T {{\varvec{i}}}_b \end{aligned} \end{aligned}$$
(9)

Matrix \({\varvec{k}}_1\) links phase linkage fluxes and vector \({\varvec{k}}_2\) links the capacitor voltage with appropriate branches of the electric circuit. Using a standard approximation for magnetic vector potential i.e. \(A\approx \sum _{i=1}^3 {N_i \varphi _i}\), first-order triangular elements and the Galerkin weighted residual approach [13–15] equation (6) is written in the discrete form:

$$\begin{aligned}&v \int \limits _{\Omega _q } {\left( {\nabla N_i \cdot \nabla N_j } \right)} \varphi _i {\mathrm{d}}\Omega =\sum _u {\sum _{n=1}^{2pQ_s } {\frac{n_t \eta _u \eta _n i_u }{S_n }} } \nonumber \\&\quad \times \int \limits _{\Omega _q } {N_i {\mathrm{d}}\Omega } +\cdots +\int \limits _{\Omega _q } {\left( {H_{cx} \frac{\partial N_i }{\partial y}-H_{cy} \frac{\partial N_i }{\partial x}} \right)} {\mathrm{d}}S \end{aligned}$$
(10)

Consequently, the vector of phase linkage fluxes is written as:

$$\begin{aligned} \lambda _u =\sum _{q=1}^{N_{\mathrm{s}} } {\left( {\frac{\ell n_{\mathrm{t}} }{n_{\mathrm{s}} }\sum _{n=1}^{2pQ_s } {\frac{\eta _n }{S_n }\int \limits _{S_n } {\sum _{i=1}^3 {N_i \varphi _i } {\mathrm{d}}S} } } \right)} _q \end{aligned}$$
(11)

or in the more general form:

$$\begin{aligned} {\varvec{\lambda }}={{\varvec{D}}}{\varvec{\varphi }}, \end{aligned}$$
(12)

where \({{\varvec{D}}}\!=\![{{{\varvec{D}}}_1,{{\varvec{D}}}_2,{{\varvec{D}}}_q ,\ldots , {{\varvec{D}}}_{n_{\mathrm{s}}}} ],{\varvec{\varphi }}\!=\![ {\varvec{\varphi }}_1,{\varvec{\varphi }}_2 ,{\varvec{\varphi }}_{q,} \ldots ,\) \({\varvec{\varphi }}_{n_{\mathrm{s}} } ]^{T} \) and \(D_{qij} \!=\!\delta _j \frac{\ell n_t \eta _n \eta _u }{S_n N_{\mathrm{s}} }\int \nolimits _{\Omega _q} {N_i d\Omega }, \delta _j \!=\!\left\{ {\begin{array}{l@{\quad }l} 0&\text{ if}\,\eta _u \ne 0 \\ 1&\text{ otherwise} \\ \end{array}}\right.\). Using loop analysis method for an electric circuit in Fig. 3, and considering (9) and (12), one obtains:

$$\begin{aligned} \begin{aligned}&{{\varvec{k}}}_l^T {{\varvec{u}}}_s ={{\varvec{k}}}_l^T {{\varvec{Rk}}}_l {{\varvec{i}}}_l +{{\varvec{k}}}_l^T {{\varvec{Lk}}}_l \frac{\mathrm{d}{{\varvec{i}}}_l}{\mathrm{d}t}+{{\varvec{k}}}_l^T {{\varvec{k}}}_1 \frac{\mathrm{d}}{\mathrm{d}t}{{\varvec{D}}}{\varvec{\varphi }}+{{\varvec{k}}}_l^T {{\varvec{k}}}_2 u_{cf} \\&0=C_f \frac{\mathrm{d}u_{cf} }{\mathrm{d}t}+{{\varvec{k}}}_2^T {{\varvec{k}}}_l {{\varvec{i}}}_l, \end{aligned} \end{aligned}$$
(13)

where \({{\varvec{k}}}_{l}\) is a loop matrix which transforms the circuit branch currents into a vector of loop currents \({{\varvec{i}}}_{l}\). Using backward Euler formula [13] for approximation of time-derivatives in (12) results in the time-stepping system of field and circuit equations:

$$\begin{aligned}&\left[ {{\begin{array}{ccc} {{\varvec{S}}}&{-{{\varvec{D}}}^{T}{{\varvec{k}}}_1^T {{\varvec{k}}}_l^T \ell ^{-1}}&{{\varvec{0}}}\\ \\ {\frac{{{\varvec{k}}}_l^T {{\varvec{k}}}_1 {{\varvec{D}}}}{\varDelta t}}&{{{\varvec{k}}}_l^T \left( {{{\varvec{R}}}+\frac{1}{\varDelta t}{{\varvec{L}}}} \right){{\varvec{k}}}_l }&{{{\varvec{k}}}_l^T {{\varvec{k}}}_2 } \\ \\ 0&{{{\varvec{k}}}_2^T {{\varvec{k}}}_l }&{\frac{C_f }{\varDelta t}} \\ \end{array} }} \right]_t \left[ {{\begin{array}{c} {\varvec{\varphi }} \\ \\ {{{\varvec{i}}}_l } \\ \\ {u_{Cf} } \\ \end{array} }} \right]_t\nonumber \\&\quad =\left[ {{\begin{array}{c} {\varvec{\varTheta }} \\ \\ {{\varvec{k}}}_l^T {{\varvec{v}}}_b -{{\varvec{k}}}_l^T \left( {{{\varvec{R}}}-\frac{1}{\varDelta t}{{\varvec{L}}}} \right){{\varvec{k}}}_l {{\varvec{i}}}_l \\ \\ {\frac{C_f }{\varDelta t}u_{Cf} } \\ \end{array} }} \right]_{t-\varDelta t}, \end{aligned}$$
(14)

where \({{\varvec{S}}}\!=\!\text{ diag}[{{{\varvec{S}}}_1 ,{{\varvec{S}}}_2,{{\varvec{S}}}_q,\ldots ,{{\varvec{S}}}_{n_{\mathrm{s}} } } ]\), \({\varTheta }\!=\![ {\varvec{\varTheta }}_1 ,{\varvec{\varTheta }}_2,{\varvec{\Theta }}_q \ldots ,\) \({\varvec{\varTheta }}_{n_{\mathrm{s}} } ]^{T}\), \(S_{qij} =v \int \nolimits _{\Omega _q } {\nabla N_i \cdot \nabla N_j d\Omega }, \varTheta _{qi} =\int \nolimits _{\Omega _q } \left( H_{cx} \frac{\partial N_i }{\partial y}-\right.\) \(\left.H_{cy} \frac{\partial N_i }{\partial x} \right)d\varOmega \).

Fig. 3
figure 3

Circuit model of a voltage waveinverter

Full size image

The transistor switches S1–S6 are modeled as two-state resistance elements, whilst the diodes as nonlinear voltage-dependent current sources considering rudimentary static characteristics. In this way, the model allows to estimate overall efficiency of the drive including inverter power loss.

The electromagnetic torque of a motor is calculated from the Maxwell stress tensor. The modeling of rotor movement by means of elements distortion and permutation of node numbers in the machine air-gap allows for computation of time variations of phase currents, voltages and torque. Such a model provides a transient solution. If he constant rotor speed is assumed, the steady-state solution is obtained after a few periods of phase current from the beginning of computations. From the steady-state waveforms the rms and average values can be computed to provide information on power balance and losses.

4 Analysis and results

4.1 Validation of the model

The model was subdivided into seven mesh-slices in axial (\(z\)) direction. By several numerical experiments it has been confirmed that such an approximation of skew is sufficiently accurate from computational point of view. The distribution of magnetic flux over whole machine in steady-state no-load operation is shown in Fig. 4.

Fig. 4
figure 4

Magnetic flux distribution over multi mesh-slice motor model under no-load conditions considering symmetry with respect to one pole-pair

Full size image

Figure 5a–d compares waveforms of phase current and phase-to-phase voltage at full-load conditions. The measured torque at the same point of operation was equal to 8.85 Nm, and the computed average torque was equal to 9.4 Nm, which considering the undetermined mechanical power loss, is very close to measurements. An agreement between the computed values of phase current, voltage and torque confirms the adequacy of the elaborated numerical model.

Fig. 5
figure 5

Waveforms of phase current (a, b), and line-to-line voltages (c, d) at rotor speed of 170.4 rpm and supply voltage of 24.4 V: computations (a, c), measurement results (b, d)

Full size image

To support the theoretical consideration on the choice of skew angle based on (4) instead of (5), an additional calculation was carried out. A two-dimensional (space and time) Fourier decomposition for radial (\(B_\mathrm{r}\)) and tangential (\(B_\psi \)) component of an air-gap magnetic flux density is carried out as the rotor rotates at no-load. The results limited to first 20 harmonics are shown in Fig. 6.

Fig. 6
figure 6

Two-dimensional harmonic spectra of components of an air-gap flux density: a, b normal and tangential component for pole width-to-pole-pitch equal to 0.778, c, d normal and tangential component for pole width-to-pole-pitch equal to 0.6, e, f normal and tangential component for pole width-to-pole-pitch equal to 0.9

Full size image

In the analysis the three lot-fill factors are considered. A first case (Fig. 6a, b) refers to the machine with specifications given in Table 2, with the slot fill factor equal to 0.778. The two remaining cases are referred to the machines having slot-fill factors equal to 0.6 and 0.9 (see Fig. 6c, d and Fig 6e, f, respectively). Owing to the fact that the torque is in proportion to a product \(B_\mathrm{r} B_\psi \), it can be seen in all figures that the most influential is harmonic \(Q/p+1\) (equal here to 7) with no matter what the slot-fill factor is. This confirms that Eq. (4) is the best choice to calculate the skew angle for such a motor.

4.2 Operation at no-load conditions

As it can be observed in Fig. 1b, c, the stator sheet stack of the physical motor is skewed by one slot pitch. From the analysis carried out in the introductory section, it is clear that a relative skew for the considered motor is 0.857 of slot-pitch width (see Table 1). To examine the effect of this change, the calculations were performed for different cases. From the results of calculations, which are exposed in Fig. 7, it can be noticed that skewing the stator by angle calculated from (4) reduces cogging torque much better than skewing it by one slot-pitch. The cogging torque reduction is nearly total.

Fig. 7
figure 7

Cogging torque calculated for two different skew angles and for the motor without skew

Full size image

The skew by one slot pitch gives the value of fundamental skew factor of 0.955, whilst the second option gives \(k_{sk1}\) equal to 0.967. In the considered motor, the fundamental winding factor is equal to the skew factor due to unity fundamental coil-span and distribution factors.

Figure 8 compares computed waveforms of phase back emf. A smaller skew angle results in more trapezoidal waveforms of back emf rather than in meaningful rise in magnitude. Because a reduction of the cogging torque is very high, it will be potentially useful to expand the width of magnet pole to full pole-pitch. This makes the waveform of phase back emf better, nearly trapezoidal shape.

Fig. 8
figure 8

Waveforms of phase back emf calculated for two different skew angles and for motor without skew at rotational speed of 170.4 rpm

Full size image

Expansion of the pole width in the latter to the length of the pole-pitch results in drop of efficiency from 82 to 81.1 % (see Fig. 9), which is due to higher value of the core loss. As it was already mentioned, the above values of motor efficiency were calculated taking into account the inverter power loss. Variations of instantaneous core loss for the same conditions of operation are shown in Fig. 10. Averaging the waveforms in time gives the value of 1.92 W for the motor without a skewed stator and, respectively, 1.66 and 1.65 W for the two remaining motor versions.

Fig. 9
figure 9

Efficiency (a), and core loss (b) versus output power at supply voltage of 24.4 V

Full size image
Fig. 10
figure 10

Variations of core loss versus time for different skew angles at rotor speed of 170.4 rpm and supply voltage of 24.4 V

Full size image

Expansion of pole width causes a rise in core loss to 1.90 W, which is due to the higher rms value of magnetic flux density in the motor air-gap as compared to other motor versions. Also from this point of view, it is better to keep the ratio of pole width to the pole-pitch at a typical value of approximately 0.8 rather than increase it to unity. An obvious effect of skewing is a reduced pulsation of the electromagnetic torque. From the results of instantaneous electromagnetic torque computations plotted in Fig. 11, it is clear that the skew angle calculated from Eq. (4) provides the smallest torque pulsations which are practically due only to commutation effects.

Fig. 11
figure 11

Variations of electromagnetic torque vs. time for different skew options at constant rotor speed of 170.4 rpm and supply voltage of 24.4 V

Full size image

A side effect of skewing is a reduction of the magnitude of axial component of current density by the factor of sec \(\alpha _{sk}\) which can be considered favorable in applications, where the demagnetization effects are particularly important.

5 Conclusions

Theoretical considerations and computations using a quasi-3D multi mesh-slice finite element model show that the best angle of skew of the sheet pack for the three-phase integer-slot permanent magnet machine with the surface-mounted magnets can be determined from a simple analytic formula. Application of a skew angle determined in such a way a very high reduction of electromagnetic torque pulsations caused by the angular variation of the equivalent magnetic reluctance of an air-gap.

The results of analysis have led to a few useful conclusions, but it is worth noting that these are based merely on a numerical experiment. The possibility of accomplishment of such an effect in a real machine is the matter of accuracy in the manufacturing process. This is because sensitivity of the magnitude of the cogging torque to the variation of the skew angle is very high.

Because an amplitude of the fundamental harmonic of the cogging torque is in proportion to the product of magnitudes of the two most important harmonics of magnetic flux density, which were identified in the preceding sections, it is possible to estimate the amplitudes of the cogging torque in skewed motor (\(T_{esk}\)) related to that in the motor without a skew (\(T_{ens}\)) as:

$$\begin{aligned} \frac{T_{esk} }{T_{ens} }\ge k_{sk1} k_{sk\,\left( {\text{ lcm}\left( {2,Q/p} \right)+1} \right)} \end{aligned}$$
(15)

Using the specifications of the machine considered and (15), it can be shown that discrepancy in a skew angle by 5 % from value given by (4) is responsible for the cogging torque magnitude, which is at least 16 % of that in the motor without a skew. This prediction agrees with the results presented in Fig. 7.

The results presented were obtained for a fractional power machine due to limitations of laboratory facilities but these should be addressed particularly to larger machines where the problem of reduction of core loss and mechanical vibrations is crucial.