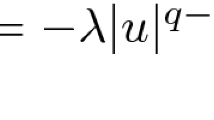Abstract
For Ξ∈R n,t∈R andf∈S(R n) define\(\left( {S^2 f} \right)\left( t \right)\left( \xi \right) = \exp \left( {it\left| \xi \right|^2 } \right)\hat f\left( \xi \right)\). We determine the optimal regularitys 0 such that
holds whereC is independent off∈S(R n) or we show that such optimal regularity does not exist. This problem has been treated earlier, e.g. by Ben-Artzi and Klainerman [2], Kato and Yajima [4], Simon [6], Vega [9] and Wang [11].
Our theorems can be generalized to the case where the exp(it|ξ|2) is replaced by exp(it|ξ|a),a≠2.
The proof uses Parseval's formula onR, orthogonality arguments arising from decomposingL 2(R n) using spherical harmonics and a uniform estimate for Bessel functions. Homogeneity arguments are used to show that results are sharp with respect to regularity.
Similar content being viewed by others
References
Ben-Artzi, M. andDevinatz, A., Local smoothing and convergence properties of Schrödinger type equations,J. Funct. Anal. 101 (1991), 231–254.
Ben-Artzi, M. andKlainerman, S., Decay and regularity for the Schrödinger equation,J. Anal. Math. 58 (1992), 25–37.
Hörmander, L.,The Analysis of Linear Partial Differential Operators I, 2nd ed., Springer-Verlag, Berlin-Heidelberg-New York, 1990.
Kato, T. andYajima, K., Some examples of smooth operators and the associated smoothing effect,Rev. Math. Phys. 1 (1989), 481–496.
Kenig, C. E., Ponce, G. andVega, L., Oscillatory integrals and regularity of dispersive equations,Indiana Univ. Math. J. 40 (1991), 33–69.
Simon, B., Best constants in come operator smoothness estimates,J. Funct. Anal. 107 (1992), 66–71.
Sjölin, P., Regularity of solutions to the Schrödinger equation,Duke Math. J. 55 (1987), 699–715.
Stein, E. M. andWeiss, G.,Introduction to Fourier Analysis on Euclidean Spaces, Princeton Univ. Press, Princeton, N. J., 1971.
Vega, L., Schrödinger equations: pointwise convergence to the initial data,Proc. Amer. Math. Soc. 102 (1988), 874–878.
Walther, B. G., Maximal estimates for oscillatory integrals with concave phase, inHarmonic Analysis and Operator Theory (Marcantognini, A. M., Mendoza, G. A., Morán, M. D., Octavio, A., and Urbina, W. O., eds.), Contemp. Math.189, pp. 485–495, Amer. Math. Soc., Providence, R. I., 1995.
Wang, S. L., On the weighted estimate of the solution associated with the Schrödinger equation,Proc. Amer. Math. Soc. 113 (1991), 87–92.
Author information
Authors and Affiliations
Additional information
Part of this research was carried out in July 1994 when I enjoyed a stay at Johannes Kepler Universität, Linz. I would like to thank Jim Cooper, Eva Matoušková, Paul Müller, Charles Stegall, Michael Schmuckenschläger and Renata Mühlbachler for having created a stimulating and friendly atmosphere in the functional analysis group at Linz. I would also like to thank Professor Per Sjölin for valuable comments and for encouraging me to carry out the investigation presented here, Professor Krzysztof Stempak, Uniwersytet Wrocławski, Wrocław for help regarding improvements of the presentation and the referee for comments and criticism.
Rights and permissions
About this article
Cite this article
Walther, B.G. A sharp weightedL 2-estimate for the solution to the time-dependent Schrödinger equation. Ark. Mat. 37, 381–393 (1999). https://doi.org/10.1007/BF02412222
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02412222