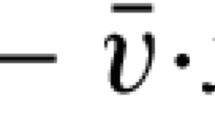Abstract
A primal–dual decomposition method is presented to solve the separable convex programming problem. Convergence to a solution and Lagrange multiplier vector occurs from an arbitrary starting point. The method is equivalent to the proximal point algorithm applied to a certain maximal monotone multifunction. In the nonseparable case, it specializes to a known method, the proximal method of multipliers. Conditions are provided which guarantee linear convergence.
Similar content being viewed by others
References
K.J. Arrow and L. Hurwicz, “Decentralization and computation in resource allocation”, in: R.W. Pfouts, ed.,Essays in economics and econometrics, University of North Carolina Press, Chapel Hill, N.C.; also in K.J. Arrow and L. Hurwicz, eds.,Studies in resource allocation processes (Cambridge University Press, 1977).
D.P. Bertsekas, “Convexification procedures and decomposition methods for nonconvex optimization problems”,Journal of Optimization Theory and Applications 29 (1979), 169–197.
G. Cohen, “Optimization by decomposition and coordination: A unified approach”, IEEE Transactions on Automatic Control, Vol. AC-23 (1978) 222–232.
G. Cohen, “Auxiliary problem principle and decomposition of optimization problems”,Journal of Optimization Theory and Applications 32 (1980) 277–305.
G.B. Dantzig and P. Wolfe, “Decomposition principle for linear programs”,Operations Research 8 (1960) 101–111.
G.B. Dantzig,Linear programming and extensions (Princeton University Press, Princeton, NJ, 1963).
I. Ekeland and R. Temam, Convex analysis and variational problems (North-Holland, 1976).
H. Everett, “Generalized Lagrange multiplier method for solving problems of optimum allocation of resources”,Operations Research 11 (1963) 399–417.
A.V. Fiacco, “Sensitivity analysis for nonlinear programming using penalty methods”,Mathematical Programming 10 (1976) 287–311.
W. Findeisen, F.N. Bailey, M. Brdyś, K. Malinowski, P. Tatjewski and A. Woźniak,Control and coordination in hierarchical systems (John Wiley & Sons, 1980).
M. Fortin and R. Glowinski, “On decomposition-coordination methods using an augmented Lagrangian”, in: M. Fortin and R. Glowinski, eds.,Augmented Lagrangian methods: Applications to the numerical solution of boundary-value problems, Studies in Mathematics and its Applications 15 (North-Holland, 1983).
M. Frank and P. Wolfe, “An algorithm for quadratic programming”,Naval Research Logistics Quarterly 3 (1956) 95–110.
D. Gabay and B. Mercier, “A dual algorithm for the solution of nonlinear variational problems via finite element approximation”,Computers and Mathematics with Applications 2 (1976) 17–40.
D. Gabay, “Applications of the method of multipliers to variational inequalities”, in: M. Fortin and R. Glowinski, eds.,Augmented Lagrangian methods: Applications to the numerical solution of boundary-value problems (North-Holland, Amsterdam, 1983).
A.M. Geoffrion, “Primal resource-directive approaches for optimizing nonlinear decomposable systems”,Operations Research 18 (1970) 375–403.
A. Geoffrion, “Large-scale linear and nonlinear programming”, in: D.A. Wismer, ed.,Optimization methods for large-scale systems with applications (McGraw-Hill, New York, 1971).
M.R. Hestenes, “Multiplier and gradient methods”,Journal of Optimization Theory and Applications (1969) 303–320.
L.S. Lasdon,Optimization theory for large systems (Macmillan, Toronto 1970).
L.S. Lasdon, “Decomposition in resource allocation”, in: D.M. Himmelblau, ed.,Decomposition of large-scale problems (North-Holland, 1973) 207–231.
F.J.R. Luque, “Asymptotic convergence analysis of the proximal point algorithm”,SIAM Journal of Control and Optimization 22 (1984) 277–293.
B. Martinet, “Determination approchée d'un point fixe d'une application pseudo-contractante. Cas de l'application prox”,Comptes Rendus des Séances de l'Académie des Sciences, Série A 274 (1972) 163–165.
G.J. Minty, “Monotone (nonlinear) operators in Hilbert space”,Duke Mathematical Journal 29 (1962) 341–346.
M.J.D. Powell, “A method for nonlinear constraints in minimization problems”, in: R. Fletcher, ed.,Optimization (Academic Press, NY, 1969) 283–298.
S.M. Robinson, “Perturbed Kuhn-Tucker points and rates of convergence for a class of nonlinear programming problems”,Mathematical Programming 7 (1974) 1–16.
R.T. Rockafellar, “On the maximal monotonicity of subdifferential mappings”,Pacific Journal of Mathematics 33 (1970) 209–216.
R.T. Rockafellar,Convex analysis (Princeton University Press, Princeton, N.J. 1970).
R.T. Rockafellar, “The multiplier method of Hestenes and Powell applied to convex programming”,Journal of Optimization Theory and Applications 12 (1973) 555–562.
R.T. Rockafellar, “Augmented Lagrangians and applications of the proximal point algorithm in convex programming”,Mathematics of Operations Research 1 (1976) 97–116.
R.T. Rockafellar, “Monotone operators and the proximal point algorithm”,SIAM Journal on Control and Optimization 14 (1976) 877–898.
R.T. Rockafellar, “Monotone operators and augmented Lagrangian methods in nonlinear programming”, in: O.L. Mangasarian et al., eds.,Nonlinear Programming ·3 (Academic Press, NY, 1978) 21–25.
R.T. Rockafellar, “Solving a nonlinear program by way of a dual problem”,Symposia Mathematica 19 (1976) 135–160.
J.E. Spingarn, “Fixed and variable constraints in sensitivity analysis”, SIAM Journal on Control and Optimization 18 (1980) 297–310.
J.E. Spingarn, “A proximal algorithm for decomposable convex programming”, summary abstract of this paper in Abstracts of the American Mathematical Society 6, October 1982.
J.E. Spingarn, “Partial inverse of a monotone operator”,Applied Mathematics and Optimization 10 (1983) 247–265.
J.E. Spingarn, “A primal-dual projection method for solving systems of linear inequalities”,Linear Algebra and its Applications 65 (1985) 45–62.
J.E. Spingarn, “A projection method for least square solutions to overdetermined systems of linear inequalities”, to appear.
G. Stephanopoulos and W. Westerberg, “The use of Hestenes' method of multipliers to resolve dual gaps in engineering system optimization”,Journal of Optimization Theory and Applications 15 (1975) 285–309.
H. Uzawa, “Iterative methods for concave programming”, in: K. Arrow, L. Hurwicz, and H. Uzawa, eds.,Studies in Linear and Nonlinear Programming (Stanford University Press, Stanford, Ca, 1958).
N. Watanabe, Y. Nishimura and M. Matsubara, “Decomposition in large system optimization using the method of multipliers”,Journal of Optimization Theory and Applications 25 (1978) 181–193.
Author information
Authors and Affiliations
Additional information
This research was sponsored, in part, by the Air Force Office of Scientific Research under grant 80-0195.
Rights and permissions
About this article
Cite this article
Spingarn, J.E. Applications of the method of partial inverses to convex programming: Decomposition. Mathematical Programming 32, 199–223 (1985). https://doi.org/10.1007/BF01586091
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01586091