Abstract
Weighted essentially non-oscillatory (WENO) schemes are a class of high-order shock capturing schemes which have been designed and applied to solve many fluid dynamics problems to study the detailed flow structures and their evolutions. However, like many other high-order shock capturing schemes, WENO schemes also suffer from the problem that it can not easily converge to a steady state solution if there is a strong shock wave. This is a long-standing difficulty for high-order shock capturing schemes. In recent years, this non-convergence problem has been studied extensively for WENO schemes. Numerical tests show that the key reason of the non-convergence to steady state is the slight post shock oscillations, which are at the small local truncation error level but prevent the residue to settle down to machine zero. Several strategies have been proposed to reduce these slight post shock oscillations, including the design of new smoothness indicators for the fifth-order WENO scheme, the development of a high-order weighted interpolation in the procedure of the local characteristic projection for WENO schemes of higher order of accuracy, and the design of a new type of WENO schemes. With these strategies, the convergence to steady states is improved significantly. Moreover, the strategies are applicable to other types of weighted schemes. In this paper, we give a brief review on the topic of convergence to steady state solutions for WENO schemes applied to Euler equations.
Similar content being viewed by others
1 Introduction
Over the past few decades, computational fluid dynamics (CFD) has become an important tool to study flow structures and aerodynamic forces through solving the compressible Euler or Navier-Stokes equations. Steady states are common in aerodynamics in which the non-viscous flow fields are governed by the following Euler equations:
where U is the vector of the conserved variables, Fi(U) is the nonlinear flux function in the i-th direction, and d is the spatial dimension. Among numerous methods to obtain a numerical solution of (1), one possible choice is to solve the following unsteady Euler equations by a time marching method:
When the time derivative or the residue of the unsteady Euler Eq. (2) becomes small enough (ideally at or close to machine zero), a numerical solution of the steady state Eq. (1) is obtained.
Shock waves are a key structure of supersonic flows. Across a shock wave, the physical variables are discontinuous. In the history of CFD, the design of numerical schemes that can capture shock waves well has been a tough problem. Many classical numerical schemes would produce severe spurious oscillations near shock waves. To eliminate or reduce such severe spurious oscillations, shock capturing schemes were carefully designed. The most popular shock capturing schemes include total variation diminishing (TVD) schemes [1], essentially non-oscillatory (ENO) schemes [2–4], and weighted ENO (WENO) schemes [5–7]. The TVD schemes were proposed by Harten [1]. Through the application of suitable limiters, TVD schemes can achieve the total variation diminishing property, which makes it very popular in the simulation of supersonic flows including strong shock waves. The non-oscillatory and no-free-parameter dissipation (NND) difference scheme, proposed by Zhang et al. [8–10], is a special type of TVD schemes. Through analyzing the evolution of the numerical error for Navier-Stokes equations, Zhang [8] found the relationship between the coefficients of the modified equation and the spurious oscillation at both sides of the shock waves. Then, he proposed the NND scheme through controlling the oscillation around the shock waves by a limiter. It was proved that the NND scheme has the TVD property [9]. However, all TVD schemes degenerate to first-order accuracy near smooth extrema due to the application of the TVD limiters [11].
ENO schemes are a type of high-order shock capturing schemes that was proposed by Harten et al. [2]. Instead of using a fixed stencil to reconstruct the numerical fluxes, the locally smoothest stencil among several candidates is used in ENO schemes. The smoothness of a stencil is measured by the corresponding divided differences. The ENO scheme has the property of being self similar and parameter-free, uniformly high-order accurate and very robust with essentially no oscillations near shock waves. However, there are still several drawbacks that can be improved. For example, the stencil might be changed even by a round-off error perturbation near zeroes of the solution and its derivatives. This may result in a loss of accuracy of the scheme when it is applied to a hyperbolic PDE. In the process of choosing the stencil, several candidate stencils are considered, but only one of them, the so called smoothest stencil in some sense, is actually used in the reconstruction of the numerical flux. This means that ENO schemes could not achieve the optimal accuracy order associated with the combined set of all the cells considered in the selection.
WENO schemes [5–7] are an extension of the ENO schemes. Instead of using only the smoothest stencil, a WENO scheme uses all candidate stencils through a convex combination to approximate the fluxes. The accuracy is improved to the optimal order in smooth regions while the essentially non-oscillatory property near discontinuities is maintained. WENO schemes have been extensively applied in many areas including CFD.
However, almost all high-order shock capturing schemes suffer from the problem that they can not easily converge to steady state solutions for compressible flow if there is a strong shock wave. To be more specific, in terms of the measurement of convergence, the residue can not settle down to a satisfactory value (ideally machine zero) but would hang at a relatively high local truncation error level. The reason is that there are slight spurious oscillations in the neighborhood region of the shock waves. For TVD schemes, because of the use of limiters, the numerical fluxes of the TVD schemes are less smooth. This makes them difficult to converge to steady states. In ENO schemes, the numerical flux is not smooth either when the stencil pattern changes at neighboring points, causing difficulty in convergence to steady states as well. Even though the numerical flux of WENO schemes is smoother than that of ENO schemes, the WENO schemes could also suffer from the same problem, especially for multi-dimensional flows with strong shocks.
In recent years, the issue of the lack of convergence to steady state solutions for WENO schemes is studied extensively [12–15]. In [15], Zhang and Shu studied the mechanism of the non-convergence of the fifth-order WENO scheme, and found that there is a relationship between the smoothness indicators and the post-shock oscillations. A new smoothness indicator was proposed for the fifth-order WENO scheme. With this new smoothness indicator, the residue can settle down to machine zero for many test problems. In [13], Zhang et al. studied the non-convergence of WENO schemes of higher orders of accuracy. They found that there is some relationship between the local characteristic projection and the appearance of post shock oscillations. A high-order upwind-biased weighted interpolation is proposed to obtain the physical values in the middle of two grid points when computing the Jacobian matrix and its eigenvectors during the local characteristic projection. These strategies can be applied to other types of weighted schemes as well [12, 14]. In more recent years, Zhu et al. [16–22] proposed new types of WENO schemes with the application of a series of unequal-sized spatial stencils. Such new WENO schemes have very nice convergence property to steady state solutions.
In this paper, we give a brief review on the convergence to steady state solutions of WENO schemes. The paper is organized as follows. In Section 2, we give an overview of the WENO methodology. The mechanism of non-convergence of WENO schemes to steady state solutions is explained in Section 3. Two techniques to improve the convergence property of WENO schemes are presented in Section 4. Section 5 describes the application of these techniques for improving steady state convergence to other types of weighted schemes including the fast sweeping WENO schemes and weighted compact schemes. Section 6 describes the new type of WENO schemes proposed by Zhu et al. [16, 19], emphasizing its nice property in steady state convergence. Section 7 contains our perspectives and discussions on the problem of steady state convergence for high-order WENO schemes.
2 Methodology of the WENO schemes
In this section, we give a brief overview of the finite difference WENO schemes including the numerical fluxes, the smoothness indicators, and the discretization of the time derivative.
2.1 Numerical fluxes of the WENO schemes
We use the one-dimensional scalar conservative law
as an example to explain the reconstruction of the numerical fluxes for finite difference WENO schemes. In general, the physical flux f(u) can be split into two parts, either globally or locally,
where, \(\frac {df^{+}(u)}{du} \geq 0\) and \(\frac {df^{-}(u)}{du} \leq 0\). The Lax-Friedrichs flux splitting is the simplest and commonly used flux splitting method, which is given by
where α= max|f′(u)| with the maximum taken over some relevant range of u.
For simplicity, we assume f′(u)≥0 in (3) to show the WENO procedure for approximating the flux f+(u). The formulae for the approximation of f−(u) are symmetric with respect to the middle point \(x_{i+\frac {1}{2}}\). The computational domain [xL,xR] is divided to a uniform mesh of △x=xj+1−xj=const.
For finite difference WENO schemes, the spatial derivative f(u)x at the point x=xi in (3) is approximated by a conservative finite difference formula
where the numerical flux \(\hat {f}_{i+\frac {1}{2}}\) approximates \(h_{i+\frac {1}{2}}\) to high-order accuracy, with h(x) defined by Shu and Osher in [4] through the indirect requirement
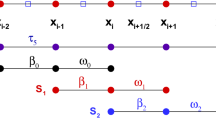
In a (2r−1)-point upwind-biased stencil S2r−1={xi−r+1,...,xi+r−1} for the middle point \(x_{i+\frac {1}{2}}\), a (2r−1)-th order numerical flux can be reconstructed as follows:
The big stencil S2r−1 can be divided into r sub-stencils
In each of these sub-stencils, an r-th order reconstruction can be obtained
where
Here, \(a^{r}_{k,l}, \,\, 0\leq k,l\leq r-1\), are constant coefficients.
Using these r sub-stencils as candidates, the ENO scheme chooses the smoothest sub-stencil to approximate the flux. The obtained numerical flux is only r-th order accurate which is given by (9) with the chosen k. In fact, if all of these sub-stencils are used, the numerical flux can achieve the optimal accuracy order 2r−1, which is given by (8). Through simple derivation, one can find that q2r−1 can also be obtained by a linear combination of \(\hat {f}^{(k)}_{i+\frac {1}{2}}\)
Here \(d_{k}=d_{k}^{r} (k=0,..,r-1)\) are constant coefficients, which are called the linear weights. The formula (10) is the same as the formula (8). It results in a linear scheme, which can not be used to compute the flow field with strong discontinuities. Through introducing the nonlinear weights ωk (k=0,...,r−1) to replace the linear weights, Liu et al. [7] proposed the WENO scheme with the numerical flux as follows:
The nonlinear weights ωk are defined by
where
Here ε is a small positive number which is introduced to avoid the denominator to become zero and p is an empirical parameter. Usually we take ε=10−6 and p=2. ISk is the smoothness indicator to measure the smoothness of the flux function in the k-th sub-stencil. The smoothness indicator is not unique. The choice of the smoothness indicator can have influence over the accuracy and the convergence towards the steady state [6, 7, 15, 23]. WENO schemes can achieve optimal order of accuracy in smooth regions while the essentially non-oscillatory property is maintained in the region near discontinuities. In [7], Liu et al. used the undivided differences to compute the smoothness indicator
Here f[j,l] are the l-th order undivided differences:
Using this smoothness indicator, the accuracy order of the WENO scheme is only r+1, not the optimal 2r−1. Jiang and Shu [6] introduced the following smoothness indicator:
where fk(x) is the reconstruction polynomial based on the sub-stencil \(S^{2r-1}_{k}\). With this smoothness indicator, the WENO scheme can achieve the optimal accuracy order.
a. The fifth-order WENO scheme
The fifth-order WENO scheme (r=3) has been applied most extensively (among all WENO schemes) in the computation of aerodynamics and in scientific computation of many other areas after it was developed by Jiang and Shu [6]. The three third-order numerical fluxes in the three sub-stencils are
The linear weights are
and the smoothness indicators are
Henrick et al. [23] noticed that the WENO scheme with the smoothness indicator (19) may lose accuracy at certain smooth extrema. To recover the accuracy order at these smooth extrema, they introduced a mapping function:
where dk∈(0,1] and k=0,1,2. The function gk(ω) is monotonically increasing with a finite slope and gk(0)=0, gk(1)=1, gk(dk)=dk, gk′(dk)=0, and gk″(dk)=0. The mapped weights are given by:
where ωk are computed by (12) and (19). This mapped WENO scheme can improve accuracy at smooth extrema. We refer to [23] for more details.
b. Seventh-order WENO scheme
In the case of r=4, the seventh-order WENO scheme was obtained by Balsara and Shu [5]. The four fourth-order numerical fluxes from the four sub-stencils are
The linear weights are given by
and the smoothness indicators are
2.2 Local characteristic decomposition for conservative law systems
In the previous subsection, we have described the WENO procedure for obtaining numerical fluxes for finite difference WENO schemes for solving scalar conservation laws. For Euler equations or other systems of conservation laws, the numerical fluxes are often reconstructed in the local characteristic fields, which makes the scheme more robust to capture strong shock waves or other discontinuities.
The procedure of the local characteristic projection may be confusing, hence we will use the one-dimensional Euler equations to show its details. The 1-D Euler equations have the following form:
where the conservative variable U has the form U=(ρ,ρu,E)T. F(U)=(ρu,ρu2+p,u(E+p))T is the flux, and ρ, u, p, and E are the density, velocity, pressure, and the total energy, respectively. The pressure is related to the total energy by the equation of states \(E=\frac {p}{\gamma -1} + \frac {1}{2} \rho u^{2} \) for the ideal gas.
Let \(A=\frac {\partial F}{\partial U}\) be the Jacobian matrix. The rows of the matrix L are the left eigenvectors of A, while the columns of the matrix R are the right eigenvectors of A. D is the diagonal matrix containing the eigenvalues of A. Then L=R−1, and
The procedure to reconstruct the WENO flux in the characteristic fields consists of the following steps:
Step 1.1: Compute L and R, the matrices of the left and right eigenvectors, at the middle point of the two grids \(x_{i+\frac {1}{2}}\). These matrices are used only to evaluate the numerical flux at \(i+\frac {1}{2}\). Project the flux F(U) (those needed by any of the reconstruction stencils) into the characteristic fields by multiplying with the left eigenvector matrix L:
For the fifth-order scheme computing the left-biased stencil, r=3.
Step 1.2: Apply the scalar WENO procedure to each component of the characteristic flux Gi+j to obtain the WENO reconstruction in the characteristic field. If we use (Gi+j)s to denote the s-th component of the vector Gi+j, then
Notice that each component s has its own smoothness indicator and hence its own nonlinear weight ωk,s, even though the linear weights are the same for all components. The nonlinear weight ωk,s is computed in the local characteristic field, using (Gi+j)s.
Step 1.3: Project the WENO reconstruction back to the physical space by
In this procedure, a key ingredient is the choice of the values of the conserved variables at \(x_{i+\frac {1}{2}}\), in the computation of the left and right eigenvectors L and R in the first step above. Jiang and Shu [6] suggested that they are computed by the Roe average [24] from the physical values at the two neighboring points xi and xi+1. The Roe average is given by
and then the left and right eigenvectors L and R of the Jacobian matrix A can be computed by
2.3 Time discretization
After the spatial derivative is discretized with the WENO scheme, a set of ordinary differential equations is obtained as:
The operator L(u) is represented in (6). This set of ordinary differential equations can be discretized by a third-order TVD Runge-Kutta method [3, 25] as follows:
3 The slight post-shock oscillations of WENO schemes and the convergence to steady state solutions
Almost all high-order shock capturing schemes suffer from the problem that there are small post-shock oscillations, which are the culprit for the failure of the numerical residue to settle down to machine zero. In [15], Zhang and Shu studied the mechanism of the post-shock oscillations and their effects on the convergence property through numerical tests and heuristic analysis. In this section, we give a brief review to the numerical experiments using the fifth-order WENO scheme as an example to show these post-shock oscillations of WENO schemes. These slight post-shock oscillations have big influence over the convergence property of WENO schemes to steady states. The post-shock oscillations of higher order WENO schemes are more severe.
Two typical examples are tested in this section. One is the one-dimensional steady shock wave and the other is the two-dimensional isentropic vortex.
3.1 One-dimensional steady shock
Our first example is a one-dimensional stationary shock wave. The governing equation is the system of Euler Eq. (25). The ratio of specific heat is set to be γ=1.4.
The computational domain is x∈[−1,1], which is divided into 400 uniformly spaced grid. The flow Mach number on the left of the shock is M∞=2. The shock wave is located at x=0. The initial state is given by the Rankine-Hugoniot jump condition [26]:
where
The initial state is the exact solution of the one-dimensional steady Euler equations. It should keep the same shape for t≥0 when we run the code. However, because of the usage of the Lax-Friedrichs flux splitting, the initial condition is not a steady numerical solution of the WENO scheme. The shock wave is smeared across a few grid points. Figure 1 is the numerical density distribution along the computational domain. The code is run to the non-dimensional time t=120. We can see that the numerical result is essentially non-oscillatory: no noticeable oscillations can be observed. The profile of the numerical shock wave is quite sharp and appears monotone to the eye. From an engineering point of view, this result is quite satisfactory. Figure 2 contains the zoomed view (left) of the density distribution at the downstream of the shock wave and the time evolution (right) of the density at the point x=0.01. We can see clearly that there are slight spurious oscillations downstream of the shock wave. The amplitude of the spurious oscillations is at the level around 10−3, which is about the size of the local truncation error of the scheme. This is the well known post-shock oscillation that appears downstream of slowly moving or steady numerical shocks. It is the culprit for the failure of high-order shock capturing schemes to converge to ideal steady states.
Figure 3 contains the time evolution of the average residue, which is defined as:
where Ri is the local residue defined as
and N is the total number of grid points.
We can see that the convergence property is not so satisfactory. Instead of converging to machine zero or to a small enough value, the average residue hangs around 10−2.2. Even though the flow variables do not change much in the long time running, the non-decreasing of the average residue after it reaches around 10−2.2 is a concern. This is because one can no longer use the size of the average residue to determine when to stop the computation, and must rely on experience including a visual comparison of the flow variables after many time steps to make this determination. Moreover, if we use this scheme to compute shock associated noises, the slight post-shock oscillation may be much stronger than the shock associated noises. Hence, it will influence the accuracy of the computation for the shock associated noises.
3.2 Two-dimensional isentropic vortex
The second example is a two-dimensional isentropic vortex, which is a smooth exact solution of two-dimensional steady Euler equations. We use this example to reveal the convergence of WENO scheme to steady smooth flows. The parameters of the vortex is the same as that in [27, 28]:
tangential velocity: \(u_{\theta } (r)=M_{\upsilon } r e^{\left (1-r^{2}\right)/2}\),
radial velocity: ur=0,
pressure: \(p(r)=\frac {1}{\gamma }[1-\frac {\gamma -1}{2} M_{\upsilon }^{2} e^{1-r^{2}}]^{\frac {\gamma }{\gamma -1}}\),
density: \(\rho (r)=[1-\frac {\gamma -1}{2}M_{\upsilon }^{2} e^{1-r^{2}}]^{\frac {1}{\gamma -1}}\), where \(r= \sqrt {(x-x_{v})^{2} + (y-y_{v})^{2}}\). The center of the vortex is (xv,yv)=(0,0). The strength of the vortex is set to be Mυ=0.25. The values at the ghost points in our computation are fixed as the exact solution. The computational domain is −4≤x≤4 and −4≤y≤4. A 400×400 equally spaced grid is used and the code is run to non-dimensional time t=50.
Figure 4 is the time evolution of the average residue. It converges to about 10−11, which is close to machine zero and is clearly small enough for us to use it as a criterion to stop the run. Figure 5 contains the density contours (dashed lines) and streamlines (solid lines with arrows). It can be seen that the streamlines and density contours are very smooth near the boundary.
Reproduced from [15]. The density contours (dashed lines from 0.9 to 1.0 with 30 levels) and streamlines (solid lines with arrows) of a two-dimensional isentropic vortex
The above two examples suggest that the reason for the non-convergence of the WENO scheme to steady state solutions of Euler equations is the slight post-shock oscillation. If we can find a technique to remove or reduce this post-shock oscillation, we could improve the convergence to steady states.
4 Strategies to improve the convergence to steady state solution for WENO schemes
4.1 A new smoothness indicator for the fifth-order WENO scheme
In [15], Zhang and Shu studied the relationship between the smoothness indicator and the appearance of the post-shock oscillation for the fifth-order WENO scheme. It was found that the choice of the smoothness indicator is one reason to influence the appearance of the post-shock oscillations of the WENO schemes. Based on the physical analysis of the simple solution of the numerical shock and the characteristics of the different parts of the smoothness indicator, a new smoothness indicator was proposed for the fifth-order WENO scheme. With the new smoothness indicator, the slight post-shock oscillation of the fifth-order WENO scheme can be removed for some typical cases or reduced significantly for some other cases. Therefore, the convergence property to steady state can be improved significantly.
To be more specific, the smoothness indicators given by (19) can be expanded as:
Each of these formulae contains two parts P1 and P2. The first term \(P_{1}=\frac {1}{4}\left (2f'\triangle x \pm \frac {2}{3}f'''\triangle x^{3}\right)^{2}\) includes the contribution from the first and third derivatives. The dominating contribution is from the first derivative. The second term is the second derivative \(P_{2}=\frac {13}{12}\left (f''\triangle x^{2}\right)^{2}\). The patterns of P1 and P2 are quite different in the neighborhood region of a shock wave. Using a step function with one transition point as an example for the numerical shock wave, the behavior of the first and the second derivatives can be analyzed. Because the shock wave is always smeared in the numerical solution, the transition point is necessary for the numerical shock wave. Supposing the shock wave is located at x=0, which is the transition point. The first derivative takes the positive value in the neighborhood region of the shock wave and the absolute value takes its maximum at the center of the shock wave. Hence, based on the definition of the smoothness indicator, it is a good choice to indicate the (lack of) smoothness here. However, the second derivative takes a zigzag pattern in the neighborhood region of the shock wave. The absolute value of the second derivative takes its local maxima at both sides from the center of the numerical shock wave. At the center of the shock wave, the absolute value of the second derivative takes its minimum. Based on the concept of the introduction of the smoothness indicator, the second derivative is not a good choice in the neighborhood region of the shock wave to indicate the (lack of) smoothness here.
Based on this heuristic analysis, a new smoothness indicator for the fifth-order WENO scheme was proposed by just removing the contribution of the second derivatives in (19). It has the following form:
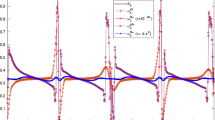
With this technique, the same one-dimensional shock wave as in (35) is computed. The numerical solution is plotted in Fig. 6, which contains the zoomed density distribution near the shock region and the time evolution of the residue. We can observe that the post-shock oscillation is removed and the residue can settle down to machine zero.
The numerical solution of the 1D steady shock wave with Mach number M∞=2 using the fifth-order WENO scheme with the new smoothness indicator (39). Left: zoomed density distribution downstream of the shock wave and its comparison with the traditional WENO scheme. WENO-JS represents the numerical result of the traditional WENO scheme [6]. WENO-ZS represents the result from the WENO scheme with the new smoothness indicator. Right: the time evolution of the average residue of WENO-ZS
4.2 Upwind-biased interpolation
The new smoothness indicator proposed in [15] is only suitable for the fifth-order WENO scheme. It can not be applied to higher order WENO schemes. Moreover, even for the fifth-order WENO scheme, it may lead to the degeneration of the order of accuracy at some smooth extrema.
In [14], Zhang et al. studied the convergence property for higher order WENO schemes. They found that the post-shock oscillation is much stronger in the higher order WENO schemes and the non-convergence problem is more serious than that of the fifth-order WENO scheme. Through numerical tests, they found that the Roe averaging method in the local characteristic projection is a key reason to the appearance of the post-shock oscillation. Hence, they proposed an upwind-biased interpolation instead of the Roe averaging method in the local characteristic decomposition procedure. That is, (31) is replaced by:
Here, u denotes the velocity in the Euler equations. U(1) and U(2) are the interpolated values on the cell interface, which are computed either by the first-order, the second-order one-sided interpolation or the higher order upwind-biased WENO interpolation.
The first-order one-sided interpolation is:
The second-order one-sided interpolation is:
The procedure of the WENO interpolation is very similar to the WENO reconstruction. They use the same stencil and sub-stencils. In the large stencil, a higher order interpolation formula can be obtained; and in the sub-stencils, several lower order interpolations can be obtained. Using a similar convex combination, the WENO interpolation with the same order of accuracy as that on the large stencil can be obtained. In the following, only WENO interpolation procedure for U(1) based on the left-biased stencil is presented. The formulae to interpolate U(2) based on the right-biased stencil are symmetric with respect to \(x_{i+\frac {1}{2}}\) and will not be shown. The detailed formulae for U(1) are as follows.
where \(\hat {U}^{(k)}_{i+\frac {1}{2}}\) is the lower order interpolation on each sub-stencil given by
with constant coefficients ckj. In the following, the fifth-order and seventh-order interpolations are listed.
a. Fifth-order WENO interpolation
In the case of r=3, the linear fifth-order interpolation is given by
The three third-order interpolations from the three sub-stencils are
The linear weights are given by
and the formulae of the smoothness indicators for the fifth-order WENO interpolation are the same as those of the fifth-order WENO reconstruction given by (19).
b. Seventh-order weighted interpolation
In the case of r=4, the linear seventh-order interpolation is given by
The four fourth-order interpolations from the four sub-stencils are
The linear weights are
and the smoothness indicators are
This new local characteristic decomposition procedure can be applied to different variants of WENO schemes, such as the one using the smoothness indicator proposed in [15], the one using the mapped technique proposed in [23], and the improved WENO scheme in [29].
With this technique, the same problem of the one-dimensional steady shock wave of Mach number 2 is computed. Figures 7 and 8 contain the numerical results for the fifth-order WENO scheme and the seventh-order WENO scheme, respectively. From these numerical tests, we can conclude: (1) Upwind-biased interpolation is suitable for all WENO schemes, including the traditional WENO scheme [6] (represented by WENO here), mapped WENO scheme [23] (MWENO), the improved WENO scheme by Don and Borges in [30] (ZWENO), and WENO schemes with general orders of accuracy. (2) For the fifth-order WENO scheme, the post-shock oscillation is reduced significantly and the residue can settle down to machine zero. (3) The post-shock oscillation is much stronger in higher order WENO schemes than those of fifth-order WENO scheme. With the upwind-biased interpolation, the post-shock oscillation is reduced significantly and the residue can go to a very small value close to machine zero.
Reproduced from [13]. Numerical solution of the 1D steady shock wave with Mach number M∞=2 using the fifth-order WENO scheme with the upwind-biased interpolation. Left: zoomed density distribution downstream of the shock wave. Right: the time evolution of the average residue
Reproduced from [13]. Numerical solution of the 1D steady shock wave with Mach number M∞=2 using the seventh-order WENO scheme with the upwind-biased interpolation. Left: zoomed density distribution downstream of the shock wave. Right: the time evolution of the average residue
Unfortunately, these strategies are not good enough for more complicated engineering problems. In [14, 15], several two-dimensional complex problems were tested for the WENO schemes with these strategies. The problems contain 135∘ oblique shock wave, regular shock reflection on a wall, a supersonic flow past a forward step, and a supersonic flow past a plate. Except for the 135∘ oblique shock wave case, the convergence for the other problems is not ideal, even though there are significant improvements compared with the traditional WENO schemes. The tests show that the convergence is sensitive to whether the numerical meshes are aligned with the shock wave. For the case of the 135∘ oblique shock wave, the initial shock wave is located exactly on the grid points with Δx=Δy. Periodic boundary condition along this direction is used. The post shock oscillation and the time evolution of the residue are then quite similar with those in the one-dimensional case. For the other three cases, the results are not so good. There are two factors which may influence the convergence property. One is the numerical grid. If the grid lines are aligned with the shock wave, the result is close to that in the one-dimensional case, and the convergence property is good. Boundary is the second factor that influences the convergence property, especially the solid wall boundary. For Navier-Stokes equations, in the neighborhood region of a wall, there is a boundary layer. If a shock wave can impinge on the wall, there will be shock boundary layer interaction. Separation may appear and the flow may become unsteady, leading to issues beyond our interest in this paper. Even for Euler equations, for which the viscous effect is neglected, if the grid lines near the boundary intersect with the shock wave, the numerical solution is very difficult to converge.
5 Application of the techniques to improve the convergence property to other types of weighted schemes
5.1 Fast sweeping WENO schemes
The fast sweeping method is a typical method to increase the convergence rate towards steady states. The main idea of the fast sweeping method is to combine the finite difference scheme and Gauss-Seidel iterations with alternating sweeping directions.
In [31–36], fast sweeping methods were developed for Eikonal equations and Hamilton-Jacobi equations. Combining the technique of the fast sweeping method and the strategies to improve the convergence to steady state solutions for WENO schemes [13, 15], Wu et al. [37] developed a high-order fixed-point sweeping WENO method for steady state Euler equations. Different from other fast sweeping methods, the fixed-point iterative sweeping method has the advantages that they have explicit forms and do not involve inverse operation of nonlinear local systems. Numerical experiments show that the convergence to steady state solutions is much faster than the regular time-marching approach.
For the two-dimensional time dependent Euler Eq. (2), the semi-discretized equation is
A Jacobi type Euler forward fixed-point iterative scheme is as the following:
Here, L represents the difference operator of the WENO scheme. The corresponding fast sweeping scheme can be written as:
where the Gauss-Seidel philosophy is used here, which means that the newest value of U, denoted by U∗, is used in the iteration. U∗ could either be \(U^{n}_{k,l}\) or \(U^{n+1}_{k,l}\) depending on the current sweeping direction. The iterations do not just proceed in only one direction i=1:N,j=1:M as in the time-marching approach (53), but in the following four alternating directions repeatedly, (1)i=1:N,j=1:M;(2)i=N:1,j=1:M;(3)i=N:1,j=M:1;(4)i=1:N,j=M:1.
For the third-order TVD Runge-Kutta scheme,
the RK type fixed-point sweeping scheme has the form
In the three stage iterations of (56), the newest value is also used in the current sweeping directions, which are represented by U∗, U∗∗, and U∗∗∗ respectively in each stage.
The feature of the numerical solution in the neighborhood region of the shock waves and the convergence property for the flow with shock waves in the fast sweeping WENO method are similar with those of WENO schemes. The use of the strategies to improve the convergence property of WENO schemes can also reduce the post-shock oscillation and improve the convergence ability. The fast sweeping technique can relax the stability condition and allow a larger CFL number, therefore leading to an increased convergence rate and decreased CPU time. The one-dimensional steady shock wave of Mach number 2 was computed in [37]. The amplitude of the post-shock oscillation, convergence property, the CPU costs, and the largest permitted CFL number were compared for different methods. Figure 9 contains the time evolution of the residues of different iterative methods. The spatial discretization is the fifth-order WENO scheme with the new smoothness indicator. We can observe that the largest CFL number of the Euler forward method is only 0.3. When the fast sweeping is used, a much larger CFL number, 1.1, is permitted. The CPU cost is saved. More details can be found in [37].
Reproduced from [37]. The evolution of the average residue in terms of iterations of the 1D steady shock by various ZSWENO schemes and CFL numbers
5.2 Weighted compact schemes
Linear compact schemes [38] are a typical type of high-order numerical schemes. They have the feature of high-order, low dissipation, and have been applied in many areas. However, linear compact schemes can not simulate flows containing strong shock waves. Combining linear compact schemes and WENO schemes, a series of weighted compact schemes were developed in [14, 39, 40]. The weighted compact scheme was developed based on the cell-centered compact scheme proposed by Lele [38],
The left hand side of the linear compact scheme (57) is a linear combination of the spatial derivatives \(f^{\prime }_{i}\) at some grid nodes and the right hand side is a linear combination of some cell-centered values \(f_{i+\frac {1}{2}}\). If β=0, c=0, a fourth order tridiagonal compact scheme is obtained with: \(a=\frac {3}{8}(3-2\alpha)\), \(b=\frac {1}{8}(22\alpha -1)\). The corresponding scheme is:
If \(\alpha =\frac {9}{62}\), we obtain a sixth-order tridiagonal scheme. Especially, if \(\alpha =\frac {1}{22}\), the coefficient b vanishes. It results in the most compact scheme as follows:
In (57), (58) and (59), the right hand side cell-centered values are unknowns. In [38], Lele proposed a compact formula to interpolate the unknown values on cell-centers from the values of neighboring grids. The obtained compact scheme is linear. Instead of using compact interpolation, Deng and Zhang [39] and Zhang et al. [14, 40] used WENO interpolation to compute the cell-centered values. The obtained schemes are the weighted compact schemes. The detailed formulae for the WENO interpolation are given by (43) and (44) in Section 4.2.
In [12, 14], Zhang et al. studied the convergence property to steady state solutions of Euler equations for weighted compact schemes. It is shown that the weighted compact schemes suffer from the same problem as WENO schemes. There is still slight post-shock oscillations, preventing the residue from settling down to a satisfactory small value. Because the WENO interpolation is quite similar with the WENO reconstruction, the strategies to improve the convergence to steady state solution for the WENO schemes are applicable also to weighted compact schemes. The same one-dimensional steady shock wave was computed in [12, 14] to test the behavior of the numerical solution, the post-shock oscillation, and the convergence feature of the weighted compact scheme with the strategies to improve the convergence property of WENO schemes. Similar conclusions were obtained. The post-shock oscillation is reduced significantly and the residue can go to a small value close to machine zero. The details can be found in [12, 14].
6 A new type of WENO schemes
6.1 The new WENO schemes
A new type of WENO schemes was developed by Zhu et al. [16, 17, 19]. They have nice convergence property for steady state computation. We also use the one-dimensional hyperbolic conservation laws (3) as an example to explain the new fifth-order WENO schemes [16, 17, 19]. Thus we have the associated semidiscretization of (6) and reformulate it as (33). Since the fifth-order version is taken as an example in this paper, we require \(\frac {1}{\Delta x} \left (\hat {f}_{i+1/2}-\hat {f}_{i-1/2}\right)\) to be a fifth-order approximation to f(u)x. For upwinding and stability, we also split the flux f(u) into f(u)=f+(u)+f−(u) and then approximate each of them separately using its own wind direction. The simple Lax-Friedrichs flux splitting is used again. All the one-dimensional and two-dimensional finite difference WENO schemes are based on the simple reconstruction procedure detailed below. Suppose we are given the cell averages \(\bar {w}_{j} = \frac {1}{\Delta x} \int _{x_{j-1/2}}^{x_{j+1/2}} w(x) dx\) for all j and would like to obtain a fifth-order WENO polynomial approximation wi(x) defined on Ii=[xi−1/2,xi+1/2], based on an upwind-biased stencil consisting of Ij=[xj−1/2,xj+1/2] with j=i−2,...,i+2. The procedure in [16, 17], with similar ideas in earlier references [41–43] as well, is summarized as follows.
Step 2.1: We choose the following big spatial stencil S1={Ii−2,...,Ii+2} and reconstruct a quartic polynomial f1(x) satisfying
We also choose two smaller spatial stencils S2={Ii−1,Ii} and S3={Ii,Ii+1}, and reconstruct two linear polynomials satisfying
and
Step 2.2: We rewrite the quartic polynomial f1(x) as:
Clearly, (63) holds true for arbitrarily positive linear weights γℓ on the condition that \(\sum _{\ell =1}^{3}\gamma _{\ell }=1\).
Step 2.3: We compute the smoothness indicators ISk, k=1,2,3, which measure how smooth the functions fk(x), k=1,2,3, are in the interval [xi−1/2,xi+1/2], by using the classical recipe for the smoothness indicators (16).
Step 2.4: We calculate the nonlinear weights, by adopting the strategy in WENO-Z as specified in [29, 30, 44]
and
Here ε is defined as a tiny positive number as before.
Step 2.5: We replace the linear weights in (63) with the nonlinear weights (65), and the final reconstruction polynomial wi(x) is given by
The construction of the numerical flux \(\hat {f}^{-}_{i{+}1/2}\) is mirror-symmetric with respect to xi+1/2. Finally, the semidiscrete scheme (3) is discretized in time by (34).
Let us mention a few features and advantages of the new WENO schemes. The first is that the linear weights can be any positive numbers on the condition that their sum is one. The second is their simplicity and easy extension to multi-dimensions. The third is that three unequal-sized central/biased spatial stencils are used in the WENO spatial reconstructions. The fourth is such new WENO schemes could maintain fifth-order accuracy in smooth regions and degrade to second-order accuracy in non-smooth regions, which are different from the fifth-order classical WENO schemes [6] (whose degenerated order is three). The last is that the number of spatial stencils is no bigger than that of the same fifth-order classical finite difference or finite volume WENO schemes [6]. We refer to [16–18, 20, 22] for more details on these new finite difference and finite volume WENO schemes on structured and unstructured meshes.
6.2 The convergence to steady state solution of the new WENO schemes
This new type of WENO schemes uses a convex combination of a quartic polynomial with two linear polynomials on unequal-sized spatial stencils in one dimension and two dimensions. Such new finite difference WENO schemes use the same information as the classical WENO scheme [6] and yield the same fifth-order in smooth regions, yet they have a few advantages over the classical WENO scheme [6], one of them being that the new WENO schemes can provide a unified polynomial approximation in the whole cell with the same nonlinear weights, comparing with the classical WENO scheme which involves different linear and nonlinear weights for different points on the cell boundaries. Computational results in [16, 17] indicate that this new type of WENO schemes works well for time-dependent test problems, but this is not what we would like to focus on in this paper.
In this section, we would like to study the performance of this new type of WENO schemes for steady state computation. Because of the global nature (the whole cell is approximated by the same WENO polynomial) and the smoothness of nonlinear weights (which is a signature advantage of WENO schemes versus ENO schemes and was already identified as the reason for better steady state computation in [6]), as well as the fact that two of the three sub-stencils in the WENO reconstruction correspond to low order linear polynomials, the new type of WENO schemes could converge to steady state solutions with close to machine zero residue for many standard test problems, including shocks, contact discontinuities, rarefaction waves or their interactions, and with these complex waves passing through the boundaries of the computational domain. This list includes many of the tough test problems mentioned in the previous sections, which cannot be successfully handled by the two strategies there. To the best of our knowledge, this appears to be the first class of high-order WENO schemes whose residue could settle down (close) to machine zero for a large class of two-dimensional test cases with standard Runge-Kutta time discretization [3, 25]. Of course, other time marching methods as well as special tools such as preconditioning to speed up steady state convergence could make the steady state convergence more efficient, however this is not the focus of the current paper and hence will not be further explored. We refer to [19, 21] for more details.
6.3 Shock reflection problem
In this section, we perform one typical example to test the steady state computation performance of the new fifth-order finite difference WENO scheme [16, 19] and term it as ZQSWENO scheme. We also make a comparison with the fifth-order classical finite difference WENO scheme [6] and term it as JSWENO scheme. The CFL number is 0.6. The average residue is defined as
where R∗i are local residuals of different conservative variables, that is, \(R1_{i}=\frac {\partial \rho }{\partial t}|_{i}=\frac {\rho _{i}^{n+1} -\rho _{i}^{n}}{\Delta t}\), \(R2_{i}=\frac {\partial (\rho u)}{\partial t}|_{i}=\frac {{(\rho u)}_{i}^{n+1} -{(\rho u)}_{i}^{n}}{\Delta t}\), \(R3_{i}=\frac {\partial (\rho v)}{\partial t}|_{i}=\frac {{(\rho v)}_{i}^{n+1} -{(\rho v)}_{i}^{n}}{\Delta t}\), \(R4_{i}=\frac {\partial E}{\partial t}|_{i}=\frac {E_{i}^{n+1} -E_{i}^{n}}{\Delta t}\), and N is the total number of grid points. Notice that here we are using a single index i to list all the two-dimensional grid points. The linear weights are set as γ1=0.98 and γ2=γ3=0.01 in this section.
The computational domain is a rectangle of length 4 and height 1. The boundary conditions are that of a reflection condition along the bottom boundary, supersonic outflow along the right boundary and Dirichlet conditions on the other two sides:
Initially, we set the solution in the entire domain to be that at the left boundary. We show the density contours with 15 equally spaced contour lines from 1.10 to 2.58 in Fig. 10, after numerical steady state is reached. The history of the residue (67) as a function of time is also shown in Fig. 10. The difference between the two types of WENO schemes can be clearly observed from the residue history. It can be observed that the average residue of the JSWENO scheme can only settle down to a value around 10−1, while the average residue of the ZQSWENO scheme with ε=10−2, ε=10−4, ε=10−6, ε=10−8, and ε=10−10 can settle down to a value around 10−12.5, close to machine zero.
7 Conclusion
The convergence to steady state solutions is a key problem for shock capturing schemes. It becomes more difficult for high-order shock capturing WENO schemes. The key reason is there is a slight post-shock oscillation.
Two techniques have been developed to improve the convergence to steady state solutions of Euler equations for high-order WENO schemes. One is a new smoothness indicator, which was proposed for the fifth-order WENO scheme. The other is an upwind-biased interpolation, introduced to compute the physical value at the cell interface in the procedure of the local characteristic projection replacing the traditional Roe average for general WENO schemes. With these techniques, the slight post shock oscillation can be removed or reduced significantly. The convergence property to steady state solution is improved. Moreover, these two techniques are applicable to other weighted schemes such as the fast sweeping WENO schemes and weighted compact schemes.
A new type of WENO schemes has also been proposed. Due to the usage of unequal-sized sub-stencils and polynomials of different degrees in different sub-stencils, these new WENO schemes have very nice convergence property for steady state computation. The residue can reach a tiny value close to machine zero for a large class of test problems, including the difficult two-dimensional problems where the shocks pass through the boundary of the computational domain.
In the viewpoint of applications, the convergence to steady state solution of high-order WENO schemes is still a difficult problem for complex engineering problems. However, with the advance made over the past years, as reviewed in this paper, especially the new type of WENO schemes summarized in Section 6, we have a good hope to overcome this difficulty of convergence to steady state solutions for complex engineering problems.
Availability of data and materials
All data and materials are available from the authors of this paper.
References
Harten A (1983) High resolution schemes for hyperbolic conservation laws. J Comput Phys 49:357–393.
Harten A, Engquist B, Osher S, Chakravarthy S (1987) Uniformly high order essentially non-oscillatory schemes, III. J Comput Phys 71:231–303.
Shu C-W, Osher S (1988) Efficient implementation of essentially non-oscillatory shock capturing schemes. J Comput Phys 77:439–471.
Shu C-W, Osher S (1989) Efficient implementation of essentially non- oscillatory shock capturing schemes II. J Comput Phys 83:32–78.
Balsara DS, Shu C-W (2000) Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J Comput Phys 160:405–452.
Jiang G-S, Shu C-W (1996) Efficient implementation of weighted ENO schemes. J Comput Phys 126:202–228.
Liu XD, Osher S, Chan T (1994) Weighted essentially non-oscillatory schemes. J Comput Phys 115:200–212.
Zhang HX (1984) The exploration of the spatial oscillations in finite difference solutions for Navier-Stokes shocks. ACTA Aerodyn Sin 1(1):12–19. (in Chinese).
Zhang HX (1988) Non-oscillatory and non-free-parameter dissipation difference scheme. ACTA Aerodyn Sin 6(2):143–165. (in Chinese).
Zhang HX, Zhuang FG (1991) NND schemes and their applications to numerical simulation of two and three dimensional flow. Adv Appl Mech 29:193–256.
Osher S, Chakravarthy C (1984) High resolution schemes and the entropy condition. SIAM J Numer Anal 21:955–984.
Zhang S, Deng X, Mao M, Shu C-W (2013) Improvement of convergence to steady state solutions of Euler equations with weighted compact nonlinear schemes. Acta Math Applicatae Sin Engl Ser 29:449–464.
Zhang S, Jiang S, Shu C-W (2011) Improvement of convergence to steady state solutions of Euler equations with the WENO schemes. J Sci Comput 47:216–238.
Zhang S, Jiang S, Shu C-W (2008) Development of nonlinear weighted compact schemes with increasingly higher order accuracy. J Comput Phys 227:7294–7321.
Zhang S, Shu C-W (2007) A new smoothness indicator for the WENO schemes and its effect on the convergence to steady state solution. J Sci Comput 31:273–305.
Zhu J, Qiu J (2016) A new fifth order finite difference WENO scheme for solving hyperbolic conservation laws. J Comput Phys 318:110–121.
Zhu J, Qiu J (2017) A new type of finite volume WENO schemes for hyperbolic conservation laws. J Sci Comput 73:1338–1359.
Zhu J, Qiu J (2017) A new third order finite volume weighted essentially non-oscillatory scheme on tetrahedral meshes. J Comput Phys 349:220–232.
Zhu J, Shu C-W (2017) Numerical study on the convergence to steady state solutions of a new class of high order WENO schemes. J Comput Phys 349:80–96.
Zhu J, Shu C-W (2018) A new type of multi-resolution WENO schemes with increasingly higher order of accuracy. J Comput Phys 375:659–683.
Zhu J, Shu C-W (2019) Numerical study on the convergence to steady state solutions of a new class of finite volume WENO schemes: Triangular meshes. Shock Waves 29:3–25.
Zhu J, Shu C-W (2019) A new type of multi-resolution WENO schemes with increasingly higher order of accuracy on triangular meshes. J Comput Phys 392:19–33.
Henrick AK, Aslam TD, Powers JM (2005) Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points. J Comput Phys 207:542–567.
Roe PL (1981) Approximate Riemann solvers, parameter vectors, and difference schemes. J Comput Phys 43:357–372.
Shu C-W (1988) Total-Variation-Diminishing time discretizations. SIAM J Sci Stat Comput 9:1073–1084.
Saad MA (1993) Compressible Fluid Flow, Prentice Hall, Englewood Cliffs, NJ, USA.
Shu C-W (1998) Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In: Cockburn B, Johnson C, C-W Shu, Tadmor E, Quarteroni A (eds)Advanced Numerical Approximation of Nonlinear Hyperbolic Equations, 325–432.. Springer. Lecture Notes in Mathematics.
Zhang S, Zhang Y-T, Shu C-W (2005) Multistage interaction of a shock wave and a strong vortex. Phys Fluid 17:116101.
Borges R, Carmona M, Costa B, Don WS (2008) An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J Comput Phys 227:3191–3211.
Don WS, Borges R (2013) Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes. J Comput Phys 250:347–372.
Qian J, Zhang Y-T, Zhao H-K (2007) Fast sweeping method for Eikonal equations on triangular meshes. SIAM J Numer Anal 45:83–107.
Qian J, Zhang Y-T, Zhao H-K (2007) A fast sweeping method for static convex Hamilton-Jacobi equations. J Sci Comput 31:237–271.
Wu L, Zhang Y-T (2015) A third order fast sweeping method with linear computational complexity for Eikonal equations. J Sci Comput 62:198–229.
Xiong T, Zhang M, Zhang Y-T, Shu C-W (2010) Fast sweeping fifth order WENO scheme for static Hamilton-Jacobi equations with accurate boundary treatment. J Sci Comput 45:514–536.
Zhang Y-T, Zhao H-K, Qian J (2005) High order fast sweeping methods for static Hamilton-Jacobi equations. J Sci Comput 29:25–56.
Zhao H-K (2004) A fast sweeping method for Eikonal equations. Math Comput 73:603–627.
Wu L, Zhang Y-T, Zhang S, Shu C-W (2016) High order fixed-point sweeping WENO methods for steady state of hyperbolic conservation laws and its convergence study. Commun Comput Phys 20:835–869.
Lele SK (1992) Compact finite difference schemes with spectral-like resolution. J Comput Phys 103:16–42.
Deng X, Zhang H (2000) Developing high-order weighted compact nonlinear schemes. J Comput Phys 165:22–44.
Liu X, Zhang S, Zhang H, Shu C-W (2015) A new class of central compact schemes with spectral-like resolution II: Hybrid weighted nonlinear schemes. J Comput Phys 284:133–154.
Capdeville G (2008) A central WENO scheme for solving hyperbolic conservation laws on non-uniform meshes. J Comput Phys 227:2977–3014.
Levy D, Puppo G, Russo G (1999) Central WENO schemes for hyperbolic systems of conservation laws, M2AN. Math Model Numer Anal 33:547–571.
Levy D, Puppo G, Russo G (2000) Compact central WENO schemes for multidimensional conservation laws. SIAM J Sci Comput 22(2):656–672.
Castro M, Costa B, Don WS (2011) High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws. J Comput Phys 230:1766–1792.
Acknowledgements
No.
Funding
The work of the first author was supported by NSFC grant 11732016. The research of the second author was supported by NSFC grant 11872210. The research of the third author was supported by NSF grant DMS-1719410.
Author information
Authors and Affiliations
Contributions
Authors’ contributions
All authors read and approved the final manuscript.
Authors’ information
The information of all authors are included in the first page of this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, S., Zhu, J. & Shu, CW. A brief review on the convergence to steady state solutions of Euler equations with high-order WENO schemes. Adv. Aerodyn. 1, 16 (2019). https://doi.org/10.1186/s42774-019-0019-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s42774-019-0019-2