Introduction

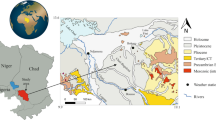
The lower loess layer is naturally higher than a nearby riverbed due to its origin through wind mobilization of sand and the entire Loess Plateau is composed of a series of independent hydrogeological units bounded by river valleys (Xu et al. 2020; Wang et al. 2017). Under natural condition, rainfall is typically the only source of groundwater recharge in the Chinese Loess Plateau. However, the mode for rainwater infiltration through the thick vadose zone between preferential flow and piston flow remains contentious (Li et al. 2017; Wang et al. 2018). This disagreement stems from the intuitive observation of water seepage along the joints and cracks in the loess profile. The argument for piston flow was due to many field observations and artificial rainfall experiments had shown that the depth of the wetting front in loess was limited, generally around 2 m and no more than 4 m (Li et al. 2016; Tu et al. 2009; Xu et al. 2011). Studies based on long-term monitoring in the Chinese Plateau by Hou et al. (2017, 2019, 2020) and Zhang et al. (2014) found that the depth at which soil moisture was most sensitive to rainfall and evaporation-transpiration was only 2.0 m, whereas water content below 2.0 m remained constant over time. Figure 1 shows the results of up-to-date data. The monitored data for the Bet Dagan and Rio Galeria basins similarly demonstrated that the response of soil water content to precipitation events began to weaken at a depth exceeding 0.3 m, regardless of whether the response was measured during the dry season or rainy season, and water content remained basically unchanged at a depth exceeding 1 m (Russo and Fiori 2008). The upper wetting zone is commonly referred to as the “active zone”, whereas the underlying zone with an unchanged water content is referred to as the “steady zone”. Past scientific understanding had been that piston flow occurred in the active zone, whereas there was no flow in the steady zone (Gazis and Feng 2004).

Fig. 1
figure 1

Conceptual diagram representing two regions of the unsaturated zone

Full size image

On the other hand, deep vertical joints, larger root pores and animal holes were widely spread in loess slopes (Derbyshire 2011; Zhang and Liu 2010; Zhuang et al. 2017), which motivated for the theory that rainwater rendered to flow along the joints, pores, and holes, referred to as “preferential flow”. However, to date, field observations and measurements have not supported this assumption. Wu et al. (2011) conducted in-situ infiltration tests across fractures in loess ground and did not identify a hydraulic connection between flow in wide fissures and groundwater. A study by Xu and Zhao (1993) on rainfall seepage in an excavated profile with fissures suggested that fissures and macro-pores did not play a key role in water diversion. The vague understanding of preferential flow can be attributed to confusion over the condition of saturation and unsaturation. It is easy to demonstrate that preferential flow occurs in saturated soil. But in unsaturated soils, the macro spaces, such joints, large pores and holes, have zero potential while the micro pores have potential. The smaller pore typically has a lower potential. Consequently, water will fill the minor pores first, then expand the bigger ones in order. During the heavy rain period, a saturated zone can temporarily form in shallow ground, with preferential flows forming along some macro paths. However, the preferential flow in macro pores diminishes immediately when saturated flow changes to unsaturated flow.

Loess is a typical unsaturated soil which is sensitive to moisture (Li et al. 2015). Preferential flow occurs temporarily on the ground surface during rain events. Uniform unsaturated seepage, namely piston flow, is the dominant mode of flow in the thick loess vadose zone.

However, it was difficult to observe piston flow in both active and steady zones (Cheng et al. 2018; Basara and Crawford 2010), and this difficulty may have contributed to misunderstanding regarding the existence of flow in the steady zone. The Richards equation described water flow in unsaturated porous media and can help explain this phenomenon (Richards 1931). The use of the Richards equation readily shows that the active zone has transient flow, whereas the steady zone has steady flow. In a natural profile, intermittent rainfall infiltration could form transient flow in the shallow active zone, which transitioned to steady flow in the underlying steady zone (Hou et al. 2017, 2020). Following steady flow, there was a constant flow of water downward to recharge groundwater (Huang et al. 2017, 2020).

The present study uses a hydraulic model by Zhang et al. (2019) to visually demonstrate the transition of water flow from transient flow behavior in the active zone to the steady flow behavior in the steady zone under multiple infiltration events. Furthermore, a differential solution for Richards equation is provided to simulate the flow in the vadose zone under a magnified rainfall series. The result demonstrates the behaviors of water flow in the vadose zone as mentioned above.

The hydraulic model

Figure 2 is a schematic conceptual representation of the hydraulic model. The model is composed of a set of open water tanks with a small outlet at the bottom of each tank. In the model, a tank represents a soil unit, the tank itself represents the soil skeleton, and the water in the tank represents water in a soil unit. The water-saturated tank represents a saturated soil unit. A set of vertically aligned tanks represents a soil column.

Fig. 2
figure 2

Representation of a soil column using the hydraulic model in the current study

Full size image

Water supplied to the top tank will successively flow to the tanks below. All tanks have the same cross-section area and height. The water level relative to the height of the tank corresponds to the water content of the soil unit, and the velocity of the change in water level of each tank corresponds to the permeability of the soil unit. The successive flow of water from the top tank to those below reflects the properties of the one-dimensional infiltration process in the vadose zone. The water levels of the tanks should be controlled without overflow to simulate unsaturated flow.

Experiment with the hydraulic model

As shown in Fig. 3, the experiment was conducted using nine glass tanks vertically fixed onto a wooden board at 10 mm intervals. Each tank had a diameter and height of 36 mm and 180 mm, respectively. A water level scale was marked onto the wall of each tank. A water supply bottle connected to a faucet was installed above the tanks. As an initial condition, all tanks had a water level of 30 mm. The boundary condition of the experiment was an intermittent water supply to the top tank C0 for simulating rainfall events, as shown in the first row in Fig. 3. As the water supply was initiated, the water level of each tank was recorded every 30 s. In total, 3,000 s of data were recorded.

Fig. 3
figure 3

Water levels in the tanks of the hydraulic model over time under an intermittent supply

Full size image

The graphs on the left-hand side of Fig. 3 show water levels of the tanks over time. The water level in C1 fluctuated widely as a direct response to water supply C0. The variation in the water level of C2 was more gentle than that in C1. An examination of the variation in water level of the tanks from C1 to C8 showed that variation in water level progressively decreased from the upper to lower tanks. The water level in the last 2 tanks (C7 and C8) stabilized at 10 mm after 2000 s. Since the water level of C8 was constant, it could be inferred that any tanks below C8 would also have constant water levels.

The water level changes of different amplitudes in some tanks imply that both the water content and permeability of the soil zone represented by each tank are variable, which reflect the behavior of the active zone with transient flow. Meanwhile, the ones with the constant water level reflect the behavior of the steady zone with a steady flow. The overall profile of the tanks shows a change in the water level from an active zone to a steady zone, which is associated with the transition from transient flow to steady flow.

Since rainfall events are permanent features in nature, the final state in the experiment corresponds to the natural state. The variations in water content in the experiment are consistent with in-situ observations in the soil profile. The experiment conducted in the present study directly demonstrates that there is water flow in both the transient and steady zones. However, this flow is difficult to observe or monitor in a natural soil profile.

Numerical solution for the hydraulic model

The present study conducts a theoretical numerical solution for the model to demonstrate the reasons for the ability of the hydraulic model to represent the behavior of unsaturated flow. The following differential expression is deduced from the model (Zhang et al. 2019):

$$\frac{{\Delta q_{i} }}{\Delta t} = \frac{\Delta }{\Delta z}\left[ {k(H) \, \left( {\frac{\Delta H}{{\Delta z}} - 1} \right)} \right]$$
(1)

In Eq. (1), qi is the ratio of water quantity in the ith tank to the total volume, z is the height of the tank, H is the water head in the tank, and k(H) is equivalent to the hydraulic conductivity function, which is expressed as follows:

$$k(H) = \frac{{r_{i}^{2} }}{{R^{2} }}\sqrt {2gh_{i} } \frac{\Delta z}{{h_{i} + \Delta z}}$$
(2)

In Eq. (2), hi is the water level of the ith tank, ri is the outlet radius of the ith tank, R is the radius of the tank, and each tank has the same radius.

The Richards equation (Richards 1931) for vertical one-dimensional flow in unsaturated soils is:

$$\frac{\partial \theta }{{\partial t}} = \frac{\partial }{\partial z}\left[ {k(H) \, \left( {\frac{dH}{{dz}} - 1} \right)} \right]$$
(3)

In Eq. (3), z is the vertical coordinate (downward is positive), θ is the volumetric water content of soil, H is the pressure head, and k(H) is the hydraulic conductivity function.

Comparing Eqs. (1) and (3) shows their similarity in form and physical context. The left-hand sides of both equations represent the rate of variation in water content to duration, whereas the right-hand sides of both equations, ΔH/Δz or ∂H/∂z, correspond to the hydraulic gradient. k(H) is the function of the water level hi as shown in Eq. (2) and is correlated to the water content hi/z or pressure head (H =  − hi) of the tank. Therefore, k(H) is equivalent to the hydraulic conductivity function, which is also a function of the water content and pressure head.

Substituting Eq. (2) and qi = hi/z, H =  − hi into Eq. (1), the first-order differential equation of Eq. (1) for time t and coordinate z can be written as Eq. (4):

$$h_{i}^{t} = h_{i}^{t - 1} + \frac{{\sqrt {2g} }}{{R^{2} }}\left( {r_{i - 1}^{2} \sqrt {h_{i - 1}^{t - 1} } - r_{i}^{2} \sqrt {h_{i}^{t - 1} } } \right)\Delta t$$
(4)

Equation (4) can be used to calculate the water level of each tank from the upper-most tank downward.

The calculation begins from t = 1. In this case, hi0 (i = 1, 2, …, n) for the right-hand side of Eq. (4) are given as initial conditions, R and ri are fixed, and g is 9800 mm/s2. Given the boundary condition h0t at the time intervals t = kΔt (k = 1, 2, …, m), the water level hit can be calculated in the order of h11, h21, …, hn1; h12, h22, …, hn2; … h1m, h2m, …, hnm. Figure 4 demonstrates the calculation steps.

Fig. 4
figure 4

Flow chart demonstrating the process used to derive the numerical solution for the model

Full size image

The outlet radii of the tanks are set as two cases to simulate the flow behaviors in uniform and layered soils, respectively, as shown in Table 1. In case 1, all tanks have the same outlet radius ri, which represents a uniform soil column with the same hydraulic conductivity function among the soil units. In case 2, each tank has a different outlet radius ri, which represents a layered soil column with different hydraulic conductivity functions among the soil units. The initial condition of the water content is also set as two states. Under state 1, the water levels of all the tanks are set to zero, whereas under state 2, the water levels are set according to the values listed in Table 1. The daily rainfall data recorded at the monitoring site in the Central Chinese Loess Plateau, from March 2018 to March 2019, are used as reference data for the boundary condition. The present study applies daily precipitation data, but the time interval of one day is zoomed to 1 s in the simulation. The long-term effect of water flow in the vadose zone is achieved by repeatedly applying one year of daily precipitation over 5 years. Since the time interval of the experiment is set to 1 s, the total duration of the experiment is 5 cycles of 365 s.

Table 1 The properties of the model
Full size table

Analysis of the results

The simulated results are summarized in Fig. 5. The dashed lines indicate the case under which the initial water levels of all tanks are zero, whereas the solid lines indicate the case under which the tanks have different initial water levels. The green lines show the case under which all tanks have the same outlet radius (ri = 1.70 mm), whereas the red lines show the case under which each tank has a different outlet radius.

Fig. 5
figure 5

Change in water level in the system under two cases of initial tank water level

Full size image

Comparison of the results for an identical initial condition (state 1, zero water level, dashed line) with those generated under different initial conditions (state 2, different water levels, solid line) shows that the final flow state of each tank is independent of the initial condition. Regardless of identical (zero) or different initial water levels, the final water levels of the upper tanks will eventually reach a state of periodic fluctuation, whereas those of the lower tanks tend to stabilize. The dashed line and corresponding solid line eventually converge. However, hysteresis can be observed on the curves under which the lower tanks require more time to reach the final state.

Table 1 shows the conditions under which all tanks have the same outlet radius (case 1, green lines) and under which each tank has a different outlet radius (case 2, red lines). And the simulated results in Fig. 5 show that the tanks with larger outlet radii (case 2, C1 to C4, red lines) have lower water levels, whereas those with smaller outlet radii (case 1, C1 to C4, green lines) have higher levels. The same regularity in water level appears in the C7 and C8. Both C7 and C8 have higher water levels, whereas they have a smaller and larger outlet radius under case 2 (red lines) and case 1 (green lines), respectively. Tanks with an identical outlet radius (in both cases, C5 and C6) show similar water levels. The green and red line for C5 and C6 are close and finally converged. The simulated results reflect the flow behavior in unsaturated soils. A soil layer with good hydraulic conductivity and low water retaining capacity is represented by the tanks with a larger outlet radius, whereas the soil layer with low hydraulic conductivity and high water retaining capacity is represented by tanks with a small outlet radius.

Figure 6 shows the soil water retention curves (SWRC) of the silt and sand, which clearly illustrate the difference in the ability of each of the two soils to retain water. Under the same water content (e.g., 17.5%), the soil suction of silt (40 kPa) would far exceed that of sand (2 kPa), representing a much lower permeability of the silt.

Fig. 6
figure 6

Representative soil water retention curves (SWRC) of sand and silt from China

Full size image

The variations in the water levels of the tanks tend to decrease from the upper to lower tanks, regardless of their initial condition. The water level in C0 represents the influence of rainfall events. There is a continuous fluctuation in the water level of C1, with a short time lag relative to C0. The water levels in C2 and C3 show continuous and smooth fluctuation with a time lag relative to the tanks above, whereas C4 to C6 show similar trends in water level variation. The amplitudes of water level in tanks C1 to C6 rapidly decrease from the top tank to the bottom tank. The water levels of C7 and C8 eventually reach a steady state. As mentioned above, the final water levels of the tanks are independent of initial conditions. Based on the final state, the model column can be divided into two zones, namely the active zone and the steady zone.

The water levels in the active zone are influenced by the boundary condition, whereas those in the steady zone are constant with a steady water flow. The flow velocity of each tank in the steady zone is equal to the average boundary recharge. As demonstrated by the monitoring results shown in Fig. 1, the flow behaviors simulated by the model are similar to those observed in natural soil layers. The hydraulic model provides strong evidence for the existence of steady flow, which acts as a typical source of groundwater recharge in the loess region.

Discussion

Figure 7(a) shows the in-situ monitoring results of water content of the soil profile in the central Chinese Loess plateau (Hou et al. 2020). Figure 7(b) shows the simulated results using the monitored precipitation data. The simulated water content of the soil profile is consistent with the observed water content. The mechanism of the similarity between the results of the physical model and the natural situation is discussed below.

Fig. 7
figure 7

Comparison of soil water content and calculated value using rainfall data

Full size image

To solve Eq. (3), two key soil constitutive functions should be provided in advance, namely the SWRC and hydraulic conductivity function (HCF) (Fredlund 2006; Lu and Likos 2006). These functions can use the empirical equations, such as the commonly used SWRC and HCF equations provided by van Genuchten (1980) and Fredlund et al. (1994), and the parameters should be fitted using laboratory test data. The equivalent SWRC and HCF for the hydraulic model can be deduced based on the principle of the model. Supposing that the equivalent SWRC is expressed as equivalent matric suction against the degree of saturation and that HCF is expressed as the equivalent hydraulic conductivity against the degree of saturation, then the water level height of the ith tank is hi, and its degree (Si) of saturation is:

$${S}_{i}=\frac{{h}_{i}}{\Delta z}$$
(5)

The equivalent matric suction (ψi) is:

$$\psi_{i} = \Delta z - h_{i}$$
(6)

Therefore, the equivalent SWRC of the tank is

$$\psi_{i} = (1 - S_{i} )\Delta z$$
(7)

From Eqs. (2) and (5), the equivalent HCF of the tank can also be easily obtained:

$$k(S_{i} ) = \frac{{r_{i}^{2} }}{{R_{i}^{2} }}\sqrt {2gS_{i} \Delta z} \frac{1}{{S_{i} + 1}}$$
(8)

Suppose Δz is unity, then Eqs. (7) and (8) can be simplified to:

$$\psi_{i} = 1 - S_{{\text{i}}}$$
(9)
$$k(s_{i} ) = \frac{{r_{i}^{2} }}{{R_{i}^{2} }}\sqrt {2gS_{i} } \frac{1}{{S_{i} + 1}}$$
(10)

Figure 8 shows the curves of Eqs. (9) and (10). Equation (9) is a linear function in which the equivalent matric suction linearly increases with decreasing saturation, similar to the trend in SWRC variation for real soil. However, it is difficult to fit a linear SWRC function for real soil. In addition, Eq. (10) shows that the trend of HCF is similar to that of real soil. However, the HCF cannot be applied in real soils. The advantage of the model is that it can visually show the two-dimensional profile of water flow in the vadose zone and can help to clarify the argument between piston flow and preferential flow.

Fig. 8
figure 8

Equivalent matric suction and hydraulic conductivity function against degree of saturation of the model

Full size image

Conclusions

The paper uses a hydraulic model to simulate the flow behavior in the vadose zone. The mathematical expression of the hydraulic model is deduced and is similar to the Richards governing equation. The experiment and mathematical solutions demonstrate that under a condition of intermittent precipitation events, the model column can be divided into two zones, namely active zone and steady zone. The water content in the active zone changes the variation of the boundary conditions (e.g., precipitation, evaporation in natural conditions), whereas it keeps constant in the steady zone. The results of the model are consistent with the soil water content profile observed in the field. The model can overcome the difficulty of observing unsaturated flow in nature by visually demonstrating the two-dimensional profile of water flow in both the active and steady zones, and particularly the transition from transient water flow to steady flow.