1 Introduction

Although a number of researches have been conducted to evaluate shear strength of reinforced concrete beams for the last century, it is still hard to well predict actual shear strength because shear behavior of reinforced concrete beams is very complicating due to many parameters such as concrete compressive strength, stirrup ratio, shear span-to-depth ratio, longitudinal reinforcement ratio, and so on (Kim 2004; Lee et al. 2010; Labib et al. 2013; Russo et al. 2013; Mofidi and Chaallal 2014; Jeong and Kim 2014; Chiu et al. 2016; El-Sayed and Shuraim 2016). On evaluating shear strength of reinforced concrete beams, even shear design provisions around the world are much different through each other, even from theoretical basis, specifically for reinforced concrete beams with stirrups (Eurocode 2 2004; ACI 318 2014; CSA A23.3 2014).

For reinforced concrete beams with stirrups and with not small shear span-to-depth ratio, ACI 318-14 (2014) simply evaluates shear strength as sum of concrete and stirrup contributions (V c and V s , respectively), based on 45° truss model. In this provision, V c is affected neither by stirrup ratio nor by deformation due to flexure since only force equilibrium is considered. Eurocode 2 (2004) acknowledges only contribution of stirrups on evaluating shear strength of reinforced concrete beams with stirrups, based on variable angle truss model. In Eurocode 2, only force equilibrium is considered with variable diagonal angle of compression strut while deformation due to flexure is not considered. CSA A23.3 (2014) is based on the variable truss angle model as like Eurocode 2, but it considers effect of deformation due to flexure on evaluating contribution of concrete and stirrups for shear strength. CSA A23.3 considers that deformation of web due to flexure affects shear strengths provided by concrete and stirrups since it was developed through simplifying the Modified Compression Field Theory (Vecchio and Collins 1986), which can consider compatibility and equilibrium together.

For reinforced concrete beams with small shear span-to-depth ratio, ACI 318-14 recommends to employ strut-and-tie model. On the other hand, Eurocode 2 provides a simple method; applied shear force within short shear span can be artificially reduced so that more shear force can be resisted by acknowledging effect of arch action.

As summarized in the above and Table 1, even theoretical basis is quite different through the shear design provisions, so predictions show relatively lots of scatter on shear strength of reinforced concrete beams with stirrups. Therefore, this paper focuses on development of an analytical model which can rationally considers effect of arch action, contribution of concrete, and diagonal angle of compression strut in reinforced concrete web all together. In order to simply evaluate effects of the main parameters, the analytical model is developed to be much simpler than section analysis with layers model (Bentz 2001; Guner and Vecchio 2008).

Table 1 Comparison through shear design provisions for RC beams with stirrups.
Full size table

2 Development of Single Web Shear Element Model

2.1 Idealization of a RC Beam for Modelling

To evaluate shear strength of a reinforced concrete beam with stirrups subjected to flexural shear, the reinforced concrete beam is idealized to have three layers; top compression chord, single web shear element, and bottom tension chord, as illustrated in Fig. 1.

Fig. 1
figure 1

Idealization of a RC beam.

Full size image

In the idealized reinforced concrete beam under the concentrated load (P) in Fig. 1, the followings are fundamentally assumed; (1) the top compression and bottom tension chords fully resist the flexural moment caused by the concentrated load; (2) the web shear element along with the top compression chord supports shear stress developed in the RC beam. Based on the assumption that the top compression chord is not cracked while the web shear element is cracked, shear stress exhibits parabolic distribution through the non-cracked region based on Gere and Goodno (2013) while it exhibits a uniform distribution through the web shear element, as presented in Vecchio and Collins (1988) where shear stress distribution was analyzed for RC beams with rectangular section; and (3) critical section is located at the middle of the main diagonal crack based on Collins et al. (1996). Figure 2 illustrates the idealized shear stress distribution along depth.

Fig. 2
figure 2

Idealized shear stress distribution in a RC beam.

Full size image

2.2 Flexural Behavior with Top and Bottom Chords

Adopting Bernoulli’s hypothesis, linear longitudinal strain distribution along the cross section of the RC beam can be considered. To satisfy force equilibrium to the longitudinal direction, compression at the top of the section is assumed to be fully resisted by the concrete section while the tension at the bottom of the section is resisted by the longitudinal tensile reinforcement. Thus, the following equation can be derived;

$$ - \varepsilon_{c} \cdot E_{c} \cdot A_{c,top} = \varepsilon_{s} \cdot E_{s} \cdot A_{s} $$
(1)

where \( \varepsilon_{c} \) and \( \varepsilon_{s} \) are the longitudinal strains at the top and bottom chords due to the bending moment. In satisfying the above equation, it should be noted that the concrete and main longitudinal tensile reinforcement still exhibit a linear–elastic behavior as most reinforced concrete beams in literature exhibit shear failure before yielding. If nonlinearity is exhibited due to significant flexural bending moment, Eq. (1) should be modified accordingly to consider the stress–strain response of the concrete and reinforcements.

After diagonal cracking, the web shear element is subjected to additional longitudinal compressive force. The longitudinal compressive force on the web shear element due to shear force is defined as follows:

$$ N_{x} = \sigma_{x} \cdot b_{w} \cdot z $$
(2)

where N x is longitudinal compressive force on the web shear element due to shear force.

The longitudinal compressive force on the web shear element due to shear force is assumed to be equally shared by the top and bottom chords in order to satisfy force equilibrium through the section. Taking the flexural moment applied on the critical section, M, and considering the shear force contribution, the subsequent equations for strains at the top and bottom chords are derived considering the effect of the longitudinal compressive force on the web shear element:

$$ \varepsilon_{c} + \Delta \varepsilon_{c} = - \left( {\frac{M}{z} + \frac{{N_{x} }}{2}} \right)\left( {\frac{1}{{E_{c} \cdot A_{c,top} }}} \right) $$
(3)

and

$$ \varepsilon_{s} + \Delta \varepsilon_{s} = \left( {\frac{M}{z} + \frac{{N_{x} }}{2}} \right)\left( {\frac{1}{{E_{s} \cdot A_{s} }}} \right) $$
(4)

where \( \Delta \varepsilon_{c} \) and \( \Delta \varepsilon_{s} \) are the additional longitudinal strains at the top and bottom chords due to the shear force, and z is the internal lever arm length which can be chosen to 0.9 times the effective depth of the section. From Eqs. (1)–(4), the strains at the top and bottom chords can be calculated for a given flexural moment at the section.

2.3 Longitudinal Strain and Shear Stress at a Shear Critical Section

Using Eqs. (1)–(4), the longitudinal strain at the mid-depth \( \varepsilon_{x} \), can be calculated as following:

$$ \varepsilon_{x} = \frac{{\left( {\varepsilon_{c} + \Delta \varepsilon_{c} + \varepsilon_{s} + \Delta \varepsilon_{s} } \right)}}{2} = \left( {\frac{1}{{E_{s} \cdot A_{s} }} + \frac{1}{{E_{c} \cdot A_{c,top} }}} \right) \cdot \left( {\frac{M}{z} + \frac{{N_{x} }}{2}} \right) $$
(5)

This calculation is done by employing numerical analysis until the force equilibrium to the longitudinal direction is satisfied. The calculated longitudinal strain serves as representative longitudinal strain in the web shear element. Therefore, it is taken into an account for shear analysis of the web shear element.

By considering the shear stress distribution as described in Fig. 2, the contribution of the top compression chord on the shear force is calculated to 0.07 V by considering geometrical shape of shear stress distribution. Therefore, 0.93 V is resisted by the web shear element. Since the shear stress distribution is constant through the web shear element, the shear stress acting on the web shear element can be evaluated as following;

$$ \tau_{xy} = 0.93\frac{V}{b \cdot z} $$
(6)

where V is the shear force in the critical section.

Taking the shear span in the RC beam subjected to a concentrated load, the flexural moment is observed to vary while the shear force remains constant. Therefore, location of shear critical section should be reasonably chosen for the analysis. When the principal tensile direction in the web shear element is θ, it can be considered that the critical section has a distance of 0.5d cotθ from the concentrated load (Collins et al. 1996), as illustrated in Fig. 2. In addition, when the shear span-to-depth ratio is small, the shear force acting on the web shear element can be significantly reduced by arch action (Park and Paulay 1975). Consequently, by adopting the coefficient to consider the arch action introduced in Eurocode 2 (2004), the actual shear force at the critical section can be calculated as follows:

$$ V = \frac{{\beta_{a/d} M}}{a - 0.5d\cot \theta }\quad {\text{for}}\quad \cot \theta \le a/d $$
(7a)

where \( \beta_{a/d} = a/2d \), not less than 0.25 and not larger than 1.0.

When the shear span-to-depth ratio is too small, the principal tensile direction in the web shear element is limited to \( d\cot \theta \le a \). In this case, the shear critical section should be chosen at the middle in the shear span, so the actual shear force for a given flexural moment can be calculated as following:

$$ V = \frac{{\beta_{a/d} M}}{0.5a}\quad {\text{for}}\quad \cot \theta > a/d $$
(7b)

2.4 Shear Analysis for the Web Shear Element

From the flexural analysis with the top and bottom chords, two parameters are essential to the shear analysis for the web shear element at the critical section; the shear stress acting on the web shear element and the longitudinal strain at the mid-depth. These are calculated for a given flexural moment. Then, the subsequent shear analysis of the web shear element can be done by employing the MCFT (Vecchio and Collins 1986), which adequately predicts structural behavior of a reinforced concrete element subjected to bi-axial stress while considering compatibility, equilibrium, and constitutive relations of the materials together.

Taking the finite element implementation procedure with the MCFT derived by Vecchio (1990), which employs a secant material stiffness formulation, the relationship between the stresses and strains in the web shear element can be expressed as:

$$ \left\{ \sigma \right\} = \left[ D \right]\left\{ \varepsilon \right\} $$
(8)

where \( \{ \sigma \} = \{ \sigma_{x} ,\sigma_{y} ,\sigma_{xy} \}^{T} \) denotes the longitudinal, transverse, and shear stresses, \( \{ \varepsilon \} = \{ \varepsilon_{x} ,\varepsilon_{y} ,\gamma_{xy} \}^{T} \) is longitudinal, transverse, and shear strains, and [D] is a stiffness matrix of the web shear element.

Since the web shear element can be considered as a plane stress element, [D] can be expressed as a 3 × 3 matrix which can be evaluated for given strains \( \left\{ \varepsilon \right\} \) through considering constitutive relations of the materials, concrete and steel reinforcements. Therefore, Eq. (8) becomes

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\tau_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & {D_{13} } \\ {D_{21} } & {D_{22} } & {D_{23} } \\ {D_{31} } & {D_{23} } & {D_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} $$
(9)

In the above equation, known variables are the longitudinal strain at the mid-depth \( \varepsilon_{x} \) and the shear stress acting on the web shear element \( \tau_{xy} \), which are calculated from the flexural analysis. In addition, when the shear span-to-depth ratio is not so small, the transverse stress of the web shear element \( \sigma_{y} \) can be assumed to 0. Therefore, Eq. (8) has three known variables \( \left( {\varepsilon_{x} ,\sigma_{y} ,\gamma_{xy} } \right) \) and three unknown variables \( \left( {\sigma_{x} ,\varepsilon_{y} ,\gamma_{xy} } \right) \), so it can be decomposed to two parts, then transformed as follows:

$$ \sigma_{x} = D_{11} \varepsilon_{x} + D_{12} \varepsilon_{y} + D_{13} \gamma_{xy} $$
(10)
$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {D_{22} } & {D_{23} } \\ {D_{32} } & {D_{33} } \\ \end{array} } \right]^{ - 1} \left[ {\left\{ {\begin{array}{*{20}c} {\sigma_{y} } \\ {\tau_{xy} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {D_{21} } \\ {D_{31} } \\ \end{array} } \right\}\varepsilon_{x} } \right] $$
(11)

In the above equations, the entries in the stiffness matrix (from D11 to D33) are evaluated for given strains in the web shear element. This indicates that Eqs. (10) and (11) can be solved for the unknown variables \( \sigma_{x} \),\( \varepsilon_{y} \), and γ xy . Consequently, stresses and strains in the web shear element at a critical section can be calculated for a given flexural moment.

2.5 Stiffness Matrix [D] for the Web Shear Element

As the web shear element is composed of both concrete and reinforcement, the stiffness matrix [D] is evaluated through the superposition of a stiffness matrix for concrete [D c ] and a stiffness matrix for steel reinforcements [D s ] described as follows:

$$ [D] = [D_{c}]+ [D_{s} ] $$
(12)

2.5.1 Development of the Stiffness Matrix for the Steel Reinforcements, [Ds]

Since most reinforced concrete beams with stirrups have longitudinal and transverse reinforcements without any inclined steel reinforcements, the stiffness matrix for steel reinforcements can be simply evaluated from the following equation.

$$ \left[ {D_{s} } \right] = \left[ {\begin{array}{*{20}c} {\rho_{sx} \overline{{E_{sx} }} } & 0 & 0 \\ 0 & {\rho_{sy} \overline{{E_{sy} }} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] $$
(13)

where \( \rho_{sx} \) is an equivalent longitudinal reinforcement ratio in the web shear element, \( \rho_{sy} \) is a stirrup ratio, \( \overline{{E_{sx} }} \) and \( \overline{{E_{sy} }} \) are secant stiffness for the longitudinal reinforcements and stirrups. Regarding \( \rho_{sx} \), several researches assumed that the main tensile longitudinal reinforcements excluding the area required to resist the bending moment can be acknowledged to have contribution on the longitudinal behavior of the web shear element (Paul et al. 1988; Lee and Kim 2004). However, this assumption undesirably affects the longitudinal stiffness in the web shear element, specifically resulted by large bending moments. In this paper, therefore, equivalent yield strength of the longitudinal reinforcement in the web shear element is employed by excluding the tensile stress of the main longitudinal reinforcement due to the bending moment, instead of reducing the equivalent longitudinal reinforcement ratio. Consequently, as the steel reinforcements in the web shear element undergo an elasto-plastic behavior, the secant stiffness of the reinforcement in the web shear element can be evaluated in both directions with the followings:

$$ \overline{{E_{sx} }} = \frac{{f_{sx} }}{{\varepsilon_{x} }} \le \frac{{f_{sxy} - \varepsilon_{s} E_{s} }}{{\varepsilon_{x} }} $$
(14)
$$ \overline{{E_{sy} }} = \frac{{f_{sy} }}{{\varepsilon_{y} }} \le \frac{{f_{syy} }}{{\varepsilon_{y} }} $$
(15)

where \( f_{sx} \) and \( f_{sy} \) are stresses of longitudinal and transverse reinforcements in the web shear element, respectively. \( E_{sx} \) and \( E_{sy} \) are the elastic moduli of the longitudinal and transverse reinforcements, respectively, and \( f_{sxy} \) and \( f_{syy} \) are the yield strengths of the steel reinforcements.

2.5.2 Stiffness Matrix for Concrete, [Dc]

To develop the stiffness matrix for concrete [D c ], the principal strains and its angles in the web shear element should be calculated, subsequently the principal stresses associated with these strains can then be evaluated using the constitutive relations for concrete. For the strains \( \varepsilon_{x} \), \( \varepsilon_{y} \), and \( \gamma_{xy} \) in the web shear element, the principal strains \( \varepsilon_{1} \) and \( \varepsilon_{2} \), and principal tensile direction θ can be calculated as followings:

$$ \varepsilon_{1} = \frac{{\varepsilon_{x} + \varepsilon_{y} }}{2} + R $$
(16)
$$ \varepsilon_{2} = \frac{{\varepsilon_{x} + \varepsilon_{y} }}{2} - R $$
(17)
$$ \theta = \frac{1}{2}\cos^{ - 1} \left( {\frac{{\varepsilon_{y} - \varepsilon_{x} }}{2R}} \right) $$
(18)

where R is a radius of strain Mohr’s circle, which can be calculated from

$$ R = \sqrt {\left( {\frac{{\varepsilon_{x} - \varepsilon_{y} }}{2}} \right)^{2} + \left( {\frac{{\gamma_{xy} }}{2}} \right)^{2} } $$
(19)

The principal compressive stress of concrete \( f_{c2} \) can be evaluated from the principal compressive strain \( \varepsilon_{2} \), with the consideration of the compression softening effect that the compressive behavior of concrete is softened by increasing lateral tensile strain in a cracked reinforced concrete as presented in Fig. 3 (Vecchio and Collins 1993). Based on Hognestad’s model (Hognestad 1951), the stress–strain response of concrete along the principal compressive direction can be calculated as following:

$$ f_{c2} = f_{p} \left[ {2\frac{{\varepsilon_{2} }}{{\varepsilon_{p} }} - \left( {\frac{{\varepsilon_{2} }}{{\varepsilon_{p} }}} \right)^{2} } \right]\quad {\text{for}}\quad \varepsilon_{2} \ge \varepsilon_{p} $$
(20a)
$$ f_{c2\hbox{max} } = \beta_{p} f_{c} \quad {\text{for}}\quad \varepsilon_{2} < \varepsilon_{p} $$
(20b)

where \( f_{p} = \beta_{p} f^{\prime}_{c} \) for the peak compressive stress of concrete, \( \varepsilon_{p} = \beta_{p} \varepsilon_{c} \) for the strain corresponding to \( f_{p} \), and \( \beta_{p} \) is a factor to consider the compression softening effect, which depends on the principal compressive and tensile strains together presented in the following equation (Vecchio and Collins 1986).

$$ \beta_{p} = \frac{1}{{0.8 - 0.34\frac{{\varepsilon_{1} }}{{\varepsilon_{c} }}}} \le 1.0 $$
(21)
Fig. 3
figure 3

Principal compressive stress–strain response of concrete (Vecchio and Collins 1993).

Full size image

Considering the principal tensile direction, the tensile response of the concrete behaves differently before and after cracking. The stress–strain relationship follows a linear–elastic behavior before cracking, while tensile stress decays slowly as the tensile strain increases after cracking due to the bond interaction between the concrete and the reinforcement; this is known as the tension stiffening effect. By adopting the tension stiffening model proposed by Vecchio and Collins (1982) in Fig. 4, the principal tensile stress of concrete in the web shear element can be calculated as follows:

$$ f_{c1} = E_{c} \varepsilon_{1} \quad {\text{for}}\quad \varepsilon_{1} \le \varepsilon_{cr} $$
(22a)
$$ f_{c1} = \frac{{f_{cr} }}{{1 + \sqrt {200\varepsilon_{1} } }} \le f_{c1,\hbox{max} } \quad {\text{for}}\quad \varepsilon_{1} > \varepsilon_{cr} $$
(22b)

where \( f_{cr} \) is the cracking strength of concrete, and \( \varepsilon_{cr} \) is the cracking strain calculated from \( \varepsilon_{cr} = {{f_{cr} } \mathord{\left/ {\vphantom {{f_{cr} } {E_{c} }}} \right. \kern-0pt} {E_{c} }} \) where E c is the elastic modulus of concrete.

Fig. 4
figure 4

Principal tensile stress–strain response of concrete (Vecchio and Collins 1982).

Full size image

In Eq. (22b), \( f_{{c1,{ \hbox{max} }}} \) is the maximum limit of the tension stiffening effect, which considers local yielding of the steel reinforcements along crack. For the web shear element containing longitudinal and transverse steel reinforcements, \( f_{{c1,{ \hbox{max} }}} \) is calculated as following:

$$ f_{c1,\hbox{max} } = \rho_{sx} \left( {f_{sxy} - \varepsilon_{s} E_{s} - f_{sx} } \right)\cos^{2} \theta + \rho_{sy} \left( {f_{syy} - f_{sy} } \right)\sin^{2} \theta $$
(23)

Upon deriving the principal stresses in the concrete, the stiffness matrix for the concrete in the web shear element can then be developed using the secant stiffness formulation given as:

$$ \left[ {D_{c} } \right]' = \left[ {\begin{array}{*{20}c} {\overline{{E_{C1} }} } & 0 & 0 \\ 0 & {\overline{{E_{C2} }} } & 0 \\ 0 & 0 & {\overline{{G_{c} }} } \\ \end{array} } \right] $$
(24)

where \( \overline{{E_{C1} }} = f_{c1} /\varepsilon_{1} \), \( \overline{{E_{C2} }} = f_{c2} /\varepsilon_{2} \), and \( \overline{{G_{c} }} = \overline{{E_{C1} }} \overline{{E_{C2} }} /\left( {\overline{{E_{C2} }} + \overline{{E_{C2} }} } \right) \) as illustrated in Figs. 3 and 4.

To express \( \left[ {D_{c} } \right]^{\prime } \) along the longitudinal direction, the principal tensile stress angle, θ, is used to develop a transformation matrix given as:

$$ \left[ {T_{c} } \right] = \left[ {\begin{array}{*{20}c} {\cos^{2} \theta } & {\sin^{2} \theta } & {\cos \theta \sin \theta } \\ {\sin^{2} \theta } & {\cos^{2} \theta } & { - \cos \theta \sin \theta } \\ { - 2\cos \theta \sin \theta } & {2\cos \theta \sin \theta } & {\left( {\cos^{2} \theta - \sin^{2} \theta } \right)} \\ \end{array} } \right] $$
(25)

This is then combined with the local stiffness matrix for concrete \( \left[ {D_{c} } \right]' \) to give the global stiffness matrix for concrete [D c ] using the equation:

$$ [D_{c} ] = [T_{c} ]^{T} [D_{c} ]^{\prime}[T_{c} ] $$
(26)

2.6 Analysis Algorithm

In Fig. 5, the analysis algorithm describing the overall process of the proposed model to evaluate shear strength of RC beams is presented. The algorithm can be divided into two parts; the flexural analysis part and the shear analysis part.

Fig. 5
figure 5

Analysis algorithm.

Full size image

In the analysis algorithm, the longitudinal strain \( \varepsilon_{x} \) at mid-depth in a shear critical section is initially given. With the given \( \varepsilon_{x} \), the compressive strain at the top chord \( \varepsilon_{c} \) is assumed, then forces at the top and bottom chords can be calculated. Through iterative procedure, strain at the top chord satisfying force equilibrium along the critical section can be found. Then, shear stress along the web shear element \( \tau_{xy} \) can be calculated, which will be used as input for the shear analysis part. For the shear analysis part, the transverse strain \( \varepsilon_{y} \) and shear strain \( \gamma_{xy} \) are initially assumed. Through the shear analysis procedure for the web shear element, \( \varepsilon_{y} \) and \( \gamma_{xy} \) can be checked for convergence. If convergence is attained, it is indicated that the reinforced concrete beam can resist the applied load. To find the ultimate shear capacity, the longitudinal strain at the mid-depth \( \varepsilon_{x} \) is gradually increased, and the whole procedure is repeated again until \( \varepsilon_{y} \) and \( \gamma_{xy} \) diverge. When divergence is occurred, the shear force at the last analysis step just before the divergence can be defined as ultimate shear capacity of the reinforced concrete beam. The analysis was conducted with Matlab (2010).

3 Verification of the Proposed Model

3.1 Database for the Verification

Verification of the proposed model was conducted with 201 test results of RC beams with a rectangular cross section and stirrups exhibiting shear failure before yielding of the main longitudinal reinforcement (Clark 1951; Bresler and Scordelis 1963; Delbaiky and Elniema 1982; Smith and Vantsiotis 1982; Mphonde and Franz 1984; Hsiung and Frantz 1985; Elzanaty et al. 1986; Narayanan and Darwish 1987; Johnson and Ramirez 1989; Mau and Hsu 1989; Roller and Russell 1990; Saram and Al-Musawi 1992; Xie et al. 1994; Kriski 1996; Yoon et al. 1996; Shin et al. 1996; McGormley et al. 1996; Tan et al. 1997; Kong and Rangan 1998; Collins and Kuchma 1999; Peng 1999; Oh and Shin 2001; Angelakos et al. 2001; Tompos and Frosch 2002; Cho 2003). The shear strength based on Eurocode 2 (2004), ACI 318-14 (2014) and CSA A23.3 (2014) are also evaluated on these specimens, and compared against the results from the proposed model.

Parameters known to affect the shear strength of RC beams are also investigated to check whether the proposed model adequately accounts for their contribution in calculating the shear strength of the RC beams. These parameters are shown in the Table 2. Noted that the database in the table consists of 129 beams with \( a/d > 2.0 \) and 72 beams with \( a/d \le 2.0 \).

Table 2 Range of parameters in the test results for verification.
Full size table

3.2 Comparison Results

The results with the proposed model for 201 RC beams showed a mean value of 1.16 and a coefficient of variance (CoV) of 0.22 on the comparison between the experimental results and predicted values. A graphical representation of this result is presented in Fig. 6. To investigate the adequacy of the proposed model on prediction of shear strength for RC beams, comparison results with the predictions by the ACI 318-14 (2014), Eurocode 2 (2004) and CSA A23.3 (2014) were also presented in the figure. ACI 318-14 gave a mean value of 1.37 and a CoV of 0.31 while those of the Eurocode 2 gave a mean value of 1.39 and a CoV of 0.36, and those of CSA A23.3 was 1.39 and 0.32, respectively; the three shear design provisions showed larger values for the mean as well as CoV than those of the proposed model as presented in Table 3.

Fig. 6
figure 6

Shear strength prediction results.

Full size image
Table 3 Comparison between model predictions (prediction/test).
Full size table

Significant difference among the proposed model and the code provisions can also be found through Figs. 7, 8, 9, and 10 where effects of main parameters on shear strength were investigated. As can be seen in Fig. 7 and 8, no clear tendency was investigated with the effect of concrete compressive strength and member depth on the predictions for shear strength. On the other hand, as compared in Fig. 9, the effect of shear span-to-depth ratio was quite clear; ACI 318-14 and CSA A23.3 significantly underestimated shear strength of reinforced concrete beams with shear span-to-depth ratio less than 2. Unlike these two design provisions, predictions by Eurocode 2 were not significantly affected although it showed lots of scatter from the test results. In the case of the proposed model, predictions showed good agreement with the test results regardless of shear span-to-depth ratio as it considered the effect of arch action with Eq. (7a).

Fig. 7
figure 7

Variation in concrete compressive strength effect.

Full size image
Fig. 8
figure 8

Variation in effect of member size.

Full size image
Fig. 9
figure 9

Variation in effect of shear span-to-depth ratio.

Full size image
Fig. 10
figure 10

Variation in effect of shear reinforcement contribution.

Full size image

In addition, clear tendency was investigated with the effect of shear reinforcement ratio on the predictions for shear strength. As can be seen in Fig. 10, Eurocode 2 significantly underestimated shear strength of reinforced concrete beams with small shear reinforcement ratio because concrete contribution was not acknowledged. On the other hand, the proposed model still showed good agreement with the test results since concrete contribution was rationally acknowledged through the analysis of web shear element by employing the MCFT. It is noted that scatters with ACI 318-14 and CSA A23.3 were mainly due to the effect of shear span-to-depth ratio as investigated in Fig. 9, not due to the effect of shear reinforcement ratio.

Figure 11 shows more detailed investigations focused on angle of concrete compressive strut or diagonal crack which means how many stirrups have contribution on shear strength. As can be seen in the figure, the diagonal crack angle was constant to 45° according to ACI 318-14 while it was evaluated to 22° in most cases according to Eurocode 2. From these results, it can be inferred that shear strength provided by stirrups is generally underestimated by ACI 318-14 while overestimated by Eurocode 2. On the other hand, the proposed model and CSA A23.3 showed similar evaluation results on the diagonal crack angle since they were developed through simplification of the MCFT, although more scatter was found with the proposed model.

Fig. 11
figure 11

θ value variation in effect of stirrup reinforcement ratio.

Full size image

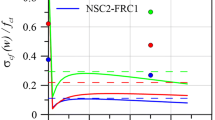
In addition to the diagonal crack angle, contribution of concrete on the shear strength was also investigated with a coefficient β, which is used in CSA A23.3 to evaluate the concrete contribution. The coefficient β can be evaluated from the following equation;

$$ \beta = \frac{{V_{n} - V_{s} }}{{\sqrt {f^{\prime}_{c} } bd}} $$
(27)

Figure 12 shows β values evaluated from the proposed model and the code provisions. As can be seen in the figure, β was constant by ACI 318-14 and Eurocode 2; 0.18 and 0.00, respectively. CSA A23.3 evaluated some variation on β mainly due to the flexural effect on the web. β was predicted within some range regardless of shear span-to-depth ratio. Since the effect of arch action was not considered, CSA A23.3 generally tended to underestimate shear strength of reinforced concrete beams with short shear span-to-depth ratio. On the other hand, the proposed model evaluated that β increased as shear span-to-depth ratio decreased when the shear span-to-depth ratio was smaller than 2, since it took the effect of arch action into the account.

Fig. 12
figure 12

β value variation in effect of a/d and \( f_{c}^{'} \).

Full size image

As investigated in Figs. 11 and 12, it can be concluded that the proposed model well captured stirrup and concrete contributions together through rational evaluation on diagonal crack angle and β coefficient. Consequently, this was resulted in comparison results that the proposed model showed good agreement with the test results on shear strength of reinforced concrete beams with stirrups.

4 Conclusion

In this paper, a rational analysis model to evaluate shear strength of reinforced concrete beams with stirrups has been developed. To develop the analysis model, a reinforced concrete beam was idealized with top and bottom chords and a single web shear element, which were designated to resist flexural bending moment and shear force, respectively. With consideration of the top and bottom chords, simple flexural analysis was employed, which gave longitudinal strain at the mid depth in a shear critical section. With the strain at the mid-depth, shear analysis was conducted for the single web shear element which was treated as a cracked orthotropic reinforced concrete element. For the shear analysis, finite element analysis procedure based on the MCFT was modified accordingly to consider the strain at the mid-depth. Thus, interaction between flexural and shear behaviors in a reinforced concrete beam could be rationally considered.

For verification of the developed analysis model, 201 reinforced concrete beams with stirrups exhibiting shear failure were analyzed. The comparison between the test results and predictions showed that the proposed analysis model well predicted the actual shear capacities of reinforced concrete beams while the shear design provisions such as ACI 318-14, Eurocode 2, and CSA A23.3 showed significant scatter on the predictions. Furthermore, contributions of stirrups and concrete, which were noted to θ and β, respectively, were evaluated with the proposed analysis model, and compared with the shear design provisions. It was investigated that the proposed analysis model well captured effect of main parameters on θ as like CSA A23.3, and it well reflected concrete contribution on shear strength, especially for beams with small shear span-to-depth ratio.

Although the developed analysis model is more complicating than the shear design provisions, contributions of concrete and stirrups at the ultimate can be rigorously evaluated, so it might be useful to develop more rational shear design provisions through simplification. In addition, through simple modification, the proposed analysis model would be useful to evaluate shear strength of reinforced concrete beams with advanced materials such as steel fibers, FRP sheets, and so on.

Since the developed analysis procedure considers linear-elastic behavior for the top and compression chords, the developed analysis procedure should be adequately modified to more precisely evaluate shear strength of reinforced concrete beams exhibiting yielding of main longitudinal rebars or crushing of top compression chord.