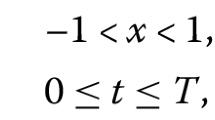1 Introduction

The use of the fractional-order derivative has become popular due to its nonlocality property, which is an intrinsic property of many complex systems. The fractional-order derivative has recently been applied in modeling different phenomena including viscoelasticity, financial modeling, nanotechnology, control theory of dynamical systems, random walk, anomalous transport, biological modeling, and anomalous diffusion as well. For further applications of the fractional order derivative in the fields of engineering, physical sciences, we may refer to [1–11] and [12–16] and the references cited therein.

The fractional partial differential equations (FPDEs) have been deployed in recent years as a powerful tool in nonlocality and spatial heterogeneity modelling. Many applications of the fractional models can be found in [17–21]. The fractional diffusion equation assumed in this paper covers not only the classic state of the heat equation but also the kernel of many other FPDEs. This equation describes the anomalous diffusion of particles. For applications of this equation, we refer to the one presented in [22], which describes the transfer processes with a long memory and the water transport in the soil model [23]. Many mathematical models are usually based on the diffusion model such as the diffusion equation on fractals [24], Fischer information theory [25], and so on. Moreover, the implication of the fractional in time (sub-diffusion) and fractional in space (super-diffusion) has been observed in the solution profiles in many fractional models [26, 27]. The superior capabilities of fractional differential equations to accurately model such processes have raised significant interest in assaying numerical methods for obtaining the solutions to such problems [28–30]. The analysis we present in this paper depends on the following time-fractional diffusion-wave problem:

$$\begin{aligned}& \partial ^{\alpha}_{t} u(x,t)=\Delta u(x,t)-u(x,t)+f(x,t),\quad (x,t) \in \Omega \times J, \end{aligned}$$
(1.1)
$$\begin{aligned}& u(0,t)=0, \qquad u(b,t)=0,\quad t \in \overline{J}, \end{aligned}$$
(1.2)
$$\begin{aligned}& u(x,0)=\phi _{1}(x), \qquad \partial _{t}u(x,0)=\phi _{2}(x),\quad x \in \overline{\Omega}, \end{aligned}$$
(1.3)

where \(\Omega =[0,b]\) is a bounded domain in R; \(J=(0,T]\) is the time interval satisfying \(0< T<+\infty \); \(u:\overline{\Omega} \times \overline{J} \rightarrow \mathbf{R}\) is a sufficiently differentiable function, and \(1< \alpha < 2\) is the order of the fractional derivative, and the time-fractional derivative \(\partial ^{\alpha}_{t}\) is the Caputo fractional derivative of order \(1<\alpha <2 \) defined by

$$\begin{aligned} \partial _{t}^{\alpha}u(x,t)=\frac{1}{\Gamma (2-\alpha )} \int _{0}^{t} \frac{\partial ^{2} u(x,s)}{\partial s^{2}} \frac{ds}{(t-s)^{\alpha -1}}. \end{aligned}$$

The reproducing theory was investigated by Mercer in 1909 [31]. He named functions satisfying the reproducing property as “positive definite kernels”. Around 1948, Aronszajn [32] systematized the concept of reproducing kernels. From 1980, Cui and co-workers [33, 34] have been pioneers and beginners in the numerical analysis of linear and nonlinear problems using the “reproducing kernel Hilbert space method”. Recently, a lot of research has been done to solve several linear and nonlinear problems using the theory of reproducing kernel [35–46].

The aim of this paper is to introduce a finite difference/pseudo-spectral method based on reproducing kernel (RK) for solving the time-fractional diffusion-wave equation (1.1)–(1.3). This paper spreads over four sections, including the introduction. In Sect. 2, we present a finite difference/pseudo-spectral method based on a reproducing kernel (RK) for solving the time-fractional diffusion-wave equation. In Sect. 2, we solve some test problems and derive several results. In Sect. 4, we present some concluding remarks.

2 Implementation of the method

2.1 Discretization of Caputo derivative and semi-discrete scheme

First, we obtain the semi-discrete scheme for (1.1)–(1.3). The discretization of J̅ is performed with a constant time step \(\tau =\frac{T}{N}\), where \(N \in \mathcal{N}^{*}\). Denote \(t_{n}=n \tau \) for \(N=0:N\). Let \(u^{n}=u(x,t_{n})\). For a discrete function \(\{u^{n}\}_{n=0}^{N+1}\), we provide some preliminaries concerning the approximation of the time fractional derivative \(\partial _{t}^{\alpha} u(x,t)\) with \(1<\alpha <2\). A Caputo derivative approximation formula (CDAF) for \(\partial _{t}^{\alpha} u(x,t_{n+1})\) with \(1<\alpha <2\) can be defined as a linear combination of the discrete second time derivatives \(\{\partial ^{2} u^{j}\}_{j=1}^{n+1}\) [47]

$$\begin{aligned} \partial _{t}^{\alpha}u^{n+1}= \frac{\tau ^{2-\alpha}}{\Gamma (3-\alpha )} \sum _{j=0}^{n}b_{j} \partial ^{2}u^{n+1-j}+\mathcal{R}_{1}^{n+1}(u), \end{aligned}$$
(2.1)

where

$$ b_{j}=(j+1)^{2-\alpha}-j^{2-\alpha},$$

and \(\mathcal{R}_{1}^{n+1}(u)\) is the local truncation error such that

$$ \bigl\vert \mathcal{R}_{1}^{n+1}(u) \bigr\vert \leq C_{u} \tau ^{3-\alpha} \text{or} \mathcal{R}_{1}^{n+1}(u)=O \bigl( \tau ^{3-\alpha}\bigr).$$

The following lemma summarizes some properties of the coefficients \(b_{j}\) which will be used in this paper.

Lemma 2.1

(See [47]. Properties of the coefficients \(b_{j}^{n+1}\))

For any \(1 < \alpha <2\), the coefficients of \(b_{j}^{n+1}\) satisfy the following properties:

  • \(b_{j}>0\), \(j=0,1,\ldots ,n\),

  • \(1=b_{0}>b_{1}>\cdots >b_{n}\) and \(b_{n} \rightarrow 0\) as \(n\rightarrow \infty \),

  • \(\sum_{j=0}^{n}(b_{j}-b_{j+1})=1\).

Substituting (2.1) into (1.1) gives

$$\begin{aligned}& a(\alpha ,\tau ) \bigl(u^{n+1}-2u^{n}+u^{n-1} \bigr)+a(\alpha ,\tau )\sum_{j=1}^{n} b_{j}\bigl(u^{n+1-j}-2u^{n-j}+u^{n-1-j}\bigr) \\& \quad =\Delta u^{n+1}(x)-u^{n+1}(x)+ f^{n+1}(x)+R^{n+1}(u), \end{aligned}$$
(2.2)

where \(a(\alpha ,\tau )=\frac{1}{\tau ^{\alpha}\Gamma (3-\alpha )}\) and \(f^{n+1}(x)=f(x,t_{n+1})\).

Replacing \(u^{n+1}\) by the approximate solution \(U^{n+1}\), we can obtain the following semi-discrete problem.

Scheme I

Given \(U^{0}=\phi _{1}(x)\), \(U^{-1}=U^{1}-2\tau \phi _{2}(x)\) and find \(U^{n+1}\) (\(n=0,1,2,\ldots ,N-1\)) such that

$$\begin{aligned} \textstyle\begin{cases} a(\alpha ,\tau )(U^{n+1}-2U^{n}+U^{n-1})+a(\alpha ,\tau )\sum_{j=1}^{n}b_{j}(U^{n+1-j}-2U^{n-j}+U^{n-1-j}) \\ \quad =\Delta U^{n+1}(x)-U^{n+1}(x)+ f^{n+1}(x), \\ U^{n+1}|_{x \in \partial \Omega}=0,\quad -1\leq n \leq N-1. \end{cases}\displaystyle \end{aligned}$$

For the convenience of discussion, define the linear operator L as follows:

$$\begin{aligned} \textrm{L} (*)=\textstyle\begin{cases} ((2a(\alpha ,\tau )+1)-\Delta ) (*),& n=0, \\ ((a(\alpha ,\tau )+1)-\Delta )(*),& 1\leq n \leq N-2. \end{cases}\displaystyle \end{aligned}$$

Therefore, a semi-discrete problem can be converted into the following equivalent:

$$\begin{aligned} \textrm{L} U^{n+1}(x)=F^{n+1}(x),\quad 0\leq n \leq N-1, \end{aligned}$$
(2.3)

where

$$ F^{n+1}(x)=\textstyle\begin{cases} -a(\alpha ,\tau )(-2\phi _{1}(x)-2\tau \phi _{2}(x))+ f^{1}(x),\quad n=0, \\ -a(\alpha ,\tau )(-2U^{n}+U^{n-1})-a(\alpha ,\tau )\sum_{j=1}^{n}b_{j}(U^{n+1-j} \\ \quad {}-2U^{n-j}+U^{n-1-j})+ f^{n+1}(x),\quad 1\leq n \leq N-2. \end{cases} $$

2.2 A pseudo-spectral kernel-based method

Now, we employ a pseudo-spectral method based on RK to discrete the space direction and obtain a full-discrete scheme of (2.3). To obtain this, we need some notations and preliminaries.

We now give background material and preliminaries, which are used in the following sections. Recall that a real reproducing kernel Hilbert space (RKHS) on a nonempty abstract set Ω is a particular type of a real Hilbert space H of functions that satisfies the following additional property (called reproducing kernel property): for each \(x\in \Omega \), there exists \(K(x,\cdot)\in \mathsf{H}\) (\(R:\Omega \times \Omega \longrightarrow \mathbf{R} \)) such that, for every \(u \in \mathsf{H}\), one has

$$\begin{aligned} u(x)=\bigl(u(\cdot),K(x,\cdot)\bigr)_{\mathsf{H}},\quad \forall u \in \mathsf{H}, \forall x \in \Omega . \end{aligned}$$
(2.4)

Definition 2.2

(See [40])

A Hilbert space H of real functions on a set Ω is called an RKHS if there exists an RK \(K(x,\cdot)\) of H.

Theorem 2.3

(See [40])

Suppose that \(\boldsymbol{\mathsf{H}}\) is an RKHS with RK \(K:\Omega \times \Omega \longrightarrow \mathbf{R} \). Then \(K(x,\cdot)\) is positive definite. Moreover, \(K(x,\cdot)\) is strictly positive definite if and only if the point evaluation functionals \(\bigl\{ \scriptsize{ \begin{array}{l@{\quad}l} I_{x}: \boldsymbol{\mathsf{H}}\longrightarrow \mathbf{R}, \\ I_{x}(u)=u(x) \end{array}}\) are linearly independent in \(\boldsymbol{\mathsf{H}}^{*}\), where \(\boldsymbol{\mathsf{H}}^{*}\) is the space of bounded linear functionals on \(\boldsymbol{\mathsf{H}}\).

Definition 2.4

(See [40]. One-dimensional RKHS)

The inner product space \(\boldsymbol{\mathsf{H}}_{p}[0,b]\) for a function u is defined as

$$\begin{aligned} \boldsymbol{\mathsf{H}}_{p}[0,b]=\bigl\{ u|u(x),u^{\prime }(x),u^{\prime \prime }(x)\in AC[0,b], u^{\prime \prime \prime }(x) \in L^{2}[0,b],u(0)=u(b)=0, x\in [0,b]\bigr\} . \end{aligned}$$

The inner product in \(\boldsymbol{\mathsf{H}}_{p}[0,b]\) is in the form

$$\begin{aligned} \langle u,v\rangle _{\boldsymbol{\mathsf{H}}_{p}}=u(0)v(0)+u(b)v(b)+u^{\prime }(0)v^{\prime }(0)+ \int _{a}^{b}u^{\prime \prime \prime }(x)v^{\prime \prime \prime }(x)\,dx, \end{aligned}$$
(2.5)

and the norm \(\|u\|_{\boldsymbol{\mathsf{H}}}\) is defined by

$$\begin{aligned} \Vert u \Vert _{\boldsymbol{\mathsf{H}}_{p}}=\sqrt{\langle u,u\rangle _{\mathsf{H}}}, \end{aligned}$$
(2.6)

where \(u,v\in \boldsymbol{\mathsf{H}}_{p}[0,b]\).

The space \(\boldsymbol{\mathsf{H}}_{p}[0,b]\) is an RKHS and the RK \(K_{y}(x)\) can be denoted by [40]

$$\begin{aligned} K_{y}(x)= \textstyle\begin{cases} \frac{1}{120b^{2}}(b-x)y(120bx+x(6b^{2}x-120-4bx^{2}+x^{3})y \\ \quad {}-5bxy^{3}+(b+x)y^{4}), \quad y< x, \\ \frac{1}{120b^{2}}(b-y)x(120by+y(6b^{2}y-120-4by^{2}+y^{3})x \\ \quad {}-5byx^{3}+(b+y)x^{4}), \quad y\geq x. \end{cases}\displaystyle \end{aligned}$$
(2.7)

With the help of pseudo-spectral method based on RK, we will illustrate how to derive the numerical solution. Now, we will give the representation of a numerical solution to the semi-discrete problem (2.3) in the RKHS \(\boldsymbol{\mathsf{H}}_{p}[0,b]\). Let \(\mathcal{B}_{M}=\{x_{j}\}_{j = 1}^{M}\) be a distinct subset of Ω̅. We consider the finite-dimensional space

$$\begin{aligned} \mathcal{U}_{M}=\operatorname{\textbf{span}}\bigl\{ \psi _{j}(x)=K_{y}(x)|_{y=x_{j}}, x_{j} \in \mathcal{B}_{M}\bigr\} \subset \boldsymbol{\mathsf{H}}_{p}[0,b], \end{aligned}$$

where \(K_{y}(x)\) is the RK constructed in \(\boldsymbol{\mathsf{H}}_{p}[0,b]\).

The semi-discrete problem can be written into following equivalent form \(\boldsymbol{\mathsf{H}}_{p}[0,b]\) to \(C[0,b]\):

$$\begin{aligned} \textrm{L} U^{n+1}(x)=F^{n+1}(x),\quad 0\leq n \leq N-1, \end{aligned}$$

where

$$ F^{n+1}(x)=\textstyle\begin{cases} -a(\alpha ,\tau )(-2\phi _{1}(x)-2\tau \phi _{2}(x))+ f^{1}(x),\quad n=0, \\ -a(\alpha ,\tau )(-2U^{n}+U^{n-1})-a(\alpha ,\tau )\sum_{j=1}^{n}b_{j}(U^{n+1-j} \\ \quad {}-2U^{n-j}+U^{n-1-j})+ f^{n+1}(x),\quad 1\leq n \leq N-2, \end{cases} $$

and \(F^{n+1}\in C[0,b]\) as \(u^{k}\in \boldsymbol{\mathsf{H}}_{p}[0,b]\).

An approximant \(U_{M}^{n+1}\) to \(U^{n+1}\) can be obtained by calculating a truncated series based on trial functions as follows:

U n + 1 ( x ) ≈ U M n + 1 ( x ) : = ∑ j = 1 M α j n + 1 ψ j ( x ) = [ ψ 1 ( x ) , ψ 2 ( x ) , … , ψ M ( x ) ] ( α 1 n + 1 α 2 n + 1 ⋮ α M n + 1 ) .
(2.8)

To determine the interpolation coefficients \(\{\alpha ^{n+1}_{j}\}_{j=1}^{M}\), the set of collocation conditions is used by applying (2.3) to \(\mathcal{B}_{M}\). Thus

$$ \lambda _{i}\bigl[U_{M}^{n+1} \bigr]:=\textrm{L} U_{M}^{n+1}(x_{i})=\sum _{j=1}^{M} \alpha ^{n+1}_{j} \textrm{L}\psi _{j}(x_{i})=F^{n+1}(x_{i}),\quad i=1,2, \ldots ,M, $$
(2.9)

where the functional \(\lambda _{i}\), (\(1\leq i \leq M\)) is defined by applying the differential operator followed by a point evaluation at \(x_{i} \in \mathcal{B}_{n}\). In general, a single set \(\Lambda _{M}:=\{\lambda _{i}\}_{i=1}^{M}\) of functionals contains several types of differential operators.

The arising collocation matrix K is unsymmetric and has the ij-entries:

$$ \textbf{K}_{ij}:=\lambda _{i}[\psi _{j}]=\lambda ^{x}_{i} K_{y}(x)|_{y=x_{j}},\quad 1 \leq i,j \leq M, $$
(2.10)

where the subscript x in \(\lambda ^{x}_{j}\) indicates that \(\lambda ^{x}_{j}\) applies to the function of x.

Therefore the unknown coefficients \(\alpha ^{n+1}_{j}\), \(j=1,2,\ldots ,M\), can be obtained by solving the following system:

$$\begin{aligned}& \textbf{K}[\alpha ]^{n+1}=\textbf{F}^{n+1}, \end{aligned}$$

where

$$\begin{aligned}& [\alpha ]^{n+1}=\bigl[\alpha _{1}^{n+1},\alpha _{2}^{n+1},\ldots ,\alpha _{M}^{n+1} \bigr]^{T},\\& \textbf{F}^{n+1}=\bigl[F^{n+1}(x_{1}),F^{n+1}(x_{2}), \ldots ,F^{n+1}(x_{M})\bigr]^{T}, \end{aligned}$$

and

K= ( λ 1 x K y ( x ) | y = x 1 λ 2 x K y ( x ) | y = x 1 ⋯ λ M x K y ( x ) | y = x 1 λ 1 x K y ( x ) | y = x 2 λ 2 x K y ( x ) | y = x 2 ⋯ λ M x K y ( x ) | y = x 2 ⋮ ⋮ ⋱ ⋮ λ 1 x K y ( x ) | y = x M λ 2 x K y ( x ) | y = x M ⋯ λ M x K y ( x ) | y = x M ) .
(2.11)

We know that

$$\begin{aligned} \textbf{U}^{n+1}=\textbf{A}[\alpha ]^{n+1}, \end{aligned}$$
(2.12)

where

$$\begin{aligned} \textbf{A}=[A_{ij}]_{M \times M},\qquad A_{ij}=\psi _{j}(x_{i}) \end{aligned}$$

and

$$\begin{aligned} \textbf{U}^{n+1}=\bigl[U^{n+1}(x_{1}),U^{n+1}(x_{2}), \ldots ,U^{n+1}(x_{M})\bigr]^{T}. \end{aligned}$$

The following matrix vector form is achieved by differentiating (2.12) with respect to x and evaluating it at the point girds \(x_{i}\in \mathcal{B}_{M}\):

$$\begin{aligned} \Delta \textbf{U}^{n+1}=\textbf{A}_{xx}[\alpha ]^{n+1}, \end{aligned}$$

where

$$\begin{aligned} \Delta \textbf{U}^{n+1}=\bigl[\Delta U^{n+1}(x_{1}), \Delta U^{n+1}(x_{2}), \ldots ,\Delta U^{n+1}(x_{M}) \bigr]^{T} \end{aligned}$$

and

$$\begin{aligned} \textbf{A}_{xx}=[A_{xx,ij}]_{M \times M},\qquad A_{xx,ij}= \frac{\partial ^{2}\psi _{j}}{\partial x^{2}}|_{x=x_{i}}. \end{aligned}$$

Now, from \(\textbf{U}^{n+1}=\textbf{A}[\alpha ]^{n+1}\) we have

$$\begin{aligned}{} [\alpha ]^{n+1}=\textbf{A}^{-1}\textbf{U}^{n+1}, \end{aligned}$$

and therefore

$$\begin{aligned} \Delta \textbf{U}^{n+1}=\textbf{A}_{xx} \textbf{A}^{-1}\textbf{U}^{n+1}. \end{aligned}$$
(2.13)

Now, by using (2.13), we can write

$$\begin{aligned} \textbf{K} \textbf{U}^{n+1}=\textbf{F}^{n+1},\quad 0 \leq n \leq N-2, \end{aligned}$$

where

$$\begin{aligned} \textbf{K}=\textstyle\begin{cases} ((2a(\alpha ,\tau )+1)\textbf{I}-\textbf{A}_{xx}\textbf{A}^{-1} ) ,& n=0, \\ ((a(\alpha ,\tau )+1)\textbf{I}-\textbf{A}_{xx}\textbf{A}^{-1} ),& 1\leq n \leq N-2, \end{cases}\displaystyle \end{aligned}$$
(2.14)

and

$$ \textbf{F}^{n+1}=\textstyle\begin{cases} a(\alpha ,\tau )(2\Phi _{1}+2\tau \Phi _{2})+ \textbf{f}^{1},\quad n=0, \\ -a(\alpha ,\tau )(-2\textbf{U}^{n}+\textbf{U}^{n-1})-a(\alpha ,\tau ) \sum_{j=1}^{n}b_{j}(\textbf{U}^{n+1-j} \\ \quad {}-2\textbf{U}^{n-j}+\textbf{U}^{n-1-j})+ \textbf{f}^{n+1}, \quad 1\leq n \leq N-2, \end{cases} $$

in which

$$\begin{aligned} \textbf{f}^{n+1}=\bigl[ f^{n+1}(x_{1}), f^{n+1}(x_{2}),\ldots ,f^{n+1}(x_{M}) \bigr]^{T} \end{aligned}$$

and

$$\begin{aligned} \Phi _{j}=\bigl[ \phi _{j}(x_{1}), \phi _{j}(x_{2}),\ldots ,\phi _{j}(x_{M}) \bigr]^{T},\quad j=1,2. \end{aligned}$$

2.3 Nonsingularity of the collocation matrix

Lemma 2.5

(See [40])

Let \(K_{y}(x)\) be the reproducing kernel of the space \(\boldsymbol{\mathsf{H}}_{p}[0,b]\), then

$$ \frac{\partial ^{i+j}K_{y}(x)}{\partial x^{i} \partial y^{j}}, \quad 0 \leq i+j \leq 2, $$
(2.15)

is absolutely continuous with respect to x and y.

Lemma 2.6

Let \(\{x_{j}\}_{j=1}^{\infty}\) be dense in the domain \([0,b]\) and the set of functions \(\{\lambda ^{x}_{j} K(x,\cdot)\}_{j=1}^{M}\) be linearly independent on the reproducing kernel space \(\boldsymbol{\mathsf{H}}_{p}[0,b]\). Then the set of vectors \(\{( \lambda ^{x}_{j} K_{y}(x)|_{y=x_{1}},\lambda ^{x}_{j} K_{y}(x)|_{y=x_{2}}, \ldots )^{T}\}_{j=1}^{M}\) is linearly independent.

Proof

If \(\{c_{j}\}_{j=1}^{M}\) satisfies \(\sum_{j=1}^{M}c_{j}( \lambda ^{x}_{j} K_{y}(x)|_{y=x_{1}},\lambda ^{x}_{j} K_{y}(x)|_{y=x_{2}},\ldots )^{T}=0\), one can deduce that

$$\begin{aligned} \sum_{j=1}^{M}c_{j} \lambda ^{x}_{j} K_{y}(x)|_{y=x_{i}}=0, \quad i\geq 1. \end{aligned}$$
(2.16)

From Lemma 2.5 it is clear that the functions \(\lambda ^{x}_{j} K(x,\cdot)\) for \(\lambda _{j} \in \Lambda _{M}\) are continuous. Furthermore, note that \(\{x_{i}\}_{i \geq 1}\) is a dense set. Therefore \(\sum_{j=1}^{M}c_{j} \lambda ^{x}_{j} K(x,\cdot)=0\), which implies that \(c_{j}=0\) (\(j=1,2,\ldots ,M\)). This completes the proof. □

From Lemma 2.6 we can extract the following theorem.

Theorem 2.7

Let the set of functions \(\{\lambda ^{x}_{j} K(x,\cdot)\}_{j=1}^{M}\) be linearly independent on \(\boldsymbol{\mathsf{H}}_{p}[0,b]\). Then there exist m points \(\mathcal{B}_{n}=\{x_{j}\}_{j=1}^{M}\) such that the collocation matrix K is nonsingular.

Lemma 2.8

Let the set of functionals \(\{\lambda _{j}\}_{j=1}^{M}\) be linearly independent on \(\boldsymbol{\mathsf{H}}_{p}[0,b]\). Then the set of functions \(\{\lambda ^{x}_{j} K(x,\cdot)\}_{j=1}^{M}\) is linearly independent.

Proof

If \(\{c_{j}\}_{j=1}^{M}\) satisfies \(\sum_{j=1}^{M}c_{j}\lambda ^{x}_{j} K(x,\cdot)=0\), then we get

$$\begin{aligned} 0 =&\Biggl\langle U(\cdot),\sum_{j=1}^{M}c_{j} \lambda ^{x}_{j} K(x,\cdot)\Biggr\rangle _{ \boldsymbol{\mathsf{H}}_{p}} \\ =&\sum _{j=1}^{M}c_{j}\lambda ^{x}_{j} \bigl\langle U(\cdot), K(x,\cdot)\bigr\rangle _{\boldsymbol{\mathsf{H}}_{p}} \\ =&\sum_{j=1}^{M}c_{j}\lambda _{j}[U], \quad \forall U \in \boldsymbol{\mathsf{H}}_{p}[0,b], \end{aligned}$$
(2.17)

which implies that \(c_{j}=0\) (\(j=1,2,\ldots ,M\)), and this completes the proof. □

From Lemma 2.8 and Theorem 2.7, we can derive the following theorem.

Theorem 2.9

Let the set of functionals \(\{\lambda _{j}\}_{j=1}^{M}\) be linearly independent on \(\boldsymbol{\mathsf{H}}_{p}[0,b]\). Then there exist n points \(\mathcal{B}_{n}=\{x_{j}\}_{j=1}^{n}\) such that the collocation matrix K is nonsingular.

2.4 Error analysis

Suppose that \(\mathcal{B}_{M}=\{x_{i}\}_{i = 1}^{M}\) and \(\mathcal{U}_{M}=\operatorname{Span}\{\psi _{1},\psi _{2},\ldots , \psi _{M}\}\). Applying the Gram–Schmidt orthogonalization process to \(\{\psi _{1},\psi _{2},\ldots , \psi _{M}\}\), we can obtain

$$\begin{aligned} \overline{\psi}_{i}(x)=\sum _{k=1}^{i}\beta _{ik}\psi _{k}(x),\quad ( \beta _{ii}>0,i=1,2,\ldots ,M). \end{aligned}$$
(2.18)

Therefore \(\{\overline{\psi}_{1},\overline{\psi}_{2},\ldots , \overline{\psi}_{n} \}\) is an orthonormal basis for \(\mathcal{U}_{M}\).

Therefore, we can write the interpolant \(U_{M}^{n+1}(x)\) to \(U^{n+1}\) at \(\mathcal{B}_{n}\) in the following form:

$$ U^{n+1}(x)\approx U_{M}^{n+1}(x)= \sum_{i=1}^{m}U^{n+1}(x_{i}) \overline{\psi}_{i}(x). $$
(2.19)

Theorem 2.10

Suppose that \(U_{M}^{n+1}(x) \in \boldsymbol{\mathsf{H}}_{p}[0,b]\) and \(U^{n+1}(x)\) are the approximate solution and exact solution for (2.3), respectively. Then, for any \(U^{n+1}(x) \in \boldsymbol{\mathsf{H}}_{p}[0,b]\), we have

$$\begin{aligned} \bigl\vert U^{n+1}(x)-U_{M}^{n+1}(x) \bigr\vert \leq \bigl\Vert U^{n+1} \bigr\Vert _{\boldsymbol{\mathsf{H}}_{p}} \Biggl\Vert K(x,\cdot)-\sum_{i=1}^{M}\overline{ \psi}_{i}(x)\psi _{i} \Biggr\Vert _{ \boldsymbol{\mathsf{H}}_{p}}. \end{aligned}$$
(2.20)

Proof

Using the reproducing property, we have

$$\begin{aligned} U_{M}^{n+1}(x) =&\sum_{i=1}^{M}U^{n+1}(x_{i}) \overline{\psi}_{i}(x) \\ =&\sum_{i=1}^{M}\bigl\langle U^{n+1},\psi _{i}\bigr\rangle _{ \boldsymbol{\mathsf{H}}_{p}}\overline{ \psi}_{i}(x) \\ =& \Biggl\langle U^{n+1},\sum_{i=1}^{M} \overline{\psi}_{i}(x)\psi _{i} \Biggr\rangle _{\boldsymbol{\mathsf{H}}_{p}}. \end{aligned}$$
(2.21)

Thus

$$\begin{aligned} \bigl\vert U^{n+1}(x)-U_{M}^{n+1}(x) \bigr\vert =& \Biggl\vert \Biggl\langle U^{n+1},K(x,\cdot)-\sum _{i=1}^{M} \overline{\psi}_{i}(x)\psi _{i}\Biggr\rangle _{\boldsymbol{\mathsf{H}}_{p}} \Biggr\vert \\ \leq& \bigl\Vert U^{n+1} \bigr\Vert _{\boldsymbol{\mathsf{H}}_{p}} \Biggl\Vert K(x,\cdot)-\sum_{i=1}^{M} \overline{ \psi}_{i}(x)\psi _{i} \Biggr\Vert _{\boldsymbol{\mathsf{H}}_{p}}. \end{aligned}$$
(2.22)

Thus, the proof is completed. □

Lemma 2.11

(See [48])

Suppose that \(u \in C^{3}[0,b]\) and \(\mathcal{B}_{M}=\{x_{i}\}_{i = 1}^{M} \subset [0,b] \) is a distinct subset of \([0,b]\), then

$$ \Vert U \Vert _{L^{2}[0,b]} \leq d \max _{x_{j} \in \mathcal{B}_{n}} \bigl\vert U(x_{j}) \bigr\vert +ch^{3} \biggl\Vert \frac{d^{3}U}{dx^{3}} \biggr\Vert _{L^{2}[0,b]},\quad h=\sup_{x \in [0,b]}\min_{x_{j} \in \mathcal{B}_{M}} \Vert x-x_{j} \Vert , $$
(2.23)

where c and d are real constants.

Theorem 2.12

If \(U^{n+1}_{M}\) is the approximate solution of (2.3) in the space \(\boldsymbol{\mathsf{H}}_{p}\). Then the following relation holds:

$$\begin{aligned} \bigl\Vert U^{n+1}-U_{M}^{n+1} \bigr\Vert _{L^{2}[0,b]} \leq ch^{3} \bigl\Vert U^{n+1} \bigr\Vert _{ \boldsymbol{\mathsf{H}}_{p}}, \end{aligned}$$
(2.24)

where c is a real constant.

Proof

According to Lemma 2.11, we have

$$\begin{aligned}& \bigl\Vert U^{n+1}-U_{M}^{n+1} \bigr\Vert _{L^{2}[0,b]} \\& \quad \leq d \max_{x_{j} \in \mathcal{B}_{n}} \bigl\vert U^{n+1}(x_{j})-U_{M}^{n+1}(x_{j}) \bigr\vert \\& \qquad {} +ch^{3} \biggl\Vert \frac{d^{3}U^{n+1}}{dx^{3}}- \frac{d^{3}U_{M}^{n+1}}{dx^{3}} \biggr\Vert _{L^{2}[0,b]} \\& \quad \leq ch^{3} \bigl\Vert U^{n+1}-U_{M}^{n+1} \bigr\Vert _{\boldsymbol{\mathsf{H}}_{p}}, \end{aligned}$$
(2.25)

where d and c are constants.

We know that

$$\begin{aligned} \bigl\Vert U^{n+1} \bigr\Vert ^{2}_{\boldsymbol{\mathsf{H}}_{p}}= \bigl\Vert U^{n+1}-U_{M}^{n+1} \bigr\Vert ^{2}_{ \boldsymbol{\mathsf{H}}_{p}}+ \bigl\Vert U_{M}^{n+1} \bigr\Vert ^{2}_{\boldsymbol{\mathsf{H}}_{p}}+2 \langle U-U_{M},U_{M} \rangle _{\boldsymbol{\mathsf{H}}_{p}}. \end{aligned}$$

Since

$$\begin{aligned} \langle U-U_{M},U_{M}\rangle _{\boldsymbol{\mathsf{H}}_{p}} =&\Biggl\langle U-U_{M}, \sum_{j=1}^{M} \alpha ^{n+1}_{j}\psi _{j}\Biggr\rangle _{ \boldsymbol{\mathsf{H}}_{p}} \\ =&\sum_{j=1}^{M}\alpha ^{n+1}_{j}\bigl\langle U-U_{M},K(\cdot ,x_{j}) \bigr\rangle _{ \boldsymbol{\mathsf{H}}_{p}} \\ =&\sum_{j=1}^{M} \alpha ^{n+1}_{j} (U-U_{M}) (x_{j})=0, \end{aligned}$$

then

$$\begin{aligned} \bigl\Vert U^{n+1} \bigr\Vert ^{2}_{\boldsymbol{\mathsf{H}}_{p}}= \bigl\Vert U^{n+1}-U_{M}^{n+1} \bigr\Vert ^{2}_{ \boldsymbol{\mathsf{H}}_{p}}+ \bigl\Vert U_{M}^{n+1} \bigr\Vert ^{2}_{\boldsymbol{\mathsf{H}}_{p}}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \bigl\Vert U^{n+1}-U_{M}^{n+1} \bigr\Vert _{\boldsymbol{\mathsf{H}}_{p}} \leq \bigl\Vert U^{n+1} \bigr\Vert _{ \boldsymbol{\mathsf{H}}_{p}}. \end{aligned}$$
(2.26)

Now, from (2.25) and (2.26), we can obtain

$$\begin{aligned}& \bigl\Vert U^{n+1}-U_{M}^{n+1} \bigr\Vert _{L^{2}[0,b]} \leq ch^{3} \bigl\Vert U^{n+1} \bigr\Vert _{ \boldsymbol{\mathsf{H}}_{p}}. \end{aligned}$$
(2.27)

Thus, the proof is completed. □

3 Illustrative test problems

We have studied some example tests to illustrate the performance of the proposed methods. We show the stability and accuracy of the proposed method for different values of M and N.

As the exact solution is known, the root mean square error \(L_{rms}\) and the maximum absolute error \(L_{\infty}\) are measured with the following formulas:

$$\begin{aligned} L_{rms}= \sqrt{\frac{1}{M}\sum _{i=1}^{M} \bigl\vert u^{N}(x_{i})-U^{N}_{M}(x_{i}) \bigr\vert ^{2}} \end{aligned}$$

and

$$\begin{aligned} L_{\infty}= \max_{1\leq i \leq M} \bigl\vert u^{N}(x_{i})-U^{N}_{M}(x_{i}) \bigr\vert . \end{aligned}$$

Example 3.1

In this example, we deal with the following problem:

$$\begin{aligned}& \partial ^{\alpha}_{t} u(x,t)=\Delta u(x,t)-u(x,t)+f(x,t),\quad (x,t) \in (0,1) \times (0,1], \end{aligned}$$
(3.1)
$$\begin{aligned}& u(0,t)=0,\qquad u(1,t)=0,\quad t \in [0,1], \end{aligned}$$
(3.2)
$$\begin{aligned}& u(x,0)=0, \qquad \partial _{t}u(x,0)=0,\quad x \in [0,1], \end{aligned}$$
(3.3)

where

$$\begin{aligned} f(x,t)=\sin (\pi x) \biggl(\frac{2 t^{-\alpha +2}}{\Gamma (-\alpha +3)} +t^{2} \pi ^{2} +t^{2} \biggr). \end{aligned}$$

The exact solution u is given by \(u(x,t)=t^{2} \sin (\pi x)\). The proposed method in the previous section is tested on this problem with \(\{t_{n}=\frac{n}{N} \}_{n=0}^{N}\), \(N=100\), \(\{x_{i}=\frac{i}{M+1}\}_{i=1}^{M}\), \(M=5,10,20,40\).

We consider the RKHS \(\boldsymbol{\mathsf{H}}_{p}[0,1]\) with the following RK:

$$\begin{aligned} K_{x}(y)= \textstyle\begin{cases} \frac{1}{120}(1-x)y(120x+x(6x-120-4x^{2}+x^{3})y-5xy^{3}+(1+x)y^{4}), & y< x, \\ \frac{1}{120}(1-y)x(120y+y(6y-120-4y^{2}+y^{3})x-5yx^{3}+(1+y)1x^{4}), & y\geq x. \end{cases}\displaystyle \end{aligned}$$

In Tables 1 and 2, we present, the root mean square error \(L_{rms}\), the maximum absolute error \(L_{\infty}\), and the convergence ratio in the computed solutions for Example 3.1 with \(\alpha =1.2,1.4,1.8,1.9\). In a considerable number of cases, an exciting agreement between the results is observed, which confirms the excellent validity of the proposed method.

Table 1 The maximum absolute error \(L_{\infty}\) for different values of α with \(N=100\) (Example 3.1).
Full size table
Table 2 The root mean square error \(L_{rms}\) for different values of α with \(N=100\) (Example 3.1).
Full size table

Example 3.2

In this example, we deal with the following problem:

$$\begin{aligned}& \partial ^{\alpha}_{t} u(x,t)=\Delta u(x,t)-u(x,t)+f(x,t),\quad (x,t) \in (0,2) \times (0,1], \end{aligned}$$
(3.4)
$$\begin{aligned}& u(0,t)=0, \qquad u(2,t)=0, \quad t \in [0,1], \end{aligned}$$
(3.5)
$$\begin{aligned}& u(x,0)=0, \qquad \partial _{t}u(x,0)=0,\quad x \in [0,1], \end{aligned}$$
(3.6)

where

$$\begin{aligned} f(x,t)= \frac{e^{-x}(8t^{2-\alpha}\sin (\frac{\pi}{2}x)+4t^{2}\cos (\frac{\pi}{2}x)\pi \Gamma (3-\alpha )+t^{2}\sin (\frac{\pi}{2}x)\pi ^{2}\Gamma (3-\alpha ))}{4\Gamma (3-\alpha )}. \end{aligned}$$

The exact solution u is given by \(u(x,t)=t^{2} e^{-x}\sin (\frac{\pi}{2}x)\). The proposed method in the previous section is tested on this problem with \(\{t_{n}=\frac{n}{N} \}_{n=0}^{N}\), \(N=120\), \(\{x_{i}=\frac{2i}{M+1}\}_{i=1}^{M}\), \(M=5,10,20,40\).

We consider the RKHS \(\boldsymbol{\mathsf{H}}_{p}[0,2]\) with the following RK:

$$\begin{aligned} K_{x}(y)= \textstyle\begin{cases} \frac{1}{480}(2-x)y(240x+x(24x-120-8x^{2}+x^{3})y-10xy^{3}+(2+x)y^{4}), & y< x, \\ \frac{1}{120}(2-y)x(240y+y(24y-120-8y^{2}+y^{3})x-10yx^{3}+(2+y)x^{4}), & y\geq x. \end{cases}\displaystyle \end{aligned}$$

In Tables 3 and 4, we present the root mean square error \(L_{rms}\), the maximum absolute error \(L_{\infty}\), and the convergence ratio in the computed solutions for Example 3.2 with \(\alpha =1.3,1.5,1.7,1.95\). In a considerable number of cases, an exciting agreement between the results is observed, which confirms the excellent validity of the proposed method.

Table 3 The maximum absolute error \(L_{\infty}\) for different values of α with \(N=100\) (Example 3.2).
Full size table
Table 4 The root mean square error \(L_{rms}\) for different values of α with \(N=100\) (Example 3.2).
Full size table

4 Conclusion

In this paper, a finite difference/pseudo-spectral method is presented to solve time-fractional diffusion-wave equation. The method is based on a finite difference method in a temporal direction to obtain a semi-discrete configuration, whereas a pseudo-spectral method based on RK introduces spatial discretization. The implementation of the proposed method is very simple and has reasonable accuracy. It can be seen from the error norms and numerical results that the proposed method for solving time-fractional diffusion-wave equation is an excellent method.