1 Introduction

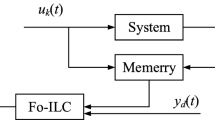
Iterative learning control (ILC) has become one of the most active fields in intelligent control methodology since the early study for robotic systems trajectory tracking in [1]. The mechanism of the ILC is that, for a control system which repeatedly operates over a finite time interval, in order to enable the system to achieve perfectly tracking as the iteration number increases successively, the ILC unit utilizes the information from the previous operation to modify an unsatisfactory control input signal. One of the important advantages of the ILC is that it requires less prior knowledge to generate iteratively a sequence of control input signals [2–6].

The fractional order iterative learning control (FOILC) is the latest trend in ILC research, it not only retains the advantages of the classical ILC, but also offers potential for better performances in a variety of complex physical processes [7–9]. Even since the above literature suggested this good learning performance, there have been made some efforts to synthesize a better FOILC updating law for various types of fractional order systems, and we have witnessed some progress in the following 16 years [10–16]. However, there still remain some restrictions which hinder further applications of the FOILCs in practice.

The obvious restriction of FOILCs is about the initial state value of the controlled fractional order system. It should be noted that perturbed initial state would degrade the tracking performance [17–19]. In the existing literature, requirements are that the initial state value should be equal to the desired one at each iteration. However, due to the effect of unavoidable noise or unidentified friction in practical engineering, the system cannot guarantee the initial value of state to the desired point. That means the initial state shift exists in the practice system, which motivates us for our study.

Besides, in the existing literature, the tracking error is analyzed in the sense of λ-norm. However, Lee and Bien [20] reported that the so-called λ-norm may not be a satisfactory measure of error in application. This is because of the λ-norm is a time decreasing weighted sup-norm, although the error becomes larger and larger near the terminal time, its λ-norm still decreases. In other words, the λ-norm may conceal the maximum absolute magnitude of the error signal, which would be very detrimental to engineering systems [21]. In order to avoid the above-mentioned phenomenon, for the Lebesgue-p norm it was reported in [22] that it is more suitable for error measure on performance than the λ-norm. Consequently, it is crucial to investigate the error measure with respect to Lebesgue-p norm in FOILCs. Recall that, for a time-varying vector function \(f: [ 0,T ] \to R^{m}\), \(f ( t ) = [ f^{1} ( t ), \ldots,f^{m} ( t ) ]^{\mathrm{T}}\), the λ-norm is defined as [18]

$$\bigl\Vert f ( \cdot ) \bigr\Vert _{\lambda} = \sup _{0 \le t \le T}e^{ - \lambda t} \Bigl( \max_{1 \le i \le m} \bigl\vert f^{i} ( t ) \bigr\vert \Bigr),\quad \lambda > 0, $$

and the Lebesgue-p norm is defined as

$$\bigl\Vert f ( \cdot ) \bigr\Vert _{p} = \biggl[ \int_{0}^{T} \Bigl( \max_{1 \le i \le m} \bigl\vert f^{i} ( t ) \bigr\vert \Bigr)^{p}\,dt \biggr]^{\frac{1}{p}},\quad 1 \le p \le \infty. $$

Motivated by the limitation of the initial state value of FOILCs and the mentioned drawback of the λ-norm, in this paper, we address the initial state shift problem for a more realistic situation by alleviating the requirement so that the initial state \(x_{k} ( 0 )\) at each iteration k lies in a neighborhood of a random initial point \(x_{0}\). The main contribution of this paper is to consider the initial state shift for a class of fractional order linear systems, and then incorporate a rectifying action into various proportional-α-order-derivative-type ILC algorithms to alleviate the tracking error caused by such a shift. The algorithms include the first- and second-order as well as feedback-based proportional-α-order-derivative-type ILCs. It is also important to note that many new theoretic analysis methods are explored to analyze the tracking performance in the sense of the Lebesgue-p norm.

The remainder of this paper is organized in five parts. In Section 2, the definitions and some properties of fractional order derivatives and some lemmas are revisited. In Section 3, FOILC schemes with rectifying action are presented and the main result on the tracking performance of the proposed schemes are discussed. In Section 4, numerical examples are given to illustrate the performance of the proposed schemes. Finally, a brief conclusion is given in Section 5.

2 Preliminaries

Definition 2.1

([23])

For an arbitrary integrable function \(f ( t ):[ 0,\infty ) \to R\), the left-sided and the right-sided fractional integrals are defined as

$$\begin{gathered} {}_{0}I_{t}^{\alpha} f ( t ) = \frac{1}{\Gamma ( \alpha )} \int_{0}^{t} \frac{f ( \tau )}{ ( t - \tau )^{1 - \alpha}} \,\mathrm{d}\tau,\quad t \in [ 0,\infty ), \\ {}_{t}I_{T}^{\alpha} f ( t ) = \frac{1}{\Gamma ( \alpha )} \int_{t}^{T} \frac{f ( \tau )}{ ( \tau - t )^{1 - \alpha}} \,\mathrm{d}\tau,\quad t \in [ 0,\infty ), \end{gathered} $$

where \(\Gamma ( \cdot )\) is the Gamma function and \(\Gamma ( \alpha ) = \int_{0}^{\infty} x^{\alpha - 1} e^{ - x}\,\mathrm{d}x\); \({}_{0}I_{t}^{\alpha}\), \({}_{t}I_{T}^{\alpha} \) are the left-sided and right-sided fractional integral of order α (\(\alpha > 0 \)) on \([ 0,{t} ]\), \([ t,T ]\), respectively.

Property 2.1

([23])

If \(\alpha > 0\), then \({}_{0}I_{t}^{\alpha} t^{\gamma} = \frac{\Gamma ( \gamma + 1 )}{\Gamma ( \gamma + 1 + \alpha )}t^{\gamma + \alpha} \), \(\gamma > - 1\), \(t > 0\).

Definition 2.2

([23])

For a given number \(\alpha > 0\), the left-sided and the right-sided α-order Caputo-type derivatives of the function \(f ( t ): [ 0,\infty ) \to R\) are defined as

$$\begin{gathered} {}_{0}^{C}D_{t}^{\alpha} f ( t ) = \frac{1}{\Gamma ( n - \alpha )} \int_{0}^{t} \frac{f^{ ( n )} ( \tau )}{ ( t - \tau )^{\alpha - n + 1}}\,\mathrm{d}\tau,\quad n - 1 < \alpha < n,t \in [ 0,\infty ), \\ {}_{t}^{C}D_{T}^{\alpha} f ( t ) = ( - 1 )^{n}\frac{1}{\Gamma ( n - \alpha )} \int_{t}^{T} \frac{f^{ ( n )} ( \tau )}{ ( \tau - t )^{\alpha - n + 1}} \,\mathrm{d}\tau,\quad n - 1 < \alpha < n,t \in [ 0,\infty ), \end{gathered} $$

where n is an integer and \(f^{ ( n )} ( t ) = \frac{\mathrm{d}^{n}}{\mathrm{d}t^{{n}}}f ( t )\); \({}_{0}^{C}D_{t}^{\alpha}\), \({}_{t}^{C}D_{T}^{\alpha} \) are the left-sided and right-sided Caputo-type derivatives of order α on \([ 0,{t} ]\), \([ t,T ]\), respectively.

For convenience, we denote \({}_{0}D_{t}^{\alpha} = {}_{0}^{C}D_{t}^{\alpha} \) and \({}_{t}D_{T}^{\alpha} = {}_{t}^{C}D_{T}^{\alpha} \) in the following.

Property 2.2

([23])

If \(\alpha > 0\), \(f ( t )\) is continuous on \([ 0,\infty )\), then \({}_{0}D_{t}^{\alpha} ({}_{0}I_{t}^{\alpha} f(t)) = f ( t )\) and \({}_{t}D_{T}^{\alpha} ({}_{t}I_{T}^{\alpha} f(t)) = f ( t )\).

Property 2.3

([16])

If \(0 < \alpha < 1\), \(f ( t )\) is continuous on \([ 0,\infty )\), then \({}_{0}D_{t}^{1 - \alpha} {}_{0}D_{t}^{\alpha} f ( t ) = f^{ ( 1 )} ( t )\), where \(f^{ ( 1 )} ( t ) = \frac{\mathrm{d}}{\mathrm{d}t}f ( t )\).

Definition 2.3

([23])

A single-parameter Mittag-Leffler function is defined by

$$E_{\alpha} (z) = \sum_{k = 0}^{\infty} \frac{z^{k}}{\Gamma ( k\alpha + 1 )},\quad \alpha > 0, z \in C^{n \times n}. $$

A two-parameter Mittag-Leffler function is defined by

$$E_{\alpha,\beta} (z) = \sum_{k = 0}^{\infty} \frac{z^{k}}{\Gamma ( k\alpha + \beta )},\quad \alpha > 0,\beta > 0, z \in C^{n \times n}. $$

It is obvious that \(E_{\alpha} ( z ) = E_{\alpha,1} ( z )\) and \(E_{1,1} ( z ) = e^{z}\).

Lemma 2.1

([16])

The series \(E_{\alpha,\beta} (z)\) (\(\alpha > 0\), \(\beta > 0\)) is absolutely convergent on \(\Vert z \Vert < \infty\).

Lemma 2.2

([23], Fractional integration by parts)

For continuous functions \(f ( t )\), \(g ( t )\) on \([ 0,T ]\), the derivatives \({}_{0}D_{t}^{\alpha} f ( t )\) and \({}_{0}D_{t}^{\alpha} g ( t )\) exist at every point \(t \in [ 0,T ]\) and are continuous. Then we have

$$\int_{0}^{T} \bigl( {}_{0}D_{t}^{\alpha} f ( t ) \bigr) g ( t )\,\mathrm{d}t = \int_{0}^{T} f ( t ) \bigl( {}_{t}D_{T}^{\alpha} g ( t ) \bigr)\,\mathrm{d}t. $$

Lemma 2.3

([24], Generalized Young inequality of convolution integral)

For Lebesgue integrable scalar functions \(g,h: [ 0,T ] \in R\), the generalized Young inequality of their convolution integral is

$$\bigl\Vert g * h ( \cdot ) \bigr\Vert _{r} \le \bigl\Vert g ( \cdot ) \bigr\Vert _{q} \bigl\Vert h ( \cdot ) \bigr\Vert _{p}, $$

where \(1 \le p,q,r \le \infty\) satisfy \(\frac{1}{r} = \frac{1}{p} + \frac{1}{q} - 1\). Particularly, when \(r = p\) and thus \(q = 1\), then the inequality of convolution integral is

$$\bigl\Vert g * h ( \cdot ) \bigr\Vert _{p} \le \bigl\Vert g ( \cdot ) \bigr\Vert _{1} \bigl\Vert h ( \cdot ) \bigr\Vert _{p}. $$

Lemma 2.4

([25])

Let \(\{ a_{k},k = 1,2, \ldots \}\) be a real sequence defined as

$$a_{k} \le \rho_{1}a_{k - 1} + \rho_{2}a_{k - 2} + \cdots + \rho_{M}a_{k - M} + d_{k},\quad k \ge M + 1, $$

with initial conditions

$$a_{1} = \bar{a}_{1},\qquad a_{2} = \bar{a}_{2},\qquad \ldots, \qquad a_{M} = \bar{a}_{M}, $$

where \(d_{k}\) is a specified real sequence. If \(\rho_{1},\rho_{2}, \ldots,\rho_{M}\) are nonnegative numbers satisfying

$$\rho = \sum_{j = 1}^{M} \rho_{j} < 1. $$

Then:

  1. (1)

    \(d_{k} \le \bar{d}\), \(k \ge M + 1\) implies that \(a_{k} \le \max \{ \bar{a}_{1},\bar{a}_{2}, \ldots,\bar{a}_{M} \} + \frac{\bar{d}}{1 - \rho}\), \(k \ge M + 1\),

  2. (2)

    \(\lim_{k \to \infty} \sup d_{k} \le d_{\infty}\) implies that \(\lim_{k \to \infty} \sup a_{k} \le \frac{d_{\infty}}{1 - \rho}\).

3 Rectifying action-based proportional-α- order-derivative-type (\(\mathrm{PD}^{\alpha}\)-type) ILCs

Consider the following α-order (\(0 < \alpha < 1\)) linear time-invariant systems:

$$ \textstyle\begin{cases} {}_{0}D_{t}^{\alpha} x_{k} ( t ) = Ax_{k} ( t ) + Bu_{k} ( t ), \\ y_{k} ( t ) = Cx_{k} ( t ),\quad t \in [0,T], \end{cases} $$
(1)

where k is the kth repetitive operation symbol, \({}_{0}D_{t}^{\alpha} \) is the Caputo derivative with lower limit zero of order α and \([ 0,T ]\) is an operation time interval, \(x_{k} ( t ) \in R^{n}\), \(u_{k} ( t ) \in R\) and \(y_{k} ( t ) \in R\) are the state vector, control input and output of the system, respectively. A, B and C are matrices with appropriate dimensions and it is assumed that CB is a full-rank matrix.

The solution of the fractional order system (1) can be written in the following form [26]:

$$x_{k} ( t ) = \Phi_{\alpha,1} ( t )x_{k} ( 0 ) + \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau )Bu_{k} ( \tau )\,\mathrm{d}\tau, $$

where \(\Phi_{\alpha,\beta} ( t ) = t^{\beta - 1}E_{\alpha,\beta} (At^{\alpha} )\) (\(\alpha > 0\), \(\beta > 0\)) stands for the state transition matrix of fractional order system (1).

In this paper, the initial state value satisfies \(x_{k} ( 0 ) \in N ( x_{0} )\), where \(N ( x_{0} )\) is a neighborhood of \(x_{0}\). Specifically, it is assumed that the initial state value satisfies the following condition:

$$ \Biggl\Vert \frac{1}{k}\sum_{i = 1}^{k} x_{i} ( 0 ) - x_{0} \Biggr\Vert _{p} \le \beta o \biggl( \frac{1}{k} \biggr), $$
(2)

where β denotes a positive constant, and \(\lim_{k \to \infty} o ( \frac{1}{k} ) / \frac{1}{k} = 0\).

It is noted that the proportional-α-order-derivative-type (\(\mathrm{PD}^{\alpha} \)-type) ILC algorithm (3) which has been investigated in [8],

$$ u_{k + 1} ( t ) = u_{k}(t) + L_{p}e_{k}(t) + L_{d}{}_{0}D_{t}^{\alpha} e_{k}(t), $$
(3)

can ensure the system output \(y_{k} ( t )\) to track a desired trajectory \(y_{d} ( t )\) precisely as the operation number k goes to infinity with the initial state being resettable. But it cannot guarantee the precisely tracking with the initial state shift. Here, \(L_{p}\) and \(L_{d}\) are termed the proportional and α-order derivative learning gains, respectively. The expression \(e_{k} ( t ) = y_{d} ( t ) - y_{k} ( t )\) denotes the tracking error of the fractional order system (1).

Then, in order to generate an upgraded control input \(u_{k} ( t )\) to stimulate the system \(y_{k} ( t )\) to track a desired \(y_{d} ( t )\) as precisely as possible, we adopt a rectifying action to compensate for the proportional-α-order-derivative-type (\(\mathrm{PD}^{\alpha} \)-type) ILCs to suppress the tracking error caused by the initial state shift. The adopted rectifying action \(\delta_{k} ( t )\) is an iteration-dependent function sequence as follows:

$$\delta_{k} ( t ) = \textstyle\begin{cases} \frac{t^{1 - \alpha}}{\varepsilon_{k}},& 0 \le t \le \varepsilon_{k}; \\ 0,& \varepsilon_{k} < t \le T, \end{cases} $$

for engineering applicability, it is assumed that the sequence obeys \(\vert \delta_{k} ( t ) \vert \le 1 / \varepsilon_{k}^{\alpha} \le M\), where M is the tolerance of the system input capability.

To this end, the rectifying first- and second-order as well as the feedback-based proportional-α-order-derivative-type (\(\mathrm{PD}^{\alpha} \)-type) ILC algorithms are considered and we suppose that \(y_{d} ( 0 ) \ne Cx_{0}\).

The rectifying action-based first-order proportional-α-order-derivative-type (\(\mathrm{PD}^{\alpha} \)-type) ILC algorithm is used of the latest historical tracking error and its α-order derivative, which is given as follows:

$$ u_{k + 1} ( t ) = u_{k}(t) + L_{p_{1}}e_{k}(t) + L_{d_{1}}{}_{0}D_{t}^{\alpha} e_{k}(t) + K\delta_{k} ( t ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). $$
(4)

Here, \(L_{p_{1}}\) and \(L_{d_{1}}\) are termed the first-order proportional and α-order derivative learning gains, respectively. K is the rectifying gain.

The rectifying action-based second-order proportional-α-order-derivative-type (\(\mathrm{PD}^{\alpha} \)-type) ILC algorithm is used of control inputs, tracking errors and their α-order derivatives of the latest two adjacent operations, given by

$$ \begin{aligned}[b] u_{k + 1} ( t ) &= c_{1} \bigl( u_{k}(t) + L_{p_{1}}e_{k}(t) + L_{d_{1}}{}_{0}D_{t}^{\alpha} e_{k}(t) \bigr) \\ &\quad {} + c_{2} \bigl( u_{k - 1}(t) + L_{p_{2}}e_{k - 1}(t) + L_{d_{2}}{}_{0}D_{t}^{\alpha} e_{k - 1}(t) \bigr) \\ &\quad {} + K\delta_{k} ( t ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). \end{aligned} $$
(5)

Here, \(L_{p_{2}}\) and \(L_{d_{2}}\) denote the second-order proportional and α-order derivative learning gains, respectively. The weighing coefficients \(c_{1}\) and \(c_{2}\) satisfy \(0 \le c_{1},c_{2} \le 1\) and \(c_{1} + c_{2} = 1\).

It is observed that, when \(c_{2}\) is null, the rectifying second-order algorithm (5) degenerates to the rectifying first-order algorithm (4). Due to the algorithm (4) being a special case of the algorithm (5), we only analyze the tracking performance of the algorithm (5) in the following.

The rectifying action-based proportional-α-order-derivative-type (\(\mathrm{PD}^{\alpha} \)-type) ILC algorithm with feedback information is used of the latest historical and current tracking errors and their α-order derivatives, given by

$$ \begin{aligned}[b] u_{k + 1} ( t ) &= u_{k}(t) + L_{p_{1}}e_{k}(t) + L_{d_{1}}{}_{0}D_{t}^{\alpha} e_{k}(t) \\ &\quad {} + L_{p_{0}}e_{k - 1}(t) + L_{d_{0}}{}_{0}D_{t}^{\alpha} e_{k - 1}(t) \\ &\quad {} + K\delta_{k} ( t ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). \end{aligned} $$
(6)

Here, \(L_{p_{0}}\) and \(L_{d_{0}}\) denote the feedback learning gains, respectively.

Before showing the effect of the initial state shift, we need the following lemmas.

Lemma 3.1

\({}_{\tau} D_{t}^{1 - \alpha} ( \Phi_{\alpha,1} ( t - \tau ) ) = \Phi_{\alpha,\alpha} ( t - \tau )\), \(0 < \alpha < 1\).

Proof

It is obtained from Lemma 2.1 that the series \(\Phi_{\alpha,1} ( t - \tau )\) is absolutely convergent for all \(0 \le t, \tau < \infty\). Then we can differentiate the series \(\Phi_{\alpha,1} ( t - \tau )\) with respect to the variable τ term by term.

It is easy to see from the definition of the right-sided Caputo derivative that

$${}_{\tau} D_{t}^{1 - \alpha} ( t - \tau )^{k\alpha} = - \frac{1}{\Gamma ( \alpha )} \int_{\tau}^{t} \frac{\frac{\mathrm{d}}{\mathrm{d}\nu} ( t - \nu )^{k\alpha}}{ ( \nu - \tau )^{1 - \alpha}} \,\mathrm{d}\nu= \frac{k\alpha}{ \Gamma ( \alpha )} \int_{\tau}^{t} ( \nu - \tau )^{\alpha - 1} ( t - \nu )^{k\alpha - 1}\,\mathrm{d}\nu. $$

Let \(\nu = s ( t - \tau ) + \tau\), we can get

$$\begin{aligned} {}_{\tau} D_{t}^{1 - \alpha} ( t - \tau )^{k\alpha} &= \frac{k\alpha}{\Gamma ( \alpha )} \int_{\tau}^{t} ( \nu - \tau )^{\alpha - 1} ( t - \nu )^{k\alpha - 1}\,\mathrm{d}\nu\\ &= \frac{k\alpha}{\Gamma ( \alpha )} \int_{0}^{1} ( t - \tau )^{k\alpha + \alpha - 1}s^{\alpha - 1} ( 1 - s )^{k\alpha - 1}\,\mathrm{d}s \\ &= \frac{k\alpha}{\Gamma ( \alpha )}B ( \alpha,k\alpha ) ( t - \tau )^{k\alpha + \alpha - 1} = \frac{\Gamma ( k\alpha + 1 )}{\Gamma ( k\alpha + \alpha )} ( t - \tau )^{k\alpha + \alpha - 1}, \end{aligned} $$

where \(B ( \alpha,\beta ) = \int_{0}^{1} t^{\alpha - 1} ( 1 - t )^{\beta - 1}\,\mathrm{d}t\) is the Beta function and \(B ( \alpha,\beta ) = \frac{\Gamma ( \alpha )\Gamma ( \beta )}{\Gamma ( \alpha + \beta )}\) (\(\alpha > 0\), \(\beta > 0\)).

This means that

$$\begin{aligned} {}_{\tau} D_{t}^{1 - \alpha} \bigl( \Phi_{\alpha,1} ( t - \tau ) \bigr)& = {}_{\tau} D_{t}^{1 - \alpha} \sum _{k = 0}^{\infty} \frac{A^{k} ( t - \tau )^{k\alpha}}{\Gamma ( k\alpha + 1 )}= \sum _{k = 0}^{\infty} \frac{A^{k}{}_{\tau} D_{t}^{1 - \alpha} ( t - \tau )^{k\alpha}}{\Gamma ( k\alpha + 1 )} \\ &= \sum_{k = 0}^{\infty} \frac{A^{k} ( t - \tau )^{k\alpha + \alpha - 1}}{\Gamma ( k\alpha + \alpha )}= ( t - \tau )^{\alpha - 1}\sum_{k = 0}^{\infty} \frac{A^{k} ( t - \tau )^{k\alpha}}{\Gamma ( k\alpha + \alpha )}= \Phi_{\alpha,\alpha} ( t - \tau ). \end{aligned} $$

This completes the proof. □

Lemma 3.2

\(\frac{\mathrm{d}}{\mathrm{d}\tau} \Phi_{\alpha,1} ( t - \tau ) = - \Phi_{\alpha,\alpha} ( t - \tau )A\), \(\alpha > 0\).

Proof

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau} \Phi_{\alpha,1} ( t - \tau ) &= \frac{\mathrm{d}}{\mathrm{d}\tau} \sum_{k = 0}^{\infty} \frac{A^{k} ( t - \tau )^{k\alpha}}{\Gamma ( k\alpha + 1 )}= - \sum_{k = 1}^{\infty} \frac{k\alpha A^{k} ( t - \tau )^{k\alpha - 1}}{\Gamma ( k\alpha + 1 )} \\ &= - ( t - \tau )^{\alpha - 1} \Biggl( \sum_{k = 1}^{\infty} \frac{A^{k - 1} ( t - \tau )^{(k - 1)\alpha}}{\Gamma ( (k - 1)\alpha + \alpha )} \Biggr) A= - \Phi_{\alpha,\alpha} ( t - \tau )A. \end{aligned} $$

This completes the proof. □

Now, the effect of initial state shift for the rectifying second-order and feedback-based proportional-α-order-derivative-type (\(\mathrm{PD}^{\alpha} \)-type) ILC algorithms will be shown.

3.1 Rectifying action-based second-order\(\mathrm{PD}^{\alpha}\)-type ILC

Theorem 3.1

Suppose that the rectifying action-based second-order \(\mathrm{PD}^{\alpha} \)-type ILC algorithm (5) is applied to the fractional order system (1) and that the initial state at each iteration satisfies the condition (2). If the system matrices A, B, C and the order α together with the learning gains \(L_{p_{1}}\), \(L_{d_{1}}\), \(L_{p_{2}}\) and \(L_{d_{2}}\) satisfy the following conditions \(\rho_{1} < 1\) and \(\rho_{2} < 1\), then we get

$$\lim_{k \to \infty} \sup \bigl\Vert e_{k + 1} ( \cdot ) \bigr\Vert _{p} \le \frac{\Delta_{2}}{1 - \bar{\rho}}, $$

where

$$\begin{gathered} \rho_{1} = \vert 1 - CBL_{d_{1}} \vert + \bigl\Vert C\Phi_{\alpha,\alpha} ( \cdot ) ( BL_{p_{1}} + ABL_{d_{1}} ) \bigr\Vert _{1}, \\ \rho_{2} = \vert 1 - CBL_{d_{2}} \vert + \bigl\Vert C \Phi_{\alpha,\alpha} ( \cdot ) ( BL_{p_{2}} + ABL_{d_{2}} ) \bigr\Vert _{1}, \\ \bar{\rho} = {c}_{1}\rho_{1} + {c}_{2} \rho_{2}, \\ \Delta_{2} = \bigl\Vert C\Phi_{\alpha,1} ( \cdot )B ( c_{1}L_{d_{1}} + c_{2}L_{d_{2}} ) - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \bigr\Vert _{1} \bigl\Vert y_{d} ( 0 ) - Cx_{0} \bigr\Vert _{p}. \end{gathered} $$

Proof

From the solution of the fractional order system (1) and algorithm (5), the output error for \(k + 1\) can be written as

$$\begin{aligned} e_{k + 1} ( t ) &= y_{d} ( t ) - y_{k + 1} ( t ) \\ &= c_{1} \bigl( y_{d} ( t ) - y_{k} ( t ) \bigr) + c_{2} \bigl( y_{d} ( t ) - y_{k - 1} ( t ) \bigr) - \bigl( y_{k + 1} ( t ) - c_{1}y_{k} ( t ) - c_{2}y_{k - 1} ( t ) \bigr) \\ &= c_{1}e_{k} ( t ) + c_{2}e_{k - 1} ( t ) - C \bigl( x_{k + 1} ( t ) - c_{1}x_{k} ( t ) - c_{2}x_{k - 1} ( t ) \bigr) \\ &= c_{1}e_{k} ( t ) + c_{2}e_{k - 1} ( t ) - C\Phi_{\alpha,1} ( t ) \bigl( x_{k + 1} ( 0 ) - c_{1}x_{k} ( 0 ) - c_{2}x_{k - 1} ( 0 ) \bigr) \\ &\quad {} - C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( u_{k + 1} ( \tau ) - c_{1}u_{k} ( \tau ) - c_{2}u_{k - 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\ &\begin{aligned}[b]&= c_{1}e_{k} ( t ) + c_{2}e_{k - 1} ( t ) - C\Phi_{\alpha,1} ( t ) \bigl( x_{k + 1} ( 0 ) - c_{1}x_{k} ( 0 ) - c_{2}x_{k - 1} ( 0 ) \bigr) \\ &\quad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( c_{1}L_{p_{1}}e_{k} ( \tau ) + c_{2}L_{p_{2}}e_{k - 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\ & \quad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( c_{1}L_{d_{1}}{}_{0}D_{\tau}^{\alpha} e_{k} ( \tau ) + c_{2}L_{d_{2}}{}_{0}D_{\tau}^{\alpha} e_{k - 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\ &\quad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) BK \delta_{k} ( \tau ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau.\end{aligned} \end{aligned}$$
(7)

Then, from Lemma 3.1, fractional integration by parts, Property 2.3 and Lemma 3.2, the second last term in the right side of (7) is rearranged as

$$ \begin{gathered}[b] - C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( c_{1}L_{d_{1}}{}_{0}D_{\tau}^{\alpha} e_{k} ( \tau ) + c_{2}L_{d_{2}}{}_{0}D_{\tau}^{\alpha} e_{k - 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\ \quad = - c_{1} \cdot C \int_{0}^{t} {}_{\tau} D_{t}^{1 - \alpha} \bigl( \Phi_{\alpha,1} ( t - \tau ) \bigr) BL_{d_{1}}{}_{0}D_{\tau}^{\alpha} e_{k} ( \tau )\,\mathrm{d}\tau \\ \qquad{}- c_{2} \cdot C \int_{0}^{t} {}_{\tau} D_{t}^{1 - \alpha} \bigl( \Phi_{\alpha,1} ( t - \tau ) \bigr) BL_{d_{2}}{}_{0}D_{\tau}^{\alpha} e_{k - 1} ( \tau )\,\mathrm{d}\tau \\ \quad= - c_{1} \cdot C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau )BL_{d_{1}} \cdot {}_{0}D_{\tau}^{1 - \alpha} {}_{0}D_{\tau}^{\alpha} e_{k} ( \tau ) \,\mathrm{d}\tau \\ \qquad{}- c_{2} \cdot C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau )BL_{d_{2}} \cdot {}_{0}D_{\tau}^{1 - \alpha} {}_{0}D_{\tau}^{\alpha} e_{k - 1} ( \tau ) \,\mathrm{d}\tau \\ \quad = - c_{1} \cdot C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau )BL_{d_{1}}\,\mathrm{d} \bigl( e_{k} ( \tau ) \bigr) - c_{2} \cdot C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau )BL_{d_{2}}\,\mathrm{d} \bigl( e_{k - 1} ( \tau ) \bigr) \\ \quad = - c_{1} \cdot C\Phi_{\alpha,1} ( t - \tau )BL_{d_{1}}e_{k} ( \tau ) \vert _{\tau = 0}^{\tau = t} - c_{2} \cdot C\Phi_{\alpha,1} ( t - \tau )BL_{d_{2}} e_{k - 1} ( \tau ) \vert _{\tau = 0}^{\tau = t} \\ \qquad{} - c_{1} \cdot C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau )ABL_{d_{1}}e_{k} ( \tau )\,\mathrm{d}\tau - c_{2}C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau )ABL_{d_{2}}e_{k - 1} ( \tau )\,\mathrm{d}\tau\\ \quad = - CB \bigl( c_{1}L_{d_{1}}e_{k} ( t ) + c_{2}L_{d_{2}}e_{k - 1} ( t ) \bigr) \\ \qquad {} + C\Phi_{\alpha,1} ( t )B \bigl( c_{1}L_{d_{1}}e_{k} ( 0 ) + c_{2}L_{d_{2}}e_{k - 1} ( 0 ) \bigr) \\ \qquad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau )AB \bigl( c_{1}L_{d_{1}}e_{k} ( \tau ) + c_{2}L_{d_{2}}e_{k - 1} ( \tau ) \bigr)\,\mathrm{d}\tau. \end{gathered} $$
(8)

Substituting (8) into (7) yields

$$ \begin{aligned}[b] e_{k + 1} ( t ) &= c_{1} ( 1 - CBL_{d_{1}} )e_{k} ( t ) + c_{2} ( 1 - CBL_{d_{2}} )e_{k - 1} ( t ) \\ &\quad {}- c_{1}C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) ( BL_{p_{1}} + ABL_{d_{1}} )e_{k} ( \tau )\,\mathrm{d}\tau \\ &\quad {}- c_{2}C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) ( BL_{p_{2}} + ABL_{d_{2}} )e_{k - 1} ( \tau )\,\mathrm{d}\tau \\ &\quad {}- C\Phi_{\alpha,1} ( t ) \bigl( x_{k + 1} ( 0 ) - c_{1}x_{k} ( 0 ) - c_{2}x_{k - 1} ( 0 ) \bigr) \\ &\quad {}+ C\Phi_{\alpha,1} ( t )Bc_{1}L_{d_{1}}e_{k} ( 0 )+ C\Phi_{\alpha,1} ( t )Bc_{2}L_{d_{2}}e_{k - 1} ( 0 ) \\ &\quad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) BK \delta_{k} ( \tau ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau. \end{aligned} $$
(9)

Then we consider the last term in the right side of equality (9). By Lemma 3.1 and fractional integration by parts, we have

$$ \begin{gathered}[b] C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) BK \delta_{k} ( \tau ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau \\ \quad = C \int_{0}^{t} {}_{\tau} D_{t}^{1 - \alpha} \bigl( \Phi_{\alpha,1} ( t - \tau ) \bigr) BK\delta_{k} ( \tau ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau \\ \quad = C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau ) BK{}_{0}D_{\tau}^{1 - \alpha} \bigl( \delta_{k} ( \tau ) \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d} \tau. \end{gathered} $$
(10)

(1) If \(0 \le t \le \varepsilon_{k}\), then \(\delta_{k} ( t ) = \frac{t^{1 - \alpha}}{\varepsilon_{k}}\). When \(\gamma = 0\), from Property 2.1, we can obtain

$$ {}_{0}I_{t}^{1 - \alpha} 1 = \frac{1}{\Gamma ( 2 - \alpha )}t^{1 - \alpha}, $$
(11)

hence, by equation (11), Property 2.2 and the mean theory of definite integral, there exists an instant \(\zeta_{k} ( t ) \in [ 0,t ]\) such that

$$ \begin{gathered}[b] C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau ) BK{}_{0}D_{\tau}^{1 - \alpha} \bigl( \delta_{k} ( \tau ) \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d} \tau \\ \quad = \frac{1}{\varepsilon_{k}} \cdot C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau ) BK{}_{0}D_{\tau}^{1 - \alpha} \bigl( \Gamma ( 2 - \alpha ){}_{0}\mathrm{I}_{\tau}^{1 - \alpha} 1 \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau \\ \quad = \frac{1}{\varepsilon_{k}} \cdot C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau ) BK \Gamma ( 2 - \alpha ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr) \,\mathrm{d}\tau \\ \quad = \frac{t}{\varepsilon_{k}} \cdot C\Phi_{\alpha,1} \bigl( t - \zeta_{k} ( t ) \bigr)BK\Gamma ( 2 - \alpha ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). \end{gathered} $$
(12)

(2) If \(\varepsilon_{k} < t \le T\), then \(\delta_{k} ( t ) = 0\). Analogously, there exists an instant \(\xi_{k} \in [ 0,\varepsilon_{k} ]\) such that

$$ \begin{gathered}[b] C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau ) BK{}_{0}D_{\tau}^{1 - \alpha} \bigl( \delta_{k} ( \tau ) \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d} \tau \\ \quad = C \int_{0}^{\varepsilon_{k}} \Phi_{\alpha,1} ( t - \tau ) BK{}_{0}D_{\tau}^{1 - \alpha} \bigl( \delta_{k} ( \tau ) \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d} \tau \\ \qquad {}+ C \int_{\varepsilon_{k}}^{t} \Phi_{\alpha,1} ( t - \tau ) BK{}_{0}D_{\tau}^{1 - \alpha} \bigl( \delta_{k} ( \tau ) \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d} \tau \\ \quad = \frac{1}{\varepsilon_{k}} \cdot C \int_{0}^{\varepsilon_{k}} \Phi_{\alpha,1} ( t - \tau ) BK{}_{0}D_{\tau}^{1 - \alpha} \bigl( \Gamma ( 2 - \alpha ){}_{0}\mathrm{I}_{\tau}^{1 - \alpha} 1 \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau \\ \quad = \frac{1}{\varepsilon_{k}} \cdot C \int_{0}^{\varepsilon_{k}} \Phi_{\alpha,1} ( t - \tau ) BK \Gamma ( 2 - \alpha ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr) \,\mathrm{d}\tau \\ \quad = C\Phi_{\alpha,1} ( t - \xi_{k} )BK\Gamma ( 2 - \alpha ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). \end{gathered} $$
(13)

Let

$$H_{k} ( t ) = \textstyle\begin{cases} \frac{t}{\varepsilon_{k}}\Phi_{\alpha,1} ( t - \zeta_{k} ( t ) ),& 0 \le t \le \varepsilon_{k}, \\ \Phi_{\alpha,1} ( t - \xi_{k} ),& \varepsilon_{k} < t \le T. \end{cases} $$

Then, considering the facts of (12) and (13), the above equality (10) is

$$ C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) BK \delta_{k} ( \tau ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau = CH_{k} ( t )BK\Gamma ( 2 - \alpha ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). $$
(14)

Notice that

$$\begin{aligned}& e_{k} ( 0 ) = \bigl( y_{d} ( 0 ) - Cx_{0} \bigr) - \bigl( Cx_{k} ( 0 ) - Cx_{0} \bigr), \end{aligned}$$
(15)
$$\begin{aligned}& e_{k - 1} ( 0 ) = \bigl( y_{d} ( 0 ) - Cx_{0} \bigr) - \bigl( Cx_{k - 1} ( 0 ) - Cx_{0} \bigr). \end{aligned}$$
(16)

Substituting (14), (15) and (16) into (9) yields

$$ \begin{aligned}[b] e_{k + 1} ( t ) &= c_{1} ( 1 - CBL_{d_{1}} )e_{k} ( t ) + c_{2} ( 1 - CBL_{d_{2}} )e_{k - 1} ( t )\\ &\quad {} - c_{1}C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) ( BL_{p_{1}} + ABL_{d_{1}} )e_{k} ( \tau )\,\mathrm{d}\tau \\ &\quad {}- c_{2}C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) ( BL_{p_{2}} + ABL_{d_{2}} )e_{k - 1} ( \tau )\,\mathrm{d}\tau \\ &\quad {}- C\Phi_{\alpha,1} ( t ) \bigl( x_{k + 1} ( 0 ) - c_{1}x_{k} ( 0 ) - c_{2}x_{k - 1} ( 0 ) \bigr) \\ &\quad {}- C\Phi_{\alpha,1} ( t )Bc_{1}L_{d_{1}} \bigl( Cx_{k} ( 0 ) - Cx_{0} \bigr) \\ &\quad {} - C\Phi_{\alpha,1} ( t )Bc_{2}L_{d_{2}} \bigl( Cx_{k - 1} ( 0 ) - Cx_{0} \bigr) \\ &\quad {}+ \bigl( C\Phi_{\alpha,1} ( t )B ( c_{1}L_{d_{1}} + c_{2}L_{d_{2}} ) - CH_{k} ( t )BK\Gamma ( 2 - \alpha ) \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). \end{aligned} $$
(17)

Taking the Lebesgue-p norm on both sides of (17) and adopting the generalized Young inequality of convolution integral, we get

$$ \begin{aligned}[b] \bigl\Vert e_{k + 1} ( \cdot ) \bigr\Vert _{p} &\le c_{1}\rho_{1} \bigl\Vert e_{k} ( \cdot ) \bigr\Vert _{p} + c_{2} \rho_{2} \bigl\Vert e_{k - 1} ( \cdot ) \bigr\Vert _{p} \\ &\quad {}+ \bigl\Vert C\Phi_{\alpha,1} ( \cdot ) \bigl( x_{k + 1} ( 0 ) - c_{1}x_{k} ( 0 ) - c_{2}x_{k - 1} ( 0 ) \bigr) \bigr\Vert _{p} \\ &\quad {} + \bigl\Vert C\Phi_{\alpha,1} ( \cdot )Bc_{1}L_{d_{1}}C \bigl( x_{k} ( 0 ) - x_{0} \bigr) \bigr\Vert _{p} \\ &\quad {}+ \bigl\Vert C\Phi_{\alpha,1} ( \cdot )Bc_{2}L_{d_{2}}C \bigl( x_{k - 1} ( 0 ) - x_{0} \bigr) \bigr\Vert _{p} + \Delta_{2}, \end{aligned} $$
(18)

recall that, from the inequality (2), by definition \(\lim_{k \to \infty} o ( \frac{1}{k} ) / \frac{1}{k} = 0\), we have

$$ \lim_{k \to \infty} \Biggl\Vert \sum_{i = 1}^{k} \bigl( x_{i} ( 0 ) - x_{0} \bigr) \Biggr\Vert _{p} = 0, $$
(19)

according to the triangular inequality property of the Lebesgue-p norm, and equality (19) yields

$$ \begin{aligned}[b] \lim_{k \to \infty} \bigl\Vert x_{k} ( 0 ) - x_{0} \bigr\Vert _{p} &= \lim _{k \to \infty} \Biggl\Vert \sum_{i = 1}^{k} \bigl( x_{i} ( 0 ) - x_{0} \bigr) - \sum _{i = 1}^{k - 1} \bigl( x_{i} ( 0 ) - x_{0} \bigr) \Biggr\Vert _{p} \\ &\le \lim_{k \to \infty} \Biggl\Vert \sum _{i = 1}^{k} \bigl( x_{i} ( 0 ) - x_{0} \bigr) \Biggr\Vert _{p} + \lim_{k \to \infty} \Biggl\Vert \sum_{i = 1}^{k - 1} \bigl( x_{i} ( 0 ) - x_{0} \bigr) \Biggr\Vert _{p} = 0, \end{aligned} $$
(20)

then, from equality (20), we have

$$ \begin{gathered}[b] \lim_{k \to \infty} \bigl\Vert C \Phi_{\alpha,1} ( \cdot ) \bigl( x_{k + 1} ( 0 ) - x_{k} ( 0 ) \bigr) \bigr\Vert _{p} \\ \quad \le \lim_{k \to \infty} \bigl\Vert C\Phi_{\alpha,1} ( \cdot ) \bigr\Vert _{1} \bigl( \bigl\Vert x_{k + 1} ( 0 ) - x_{0} \bigr\Vert _{p} + \bigl\Vert x_{k} ( 0 ) - x_{0} \bigr\Vert _{p} \bigr).\end{gathered} $$
(21)

Therefore

$$ \lim_{k \to \infty} \bigl\Vert C\Phi_{\alpha,1} ( \cdot ) \bigl( x_{k + 1} ( 0 ) - x_{k} ( 0 ) \bigr) \bigr\Vert _{p} = 0. $$
(22)

In this analogy, we can easily get

$$ \begin{gathered} \lim_{k \to \infty} \bigl\Vert C\Phi_{\alpha,1} ( \cdot )Bc_{1}L_{d_{1}}C \bigl( x_{k} ( 0 ) - x_{0} \bigr) \bigr\Vert _{p} = 0, \\ \lim_{k \to \infty} \bigl\Vert C\Phi_{\alpha,1} ( \cdot )Bc_{2}L_{d_{2}}C \bigl( x_{k - 1} ( 0 ) - x_{0} \bigr) \bigr\Vert _{p} = 0, \\ \lim_{k \to \infty} \bigl\Vert C\Phi_{\alpha,1} ( \cdot ) \bigl( x_{k + 1} ( 0 ) - c_{1}x_{k} ( 0 ) - c_{2}x_{k - 1} ( 0 ) \bigr) \bigr\Vert _{p} = 0. \end{gathered} $$
(23)

It is obvious that \(\bar{\rho} = {c}_{1}\rho_{1} + {c}_{2}\rho_{2}\) under the assumption that \(\rho_{1} < 1\), \(\rho_{2} < 1\), then, from (23) and Lemma 2.4, inequality (18) leads to

$$ \lim_{k \to \infty} \sup \bigl\Vert e_{k + 1} ( \cdot ) \bigr\Vert _{p} \le \frac{\Delta_{2}}{1 - \bar{\rho}}. $$
(24)

This completes the proof. □

Remark 3.1

Inequality (24) shows that the FOILC scheme (5) is able to drive the tracking error into a bound. It is worth noting that the upper bound is mainly determined by the parameter ρ̄ and the term \(\Delta_{2} = \Vert C\Phi_{\alpha,1} ( \cdot )B ( c_{1}L_{d_{1}} + c_{2}L_{d_{2}} ) - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \Vert _{1} \Vert y_{d} ( 0 ) - Cx_{0} \Vert _{p}\). Therefore, the upper bound can be confined to a smaller level by two steps. The first step is to choose the learning gains \(L_{p_{1}}\), \(L_{d_{1}}\), \(L_{p_{2}}\), \(L_{d_{2}}\), so that ρ̄ is sufficiently small. The second step is to select the rectifying gain K so that \(\Vert C\Phi_{\alpha,1} ( \cdot )B ( c_{1}L_{d_{1}} + c_{2}L_{d_{2}} ) - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \Vert _{1}\) is sufficiently small.

Remark 3.2

Regarding the selection of the rectifying gain K, it is easy to observe that the definition of \(H_{k} ( t )\) is close to the function \(\Phi_{\alpha,1} ( t )\). Thus, we can choose the rectifying gain K so as to approximate \(\frac{c_{1}L_{d_{1}} + c_{2}L_{d_{2}}}{\Gamma ( 2 - \alpha )}\), with the result that \(\Vert C\Phi_{\alpha,1} ( \cdot )B ( c_{1}L_{d_{1}} + c_{2}L_{d_{2}} ) - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \Vert _{1}\) is sufficiently small.

Remark 3.3

In the case when \(c_{2}\) is null, the proposed rectifying second-order scheme (5) degenerates to the rectifying first-order scheme (4). Thus, the convergent condition becomes \(\rho_{1} < 1\) and the upper bound of output error is \(\frac{\Delta_{1}}{1 - \rho_{1}}\), where \(\Delta_{1} = \Vert C\Phi_{\alpha,1} ( \cdot )BL_{d_{1}} - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \Vert _{1} \Vert y_{d} ( 0 ) - Cx_{0} \Vert _{p}\). We can find that the second-order scheme (5) has more freedom in choosing the learning gains to make ρ̄ and \(\Delta_{2}\) is smaller than \(\rho_{1}\) and \(\Delta_{1}\), with the result that the upper bound \(\frac{\Delta_{2}}{1 - \bar{\rho}} \) is smaller than \(\frac{\Delta_{1}}{1 - \rho_{1}}\).

Remark 3.4

It is obvious that, for the case when \(y_{d} ( 0 ) = Cx_{0}\), the deduction of Theorem 3.1 guarantees that the output error asymptotically approaches zero, where the initial state shift of the fractional order system exists and satisfies the constraint (2).

3.2 Rectifying action-based \(\mathrm{PD}^{\alpha}\)-type ILC with feedback informantion

Theorem 3.2

Suppose that the algorithm (6) is applied to the system (1) and the initial state value at each iteration satisfies the condition (2). If the system matrices A, B, C and the order α together with the learning gains \(L_{p_{1}}\) and \(L_{d_{1}}\), feedback gains \(L_{p_{0}}\) and \(L_{d_{0}}\) satisfy the condition \(\tilde{\rho} = \rho_{0}\rho_{1} < 1\), then we get

$$\lim_{k \to \infty} \sup \bigl\Vert e_{k + 1} ( \cdot ) \bigr\Vert _{p} \le \frac{\rho_{0}\Delta_{0}}{1 - \tilde{\rho}}, $$

where

$$\begin{gathered} \rho_{0} = \bigl( \vert 1 + CBL_{d_{0}} \vert - \bigl\Vert C\Phi_{\alpha,\alpha} ( \cdot ) ( BL_{p_{0}} + ABL_{d_{0}} ) \bigr\Vert _{1} \bigr)^{ - 1}, \\ \rho_{1} = \vert 1 - CBL_{d_{1}} \vert + \bigl\Vert C \Phi_{\alpha,\alpha} ( \cdot ) ( BL_{p_{1}} + ABL_{d_{1}} ) \bigr\Vert _{1}, \\ \Delta_{0} = \bigl\Vert C\Phi_{\alpha,1} ( \cdot )B ( L_{d_{1}} + L_{d_{0}} ) - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \bigr\Vert _{1} \bigl\Vert \bigl( y_{d} ( 0 ) - Cx_{0} \bigr) \bigr\Vert _{p}. \end{gathered} $$

Proof

Consider the formulation of rule (6) and the dynamic system (1), we get the \(k + 1\)th output error

$$ \begin{aligned}[b] e_{k + 1} ( t ) &= y_{d} ( t ) - y_{k + 1} ( t ) \\ &= y_{d} ( t ) - y_{k} ( t ) - \bigl( y_{k + 1} ( t ) - y_{k} ( t ) \bigr) \\ &= e_{k} ( t ) - C \bigl( x_{k + 1} ( t ) - x_{k} ( t ) \bigr) \\ &= e_{k} ( t ) - C\Phi_{\alpha,1} ( t ) \bigl( x_{k + 1} ( 0 ) - x_{k} ( 0 ) \bigr) - C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( u_{k + 1} ( \tau ) - u_{k} ( \tau ) \bigr)\,\mathrm{d}\tau\hspace{-20pt} \\ & = e_{k} ( t ) - C\Phi_{\alpha,1} ( t ) \bigl( x_{k + 1} ( 0 ) - x_{k} ( 0 ) \bigr) \\ &\quad {} - C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( L_{p_{1}}e_{k} ( \tau ) + L_{p_{0}}e_{k + 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\ &\quad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( L_{d_{1}}{}_{0}D_{\tau}^{\alpha} e_{k} ( \tau ) + L_{d_{0}}{}_{0}D_{\tau}^{\alpha} e_{k + 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\ &\quad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) BK \delta_{k} ( \tau ) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr)\,\mathrm{d}\tau. \end{aligned} $$
(25)

Then, from Lemma 3.1, fractional integration by parts, Property 2.3 and Lemma 3.2, the second last term in the right-hand side of (25) can be rearranged as follows:

$$\begin{aligned}& C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) B \bigl( L_{d_{1}}{}_{0}D_{\tau}^{\alpha} e_{k} ( \tau ) + L_{d_{0}}{}_{0}D_{\tau}^{\alpha} e_{k + 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\& \quad = C \int_{0}^{t} {}_{\tau} D_{t}^{1 - \alpha} \bigl( \Phi_{\alpha,1} ( t - \tau ) \bigr) B \bigl( L_{d_{1}}{}_{0}D_{\tau}^{\alpha} e_{k} ( \tau ) + L_{d_{0}}{}_{0}D_{\tau}^{\alpha} e_{k + 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\& \quad = C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau )B \bigl( L_{d_{1}} \cdot {}_{0}D_{\tau}^{1 - \alpha} {}_{0}D_{\tau}^{\alpha} e_{k} ( \tau ) + L_{d_{0}} \cdot {}_{0}D_{\tau}^{1 - \alpha} {}_{0}D_{\tau}^{\alpha} e_{k + 1} ( \tau ) \bigr) \,\mathrm{d}\tau \\& \quad = C \int_{0}^{t} \Phi_{\alpha,1} ( t - \tau )B \bigl( L_{d_{1}}\,\mathrm{d}e_{k} ( \tau ) + L_{d_{0}} \,\mathrm{d}e_{k + 1} ( \tau ) \bigr) \\& \quad = C\Phi_{\alpha,1} ( t - \tau )B \bigl( L_{d_{1}}e_{k} ( \tau ) + L_{d_{0}}\,\mathrm{d}e_{k + 1} ( \tau ) \bigr) \vert _{\tau = 0}^{\tau = t} \\& \qquad {}- C \int_{0}^{t} \frac{\mathrm{d}}{\mathrm{d}\tau} \bigl( \Phi_{\alpha,1} ( t - \tau ) \bigr)B \bigl( L_{d_{1}}e_{k} ( \tau ) + L_{d_{0}}e_{k + 1} ( \tau ) \bigr)\,\mathrm{d}\tau \\& \quad = CBL_{d_{1}}e_{k} ( t ) + CBL_{d_{0}}e_{k + 1} ( t ) - C\Phi_{\alpha,1} ( t )BL_{d_{1}}e_{k} ( 0 ) - C \Phi_{\alpha,1} ( t )BL_{d_{0}}e_{k + 1} ( 0 ) \\& \qquad {} + C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau )AB \bigl( L_{d_{1}}e_{k} ( \tau ) + L_{d_{0}}e_{k + 1} ( \tau ) \bigr)\,\mathrm{d}\tau. \end{aligned}$$
(26)

Similar to the proof of Theorem 3.1, one can easily get

$$ \begin{gathered}[b] ( 1 + CBL_{d_{0}} )e_{k + 1} ( t ) \\ \quad = ( 1 - CBL_{d_{1}} )e_{k} ( t )- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) ( BL_{p_{1}} + ABL_{d_{1}} ) e_{k} ( \tau )\,\mathrm{d}\tau \\ \qquad {}- C \int_{0}^{t} \Phi_{\alpha,\alpha} ( t - \tau ) ( BL_{p_{0}} + ABL_{d_{0}} ) e_{k + 1} ( \tau )\,\mathrm{d}\tau\\ \qquad {}- C\Phi_{\alpha,1} ( t ) \bigl( x_{k + 1} ( 0 ) - x_{k} ( 0 ) \bigr) - C\Phi_{\alpha,1} ( t )BL_{d_{1}} \bigl( Cx_{k} ( 0 ) - Cx_{0} \bigr) \\ \qquad {} - C\Phi_{\alpha,1} ( t )BL_{d_{0}} \bigl( Cx_{k + 1} ( 0 ) - Cx_{0} \bigr) \\ \qquad {}+ \bigl( C\Phi_{\alpha,1} ( t )BL_{d_{1}} + C \Phi_{\alpha,1} ( t )BL_{d_{0}} - CH_{k} ( t )BK\Gamma ( 2 - \alpha ) \bigr) \bigl( y_{d} ( 0 ) - Cx_{0} \bigr). \end{gathered} $$
(27)

Taking the Lebesgue-p norm on both sides of (27) and adopting the generalized Young inequality of the convolution integral, we get

$$ \begin{gathered}[b] \bigl( \vert 1 + CBL_{d_{0}} \vert - \bigl\Vert C\Phi_{\alpha,\alpha} ( \cdot ) ( BL_{p_{0}} + ABL_{d_{0}} ) \bigr\Vert _{1} \bigr) \bigl\Vert e_{k + 1} ( \cdot ) \bigr\Vert _{p} \\ \quad \le \bigl( \vert 1 - CBL_{d_{1}} \vert + \bigl\Vert C \Phi_{\alpha,\alpha} ( \cdot ) ( BL_{p_{1}} + ABL_{d_{1}} ) \bigr\Vert _{1} \bigr) \bigl\Vert e_{k} ( \cdot ) \bigr\Vert _{p} \\ \qquad {}+ \bigl\Vert C\Phi_{\alpha,1} ( \cdot ) \bigl( x_{k + 1} ( 0 ) - x_{k} ( 0 ) \bigr) \bigr\Vert _{p}+ \bigl\Vert C \Phi_{\alpha,1} ( \cdot )BL_{d_{1}} \bigl( Cx_{k} ( 0 ) - Cx_{0} \bigr) \bigr\Vert _{p} \\ \qquad {}+ \bigl\Vert C\Phi_{\alpha,1} ( \cdot )BL_{d_{0}} \bigl( Cx_{k + 1} ( 0 ) - Cx_{0} \bigr) \bigr\Vert _{p} + \Delta_{0}, \end{gathered} $$
(28)

then inequality (28) can be rewritten as

$$ \begin{aligned}[b] \bigl\Vert e_{k + 1} ( \cdot ) \bigr\Vert _{p} &\le \tilde{\rho} \bigl\Vert e_{k} ( \cdot ) \bigr\Vert _{p}+ \rho_{0} \bigl\Vert C\Phi_{\alpha,1} ( \cdot ) \bigl( x_{k + 1} ( 0 ) - x_{k} ( 0 ) \bigr) \bigr\Vert _{p} \\ &\quad {}+ \rho_{0} \bigl\Vert C\Phi_{\alpha,1} ( \cdot )BL_{d_{1}} \bigl( Cx_{k} ( 0 ) - Cx_{0} \bigr) \bigr\Vert _{p} \\ &\quad {}+ \rho_{0} \bigl\Vert C\Phi_{\alpha,1} ( \cdot )BL_{d_{0}} \bigl( Cx_{k + 1} ( 0 ) - Cx_{0} \bigr) \bigr\Vert _{p} + \rho_{0}\Delta_{0}. \end{aligned} $$
(29)

Similar to the derivation of the (23), it is easy to get

$$\lim_{k \to \infty} \bigl\Vert C\Phi_{\alpha,1} ( \cdot )BL_{d_{0}}C \bigl( x_{k + 1} ( 0 ) - x_{0} \bigr) \bigr\Vert _{p} = 0. $$

From the assumption that \(\tilde{\rho} < 1\) and Lemma 2.4, we have

$$ \lim_{k \to \infty} \sup \bigl\Vert e_{k + 1} ( \cdot ) \bigr\Vert _{p} \le \frac{\rho_{0}\Delta_{0}}{1 - \tilde{\rho}}. $$
(30)

This completes the proof. □

Remark 3.5

Inequality (30) shows that the limit superior of the output error is controlled depends on the magnitude ρ̃ and the term \(\Delta_{0} = \Vert C\Phi_{\alpha,1} ( \cdot )B ( L_{d_{1}} + L_{d_{0}} ) - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \Vert _{1} \Vert y_{d} ( 0 ) - Cx_{0} \Vert _{p}\). Hence, the reduction of the output error should be done based on the suitable choice of learning gains \(L_{p_{1}}\), \(L_{d_{1}}\), \(L_{p_{0}}\), \(L_{d_{0}}\) leading to ρ̃ being sufficiently small.

In addition, it is observed that the \(H_{k} ( t )\) is approximate to the function \(\Phi_{\alpha,1} ( t )\). Therefore, the properly selection of the rectifying gain K leads to K being closer to the value \(\frac{L_{d_{1}} + L_{d_{0}}}{\Gamma ( 2 - \alpha )}\). It leads to \(\Delta_{0} = \Vert C\Phi_{\alpha,1} ( \cdot )B ( L_{d_{1}} + L_{d_{0}} ) - CH_{k} ( \cdot )BK\Gamma ( 2 - \alpha ) \Vert _{1} \Vert y_{d} ( 0 ) - Cx_{0} \Vert _{p}\) being small enough and thus the superior limit of the output errors is also sufficiently small concurrently.

Remark 3.6

In the case when \(L_{p_{0}} = L_{d_{0}} = 0\), the proposed rectifying feedback-based scheme (6) degenerates to the rectifying first-order scheme (4), with the result that the convergent condition becomes \(\rho_{1} < 1\) and the upper bound of the output error is \(\frac{\Delta_{1}}{1 - \rho_{1}}\). It is found that if the learning gains \(L_{p_{0}}\), \(L_{d_{0}}\) are chosen in such a way that \(\rho_{0} < 1\) and \(\Delta_{0} < \Delta_{1}\), then we have an upper bound \(\frac{\rho_{0}\Delta_{0}}{1 - \tilde{\rho}} \) that is smaller than \(\frac{\Delta_{1}}{1 - \rho_{1}}\).

4 Numerical simulations

In this simulation, we consider the fractional order linear system with the Caputo derivative (fractional order \(\alpha = 4 / 5\)),

$$ \textstyle\begin{cases} A = \bigl[ {\scriptsize\begin{matrix}{} 0 & 1 \cr - 2 & - 3 \end{matrix}} \bigr],\qquad B = \bigl[ {\scriptsize\begin{matrix}{} 0 \cr 1 \end{matrix}} \bigr], \\ C = [ { 0 \ 1 } ], \end{cases} $$
(31)

the desired trajectory is \(y_{d} ( t ) = 12t^{2}(1 - t)\), \(t \in [ 0,1 ]\) and the beginning control input set as \(u_{1} ( t ) = 0\), \(t \in [ 0,1 ]\).

The random initial state are produced as

$$\textstyle\begin{cases} x_{0} = [ 0 \ 0.1 ]^{T}, \\ x_{k} ( 0 ) = x_{0} + \frac{0.1}{k^{2}} ( \mathit{rand} - 0.5 ), \end{cases} $$

where ‘rand’ stands for a randomly generated scalar number on the interval \(( 0,1 )\). The rectifying function is set as

$$\delta_{k} ( t ) = \textstyle\begin{cases} \frac{t^{1 / 5}}{0.1 - \frac{0.05}{k^{2}}},& 0 \le t \le 0.1 - \frac{0.05}{k^{2}}, \\ 0,& 0.1 - \frac{0.05}{k^{2}} < t \le 1. \end{cases} $$

To better illustrate the rectifying action of our proposed \(\mathrm{PD}^{4 / 5}\)-type ILC scheme (4) by comparison, first, the \(\mathrm{PD}^{4 / 5}\)-type ILC without a rectifying action (3) is used. We set first-order learning gains \(L_{p_{1}} = 0.1\), \(L_{d_{1}} = 1.2\), respectively. The rectifying gain \(K = 1.1\). We calculate that \(\rho_{1} = 0.7491 < 1\). Figures 1-3 present the tracking performances of the rectifying action-based first-order scheme (4) and the first-order scheme without a rectifying action (3) at the third, fifth and the tenth iterations, respectively, where the dashed curve denotes the desired trajectory, the dash-dotted curve denotes the output produces by the scheme (3) and the solid curve denotes the output produces by the scheme (4), respectively. It is shown that the rectifying action-based first-order scheme (4) is able to stir the system output to track the desired trajectory much better than the \(\mathrm{PD}^{4 / 5}\)-type scheme without a rectifying action (3). Figure 4 shows tracking errors of the above schemes in the sense of the Lebesgue-2 norm. It is shown that the rectifying action can suppress the tracking error incurred by the initial shift effectively.

Figure 1
figure 1

Tracking perfermance at 3th iterative.

Full size image
Figure 2
figure 2

Tracking perfermance at 5th iterative.

Full size image
Figure 3
figure 3

Tracking performance at tenth iterative.

Full size image
Figure 4
figure 4

Tracking error comparison.

Full size image

In order to compare the tracking errors of the rectifying first-order scheme (4) with the rectifying second-order scheme (5), the first- and second-order learning gains are chosen as \(L_{p_{1}} = 0.9\), \(L_{d_{1}} = 0.3\), \(L_{p_{2}} = 1.7\) and \(L_{d_{2}} = 0.9\), respectively. The rectifying gain is \(K = 0.9\) and the weighting coefficients are chosen as \(c_{1} = 0.2\), \(c_{2} = 0.8\). It is calculated that \(\rho_{1} = 0.8216 < 1\), \(\rho_{2} = 0.1689 < 1\) and thus \(\bar{\rho} = c_{1}\rho_{1} + c_{2}\rho_{2} = 0.2994 < 1\). The corresponding tracking error comparison between rectifying action-based schemes (4) and (5) in Lebesgue-2 norm is shown in Figure 5. It is shown that asymptotic tracking error of the rectifying second-order scheme (5) is smaller than the rectifying first-order scheme (4).

Figure 5
figure 5

Tracking error comparison.

Full size image

In terms of the comparison of the tracking errors of the rectifying first-order scheme (4) and the rectifying feedback-based scheme (6), the first-order learning gains are identically chosen as \(L_{p_{1}} = 0.9\), \(L_{d_{1}} = 0.3\), and the feedback gains are chosen as \(L_{p_{0}} = 1\), \(L_{d_{0}} = 0.3\), respectively. It is computed that \(\rho_{1} = 0.8704 < 1\), \(\rho_{0} = 0.8216 < 1\) and thus \(\tilde{\rho} = \rho_{0}\rho_{1} ={ 0.7151 < 1}\). The corresponding tracking error comparison between rectifying action-based schemes (4) and (6) in Lebesgue-2 norm is shown in Figure 6. It is shown that asymptotic tracking error of the rectifying feedback-based scheme (6) is smaller than the rectifying first-order scheme (4).

Figure 6
figure 6

Tracking error comparison.

Full size image

5 Conclusion

In this paper, a new rectifying action was introduced into various \(\mathrm{PD}^{\alpha} \)-type ILC schemes and the tracking performances against the initial state shift were investigated for a class of fractional order linear systems. The proposed \(\mathrm{PD}^{\alpha} \)-type ILC schemes were shown to be an extended form of first- and second-order as well as feedback-based \(\mathrm{PD}^{\alpha} \)-type ILC schemes. The tracking performances were analyzed in the form of the Lebesgue-p norm by the technique of the generalized Young inequality of the convolution integral and fractional integration by parts. These analyses show that effect of the initial state shift can be more effectively controlled in various ways and the tracking performances can be improved according to the proper choice of the learning gains.