1 Introduction

The pollution levels in a stream can be measured via data collection. This is rather difficult and complex, and the results obtained deviate in measurement from one point in each time/place to another when the water flow in the stream is not uniform. In water quality modeling for a non-uniform flow stream, the governing equations used are the hydrodynamic model and the dispersion model. The one-dimensional shallow water equation and the advection-dispersion-reaction equation govern the first and the second models, respectively.

Numerous numerical techniques for solving such models are available. In [1], a finite element method for solving a steady water pollution control to achieve a minimum cost is used. Numerical techniques for solving the uniform flow of a stream water quality model, especially the one-dimensional advection-dispersion-reaction equation, are presented in [2–5], and [6].

The non-uniform flow model requires the velocity of the current at any point and any time in the domain. A hydrodynamic model provides the velocity field and tidal elevation of the water. In [7–9], and [10], the hydrodynamic model and the advection-dispersion equation are used to approximate the velocity of the water current in a bay, uniform reservoir and stream, respectively. Among these numerical techniques, finite difference methods, including both explicit and implicit schemes, are mostly used for one-dimensional domains, such as longitudinal stream systems [11, 12].

There are two mathematical models used to simulate water quality in non-uniform water flow systems. The first is the hydrodynamic model. This provides the velocity field and the water elevation. The second is the dispersion model. This gives the pollutant concentration field. The traditional Crank-Nicolson method is used in the hydrodynamic model. At each step, the calculated flow velocity fields of the first model are inputs into the second model [9, 10, 13].

Numerical techniques to solve the non-uniform flow of stream water containing one-dimensional advection-dispersion-reaction equation are presented in [10]. The fully implicit scheme (the Crank-Nicolson method) is used to solve the hydrodynamic model and the backward time-central space (BTCS) for the dispersion model. In [13], the Crank-Nicolson method is also used to solve the hydrodynamic model while the explicit Saulyev scheme is used to solve the dispersion model.

Research on finite difference techniques for the dispersion model have concentrated on computation accuracy and numerical stability. Many complicated numerical techniques, such as the QUICK scheme, the Lax-Wendroff scheme, and the Crandall scheme, have been studied to increase performance. These techniques focus on their advantages in terms of stability and higher-order accuracy [3].

Simple finite difference schemes are becoming more attractive for model use. Simple explicit methods include the forward time-central space (FTCS) scheme, the MacCormack scheme, and the Saulyev scheme. Implicit schemes include the BTCS and the Crank-Nicolson scheme [12]. These schemes are either first-order or second-order accurate and have advantages in programming and computing without losing much accuracy, thus they are used for many model applications [3].

A third-order upwind scheme for the advection-diffusion equation using a simple spreadsheet simulation is proposed in [14]. In [15], a new flux splitting scheme is proposed. The scheme is robust and converges as fast as the Roe splitting scheme. The Godunov mixed method for advection-dispersion equations is introduced in [16]. A time-splitting approach for the advection-dispersion equations is also considered. In addition, [17] proposes time-split methods for multi-dimensional advection-diffusion equations in which advection is approximated by a Godunov-type procedure, and diffusion is approximated by a low-order mixed finite element method. In [18], a flux-limiting solution technique for the simulation of a reaction-diffusion-convection system is proposed. A composite scheme to solve scalar transport equations in a two-dimensional space, that accurately resolves sharp profiles in the flow, is introduced. The total variation diminishing implicit Runge-Kutta method for dissipative advection-diffusion problems in astrophysics is proposed in [19]. They derive dissipative space discretizations and demonstrate that, together with specially adapted total-variation-diminishing or strongly stable Runge-Kutta time discretizations with adaptive step-size control, these yield reliable and efficient integrators for the underlying multi-dimensional non-linear evolution equations.

We propose simple revisions to a new fourth-order scheme that improve its accuracy for the problem of water quality measurement in a non-uniform water flow in a stream. In the following sections, the formulation of a new fourth-order scheme is introduced. The proposed revision of a new fourth-order scheme with the Saulyev method is described.

The result from the hydrodynamic model is the water flow velocity used in the advection-dispersion-reaction equation to determine the pollutant concentration field. Friction forces, due to the drag of the sides of the stream, are considered. The theoretical solution to the model at the end point of the domain that guarantees the accuracy of the approximate solution is presented in [9, 10], and [13].

The stream has a simple one space dimension, as shown in Figure 1. By averaging the equation over the depth, discarding the term due to the Coriolis force, it follows that the one-dimensional shallow water and the advection-dispersion-reaction equations are applicable. We use the Crank-Nicolson scheme, the traditional FTCS, and a couple of new fourth-order schemes and the Saulyev method to approximate the velocity, the elevation, and the pollutant concentration from the first and the second models, respectively.

Figure 1
figure 1

A shallow water system.

Full size image

2 Model formulation

2.1 The hydrodynamic model

In this section, we derive a simple hydrodynamic model describing the water current and elevation by the one-dimensional shallow water equation. We make the usual assumption in the continuity and momentum balance, i.e., we assume that the Coriolis and shearing stresses are small, and the surface wind is soft [7, 9, 10, 20]. We obtain the one-dimensional shallow water equations

$$\begin{aligned} &\frac{\partial \zeta}{\partial t} + \frac{\partial }{\partial x} \bigl[(h+ \zeta)u\bigr] = 0, \end{aligned}$$
(1)
$$\begin{aligned} &\frac{\partial u}{\partial t} + g \frac{\partial \zeta}{\partial x} = 0, \end{aligned}$$
(2)

where x is the longitudinal distance along the stream (m), t is time (s), \(h(x)\) is the depth measured from the mean water level to the stream bed (m), \(\zeta(x,t)\) is the elevation from the mean water level to the temporary water surface or the tidal elevation (m/s), and \(u(x,t)\) is the velocity components (m/s), for all \(x \in [0,l]\).

Assuming that h is a constant and that \(\zeta \ll h\), equations (1) and (2) reduce to

$$\begin{aligned} &\frac{\partial \zeta}{\partial t} + h\frac{\partial u}{\partial x} \doteq 0, \end{aligned}$$
(3)
$$\begin{aligned} &\frac{\partial u}{\partial t} + g \frac{\partial \zeta}{\partial x} = 0. \end{aligned}$$
(4)

We obtain a dimensionless equation by letting \(U = u / \sqrt{gh}\), \(X = x/l\), \(Z = \zeta / h\) and \(T = t \sqrt{gh}/l\). Substituting these expressions into equations (3) and (4) leads to

$$\begin{aligned} &\frac{\partial Z}{\partial T} + \frac{\partial U}{\partial X} = 0 , \end{aligned}$$
(5)
$$\begin{aligned} &\frac{\partial U}{\partial T} + \frac{\partial Z}{\partial X} = 0. \end{aligned}$$
(6)

In [9, 10], and [13], a damping term is introduced into equations (5) and (6) to represent the frictional forces due to the drag of sides of the stream. We have

$$\begin{aligned} &\frac{\partial Z}{\partial T} + \frac{\partial U}{\partial X} = 0, \end{aligned}$$
(7)
$$\begin{aligned} &\frac{\partial U}{\partial T} + \frac{\partial Z}{\partial X} = -U. \end{aligned}$$
(8)

The initial conditions at \(t=0\) and \(0\leq X\leq 1\) are \(Z= 0\) and \(U=0\). The boundary conditions for \(t>0\) are \(Z = e^{it}\) at \(X=0\) and \(\frac{\partial Z}{\partial X} =0\) at \(X=1\). Equations (7) and (8) are called the damped equations. We solve the damped equations using a finite difference method in \([0,1]\times [0,T]\). Since Z may be used to represent the vertical coordinate, U may be used to represent the approximated solutions, and T may be used to represent the time at which the maximum error of computed solutions is found, it is convenient to use \(u, d, t\) and x for \(U, Z, T\) and X, respectively. We have

$$\begin{aligned} &\frac{\partial u}{\partial t} + \frac{\partial d}{\partial x} = -u, \end{aligned}$$
(9)
$$\begin{aligned} &\frac{\partial d}{\partial t} + \frac{\partial u}{\partial x} = 0. \end{aligned}$$
(10)

The initial conditions are \(u=0\) and \(d=0\) at \(t=0\). The boundary conditions are \(d(0,t)=f(t)\) and \(\frac{\partial d}{\partial x}=0\) at \(x=1\).

2.2 Dispersion model

In a stream water quality model, the governing equation is the dynamic one-dimensional advection-dispersion equation. A simplified representation, averaging the equation over the depths, as shown in [2–4, 10], and [6], is

$$ \frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} = D\frac{\partial^{2} C}{\partial x^{2}}. $$
(11)

Here \(C(x,t)\) is the concentration averaged over the depth at the point x at time t (mg/L), D is the diffusion coefficient (m2/s), and \(u(x,t)\) is the velocity component (m/s), for all \(x \in [0,L]\). The initial conditions and the left boundary conditions are usually determined by observations. The initial pollutant concentration is \(C(x,0) = C_{0}\) at \(t=0\) for all \(x>0\), where \(C_{0}\) is a positive constant. The released pollutant concentration on the left boundary condition is given by \(C(0,t) = r(t)\) at \(x=0\), where \(r(t)\geq0\). The observed rate of change of the pollutant concentration on the right boundary is assumed to be a constant \(\frac{\partial C}{\partial x} = S_{0}\) at \(x=L\), where \(S_{0}\) is an arbitrary constant.

3 Crank-Nicolson method for the hydrodynamic model

The hydrodynamic model provides the velocity field and the elevation of the water. The calculated results of this model are the inputs into the dispersion model, which determine the pollutant concentration. We follow the numerical techniques of [9]. To find the water velocity and the water elevation from equations (9) and (10), we make a change of variables, \(v=e^{t} u\). Substituting this into equations (9) and (10), we obtain

$$\begin{aligned} &\frac{\partial v}{\partial t} + e^{t}\frac{\partial d}{\partial x} = 0, \end{aligned}$$
(12)
$$\begin{aligned} &\frac{\partial d}{\partial t} + e^{-t}\frac{\partial v}{\partial x} = 0. \end{aligned}$$
(13)

Equations (12) and (13) can be written in matrix form as follows:

$$ \begin{pmatrix} v \\ d \end{pmatrix}_{t} + \begin{bmatrix} 0 & e^{t} \\ e^{-t} & 0 \end{bmatrix}\begin{pmatrix} v \\ d \end{pmatrix}_{x} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}. $$
(14)

That is,

$$ U_{t} + A U_{x} = \bar{0}, $$
(15)

where

$$\begin{aligned} &A = \begin{bmatrix} 0 & e^{t} \\ e^{-t} & 0 \end{bmatrix}, \end{aligned}$$
(16)
$$\begin{aligned} &U = \begin{pmatrix} v\\ d \end{pmatrix} \quad \mbox{and}\quad \begin{pmatrix} v \\ d \end{pmatrix}_{t} = \begin{pmatrix} \partial v/\partial t \\ \partial d/\partial t \end{pmatrix}, \end{aligned}$$
(17)

with initial conditions \(d=v=0\) at \(t=0\). The left boundary condition at \(x=0,\ t> 0\) is specified: \(d(0,t) = f(t)\) and \(\frac{\partial v}{\partial x} = -e^{t} \frac{df}{dt}\). The right boundary condition at \(x=1,\ t> 0\) is specified: \(\frac{\partial d}{\partial x} = 0\) and \(v(0,t) = 0\).

We now discretize equation (15) by dividing the interval \([0,1]\) into M subintervals such that \(M\Delta x=1\) and the interval \([0,T]\) into N subintervals such that \(N\Delta t = T\). We then approximate \(d(x_{i},t_{n})\) by \(d_{i}^{n}\), the value of the difference approximation of \(d(x,t)\) at the point \(x=i\Delta x\) and \(t = n\Delta t\), where \(0\leq i \leq M\) and \(0 \leq n \leq N\). We similarly define \(v_{i}^{n}\) and \(U_{i}^{n}\). The grid point \((x_{n},t_{n})\) is defined by \(x_{i} = i\Delta x\) for all \(i=0,1,2,\dots,M\) and \(t_{n}=n\Delta t\) for all \(n=0,1,2,\dots,N\) in which M and N are positive integers. Applying the Crank-Nicolson method [21] to equation (15), the following finite difference equation is obtained:

$$ \biggl[I-\frac{1}{4}\lambda A (\Delta_{x} + \nabla_{x})\biggr] U_{i}^{n+1} = \biggl[I + \frac{1}{4} \lambda A (\Delta_{x} + \nabla_{x}) \biggr] U_{i}^{n}, $$
(18)

where

$$ U_{i}^{n} = \begin{pmatrix} v_{i}^{n} \\ d_{i}^{n} \end{pmatrix}, \qquad \Delta_{x} U_{i}^{n} = U_{i+1}^{n} - U_{i}^{n}\quad \textrm{and}\quad \nabla_{x} U_{i}^{n} = U_{i}^{n} - U_{i-1}^{n}. $$
(19)

I is the unit matrix of order two and \(\lambda = \Delta t/ \Delta x\). Applying the initial and boundary conditions given in equations (12) and (13), we have

$$ G^{n+1} \bar{U}^{n+1} = E^{n} \bar{U}^{n} + F^{n}, $$
(20)

where

$$\begin{aligned} &G^{n+1} = \begin{bmatrix} 1 & 0 & 0 & -\frac{\lambda}{4} a_{1}^{n+1} & 0 & 0 & \\ \frac{\lambda}{4} a_{2}^{n+1} & 1 & -\frac{\lambda}{4} a_{2}^{n+1} & 0 & 0 & 0 &\\ 0 & \frac{\lambda}{4} a_{1}^{n+1} & 1 & 0 & 0 & -\frac{\lambda}{4} a_{1}^{n+1} &\\ \frac{\lambda}{4} a_{2}^{n+1} & 0 & 0 & 1 & -\frac{\lambda}{4} a_{2}^{n+1} & 0 &\\ \ddots & \ddots & \ddots & \ddots & \ddots & \ddots \\ &0 & 0 & 0 & \frac{\lambda}{4} a_{1}^{n+1} & 1 & - \frac{\lambda}{4} a_{1}^{n+1} \\ &0 & 0 & \frac{\lambda}{4} a_{2}^{n+1} & 0 & 0 & 1 \end{bmatrix}, \\ &E^{n} = \begin{bmatrix} 1 & 0 & 0 & -\frac{\lambda}{4} a_{1}^{n} & 0 & 0 & \\ -\frac{\lambda}{4} a_{2}^{n} & 1 & \frac{\lambda}{4} a_{2}^{n} & 0 & 0 & 0 &\\ 0 & -\frac{\lambda}{4} a_{1}^{n} & 1 & 0 & 0 & \frac{\lambda}{4} a_{1}^{n} &\\ -\frac{\lambda}{4} a_{2}^{n} & 0 & 0 & 1 & \frac{\lambda}{4} a_{2}^{n} & 0 &\\ \ddots & \ddots & \ddots & \ddots & \ddots & \ddots \\ &0 & 0 & 0 & -\frac{\lambda}{4} a_{1}^{n} & 1 & \frac{\lambda}{4} a_{1}^{n} \\ &0 & 0 & -\frac{\lambda}{4} a_{2}^{n} & 0 & 0 & 1 \end{bmatrix}, \qquad \bar{U}^{n} = \begin{pmatrix} U_{1}^{n} \\ U_{2}^{n} \\ \vdots \\ U_{M-1}^{n} \end{pmatrix}, \\ &F^{n} = \begin{pmatrix} -\frac{\lambda}{4} a_{1}^{n+1} f (t_{n+1}) - \frac{\lambda}{4}a_{1}^{n} f (t_{n}) \\ -\frac{\lambda}{4}a_{2}^{n+1} \Delta x e^{-t_{n+1}} \frac{df}{dt} (t_{n+1}) - \frac{\lambda}{4} a_{2}^{n} \Delta x e^{-t_{n}} \frac{df}{dt} (t_{n}) \\0 \\ 0 \\ \vdots \\0 \\ 0 \end{pmatrix}, \end{aligned}$$

where \(a_{1}^{n} = e^{t_{n}}, a_{2}^{n} = e^{-t_{n}}\) and \(t_{n} = n\Delta t\) for all \(n = 0,1,2,\ldots, N\). The Crank-Nicolson scheme is unconditionally stable [12, 21].

4 A new fourth-order scheme with a Saulyev method for the advection-dispersion equation

Applying a new fourth-order technique [22] to equation (11), the discretization of each term is obtained as follows:

$$\begin{aligned} &C \cong C_{i}^{n}, \end{aligned}$$
(21)
$$\begin{aligned} &\frac{\partial C}{\partial t} \cong \frac{C_{i}^{n+1} - C_{i}^{n}}{\Delta t}, \end{aligned}$$
(22)
$$\begin{aligned} &\frac{\partial C}{\partial x} \cong F_{i}^{n} \frac{C_{i+2}^{n}-C_{i}^{n}}{2\Delta x} + G_{i}^{n}\frac{C_{i}^{n}-C_{i-2}^{n}}{2\Delta x} - H_{i}^{n} \frac{C_{i+1}^{n}-C_{i-1}^{n}}{2\Delta x}, \end{aligned}$$
(23)
$$\begin{aligned} &\frac{\partial^{2} C}{\partial x^{2}} \cong P_{i}^{n}\frac{C_{i+1}^{n}-2C_{i}^{n}+C_{i-1}^{n}}{(\Delta x)^{2}} + Q_{i}^{n}\frac{C_{i+2}^{n}-2C_{i}^{n}+C_{i-2}^{n}}{(\Delta x)^{2}} , \end{aligned}$$
(24)
$$\begin{aligned} &u \cong \widehat{U}_{i}^{n} , \end{aligned}$$
(25)

where

$$\begin{aligned} &\lambda = \frac{D\Delta t}{(\Delta x)^{2}}, \\ &\gamma_{i}^{n} = \frac{\Delta t}{\Delta x}\widehat{U}_{i}^{n}, \\ &F_{i}^{n} =\frac{(12\lambda+2(\gamma_{i}^{n})^{2}-3\gamma_{i}^{n}-2)}{12}, \\ &G_{i}^{n} = \frac{(12\lambda+2(\gamma_{i}^{n})^{2}+3\gamma_{i}^{n}-2)}{12}, \\ &H_{i}^{n} = \frac{((\gamma_{i}^{n})^{2}+6\lambda-4)}{3}, \\ &P_{i}^{n} = \frac{(-(\gamma_{i}^{n})^{4}+4(\gamma_{i}^{n})^{2}-12\lambda^{2}-12\lambda(\gamma_{i}^{n})^{2}+8\lambda)}{6\lambda}, \\ &Q_{i}^{n} = \frac{((\gamma_{i}^{n})^{4}-4(\gamma_{i}^{n})^{2}+12\lambda^{2}+12\lambda(\gamma_{i}^{n})^{2}-2\lambda)}{6\lambda}. \end{aligned}$$

Substituting equations (21)-(25) into equation (11), we obtain

$$\begin{aligned} &\frac{C_{i}^{n+1} - C_{i}^{n}}{\Delta t} + \widehat{U}_{i}^{n} \biggl(F_{i}^{n} \frac{C_{i+2}^{n}-C_{i}^{n}}{2\Delta x} + G_{i}^{n} \frac{C_{i}^{n}-C_{i-2}^{n}}{2\Delta x} - H_{i}^{n}\frac{C_{i+1}^{n}-C_{i-1}^{n}}{2\Delta x}\biggr) \\ &\quad = D\biggl(P_{i}^{n}\frac{C_{i+1}^{n}-2C_{i}^{n}+C_{i-1}^{n}}{(\Delta x)^{2}} + Q_{i}^{n}\frac{C_{i+2}^{n}-2C_{i}^{n}+C_{i-2}^{n}}{(\Delta x)^{2}}\biggr), \end{aligned}$$
(26)

for \(2\leq i \leq M-2\) and \(0\leq n \leq N-1\). Equation (26) can be written in an explicit form of finite difference equations as follows:

$$\begin{aligned} C_{i}^{n+1} =& \biggl(\frac{1}{2} \gamma_{i}^{n} G_{i}^{n} +\lambda Q_{i}^{n}\biggr)C_{i-2}^{n} + \biggl(- \frac{1}{2}\gamma_{i}^{n} H_{i}^{n} + \lambda P_{i}^{n}\biggr)C_{i-1}^{n} \\ &{} + \biggl(1+\frac{1}{2}\gamma_{i}^{n} F_{i}^{n} -\frac{1}{2}\gamma_{i}^{n} G_{i}^{n} -2\lambda P_{i}^{n} -\lambda Q_{i}^{n}\biggr)C_{i}^{n} + \biggl( \frac{1}{2}\gamma_{i}^{n} H_{i}^{n} +\lambda P_{i}^{n}\biggr) C_{i+1}^{n} \\ &{} + \biggl(-\frac{1}{2}\gamma_{i}^{n} F_{i}^{n} +\lambda Q_{i}^{n} \biggr)C_{i+2}^{n}, \end{aligned}$$
(27)

for \(2\leq i \leq M-2\) and \(0\leq n \leq N-1\). For \(i=1, M-1\) and M, the new fourth-order finite difference equation (27) cannot be employed to calculate the value \(C_{i}^{n}\) on the grid point next to left and right boundaries of the domain of the solution. An alternate appropriate finite difference method, such as the Saulyev method, is employed to approximate their values as discussed in the following section.

4.1 The employment of a Saulyev method to the left and the right boundary conditions

The Saulyev scheme is unconditionally stable [5, 22]. Applying the Saulyev technique [5] to equation (11), we obtain the following discretization:

$$\begin{aligned} &C \cong C_{i}^{n}, \end{aligned}$$
(28)
$$\begin{aligned} &\frac{\partial C}{\partial t} \cong \frac{C_{i}^{n+1} - C_{i}^{n}}{\Delta t}, \end{aligned}$$
(29)
$$\begin{aligned} &\frac{\partial C}{\partial x} \cong \frac{C_{i+1}^{n} - C_{i-1}^{n+1}}{2\Delta x}, \end{aligned}$$
(30)
$$\begin{aligned} &\frac{\partial^{2} C}{\partial x^{2}} \cong \frac{C_{i+1}^{n} -C_{i}^{n}-C_{i}^{n+1} + C_{i-1}^{n+1}}{(\Delta x)^{2}}, \end{aligned}$$
(31)
$$\begin{aligned} &u \cong \widehat{U}_{i}^{n}. \end{aligned}$$
(32)

Substituting equations (28)-(32) into equation (11), we obtain

$$ \frac{C_{i}^{n+1}-C_{i}^{n}}{\Delta t} + \widehat{U}_{i}^{n}\biggl( \frac{C_{i+1}^{n}-C_{i-1}^{n+1}}{2\Delta x}\biggr) = D \biggl(\frac{C_{i+1}^{n}-C_{i}^{n}-C_{i}^{n+1}+C_{i-1}^{n+1}}{(\Delta x)^{2}}\biggr), $$
(33)

for \(1\leq i \leq M\) and \(0\leq n \leq N-1\).

For \(i=1\), we put the known value of the left boundary \(C_{0}^{n+1}=r_{0}^{n+1}\) into equation (33) on the right hand side, and we obtain

$$ C_{1}^{n+1} = \biggl(\frac{1}{1+\lambda}\biggr) \biggl(\biggl( \frac{1}{2}\gamma_{1}^{n}+\lambda\biggr)r_{0}^{n+1} + (1-\lambda)C_{1}^{n} + \biggl(\lambda- \frac{1}{2}\gamma_{1}^{n}\biggr)C_{2}^{n}\biggr). $$
(34)

For \(i=M-1\), we obtain an explicit form of equation (33). We have

$$\begin{aligned} C_{M-1}^{n+1} = \biggl(\frac{1}{1+\lambda}\biggr) \biggl(\biggl( \frac{1}{2}\gamma_{M-1}^{n}+\lambda\biggr)C_{M-2}^{n+1} + (1-\lambda)C_{M-1}^{n} + \biggl(\lambda-\frac{1}{2} \gamma_{M-1}^{n}\biggr)C_{M}^{n}\biggr). \end{aligned}$$
(35)

For \(i=M\), substitution of the approximate unknown value of the right boundary by a traditional central difference approximation [23] with the known derivative the right boundary condition gives

$$ C_{M+1}^{n} = C_{M-1}^{n} + 2\Delta x S_{0}. $$
(36)

Substituting equation (36) into equation (33), we obtain

$$ C_{M+1}^{n+1} = \biggl(\frac{1}{1+\lambda}\biggr) \biggl(2 \lambda C_{i-1}^{n} + (1-\lambda) C_{i}^{n} + \biggl(\lambda-\frac{1}{2}\gamma_{i}^{n}\biggr) (2 \Delta x S_{0})\biggr). $$
(37)

From equations (34) and (37), we see that the technique does not generate fictitious points along either side of the solution domain. It follows that the new fourth-order finite difference equation (27), with the employed Saulyev finite difference equations (34)-(35) and (37), can be used to calculate the values \(C_{i}^{n}\) on grid points of the solution domain.

5 Numerical experiment

The uniform flow of advection-diffusion is considered in a uniform stream of constant cross-section and bottom slope. The flow velocity and diffusion coefficient are taken to be \(U=0.01\) m/s and \(D=0.001\) m2/s. We assume that the length of the stream is \(L=100\) m. We assume that the pollutant concentration level at the left end is

$$ C(0,1) = 1. $$
(38)

We assume that there is no rate of change of pollutant on the right end as follows:

$$ \frac{\partial C}{\partial x}(L,t) = 0. $$
(39)

The theoretical solution to the problem is [24, 25]

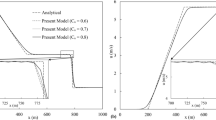
$$ C(x,t) = \frac{1}{2}\operatorname{erfc} \biggl(\frac{x-Ut}{\sqrt{4Dt}} \biggr) + \frac{1}{2}e^{\frac{Ux}{D}}\operatorname{erfc} \biggl(\frac{x+Ut}{\sqrt{4Dt}} \biggr). $$
(40)

The accuracy of the proposed new fourth-order scheme with employed Saulyev method and the theoretical methods is compared in Table 1 and Figure 2. They are not very sensitive to spatial and time discretization sizes as shown in Figures 3-4, while the time and location are fixed at \(x = 1.0 \) and \(t = 40.00 \) in Table 2.

Figure 2
figure 2

The comparison of the exact solution and the new fourth-order scheme at \(\pmb{C(1.0,t)}\) while \(\pmb{(\Delta x=0.0500, \Delta t=0.0250, \frac{\Delta t}{(\Delta x)^{2}} =10.00)}\) and \(\pmb{(\Delta x=0.0250, \Delta t=0.0125, \frac{\Delta t}{(\Delta x)^{2}}=20.00)}\) for all \(\pmb{0\leq t \leq 15}\) .

Full size image
Figure 3
figure 3

The comparison of the exact solution and the new fourth-order scheme at \(\pmb{C(0.5,t)}\) while \(\pmb{(\Delta x=0.2000, \Delta t=0.1000, \frac{\Delta t}{(\Delta x)^{2}} =2.50)}\) and \(\pmb{(\Delta x=0.0100, \Delta t=0.0500, \frac{\Delta t}{(\Delta x)^{2}}=5.00)}\) for all \(\pmb{0\leq t\leq 12.50}\) .

Full size image
Figure 4
figure 4

The comparison of the exact solution and the new fourth-order scheme at \(\pmb{C(1.0,t)}\) while \(\pmb{(\Delta x=0.0500, \Delta t=0.0250, \frac{\Delta t}{(\Delta x)^{2}} =10.00)}\) and \(\pmb{(\Delta x=0.0250, \Delta t=0.0125, \frac{\Delta t}{(\Delta x)^{2}}=20.00)}\) for all \(\pmb{0\leq t\leq 12.50}\) .

Full size image
Table 1 The error defined by \(\pmb{\operatorname{error}(T_{\mathrm{mxe}}) = \max \vert C(0.50,t)-\widetilde{C}(0.5,t) \vert }\) for all \(\pmb{0\leq t \leq 5}\) , for some \(\pmb{T_{\mathrm{mxe}}\in [0,5]}\) , where C and \(\pmb{\widetilde{C}}\) are theoretical solutions and new fourth-order scheme solutions, respectively
Full size table
Table 2 The comparison sensitivity to discretization sizes of approximated pollutant concentrations while time discretizations are halved
Full size table

The proposed technique gives the accurate results that depend on some spatial discretization sizes. It is a remarkably simple alteration to the fourth-order method so as to make it more accurate without any significant loss of computational efficiency.

6 Application to a non-uniform flow stream water quality assessment

Consider the measurement of a pollutant concentration C in a non-uniform flow stream. The stream is aligned with a longitudinal distance of 1.0 (km) and a depth of 1.0 (m). There is a plant which discharges waste water into the stream and the pollutant concentration at the discharge point is \(C(0,t) = C_{0} = 1\) (mg/L) at \(x=0\) for all \(t>0\), there is no rate of change of pollutant level \(\frac{\partial C}{\partial x}=0\) at \(x=1.0\) for all \(t>0\), and there is no initial pollutant \(C(x,0) = 0 \) (mg/L) at \(t=0\). The elevation of water at the discharge point can be described as a function \(d(0,t) = f(t) = \sin t\) (m) for all \(t>0\), and the elevation does not change at \(x = 1.0\) (km). The physical parameter of the pollutant matter is a diffusion coefficient \(D=0.1\) (m2/s).

In the analysis conducted in this study, we mesh the stream into 40 elements with \(\Delta x = 0.05\) and the time increment is 0.4 s with \(\Delta t = 0.00125\), characterizing a one-dimensional flow. Using the Crank-Nicolson method of [9, 10], and [13], the water flow velocity \(u(x,t)\) is shown in Table 3 and Figure 5.

Figure 5
figure 5

The approximated water flow velocity \(\pmb{u(x,t)}\) (m/s) in a uniform channel using the Crank-Nicolson method, for all \(\pmb{0\leq t \leq 133}\) min, \(\pmb{\Delta x = 0.05}\) , \(\pmb{\Delta t = 0.00125}\) , \(\pmb{\Delta t/\Delta x=0.50}\) .

Full size image
Table 3 The velocity of water flow \(\pmb{u(x,t)}\) , \(\pmb{\Delta x = 0.05}\) , \(\pmb{\Delta t = 0.00125}\)
Full size table

Next, the approximate water velocity can be added to the new fourth-order scheme, employing the Saulyev method to the left boundary near the discharge point, and the right boundary as in equation (27). The approximation of pollutant concentrations C of the proposed scheme is shown in Table 4 and Figure 6.

Figure 6
figure 6

The approximated pollutant concentration using the new fourth-order scheme and employing the Saulyev scheme, for all \(\pmb{0\leq t \leq 133}\) min, \(\pmb{\Delta x = 0.05}\) , \(\pmb{\Delta t = 0.00125}\) , \(\pmb{\Delta t/\Delta x=0.50}\) .

Full size image
Table 4 The pollutant concentration \(\pmb{C(x,t)}\) using the new fourth-order scheme and employing Saulyev scheme, Δ x = 0.05, Δ t = 0.00125
Full size table

They are not very sensitive to spatial and time discretization sizes as shown in Figure 7, while all discretization cases are halved and their ratios \(\Delta t /(\Delta x)^{2}\) are increased. The proposed technique gives good agreement results. The technique can be used to solve some water quality measurement problems that are limited by space and time discretizations. The proposed method, a fourth-order accurate finite difference scheme, is more accurate and is more efficient than the conventional second-order accurate finite difference techniques such as the FTCS explicit finite difference scheme and the Saulyev explicit finite difference scheme that are proposed in [13].

Figure 7
figure 7

The approximated pollutant concentration using the new fourth-order scheme and employing the Saulyev scheme at \(\pmb{x= 500}\) m for all \(\pmb{0\leq t \leq 133}\) min while \(\pmb{(\Delta x = 0.05, \Delta t = 0.000625, \Delta t/(\Delta x)^{2}=0.25)}\) , \(\pmb{(\Delta t = 0.00125, \Delta t/(\Delta x)^{2}=2.0)}\) , \(\pmb{(\Delta x = 0.025, \Delta t = 0.000625, \Delta t/(\Delta x)^{2}=1.0)}\) and \(\pmb{(\Delta x = 0.05, \Delta t = 0.00125, \Delta t/(\Delta x)^{2}=0.50)}\) .

Full size image

7 Conclusions

In this paper, the unconditionally stable Crank-Nicolson method is proposed to solve a one-dimensional hydrodynamic model with damped force due to the drag of stream sides. The one-dimensional advection-diffusion equation in a non-uniform flow in the stream is solved by using a new fourth-order scheme employing the unconditionally stable Saulyev method near the left and right boundary conditions. The new fourth-order scheme gives accurate results without any significant loss of computational efficiency. The results obtained indicate that the proposed new fourth-order scheme, coupled with the unconditionally stable Saulyev method, improves the prediction accuracy compared to that of the traditional computation techniques.