1 Introduction

Fractional calculus (FC) has become an alternative mathematical method to describe models with nonlocal behavior. In the last decade, considerable interest in fractional differential equations has been stimulated due to their numerous applications in the areas of physics and engineering [1–15]. Several numerical and analytical methods have been developed to study the solutions of nonlinear fractional partial differential equations, fractional sub-equation methods [16–18], the homotopy perturbation methods [19–21], the variational iteration methods [22–27], homotopy perturbation transform methods [28, 29], Adomian descomposition methods [30–33], and other analytical approaches that could be of interest for the reader are presented in [34–38]. It worth noting that there exist only two main definitions of the fractional derivative; the first was proposed by Riemann and Liouville and is the derivative of the convolution of a given function and a power law kernel, the second one was suggested by Caputo and it is the convolution of the local derivative of a given function with power law function [39].

Due to the fact that the power law cannot be used to model all the physical problems, Caputo and Fabrizio [40] have suggested an alternative concept of differentiation using the exponential decay as kernel instead of the power law. This new differentiation has also attracted attention of many scholars but was also disqualified for classification as a fractional derivative due to the fact that the kernel was not nonlocal; however, it is clear that many problems in nature also follow the exponential decay law which indeed has no singularity; therefore this derivative is significantly useful in modeling such real world problems [41–44].

The homotopy analysis method (HAM), proposed by Liao, has been successfully applied to solving many problems in physics and science [45–48], this method transforms a problem into an infinite number of linear problems without using the perturbation techniques. The Laplace homotopy analysis method (LHAM) is a combination of HAM and Laplace transform [49, 50]. The homotopy perturbation method is also combined with the well-known Laplace transformation method and the variational iteration method to produce a highly effective technique (homotopy perturbation transform method) for handling many nonlinear problems [51].

In this paper, we use the homotopy perturbation transform method (HPTM) to solve nonlinear fractional partial differential equations using the fractional operator of Caputo-Fabrizio type. The basic definitions of fractional calculus are given in Section 2, several test problems that show the effectiveness of the proposed method are given in Section 3, and finally the conclusion is given in Section 4.

2 Basic tools

The Liouville-Caputo fractional derivative is defined for \((\gamma>0)\) as

$$ ^{C}_{0}{\mathcal{D}}_{t}^{\mu} f(t) = \frac{1}{\Gamma(n - \mu )} \int_{0}^{t} (t-s)^{n-\mu-1}f^{(n)}(s) \,ds, $$
(1)

where \({}^{C}_{0}{\mathcal{D}}_{t}^{\mu}\) is a Liouville-Caputo fractional derivative with respect to t, \(f^{(n)}\) is the derivative of integer nth order of f, \(n = 1,2,\ldots\in N\), and \(n-1< \mu\leq n\).

Now, if the kernel \((t-s)^{n-\mu-1}\) is changed for the function \(\exp (-\mu(t-s)/(1-\mu))\), and \(\frac{1}{\Gamma(n-\mu)}\) for \(\frac{(2-\alpha )M(\alpha)}{2(1-\alpha)}\) in equation (1), we can show the new definition of fractional operator proposed by Caputo and Fabrizio (CF), which is expressed as follows [40, 41]:

$$ ^{\mathrm{CF}}_{0}{\mathcal{D}}_{t}^{\mu} f(t)= \frac{(2-\mu)M(\mu)}{2(1-\mu)} \int _{0}^{t} \exp \biggl(\frac{-\mu}{1-\mu} (t-s) \biggr)f^{(n)}(s) \,ds, $$
(2)

where \(M(\alpha)\) is a normalization function such that \(M(0)=M(1)=1\). This new definition does not have singularities at \(t=s\).

If \(0<\mu\leq1\) and \(n\in\mathbb{N}\), then we define the Laplace transform for the CF fractional operator as follows [40]:

$$\begin{aligned} &\mathcal{L} \bigl[_{0}^{\mathrm{CF}}D_{t}^{ (n+\mu )}f (t ) \bigr](s) \\ & \quad=\frac{1}{1-\mu}\mathcal{L} \bigl[f^{ (n+1 )} (t ) \bigr] \mathcal{L} \biggl[\exp \biggl(-\frac{\mu}{\mu-1} t \biggr) \biggr] \\ & \quad=\frac{s^{n+1}\mathcal{L} [f (t ) ]-s^{n}f (0 )-s^{n-1} f ' (0 )\ldots-f^{ (n )} (0 )}{s+\mu (1-s )}. \end{aligned}$$
(3)

3 General description of the method using the operator of Caputo-Fabrizio type

Consider the following nonlinear partial differential equation in the Caputo-Fabrizio sense:

$$\begin{aligned} ^{\mathrm{CF}}_{0}{\mathcal{D}}_{t}^{(n+\mu)} u (x,t )+\beta u (x,t )+ \varphi u (x,t )=\kappa (x,t ), \quad m-1< \mu+n\leq m, \end{aligned}$$
(4)

with initial conditions

$$ \frac{\partial^{h}u (x,0 )}{\partial t^{h}}=f_{h} (x ) ,\quad h=0,1,\ldots,m-1. $$
(5)

Applying the Laplace transform (3) in (4) yields

$$\begin{aligned} \mathcal{L} \bigl[u(x,t) \bigr] & = \Theta(x,s)- \biggl(\frac{s+\mu (1-s)}{s^{n+1}} \biggr) \mathcal{L} \bigl[\beta u (x,t ) + \varphi u (x,t ) \bigr], \end{aligned}$$
(6)

where

$$\begin{aligned} \Theta(x,s)& = \frac{1}{s^{n+1}} \bigl[s^{n} f_{0} (x )+s^{n-1} f_{1} (x )+ \cdots+ f_{n}(x) \bigr] + \frac{s+\mu (1-s )}{s^{n+1}} \widetilde{\kappa}(x,s). \end{aligned}$$
(7)

Applying the Laplace inverse operator on both sides of (6) yields

$$\begin{aligned} u(x,t) & = \Theta(x,t)- \mathcal{L}^{-1} \biggl[ \biggl( \frac{s+\mu (1-s)}{s^{n+1}} \biggr) \mathcal{L} \bigl[\beta u (x,t ) + \varphi u (x,t ) \bigr] \biggr], \end{aligned}$$
(8)

where \(\Theta(x,t)\) represents the term arising from the source term. Now, we apply the HPTM to obtain the solution of equation (8) starting by the hypothesis that \(u(x,t)\) is a solution of this equation, which we express as

$$\begin{aligned} u(x,t) = \sum_{n=0}^{\infty} z^{n}u_{n}(x,t), \end{aligned}$$
(9)

where \(u_{n}(x,t)\) are known functions, the nonlinear term can be decomposed as

$$\begin{aligned} \varphi u(x,t) = \sum_{n=0}^{\infty} z^{n}H_{n}(x,t), \end{aligned}$$
(10)

the polynomials \(H_{n}(x,t)\) are given by [52]

$$\begin{aligned} H_{n}(u_{0},u_{1}, \ldots,u_{n}) =\frac{1}{n!}\frac{\partial^{n}}{\partial z^{n}} \Biggl[\varphi \Biggl( \sum_{i=0}^{\infty} z^{i}u_{i} \Biggr) \Biggr]_{z=0},\quad n=0,1,2,\ldots; \end{aligned}$$
(11)

substituting (9) and (10) into (8) we get

$$ \sum_{n=0}^{\infty}u_{n}(x,t)= \Theta(x,t)- z \mathcal{L}^{-1} \Biggl[ \biggl(\frac{s+\mu(1-s)}{s^{n+1}} \biggr) \mathcal{L} \Biggl[\beta\sum_{n=0}^{\infty} z^{n}u_{n}(x,t)+ \sum_{i=0}^{\infty} z^{n}H_{n} \Biggr] \Biggr]. $$
(12)

Comparing the coefficients of like powers of z yields

$$\begin{aligned} \begin{aligned} &z^{0}: u_{0} (x,t ) = \Theta(x,t), \\ &z^{1}: u_{1} (x,t ) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s^{n+1}} \biggr) \mathcal{L} \bigl[\beta u_{0}(x,t)+ H_{0}(u) \bigr] \biggr], \\ &z^{2}: u_{2} (x,t ) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s^{n+1}} \biggr) \mathcal{L} \bigl[\beta u_{1}(x,t)+ H_{1}(u) \bigr] \biggr], \\ &z^{3}: u_{3} (x,t ) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s^{n+1}} \biggr) \mathcal{L} \bigl[\beta u_{2}(x,t)+ H_{2}(u) \bigr] \biggr], \\ &\phantom{z^{3}: u_{3} (x,t )} \vdots \\ &z^{n+1}: u_{n+1} (x,t ) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac {s+\mu(1-s)}{s^{n+1}} \biggr) \mathcal{L} \bigl[\beta u_{n}(x,t)+ H_{n}(u) \bigr] \biggr]. \end{aligned} \end{aligned}$$
(13)

4 Applications

We present the solutions obtained by the application of the HPTM with Caputo-Fabrizio fractional operator for some NFPDEs.

Example 1

Regarding the following nonlinear KdV equation in the Caputo-Fabrizio sense:

$$ {^{\mathrm{CF}}_{0}{\mathcal{D}}_{t}^{\mu}}u(x,t)=-u \frac{\partial u}{\partial x} - u\frac{\partial^{3} u}{\partial x^{3}},\quad 0< \mu\leq 1, $$
(14)

with the initial condition

$$\begin{aligned} u (x,0 )=x, \end{aligned}$$
(15)

applying the Laplace transform to (14) and considering the condition (15), we have

$$\begin{aligned} \mathcal{L} \bigl[u(x,t) \bigr] & = \frac{1}{s} u(x,0) - \biggl( \frac{s+\mu (1-s)}{s} \biggr)\mathcal{L} \biggl[u\frac{\partial u}{\partial x} + u \frac {\partial^{3} u}{\partial x^{3}} \biggr]. \end{aligned}$$
(16)

Applying the inverse of the Laplace transform to (16) yields

$$\begin{aligned} u(x,t) & = u(x,0) - \mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr)\mathcal{L} \biggl[u\frac{\partial u}{\partial x} + u\frac{\partial^{3} u}{\partial x^{3}} \biggr] \biggr]. \end{aligned}$$
(17)

Now, we apply the HPTM

$$\begin{aligned} \sum_{n=0}^{\infty}u_{n}(x,t)& = x - z \mathcal{L}^{-1} \Biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \mathcal{L} \Biggl[ \sum_{n=0}^{\infty} z^{n}H_{n}(u) + \sum_{i=0}^{\infty} z^{n}H_{n}(u) \Biggr] \Biggr], \end{aligned}$$
(18)

where \(H_{n}(u)\) are the polynomials that represent the nonlinear terms defined in (11). The polynomials \(H_{n}(u)\) are calculated in the following form:

$$\begin{aligned} \begin{aligned} &H_{0}(u) = u_{0}\frac{\partial}{\partial x}(u_{0})+u_{0} \frac{\partial ^{3} }{\partial x^{3}}(u_{0}), \\ &H_{1}(u) = \frac{\partial}{\partial z} \biggl[(u_{0}+ z u_{1}) \frac {\partial}{\partial x}(u_{0} + z u_{1})+(u_{0} + z u_{1})\frac{\partial ^{3} }{\partial x^{3}}(u_{0}+ z u_{1}) \biggr]_{z=0} \\ &\phantom{H_{1}(u) =} = u_{0}\frac{\partial}{\partial x}(u_{1})+ u_{1} \frac{\partial }{\partial x}(u_{0})+ u_{0}\frac{\partial^{3}}{\partial x^{3}}(u_{1})+u_{1} \frac{\partial^{3}}{\partial x^{3}}(u_{0}), \\ &H_{2}(u)=\frac{1}{2} \frac{\partial^{2}}{\partial z^{2}} \biggl[ \bigl(u_{0}+ z u_{1}+ z^{2} u_{2}\bigr) \frac{\partial}{\partial x}\bigl(u_{0} + z u_{1} + z^{2} u_{2}\bigr) \biggr]_{z=0} \\ &\phantom{H_{2}(u)={}}+\frac{1}{2} \frac{\partial^{2}}{\partial z^{2}} \biggl[\bigl(u_{0}+ z u_{1}+ z^{2} u_{2}\bigr) \frac{\partial^{3}}{\partial x^{3}} \bigl(u_{0} + z u_{1} + z^{2} u_{2} \bigr) \biggr]_{z=0} \\ &\phantom{H_{2}(u)} = u_{0}\frac{\partial}{\partial x}(u_{2})+ u_{1} \frac{\partial }{\partial x}(u_{1}) + u_{2}\frac{\partial}{\partial x}(u_{0}) \\ &\phantom{H_{2}(u)={}} + u_{0}\frac{\partial^{3}}{\partial^{3} x}(u_{2})+ u_{1} \frac{\partial ^{3}}{\partial x^{3}}(u_{1}) + u_{2}\frac{\partial^{3}}{\partial x^{3}}(u_{0}) \\ &\phantom{H_{2}(u)} \vdots \end{aligned} \end{aligned}$$
(19)

thus, \(H_{0}(u)= x\).

Comparing the coefficients of z in equation (18), we have

$$\begin{aligned} \begin{aligned} &z^{0}: u_{0}(x,t) = x, \\ &z^{1}: u_{1}(x,t) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s} \biggr) \mathcal{L} \bigl[ H_{0}(u)+ K_{n}(u) \bigr] \biggr] \\ &\phantom{z^{1}: u_{1}(x,t)} = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \mathcal{L} [ x ] \biggr] \\ &\phantom{z^{1}: u_{1}(x,t)} = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \frac{x}{s} \biggr] \\ &\phantom{\phantom{z^{1}: u_{1}(x,t)}} = -\mathcal{L}^{-1} \biggl[\frac{x \mu}{s^{2}} + \frac{(1-\mu)x}{s} \biggr] \\ &\phantom{z^{1}: u_{1}(x,t)} = -x\mu t- x (1-\mu), \\ &z^{2}: u_{2}(x,t) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s} \biggr) \mathcal{L} \bigl[ -2\mu x t - 2 x(1-\mu) \bigr] \biggr] \\ &\phantom{z^{2}: u_{2}(x,t)} = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \biggl[\frac {-2\mu x}{s^{2}} - \frac{2 x(1-\mu)}{s} \biggr] \biggr] \\ &\phantom{z^{2}: u_{2}(x,t)} =-2\mu x\mathcal{L}^{-1} \biggl[\frac{s+\mu(1-s)}{s^{3}} \biggr]+ 2x(1-\mu )\mathcal{L}^{-1} \biggl[\frac{s+\mu(1-s)}{s^{2}} \biggr] \\ &\phantom{z^{2}: u_{2}(x,t)} = -2\mu x \mathcal{L}^{-1} \biggl[\frac{\mu}{s^{3}} + \frac{(1-\mu )}{s^{2}} \biggr] + 2x(1-\mu)\mathcal{L}^{-1} \biggl[ \frac{\mu}{s^{2}} + \frac {(1-\mu)}{s} \biggr] \\ &\phantom{z^{2}: u_{2}(x,t)} = \mu^{2} x t^{2} + 4\mu(1-\mu)x t + 2(1- \mu)^{2} x \\ &\phantom{z^{2}: u_{2}(x,t)} \vdots \end{aligned} \end{aligned}$$
(20)

so the approximate solution of \(u(x,t)\) is given by

$$\begin{aligned} u(x,t) & = \sum_{n=0}^{\infty}u_{n}(x,t) \\ & = x \bigl(1-\mu t- (1-\mu) + \mu^{2} t^{2} + 4\mu(1-\mu)t +2\bigl(1-\mu^{2}\bigr) + \cdots \bigr). \end{aligned}$$
(21)

Therefore the analytical solution when \(\mu\to1\), is given by

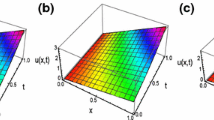
$$\begin{aligned} u(x,t) &= x \bigl(1 -t + t^{2} - t^{3} + \cdots \bigr) \\ & = x \sum_{k=0}^{\infty}(-1)^{k} t^{k} \\ & =\frac{x}{1+ t}. \end{aligned}$$
(22)

Figure 1 shows the numerical evaluation of (21).

Figure 1
figure 1

Numerical evaluation of ( 21 ).

Full size image

Example 2

Next, the following nonlinear KdV equation in the Caputo-Fabrizio sense is analyzed:

$$\begin{aligned} {^{\mathrm{CF}}_{0}{\mathcal{D}}_{t}^{\mu}}u(x,t) = -u\frac{\partial u}{\partial x} - \frac{\partial^{3} u}{\partial x^{3}} +x^{2} + 2 x^{3} t^{2}, \quad 0< \mu\leq1, \end{aligned}$$
(23)

with the initial condition

$$\begin{aligned} u (x,0 )=0. \end{aligned}$$
(24)

Applying the Laplace transform to (23) and considering the condition (24), we obtain

$$\begin{aligned} \mathcal{L} \bigl[u(x,t) \bigr] & = \biggl( \frac{s+\mu(1-s)}{s} \biggr) \biggl[ \frac{x^{2}}{s}+\frac{4 x^{3}}{s^{3}} \biggr] - \biggl(\frac{s+\mu (1-s)}{s} \biggr) \mathcal{L} \biggl[u\frac{\partial u}{\partial x} + \frac {\partial^{3} u}{\partial x^{3}} \biggr]. \end{aligned}$$
(25)

Applying the inverse of the Laplace transform to the above equation yields

$$\begin{aligned} u(x,t) ={}& x^{3} \biggl(\frac{2 \mu t^{3}}{3}-2 \mu t^{2}+2 t^{2} \biggr)+x^{2} (-\mu +\mu t+1) \\ &{} - \mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \mathcal{L} \biggl[u\frac{\partial u}{\partial x} + \frac{\partial^{3} u}{\partial x^{3}} \biggr] \biggr]. \end{aligned}$$
(26)

Now, we apply the HPTM to (26)

$$\begin{aligned} \sum_{n=0}^{\infty}u_{n}(x,t) = {}&x^{3} \biggl(\frac{2 \mu t^{3}}{3}-2 \mu t^{2}+2 t^{2} \biggr)+x^{2} (-\mu +\mu t+1) \\ &{}-z \mathcal{L}^{-1} \Biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \mathcal{L} \Biggl[ \sum_{n=0}^{\infty} z^{n}H_{n}(u) + \biggl(\sum_{n=0} z^{n} u_{n}(x,t) \biggr)_{xxx} \Biggr] \Biggr], \end{aligned}$$
(27)

where the polynomials \(H_{n}(u)\) can be expressed in the following form:

$$\begin{aligned} \begin{aligned} &H_{0}(u) = u_{0}\frac{\partial}{\partial x}(u_{0}), \\ & H_{1}(u) = \frac{\partial}{\partial z} \biggl[(u_{0}+ z u_{1}) \frac {\partial}{\partial x}(u_{0} + z u_{1}) \biggr]_{z=0} \\ &\phantom{H_{1}(u)} = u_{0}\frac{\partial}{\partial x}(u_{1})+ u_{1} \frac{\partial }{\partial x}(u_{0}), \\ &H_{2}(u) =\frac{1}{2} \frac{\partial^{2}}{\partial z^{2}} \biggl[ \bigl(u_{0}+ z u_{1}+ z^{2} u_{2}\bigr) \frac{\partial}{\partial x}\bigl(u_{0} + z u_{1} + z^{2} u_{2}\bigr) \biggr]_{z=0} \\ &\phantom{H_{1}(u)} = u_{0}\frac{\partial}{\partial x}(u_{2})+ u_{1}\frac{\partial }{\partial x}(u_{1}) + u_{2} \frac{\partial}{\partial x}(u_{0}) \\ &\phantom{H_{1}(u)} \vdots \end{aligned} \end{aligned}$$
(28)

Comparing the coefficients of z in (27), we have

$$\begin{aligned} & z^{0}: u_{0}(x,t) = x^{3} \biggl( \frac{2 \mu t^{3}}{3}-2 \mu t^{2}+2 t^{2} \biggr)+x^{2} (-\mu +\mu t+1), \\ & z^{1}: u_{1}(x,t) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s} \biggr) \mathcal{L} \biggl[ H_{0}(u) + \frac{\partial ^{3}u_{0}}{\partial x^{3}} \biggr] \biggr] \\ &\phantom{z^{1}: u_{1}(x,t)} = -\frac{4 \mu^{3} t^{7} x^{5}}{21} - 6 t \bigl(\mu^{3} x^{3}-2 \mu^{2} x^{3}+\mu x^{3} \bigr)+2 \bigl( \mu^{3} x^{3}-3 \mu^{2} x^{3} +3 \mu x^{3}-x^{3} \bigr) \\ &\phantom{\phantom{z^{1}: u_{1}(x,t)}=}{} + 2 t^{2} \bigl(-6 \mu^{2}+12 \mu+5 \mu^{3} x^{4}-15 \mu^{2} x^{4}+15 \mu x^{4}-5 x^{4}+2 \mu^{3} x^{3}-2 \mu^{2} x^{3}-6 \bigr) \\ &\phantom{z^{1}: u_{1}(x,t)={}} + \frac{8 t^{6}}{3} \bigl(\mu^{3} x^{5}-\mu^{2} x^{5} \bigr) \\ &\phantom{z^{1}: u_{1}(x,t)={}} -\frac{2 t^{3}}{3} \bigl(-12 \mu^{2}+12 \mu+25 \mu^{3} x^{4}-50 \mu^{2} x^{4}+25 \mu x^{4}+\mu^{3} x^{3} \bigr) \\ &\phantom{z^{1}: u_{1}(x,t)={}} + \frac{t^{4}}{3} \bigl(-3 \mu^{2}+36 \mu^{3} x^{5}-108 \mu^{2} x^{5}+108 \mu x^{5}-36 x^{5}+20 \mu^{3} x^{4}-20 \mu^{2} x^{4} \bigr) \\ &\phantom{z^{1}: u_{1}(x,t)={}} -\frac{2 t^{5}}{15} \bigl(78 \mu^{3} x^{5}-156 \mu^{2} x^{5}+78 \mu x^{5}+5 \mu^{3} x^{4} \bigr), \\ &z^{2}: u_{2}(x,t) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s} \biggr) \mathcal{L} \biggl[ H_{1}(u) + \frac{\partial ^{3}u_{1}}{\partial x^{3}} \biggr] \biggr] \\ &\phantom{z^{2}: u_{2}(x,t)} = -2 \biggl(-6 \mu^{4}+24 \mu^{3}-36 \mu^{2} + 24 \mu-\frac{1}{2} \mu^{4} t^{4} + 6 \bigl(\mu^{4}-\mu^{3} \bigr) t^{3} \\ &\phantom{z^{2}: u_{2}(x,t)={}} - 21 \bigl(\mu^{4}-2 \mu ^{3}+\mu^{2} \bigr) t^{2}+24 \mu^{4} t-72 \mu^{3} t+72 \mu^{2} t-24 \mu t-6 \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)={}} -2 x \biggl(-\frac{3}{2} \mu^{4} t^{6}+ \frac{134}{5} \bigl(\mu^{4}-\mu ^{3} \bigr) t^{5}-144 \mu^{4} t^{4}+288 \mu^{3} t^{4}-144 \mu^{2} t^{4} \\ &\phantom{z^{2}: u_{2}(x,t)={}} + 264 \bigl(\mu^{4}-3 \mu^{3}+3 \mu^{2}-\mu \bigr) t^{3}-132 \bigl(\mu^{4} - 4 \mu^{3}+6 \mu^{2}-4 \mu+1 \bigr) t^{2} \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)={}} -2 x^{2} \biggl(-\frac{47}{56} \mu^{4} t^{8}+\frac{138}{7} \bigl(\mu^{4}-\mu ^{3} \bigr) t^{7} - 149 \mu^{4} t^{6}+298 \mu^{3} t^{6}-149 \mu^{2} t^{6} \\ &\phantom{z^{2}: u_{2}(x,t)={}} + \frac{2{,}136}{5} \bigl(\mu^{4}-3 \mu^{3}+3 \mu^{2}-\mu \bigr) t^{5} \\ &\phantom{z^{2}: u_{2}(x,t)={}} -396 \bigl(\mu^{4} t^{4}-4 \mu^{3} t^{4}+6 \mu^{2} t^{4}-4 \mu t^{4}+t^{4} \bigr) \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)={}} -2 x^{4} \biggl(5 \mu^{5}-25 \mu^{4}+50 \mu^{3}-50 \mu^{2}+25 \mu -\frac{1}{3} \mu^{5} t^{5} \\ &\phantom{z^{2}: u_{2}(x,t)={}} +\frac{55}{12} \bigl(\mu^{5} t^{4}-\mu^{4} t^{4} \bigr) -20 \bigl( \mu^{5} - 2 \mu^{4}+\mu^{3} \bigr) t^{3} \\ &\phantom{z^{2}: u_{2}(x,t)={}} + 35 \bigl(\mu ^{5}-3 \mu^{4}+3 \mu^{3}- \mu^{2} \bigr) t^{2}-25 \mu^{5} t+100 \mu^{4} t \\ &\phantom{z^{2}: u_{2}(x,t)={}} -150 \mu ^{3} t+100 \mu^{2} t-25 \mu t-5 \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)={}} -2 x^{5} \biggl(-\frac{10}{21} \mu^{5} t^{7}+9 \mu^{5} t^{6}-9 \mu^{4} t^{6}-\frac{276}{5} \bigl(\mu^{5}-2 \mu^{4}+ \mu^{3} \bigr) t^{5} \\ &\phantom{z^{2}: u_{2}(x,t)={}} +136 \mu^{5} t^{4} - 408 \mu^{4} t^{4} + 408 \mu^{3} t^{4} \\ &\phantom{z^{2}: u_{2}(x,t)={}} - 136 \mu^{2} t^{4}-134 \bigl(\mu ^{5}-4 \mu^{4}+6 \mu^{3}-4 \mu^{2}+\mu \bigr) t^{3} \\ &\phantom{z^{2}: u_{2}(x,t)={}} +42 \bigl(\mu^{5}-5 \mu^{4}+10 \mu^{3}-10 \mu^{2}+5 \mu-1 \bigr) t^{2} \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)={}} -2 x^{6} \biggl(-\frac{20}{81} \mu^{5} t^{9}+6 \mu^{5} t^{8}-6 \mu^{4} t^{8}-\frac{2{,}204}{45} \bigl(\mu^{5}-2 \mu^{4}+ \mu^{3} \bigr) t^{7} \\ &\phantom{z^{2}: u_{2}(x,t)={}} +\frac{7{,}546}{45} \bigl( \mu^{5} t^{6}-3 \mu^{4} t^{6} + 3 \mu^{3} t^{6} - \mu^{2} t^{6} \bigr) \\ &\phantom{z^{2}: u_{2}(x,t)={}}-\frac{1{,}204}{5} \bigl( \mu^{5}-4 \mu^{4}+6 \mu^{3}-4 \mu ^{2} + \mu \bigr) t^{5}+112 \mu^{5} t^{4}-560 \mu^{4} t^{4} \\ &\phantom{z^{2}: u_{2}(x,t)={}}+1{,}120 \mu^{3} t^{4} - 1{,}120 \mu^{2} t^{4}+560 \mu t^{4}-112 t^{4} \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)={}}-2 x^{7} \biggl(-\frac {32}{693} \mu^{5} t^{11} + \frac{48}{35} \bigl(\mu^{5} t^{10} - \mu^{4} t^{10} \bigr) - \frac{13{,}312}{945} (\mu^{5} t^{9} -2 \mu^{4} t^{9} +\mu^{3} t^{9} ) \\ &\phantom{z^{2}: u_{2}(x,t)={}}+ \frac{952}{15} \bigl( \mu^{5} t^{8} - 3 \mu^{4} t^{8} + 3 \mu^{3} t^{8} - \mu^{2} t^{8} \bigr) \\ &\phantom{z^{2}: u_{2}(x,t)={}}- \frac{4{,}512}{35} \bigl( \mu^{5} - 4\mu^{4} + 6 \mu^{3} - 4 \mu^{2} + \mu \bigr) t^{7} + 96 \mu^{5} t^{6} - 480 \mu^{4} t^{6} \\ &\phantom{z^{2}: u_{2}(x,t)={}}+960 \mu^{3} t^{6}-960 \mu ^{2} t^{6}+480 \mu t^{6}- 96 t^{6} \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)={}}\vdots \end{aligned}$$
(29)

so the approximate solution of \(u(x,t)\) is given by

$$\begin{aligned} u(x,t) & =\sum_{n=0}^{\infty}u_{n}(x,t)= u_{0} + u_{1} + u_{2} + \cdots. \end{aligned}$$
(30)

Therefore the analytical solution when \(\mu\to1\) is given by

$$\begin{aligned} u(x,t) = x^{2} t . \end{aligned}$$
(31)

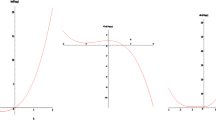
Figure 2 shows the numerical evaluation of (30).

Figure 2
figure 2

Numerical evaluation of ( 30 ).

Full size image

Example 3

We consider the following nonlinear Burger equation in the Caputo-Fabrizio sense:

$$\begin{aligned} {^{\mathrm{CF}}_{0}{\mathcal{D}}_{t}^{\mu}}u(x,t) + u\frac{\partial u}{\partial x} = \eta\frac{\partial^{2} u}{\partial x^{2}},\quad 0< \mu\leq1, \end{aligned}$$
(32)

subject to the initial condition

$$\begin{aligned} u(x,0) = n x, \quad n\in\mathbb{N}. \end{aligned}$$
(33)

Applying the Laplace transform to (32) and considering the condition (33), we have

$$\begin{aligned} \mathcal{L} \bigl[u(x,t) \bigr] = \frac{1}{s} u(x,0) - \biggl( \frac{s+\mu (1-s)}{s} \biggr)\mathcal{L} \biggl[u\frac{\partial u}{\partial x} - \eta \frac{\partial^{2} u}{\partial x^{2}} \biggr]. \end{aligned}$$
(34)

Applying the inverse of the Laplace transform to the above equation yields

$$\begin{aligned} u(x,t) = u(x,0) - \mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr)\mathcal{L} \biggl[u\frac{\partial u}{\partial x} - \eta\frac {\partial^{2} u}{\partial x^{2}} \biggr] \biggr]. \end{aligned}$$
(35)

Now, we apply the HPTM to (35)

$$\begin{aligned} \sum_{n=0}^{\infty}u_{n}(x,t)& = n x - z \mathcal {L}^{-1} \Biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \mathcal{L} \Biggl[ \sum_{n=0}^{\infty} z^{n}H_{n}(u) - \eta\frac{\partial^{2} u}{\partial x^{2}}\sum _{i=0}^{\infty} z^{n}u_{n}(x,t) \Biggr] \Biggr], \end{aligned}$$
(36)

where \(H_{n}(u)\) are the polynomials defined in equation (11), which represent the nonlinear terms. The polynomials \(H_{n}(u)\) are calculated in the following form:

$$\begin{aligned} \begin{aligned} &H_{0}(u) = u_{0}\frac{\partial}{\partial x}(u_{0}), \\ &H_{1}(u) = \frac{\partial}{\partial z} \biggl[(u_{0}+ z u_{1}) \frac {\partial}{\partial x}(u_{0} + z u_{1}) \biggr] \\ &\phantom{H_{1}(u)} = u_{0}\frac{\partial}{\partial x}(u_{1})+ u_{1} \frac{\partial }{\partial x}(u_{0}), \\ &H_{2}(u) =\frac{1}{2} \frac{\partial^{2}}{\partial z^{2}} \biggl[ \bigl(u_{0}+ z u_{1}+ z^{2} u_{2}\bigr) \frac{\partial}{\partial x}\bigl(u_{0} + z u_{1} + z^{2} u_{2}\bigr) \biggr] \\ &\phantom{H_{2}(u)} = u_{0}\frac{\partial}{\partial x}(u_{2})+ u_{1} \frac{\partial }{\partial x}(u_{1}) + u_{2}\frac{\partial}{\partial x}(u_{0}) \\ & \phantom{H_{2}(u)}\vdots \end{aligned} \end{aligned}$$
(37)

thus, \(H_{0}(u)=n^{2} x\) and \(u_{0}(x,t)=0\).

Comparing the coefficients of z in (36), we have

$$\begin{aligned} \begin{aligned} &z^{0}: u_{0}(x,t) = n x, \\ &z^{1}: u_{1}(x,t) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s} \biggr) \mathcal{L} ( n x ) \biggr] \\ &\phantom{z^{1}: u_{1}(x,t)} = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \biggl( \frac{n x}{s} \biggr) \biggr] \\ &\phantom{z^{1}: u_{1}(x,t)} = -n^{2} x (1 -\mu+ \mu t ), \end{aligned} \end{aligned}$$
(38)
$$\begin{aligned} \begin{aligned} &z^{2}: u_{2}(x,t) = -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s} \biggr) \mathcal{L} \bigl[ -2 n^{3} x (-\mu+ \mu t+1) \bigr] \biggr] \\ &\phantom{z^{2}: u_{2}(x,t)}= -\mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s} \biggr) \biggl( -2 n^{3} x \biggl(\frac{\mu}{s^{2}}-\frac{\mu}{s}+ \frac{1}{s} \biggr) \biggr) \biggr] \\ &\phantom{z^{2}: u_{2}(x,t)} =2 n^{3} x \biggl(\mu^{2}-2 \mu+\frac{\mu^{2} t^{2}}{2}-2 \bigl(\mu ^{2}-\mu \bigr) t+1 \biggr) \\ &\phantom{z^{2}: u_{2}(x,t)} \vdots \end{aligned} \end{aligned}$$
(39)

the approximate solution of \(u(x,t)\) is given by

$$\begin{aligned} u(x,t) & = \sum_{n=0}^{\infty}u_{n}(x,t) \\ & = u_{0} + u_{1} + u_{2} + \cdots. \end{aligned}$$
(40)

Therefore the analytical solution when \(\mu\to1\) is given by

$$\begin{aligned} u(x,t)& = nx \bigl[1- n t + n^{2} t^{2} - n^{3} t^{3} + \cdots \bigr] \\ & = x \sum_{k=0}^{\infty} (-1)^{k}n^{k+1} t^{k} \\ & = \frac{nx}{1 + n t}. \end{aligned}$$
(41)

Figure 3 shows the numerical evaluation of (40).

Figure 3
figure 3

Numerical evaluation of ( 40 ).

Full size image

Example 4

Consider the following nonlinear Klein-Gordon equation in the Caputo-Fabrizio sense:

$$\begin{aligned} {^{\mathrm{CF}}_{0}{\mathcal{D}}_{t}^{\mu+1}}u(x,t) = \frac{\partial^{2} u}{\partial x^{2}} - u^{2} + x^{2}t^{2},\quad 0< \mu \leq1, \end{aligned}$$
(42)

subject to the initial condition

$$\begin{aligned} \begin{aligned} &u(x,0) = 0, \\ &u_{t}(x,0) = x. \end{aligned} \end{aligned}$$
(43)

Applying the Laplace transform to (42) and considering the condition (43), we have

$$\begin{aligned} \mathcal{L} \bigl[u(x,t) \bigr] & = \frac{1}{s^{2}} u_{t}(x,0) + 2 \biggl(\frac {s+\mu(1-s)}{s^{5}} \biggr)x^{2} + \biggl(\frac{s+\mu(1-s)}{s^{2}} \biggr)\mathcal {L} \biggl[\frac{\partial^{2} u}{\partial x^{2}} - u^{2} \biggr]. \end{aligned}$$
(44)

Applying the inverse of the Laplace transform to the above equation yields

$$\begin{aligned} u(x,t) = x t + \frac{\mu t^{4} x^{2}}{12}+ \frac{(1-\mu)t^{3} x^{2}}{3} + \mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu(1-s)}{s^{2}} \biggr)\mathcal{L} \biggl[ \frac{\partial^{2} u}{\partial x^{2}} - u^{2} \biggr] \biggr]. \end{aligned}$$
(45)

Now, we apply the HPTM to (45)

$$\begin{aligned} \sum_{n=0}^{\infty}u_{n}(x,t) ={}& x t + \frac{\mu t^{4} x^{2}}{12}+ \frac {(1-\mu)t^{3} x^{2}}{3} \\ &{} + z \mathcal{L}^{-1} \Biggl[ \biggl(\frac{s+\mu(1-s)}{s^{2}} \biggr) \mathcal{L} \Biggl[\frac{\partial^{2} u}{\partial x^{2}} \sum_{n=0}^{\infty} z^{n}u_{n}(x,t) - \sum_{i=0}^{\infty} z^{n}H_{n}(x,t) \Biggr] \Biggr], \end{aligned}$$
(46)

where \(H_{n}(u)\) are the polynomials defined in equation (11), that represent the nonlinear terms. The polynomial \(H_{n}(u)\) are calculated in the following form:

$$\begin{aligned} \begin{aligned} &H_{0}(u) = (u_{0})^{2}, \\ &H_{1}(u) = \frac{\partial}{\partial z} \bigl[(u_{0}+ z u_{1})^{2} \bigr] \\ &\phantom{H_{1}(u)} = 2 u_{0} u_{1} \\ &\phantom{H_{1}(u)} \vdots \end{aligned} \end{aligned}$$
(47)

thus, \(H_{0}(u)= (x t + \frac{\mu t^{4} x^{2}}{12}+ \frac{(1-\mu )t^{3} x^{2}}{3} )^{2}\).

Comparing the coefficients of z in (46), we have

$$\begin{aligned} & z^{0}: u_{0}(x,t)= x t + \frac{\mu t^{4} x^{2}}{12}+ \frac{(1-\mu )t^{3} x^{2}}{3} , \\ &z^{1}: u_{1}(x,t) \\ &\quad = \mathcal{L}^{-1} \biggl[ \biggl(\frac{s+\mu (1-s)}{s^{2}} \biggr) \mathcal{L} \biggl(-\frac{2 x^{2}}{s^{3}} + \frac{4(1-\mu )}{s^{4}} -\frac{16 x^{3} (1-\mu)}{s^{5}} \\ & \qquad{}- \frac{80x^{4} (1-\mu)^{2}}{s^{7}} + \frac{4\mu}{s^{5}} -\frac{20 x^{3} \mu }{s^{6}} - \frac{280 x^{4} (1-\mu)\mu}{s^{8}} -\frac{280 x^{4} \mu^{2}}{s^{9}} \biggr) \biggr] \\ & \quad= -\frac{t^{4} x^{2} \mu}{12} +\frac{t^{5} (1-\mu)\mu}{30} - \frac{t^{6} x^{3} (1-\mu)\mu}{45} - \frac{t^{8} x^{4} (1-\mu)^{2} \mu}{504} \\ &\qquad{} + \frac{t^{6} \mu^{2}}{180} - \frac{x^{3} \mu^{2} t^{7}}{252}- \frac{t^{9} x^{4} (1-\mu)\mu^{2}}{1{,}296} - \frac{t^{10} x^{4} \mu^{2}}{12{,}960} \\ &\qquad{} -\frac{t^{3} x^{2} (1-\mu)}{3} + \frac{t^{4} (1-\mu)^{2}}{6} - \frac{2 t^{5} x^{3} (1-\mu)^{2}}{15} - \frac{t^{7} x^{4} (1-\mu)^{3}}{63} \\ &\qquad{} +\frac{t^{5} \mu(1-\mu) x^{4}}{30} - \frac{t^{6} x^{3} \mu(1-\mu)}{36} - \frac {t^{8} x^{4} (1-\mu)^{2} \mu}{144} - \frac{t^{9} x^{4} (1-\mu) \mu^{2}}{1{,}296}, \\ &z^{2}: u_{2}(x,t) \\ &\quad= -\mathcal{L}^{-1}\biggl[ \biggl( \frac{s+\mu (1-s)}{s^{2}} \biggr) \bigl[(u_{1})_{xx} - H_{1}(u) \bigr]\biggr] \\ &\quad =\mu \biggl[\frac{\mu^{4} t^{16} x^{6}}{18{,}662{,}400}- \frac{t^{6}}{180} \bigl(-\mu^{2}+\mu+4 \mu x^{3}-4 x^{3} \bigr)- \frac{t^{5}}{30} \bigl( \mu^{2}-2 \mu+1 \bigr) \\ & \qquad{}+ \frac{t^{8} (44 \mu^{2} x^{4}-88 \mu x^{4}+44 x^{4}-27 \mu^{3} x+66 \mu ^{2} x-39 \mu x )}{5{,}040} \\ &\qquad{} + \frac{t^{7} (5 \mu x^{3}+24 \mu^{3} x-82 \mu^{2} x+92 \mu x-34x )}{1{,}260} \\ & \qquad{}-t^{10} \bigl(304 \mu^{3} x^{5}-912 \mu^{2} x^{5}+912 \mu x^{5}-304 x^{5}-55 \mu^{2} x^{4} - 270 \mu^{4} x^{2} \\ &\qquad{} + 992 \mu^{3} x^{2}-1{,}174 \mu^{2} x^{2}+452 \mu x^{2} \bigr)/226{,}800 \\ &\qquad{} + \frac{t^{11} (555 \mu^{3} x^{5}-1{,}110 \mu^{2} x^{5}+555 \mu x^{5}-140 \mu^{4} x^{2}+392 \mu^{3} x^{2}-252 \mu^{2} x^{2} )}{831{,}600} \\ &\qquad{} - t^{9} \bigl(133 \mu^{2} x^{4}-133 \mu x^{4}+120 \mu^{4} x^{2}-550 \mu ^{3} x^{2} \\ &\qquad {}+ 930 \mu^{2} x^{2}-690 \mu x^{2}+190 x^{2}-15 \mu^{3} x+22 \mu^{2} x \bigr)/45{,}360 \\ &\qquad{} + \frac{137 t^{14} (\mu^{4} x^{6}-2 \mu^{3} x^{6}+\mu^{2} x^{6} )}{9{,}906{,}624}- \frac{t^{15} (\mu^{4} x^{6}-\mu^{3} x^{6} )}{680{,}400} \\ & \qquad{}+ t^{12} \bigl(240 \mu^{4} x^{6}-960 \mu^{3} x^{6}+1{,}440 \mu^{2} x^{6}-960 \mu x^{6}+240 x^{6} \\ & \qquad{}- 319 \mu^{3} x^{5}+319 \mu^{2} x^{5}+21 \mu^{4} x^{2}-42 \mu^{3} x^{2} \bigr) / 2{,}993{,}760 \\ &\qquad{} - \frac{t^{13} (390 \mu^{4} x^{6}-1{,}170 \mu^{3} x^{6}+1{,}170 \mu^{2} x^{6}-390 \mu x^{6}-37 \mu^{3} x^{5} )}{7{,}076{,}160} \biggr] \\ & \quad\vdots \end{aligned}$$
(48)

and the approximate solution of \(u(x,t)\) is

$$\begin{aligned} u(x,t) = \sum_{n=0}^{\infty}u_{n}(x,t) = u_{0} + u_{1} + u_{2} + u_{3} + \cdots. \end{aligned}$$
(49)

Therefore the analytical solution when \(\mu\to1\) is given by

$$\begin{aligned} u(x,t) = x t. \end{aligned}$$
(50)

Figure 4 shows the numerical evaluation of (49).

Figure 4
figure 4

Numerical evaluation of ( 49 ).

Full size image

Example 5

Consider the following nonlinear Klein-Gordon equation in the Caputo-Fabrizio sense:

$$ {^{\mathrm{CF}}_{0}{\mathcal{D}}_{t}^{\mu+1}}u(x,t)= \frac{\partial^{2} u}{\partial x^{2}} - u^{2} + t \sin(x) + t^{2} \sin^{2}(x), \quad 0< \mu \leq1, $$
(51)

subject to the initial condition

$$\begin{aligned} \begin{aligned} &u(x,0) =0, \\ &u_{t}(x,0) = \sin(x). \end{aligned} \end{aligned}$$
(52)

Applying the Laplace transform to (51) and considering the condition (52), we have

$$\begin{aligned} \mathcal{L} \bigl[u(x,t) \bigr] ={}& \frac{\sin(x)}{s^{2}} + \biggl( \frac{ s +\mu(1-s)}{s^{2}} \biggr) \biggl[\frac{\sin(x)}{s^{2}} + \frac{2 \sin ^{2}(x)}{s^{3}} \biggr] \\ &{}+ \biggl(\frac{s+\mu(1-s)}{s^{2}} \biggr)\mathcal{L} \biggl[\frac{\partial^{2} u}{\partial x^{2}} - u^{2} \biggr]. \end{aligned}$$
(53)

Applying the inverse of the Laplace transform to the above equation yields

$$\begin{aligned} u(x,t) ={} &\sin(x) t + \frac{\mu t^{4} \sin^{2}(x)}{12} +\frac{(1-\mu) t^{3} \sin ^{2}(x)}{3} + \frac{\mu t^{3} \sin(x)}{6} \\ & {}+\frac{(1-\mu) t^{2} \sin(x)}{2} + \mathcal{L}^{-1} \biggl[ \biggl(\frac {s+\mu(1-s)}{s^{2}} \biggr)\mathcal{L} \biggl[ \frac{\partial^{2} u}{\partial x^{2}} - u^{2} \biggr] \biggr]. \end{aligned}$$
(54)

Now, we apply the HPTM to (54),

$$\begin{aligned} \sum_{n=0}^{\infty}u_{n}(x,t) = {}&\sin(x) t + \frac{\mu t^{4} \sin ^{2}(x)}{12} +\frac{(1-\mu) t^{3} \sin ^{2}(x)}{3} +\frac{\mu t^{3} \sin(x)}{6} + \frac{(1-\mu) t^{2} \sin (x)}{2} \\ &{} + z \mathcal{L}^{-1} \Biggl[ \biggl(\frac{s+\mu(1-s)}{s^{2}} \biggr) \mathcal{L} \Biggl[ \sum_{n=0}^{\infty} z^{n}u_{n}(x,t) - \sum_{n=0}^{\infty} z^{n}H_{n}(x,t) \Biggr] \Biggr], \end{aligned}$$
(55)

where \(H_{n}(u)\) are the polynomials defined in (11), which represent the nonlinear terms. The polynomial \(H_{n}(u)\) are calculated in the following form:

$$\begin{aligned} \begin{aligned} &H_{0}(u) = (u_{0})^{2}, \\ &H_{1}(u) = \frac{\partial}{\partial z} \bigl[(u_{0}+ z u_{1})^{2} \bigr] \\ &\phantom{H_{1}(u)} = 2 u_{0} u_{1} \\ & \phantom{H_{1}(u)}\vdots \end{aligned} \end{aligned}$$
(56)

Comparing the coefficients of the same order in powers of p in (55), we have

$$\begin{aligned} &z^{0}: u_{0}(x,t) = \sin(x) t + \frac{\mu t^{4} \sin^{2}(x)}{12} + \frac{(1-\mu) t^{3} \sin ^{2}(x)}{3} +\frac{\mu t^{3} \sin(x)}{6} +\frac{(1-\mu) t^{2} \sin (x)}{2} , \\ &z^{1}: u_{1}(x,t) = \mathcal{L}^{-1} \biggl[ \biggl[\frac{s+\mu (1-s)}{s^{2}} \biggr] \mathcal{L} \biggl[\frac{\partial^{2} u_{0}}{\partial x^{2}} -H_{0}(u) \biggr] \biggr] \\ &\phantom{z^{1}: u_{1}(x,t) } = -\frac{\mu^{2} t^{5} \cos^{2}(x)}{15} +\frac{\mu t^{5} \cos ^{2}(x)}{15} +\frac{\mu^{2} t^{4} \cos^{2}(x)}{6} - \frac{\mu t^{4} \cos ^{2}(x)}{3} +\frac{t^{4} \cos^{2}(x)}{6} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} + \frac{ \mu^{2} t^{6} \cos^{2}(x)}{180} + \frac{\mu t^{3} \sin (x)}{6} -\frac{t^{3} \sin(x)}{6} + \frac{ \mu t^{2} \sin(x)}{2} -\frac{ t^{2} \sin(x)}{2} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} -\frac{\mu^{2} t^{5} \sin(x)}{120} +\frac{ \mu^{2} t^{4} \sin (x)}{12} -\frac{ \mu t^{4} \sin(x)}{12} - \frac{\mu^{2} t^{3} \sin(x)}{6} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} -\frac{ t^{5} \sin^{2}(x)}{20} +\frac{3 \mu t^{4} \sin^{2}(x)}{4} -\frac{5 t^{4} \sin^{2}(x)}{12}+ \frac{\mu t^{3} \sin^{2}(x)}{3} -\frac{t^{3} \sin ^{2}(x)}{3} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} -\frac{13 \mu t^{6} \sin^{2}(x)}{360}+ \frac{ \mu^{2} t^{5} \sin ^{2}(x)}{30} -\frac{ \mu t^{5} \sin^{2}(x)}{30} - \frac{5 \mu^{2} t^{4} \sin ^{2}(x)}{12} \\ & \phantom{z^{1}: u_{1}(x,t) =}{}-\frac{\mu^{2} t^{7} \sin^{2}(x)}{126} -\frac{13 \mu^{3} t^{6} \sin ^{2}(x)}{360} +\frac{\mu^{2} t^{6} \sin^{2}(x)}{18} + \frac{\mu^{3} t^{5} \sin ^{2}(x)}{20} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} -\frac{\mu^{3} t^{8} \sin^{2}(x)}{2{,}016}+\frac{\mu^{3} t^{7} \sin ^{2}(x)}{126} -\frac{ t^{6} \sin^{3}(x)}{18} + \frac{4 \mu t^{5} \sin ^{3}(x)}{15}-\frac{2 t^{5} \sin^{3}(x)}{15} \\ & \phantom{z^{1}: u_{1}(x,t) =}{}-\frac{\mu t^{7} \sin^{3}(x)}{28} -\frac{7 \mu^{2} t^{6} \sin ^{3}(x)}{60} +\frac{7 \mu t^{6} \sin^{3}(x)}{60}- \frac{2 \mu^{2} t^{5} \sin ^{3}(x)}{15} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} -\frac{ \mu^{2} t^{8} \sin^{3}(x)}{144}-\frac{\mu^{3} t^{7} \sin ^{3}(x)}{28} +\frac{17 \mu^{2} t^{7} \sin^{3}(x)}{252}+ \frac{\mu^{3} t^{6} \sin ^{3}(x)}{18} \\ & \phantom{z^{1}: u_{1}(x,t) }{}-\frac{\mu^{3} t^{9} \sin^{3}(x)}{2{,}592}+\frac{\mu^{3} t^{8} \sin ^{3}(x)}{144} +\frac{\mu t^{7} \sin^{4}(x)}{21} - \frac{ t^{7} \sin ^{4}(x)}{63} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} -\frac{\mu^{2} t^{9} \sin^{4}(x)}{648} +\frac{\mu^{2} t^{8} \sin ^{4}(x)}{56} -\frac{\mu t^{8} \sin^{4}(x)}{112} - \frac{\mu^{2} t^{7} \sin ^{4}(x)}{21} \\ &\phantom{z^{1}: u_{1}(x,t) =}{} -\frac{\mu^{3} t^{10} \sin^{4}(x)}{12{,}960}+ \frac{\mu^{3} t^{9} \sin ^{4}(x)}{648} -\frac{ \mu^{3} t^{8} \sin^{4}(x)}{112}+ \frac{\mu^{3} t^{7} \sin ^{4}(x)}{63} \\ &\phantom{z^{1}: u_{1}(x,t) } \vdots \end{aligned}$$
(57)

and the approximate solution of \(u(x,t)\) is given by

$$\begin{aligned} &u(x,t) = \sum_{n=0}^{\infty}u_{n}(x,t) \\ &\phantom{u(x,t) } = u_{0} + u_{1} + u_{2} + \cdots. \end{aligned}$$
(58)

Therefore the analytical solution when \(\mu\to1\) is

$$\begin{aligned} u(x,t) = \sin(x) t. \end{aligned}$$
(59)

Figure 5 shows the numerical evaluation of (58).

Figure 5
figure 5

Numerical evaluation of ( 58 ).

Full size image

4.1 Convergence and stability analysis

If the series (12) converges \((n=0,1,2,\ldots, n)\), where \(\Theta (x,s )\) is governed by (7), it must be the solution of equation (4). Overall, the results show that the proposed approach is unconditionally stable and convergent. The method provides a simple way to control the convergence region of the solution by introducing (11) and our approximate results agree well with exact solutions and numerical ones.

Madani in [53] have compared the approximate solutions obtained by means of HPTM in a wide range of the problem’s domain with those results obtained from the exact analytical solutions and the HAM. This comparison shows precise agreement between the HPTM and exact results. The HPTM solution is valid for a wide range of time and this suggests that the HPTM method can solve non-homogeneous equations with a high degree of accuracy by considering only few terms in the perturbed solution. On the other hand the relative error for the HAM is dramatically increased as the time value t increases, so the HAM solution validity range is restricted to a short region.

Therefore the HPTM method is a powerful new method which needs less computation time and is much easier and more convenient than the HAM, because the Laplace transform allows one in many situations to overcome the deficiency mainly caused by unsatisfied boundary or initial conditions that appear in other semi-analytical methods such as HAM [53].

5 Conclusions

In this paper, the HPTM method was developed to solve fractional nonlinear differential equations using the Caputo-Fabrizio operator. With the polynomials expansion considered in the HTPM method we obtained an infinite series solution for the fractional partial differential equations. Based on the HPTM, a general scheme was developed to obtain approximate solutions of fractional equations and the solutions are given in a series form, which converges rapidly. The methodology presented has become an important mathematical tool, motivated by the potential use for physicists and engineers working in various areas of the natural sciences.

This work shows that the HPTM method is an efficient tool for solving nonlinear fractional partial differential equations considering the fractional operator of Caputo-Fabrizio type. The HPTM yields a rapidly convergent series solution by using a few iterations [53, 54]. In this paper a Mathematica program has been used for computations and programming.