A modified proximal point algorithm involving nearly asymptotically quasi-nonexpansive mappings

Abstract

In this paper, we propose a modified proximal point algorithm based on the Thakur iteration process to approximate the common element of the set of solutions of convex minimization problems and the fixed points of two nearly asymptotically quasi-nonexpansive mappings in the framework of $\operatorname{CAT}(0)$ spaces. We also prove the Δ-convergence of the proposed algorithm. We also provide an application and numerical result based on our proposed algorithm as well as the computational result by comparing our modified iteration with previously known Sahu’s modified iteration.

1 Introduction

In this article, we assume that $\mathbb{N}$ denotes the set of all positive integers and $\mathbb{R}$ stands for the set of all real numbers. Let $\mathcal{C}$ be a nonempty subset of a $\operatorname{CAT}(0)$ space, $(\mathcal{X}, d)$ and $\mathcal{F}(\mathcal{T})$ denote the set all fixed points of a mapping $\mathcal{T}:\mathcal{C}\rightarrow \mathcal{C}$.

Fixed point theory in $\operatorname{CAT}(0)$ spaces was introduced by Kirk, afterward it attracted so many researchers of this field and has become a delightful topic of research for the past few years. Kirk proved the existence of a fixed point for a nonexpansive mapping defined on a bounded convex closed subset of a complete $\operatorname{CAT}(0)$ space (see [23]).

Let $\zeta :\mathcal{X}\rightarrow (-\infty , \infty ]$ be a proper convex function defined on $(\mathcal{X}, d)$. One of the vital problems of optimization is to find the minimizers of convex functional ζ over $\mathcal{X}$, i.e., find $\chi ^{*}\in \mathcal{X}$ such that

$$ \zeta \bigl(\chi ^{*}\bigr) = \min_{\varphi \in \mathcal{X}}\zeta ( \varphi ). $$

We denote by $\mathop{\operatorname{argmin}}_{\varphi \in \mathcal{X }}\zeta (\varphi )$ the set of minimizers of ζ.

In 1970, Martinet [27] initiated the proximal point algorithm (shortly PPA) which is a capable tool for solving this minimization problem, and after that Rockafellar [32] developed the PPA in a Hilbert space and proved that this method converges to a solution of the convex minimization problem. Recently, it has become a fascinating topic to extend the PPA for solving an optimization problem in the setting of manifolds which are an extension of Hilbert, Banach, and linear spaces. For more details on convex optimization and proximal point algorithms, see ([7–9, 13, 15, 35, 38, 41–46]).

In 2013, Bačák [6] introduced the concept of PPA in $\operatorname{CAT}(0)$ spaces, where the sequence $\{\chi _{n}\}$ is generated as follows:

$$ \textstyle\begin{cases} \chi _{1}\in \mathcal{C}, \\ \chi _{n+1} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} d^{2}(\varphi ,\chi _{n}) ),& \forall n\in \mathbb{N}, \end{cases} $$

where $\nu _{n}>0$. Later, it was proved by Ariza-Ruiz et al. [5] that if ζ has a minimizer and $\sum_{n=1}^{\infty }\nu _{n}=\infty$, then the sequence $\{\chi _{n}\}$ converges to the minimizer of ζ. This tremendous result became the reason for the success of convex analysis in $\operatorname{CAT}(0)$ spaces during past two decades by fascinating research in this direction.

In 2015, Cholamjiak [11] proposed a modified PPA by using the Halpern iteration procedure in $\operatorname{CAT}(0)$ spaces, where the sequence $\{\chi _{n}\}$ is generated as follows:

$$ \textstyle\begin{cases} \chi _{1}\in \mathcal{C}, \\ \varphi _{n} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} d^{2}(\varphi ,\chi _{n}) ), \\ \chi _{n+1} = (1 - \rho _{n})\upsilon \oplus \rho _{n}\mathcal{T} \varphi _{n}, \quad \forall n\in \mathbb{N}, \end{cases} $$

where $\nu _{n}> 0$, $\lim_{n\to \infty }\rho _{n}=0$, and $\sum_{n=1}^{\infty }\rho _{n}=\infty$, and proved that $\{\chi _{n}\}$ converges to the minimizer.

In the same year, Cholamjiak et al. [12] proposed a modified PPA by adopting the S-iteration procedure in $\operatorname{CAT}(0)$ spaces, where the sequence $\{\chi _{n}\}$ is generated as follows:

$$ \textstyle\begin{cases} \chi _{1}\in \mathcal{C}, \\ \varrho _{n} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} d^{2}(\varphi ,\chi _{n}) ), \\ \varphi _{n} = (1 - \sigma _{n})\chi _{n} \oplus \sigma _{n} \mathcal{T}_{1}\varrho _{n}, \\ \chi _{n+1} = (1 - \rho _{n})\mathcal{T}_{1}\chi _{n} \oplus \rho _{n} \mathcal{T}_{2}\varphi _{n}, \quad \forall n\in \mathbb{N}. \end{cases} $$

They proved some convergence theorems and showed that the above algorithm converges to the common fixed points of $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ and to the minimizers of a convex function ζ.

In the background of iteration processes, Mann [26], Ishikawa [21], and Halpern [20] are the three basic iterations utilized to approximate the fixed points of a nonexpansive mapping.

After these three basic iterative schemes, several researchers came up with the idea of generalized iterative schemes for the approximation of fixed points of nonlinear mappings. Here, we have a few iterations among the number of new iterative schemes: Noor iteration [28], Agarwal et al. iteration (S-iteration) [3], Abbas and Nazir iteration [2], Thakur’s iteration [39, 40], SP-iteartion [31], M-iteration [26], and so on.

In 2016, Chang et al. [10] established some strong convergence theorems for the PPA with S-iteration process to the common fixed points of asymptotically nonexpansive mappings and to the minimizer of a convex function in $\operatorname{CAT}(0)$ spaces.

In 2018, Pakkaranang et al. [30] proposed a modified PPA with SP iteration process for three asymptotically quasi-nonexpansive mappings in $\operatorname{CAT}(0)$ spaces and proved some convergence theorems.

Recently, Sahu et al. [34] introduced a modified PPA based on the S-iterative scheme to approximate a common element of the set of solutions of convex minimization problems and the set of fixed points of nearly asymptotically quasi-nonexpansive mappings in the setting of $\operatorname{CAT}(0)$ spaces, where the sequence $\{\chi _{n}\}$ is generated as follows:

$$ \textstyle\begin{cases} \chi _{1}\in \mathcal{C}, \\ \upsilon _{n} = \mathop{\operatorname{argmin}}_{\varrho \in \mathcal{C}} (\tau ( \varrho )+ \frac{1}{2\delta _{n}} d^{2}(\varrho ,\chi _{n}) ). \\ \varrho _{n} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} d^{2}(\varphi ,\upsilon _{n}) ), \\ \varphi _{n} = (1 - \sigma _{n})\chi _{n} + \sigma _{n}\mathcal{T}^{n} \varrho _{n}, \\ \chi _{n+1} = (1 - \rho _{n})\mathcal{T}^{n}\chi _{n}\oplus \rho _{n} \mathcal{S}^{n}\varphi _{n}. \end{cases} $$

Motivated by the above work, we propose a modified PPA based on the Thakur iterative scheme, where the sequence $\{\chi _{n}\}$ is generated as follows:

$$ \textstyle\begin{cases} \chi _{1}\in \mathcal{C}, \\ \omega _{n} = \mathop{\operatorname{argmin}}_{\varrho \in \mathcal{C}} (\tau ( \varrho )+ \frac{1}{2\delta _{n}} d^{2}(\varrho ,\chi _{n}) ), \\ \upsilon _{n} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} d^{2}(\varphi ,\omega _{n}) ), \\ \varrho _{n} = (1 - \varsigma _{n})\chi _{n}\oplus \varsigma _{n} \mathcal{T}^{n}\upsilon _{n}, \\ \varphi _{n} = (1 - \sigma _{n})\varrho _{n}\oplus \sigma _{n} \mathcal{S}^{n}\varrho _{n}, \\ \chi _{n+1} = (1-\rho _{n})\mathcal{T}^{n}\varrho _{n}\oplus \rho _{n}{S}^{n} \varphi _{n}, \end{cases} $$

(1.1)

for all $n \geq 1$, where $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ are appropriate real sequences in the interval $(0,1)$, and $\{\nu _{n}\}$ and $\{\delta _{n}\}$ are sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. $\zeta , \tau : \mathcal{C} \rightarrow (-\infty , \infty ]$ are proper convex and lower semi-continuous functions. We also prove that the sequence $\{\chi _{n}\}$ Δ-converges to a common element of the set of solutions of convex minimization problems and the set of fixed points of two nearly asymptotically quasi-nonexpansive mappings in the framework of $\operatorname{CAT}(0)$ spaces. We also provide a numerical example and application to show the efficiency of our main result, and by using MATLAB R2018a, we also add the comparison tables for our proposed iteration and previously known Sahu’s modified iteration process.

2 Preliminaries

In this section, we recall some frequently used lemmas and concepts in our main results. A self-mapping $\mathcal{T}$ defined on $\mathcal{C}$ is said to be

• (i) nonexpansive if

  $$ d(\mathcal{T}\chi , \mathcal{T}\varphi )\leq d(\chi , \varphi ) \quad \text{for all } \chi , \varphi \in \mathcal{C}; $$

• (ii) asymptotically nonexpansive [19] if there exists a sequence of real numbers $\{\Upsilon _{n}\}$ in $[1,\infty )$ with $\lim_{n\to \infty } \Upsilon _{n} = 1$ such that

  $$ d\bigl(\mathcal{T}^{n}\chi , \mathcal{T}^{n}\varphi \bigr)\leq \Upsilon _{n} d( \chi , \varphi ) \quad \text{for all } \chi , \varphi \in \mathcal{C} \text{ and } n\in \mathbb{N}; $$

• (iii) nearly uniformly ϒ-Lipschitzian [33] if there exist a fix sequence $\{a_{n}\}$ in $[0,\infty )$ with $\lim_{n\to \infty } a_{n} = 0$ and a constant $\Upsilon _{n} \geq 0$ with $\Upsilon _{n} \leq \Upsilon$ for some $\Upsilon \in [0, \infty )$ such that

  $$ d\bigl(\mathcal{T}^{n}\chi , \mathcal{T}^{n}\varphi \bigr)\leq \Upsilon d(\chi , \varphi )+a_{n} \quad \text{for all } \chi , \varphi \in \mathcal{C} \text{ and } n\in \mathbb{N}; $$

• (iv) nearly asymptotically nonexpansive [33] if there exist $\Upsilon _{n}\geq 1$ for all $n\in \mathbb{N}$, $\lim_{n\to \infty } \Upsilon _{n} = 1$, and a fix sequence $\{a_{n}\}$ in $[0,\infty )$ with $\lim_{n\to \infty } a_{n} = 0$ such that

  $$ d\bigl(\mathcal{T}^{n}\chi , \mathcal{T}^{n}\varphi \bigr)\leq \Upsilon _{n} d( \chi , \varphi )+a_{n} \quad \text{for all } \chi , \varphi \in \mathcal{C} \text{ and } n \in \mathbb{N}; $$

• (v) nearly asymptotically quasi-nonexpansive [1, 36] if there exist $\Upsilon _{n}\geq 1$ for all $n\in \mathbb{N}$, $\lim_{n\to \infty } \Upsilon _{n} = 1$, and a fix sequence $\{a_{n}\}$ in $[0,\infty )$ with $\lim_{n\to \infty } a_{n} = 0$ and $F(\mathcal{T})\neq \emptyset$ such that

  $$ d\bigl(\mathcal{T}^{n}\chi , p\bigr)\leq \Upsilon _{n} d(\chi , p)+a_{n} \quad \text{for all } \chi \in \mathcal{C}, p\in F(\mathcal{T}) \text{ and } n\in \mathbb{N}. $$

A metric space $(\mathcal{X}, d)$ is called a $\operatorname{CAT}(0)$ space if it is geodesically connected, and every geodesic triangle in $\mathcal{X}$ is at least as “thin” as its comparison triangle in the Euclidean plane.

Lemma 2.1

([17])

Let $\mathcal{X}$ be a $\operatorname{CAT}(0)$ space, $\chi , \varphi , \varrho \in \mathcal{X}$, and $t\in [0, 1]$. Then

$$ d\bigl(t\chi \oplus (1-t)\varphi , \varrho \bigr)\leq td(\chi , \varrho )+(1-t)d( \varphi , \varrho ). $$

A geodesic space $\mathcal{X}$ is a $\operatorname{CAT}(0)$ space if and only if it satisfies the following inequality:

$$ d^{2}\bigl(t\chi \oplus (1-t)\varphi , \varrho \bigr)\leq td^{2}(\chi , \varrho )+(1-t)d^{2}(\varphi , \varrho )-t(1-t)d^{2}(\chi , \varphi ) $$

for all $\chi , \varphi , \varrho \in \mathcal{X}$ and $t \in [0, 1]$.

Let $\{\chi _{n}\}$ be a bounded sequence in $\mathcal{X}$, a complete $\operatorname{CAT}(0)$ space. For $\chi \in \mathcal{X}$, set

$$ r\bigl(\chi ,\{\chi _{n}\}\bigr)=\limsup_{n\rightarrow \infty }d( \chi ,\chi _{n}). $$

The asymptotic radius $r(\{\chi _{n}\})$ is given by

$$ r\bigl(\{\chi _{n}\}\bigr)=\inf \bigl\{ r(\chi ,\chi _{n}):\chi \in \mathcal{X}\bigr\} , $$

and the asymptotic center $A(\{\chi _{n}\})$ of $\{\chi _{n}\}$ is defined as follows:

$$ A\bigl(\{\chi _{n}\}\bigr)=\bigl\{ \chi \in \mathcal{X}: r(\chi , \chi _{n})=r\bigl(\{ \chi _{n}\}\bigr)\bigr\} . $$

It is known that if $\mathcal{C}$ is a nonempty closed convex subset of a complete $\operatorname{CAT}(0)$ space $\mathcal{X}$, then $A(\{\chi _{n}\})$ consists of exactly one point see [16].

In 2008, Kirk and Panyanak [24] gave a concept of convergence in $\operatorname{CAT}(0)$ spaces which is an analogue of weak convergence in Banach spaces and restriction of Lim’s concepts of convergence [25] to $\operatorname{CAT}(0)$ spaces.

A sequence $\{\chi _{n}\}$ in $\mathcal{X}$ is said to Δ-converge to $\chi \in \mathcal{X}$ if χ is the unique asymptotic center for every subsequence $\{\upsilon _{n}\}$ of $\{\chi _{n}\}$. In this case, we write $\Delta -\lim_{n} {\chi _{n}}=\chi$ and read as χ is the Δ-limit of $\{\chi _{n}\}$.

Lemma 2.2

([16])

Suppose that $(\mathcal{X}, d)$ is a complete $\operatorname{CAT}(0)$ space. Let $\{\chi _{n}\}$ be a bounded sequence in $\mathcal{X}$. If $A(\{\chi _{n}\}) = \{p\}$, $\{\upsilon _{n}\}$ is a subsequence of $\{\chi _{n}\}$ such that $A(\{\upsilon _{n}\}) = \{\upsilon \}$ and $d(\chi _{n}, \upsilon )$ converges, then $p=\upsilon$.

Lemma 2.3

([24])

In a complete $\operatorname{CAT}(0)$ space, every bounded sequence admits a Δ-convergent subsequence.

Definition 2.1

Let $\mathcal{C}$ be a nonempty closed convex subset of a complete $\operatorname{CAT}(0)$ space $\mathcal{X}$ and $\mathcal{T} : \mathcal{C} \rightarrow \mathcal{C}$ be a mapping. We say that the mapping $\mathcal{T}$ satisfies the demiclosedness principle if for any bounded sequence $\{\chi _{n}\}$ in $\mathcal{C}$ with $d(\chi _{n}, \mathcal{T}\chi _{n}) \rightarrow 0$ and for any its Δ-limit, $\varrho \in \mathcal{C}$, it holds that $\mathcal{T} \varrho =\varrho$.

Lemma 2.4

([1])

Let $\mathcal{C}$ be a nonempty closed convex subset of a complete $\operatorname{CAT}(0)$ space $\mathcal{X}$ and $\mathcal{T} : \mathcal{C} \rightarrow \mathcal{C}$ be a uniformly continuous nearly asymptotically nonexpansive mapping. Then $\mathcal{T}$ satisfies the demiclosedness principle.

Lemma 2.5

([37])

Let $\mathcal{X}$ be a complete $\operatorname{CAT}(0)$ space and $\upsilon \in \mathcal{X}$. Suppose that $\{t_{n}\}$ is a sequence in $[b, c]$ for some $b, c \in (0,1)$ and $\{\chi _{n}\}$, $\{\varphi _{n}\}$ are sequences in $\mathcal{X}$ such that $\limsup_{n\to \infty } d(\chi _{n}, \upsilon )\leq r$, $\limsup_{n\to \infty } d(\varphi _{n}, \upsilon ) \leq r$, and $\lim_{n\to \infty } d((1- t_{n})\chi _{n} \oplus t_{n} \varphi _{n}, \upsilon )=r$ for some $r\geq 0$. Then

$$ \lim_{n\to \infty } d(\chi _{n}, \varphi _{n})=0. $$

Let $\mathcal{C}$ be a convex subset of a $\operatorname{CAT}(0)$ space, $\mathcal{X}$. A function $\zeta :\mathcal{C}\rightarrow (-\infty , \infty ]$ is said to be convex if, for any geodesic $[\chi , \varphi ]:=\{\varsigma _{\chi , \varphi }(\nu ):0\leq \nu \leq 1\}:=\{\nu \chi \oplus (1-\nu )\varphi :0\leq \nu \leq 1\}$ joining $\chi , \varphi \in \mathcal{C}$, the function $(\zeta \circ \varsigma )$ is convex, i.e.,

$$ \zeta \bigl(\varsigma _{\chi , y}(\nu )\bigr):=\zeta \bigl(\nu \chi \oplus (1-\nu )y\bigr) \leq \nu \zeta (\chi )+(1-\nu )\zeta (y). $$

A function ζ defined on $\mathcal{C}$ is said to be lower continuous at $\varphi \in \mathcal{C}$ if

$$ \zeta (\varphi )\leq \liminf_{n\rightarrow \infty }\zeta (\chi _{n}) \quad \text{for each } \chi _{n}\rightarrow \varphi $$

and lower semi-continuous on $\mathcal{C}$ if it is lower semi-continuous at each point of $\mathcal{C}$.

Let $\mathcal{X}$ be a $\operatorname{CAT}(0)$ space and $\zeta : \mathcal{X} \rightarrow (-\infty , \infty ]$ be a proper convex and lower semi-continuous function. The Moreau–Yosida resolvent of ζ in $\operatorname{CAT}(0)$ spaces is defined as follows:

$$ \operatorname{prox}_{\nu \zeta }(\chi )=\mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} \biggl( \zeta (\varphi )+ \frac{1}{2\nu } d^{2}(\varphi ,\chi ) \biggr) $$

for all $\chi \in \mathcal{X}$ and $\nu > 0$. The mapping $\operatorname{prox}_{\nu \zeta }$ defined above is well defined for all $\nu > 0$ which is called the proximal operator of ζ with parameter $\nu > 0$ (see [22]).

Lemma 2.6

([4])

Let $(\mathcal{X}, d)$ be a complete $\operatorname{CAT}(0)$ space and $\zeta :\mathcal{C}\rightarrow (-\infty , \infty ]$ be a proper convex and lower semi-continuous function. Then, for all $\chi , \varphi \in \mathcal{X}$ and $\nu > 0$, the following identity holds:

$$ \frac{1}{2\nu }d^{2}\bigl(\operatorname{prox}_{\nu \zeta }( \chi ), \varphi \bigr)- \frac{1}{2\nu }d^{2}(\chi , \varphi )+ \frac{1}{2\nu }d^{2}\bigl(\chi , \operatorname{prox}_{\nu \zeta }( \chi )\bigr)+\zeta \bigl(\operatorname{prox}_{\nu \zeta }(\chi )\bigr) \leq \zeta (\varphi ). $$

Lemma 2.7

([22])

Let $(\mathcal{X}, d)$ be a complete $\operatorname{CAT}(0)$ space and $\zeta :\mathcal{C}\rightarrow (-\infty , \infty ]$ be a proper convex and lower semi-continuous function. Then the following identity holds:

$$ \operatorname{prox}_{\nu \zeta }(\chi ) = \operatorname{prox}_{\mu \zeta } \biggl( \frac{\nu -\mu }{\nu }\operatorname{prox}_{\nu \zeta }(\chi )\oplus \frac{\mu }{\nu }\chi \biggr) $$

for all $\chi \in \mathcal{X}$ and $0<\mu <\nu$.

Lemma 2.8

([5])

Let $(\mathcal{X}, d)$ be a complete $\operatorname{CAT}(0)$ space and $\zeta :\mathcal{C}\rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous. Then, for any $\nu > 0$,

• (a) the proximal operator $\operatorname{prox}_{\nu \zeta }$ of ζ is firmly nonexpansive, i.e.,

  $$ d\bigl(\operatorname{prox}_{\nu \zeta }(\chi ),\operatorname{prox}_{\nu \zeta }( \varphi )\bigr) \leq d\bigl((1-t)\chi \oplus t \operatorname{prox}_{\nu \zeta }( \chi ), (1-t) \varphi \oplus t \operatorname{prox}_{\nu \zeta }(\varphi ) \bigr) $$

  for all $\chi , \varphi \in \mathcal{X}$ and $t \in (0, 1)$;

• (b) the set $\mathcal{F}(\operatorname{prox}_{\nu \zeta })$ of fixed points of $\operatorname{prox}_{\nu \zeta }$ coincides with the set $\mathop{\operatorname{argmin}}_{\varphi \in \mathcal{X}} \zeta (\varphi )$ of minimizers of ζ.

Remark 1

Every firmly nonexpansive mapping is nonexpansive mapping.

Lemma 2.9

([29])

Let $\{s_{n}\}$ be the sequences of nonnegative numbers such that

$$ s_{n+1} \leq \varsigma _{n}s_{n} + \xi _{n}, $$

where $\{\varsigma _{n}\}$ and $\{\xi _{n}\}$ are sequences of nonnegative numbers such that $\varsigma _{n}\subseteq [1, \infty )$ and $\sum_{n=1}^{\infty }(\varsigma _{n}-1)<\infty$ and $\sum_{n=1}^{\infty }(\xi _{n})<\infty$. Then $\lim_{n\to \infty }s_{n}=0$ exists.

3 Main results

We begin with the following proposition.

Proposition 3.1

Let $\mathcal{C}$ be a nonempty closed convex subset of a complete CAT (0) space $(\mathcal{X},d)$. Let $\zeta , \tau : \mathcal{C} \rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous functions, and $\mathcal{T}, \mathcal{S} : \mathcal{C} \rightarrow \mathcal{C}$ be two uniformly continuous mappings satisfying the following:

• (a) $\mathcal{T}$ and $\mathcal{S}$ are nearly asymptotically quasi-nonexpansive mappings with sequence $\{(a_{n}, \Upsilon _{n})\}$ such that $\sum_{n=1}^{\infty } a_{n}<\infty$ and $\sum_{n=1}^{\infty }(\Upsilon _{n}-1)<\infty$;

• (b) $\mathcal{T}$ and $\mathcal{S}$ are nearly uniformly Γ-Lipschitzian mappings with sequence $\{(q_{n}, \Gamma )\}$.

Let $P= \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S})\cap \operatorname{argmin}_{ \varphi \in \mathcal{C}} \zeta (\varphi )\cap \operatorname{argmin}_{\varrho \in \mathcal{C}} \tau (\varrho )\neq \emptyset$. Let $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ be sequences in $(0, 1)$ such that $0 <\rho \leq \rho _{n}$, $\sigma _{n}, \varsigma _{n}\leq \sigma <1$ for all $n\in \mathbb{N}$. Let $\{\nu _{n}\}$ and $\{\delta _{n}\}$ be sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. For $\chi _{1} \in \mathcal{C}$, let $\{\chi _{n}\}$ be a sequence in $\mathcal{C}$ defined by (1.1). Then we have the following:

• (D1) $\lim_{n\rightarrow \infty }d(\chi _{n}, p)$ exists for each $p \in P$;

• (D2) $\lim_{n\rightarrow \infty }d(\chi _{n}, \mathcal{T}\chi _{n}) =\lim_{n \rightarrow \infty }d(\chi _{n}, \mathcal{S}\chi _{n})=0$.

Proof

Let $p\in P$. Then $p=\mathcal{T}p$ and $\zeta (p)\leq \zeta (\varphi )$ and $\tau (p)\leq \tau (\varrho )$ for all $\varphi , \varrho \in C$. Since, $\zeta (p)\leq \zeta (\varphi )$, it follows that

$$ \zeta (p)+ \frac{1}{2\nu _{n}} d^{2}(p,p) \leq \zeta (\varphi )+ \frac{1}{2\nu _{n}} d^{2}(\varphi ,p) $$

for all $\varphi \in C$ and hence $p =\operatorname{prox}_{\nu _{n} \zeta } (p)$ for all $n\in \mathbb{N}$. Similarly, we have $p =\operatorname{prox}_{\delta _{n} \tau } (p)$ for all $n\in \mathbb{N}$.

First, we prove that $\lim_{n\rightarrow \infty }d(\chi _{n}, p)$ exists. Note that $\upsilon _{n} =\operatorname{prox}_{\nu _{n} \zeta } (\omega _{n})$ and $\omega _{n} =\operatorname{prox}_{\delta _{n} \tau } (\chi _{n})$ for all $n\in \mathbb{N}$. By Lemma 2.8, it follows that

$$ d(\upsilon _{n},p)= d\bigl(\operatorname{prox}_{\nu _{n} \zeta } ( \omega _{n}), \operatorname{prox}_{\nu _{n} \zeta }(p)\bigr) \leq d( \omega _{n},p) $$

and

$$ d(\omega _{n},p)= d\bigl(\operatorname{prox}_{\delta _{n} \tau } (\chi _{n}), \operatorname{prox}_{\delta _{n} \tau } (p)\bigr) \leq d(\chi _{n},p). $$

Hence,

$$ d(\upsilon _{n},p)\leq d(\chi _{n},p). $$

(3.1)

By using the definition of nearly asymptotically quasi-nonexpansive mapping and (1.1), we have

$$\begin{aligned}& \begin{aligned} d(\varrho _{n}, p) & = d\bigl((1- \varsigma _{n})\chi _{n} \oplus \varsigma _{n} \mathcal{T}^{n}\upsilon _{n}, p\bigr) \\ & \leq (1-\varsigma _{n})d(\chi _{n}, p)+ \varsigma _{n} d\bigl( \mathcal{T}^{n}\upsilon _{n}, p \bigr) \\ & \leq (1-\varsigma _{n})d(\chi _{n}, p)+\varsigma _{n}\bigl[\Upsilon _{n}d( \upsilon _{n}, p)+a_{n}\bigr] \\ & \leq (1-\varsigma _{n})d(\chi _{n}, p)+\varsigma _{n}\bigl[\Upsilon _{n}d( \upsilon _{n}, p)+a_{n}\bigr] \\ & \leq (1-\varsigma _{n})d(\chi _{n}, p)+\varsigma _{n}\bigl[\Upsilon _{n}d( \chi _{n}, p)+a_{n}\bigr] \\ & \leq \Upsilon _{n} d(\chi _{n}, p)+a_{n}. \end{aligned} \end{aligned}$$

(3.2)

$$\begin{aligned}& \begin{aligned} d(\varphi _{n}, p) & = d\bigl((1-\sigma _{n})\varrho _{n} \oplus \sigma _{n} \mathcal{S}^{n}\varrho _{n}, p\bigr) \\ & \leq (1-\sigma _{n})d(\varrho _{n}, p)+ \sigma _{n} d\bigl(\mathcal{S}^{n} \varrho _{n}, p \bigr) \\ & \leq (1-\sigma _{n})d(\varrho _{n}, p)+ \sigma _{n}\bigl[\Upsilon _{n}d( \varrho _{n}, p)+a_{n}\bigr] \\ & \leq \Upsilon _{n} d(\varrho _{n}, p)+a_{n} \\ & \leq \Upsilon _{n}\bigl[\Upsilon _{n} d(\chi _{n}, p)+a_{n}\bigr]+a_{n} \\ & \leq \Upsilon _{n}^{2}d(\chi _{n}, p)+(1+ \Upsilon _{n})a_{n}. \end{aligned} \end{aligned}$$

(3.3)

Also we have

$$\begin{aligned} d(\chi _{n+1}, p) & = d\bigl((1-\rho _{n}) \mathcal{T}^{n}\varrho _{n} \oplus \rho _{n} \mathcal{S}^{n}\varphi _{n}, p\bigr) \\ & \leq (1-\rho _{n})d\bigl(\mathcal{T}^{n}\varrho _{n}, p\bigr)+ \rho _{n} d\bigl( \mathcal{S}^{n} \varphi _{n}, p\bigr) \\ & \leq (1-\rho _{n})\bigl[\Upsilon _{n}d(\varrho _{n}, p)+a_{n}\bigr]+ \rho _{n} \bigl[ \Upsilon _{n}d(\varphi _{n}, p)+a_{n}\bigr] \\ & \leq (1-\rho _{n})\Upsilon _{n}d(\varrho _{n}, p)+ \rho _{n} \Upsilon _{n}d(\varphi _{n}, p)+a_{n} \\ & \leq (1-\rho _{n})\Upsilon _{n}d(\varrho _{n}, p)+ \rho _{n} \Upsilon _{n}\bigl[ \Upsilon _{n}d(\varrho _{n}, p)+a_{n} \bigr]+a_{n} \\ \begin{aligned}& \leq \Upsilon _{n}\bigl[1+\rho _{n}( \Upsilon _{n}-1)\bigr]d(\varrho _{n}, p)+ (\rho _{n} \Upsilon _{n}+1)a_{n} \\ & \leq \Upsilon _{n}^{2}d(\varrho _{n}, p)+ (\Upsilon _{n}+1)a_{n} \end{aligned} \\ & \leq \Upsilon _{n}^{2}\bigl[\Upsilon _{n}d(\chi _{n}, p)+a_{n}\bigr]+ ( \Upsilon _{n}+1)a_{n} \\ & \leq \Upsilon _{n}^{3}d(\chi _{n}, p)+ \bigl(\Upsilon _{n}^{2}+ \Upsilon _{n}+1 \bigr)a_{n} \\ & \leq \bigl[1+\bigl(\Upsilon _{n}^{3}-1\bigr)\bigr]d( \chi _{n}, p)+ \bigl(\Upsilon _{n}^{2}+ \Upsilon _{n}+1\bigr)a_{n} \\ & \leq \bigl[1+(\Upsilon _{n}-1) \bigl(1+\Upsilon _{n}+ \Upsilon _{n}^{2}\bigr)\bigr]d( \chi _{n}, p)+ \bigl(1+\Upsilon _{n}+\Upsilon _{n}^{2} \bigr)a_{n} \\ & \leq \bigl[1+(\Upsilon _{n}-1)M_{1}\bigr]d(\chi _{n}, p)+ M_{1}a_{n}, \end{aligned}$$

(3.4)

where $M_1={sup}_{n\in \mathbb{N}}(1+{\mathrm{\Upsilon }}_n+{\mathrm{\Upsilon }}_n^2)$. By Lemma 2.9, $\lim_{n\rightarrow \infty }d(\chi _{n},p)$ exists.

(ii) Next we will prove that $\lim_{n\rightarrow \infty }d(\chi _{n}, \omega _{n}) = 0$ and $\lim_{n\rightarrow \infty }d(\chi _{n},\upsilon _{n}) = 0$. Assume that

$$ \lim_{n\rightarrow \infty }d(\chi _{n},p)=r $$

(3.5)

for some $r>0$. By Lemma 2.6, we have

$$\begin{aligned}& \frac{1}{2\delta _{n}} d^{2}\bigl(\operatorname{prox}_{\delta _{n} \tau }( \chi _{n}),p\bigr)- \frac{1}{2\delta _{n}} d^{2}(\chi _{n}, p)+ \frac{1}{2\delta _{n}} d^{2}\bigl( \chi _{n}, \operatorname{prox}_{\delta _{n} \tau }(\chi _{n}) \bigr) \\& \quad \leq \tau (p)- \tau (\chi _{n}). \end{aligned}$$

Since $\tau (p)\leq \tau (\chi _{n})$ for all $n\in \mathbb{N}$, it follows that

$$ d^{2}(\chi _{n},\omega _{n}) \leq d^{2}(\chi _{n},p)-d^{2}(\omega _{n},p) $$

(3.6)

and

$$\begin{aligned}& \frac{1}{2\nu _{n}} d^{2}\bigl(\operatorname{prox}_{\varsigma _{n} \zeta }( \omega _{n}),p\bigr)- \frac{1}{2\nu _{n}} d^{2}(\omega _{n}, p)+ \frac{1}{2\delta _{n}} d^{2}\bigl( \omega _{n}, \operatorname{prox}_{\varsigma _{n} \zeta }(\omega _{n}) \bigr) \\& \quad \leq \zeta (p)-\zeta (\omega _{n}). \end{aligned}$$

Since $\zeta (p)\leq \zeta (\omega _{n})$ for all $n\in \mathbb{N}$, it follows that

$$ d^{2}(\omega _{n}, \upsilon _{n}) \leq d^{2}(\omega _{n},p)-d^{2}( \upsilon _{n},p). $$

(3.7)

From (3.4), we have

$$\begin{aligned} d(\chi _{n+1}, p) \leq & (1-\rho _{n})\Upsilon _{n}d(\varrho _{n}, p)+ \rho _{n} \Upsilon _{n}d(\varphi _{n}, p)+a_{n} \\ \leq & (1-\rho _{n})\Upsilon _{n}\bigl[\Upsilon _{n} d(\chi _{n}, p)+a_{n}\bigr]+ \rho _{n} \Upsilon _{n}d(\varphi _{n}, p)+a_{n} \\ \leq & \Upsilon _{n}^{2}d(\chi _{n}, p)- \rho _{n}\Upsilon _{n}^{2}d( \chi _{n}, p)+ \rho _{n} \Upsilon _{n}d(\varphi _{n}, p)+\bigl[1+(1-\rho _{n}) \Upsilon _{n} \bigr]a_{n}. \end{aligned}$$

This implies that

$$ d(\chi _{n}, p)\leq \frac{1}{\rho _{n}}d(\chi _{n}, p)- \frac{1}{\rho _{n}\Upsilon _{n}^{2}}d(\chi _{n+1}, p)+ \frac{1}{\Upsilon _{n}}d(\varphi _{n}, p)+ \frac{1}{\rho _{n}\Upsilon _{n}^{2}} \bigl[1+(1-\rho _{n})\Upsilon _{n}\bigr]a_{n}. $$

By our assumption and taking $\liminf_{n\rightarrow \infty }$ on both sides, we have

$$ r =\liminf_{n\rightarrow \infty }d(\chi _{n}, p)\leq \liminf _{n \rightarrow \infty }d(\varphi _{n}, p). $$

From (3.3), we have $\limsup_{n\rightarrow \infty }d(\varphi _{n}, p)\leq \limsup_{n \rightarrow \infty }d(\chi _{n}, p)= r$. Thus,

$$ \lim_{n\rightarrow \infty }d(\varphi _{n}, p)= r. $$

(3.8)

From (3.3), we also have

$$ d(\varphi _{n}, p) \leq \Upsilon _{n}d(\varrho _{n}, p)+a_{n}. $$

By taking $\liminf_{n\rightarrow \infty }$ on both sides, we have

$$ r =\liminf_{n\rightarrow \infty }d(\varphi _{n}, p)\leq \liminf _{n \rightarrow \infty }d(\varrho _{n}, p). $$

From (3.2), we have $\limsup_{n\rightarrow \infty }d(\varrho _{n}, p)\leq \limsup_{n \rightarrow \infty }d(\chi _{n}, p)= r$. Thus,

$$ \lim_{n\rightarrow \infty }d(\varrho _{n}, p)= r. $$

(3.9)

From (3.2), this implies that

$$ \begin{aligned} &\rho _{n}d(\chi _{n}, p)\leq d(\chi _{n}, p)-d(\varrho _{n}, p)+ \rho _{n} \Upsilon _{n}d(\upsilon _{n}, p)+\rho _{n}a_{n}, \\ &d(\chi _{n}, p)\leq \frac{1}{\rho _{n}}\bigl(d(\chi _{n}, p)-d(\varrho _{n}, p)\bigr)+\Upsilon _{n}d(\omega _{n}, p)+a_{n}. \end{aligned} $$

(3.10)

Using (3.5), (3.9) and our assumptions, we get $r =\liminf_{n\rightarrow \infty }d(\chi _{n}, p)\leq \liminf_{n \rightarrow \infty }d(\omega _{n}, p)$, which together with $\limsup_{n\rightarrow \infty }d(\omega _{n}, p)\leq \limsup_{n \rightarrow \infty }d(\chi _{n}, p)=r$ gives us that

$$ \lim_{n\rightarrow \infty }d(\omega _{n},p)= r. $$

(3.11)

Hence, from (3.6), we have

$$ \lim_{n\rightarrow \infty }d(\chi _{n},\omega _{n}) =0. $$

(3.12)

From (3.2), we have

$$ \begin{aligned} &d(\varrho _{n}, p) \leq (1-\rho _{n})d(\chi _{n}, p)+\rho _{n}\bigl[ \Upsilon _{n}d(\upsilon _{n}, p)+a_{n}\bigr] \\ &d(\varrho _{n}, p) \leq d(\chi _{n}, p)-\rho _{n}d(\chi _{n}, p)+ \rho _{n}\Upsilon _{n}d(\upsilon _{n}, p)+\rho _{n}a_{n} \\ &\rho _{n}d(\chi _{n}, p)\leq d(\chi _{n}, p)-d(\varrho _{n}, p)+ \rho _{n}\Upsilon _{n}d(\upsilon _{n}, p)+\rho _{n}a_{n} \\ &d(\chi _{n}, p)\leq \frac{1}{\rho _{n}}\bigl(d(\chi _{n}, p)-d(\varrho _{n}, p)\bigr)+\Upsilon _{n}d(\upsilon _{n}, p)+a_{n} \\ &d(\chi _{n}, p)\leq \frac{1}{\rho }\bigl(d(\chi _{n}, p)-d(\varrho _{n}, p)\bigr)+ \Upsilon _{n}d(\upsilon _{n}, p)+a_{n}. \end{aligned} $$

(3.13)

Using (3.5) and (3.9), we get $r =\liminf_{n\rightarrow \infty }d(\chi _{n}, p)\leq \liminf_{n \rightarrow \infty }d(\upsilon _{n}, p)$, which together with $\limsup_{n\rightarrow \infty }d(\upsilon _{n}, p)\leq \limsup_{n \rightarrow \infty }d(\chi _{n}, p)=r$ gives us that

$$ \lim_{n\rightarrow \infty }d(\upsilon _{n}, p)= r. $$

(3.14)

Hence, from (3.7), (3.11), and (3.14), we have

$$ \lim_{n\rightarrow \infty }d(\omega _{n}, \upsilon _{n}) =0. $$

(3.15)

From (3.12) and (3.15), we get

$$\begin{aligned}& \begin{aligned} &d(\chi _{n}, \upsilon _{n}) \leq d(\chi _{n}, \omega _{n})+d( \omega _{n}, \upsilon _{n}), \\ &\lim_{n\rightarrow \infty }d(\chi _{n}, \upsilon _{n}) =0. \end{aligned} \end{aligned}$$

(3.16)

From (3.1), we have

$$ \begin{aligned} d^{2}(\varrho _{n}, p) ={} & d^{2}\bigl((1-\rho _{n})\chi _{n} \oplus \rho _{n}\mathcal{T}^{n}\upsilon _{n}, p\bigr) \\ \leq {}&(1-\rho _{n})d^{2}(\chi _{n}, p)+ \rho _{n} d^{2}\bigl(\mathcal{T}^{n} \upsilon _{n}, p\bigr)-\rho _{n}(1-\rho _{n})d^{2} \bigl(\chi _{n}, \mathcal{T}^{n} \upsilon _{n} \bigr) \\ \leq {}&(1-\rho _{n})d^{2}(\chi _{n}, p)+ \rho _{n} \bigl(\Upsilon _{n}d( \upsilon _{n}, p)+a_{n}\bigr)^{2}-\rho _{n}(1-\rho _{n})d^{2}\bigl(\chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr) \\ ={}&(1-\rho _{n})d^{2}(\chi _{n}, p)+ \rho _{n} \bigl(\Upsilon _{n}^{2}d^{2}( \upsilon _{n}, p)+\bigl(a_{n}+2\Upsilon _{n}d(\upsilon _{n}, p)\bigr)a_{n}\bigr) \\ &{}- \rho _{n}(1-\rho _{n})d^{2}\bigl(\chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr) \\ \leq {}&\Upsilon _{n}^{2}(1-\rho _{n})d^{2}( \chi _{n}, p)+ \rho _{n} \bigl( \Upsilon _{n}^{2}d^{2}(\chi _{n}, p)+M_{2}a_{n}\bigr) \\ &{}-\rho _{n}(1-\rho _{n})d^{2}\bigl( \chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr) \\ = {}&\Upsilon _{n}^{2}d^{2}(\chi _{n}, p)+M_{2}a_{n}-\rho _{n}(1- \rho _{n})d^{2}\bigl(\chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr), \end{aligned} $$

(3.17)

where $M_2={sup}_{n\in \mathbb{N}}(a_n+2{\mathrm{\Upsilon }}_{n}d({\upsilon }_n,p))$. This implies that

$$ \rho _{n}(1-\rho _{n})d^{2}\bigl( \chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr) \leq \bigl(\Upsilon _{n}^{2}d^{2}(\chi _{n}, p)-d^{2}(\varrho _{n}, p)\bigr)+ M_{2}a_{n}. $$

Hence, from (3.5), (3.9) and our assumption, we have

$$ \lim_{n\rightarrow \infty }d\bigl(\chi _{n},\mathcal{T}^{n} \upsilon _{n}\bigr) =0. $$

(3.18)

By using (3.16) and (3.18),

$$ \begin{aligned} d\bigl(\chi _{n}, \mathcal{T}^{n} \chi _{n}\bigr) & \leq d\bigl(\chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr)+d\bigl( \mathcal{T}^{n}\upsilon _{n}, \mathcal{T}^{n} \chi _{n}\bigr) \\ & \leq d\bigl(\chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr)+\Gamma d(\upsilon _{n}, \chi _{n})+q_{n} \\ & \rightarrow 0\quad \text{as } n\rightarrow \infty . \end{aligned} $$

(3.19)

From (3.2), we have

$$\begin{aligned} d^{2}(\varphi _{n}, p) = & d^{2}\bigl((1-\sigma _{n})\varrho _{n} \oplus \sigma _{n}^{n}\varrho _{n}, p\bigr) \\ \leq &(1-\sigma _{n})d^{2}(\varrho _{n}, p)+ \sigma _{n} d^{2}\bigl( \mathcal{S}^{n} \varrho _{n}, p\bigr)-\sigma _{n}(1-\sigma _{n})d^{2}\bigl( \varrho _{n}, \mathcal{S}^{n}\varrho _{n}\bigr) \\ \leq &(1-\sigma _{n})d^{2}(\varrho _{n}, p)+ \sigma _{n} \bigl(\Upsilon _{n}d( \varrho _{n}, p)+a_{n}\bigr)^{2}-\sigma _{n}(1-\sigma _{n})d^{2}\bigl(\varrho _{n}, \mathcal{S}^{n}\varrho _{n}\bigr) \\ =&(1-\sigma _{n})d^{2}(\varrho _{n}, p)+ \sigma _{n} \bigl(\Upsilon _{n}^{2}d^{2}( \varrho _{n}, p)+\bigl(a_{n}+2\Upsilon _{n}d( \varrho _{n}, p)\bigr)a_{n}\bigr) \\ &{}- \sigma _{n}(1-\sigma _{n})d^{2}\bigl( \varrho _{n}, \mathcal{S}^{n}\varrho _{n} \bigr) \\ \leq &\Upsilon _{n}^{2}(1-\sigma _{n})d^{2}( \varrho _{n}, p)+ \sigma _{n} \bigl(\Upsilon _{n}^{2}d^{2}(\varrho _{n}, p)+M_{2}a_{n}\bigr) \\ &{}- \sigma _{n}(1-\sigma _{n})d^{2}\bigl( \varrho _{n}, \mathcal{S}^{n}\varrho _{n} \bigr) \\ \leq &\Upsilon _{n}^{2}(1-\sigma _{n})d^{2}( \varrho _{n}, p)+ \sigma _{n} \Upsilon _{n}^{2}d^{2}(\varrho _{n}, p)+M_{2}a_{n}- \sigma _{n}(1-\sigma _{n})d^{2}\bigl(\varrho _{n}, \mathcal{S}^{n}\varrho _{n}\bigr) \\ = &\Upsilon _{n}^{2}d^{2}(\varrho _{n}, p)+M_{2}a_{n}-\sigma _{n}(1- \sigma _{n})d^{2}\bigl(\varrho _{n}, \mathcal{S}^{n}\varrho _{n}\bigr), \end{aligned}$$

(3.20)

where $M_2={sup}_{n\in \mathbb{N}}(a_n+2{\mathrm{\Upsilon }}_{n}d({\varrho }_n,p))$. This implies that

$$ \rho _{n}(1-\rho _{n})d^{2}\bigl( \varrho _{n}, \mathcal{S}^{n}\varrho _{n} \bigr) \leq \bigl(\Upsilon _{n}^{2}d^{2}( \varrho _{n}, p)-d^{2}(\varphi _{n}, p)\bigr)+ M_{2}a_{n}. $$

Hence, from (3.8) and (3.9), we have

$$ \lim_{n\rightarrow \infty }d^{2}\bigl(\varrho _{n}, \mathcal{S}^{n} \varrho _{n}\bigr)=0. $$

(3.21)

By using (3.18), we have

$$\begin{aligned} d(\chi _{n}, \varrho _{n}) = &d\bigl(\chi _{n}, (1-\varsigma _{n})\chi _{n} \oplus \varsigma _{n}\mathcal{T}^{n}\upsilon _{n} \bigr) \\ \leq &(1-\varsigma _{n})d(\chi _{n}, \chi _{n})+\varsigma _{n}d\bigl( \chi _{n}, \mathcal{T}^{n}\upsilon _{n}\bigr) \\ \rightarrow & 0 \quad \text{as } n\rightarrow \infty , \end{aligned}$$

(3.22)

and from (3.21) and (3.23),

$$ \begin{aligned} d(\chi _{n}, \varphi _{n}) & = d\bigl(\chi _{n}, (1-\sigma _{n})\varrho _{n} \oplus \sigma _{n}\mathcal{S}^{n}\varrho _{n} \bigr) \\ & \leq (1-\sigma _{n})d(\chi _{n}, \varrho _{n})+\sigma _{n}d\bigl(\chi _{n}, \mathcal{S}^{n}\varrho _{n}\bigr) \\ & \leq (1-\sigma _{n})d(\chi _{n}, \varrho _{n})+\sigma _{n} d(\chi _{n}, \varrho _{n})+\sigma _{n}d\bigl(\varrho _{n}, \mathcal{S}^{n}\varrho _{n}\bigr) \\ & \rightarrow 0 \quad \text{as } n\rightarrow \infty . \end{aligned} $$

(3.23)

Since $\mathcal{S}$ and $\mathcal{T}$ are nearly uniformly Γ-Lipschitzian mappings, we obtain

$$\begin{aligned}& \lim_{n\rightarrow \infty }d\bigl(\mathcal{S}^{n}\chi _{n}, \mathcal{S}^{n} \varrho _{n}\bigr)=0 \quad \text{and}\quad \lim_{n\rightarrow \infty }d\bigl( \mathcal{T}^{n}\chi _{n}, \mathcal{T}^{n} \varrho _{n}\bigr)=0. \end{aligned}$$

(3.24)

$$\begin{aligned}& \lim_{n\rightarrow \infty }d\bigl(\mathcal{S}^{n}\chi _{n}, \mathcal{S}^{n} \varphi _{n}\bigr)=0 \quad \text{and}\quad \lim_{n\rightarrow \infty }d\bigl( \mathcal{T}^{n}\chi _{n}, \mathcal{T}^{n} \varphi _{n}\bigr)=0. \end{aligned}$$

(3.25)

By using (3.21), (3.23), and (3.24), we have

$$ \begin{aligned}d\bigl(\chi _{n}, \mathcal{S}^{n} \chi _{n}\bigr) & \leq d(\chi _{n}, \varrho _{n})+d\bigl( \varrho _{n}, \mathcal{S}^{n} \varrho _{n}\bigr)+d\bigl(\mathcal{S}^{n}\varrho _{n}, \mathcal{S}^{n}\chi _{n}\bigr) \\ & \rightarrow 0 \quad \text{as } n\rightarrow \infty . \end{aligned} $$

(3.26)

From (3.19), (3.24), (3.25), and (3.26), we have

$$\begin{aligned} d(\chi _{n}, \chi _{n+1}) = &d\bigl(\chi _{n}, (1-\rho _{n})\mathcal{T}^{n} \varrho _{n} \oplus \rho _{n}\mathcal{S}^{n}\varphi _{n}\bigr) \\ \leq &(1-\rho _{n})d\bigl(\chi _{n}, \mathcal{T}^{n}\varrho _{n} \bigr)+\rho _{n}d \bigl( \chi _{n}, \mathcal{S}^{n}\varphi _{n} \bigr) \\ \leq &(1-\rho _{n})\bigl[d\bigl(\chi _{n}, \mathcal{T}^{n}\chi _{n}\bigr)+d\bigl( \mathcal{T}^{n}\chi _{n}, \mathcal{T}^{n} \varrho _{n}\bigr)\bigr] \\ &{}+\rho _{n}\bigl[d\bigl( \chi _{n}, \mathcal{S}^{n}\chi _{n}\bigr)+d\bigl( \mathcal{S}^{n}\chi _{n}, \mathcal{S}^{n} \varphi _{n}\bigr)\bigr] \\ \rightarrow & 0 \quad \text{as } n\rightarrow \infty . \end{aligned}$$

(3.27)

Using the uniform continuity of $\mathcal{T}$ in (3.19) and the definition of nearly uniformly Γ-Lipschitzian mapping $\mathcal{T}$ in (3.28), we have $\lim_{n\rightarrow \infty }d(\mathcal{T}\chi _{n}, \mathcal{T}^{n+1} \chi _{n}) =0$ and $\lim_{n\rightarrow \infty }d(\mathcal{T}^{n+1}\chi _{n}, \mathcal{T}^{n+1} \chi _{n+1}) =0$.

From (3.19) and (3.28),

$$\begin{aligned} d(\chi _{n},\mathcal{T}\chi _{n}) \leq &d( \chi _{n},\chi _{n+1})+d\bigl( \chi _{n+1}, \mathcal{T}^{n+1}\chi _{n}+1\bigr) \\ &{} +d\bigl(\mathcal{T}^{n+1}\chi _{n+1}, \mathcal{T}^{n+1}\chi _{n}\bigr)+d\bigl( \mathcal{T}^{n+1}\chi _{n}, \mathcal{T} \chi _{n}\bigr) \\ \rightarrow & 0 \quad \text{as } n\rightarrow \infty . \end{aligned}$$

(3.28)

Using the uniform continuity of $\mathcal{S}$ in (3.26) and the definition of nearly uniformly Γ-Lipschitzian mapping $\mathcal{S}$ in (3.28), we have $\lim_{n\rightarrow \infty }d(\mathcal{S}\chi _{n}, \mathcal{S}^{n+1} \chi _{n}) =0$ and $\lim_{n\rightarrow \infty }d(\mathcal{S}^{n+1}\chi _{n}, \mathcal{S}^{n+1} \chi _{n+1}) =0$.

From (3.26) and (3.28),

$$\begin{aligned} d(\chi _{n},\mathcal{S}\chi _{n}) \leq &d( \chi _{n},\chi _{n+1})+d\bigl( \chi _{n+1}, \mathcal{S}^{n+1}\chi _{n}+1\bigr) +d\bigl( \mathcal{S}^{n+1}\chi _{n+1}, \mathcal{S}^{n+1}\chi _{n}\bigr) \\ &{}+d\bigl(\mathcal{S}^{n+1}\chi _{n}, \mathcal{S} \chi _{n}\bigr) \\ \rightarrow & 0\quad \text{as } n\rightarrow \infty . \end{aligned}$$

(3.29)

This completes the proof. □

Now, we are ready to prove the main result.

Theorem 3.1

Let $\mathcal{C}$ be a nonempty closed convex subset of a complete CAT (0) space $(\mathcal{X},d)$. Let $\zeta , \tau : \mathcal{C } \rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous functions, and let $\mathcal{T}, \mathcal{S} : \mathcal{C} \rightarrow \mathcal{C}$ be uniformly continuous mappings satisfying the following:

• (a) $\mathcal{T}$ and $\mathcal{S}$ are nearly asymptotically quasi-nonexpansive mappings with sequence $\{(a_{n},\Upsilon _{n})\}$ such that $\sum_{n=1}^{\infty } a_{n}<\infty$ and $\sum_{n=1}^{\infty }(\Upsilon _{n}-1)<\infty$;

• (b) $\mathcal{T}$ and $\mathcal{S}$ are nearly uniformly Γ-Lipschitzian mappings with sequence $\{(q_{n}, \Gamma )\}$.

Let $\mathcal{T}$ and $\mathcal{S}$ satisfy the demiclosedness principle and $P= \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S})\cap \operatorname{argmin}_{ \varphi \in \mathcal{C}} \zeta (\varphi )\cap \operatorname{argmin}_{\varrho \in \mathcal{ C}} \tau (\varrho )\neq \emptyset$. Let $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ be sequences in $(0, 1)$ such that $0 <\rho \leq \rho _{n}$, $\sigma _{n}, \varsigma _{n}\leq \sigma <1$ for all $n\in \mathbb{N}$. Let $\{\nu _{n}\}$ and $\{\delta _{n}\}$ be sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. For $\chi _{1} \in C$, let $\{\chi _{n}\}$ be a sequence in C defined by (1.1). Then the sequence $\{\chi _{n}\}$ Δ-converges to an element of P.

Proof

Since $0 <\nu \leq \nu _{n}$, therefore from Lemma 2.7 and (3.12), (3.15), and (3.16), we have

$$\begin{aligned} d(\operatorname{prox}_{\nu \zeta } \chi _{n}, \chi _{n}) \leq & d(\operatorname{prox}_{ \nu \zeta } \chi _{n}, \upsilon _{n})+d(\upsilon _{n}, \omega _{n})+d( \omega _{n}, \chi _{n}) \\ = &d(\operatorname{prox}_{\nu \zeta } \chi _{n}, \operatorname{prox}_{\nu _{n} \zeta } \omega _{n})+d(\upsilon _{n}, \omega _{n})+d(\omega _{n}, \chi _{n}) \\ = &d \biggl(\operatorname{prox}_{\nu \zeta } \chi _{n}, \operatorname{prox}_{\nu \zeta } \biggl(\frac{\nu _{n}-\nu }{\nu _{n}} \operatorname{prox}_{\nu _{n} \zeta }\omega _{n} \oplus \frac{\nu }{\nu _{n}}\omega _{n} \biggr) \biggr) \\ &{}+d(\upsilon _{n}, \omega _{n})+d(\omega _{n}, \chi _{n}) \\ \leq &d\biggl(\chi _{n}, \frac{\nu _{n}-\nu }{\nu _{n}} \operatorname{prox}_{\nu _{n} \zeta }\omega _{n}\oplus \frac{\nu }{\nu _{n}}\omega _{n}\biggr)+d(\upsilon _{n}, \omega _{n})+d(\omega _{n}, \chi _{n}) \\ =& \biggl(1-\frac{\nu }{\nu _{n}}\biggr)d(\chi _{n}, \operatorname{prox}_{\nu _{n} \zeta }\omega _{n})+\frac{\nu }{\nu _{n}}d( \chi _{n}, \omega _{n}) \\ &{}+d( \upsilon _{n}, \omega _{n})+d(\omega _{n}, \chi _{n}) \\ =& \biggl(1-\frac{\nu }{\nu _{n}} \biggr)d(\chi _{n}, \upsilon _{n})+ \frac{\nu }{\nu _{n}}d(\chi _{n}, \omega _{n})+d(\upsilon _{n}, \omega _{n})+d(\omega _{n}, \chi _{n}) \\ =& \biggl(1-\frac{\nu }{\nu _{n}}\biggr)d(\chi _{n},\upsilon _{n})+ \biggl(1+ \frac{\nu }{\nu _{n}} \biggr)d(\chi _{n}, \omega _{n})+d(\upsilon _{n}, \omega _{n}) \\ \rightarrow & 0 \quad \text{as } n\rightarrow \infty . \end{aligned}$$

(3.30)

Proceeding in the same manner as above and using (3.12), we have

$$\begin{aligned} d(\operatorname{prox}_{\delta \tau } \chi _{n}, \chi _{n}) \leq & d( \operatorname{prox}_{\delta \tau } \chi _{n}, \omega _{n})+d(\omega _{n}, \chi _{n}) \\ = &d(\operatorname{prox}_{\delta \tau } \chi _{n}, \operatorname{prox}_{\delta _{n} \tau } \chi _{n})+d(\omega _{n}, \chi _{n}) \\ = &d \biggl(\operatorname{prox}_{\delta \tau } \chi _{n}, \operatorname{prox}_{\delta \tau } \biggl(\frac{\delta _{n}-\delta }{\delta _{n}} \operatorname{prox}_{\delta _{n} \tau }\chi _{n}\oplus \frac{\delta }{\delta _{n}}\chi _{n} \biggr) \biggr)+d( \omega _{n}, \chi _{n}) \\ \leq &d\biggl(\chi _{n}, \frac{\delta _{n}-\delta }{\delta _{n}} \operatorname{prox}_{\delta _{n} \tau }\chi _{n}\oplus \frac{\delta }{\delta _{n}}\chi _{n}\biggr) \\ &{}+d(\omega _{n}, \chi _{n}) \\ =& \biggl(1-\frac{\delta }{\delta _{n}}\biggr)d(\chi _{n}, \operatorname{prox}_{ \delta _{n} \tau }\chi _{n})+\frac{\delta }{\delta _{n}}d( \chi _{n}, \chi _{n})+d(\omega _{n}, \chi _{n}) \\ =& \biggl(1-\frac{\delta }{\delta _{n}} \biggr)d(\chi _{n},\omega _{n})+ \frac{\delta }{\delta _{n}}d(\chi _{n}, \chi _{n})+d(\omega _{n}, \chi _{n}) \\ =& \biggl(1-\frac{\delta }{\delta _{n}}\biggr)d(\chi _{n},\omega _{n})+ +d( \omega _{n}, \chi _{n}) \\ =& \biggl(2-\frac{\delta }{\delta _{n}}\biggr)d(\chi _{n},\omega _{n}) \\ \rightarrow & 0\quad \text{as } n\rightarrow \infty . \end{aligned}$$

(3.31)

Next we show that $w_{\Delta }(\chi _{n})=\bigcup_{\{\eta _{n}\}\subset \{\chi _{n}\}}A( \{\eta _{n}\})\subset P$. Let $\eta \in w_{\Delta }(\chi _{n})$. Then there exists a subsequence $\{\eta _{n}\}$ of $\{\chi _{n}\}$ such that $A(\eta _{n})=\{\eta \}$. Therefore, there exists a subsequence $\{\vartheta _{n}\}$ of $\{\eta _{n}\}$ such that $\Delta -\lim_{n\rightarrow \infty }\vartheta _{n} = \vartheta$ for some $\vartheta \in P$. In view of Proposition 3.1, (3.30), and (3.31), we have $\lim_{n\rightarrow \infty }d(\vartheta _{n}, \mathcal{T}\vartheta _{n})=0$, $\lim_{n\rightarrow \infty }d(\vartheta _{n}, \mathcal{S}\vartheta _{n})=0$, $\lim_{n\rightarrow \infty }d(\operatorname{prox}_{\nu \zeta } \vartheta _{n}, \vartheta _{n})=0$, $\lim_{n\rightarrow \infty }d(\operatorname{prox}_{\delta \tau } \vartheta _{n}, \vartheta _{n})=0$. Since $\mathcal{T}$ and $\mathcal{S}$ satisfy demiclosedness conditions, we have $\vartheta \in P$. Hence, by Proposition 3.1(a), $\lim_{n\rightarrow \infty }d(\chi _{n},\vartheta )$ exists, and by Lemma 2.2, we have $\eta = \vartheta$. This shows that $w_{\Delta }(\chi _{n})\subset P$. Finally, we show that the sequence $\{\chi _{n}\}$ generated by (1.1) Δ-converges to a point in P. To this end, it suffices to show that $w_{\Delta }(\chi _{n})$ consists of exactly one point. Let $\{\eta _{n}\}$ be a subsequence of $\{\chi _{n}\}$, and let $A(\{\chi _{n}\}) =\{\chi \}$. Since $\eta \in w_{\Delta }(\chi _{n})\subset P$ and $d(\chi _{n}, \eta )$ converges, we have $\chi =\eta$. Hence $w_{\Delta }(\chi _{n}) =\{\chi \}$. □

Theorem 3.2

Let $\mathcal{C}$ be a nonempty closed convex subset of a complete CAT (0) space $(\mathcal{X},d)$. Let $\zeta , \tau : \mathcal{C} \rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous functions, and let $\mathcal{T}, \mathcal{S} : \mathcal{C }\rightarrow \mathcal{C}$ be uniformly continuous nearly asymptotically nonexpansive mappings with sequence $\{(a_{n},\Upsilon _{n})\}$ such that $\sum_{n=1}^{\infty } a_{n}<\infty$ and $\sum_{n=1}^{\infty }(\Upsilon _{n}-1)<\infty$. Let $P= \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S})\cap \operatorname{argmin}_{ \varphi \in \mathcal{C}} \zeta (\varphi )\cap \operatorname{argmin}_{\varrho \in \mathcal{C}} \tau (\varrho )\neq \emptyset$. Let $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ be sequences in $(0, 1)$ such that $0 <\rho \leq \rho _{n}$, $\sigma _{n}, \varsigma _{n}\leq \sigma <1$ for all $n\in \mathbb{N}$. Let $\{\nu _{n}\}$ and $\{\delta _{n}\}$ be sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. For $\chi _{1} \in \mathcal{C}$, let $\{\chi _{n}\}$ be a sequence in $\mathcal{C}$ defined by (1.1). Then the sequence $\{\chi _{n}\}$ Δ-converges to an element of P.

Proof

$\mathcal{T}$, $\mathcal{S}$ are nearly asymptotically nonexpansive mappings with $P\neq \emptyset$. This implies that $\mathcal{T}$, $\mathcal{S}$ are nearly asymptotically quasi-nonexpansive mappings. Set $\mathrm{\Gamma }={sup}_{n\in \mathbb{N}}{\mathrm{\Upsilon }}_n$. Then $\mathcal{S}$ and $\mathcal{T}$ are nearly uniformly Γ-Lipschitzian. By Lemma 2.5, $\mathcal{T}$ and $\mathcal{S}$ satisfy the demiclosedness principle. Therefore, the proof follows from Theorem 3.1. □

Theorem 3.3

Let $\mathcal{C}$ be a nonempty closed convex subset of a complete CAT (0) space $(\mathcal{X},d)$. Let $\zeta , \tau : \mathcal{C } \rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous functions, and let $\mathcal{T}, \mathcal{S} : \mathcal{C} \rightarrow \mathcal{C}$ be uniformly continuous mappings satisfying the following:

• (a) $\mathcal{T}$ and $\mathcal{S}$ are quasi-nonexpansive mappings:

• (b) $\mathcal{T}$ and $\mathcal{S}$ are nearly uniformly Γ-Lipschitzian mappings with sequence $\{(q_{n}, \Gamma )\}$.

Let the mappings $\mathcal{T}$ and $\mathcal{S}$ satisfy the demiclosedness principle and $P= \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S})\cap \operatorname{argmin}_{ \varphi \in C} \zeta (\varphi )\cap \operatorname{argmin}_{\varrho \in C} \tau ( \varrho )\neq \emptyset$. Let $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ be sequences in $(0, 1)$ such that $0 <\rho \leq \rho _{n}$, $\sigma _{n}, \varsigma _{n}\leq \sigma <1$ for all $n\in \mathbb{N}$. Let $\{\nu _{n}\}$ and $\{\delta _{n}\}$ be sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. For $\chi _{1} \in C$, let $\{\chi _{n}\}$ be a sequence in $\mathcal{C}$ defined by (1.1). Then the sequence $\{\chi _{n}\}$ Δ-converges to an element of P.

Remark 2

If we take $\mathcal{T}^{n}=\mathcal{T}$ and $\mathcal{S}^{n}=\mathcal{S}$, then (1.1) reduces to the following iterative process:

$$ \textstyle\begin{cases} \chi _{1}\in \mathcal{C}, \\ \omega _{n} = \mathop{\operatorname{argmin}}_{\varrho \in \mathcal{C}} (\tau ( \varrho )+ \frac{1}{2\delta _{n}} d^{2}(\varrho ,\chi _{n}) ), \\ \upsilon _{n} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} d^{2}(\varphi ,\omega _{n}) ), \\ \varrho _{n} = (1 - \varsigma _{n})\chi _{n}\oplus \varsigma _{n} \mathcal{\mathcal{T}}\upsilon _{n}, \\ \varphi _{n} = (1 - \sigma _{n})\varrho _{n}\oplus \sigma _{n} \mathcal{\mathcal{S}}\varrho _{n}, \\ \chi _{n+1} = (1-\rho _{n})\mathcal{\mathcal{T}}\varrho _{n}\oplus \rho _{n}{\mathcal{S}}\varphi _{n}. \end{cases} $$

(1.1a)

Theorem 3.4

Let $\mathcal{C}$ be a nonempty closed convex subset of a complete CAT (0) space $(\mathcal{X},d)$. Let $\zeta , \tau : \mathcal{C} \rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous functions, and let $\mathcal{T}, \mathcal{S} : \mathcal{C } \rightarrow \mathcal{C}$ be nonexpansive mappings with $P= \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S}) \operatorname{argmin}_{ \varphi \in \mathcal{C}} \zeta (\varphi )\cap \operatorname{argmin}_{\varrho \in \mathcal{C}} \tau (\varrho )\neq \emptyset$. Let $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ be sequences in $(0, 1)$ such that $0 <\rho \leq \rho _{n}$, $\sigma _{n}, \varsigma _{n}\leq \sigma <1$ for all $n\in \mathbb{N}$. Let $\{\nu _{n}\}$ and $\{\delta _{n}\}$ be sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. For $\chi _{1} \in \mathcal{C}$, let $\{\chi _{n}\}$ be a sequence in $\mathcal{C}$ defined by (1.1a). Then the sequence $\{\chi _{n}\}$ Δ- converges to an element of P.

Remark 3

If we take $\tau =\zeta =0$ and $\mathcal{T}=\mathcal{S}$, then (1.1a) reduces to the Thakur iteration process in a $\operatorname{CAT}(0)$ space studied by Garodia and Uddin [18] for generalized nonexpansive mappings.

Since every Hilbert space is a complete $\operatorname{CAT}(0)$ space, we directly obtain the following result.

Corollary 3.1

Let $\mathcal{C}$ be a nonempty closed convex subset of a Hilbert space $\mathcal{X}$. Let $\zeta , \tau : \mathcal{C} \rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous functions, and let $\mathcal{T}, \mathcal{S} :\mathcal{ C} \rightarrow \mathcal{C}$ be uniformly continuous mappings satisfying the following:

• (a) $\mathcal{T}$ and $\mathcal{S}$ are nearly asymptotically quasi-nonexpansive mappings with sequence $\{(a_{n},\Upsilon _{n})\}$ such that $\sum_{n=1}^{\infty } a_{n}<\infty$ and $\sum_{n=1}^{\infty }(\Upsilon _{n}-1)<\infty$;

• (b) $\mathcal{T}$ and $\mathcal{S}$ are nearly uniformly Γ-Lipschitzian mappings with sequence $\{(q_{n}, \Gamma )\}$.

Let the mappings $\mathcal{T}$ and $\mathcal{S}$ satisfy the demiclosedness principle and $P= \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S})\cap \operatorname{argmin}_{ \varphi \in \mathcal{C}} \zeta (\varphi )\cap \operatorname{argmin}_{\varrho \in \mathcal{C}} \tau (\varrho )\neq \emptyset$. Let $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ be sequences in $(0, 1)$ such that $0 <\rho \leq \rho _{n}$, $\sigma _{n}, \varsigma _{n}\leq \sigma <1$ for all $n\in \mathbb{N}$. Let $\{\nu _{n}\}$ and $\{\delta _{n}\}$ be sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. For $\chi _{1} \in \mathcal{C}$, let $\{\chi _{n}\}$ be a sequence in $\mathcal{C}$ defined by

$$ \textstyle\begin{cases} \omega _{n} = \mathop{\operatorname{argmin}}_{\varrho \in \mathcal{C}} (\tau ( \varrho )+ \frac{1}{2\delta _{n}} \Vert \varrho -\chi _{n} \Vert ^{2} ), \\ \upsilon _{n} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} \Vert \varphi -\omega _{n} \Vert ^{2} ), \\ \varrho _{n} = (1 - \varsigma _{n})\chi _{n}+ \varsigma _{n} \mathcal{\mathcal{T}}^{n}\upsilon _{n}, \\ \varphi _{n} = (1 - \sigma _{n})\varrho _{n}+ \sigma _{n} \mathcal{\mathcal{S}}^{n}\varrho _{n}, \\ \chi _{n+1} = (1-\rho _{n})\mathcal{\mathcal{T}}^{n}\varrho _{n}+ \rho _{n}{\mathcal{S}}^{n}\varphi _{n}. \end{cases} $$

(1.1b)

Then the sequence $\{\chi _{n}\}$ weakly converges to an element of P.

4 Application

In this section, particularly using Theorem 3.4 in a Hilbert space, we obtain the following.

Theorem 4.1

Let $\mathcal{C}$ be a nonempty closed convex subset of a Hilbert space, $\mathcal{X}$. Let $\zeta ,\tau : \mathcal{C} \rightarrow (-\infty , \infty ]$ be proper convex and lower semi-continuous functions and $\mathcal{T}, \mathcal{S} : \mathcal{C} \rightarrow \mathcal{C}$ be two nonexpansive mappings with $P= \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S})\cap \operatorname{argmin}_{ \varphi \in \mathcal{C}} \zeta (\varphi )\cap \operatorname{argmin}_{\varrho \in \mathcal{C}} \tau (\varrho )\neq \emptyset$. Let $\{\rho _{n}\}$, $\{\sigma _{n}\}$, and $\{\varsigma _{n}\}$ be sequences in $(0, 1)$ such that $0 <\rho \leq \rho _{n}$, $\sigma _{n}, \varsigma _{n}\leq \sigma <1$ for all $n\in \mathbb{N}$. Let $\{\nu _{n}\}$ and $\{\delta _{n}\}$ be sequences in $(0,\infty )$ such that $0 <\nu \leq \nu _{n}$ and $0 <\delta \leq \delta _{n}$ for all $n\in \mathbb{N}$. For $\chi _{1} \in \mathcal{C}$, let $\{\chi _{n}\}$ be a sequence in $\mathcal{C}$ defined as follows:

$$ \textstyle\begin{cases} \omega _{n} = \mathop{\operatorname{argmin}}_{\varrho \in \mathcal{C}} (\tau ( \varrho )+ \frac{1}{2\delta _{n}} \Vert \varrho -\chi _{n} \Vert ^{2} ), \\ \upsilon _{n} = \mathop{\operatorname{argmin}}_{\varphi \in \mathcal{C}} (\zeta ( \varphi )+ \frac{1}{2\nu _{n}} \Vert \varphi -\omega _{n} \Vert ^{2} ), \\ \varrho _{n} = (1 - \varsigma _{n})\chi _{n}+ \varsigma _{n} \mathcal{\mathcal{T}}\upsilon _{n}, \\ \varphi _{n} = (1 - \sigma _{n})\varrho _{n}+ \sigma _{n} \mathcal{\mathcal{S}}\varrho _{n}, \\ \chi _{n+1} = (1-\rho _{n})\mathcal{\mathcal{T}}\varrho _{n}+\rho _{n}{ \mathcal{S}}\varphi _{n}. \end{cases} $$

(1.1c)

Then the sequence $\{\chi _{n}\}$ converges to an element of P.

Example 4.1

Let $\mathcal{X}={\mathbb{R}}^3$ with the Euclidean norm. Define nonexpansive mappings $\mathcal{T},\mathcal{S}:{\mathbb{R}}^3\to {\mathbb{R}}^3$ as follows:

$$\mathcal{T}(\chi ,\phi ,\varrho )=(\frac{1}{7}(4\chi -3\phi -9),\frac{1}{7}(-3\chi +4\phi -9),\frac{\varrho }{2}),(\chi ,\phi ,\varrho )\in {\mathbb{R}}^3$$

and

$$\mathcal{S}(\chi ,\phi ,\varrho )=(\frac{1}{9}(5\chi -4\phi -12),\frac{1}{9}(-4\chi +5\phi -12),\frac{\varrho }{3}),(\chi ,\phi ,\varrho )\in {\mathbb{R}}^3.$$

We define $\zeta ,\tau :{\mathbb{R}}^3\to \mathbb{R}$ by

$$\zeta (u)=\frac{1}{2}{\parallel \mathcal{A}u-b\parallel }^2\text{and}\tau (u)=\frac{1}{2}{\parallel \mathcal{B}u-c\parallel }^2,u\in {\mathbb{R}}^3,$$

where

$$\begin{array}{c}\mathcal{A}=\left(\begin{array}{ccc}-1& -1& 1\\ -1& -1& 1\\ 1& 1& -1\end{array}\right),\mathcal{B}=\left(\begin{array}{ccc}-1& -1& 0\\ -1& -1& 0\\ 0& 0& 0\end{array}\right),\hfill \\ b=(3,3,-3),c=(3,3,0).\hfill \end{array}$$

The functions ζ and τ are proper convex and lower semi-continuous. Hence, from proximity operators in [14], it follows that, for $\nu , \delta > 0$, we have

$$ \operatorname{prox}_{\nu \zeta } (u)=\bigl(I+\nu \mathcal{A}^{*} \mathcal{A}\bigr)^{-1}\bigl(u+ \nu \mathcal{A}^{*}b\bigr) $$

and

$${prox}_{\delta \tau }(u)={(I+\delta {\mathcal{B}}^{\ast }\mathcal{B})}^{-1}(u+\delta {\mathcal{B}}^{\ast }c)\text{for all }u\in {\mathbb{R}}^3.$$

Note

$$\begin{array}{rcl}P& =& \mathcal{F}(\mathcal{T})\cap \mathcal{F}(\mathcal{S})\cap \underset{\phi \in \mathcal{C}}{argmin}\zeta (\phi )\cap \underset{\varrho \in \mathcal{C}}{argmin}\tau (\varrho )\\ & =& \{(\chi ,\phi ,\varrho )\in {\mathbb{R}}^3:\chi +\phi +3=0,\varrho =0\}.\end{array}$$

Algorithm (1.1c) becomes

$$ \textstyle\begin{cases} t_{n} = (I+\delta \mathcal{B}^{*}\mathcal{B})^{-1}((\chi _{n}, \varphi _{n}, \varrho _{n})+\delta \mathcal{B}^{*}c), \\ \omega _{n} = (I+\nu \mathcal{A}^{*}\mathcal{A})^{-1}(t_{n}+\nu \mathcal{A}^{*}b), \\ \upsilon _{n} = (1 - \varsigma _{n})(\chi _{n}, \varphi _{n}, \varrho _{n}) + \varsigma _{n}\mathcal{T}\omega _{n}, \\ \psi _{n} = (1 - \sigma _{n})\upsilon _{n} + \sigma _{n} \mathcal{S} \upsilon _{n}, \\ (\chi _{n+1}, \varphi _{n+1}, \varrho _{n+1}) = (1 - \rho _{n}) \mathcal{T}\upsilon _{n} + \rho _{n} \mathcal{S}\psi _{n},\quad \forall n \in \mathbb{N}. \end{cases} $$

(4.1)

We choose the particular values of $\rho _{n}=\sigma _{n}=\varsigma _{n} = 1/2$ and $\nu _{n} = \delta _{n} = 1$ for all $n\in \mathbb{N}$. It can be clearly seen that all the presumptions of Theorem 4.1 are fulfilled. Therefrom, algorithm (4.1) converges to an element of P.

Table 1 shows the computative result for the proposed iteration and Sahu’s iteration with starting point $(-3, 1, 2)$, and it can be seen directly from the table that both iteration processes converge to the point $(-3.5, 0.5, 0)$ of P.

Table 1 Iterative values with starting point $(-3, 1, 2)$

Table 2 shows the computative result for the proposed iteration and Sahu’s iteration with starting point $(3, -1, 2)$, and it can be seen directly that both iteration processes converge to the point $(0.5, -3.5, 0)$ of P.

Table 2 Iterative values with starting point $(3, -1, 2)$

Table 3 shows the computative result for the proposed iteration and Sahu’s iteration with starting point $(3, 1, -2)$, and it can be seen directly that both iteration processes converge to the point $(-0.5, -2.5, 0)$ of P.

Table 3 Iterative values with starting point $(3, 1, -2)$

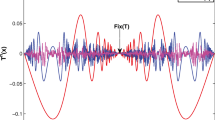
Figures 1, 2, 3 represent the behavior of errors $E(n) = \|\chi _{n} - \chi _{n+1}\|$ for the proposed iteration and Sahu’s iteration with starting points $(-3, 1, 2)$, $(3, -1, 2)$, and $(3, 1, -2)$.

Figure 1

$E(n) = \|\chi _{n} -\chi _{n+1}\|$ for iterations with initial point $(-3, 1, 2)$

Figure 2

$E(n) = \|\chi _{n} - \chi _{n+1}\|$ for iterations with initial point $(3, -1, 2)$

Figure 3

$E(n) = \|\chi _{n} - \chi _{n+1}\|$ for iteration with initial point $(3, 1, -2)$

Remark 4

From data in Tables 1–3, we see that computative results of our proposed iteration process have the lower number of iterations than the modified PPA of Sahu et al. [34], 35% on average. This shows that our proposed iteration has better convergence rate than the modified PPA iteration.

5 Conclusion

The purpose of this paper was to propose a modified proximal point algorithm based on the Thakur iteration process to approximate the common element of the set of solutions of convex minimization problems and the fixed points of two nearly asymptotically quasi-nonexpansive mappings in the framework of $\operatorname{CAT}(0)$ spaces. We proved the Δ-convergence of the proposed algorithm. We also provided an application and a numerical result based on our proposed algorithm as well as the computational result by comparing our modified iteration with previously known Sahu’s modified iteration.