Background

Heat exchanger is one of the important apparatus in heat transfer that can be found in many processed industries. The arrangement of tubes in heat exchangers determines the heat transfer performance. Besides that, the distance between the tubes, called pitchs, plays also an important role. The pitchs make the geometrical shapes: rotated triangular pitch, triangular pitch, square pitch, and rotated square pitch [Brian Spalding and Taborek 1983]. All these pitchs are obtained from two main arrangements of tubes, in-line or staggered.

The analytical models for the heat transfer of tube banks of in-line and staggered arrangement are developed by Khan et al. [2006]. These models are developed in terms of longitudinal and transverse transverse pitch and Reynolds and Prandtl numbers. In this study, the authors explore the convection heat transfer associated with crossflow over the tubes for certain value of transverse pitch.

Minter Cheng 2004 has given numerical study of the influence of the distance (transverse pitch) of two circular cylinders on heat transfer. Equations of momentum in x and y directions are solved by finite volume method. In this case, the pressure distribution is guessed and then it is corrected until all variables converge. The heat transfer increase with transverse pitch ranging from 1 to 1.5 and heat transfer decrease with transverse pitch for transverse pitch greater than 1.5. The heat transfer equals to that of single cylinders if transverse pitch is equal to two. Heat transfer of each row of the heat exchanger is not the same, the smallest value is found in the first row, and it increases in the second and third rows as shown experimentally by Mehrabian 2007.

A study concerning with a complex flows and heat transfer in the laminar flow regime around a single row of tubes in a channel is given by Cho and Son 2008. The time-dependent numerical approaches predicted the generation and evolution of vertical structures, wakes interactions, and their effects on the drag, lift, and heat transfer in the range of 20 < Re < 180.

Most heat transfer of flow around a circular cylinder occurs in the zone between the stagnation point and the separation point [Khan et al., 2005] Local variations are presented over the entire cylinder surface, including the zone beyond the separation points. At low Reynolds numbers, the heat transfer of the rear portion of a tube is at a minimum [Abdel-Raouf et al. 2010; Buyruk, 2002; Kaptan et al., 2008; Rahmani et al., 2005]. The effects of longitudinal pitch on heat transfers have been also studied by Kim 2013 and Shinya et al. 1980.

A laminar boundary layer develops from the front stagnation point of a cylinder in cross-flow and grows in thickness around the circular tube. The distributions of local heat transfer coefficients around cylinders are almost the same, except for the front half of the first row [Yan-xing et al. 2000; Tahsee et al., 2013]. Transient numerical simulations of heat transfer were performed by Horvat and Mavko 2006 for heat exchanger segments with cylindrical and ellipsoidal tubes in the staggered arrangement. The value of Stanton number is lower for the ellipsoidal form in comparison to the cylindrical form of tube cross section.

From the literature survey, the effect of transverse pitch on heat transfers in tube bundles with single row is not yet established. There is no work that has been reported on the optimum limit of transverse pitch for a bank of tubes with single row. The purpose of this study is to investigate numerically the optimum limit of transverse pitch on heat transfers from single row of circular tube banks.

Governing equations

The only analytical model of heat transfer of tube bundle in a heat exchanger is given by Khan et al. (2006) which is valid for many rows of tubes, not for single row. In this study, the author tries to explore numerically the effect of transverse pitch by solving the mathematical equations of the fluid flow and the energy.

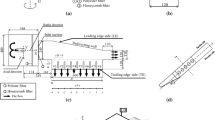
Figure 1 shows the coordinate system and parameters of this study. As shown in the figure, three isothermal heated cylinders arranged in a transverse direction (one row) to the free stream are placed in a uniform stream flow. The number of cylinders may be more than three and we investigate only the flow around a single cylinder flanked by two cylinders, so that every cylinder can be treated as a single cylinder influenced by other cylinders.

Fig. 1
figure 1

Model of single row of cylinders

Full size image

The governing equation of continuity, momentum, and energy equations in x-direction for steady incompressible flow of a Newtonian fluid with constant thermophysical properties, no heat generation, and negligible viscous dissipation are as follows:

Continuity equation:

$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 $$
(1)

Momentum equation:

$$ u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho}\frac{dp}{dx}+\upsilon \frac{\partial^2u}{\partial {y}^2} $$
(2)

Energy equation:

$$ u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\lambda \frac{\partial^2T}{\partial {y}^2} $$
(3)

With boundary conditions as follows:

  • u = v = 0, T = T S at the cylinder surface

  • u = U e , T = T ∞ far from cylinder

The dimensionless variables:

$$ {y}^{+}=\frac{y}{D}\sqrt{R_e},{u}^{+}=\frac{u}{U_{\infty }},{R}_e=\frac{U_{\infty }D}{\upsilon },{x}^{+}=\frac{x}{D},{v}^{+}=\frac{v}{U_{\infty }}\sqrt{R_e},{U_e}^{+}=\frac{U_e}{U_{\infty }},{T}^{+}=\frac{T-{T}_{\infty }}{T_S-{T}_{\infty }} $$
(4)

By introducing the dimensionless variables, Eqs. (1), (2), and (3) become

$$ \frac{\partial {u}^{+}}{\partial {x}^{+}}+\frac{\partial {v}^{+}}{\partial {y}^{+}}=0 $$
(5)
$$ {u}^{+}\frac{\partial {u}^{+}}{\partial {x}^{+}}+{v}^{+}\frac{\partial {u}^{+}}{\partial {y}^{+}}={U_e}^{+}\frac{d{U_e}^{+}}{d{x}^{+}}+\frac{\partial^2{u}^{+}}{\partial {y^{+}}^2} $$
(6)
$$ {u}^{+}\frac{\partial {T}^{+}}{\partial {x}^{+}}+{v}^{+}\frac{\partial {T}^{+}}{\partial {y}^{+}}=\frac{1}{ \Pr}\frac{\partial^2{T}^{+}}{\partial {y^{+}}^2} $$
(7)

and the boundary condition becomes (Fig. 2)

Fig. 2
figure 2

Small element in grids

Full size image
  1. 1.

    u +  = v +  = 0, T +  = 1 at the cylinder surface.

  2. 2.

    u +  = U e +, T +  = 0 far from cylinder surface.

It is noted that the boundary layer develops from the stagnation point of the cylinder surface.

Methods

The model of solution of configuration of single row of cylinders is similar to that of given by Khan et al. (2006) which the bundle of cylinders consist of a single cylinder arranged in the same distance, the same flow, and thermal characteristic around it. Therefore, only one cylinder is to be explored about the flow and the thermal behavior. We use the finite volume method Cousteix (1988) to solve Eqs. (4) and (5). The method is to integrate the equations in a small volume as shown in a black shaded area in Fig. 2. The discretization in x and y direction is represented by subscripts i and j , respectively. The number of nodes is 90 in x direction and the maximum number of nodes increases in y direction where it is 140 nodes near the separation zone. The calculation is carried out for the zone of semi-cylinder (symmetrical system) and it is not including the separation zone. The above hydrodynamic equations can be expressed as a general expression shown below

$$ \frac{\partial }{\partial {x}^{+}}\left(\varphi {u}^{+}\right)+\frac{\partial }{\partial {y}^{+}}\left(\varphi {v}^{+}\right)=S+\frac{\partial }{\partial {y}^{+}}\left(N\frac{\partial \varphi }{\partial {y}^{+}}\right) $$
(8)

where φ is the dependent variable, N is the diffusion, and S is the source term.

After integrating Eqs. (5) and (6) in small volume V in Figs. 2 and 3, we obtain the following expression:

$$ {{\displaystyle \underset{y_i}{\overset{y_s}{\int }}{\left[\varphi {u}^{+}\right]}_{x_n}^{x_{n+1}}d{y}^{+}+{\displaystyle \underset{x_n}{\overset{x_{n+1}}{\int }}{\left[\varphi {v}^{+}\right]}_{y_i}^{y_s}d{x}^{+}={\displaystyle \underset{V}{\iint }S.d{x}^{+}d{y}^{+}+{\displaystyle \underset{x_n}{\overset{x_{n+1}}{\int }}\left[N\frac{\partial u}{\partial y}\right]}}}}}_{y_i}^{y_s}d{x}^{+} $$
(9)
Fig. 3
figure 3

Element of volume of integration

Full size image

By evaluating the integration of Eq. (8), the system of equations forms a Tridiagonal matrix that can be solved easily by the Cholesky method. The integration for all elements is carried out to obtain the velocity distribution of all nodes. The first term of the right hand of Eq. (5) is obtained by the measurement of the static pressure in a wind tunnel with a section test of 40 × 40 cm2. The pressure measured at the surface of the middle cylinder then converts to velocity at the boundary layer.

Three circular cylinders of diameter 61 mm are placed, as the arrangement shown by Fig. 1, across the flow, and the pressures were measured at the surface of cylinder located in the middle. The calculation of Reynolds number is based on the maximum velocity between the cylinders. After calculation, we obtain maximum velocity U max = 15 m/s for the cylinders with smallest transverse distance and the Reynolds number is 8.4 × 104 which is laminar flow and it is less than the value of the transition Reynolds number [Lienhard et al. 2008].

The solution to the energy equation is carried out with iteration method. Equation (6) is discretized with finite difference method and then it is easily solved by the iteration method with a factor of relaxation. The finite difference scheme is applied to Eq. (6) and we obtain the following

$$ {u}_{i,j}^{+}\left(\frac{T_{i,j}^{+}-{T}_{i-1,j}^{+}}{\varDelta {x}^{+}}\right)+{v}_{i,j}^{+}\left(\frac{T_{i,j+1}^{+}-{T}_{i,j-1}^{+}}{2\varDelta {y}^{+}}\right)=\frac{1}{ \Pr}\left(\frac{T_{i,j+1}^{+}-2{T}_{i,j}^{+}+{T}_{i,j-1}^{+}}{\varDelta {y}^{+2}}\right) $$
(10)

The velocity distributions as the results of the solution of Eq. (9) are then injected into Eq. (10). We use Pr = 0.71 for all calculation in this study. The velocity distributions of the results of the solution to Eq. (9) are then injected into Eq. (10). We use Pr = 0.71 (air) for all calculations in this study.

There is no shear stress acts on the cylinder surface after the boundary-layer separation; the drag force is calculated from the stagnation point to point of separation. The drag coefficient is given by

$$ {C}_D=\frac{2.{\displaystyle \underset{0}{\overset{\pi }{\int }}{\tau}_w \sin \alpha .dA}}{{\scriptscriptstyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.\rho {U}_{\infty}^2A} $$

Or using the variables in Eq. (4), the drag coefficient becomes

$$ {C}_D.{\mathrm{Re}}^{1/2}=4.{\displaystyle \underset{0}{\overset{x_{{}^s}^{+}}{\int }}\frac{\partial {u}^{+}}{\partial {y}^{+}}} \sin \alpha .d{x}^{+} $$
(11)

and average Nusselt number is written

$$ Nu/{\mathrm{Re}}^{1/2}=\frac{1}{x^{+}}{\displaystyle \underset{0}{\overset{x_s^{+}}{\int }}{\left.\frac{\partial {T}^{+}}{\partial {y}^{+}}\right|}_{y=0}}d{x}^{+} $$
(12)

Results and discussion

The solution to the energy equation by using the iteration method needs the factor of relaxation of 0.5 and, the number of iteration is about 3400. The temperature variables at of all nodes converge on the solution where the absolute convergence is less than 10−6. The examples of velocity profiles in boundary layers for L/D = 1.42 and some value of α are illustrated in Fig. 4. The other curves that are not presented here show that velocity profiles are similar. A laminar boundary layer develops from the stagnation point and grows in thickness around the cylinder. The velocities increase with y + for all α. In the favorable gradient for α up to 92°, the profiles are strongly curved. From 92° on, the velocities far from the surface begin to decelerate and the profile becomes thicker and then S-shapes, with an early separation. The velocity profile of α = 110° is near the separation point.

Fig. 4
figure 4

Velocity profiles

Full size image

As shown by the dimensionless form of Eq. (6), the equation has no the diffusion term in x direction since the Reynolds number is sufficiently large to ensure the boundary layer structure to the flow. So the diffusion term is small compared with the other term of the equation since the term in this case is (∂2 u +/∂x +2)/Re. Equation (2) or (6) is the momentum equation valid for steady laminar flow. As shown by many literatures, for example, Lienhard (2008), for the flow around a circular cylinder with, it means 100 < Re <3.105.

The results of calculation of separation points for all transverse pitch are presented in Table 1. The separation point is located further away from the point of stagnation for small transverse pitch.

Table 1 Angle of separation for different L/D
Full size table

Figure 5 represents the effect of temperature profiles for different α for L/D = 1.42. The profiles have the common feature that the temperature decreases in a monotone fashion from the surface to a zero value far away from surface. It seems that the angles α < 69°, the temperature profiles coincide, and α ≥ 69° starts an important variation. The dimensionless temperature is always a positive value since the surface temperature of the cylinder is greater than temperature of the fluid flow as shown by the dimensionless variable of temperature (Eq. 4). It means the convection occurs from the surface to the flow. Therefore, the fluid temperature in the thermal boundary layer T ∞ ≤ T ≤ T S, in heat exchanger application where T S is the temperature of the outer surface tubes and T ∞ is the temperature of the fluid to be heated.

Fig. 5
figure 5

Dimensionless temperature profiles

Full size image

The local friction drag coefficient, CD.Re1/2, is shown in Fig. 6. It represents the shear profiles at the cylinder surface. For all L/D, the drag is zero at the stagnation point and it increases to a maximum value of certain α and then decreases rapidly to the point of separation where the drag coefficient is zero. It can be observed that for L/D = 1.17, the drag coefficient near the stagnation point is smaller and increases significantly to maximum value at α ≈ 88°. This maximum value is greater than that of all curves. We observe the smaller the transverse pitch the higher the local friction drag coefficient since the velocities are dominated by higher velocities. The maximum drag coefficient shift to the left at smaller angles and the drag coefficient profiles shift also to the left part. The curves tend to coincide when L/D increases.

Fig. 6
figure 6

Local drag coefficient

Full size image

Local drag friction represents the velocity of flow near the surface of cylinder. For small distance of the cylinders, the flow tends to accelerate near α ≈ 90° as the minimum flow area. In this case, the flow characteristic behaves as the flow passes a nozzle and a diffuser where the cross sections change rapidly. The flow for α < 90° is a favorable gradient and never separates, the expanding area produces, α > 90°, low velocity and increasing pressure, an adverse gradient.

The total drag coefficient in the form of CD.Re1/2 is shown in Fig. 7. It is obviously shown that the drag coefficient is higher for smaller L/D. The drag coefficient decreases in the increase in transverse distance. The rapid decrease is observed for L/D < 2, and then it tends to constant values of transverse distance greater than two. A higher drag coefficient is due to a higher velocity near the surface of the cylinder for small pitch ratios. It seems that starting from L/D = 2, there is no the hydrodynamic effect on pitch ratios of the tubes. The increase in drag coefficient for small transverse distance is caused by the deformation of the velocity profiles in the boundary layer, a higher velocity gradient at the wall and a thicker boundary layer.

Fig. 7
figure 7

Friction drag coefficient

Full size image

Local heat transfer represented by Nu.Re1/2 is shown in Fig. 8 for different L/D. It can be seen for small transverse pitch, L/D = 1.17, heat transfer is small near stagnation zone and then increases with α. It achieves a maximum value of about α = 70° and then decreasing to the separation point. The low heat transfer on the stagnation point is due to the small increase in velocity. The rise of the transverse pitch ratio, the heat transfer is larger than that of smaller pitch on stagnation point. It is important to be noted that near the separation point, the heat transfer increases with L/D. It seems the maximum heat transfer as L/D ≥ 2 is located and decreases with distance along the surface as boundary layer thickness increases. The low heat transfer on the stagnation point is due to the small increase in velocity. The increase of the transverse pitch makes higher heat transfer on the stagnation point. All local heat transfer profiles decrease to zero at the separation point. The similar profiles are observed for L/D ≥ 2 but a slightly lower profile for L/D = 3. All curves seem to have the intersection at α ≈ 55° since the velocity profiles have the intersection at the same α as it is shown in Fig. 6 which represents the velocity near the surface.

Fig. 8
figure 8

Local Nusselt number

Full size image

Figure 9 illustrates the average Nusselt number, Nu/Re1/2. The lowest heat transfer is obtained for the lowest distance between cylinders, and then it increases significantly up to L/D < 2. As spacing between cylinders becomes larger, the average Nusselt number seems to be constant. Though we observe a slightly decrease, it may be negligible.

Fig. 9
figure 9

Average Nusselt number

Full size image

Conclusions

Numerical calculation for the forced convection heat transfer of a tube bank of single row in the air is performed in this work. The calculation is carried out to solve the momentum equation and energy equation. The velocity at the boundary layer is calculated by the results of pressure measurements. The numerical calculation is carried out by finite volume method to solve the momentum equation, and the iteration method is used to solve the energy equation. The results obtained are found that the effect of transverse pitch for L/D < 2 has a significant change of heat transfer. The heat transfer decreases with the decrease of L/D. The pitch has no influence on heat transfer for L/D ≥ 2. This study gives the limit of distance between cylinders in design of a tube bank in a heat exchanger.