Revisiting radiation patterns in $e^+e^-$ collisions

Abstract

We propose four simple event-shape variables for semi-inclusive $e^+e^- \rightarrow 4$-jet events. The observables and cuts are designed to be especially sensitive to subleading aspects of the event structure, and allow to test the reliability of phenomenological QCD models in greater detail. Three of them, $\theta _{14}$, $\theta ^*$, and $C_2^{(1/5)}$, focus on soft emissions off 3-jet topologies with a small opening angle, for which coherence effects beyond the leading QCD dipole pattern are expected to be enhanced. A complementary variable, $M_L^2/M_H^2$, measures the ratio of the hemisphere masses in 4-jet events with a compressed scale hierarchy (Durham $y_{23}$–$y_{34}$), for which subleading $1\rightarrow 3$ splitting effects are expected to be enhanced. We consider several different parton-shower models, spanning both conventional and dipole/antenna ones, all tuned to the same $e^+e^-$ reference data, and show that a measurement of the proposed observables would allow for additional significant discriminating power between the models.

1 Introduction

General-purpose event generators (see [1–4] for recent reviews) aim to give a complete description of high-energy interactions, down to the level of individual particles. They are extensively used as research vessels for exploring new approaches to phenomenological questions within and beyond the Standard Model, and they are relied upon to provide explicit simulations of high-energy reactions in a broad variety of contexts. The achievable accuracy depends both on the inclusiveness of the chosen observable and on the sophistication of the calculation itself. An important driver for the latter is obviously the development of improved theoretical models; but it also depends crucially on the available constraints on the remaining free parameters. Using existing data to constrain these is referred to as generator tuning.

The main experimental reference for final-state radiation and fragmentation studies is the process $e^+e^- \rightarrow Z/\gamma ^* \rightarrow \mathrm {hadrons}$. Prior to and during the LEP era, a large set of event measurements were performed (see, e.g., [5–8]) and used to constrain the shower and hadronization models of the day, such as Herwig [9], Jetset/Pythia [10], and Ariadne [11]. Most of the relevant analyses were corrected to the particle level and have subsequently been encoded in Rivet [12]. This makes it straightforward to apply almost the same comprehensive battery of tests to any model today.¹ A main question we wish to examine in this study is whether the existing constraints are sufficient in the context of present-day models. The reasons to ask this question are threefold.

Firstly, current parton-shower models are, in fact, quite sophisticated, at least as far as pure final-state radiation effects are concerned. For instance, they all include color coherence (though the way this is achieved differs from model to model), the inclusion of dominant contributions of two-loop splitting kernels by suitable renormalization-scale choices (e.g., $\mu _R\propto p_\perp$), and effects of momentum conservation (again with individual models employing different “recoil” strategies), and several even incorporate further subleading aspects such as gluon-polarization or helicity-conservation effects. Their precision is therefore typically much better than their nominal “leading-logarithmic” (LL) labels indicate; in comparison with the experimental uncertainties at LEP, differences on observables dominated by LL effects are typically too small to show up clearly (cf., e.g., [24]). It is therefore interesting to study whether more information can be extracted from variables designed to remove LL contributions and isolate specific subleading aspects.

Secondly, over the last decade, several completely new parton-shower models have been formulated [25–34], in the context of a new generation of MC generators such as Herwig++ [31, 35], Pythia 8 [36], Sherpa [37], and Vincia [29]. Many of the new shower models build on the coherent QCD dipole-antenna formalism [38–41] and aim explicitly at facilitating combinations with higher-order matrix elements [32, 42–44] (so-called “matching”). These models were not present during the main era of $ee$ measurements, and hence could not directly inform the selection of observables. Thus, it is natural at this point to reconsider whether there are additional interesting observables, which could provide further non-trivial constraints on modern generators.

Thirdly, the desire for reliable descriptions of jet production and jet substructure for signal and background estimates at the LHC is causing the subleading aspects of shower models and matrix-element matching strategies to come under increasing scrutiny, in particular in the context of the interplay between matching and tuning. While all shower and matching strategies are designed to have the same leading behaviors, they do exhibit differences at subleading levels, making subleading-sensitive observables especially interesting for cross checks.

In this paper, we are interested mainly in inclusive 4-jet observables sensitive to coherence properties and to effective $1\rightarrow 3$ splittings. The starting points are the $\theta ^*$ variable proposed in [31], $\theta _{14}$ and $M_L^2/M_H^2$ proposed in [45], and the energy correlation functions proposed in [46]. The former two, $\theta ^*$ and $\theta _{14}$, are designed to be sensitive to the coherent emission of a soft fourth jet from a three-parton state (with cuts restricting the opening angles of the jets, as will be described below), with a radiation pattern dictated by color coherence. In particular, they can be used to test whether the angular distribution of the fourth jet is well described by a three-parton system represented by partons / dipoles / antennae, and how this description depends upon the choice of shower ordering variable. The latter two variables, $M_L^2/M_H^2$ (the ratio of hemisphere masses) and the energy correlation functions, have sensitivity to the effective description of $1\rightarrow 3$ splittings and the energy spectrum of the fourth jet, respectively, as will be discussed below. For all observables, we impose an explicit cut on the Durham $k_T$ resolution scale of the fourth jet, $y_{34}>0.0045$ (corresponding to $\ln (y_{34})~>~-5.4$), thus restricting it to be in the perturbative domain and avoiding possible contamination from $B$ decays.

We examine six different parton-shower models: the default angular-ordered parton shower of Herwig++ [25], the $p_\perp$- and virtuality-ordered dipole showers of Herwig++ [31], the default $p_\perp$-ordered shower of Pythia 8 [26], and the $p_\perp$- and $m_{\mathrm {ant}}^2$-ordered antenna showers of Vincia [29].

The salient properties of each shower model will be summarized briefly in Sect. 2. As a cross check, and to ensure a fair comparison between the models, we tune all of them to the same reference data in Sect. 3. The main study of soft-jet and event-shape variables is presented in Sect. 4. Finally, we round off with conclusions in Sect. 5.

2 Theory models

Parton showers are not guaranteed to respect coherence. For example, in a traditional shower based on the collinear DGLAP formalism [47–49], the linear sum of $n$ DGLAP splitting kernels (one for each parton in an $n$-parton state) can substantially overcount the amount of wide-angle soft radiation in comparison, e.g. [50], with $(n+1)$-parton matrix elements. Physically speaking, if we approximate the radiation from an $n$-parton (“color-multipole”) state by the incoherent sum of $n$ monopole terms, there is a substantial risk that highly important destructive-interference effects will be neglected, leading to double counting of soft gluon emission.

It was found in the early 1980s [51] that DGLAP-based parton showers can nonetheless be brought to agree with the correct soft limits of QCD (up to azimuthal averaging effects), by choosing the shower ordering variable to be proportional to energy times angle. This is the basis of the angular-ordered showers [25] in Herwig++, which is the first shower model we include in our study.

An alternative DGLAP-based shower model is that of Pythia 8, the second model included in our study. In this framework [26], small opening angles are reinterpreted as corresponding to highly boosted color dipoles. The resulting Lorentz-boosted DGLAP radiation patterns combined with an ordering in transverse momentum of the dipoles are used to obtain approximately coherent results.

A more formal definition of showers based on color dipoles can be obtained by replacing the DGLAP splitting kernels by intrinsically coherent radiation functions such as Catani–Seymour (CS) dipole functions [39] or QCD antenna functions (also called Lund dipoles) [38, 40]. These reproduce the leading collinear and soft singularities of QCD amplitudes for each single emission without the need of a particular phase-space restriction as present in angular-ordered showers. They can, however, differ in the ordering variable, affecting multiple emissions and hence potentially higher-order coherence properties. Another difference is the recoil strategy taken, which can lead to differences at the level of next-to-leading logarithms or beyond. In order to explore these ambiguities more fully, we include four different variants of dipole-antenna shower models in our study, two based on a dipole formalism and two based on antennae, with differences as follows.

For each radiation term, the dipole formalism identifies a single parton as the emitter, with a color partner assigned to be the spectator. The recoil is constrained to be purely longitudinal, in the rest frame of the dipole pair. By itself, the dipole radiation function only accounts for half of the soft singularity of the dipole pair, and there is no collinear singularity associated with the spectator. There is a separate radiation term in which the roles of the two are reversed, such that the sum is correct in all the infrared limits. The preferred choice of ordering variable is transverse momentum, $p_{\perp \mathrm {dip}}$, the relative transverse momentum of the splitting products with collinear direction defined by the spectator. This defines the third model included in this study. As a fourth option, we consider ordering in the virtuality of the splitting products, $q_\mathrm {dip}$ (see Table 1 for precise definitions).

Table 1 The six shower models considered in this paper. The ordering variables shown correspond to $I\rightarrow ij$ for the DGLAP models, the same as with $K$ as the spectator for the CS dipole models, and as $IK \rightarrow ijk$ for the antenna ones. We use the notation $Q_I^2 = (p_i + p_j)^2$, $Q_K^2 = (p_j+p_k)^2$, and $M_{IK}^2 = (p_I + p_K)^2 = (p_i + p_j + p_k)^2$. The Pythia 8 evolution variable is defined as $p_{\perp \mathrm {evol}}^2 = z(1-z)Q_I^2$ with $z=(M^2_{IK}-Q^2_K)/(M^2_{IK}+Q^2_I)$ the fraction of the light-cone momentum of parton $I$ carried by parton $i$, in the DGLAP functions, $P(z)$

In the antenna formalism, there is no unique distinction between emitters and spectators. Instead, a single antenna radiation function captures the collinear limits of both of the color partners together with their full soft singularity, and a $2\rightarrow 3$ kinematics map is used, which smoothly interpolates between the two collinear limits (both parents generally acquire some recoil). In this context, it has been shown explicitly [44] that the choice of $p_\perp$ as evolution variable absorbs all logarithms through second order in $\alpha _s$ (i.e., up to and including $\alpha _s^2 \ln Q^2$ corrections), hence this is the preferred choice, defining the fifth shower model in our study. As an alternative, we also consider ordering in antenna mass, which is known to exhibit an $\alpha _s^2 \ln Q^2$ discrepancy with respect to second-order QCD [44].

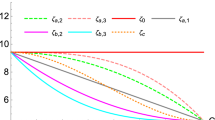
A systematic comparison of the salient differences between these six different shower models is given in Table 1. Contours of constant value of each of the corresponding evolution variables are shown in Fig. 1, over the triangular dipole branching phase space. Labeling the pre- and post-branching partons by $IK \rightarrow ijk$, the axes of the plots are defined by the dimensionless branching invariants $Q_I^2/M_{IK}^2$ and $Q_K^2/M_{IK}^2$, so that the collinear singularities lie along the axes and the soft singularity lies at (0, 0). Note that the DGLAP- and dipole-based evolution variables, 2–4, correspond to the evolution of a single parton, $I$, hence the corresponding radiation functions only have collinear singularities along the $y$ axis; the antenna evolution variables, 5–6, correspond to the evolution of the $IK$ antenna, with collinear singularities along both axes.

Fig. 1

Illustration of the progression of the shower evolution variables over the dipole phase space, for each of the models listed in Table 1. Note that 2–4 correspond to radiation functions whose only singularities lie along the $y$ axis, while 1, 5, and 6 have singularities along both the $x$ and the $y$ axes

In order to focus on the pure shower aspects and make the models more directly comparable, a few non-default choices have been made in the context of our study. In particular for Vincia, ME corrections at both LO [43] and NLO [44] were switched off, and we use the smoothly ordered showers [43] with a one-loop running of $\alpha _s$. The Herwig++ dipole-shower simulations likewise used a one-loop running and no matrix-element corrections nor NLO matching has been applied. For the default shower models (angular-ordered in Herwig++ and $p_{\perp \mathrm {evol}}$-ordered in Pythia), we use the respective default settings, which includes matrix-element corrections for the first emission, for both codes, and one-loop (two-loop) running for Pythia (Herwig++), respectively. As a cross check, we investigated the effect of including NLO matching for the $p_{\perp \mathrm {dip}}$-ordered dipole shower of Herwig++ and found that the 4-jet observables, which we study here, are not sensitive to these corrections. An enlarged set of results, including plots of the last-mentioned study and strong versus smooth ordering, will be included in [52].

3 Tuning

In order to compare the models on as equal a footing as possible, we first adjust (“tune”) the shower and hadronization parameters of each model to the same set of existing LEP measurements. We perform this tuning with the Professor [53] tuning system, via analyses that are encoded in Rivet [12], for all shower models. This relatively agnostic (automated) tuning approach also makes it possible to make (relatively) objective statements concerning whether each shower model is able to describe the existing data with a similar quality.²

The goodness-of-fit per degree of freedom provides information as regards how well data measurements are described by the predictions of Monte Carlo (MC) event generators. It is defined as

$$\begin{aligned} \frac{\chi ^2}{N_{\text {dof}}}= \frac{\sum \nolimits _\mathcal O w_\mathcal O\sum \nolimits _{b\in \mathcal O}(f_b(\vec {p})-\mathcal R_b)^2/\Delta _b^2}{\sum \nolimits _\mathcal O w_\mathcal O|{b\in \mathcal O}|}, \end{aligned}$$

(1)

with reference value $\mathcal R_b$ and total error $\Delta _b$ of the data per bin $b$ and observable $\mathcal O$. The true MC response is modeled by a set of functions $f_{b}(\vec {p})$. These functions are replaced by the true MC response $\text {MC}_{b}(\vec {p})$, if real MC runs are used. The observables’ weights $w_\mathcal O$ enter in the calculation of the goodness-of-fit as well as in the number of degrees of freedom.

3.1 Observables and parameters

As observables for the tuning we use event shapes, identified particle spectra, jet rates, particle multiplicities and $b$-quark fragmentation functions, provided by the ALEPH [5, 54], DELPHI [6] and OPAL [55] experiments and by the Particle Data Group PDG [56]. The observables and their weights can be found in Tables 4, 5, 6, 7, 8 in the appendix.

The parameters for the hadronization and shower models of Herwig++, Pythia 8 and Vincia, which we readjust here, can be found in Tables 9 and 10 in the appendix, together with a short description.

After performing a first tune with Herwig++ we obtain flat distributions in $\chi ^2$ for two parameters, the soft scale $\mu _{\text {soft},FF}$ and the smearing parameter $\text {Cl}_\text {smr}$. Therefore, we keep $\text {Cl}_\text {smr}$ fixed at its default value and set $\mu _{\text {soft},FF}$ to zero for a slight increase of the value of the shower cutoff. This approach leads to slightly smaller values in the goodness-of-fit values since the minimization works better due to the reduction of the dimensionality of the parameter space.

To get a good description of the MC response by the interpolation function of Professor, we use a fourth-order polynomial. Due to fixing those parameters which exhibit flat distributions in $\chi ^2$, as explained above, we remain with six parameters for each combination of shower and hadronization model. The minimal possible number of MC runs needed for the tuning is defined by the number of coefficients for the polynomial; here we need at least $210$ runs. To get reasonable results we perform oversampling of about a factor $3$, leading to $650$ MC runs with different randomly selected values of the parameters that are tuned. We use $500$ randomly selected runs $300$ times to interpolate the generator response and check the quality of the interpolation by comparing the $\chi ^2$ of the interpolation response with real MC runs at certain parameter values. By removing parameter regions where the interpolation did not work sufficiently well we increase the quality of the interpolation. Unfortunately we cannot remove all bad regions for Herwig++ since the values of some observables are not a smooth function of the gluon mass in the region where the MC predictions fit the data well. This is backed by the possibility of new splitting processes for higher gluon masses. We use the $300$ different run combinations again in the tuning step where the goodness-of-fit is minimized in order to obtain the parameters that describe the observables best. Afterwards we perform real MC runs for these different parameter sets and calculate the real $\chi ^2/N_\text {dof}$ to get the best tune.

3.2 Tuning results

This section presents the results of the tuning process, starting with a short overview in terms of the total $\chi ^2/N_\text {dof}$ values for the different shower models. In order to validate the results of the tuning, we apply different analysis tools. The results for the $p^2_{\perp \mathrm {dip}}$-ordered dipole shower are presented as an example for Herwig++ and for the $p_{\perp \mathrm {ant}}^2$-ordered shower as an example for Vincia. The parameter values obtained by the best tune are listed in the appendix, in Table 11 for Herwig++ and in Table 12 for Pythia 8 and Vincia. In addition, the default values and the scanned range are shown for the different parameters.

3.2.1 Quality of the overall description

The goodness-of-fit function per degree of freedom, $\chi ^2/N_\text {dof}$, is listed in Table 2 for each of the shower models included in the study, before and after tuning. The previous (default) tunes of Vincia and Pythia 8 already describe the existing LEP measurements very well. The description of the LEP data by the default angular-ordered tune of Herwig++ is fine as well. Therefore only small improvements in the quality of the description of LEP data are achieved. Note that the angular-ordered shower is the only one that describes the mean particle multiplicities better than the other observables. In the context of the string-based models, one would presumably need to include the spin- and flavor-sensitive parameters in the tuning as well, to reoptimize the agreement with the mean identified particle multiplicities. We did not look into this here, since the 4-jet observables we investigate are not sensitive to the particle composition, and since including these parameters would have greatly inflated the dimensionality of the parameter space.

Table 2 The total $\chi ^2/N_\text {dof}$ values for the different shower models, for the default values of the parameters and the best tune

For the Herwig++ dipole shower, for ordering in transverse momentum as well as for ordering in virtuality, the tuning greatly improved the quality of the description of the LEP data. The goodness-of-fit values are reduced by factors up to $17$.

In terms of the overall description of the LEP data, Vincia with ordering in transverse momentum fits the data the best, followed by Pythia 8 and Vincia with $m_{\mathrm {ant}}^2$-ordering. Especially the two $p_\perp$-ordered models achieve very similar $\chi ^2/N_\mathrm {dof}$ values and hence cannot be told apart using the present data, nor does the mass-ordered version of Vincia stand out very clearly after retuning. (Among the event shapes, the in- and out-of-plane $p_\bot$ distributions exhibit the most significant individual discrepancies with the data. We suspect color-reconnection effects may play a role for these distributions, an issue which is still very actively investigated [32, 57–61].) The three shower models interfaced to the cluster hadronization model in Herwig++ come in at somewhat higher overall $\chi ^2/N_\mathrm {dof}$ values.

We note that all the LEP measurements used Pythia [62] or Jetset [62] to generate MC event samples for the detector correction, hence there may be a small systematic bias favoring the string-based models (here Pythia 8 and Vincia). Herwig event samples were used as well, to estimate the systematic uncertainties. Therefore, the experiments claim that the observable distributions are independent of the underlying MC generator for the detector corrections within the experimental systematics.

3.2.2 Validation

The distribution of the $\chi ^2/N_\text {dof}$ values of the $300$ tunes, each based on $500$ randomly selected runs at different parameter points, are plotted in Figs. 2 and 3 for two parameters for the Herwig++ $p^2_{\perp \mathrm {dip}}$-ordered dipole shower and for Vincia with ordering in $p_{\perp \mathrm {ant}}^2$. Narrow distributions indicate that the observables are very sensitive to this parameter. Broader distributions are obtained if either the observables are less sensitive to a parameter or, as for the Lund parameters $a_L$ and $b_L$, if two parameters are highly correlated.

Fig. 2

Scatterplots for AlphaMZ and PSplit with real MC runs for the Herwig++ $p^2_{\perp \mathrm {dip}}$-ordered dipole shower. The plots show the $\chi ^2/N_\text {dof}$ values of the $300$ different run combinations with respect to the parameter value. The vertical line indicates the parameter value of the best tune and the plot boundaries are chosen to be equal to the scanned range of the parameter

Fig. 3

Scatterplots for aLund and PTsigma with real MC runs for the Vincia $p_{\perp \mathrm {ant}}^2$-ordered shower. The plots show the $\chi ^2/N_\text {dof}$ values of the $300$ different run combinations with respect to the parameter value. The vertical line indicates the parameter value of the best tune and the plot boundaries are chosen to be equal to the scanned range of the parameter

In order to verify the result of the generator tuning with Professor we perform real MC runs where we change only one parameter with randomly distributed values and set all other parameters to their new tuned value. We reproduce the histograms at the same parameter points by using the interpolation function calculated by Professor to model the MC response. The distribution of the goodness-of-fit is shown with respect to the parameter value for two different parameters for the Herwig++ $p^2_{\perp \mathrm {dip}}$-ordered dipole shower and for Vincia with ordering in $p_{\perp \mathrm {ant}}^2$ in Figs. 4 and 5. The $\chi ^2/N_\text {dof}$ value is split for the different groups of observables where the lines correspond to the interpolation result and the points to the real MC runs. The single observables enter in the calculation of the goodness-of-fit for a group of observables with the same weight as for the calculation of the overall $\chi ^2/N_\text {dof}$. By comparing the interpolation with the real generator response, the quality of the interpolation function can be evaluated as well. Figures 4 and 5 show that the parameter values of the best tune, marked by the vertical line, are clearly favored, mostly driven by event shapes. As mentioned above, we were not able to remove all regions for Herwig++ where the interpolation did not work sufficiently well. This leads to the different $\chi ^2/N_\text {dof}$ values for interpolation and MC runs. Since the quality of the interpolation is disrupted by the possibility for new splitting processes for higher gluon masses, identified particle spectra and mean multiplicities cannot be described very well. This affects of course also the other parameters. As shown in Fig. 5, the interpolation works better for Vincia, where interpolation and generator response agree perfectly.

Fig. 4

A scan of AlphaMZ and PSplit with real MC runs and the interpolation result of Professor for the Herwig++ $p^2_{\perp \mathrm {dip}}$-ordered dipole shower. All other parameters are fixed at their new tuned values. The vertical line indicates the value of the best tune of the scanned parameter. The curves show the $\chi ^2/N_\text {dof}$ for the different types of observables and the blue curve the combination of all observables. Points correspond to the real MC and lines to the interpolation result

Fig. 5

A scan of aLund and PTsigma with real MC runs and the interpolation result of Professor for the Vincia $p_{\perp \mathrm {ant}}^2$-ordered shower. All other parameters are fixed at their new tuned values. The vertical line indicates the value of the best tune of the scanned parameter. The curves show the $\chi ^2/N_\text {dof}$ for the different types of observables and the blue curve the combination of all observables. Points correspond to the real MC and lines to the interpolation result

Besides the $\chi ^2/N_\text {dof}$ distribution of the parameters we have shown here, we obtain parameters with flatter distributions as well. In addition some parameters prefer to be at the limit of the scanned range as occurring for example for the strong coupling $\alpha _{S}$ within the tuning of Pythia 8 and Vincia with $m_{\mathrm {ant}}^2$-ordering.

3.3 Eigentunes

To estimate the uncertainty in the MC predictions in connection with changing the parameter values during the tuning, so-called eigentunes are performed. The parameters are varied along the eigenvectors in parameter space where the eigenvectors are obtained by certain changes, $\Delta \chi ^2/N_\text {dof}$, in $\chi ^2/N_\text {dof}$. For each parameter two eigenvectors, one in the “$+$” and one in the “$-$” direction, exist. If the goodness-of-fit were distributed as a true $\chi ^2$ function $\Delta \chi ^2/N_\text {dof}=1$ would correspond to a one-sigma deviation and $\Delta \chi ^2/N_\text {dof}=4$ to a two-sigma deviation from the minimum (i.e., the central tune), etc.

Given, however, that none of the models achieves a $\chi ^2/N_\text {dof} \le 1$, the eigentunes can at most be used to give a rough indication of the range of accessible model variations near the respective minimum for each model. This is still valuable, as it can help us determine whether the central tunes of two (or more) different theory models could easily be retuned to give the same result or not, on a given observable (overlapping versus non-overlapping eigentune variation ranges).

We calculate two sets of eigentunes with Professor, corresponding to one- and two-sigma deviations, and perform MC runs to obtain envelopes around the central tune for each of the six different theory models. For the 4-jet observables we propose (see Sect. 4), we find that the model differences are larger than the individual eigentune envelopes. Hence we conclude that these observables do have sensitivity to distinguish between the theory models within the limits of the tuning uncertainty. For all further studies we will use the central tunes.

4 Results

We consider hadronic $Z$ events (photon ISR is switched off) and use the Durham $k_T$ clustering algorithm [63] to cluster all events back to two jets, keeping track of the intermediate clustering scales along the way. The $3\rightarrow 2$ clustering scale is denoted $y_{23} = k_{T3}^2/m_Z^2$, and so on for higher jet numbers. We require both $y_{23}$ and $y_{34}$ to be greater than $0.0045$, to obtain an inclusive 4-jet event sample with minimal contamination from $B$ decays and lower (non-perturbative) scales.

Strong ordering corresponds to $y_{23}\gg y_{34} \gg \ldots$, while events with, e.g., $y_{34}$–$y_{23}$ should be more sensitive to the ordering condition and to the effective $1\rightarrow 3$ splitting kernels. Further, we may in principle also keep track of which “side” each clustering step happens on, which can give us an additional handle on the relative contributions to the 4-jet rate from “opposite-side” $1\rightarrow 2 \otimes 1\rightarrow 2$ splittings versus “same-side” $1\rightarrow 3$ ones. Within the context of this study, however, we only explicitly used the former requirement ($y_{23}$–$y_{34}$), in the context of the definition of the $M_L^2/M_H^2$ variable, though we note that the latter (same-side vs. opposite-side sequential clusterings) is implicitly present along the $M_L^2/M_H^2$ axis.

4.1 Observable 1: $\mathbf {\theta _{14}}$

We consider the event at the stage when it has been clustered back to four jets, and order the jets in hardness. To be sensitive to coherence we constrain the angles between the jets such that the first (hardest) jet lies back-to-back to a near-collinear jet pair, formed by the second and third jet; $\theta _{12}>2\pi /3$, $\theta _{13}>2\pi /3$ and $\theta _{23}<\pi /6$. From this near-collinear 3-jet state we probe the emission angle of the soft fourth jet with respect to the first jet, $\theta _{14}$.

Before presenting the main results for $\theta _{14}$, we note that, for Herwig++ with default shower and hadronization parameters, an enhancement for small values of $\theta _{14}$ shows up due to surprisingly large non-perturbative effects. This enhancement decreases for the dipole shower due to changing the values of the hadronization parameters throughout the tuning, but unfortunately not for the angular-ordered shower. By checking the influence of the hadronization parameters on the shape of the distribution of $\theta _{14}$, we identify the mass exponent for daughter clusters, $P_\text {split}$, as the cause of the enhancement. By keeping it fixed at a value of $0.6$ during the tuning, we achieve a better agreement between hadron level and parton level for the normalized distribution of $\theta _{14}$, which we regard as physically more reasonable given the cut of $y_{34}>0.0045$. This distribution is shown in the upper row of Fig. 6 for keeping $P_\text {split}$ fixed on the right and for no constraints on the left. We see that the influence of hadronization is reduced strongly by keeping the hadronization parameter fixed. However, some sensitivity to non-perturbative effects is still left for small values of the observable $\theta _{14}$. The Herwig++ dipole shower gives similar results in the comparison of the angular observables on hadron and parton level. In addition we show this comparison in the lower row of Fig. 6 for Pythia 8 and the $p^2_{\perp \mathrm {ant}}$-ordered shower of Vincia. For Pythia 8 we can see a small enhancement for small values of $\theta _{14}$ as well, whereas the predictions of Vincia agree well with each other.

Fig. 6

A comparison of the normalized distribution of $\theta _{14}$ on hadron (red solid) and parton level (blue dashed). The upper row shows the predictions of the Herwig++ angular-ordered shower, where $P_\text {split}$ is kept fixed in the right plot and no constraints in the left plot. In the lower row the same plot is shown for Pythia 8 and the $p_{\perp \mathrm {ant}}^2$-ordered shower of Vincia

To compare the predictions of the different theory models, Fig. 7 shows the normalized distribution of $\theta _{14}$ in the upper left plot.

Fig. 7

Upper Left normalized distribution of the angular observable $\theta _{14}$. Other plots ratios of different regions with respect to the definition of the region, cf Table 3. The solid curves refer to the Herwig++ showers, the angular-ordered default shower in blue, the $p^2_{\perp \mathrm {dip}}$-ordered in green and the $q_\mathrm {dip}^2$-ordered dipole shower in red, respectively. The dashed lines refer to the Vincia shower with $m_{\mathrm {ant}}^2$-ordering in violet and $p_{\perp \mathrm {ant}}^2$-ordering in pink and to the Pythia 8 shower in teal. The ratio plots show the deviation of the showers with respect to the Herwig++ angular-ordered default shower. The vertical error bars indicate the expected $1\sigma$ statistical error with $5\cdot 10^5$ hadronic $Z$ decays

To show the differences more clearly and reduce the observable to a simpler quantity with better statistics, we divide the full $\theta _{14}$ range into three regions labeled “Towards” (small $\theta _{14}$), “Central” (intermediate $\theta _{14}$), and “Away” (large $\theta _{14}$). We may then consider the ratio between regions,

$$\begin{aligned} AS(x) = \dfrac{\sum \nolimits _{x_1<x<x_2}y(x)}{\sum \nolimits _{x_3<x<x_4}y(x)}. \end{aligned}$$

(2)

In the “Towards” region, the first and fourth jet are collinear, while they are back-to-back in the “Away” region. Events where the fourth jet is a wide-angle emission from the 3-jet system populate the “Central” region. We consider nine different possibilities for the exact divisions between the regions, listed in Table 3 and corresponding roughly to looser or tighter cuts. The ratios of the integrated $\theta _{14}$ rates for each of the nine different region definitions are shown in Fig. 7.

Table 3 Definition of the different regions for the asymmetry of $\theta _{14}$. Columns 2–5 specify the limits for the regions and the first column gives the numbering. The ratio of the central to towards region is built with the second and third column, central to away with the second and fourth and towards to away uses the fourth and fifth column

Since large non-perturbative effects occur in the towards region for the Herwig++ shower models, we consider the ratio of the central to away region to be the most robust observable. This ratio reflects the relative amount of soft wide-angle emissions to emissions where the first jet lies back-to-back to all other jets in the event. Compared to the angular-ordered shower, the Herwig++ dipole shower with $q_\mathrm {dip}^2$-ordering predicts up to $30~\%$ higher values for this ratio; a very significant difference. The predictions of the $p^2_{\perp \mathrm {dip}}$-ordered dipole shower of Herwig++ are very similar to the ones of Pythia 8 and lower than the predictions of all other shower models. Vincia with both ordering variables agrees with the result of the Herwig++ angular-ordered shower within the statistical errors.

To distinguish between the two evolution variables of Vincia we can use the ratio of the central to towards region. This ratio reflects the relative amount of soft wide-angle emission compared to collinear emission. The predictions of the $m_{\mathrm {ant}}^2$-ordered shower are about $35~\%$ higher than the ones of the $p_{\perp \mathrm {ant}}^2$-ordered shower. We expect this behavior since the $m_{\mathrm {ant}}^2$-ordered shower prefers wide-angle soft over collinear emissions, see Fig. 1, whereas the $p_{\perp \mathrm {ant}}^2$-ordered shower prefers the opposite.

The third ratio, shown in the lower right plot of Fig. 7, is the towards over away region, which is predicted very similarly by Pythia 8, Herwig++ with $p^2_{\perp \mathrm {dip}}$-ordering and Vincia with $m_{\mathrm {ant}}^2$-ordering. The predictions of these theory models are $20$ to $30~\%$ smaller than the one of the angular-ordered shower of Herwig++. The $q_\mathrm {dip}^2$-ordered shower on the other hand produces values up to $40~\%$ higher. In both ratios including the away region, we see a $10$ to $20~\%$ difference between the predictions of Pythia 8 and the $p^2_{\mathrm {ant}}$-ordered shower of Vincia, where Pythia 8 produces more events populating the away region. Thus, we conclude that these ratios have significant discriminating power between the models, including between Pythia 8 and Vincia which appeared very similar in the global analysis.

4.2 Observable 2: $\mathbf {\theta ^*}$

In addition to the cuts for the previous observable, we require the fourth jet to be close in angle to the near-collinear (23) jet pair, $\theta _{24}<\pi /2$, in order to enhance the sensitivity to coherent emission off the (23) jet system. We then define our second angular observable as the difference in opening angles, $\theta ^*=\theta _{24}-\theta _{23}$, and, similarly to above, we introduce the asymmetry,

$$\begin{aligned} \frac{N_\text {left}}{N_\text {right}} = \dfrac{\sum \nolimits _{x<x_0}y(x)}{\sum \nolimits _{x>x_0}y(x)}, \end{aligned}$$

(3)

with respect to an arbitrary dividing point, $\theta ^*=x_0$, which separates the small-$\theta ^*$ region from the large-$\theta ^*$ one. The normalized distribution of $\theta ^*$ and the asymmetry (as a function of the dividing point $x_0$) are shown in Fig. 8. Due to the additional cut on $\theta _{24}$ for this observable, the error bars are higher and thus the statistical power in discriminating the different theory models smaller. The only shower model which can be distinguished from the others is the $q_\mathrm {dip}^2$-ordered dipole shower of Herwig++. This model tends to predict more events where the difference in opening angles of the fourth and third jet is large, compared to the angular-order shower. The $p^2_{\perp \mathrm {dip}}$-ordered dipole shower of Herwig++ predicts larger values for the asymmetry and therefore more events with a smaller difference in opening angles.

Fig. 8

The plots show the normalized distribution of the difference in opening angles, $\theta ^*$, on the left and its asymmetry with respect to the asymmetry axis, $x_0$, on the right

4.3 Observable 3: $\mathbf {C_2^{(1/5)}}$

Reference [46] defines the $N$-point energy correlation function (ECF) as

$$\begin{aligned} \text {ECF}(N,\beta )=\sum _{i_1<i_2<\cdots <i_N}\left( \prod _{a=1}^NE_{i_a}\right) \left( \prod _{b=1}^{N-1}\prod _{c=b+1}^N \theta _{i_bi_c}\right) ^\beta . \end{aligned}$$

(4)

where the sum runs over all particles of a jet. To be sensitive to the global event structure we replace this sum by the sum over all jets in the event. Thus, $\theta _{i_1i_2}$ denotes the angle between two jets $i_1$ and $i_2$. The ECFs are used to build double ratios

$$\begin{aligned} C_N^{(\beta )}= \frac{\text {ECF}(N+1,\beta )\text {ECF}(N-1,\beta )}{\left( \text {ECF}(N,\beta )\right) ^2}. \end{aligned}$$

(5)

We choose a value of $\beta =1/5$ to give all angles about equal weights and to be sensitive to soft configurations. Sensitivity to collinear configurations can be achieved by choosing $\beta =2$ and giving greater angles more weight.

In the 4-jet events described in Sect. 4.1 we use the 2-point double ratio

$$\begin{aligned} C_2^{(\beta )}=\frac{\sum \nolimits _{j_1<j_2<j_3}E_{j_1}E_{j_2}E_{j_3}(\theta _{j_1j_2}\theta _{j_1j_3}\theta _{j_2j_3})^\beta }{\left( \sum \nolimits _{j_1<j_2}E_{j_1}E_{j_2}\theta _{j_1j_2}^\beta \right) ^2}\cdot E_\text {vis}, \end{aligned}$$

(6)

where the sums run over the four jets. Due to the cuts on the angles between the jets, the events look like 3-jet systems to the observable. This system contains two hard jets, jet $1$ and jet $(23)$,³ lying approximately back-to-back and a third soft jet, jet $4$. With this notation (6) can approximately be written as

$$\begin{aligned} C_2^{(\beta )} \approx \frac{E_1E_{23}E_4(\theta _{1\,23}\theta _{14}\theta _{23\,4})^\beta }{(E_1E_{23}\theta _{1\,23}^\beta +E_1E_4\theta _{14}^\beta +E_{23}E_4\theta _{23\,4}^\beta )^2}\cdot E_\text {vis}. \end{aligned}$$

(7)

Taking the small energy of jet $4$ and the large angle $\theta _{1\,23}>2\pi /3$ into account, the denominator can be reduced to its first term,

$$\begin{aligned} C_2^{(\beta )} \approx \frac{E_4(\theta _{14}\theta _{23\,4})^\beta }{E_1E_{23}\theta _{1\,23}^\beta }\cdot E_\text {vis}. \end{aligned}$$

(8)

This leaves only the angles relative to the fourth jet and the energies as free parameters. For $\beta =1/5$ all angles are weighted relatively equal and hence $C_2^{(1/5)}$ is proportional to the energy of the fourth jet, relative to the remaining energy of the event.

For the normalized distribution of the 2-point double ratio, $C_2^{(1/5)}$, we see non-perturbative effects for Herwig++ and the $m_{\mathrm {ant}}^2$-ordered shower of Vincia. For all of these shower models, hadronization and decays enlarge the number of events with a harder fourth jet, hence higher values of $C_2^{(1/5)}$.

We again use the asymmetry, as defined in Eq. (3), to condense the differences between the theory models into a ratio of integrals. The normalized distribution of the 2-point double ratio, $C_2^{(1/5)}$, and the according asymmetry are shown in Fig. 9. As indicated by the asymmetry, the $p^2_\perp$-ordered shower models of Herwig++, Pythia 8 and Vincia give similar predictions. Compared to that, the prediction of the $m_{\mathrm {ant}}^2$-ordered shower of Vincia is higher, as expected due to the preference of soft over collinear emissions during the population of phase space.

Fig. 9

The plots show the normalized distribution of the 2-point double ratio, $C_2^{(1/5)}$, on the left and its asymmetry with respect to the asymmetry axis, $x_0$, on the right

4.4 Observable 4: $\mathbf {M_L^2/M_H^2}$

To force a “compressed” scale hierarchy, we impose the cut $y_{34} > 0.5\, y_{23}$, and plot the ratio $M_L^2/M_H^2$ of the invariant masses (squared) of the jets at the end of the clustering, ordered so that $M_L^2 \le M^2_H$. With four partons at LO, the light jet mass, $M_L$, is zero if both the $4\rightarrow 3$ and the $3\rightarrow 2$ clusterings happen in the same jet, while it is non-zero otherwise. Thus, the region close to zero is sensitive to events with a $1\rightarrow 3$ splitting occurring in one of the jets, while the region above $\sim$0.25 is dominated by opposite-side $1\rightarrow 2$ splittings.

The normalized distribution of the mass ratio is shown on the left side in Fig. 10. The ratio plot shows that the difference between the theory models mainly occurs in the region for values $M_L^2/M_H^2\lesssim 0.3$, leaving smaller differences per bin for higher values due to the normalization. To condense these difference we use the asymmetry, as defined in Eq. (3), whose values are shown on the right in Fig. 10 with respect to the asymmetry axis, $x_0$. The asymmetry roughly reflects the relative amount of events with a $1\rightarrow 3$ splitting occurring in one of the jets, divided by events with opposite-side $1\rightarrow 2$ splittings.

Fig. 10

The plots show the normalized distribution of the ratio of jet masses, $M_L^2/M_H^2$, on the left and its asymmetry with respect to the asymmetry axis, $x_0$, on the right

Compared to the angular-ordered shower of Herwig++, the $p^2_{\perp \mathrm {dip}}$-ordered dipole shower and Pythia 8 predict a higher value for the asymmetry, whereas the predictions of Vincia with both ordering variables and the $q_\mathrm {dip}^2$-ordered dipole shower of Herwig++ are smaller. Both evolution variables of Vincia result in the same value for the asymmetry, whereas a difference of $5$ to $12~\%$ occurs between Pythia 8 and Vincia. For Pythia 8 and the $p^2_{\perp \mathrm {ant}}$-ordered shower of Vincia we also see differences up to nearly $20~\%$ in the bins for small mass ratios. Thus, this observable can be used to tell these theory models apart.

Note that we obtain a distribution similar to the mass ratio by using the ECF, defined in Eq. (4). The 1-point double ratio is defined as

$$\begin{aligned} C_1^{(\beta )}=\frac{\sum \nolimits _{i<j\in J}E_iE_j\theta _{ij}^\beta }{\left( \sum \nolimits _{i\in J}E_i\right) ^2}, \end{aligned}$$

(9)

where the sum runs over all particles of a jet. By building a ratio similar to the mass ratio we get

$$\begin{aligned} \frac{C_{1,L}^{(\beta )}}{C_{1,H}^{(\beta )}} = \frac{\sum \nolimits _{i<j\in J_L}E_iE_j\theta _{ij}^\beta }{\left( \sum \nolimits _{i\in J_L}E_i\right) ^2} \cdot \frac{\left( \sum \nolimits _{i\in J_H}E_i\right) ^2}{\sum \nolimits _{i<j\in J_H}E_iE_j\theta _{ij}^\beta }, \end{aligned}$$

(10)

with $C_{1,L}^{(\beta )}\le C_{1,H}^{(\beta )}$. With the expansion $\cos \theta \approx 1-\theta ^2/2$, the invariant mass squared of two particles is

$$\begin{aligned} M_{ij}^2=E_iE_j(1-\cos \theta _{ij})&\approx E_iE_j\theta _{ij}^2/2. \end{aligned}$$

(11)

By using a value of $\beta =2$, Eq. (10) is approximately equal to the mass ratio and we thus obtain similar results for the two variables.

5 Conclusions

We have studied four event-shape variables, designed to be sensitive to subleading aspects of the event structure in semi-inclusive $e^+e^- \rightarrow 4$-jet events, with a cut on $y_{34} > 0.0045$. Six different parton-shower models were compared, available through the Herwig++, Pythia 8, and Vincia Monte Carlo codes. These models span a wide range of theoretical ideas, from conventional parton showers to ones based on dipoles and antennae, with different ordering criteria, different recoil strategies, and different radiation functions.

To make the comparison as fair and unbiased as possible, we first tuned all the theory models to the same set of existing LEP measurements, using the Professor and Rivet tuning tools. We find that the existing data already provides some discriminating power, with the models using string hadronization achieving somewhat lower $\chi ^2$ values than those based on cluster hadronization.⁴ Therefore, it is important that we limit ourselves to draw conclusions only from observables that are not very sensitive to non-perturbative effects. Vincia with ordering in transverse momentum provides the best overall description of the LEP data. Using just the existing data, however, it is nearly impossible to tell, e.g., Pythia and Vincia apart, despite significant differences between the shower models. Although the Herwig++ models are easier to tell apart already using the existing data, we do also see larger differences between them in the variables proposed here, corroborating our conclusion that the new observables add significant discriminating power.

We have shown that the observables proposed here, which are sensitive to coherence properties and to effective $1\rightarrow 3$ splittings, allow for additional significant discriminating power between the different models, given a sample size of order 500k events or more. The theory models for the shower implemented in Herwig++ can clearly be told apart by most of the observables we propose. Depending on the tuning parameters, however, the cluster model may generate rather large non-perturbative corrections to the 4-jet rate, especially at low $\theta _{14}$. For the $\theta _{14}$ variable, we therefore also highlighted the integrated “Central/Away” ratio as an observable that should be particularly robust against corrections at low $\theta _{14}$. As expected and measured with the 4-jet angular observable $\theta _{14}$, we see that the $m_{\mathrm {ant}}^2$-ordered shower of Vincia predicts a higher ratio of wide-angle to collinear emissions from a 3-jet system, compared to the $p^2_{\perp \mathrm {ant}}$-ordered shower. With the same observables as well as with the ratio of jet masses, $M_L^2/M_H^2$, we can distinguish between Vincia and Pythia 8. The shower model of the latter produces more events where one hard jets lies back-to-back to the remaining jets of the event.

We round off by emphasizing that a comparison against corrected LEP data would be extremely interesting, and, we believe, of great importance to constraining the subleading properties of modern-day QCD models.

Appendix A: Tuning observables, weights, and parameters

See Tables 4, 5, 6, 7, 8, 9, 10, 11, and 12.

Table 4 Identified particle spectra and the associated weights, taken from Ref. [6]

Table 5 Event shapes and the associated weights, taken from Refs. [5] and [6]

Table 6 Jet rates and the associated weights, taken from Ref. [55]

Table 7 Observables for $b$ quarks and the associated weights, taken from Ref. [54]

Table 8 Multiplicities and the associated weights, taken from Ref. [56]

Table 9 The table lists the parameters for the Herwig++ shower and hadronization model. The shower parameters indicated by the superscript $(f)$ exist in different copies for different splitting processes and the hadronization with superscript $(f)$ exist in three copies for the different flavors: $(f)=(u,d,s),c,b$

Table 10 The table lists the parameters for the shower model of Vincia and Pythia 8 and for the Lund hadronization model of Pythia 8

Table 11 The table lists the parameters with their default value and the scanned range for the tuning of Herwig++. The last columns contain the values of the best tune

Table 12 The table lists the parameters with their default value and the scanned range for the tuning of Pythia 8 and Vincia. The last columns contain the values of the best tune