1 Introduction

The EoS of dense, strongly interacting matter is the key input for an array of astrophysical simulations of compact objects in isolation and binaries within various scenarios. A large collection of EoS is already featured on the CopmOSE database [1]. Nevertheless, the need for further developments and export of new EoS to this and other databases is necessary because of the strong constraints that emerged during the recent years and will appear in the future, notably due to the multimessenger observations of binary neutron star (BNS) mergers, isolated nearby neutron stars in X-rays and radiopulsars.

The formation of hot and neutrino-rich compact objects is predicted by numerical simulations of core-collapse supernova (SN) and BNS mergers. In the core-collapse supernova context, a hot proto-neutron star is formed during the contraction of the supernova progenitor and subsequent gravitational detachment of the remnant from the expanding ejecta [2,3,4,5,6,7,8,9]. A transient formation of dense hot matter arises in the case when the progenitor mass is large (typically tens of solar masses) and the matter collapses into a black hole [10,11,12,13].

Numerical simulations indicate that BNS mergers produce hot and dense interacting matter in the post-merger phase [14,15,16,17,18]. The outcome of a merger depends on the combined masses of merged objects and may result both in a black hole and a stable neutron star. In any case, a transient hot object is formed and, therefore, the spectrum of gravitational waves emitted in this phase (which can be observed with advanced gravitational wave instruments) will carry imprints of the EoS of hot and dense matter. This EoS also determines the stability of the remnant object and thus the outcome of the transient evolution [19] as well as the efficacy of dissipative processes [20,21,22,23,24,25,26,27] that should be included [26] in the frequently employed ideal hydrodynamics simulations.

The local properties of matter in the “hot” stage of evolution in the above astrophysical contexts is characterized by the density, temperature (or entropy), and the lepton fractions for electrons and \(\mu \)-ons. The EoS in this stage depends on multiple parameters which can be compared to the simpler one-parametric EoS of cold and \(\beta \)-equilibrated matter. Since many nuclear and astrophysical constraints are placed on the cold EoS, it is mandatory to study this limit in parallel with the finite-temperature EoS. The cold and hot regimes also differ in the fact that in the hot case neutrinos are trapped above the temperature \(T_\mathrm{tr}\simeq 5\) MeV; in this regime, the neutrino mean-free path is shorter than the size of the star [28]. As we will discuss below the composition of matter is strongly affected by the prescription for the neutrino fractions (via the fixation of the lepton number).

In this work, we report an extension of our previous study of hot hypernuclear matter [29] which builds upon the work of Ref. [30] to include non-strange \(J^P=\frac{3}{2}^+\) members of the baryons decuplet – the \(\varDelta \)-resonances. Our numerical implementation is based on the code of Ref. [30] supplemented with hidden strangeness \(\sigma ^*\) and \(\phi \) mesons which account for the interactions amongst hyperons [29]. In the hypernuclear sector, we will adopt the parameter set already discussed in Refs. [31,32,33] in the case of zero-temperature EoS. In the nucleonic sector, we will use CDF parameters corresponding to the DDME2 parameterization [34]. Heavy baryons have been studied in the zero-temperature limit in recent years because of the emerging new astrophysical and laboratory constraints [31, 32, 35,36,37,38,39,40,41], for a review see [42]. The study of the hypernuclear matter with \(\varDelta \)-resonance admixture at finite temperatures begun recently [43,44,45]. These references employed CDFs with density-dependent couplings, as we do below. However, our study differs from these works by (a) the parametrization of the CDF in the nuclear and/or hypernuclear sectors; (b) the mesonic content of the Lagrangian. Specifically Refs. [43,44,45] include \(\sigma , \omega ,\) and \(\rho \) mesons only while we will include in addition the hidden strangeness \(\sigma ^*\) and \(\phi \) mesons.

This work is organized as follows. In Sect. 2 we discuss the main elements of CDF approach at finite temperatures. The general purpose EoS is then specified for the scenarios of SN and BNS mergers in Sect. 2.3. We present the numerical results on the EoS and composition in Sect.  3. The mass-radius (hereafter M-R) relation of static cold and isentropic, hot compact stars and the astrophysical constraints are discussed in Sect.  4. In Sect.  5 we provide a summary of our main findings. We use the natural (Gaussian) units with \(\hbar = c=k_B=1\), and the metric signature \(g^{\mu \nu }=\mathrm{diag}(1,-1,-1,-1)\).

2 Relativistic density functional with density-dependent couplings

2.1 Equation of state

The Lagrangian of the stellar matter is given by

$$\begin{aligned} \mathscr {L} = \mathscr {L}_b + \mathscr {L}_d + \mathscr {L}_m + \mathscr {L}_\lambda + \mathscr {L}_\mathrm{em}, \end{aligned}$$
(1)

where the \(J_B^P = \frac{1}{2}^+\) baryon Lagrangian is given by

$$\begin{aligned} \mathscr {L}_b \,= & {} \, \sum _b{{\bar{\psi }}}_b\bigg [\gamma ^\mu \! \left( i\partial _\mu -g_{\omega b}\omega _\mu -g_{\phi b}\phi _\mu - \frac{1}{2} g_{\rho b}{\varvec{\tau }}\cdot {\varvec{\rho }}_\mu \right) \nonumber \\&- (m_b - g_{\sigma b}\sigma - g_{\sigma ^* b}\sigma ^*)\bigg ]\psi _b, \end{aligned}$$
(2)

where the b-sum is over the \(J_B^P = \frac{1}{2}^+\) baryon octet \(b\in (n,p,\varLambda , \varXi ^{0,-},\varSigma ^{0,\pm })\), \(\psi _b\) are the Dirac fields of the octet with masses \(m_b\). The mesonic fields included in theory are \(\sigma ,\sigma ^*,\omega _\mu ,\phi _\mu \), and \({\varvec{\rho }}_\mu \) with meson-baryon couplings \(g_{mb}\) where m index runs over the mesons \(m\in (\sigma , \omega , \rho , \sigma ^*, \phi )\). Later on we will specify the theory to the case where the couplings are density-dependent. The strange mesons \(\sigma ^*\) and \(\phi \) couple only to hyperons. The second term in Eq. (1) stands for the contribution of the non-strange \(J=\frac{3}{2}^+\) members of the baryons decuplet which is the quartet of \(\varDelta \)-resonances \(d \in (\varDelta ^-,\varDelta ^0,\varDelta ^+,\varDelta ^{++})\) and is given explicitly by

$$\begin{aligned} \mathscr {L}_d&= \sum _{d}{{\bar{\psi }}}^{\nu }_{d} \bigg [\gamma ^\mu \left( i\partial _\mu -g_{\omega d}\omega _\mu - \frac{1}{2} g_{\rho d}{\varvec{\tau }}\cdot {\varvec{\rho }}_\mu \right) \nonumber \\&\quad - (m_d- g_{\sigma d}\sigma )\bigg ]\psi _{d\nu } , \end{aligned}$$
(3)

where the d-summation is over the resonances described by the Rarita–Schwinger fields \(\psi _{d\nu }\).

The mesonic Lagrangian is given by

$$\begin{aligned} \mathscr {L}_m= & {} \frac{1}{2} \partial ^\mu \sigma \partial _\mu \sigma -\frac{m_\sigma ^2}{2} \sigma ^2 - \frac{1}{4}\omega ^{\mu \nu }\omega _{\mu \nu } + \frac{m_\omega ^2}{2} \omega ^\mu \omega _\mu \nonumber \\&- \frac{1}{4}{\varvec{\rho }}^{\mu \nu }\cdot {\varvec{\rho }}_{\mu \nu } + \frac{m_\rho ^2}{2} {\varvec{\rho }}^\mu \cdot {\varvec{\rho }}_\mu +\frac{1}{2} \partial ^\mu \sigma ^*\partial _\mu \sigma ^*\nonumber \\&-\frac{m_\sigma ^{*2}}{2} \sigma ^{*2}- \frac{1}{4}\phi ^{\mu \nu }\omega _{\mu \nu } + \frac{m_\phi ^2}{2} \phi ^\mu \phi _\mu , \end{aligned}$$
(4)

where \(m_{\sigma }\), \(m_{\sigma ^*}\), \(m_{\omega }\), \(m_{\phi }\) and \(m_{\rho }\) are the meson masses. The field-strength tensors for vector fields are given by

$$\begin{aligned} \omega _{\mu \nu }= & {} \partial _{\mu }\omega _{\nu } - \partial _{\mu }\omega _{\nu } ,\end{aligned}$$
(5)
$$\begin{aligned} \phi _{\mu \nu }= & {} \partial _{\mu }\phi _{\nu } - \partial _{\mu }\phi _{\nu } ,\end{aligned}$$
(6)
$$\begin{aligned} \varvec{\rho }_{\mu \nu }= & {} \partial _{\nu } \varvec{\rho }_{\mu } - \partial _{\mu }\varvec{\rho }_{\nu }. \end{aligned}$$
(7)

The leptons will be assumed non-interacting and are described by the free-field Dirac Lagrangian

$$\begin{aligned} \mathscr {L}_\lambda \,=\, \sum _{\lambda }{{\bar{\psi }}}_\lambda (i\gamma ^\mu \partial _\mu - m_\lambda )\psi _\lambda , \end{aligned}$$
(8)

where \(\psi _\lambda \) are leptonic fields and \(m_\lambda \) are their masses. In the case of cold stellar matter the lepton index \(\lambda \in (e,\mu )\) runs over electrons and \(\mu \)-ons and their antiparticles, whereas \(\tau \)-leptons can be neglected because of their large mass. For temperatures above trapping temperature \(T_\mathrm{tr}=5\) MeV electron and \(\mu \)-on neutrinos are trapped (the details of trapping depend on the local density of matter and its composition). In that case, the three flavors of left-handed neutrinos (assuming Standard Model particle content) need to be included in the Lagrangian (8). In this work, we neglect electromagnetism and drop the term \(\mathscr {L}_\mathrm{em}\) from the Lagrangian (1). It has been included elsewhere to accommodate the possibility of extremely large magnetic fields in compact stars, see [46,47,48] and references therein.

Having defined the Lagrangian (1) of the system we proceed to evaluate the partition function of the system. The evaluation is simplified by the fact that we consider a stationary system in the infinite limit, i.e., the time and space variations of the fields can be neglected. The partition function is evaluated in the mean-field approximation by keeping only the Hartree terms. With these approximations, the pressure and energy density are given by

$$\begin{aligned} P= & {} P_m+P_b+P_d+P_{\lambda } + P_{r},\end{aligned}$$
(9)
$$\begin{aligned} {\mathcal E}= & {} {\mathcal E}_m+{\mathcal E}_d+{\mathcal E}_d+{\mathcal E}_{\lambda }, \end{aligned}$$
(10)

where the contributions due to mesons and \(J_B^P = \frac{1}{2}^+\)-baryons are given by

$$\begin{aligned} P_m= & {} - \frac{m_\sigma ^2}{2} \sigma ^2 -\frac{m_\sigma ^{*2}}{2} \sigma ^{*2} + \frac{m_\omega ^2}{2} \omega _0^2 + \frac{m_\phi ^2 }{2} \phi _0^2 + \frac{m_\rho ^2 }{2} \rho _{03}^2,\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} {\mathcal E}_m= & {} \frac{m_\sigma ^2}{2} \sigma ^2 +\frac{m_\sigma ^{*2}}{2} \sigma ^{*2} + \frac{m_\omega ^2 }{2} \omega _0^2 + \frac{m_\phi ^2 }{2} \phi _0^2 + \frac{m_\rho ^2 }{2} \rho _{03}^2,\nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned} P_b= & {} \sum _{b} \frac{g_{b}}{6\pi ^2}\int _0^{\infty }\! \frac{dk\, k^4 }{E_k^{b}} \left[ f(E_k^{b}-\mu _{b}^*)+f(E_k^{b}+\mu _{b}^*)\right] , \nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned} {\mathcal E}_b= & {} \sum _{b} \frac{g_{b}}{2\pi ^2} \int _0^{\infty }\! dk \, k^2 E_k^{b}\nonumber \\&\times \left[ f(E_k^{b}-\mu _{b}^*) +f(E_k^{b}+\mu _{b}^*)\right] , \end{aligned}$$
(14)

where \(f(E) = [1+\exp (E/T)]^{-1}\) is the Fermi distribution function, \(g_b=2J_b+1 = 2 \) is the spin (\(J_b = 1/2\)) degeneracy factor of the baryon octet. The expressions for \(P_d\) and \({\mathcal E}_d\) follow from (13) and (14) via a replacement of the indices b by d and taking into account that the spin degeneracy factor is \(g_d = 4 \) for \(\varDelta \)-resonances. The lepton contribution is given by

$$\begin{aligned} P_{\lambda }= & {} \sum _{\lambda } \frac{g_{\lambda }}{6\pi ^2}\int _0^{\infty }\! \frac{dk\, k^4 }{E_k^\lambda } \left[ f(E_k^{\lambda }-\mu _\lambda )+f(E_k^{\lambda }+\mu _\lambda )\right] ,\nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned} {\mathcal E}_{\lambda }= & {} \sum _{\lambda } \frac{g_{\lambda }}{2\pi ^2} \int _0^{\infty }\!\! dk\, k^2E_k^\lambda \nonumber \\&\times \left[ f(E_k^\lambda -\mu _\lambda ) +f(E_k^\lambda +\mu _\lambda )\right] , \end{aligned}$$
(16)

where the degeneracy factor \(g_\lambda = 2J_{\lambda }+1 \) is equal 2 for electrons and \(\mu \)-ons and 1 for neutrinos of all flavors. The single-particle energies of baryons and \(\varDelta \)-resonances (which include interactions) are given by \(E_k^{b} = \sqrt{k^2+m^{*2}_{b}}\) and \(E_k^{d} = \sqrt{k^2+m^{*2}_{d}}\), respectively, where the corresponding effective (Dirac) masses are given by

$$\begin{aligned} m_{b}^* = m_b - g_{\sigma b}\sigma - g_{\sigma ^*b}\sigma ^*,\quad m_{d}^* = m_d - g_{\sigma d}\sigma , \end{aligned}$$
(17)

where the mesonic fields now correspond to their mean-field values, see Eqs. (23)–(27) below. Leptons are treated as non-interacting gas and their kinetic energies are given by \(E_k^{\lambda }=\sqrt{k^2+m_\lambda ^2}\), where \(m_\lambda \) is given by the free mass of electron or \(\mu \)-on and is assumed vanishingly small in the case of neutrinos.

For contact interactions, the mesonic mean-fields shift the value of the baryon and \(\varDelta \)-resonance non-interacting chemical potentials \(\mu _{b}\) and \(\mu _{d}\) to

$$\begin{aligned}&\mu _{b}^* = \mu _{b}- g_{\omega b}\omega _{0} - g_{\phi b}\phi _{0} - g_{\rho b} \rho _{03} I_{3b} - \varSigma ^{r}, \end{aligned}$$
(18)
$$\begin{aligned}&\mu _{d}^* = \mu _{d}- g_{\omega d}\omega _{0} - g_{\rho d} \rho _{03} I_{3d} - \varSigma ^{r}, \end{aligned}$$
(19)

where \(I_{3b/3d}\) is the third component of isospin of baryons/\(\varDelta \)-resonances and the rearrangement self-energy \(\varSigma ^r\) is given by

$$\begin{aligned} \varSigma ^r= & {} \sum _{b,d} \left( \frac{\partial g_{\omega b}}{\partial n_b} \omega _0 n_b+ \frac{\partial g_{\rho b}}{\partial n_b} I_{3b} \rho _{03} n_b+ \frac{\partial g_{\phi b}}{\partial n_b} \phi _0 n_b \right. \nonumber \\&-\left. \frac{ \partial g_{\sigma b}}{\partial n_b} \sigma n_b^s - \frac{ \partial g_{\sigma ^* b}}{\partial n_b} \sigma ^* n_b^s + b\leftrightarrow d\right) . \end{aligned}$$
(20)

This quantity adds a contribution to the pressure in a manner that guarantees the thermodynamical consistency (specifically the energy conservation and fulfillment of the Hugenholtz–van Hove theorem). The true pressure is given by Eq. (9) where the rearrangement term is

$$\begin{aligned} P_r = n_B\varSigma _{r}, \end{aligned}$$
(21)

where \(n_B\) is the net baryon density. It can be verified that the contribution from the rearrangement self-energy guarantees the validity of the thermodynamic relation

$$\begin{aligned} P = n_B^2 \frac{\partial }{\partial n_B}\left( \frac{{\mathcal E}}{n_B}\right) . \end{aligned}$$
(22)
Table 1 The values of parameters of the DDME2 CDF
Full size table

The expectation values of mesons in the mean-field and infinite system approximations are given by

$$\begin{aligned}&m_{\sigma }^2\sigma = \sum _{b} g_{\sigma b}n_{b}^s + \sum _{d} g_{\sigma d}n_{d}^s, \end{aligned}$$
(23)
$$\begin{aligned}&m_{\sigma ^{*}}^2 \sigma ^{*} = \sum _{b} g_{\sigma ^{*} b} n_{b}^s, \end{aligned}$$
(24)
$$\begin{aligned}&m_{\omega }^2\omega _{0}= \sum _{b} g_{\omega b}n_{b} +\sum _{d} g_{\omega d}n_{d}, \end{aligned}$$
(25)
$$\begin{aligned}&m_{\phi }^2\phi _{0}= \sum _{b} g_{\phi b}n_{b} , \end{aligned}$$
(26)
$$\begin{aligned}&m_{\rho }^2\rho _{03}= \sum _{b} g_{\rho b} n_{b} I_{3b}+ \sum _{d} g_{\rho d} n_{d}I_{3d}, \end{aligned}$$
(27)

where the scalar and baryon (vector) number densities are defined for the baryon octet and \(\varDelta \)-resonances as

$$\begin{aligned} n_{b}^s= & {} \langle {\bar{\psi }}_b \psi _b\rangle , \quad n_{b}= \langle {\bar{\psi }}_b \gamma ^0 \psi _b\rangle , \end{aligned}$$
(28)
$$\begin{aligned} n_{d}^s= & {} \langle {\bar{\psi }}_{d\nu } \psi ^\nu _d\rangle ,\quad n_{d}= \langle {\bar{\psi }}_{d\nu } \gamma ^0 \psi ^\nu _d\rangle , \end{aligned}$$
(29)

respectively. The explicit expressions of these expectation values at finite temperatures can be computed in a standard way, and are given in the case of spin-\(J\frac{1}{2}^+\) by

$$\begin{aligned} n_{b}= & {} \frac{g_b}{2\pi ^2}\!\!\int _0^\infty \! k^2dk \left[ f(E^b_k-\mu _b^*)-f(E^b_k+\mu _b^*)\right] , \end{aligned}$$
(30)
$$\begin{aligned} n_{b}^s= & {} \frac{g_b}{2\pi ^2}\!\!\int _0^\infty \! \frac{k^2dk\, m^*_b}{E_k^b} \left[ f(E^b_k-\mu _b^*)+f(E^b_k+\mu _b^*)\right] .\nonumber \\ \end{aligned}$$
(31)

The expressions for the \(\varDelta \)-resonances are obtained upon exchange \(b\leftrightarrow d\).

2.2 Fixing couplings

In this work, we continue to employ a model with density-dependent couplings that depend on the net baryon density \(n_B\). The influence of the temperature on the effective interactions in the theory (as well as possible contributions from fluctuations) is thus neglected. The density-dependence of the nucleon-meson couplings is

$$\begin{aligned} g_{iN}(n_B) = g_{iN}(n_\mathrm{sat})h_i(x), \end{aligned}$$
(32)

where \(n_\mathrm{sat}=0.152\) fm\(^{-3}\) is the saturation density, \(x = n_B/n_\mathrm{sat}\) and

$$\begin{aligned} h_i(x)= & {} \frac{a_i+b_i(x+d_i)^2}{a_i+c_i(x+d_i)^2},~i=\sigma ,\omega , \end{aligned}$$
(33)
$$\begin{aligned} h_\rho (x)= & {} e^{-a_\rho (x-1)}. \end{aligned}$$
(34)

The five constraints \(h_{i }(1)=1\), \(h_i^{\prime \prime }(0)=0\) and \(h^{\prime \prime }_{\sigma }(1)=h^{\prime \prime }_{\omega }(1)\) allow one to reduce the number of free parameters in isoscalar-scalar and iso-scalar-vector sector to three. In the nucleonic (hereafter N) sector, the parameters of the model are fixed from the nuclear phenomenology and properties of selected nuclei. We adopt the DDME2 model [34] with the couplings and other parameters defined in Table 1. For a review of the theory that uses density-dependent couplings for the meson-baryon interactions, see, for example, [49].

Let us turn to the hyperonic (hereafter Y) sector. We follow the established procedure to fix the couplings of the vector mesons according to the SU(6) spin-flavor symmetric model [50] and adjust the scalar meson couplings to reproduce the values of the phenomenological potential depths of various hyperons at the saturation density in isospin symmetrical nuclear matter.

Quantitatively one defines the ratios of hyperonic couplings to the corresponding nucleonic couplings, i.e., \(R_{i Y}=g_{i Y}/g_{i N} \) for \(i=\{\sigma ,\omega ,\rho \}\) and \(R_{\sigma ^* Y} =g_{\sigma ^* Y}/g_{\sigma N} \), \(R_{\phi Y}=g_{\phi Y}/g_{\omega N} \). The values of corresponding ratios are listed in Table 2. The ratio \(R_{\sigma \varLambda }\) for \(\varLambda \)-hyperons [31] is numerically close to the value determined from fits to \(\varLambda \)-hypernuclei data [51]. The commonly considered range of potentials for \(\varSigma \) and \(\varXi \) hyperons, in the sense defined above, is given by

$$\begin{aligned}&-10\le U_{\varSigma }(n_\mathrm{sat}) \le 30 ~\mathrm{MeV},\end{aligned}$$
(35)
$$\begin{aligned}&-24\le U_{\varXi }(n_\mathrm{sat}) \le 0~\mathrm{MeV}. \end{aligned}$$
(36)

The lower value of the range \(U_{\varXi }(n_\mathrm{sat}) \) was obtained from the analysis of the \(\varXi +p \rightarrow \varLambda \varLambda \) two-body capture events in \(^{12}\)C and \(^{14}\)N emulsion nuclei [52]; more shallow results were obtained from the analysis of the \(^{9}\)Be(\(K^{-},K^{+}\)) reaction, specifically, \(U_{\varXi }(n_\mathrm{sat}) =-17\) MeV [53], and on the bases of the (2+1)-flavor lattice QCD simulations close to the physical point by the Lattice19 collaboration [54]. Our adopted values of the couplings match those used previously by Ref. [31]. The remaining parameters in the hyperonic sector, which determine the density-dependence of the couplings, are the same as in the nucleonic sector. In particular, the hidden strangeness mesons are assigned masses \(m_{\sigma ^*} = 980\) MeV and \(m_{\phi } = 1019.45\) MeV, and the density-dependence of their couplings coincides with the ones of \(\sigma \)- and \(\omega \)-mesons, respectively.

Finally, let us turn to the \(\varDelta \)-resonance (hereafter \(\varDelta \)) matter. The information on the \(\varDelta \)-potential in the isospin symmetric nuclear matter is available from the analysis of the scattering of electrons and pions off nuclei and from the simulations of the heavy ion collisions. The isovector meson-\(\varDelta \)-resonance couplings are less explored. Recent work suggests for the ratios the ranges [31, 55]

$$\begin{aligned} R_{\rho \varDelta } = 1, \quad 0.8 \le R_{\omega \varDelta } \le 1.6, \quad R_{\sigma \varDelta } = R_{\omega \varDelta } \pm 0.2. \end{aligned}$$
(37)

In the following we adopt representative values

$$\begin{aligned} R_{\rho \varDelta } = R_{\omega \varDelta } = R_{\sigma \varDelta } =1. \end{aligned}$$
(38)

Note that within a certain range of the parameters the \(\varDelta \)-admixed matter undergoes spinodal instability [56]; for fixed \(R_{\rho \varDelta } = R_{\sigma \varDelta } =1\) this occurs for \(R_{\omega \varDelta } \le 0.8\), therefore the choice (38) avoids such instabilities.

Table 2 The ratios of the couplings of hyperons and \(\varDelta \)-resonances to mesons to those of nucleons in our model
Full size table

2.3 Adapting CDF to conditions in supernovas and merger remnants

Consider next matter composed of baryon octet, \(\varDelta \)-resonances, and leptons. If equilibrium is established in matter with respect to the weak processes, then the following relations for the chemical potentials of the species hold

$$\begin{aligned}&\mu _{\varLambda }=\mu _{\varSigma ^0}=\mu _{\varXi ^0}=\mu _{\varDelta ^0}=\mu _n=\mu _B, \end{aligned}$$
(39)
$$\begin{aligned}&\mu _{\varSigma ^-}=\mu _{\varXi ^-}=\mu _{\varDelta ^-}=\mu _B-\mu _Q, \end{aligned}$$
(40)
$$\begin{aligned}&\mu _{\varSigma ^+}=\mu _{\varDelta ^+}=\mu _B+\mu _Q, \end{aligned}$$
(41)
$$\begin{aligned}&\mu _{\varDelta ^{++}}=\mu _B+2\mu _Q, \end{aligned}$$
(42)

where \(\mu _B\) and \(\mu _Q=\mu _p-\mu _n\) are the baryon and charge chemical potentials. The net charge of baryons is given by the sum

$$\begin{aligned}&n_p+n_{\varSigma ^+}+2n_{\varDelta ^{++}}\nonumber \\&\quad +n_{\varDelta ^{+}}-(n_{\varSigma ^-}+n_{\varXi ^-}+n_{\varDelta ^-})=n_Q. \end{aligned}$$
(43)

Next we define the dimensionless baryon and lepton charge densities via \(Y_Q = n_Q/n_B\), \(Y_{e,\mu } = (n_{e,\mu }-n_{e^+,\mu ^+})/n_B\), where \(e^+\) refers to the positron and \(\mu ^+\) – to the anti-\(\mu \)-on. Then, the charge neutrality condition in terms of these new quantities can be written

$$\begin{aligned} Y_Q = Y_e + Y_{\mu }. \end{aligned}$$
(44)

When neutrinos are trapped in matter, i.e., are in thermal equilibrium characterized by a distribution function at matter temperature, the quantities that are fixed are the lepton numbers \(Y_{L,e} = Y_{e} + Y_{\nu _e}\) and \(Y_{L,\mu } = Y_{\mu } + Y_{\nu _\mu }\) of the electron and \(\mu \)-on families, respectively, which are conserved separately and, therefore, are associated with lepton-number chemical potentials \(\mu _{L,e} \) and \(\mu _{L,\mu }\). In the free-streaming (untrapped) neutrino regime the neutrino chemical potentials vanish and the lepton chemical potentials are equal to the charge chemical potential up to the sign. Thus, we have

$$\begin{aligned} \mu _e= & {} \mu _\mu =-\mu _Q = \mu _n-\mu _p, \quad \text {(free streaming)} \end{aligned}$$
(45)
$$\begin{aligned} \mu _e= & {} \mu _{L,e} - \mu _Q, \quad \mu _{\mu } = \mu _{L,\mu } - \mu _Q. \quad \text {(trapped)} \end{aligned}$$
(46)

The thermodynamical conditions depend on the astrophysical scenario under consideration. As well known, neutrinos are trapped when their mean-free path is shorter than the size of the system (roughly the stellar radius) [20,21,22]. The electron and \(\mu \)-on neutrino spheres (with their surfaces defined by the location of the last neutrino scattering) are not identical and, therefore, the trapping regimes may depend on the lepton family.

We will fix below the lepton number in each family separately, assuming that the neutrino oscillations are neglected and will neglect \(\tau \)-leptons as they are too massive to be relevant.

In the case of BNS mergers, the initial conditions correspond to two cold neutron stars, which are dominated by the neutron component. In this case, our working assumption is

$$\begin{aligned} Y_{L,e} = Y_{L,\mu }= 0.1, \end{aligned}$$
(47)

which is consistent with the lepton abundances in the pre-merger neutron stars.

For supernova matter the predicted electron and \(\mu \)-on lepton numbers are typically [2, 43]

$$\begin{aligned} Y_{L,e} = 0.4, \quad Y_{L,\mu } = 0. \end{aligned}$$
(48)

However, note that the electron fraction may vary significantly along the supernova profile in a time-dependent manner. Furthermore, \(\mu \)-onization in the matter can lead to a small fraction of \(\mu \)-ons (of the order \(10^{-3}\)) [57, 58] which we will neglect here.

We will show below isentropic results for the entropy per baryon \(S/A = 1\), which is a representative value of the entropy of the core of a BNS remnant [59] and of a core region of a supernova and proto-neutron star [60]. In both cases the dense core of the star maintains its low entropy, whereas the outer layers are heated by shock(s) and dissipation and may reach a larger value of S/A. The sensitivity of the EoS and composition on the value S/A has been quantified in Ref. [45] who used a somewhat different density functional.

3 Composition and EoS of hot \(NY\varDelta \) matter

We have extended the numerical code for the computation of finite temperature hypernuclear matter, as presented in Ref. [30], to include \(\varDelta \)-resonances. The numerical procedure is based on a self-consistent solution of the equations for the meson fields (23)–(27) and the scalar and baryon densities (30) and (31) for fixed values of temperature and density or, alternatively, entropy per baryon S/A and density. In the neutrino-trapped regime the lepton numbers \(Y_{L,e}\) and \(Y_{L,\mu }\) are fixed to values that are characteristic either for supernova or BNS merger physics, see Sect. 2.3.

We start the discussion with the finite-temperature EoS of dense matter which is shown in Fig. 1 for purely nucleonic, hyperonic, and \(\varDelta \)-admixed hyperonic matter. It includes the cases of low-temperature (\(T=0.1\) MeV) matter in \(\beta \)-equilibrium, which corresponds to the neutrino-free case. In addition it contains the results for \(T=50\) MeV, which corresponds to the trapped neutrino regime, for selected combinations of electron and \(\mu \)-on fractions corresponding to SN physics (\(Y_{L,\mu } = 0\), \(Y_{L,e} = 0.4\)) and BNS merger physics (\(Y_{L,\mu } =Y_{L,e} = 0.1\)). The presence of hyperons strongly softens the EoS of nucleonic matter consistent with the fact that new degrees of freedom appear and, therefore, the degeneracy pressure of neutrons is reduced. If \(\varDelta \)’s are added to hypernuclear matter, the EoS becomes stiffer in the high-density range and softer at the intermediate-density, as already observed in the zero-temperature calculations [31, 32, 36,37,38,39,40,41]. The case of constant entropy per baryon S/A is shown in Fig. 2. The softening of the EoS with the onset of hyperons and \(\varDelta \)-resonances is seen also in this case, as it is a robust consequence of the onset of additional degrees of freedom. At asymptotically high density the \(\varDelta \) admixture leads (as in the isothermal case) to a harder EoS.

Fig. 1
figure 1

Pressure as a function of the baryon density normalized by the saturation density \(n_\mathrm{sat}\). The upper panel labeled \(\mu _\nu =0\) assumes neutrino-free \(\beta \)-equilibrium matter in the cases of purely nucleonic (labeled N), hyperonic (labeled NY) and \(\varDelta \)-admixed hyperonic (labeled \(NY\varDelta \)) matter at temperature \(T=0.1\) MeV. The remaining panels show the same dependence in neutrino trapped regime at temperature \(T=50\) MeV in the two cases \(Y_{L,\mu } = Y_{L,e} = 0.1\) (middle panel); \(Y_{L,e}=0.1\), \(Y_{L,\mu }=0.1\) (lower panel). The case \(Y_{L,e} = 0.1\) is characteristic of a BNS merger remnant, whereas the case \(Y_{L,e} = 0.4\) for SN

Full size image
Fig. 2
figure 2

Same as in Fig. 1, but in each panel instead of constant temperature the entropy per baryon is fixed at \(S/A = 1\)

Full size image
Fig. 3
figure 3

Composition of matter for \(\varDelta \)-admixed hyperonic matter. The upper panel corresponds to \(\beta \)-equilibrium case at \(T=0.1\) MeV whereas the remaining panels correspond to trapped neutrino matter at \(T=50\) MeV with the lepton fractions fixed at \(Y_{L,\mu } = Y_{L,e} = 0.1\) (middle panel), and \(Y_{L,e}=0.4\), \(Y_{L,\mu }=0\) (lower panel). At \(T=0.1\) MeV the hyperons \(\varLambda \), \(\varXi ^-\) and \(\varXi ^0\) as well as \(\varDelta ^-\) an \(\varDelta ^0\) resonances appear along with the standard nucleonic (i.e. neutron-proton-electron and muon) composition. In the neutrino trapped regime the triplet \(\varSigma ^{0\pm }\) appears as well as electron and muon neutrinos (middle panel) and electron neutrinos (lower panel)

Full size image
Fig. 4
figure 4

Same as in Fig. 3, but for constant entropy per baryon \(S/A = 1\)

Full size image

Figure 3 shows the composition of finite-temperature hyperonic matter admixed with \(\varDelta \)-resonances. Hyperons \(\varLambda \), \(\varXi ^-\) and \(\varXi ^0\) appear in the given order at low temperature, with the \(\varSigma ^-\) hyperon fraction being strongly suppressed by the highly repulsive potential in nuclear matter at saturation density [61,62,63,64,65,66]. This is in contrast with the early predictions made for the free hyperonic gas, where \(\varSigma ^-\) was the first hyperon to nucleate [67] and in an early version of the present CDF work which employed a weaker repulsive potential [30]. At finite temperature \(T=50\) MeV the isospin triplet of \(\varSigma ^{\pm ,0}\) appears in amounts comparable (but sub-leading) to other hyperons for both SN and BNS merger cases.

We find that among the \(\varDelta \)-resonances only \(\varDelta ^-\) and \(\varDelta ^0\) appear in the matter (in the given order). At low temperatures, there are clearly visible thresholds of appearance of the resonances above twice the saturation density with only \(\varDelta ^-\) reaching a significant (10%) level in the intermediate density regime. At high temperatures, the fractions of both \(\varDelta ^-\) and \(\varDelta ^0\) are comparable and phenomenologically significant \((\le 10\%)\). The abundances of heavy baryons in the case of fixed entropy per baryon is shown in Fig. 4. Fixing the entropy requires the temperature to increase as the density increases and the abundances at each density correspond to a temperature that is intermediate compared to those shown in Fig. 3. As a consequence, for example, the thresholds for heavy baryons are less steep and these are shifted to lower densities compared to the \(T=0.1\) MeV \(\beta \)-equilibrium case.

Let us turn now to the fractions of leptons. In the case of BNS mergers the imposed condition \(Y_{L,e} = Y_{L,\mu } = 0.1\) implies that the fractions of electron and \(\mu \)-on are almost equal. The same applies to their neutrinos. In the SN case \(Y_{L,\mu } = 0\), and the \(\mu \)-on neutrinos are replaced by a much smaller amount of \(\mu \)-on antineutrinos, which in turn allow for a small fraction of \(\mu \)-ons to be present despite the condition \(Y_{L,\mu } = 0\) was imposed. The lepton fraction, which is intimately related to the charge neutrality condition, is affected once hyperons and \(\varDelta \)-resonances are introduced. The effect of adding \(\varXi ^-\) and \(\varDelta ^-\) to the composition in the low-temperature and \(\beta \)-equilibrated matter is that the proton fraction becomes balanced by these particles rather than leptons, and as a consequence the electron and \(\mu \)-on populations drop rapidly and eventually they become extinct at high densities. The decrease of lepton number densities with increasing baryon density is observed also in the hot, \(\beta \)-equilibrated neutrino-trapped matter, with the main difference being the fact that the lepton populations remain finite at all densities. Since the lepton fractions are fixed in this case, this has the consequence that neutrino fractions increase with density. The effect of \(\varXi ^-\) and \(\varDelta ^-\) at finite temperature is less dramatic, since electrons are present at all densities, whereas the fractions of \(\mu \)-ons depend on whether we adopt the BNS merger or SN values of lepton fractions. In the first case, the electron and \(\mu \)-on fractions are quantitatively close to each other. In the SN case, \(\mu \)-on fraction is strongly reduced but is not zero because of a population of \(\mu \)-on antineutrinos.

As well-known (see, e.g., Refs. [32, 56]), the onset of \(\varDelta ^-\) shifts the balance between the chemical potentials of particles participating in the Urca reactions \(n\rightarrow p + e+ {{\bar{\nu }}}\) and \(e+p \rightarrow n+ \nu \). The proton fraction becomes large enough (compared to the \(npe\mu \)-matter) so that the first Urca process can take place in the matter. The electron extinction implies that the first Urca process is favored (because of the absence of final state Pauli blocking of electron states) compared to the second one, which is suppressed because of the absence of the initial state electrons. Thus, the presence of \(\varDelta \)’s can promote the nucleonic Urca processes. In addition, \(\varDelta \)’s themselves participate in Urca processes as their emergence can lead to additional processes, such as \(\varDelta ^- \rightarrow n + e^- + {{\bar{\nu }}}\) or \(\varDelta ^- \rightarrow \varLambda + e^- + {{\bar{\nu }}}\) [68]. In hot matter these processes may contribute to the neutrino opacity, which is relevant in supernova context [10,11,12,13], and bulk viscous damping of density oscillations in BNS mergers [20,21,22,23,24].

Fig. 5
figure 5

Composition of \(\varDelta \)-admixed hyperonic matter as in Fig. 3. The conventions are the same except that the lepton number fractions are fixed at \(Y_{L,e}= Y_{L,\mu }=0.1\), and the panels have fixed temperatures \(T=10\), 20, and 30 MeV as labeled. The lepton number fractions are characteristic of BNS mergers

Full size image
Fig. 6
figure 6

Same as in Fig. 5, but for lepton number fractions fixed at \(Y_{L,e}= 0.4\) and \(Y_{L,\mu }=0\) which are characteristic of supernova matter

Full size image

Let us finally comment on the high-temperature and low-density limit, where our computations are limited to the density \(0.5n_\mathrm{sat}\). It is seen from Fig. 3 that in this limit hyperon and \(\varDelta \)-resonance thresholds are absent and they propagate up to the lower bound of the density range considered. A hint on the presence of these species at lower densities is provided by the recent observation that the low-density hot nuclear matter contains a significant fraction of strangeness (\(\varLambda \)-particles) as well as \(\varDelta \)-resonances in addition to clusters and free nucleons [69].

In closing our discussion of the numerical results, we would like to explore the evolution of the fractions of particles with temperature while keeping the lepton fractions constant according to Eqs. (47) and  (48). Figures 5 and 6 below address these cases.

Consider first the case of BNS merger with fixed values of lepton fractions \(Y_{L,e}= Y_{L,\mu }=0.1\) and temperature values \(T= 10, 20\) and 30 MeV as shown in the panels of Fig. 5. First note that the \(n,p,e,\mu \) fractions depend weakly on the temperature. The equality of lepton numbers implies that the electron and \(\mu \)-on fractions are almost equal. The small electron excess over \(\mu \)-ons is compensated by the \(\mu \)-on neutrino excess over the electron-neutrinos. At high densities, the neutrino fractions depend weakly on the temperature as well but at low densities their fractions decrease with increasing temperature and, eventually, become negative at temperatures between 40 and 50 MeV.

Hyperons and \(\varDelta \)-resonances have still sharply increasing fractions at the thresholds at \(T=10\) MeV similar to the low-temperature, neutrino-free regime. The main change visible in the low-density regime is the shift of the thresholds of hyperons and \(\varDelta \)-resonances to lower densities with increasing temperature. In the high-density regime, the changes with the temperature are not significant as the quantum degeneracy dominates thermal effects. In this density regime, the \(\varLambda \) is the most abundant among the heavy baryon species and its fraction exceeds that of neutron for \(n_B/n_\mathrm{sat} \ge 6.\) The \(\varXi \)-hyperons have similar to \(\varDelta ^-\) fractions \(\lesssim 10\%\), whereas the abundance of \(\varDelta ^0\) is mildly suppressed at lower temperatures and becomes comparable to that of \(\varDelta ^-\) at \(T\ge 30\) MeV. Finally, for \(T\ge 20\) MeV the \(\varSigma \) hyperons appear, but their fractions remain below \(1\%\).

Consider next the case of SN with fixed values of lepton fractions \(Y_{L,e}= 0.4\) and \(Y_{L,\mu }=0\) as shown in Fig. 6. The remarks regarding the shift of the heavy-baryon thresholds toward low densities with increasing temperature are valid also in this case. At high densities the dominance of \(\varXi ^0\) over \(\varXi ^-\) occurs earlier, the reason being the suppression of \(\varXi ^-\) fractions by electrons with preassigned lepton fraction. Indeed, electrons supply the necessary negative charge which was otherwise due to \(\varXi ^-\) hyperons. The main difference to the BNS case arises from the suppression of the \(\mu \)-on fraction to below 1%. Their non-vanishing number is due to the presence of \(\mu \)-on antineutrinos, as pointed out above. Because of this, the charge neutrality is mainly maintained by the equality of the abundances of protons and electrons, with slight departure due to the presence of \(\varXi ^-\) and \(\varDelta ^-\) at high density. The small \(\mu \)-on fraction also results in the complete dominance of the electron-neutrinos over their \(\mu \)-onic counterparts.

As pointed out in the previous work [29], where resonances were neglected, there is a special isospin degeneracy (ID) point where the fractions within each isospin multiplet coincide. We find that in the \(\varDelta \)-resonance admixed matter this feature is maintained and extended to the \(\varDelta ^{\pm }\varDelta ^{++}\), and \(\varDelta ^0\) resonances. At the ID point of the isospin multiplet of \(\varSigma ^{0,\pm }\) hyperons the fractions of \(\varSigma ^-\) and \(\varSigma ^+\) interchange their roles from being most abundant to least abundant \(\varSigma \)-hyperon with increasing density. We see that the fractions of \(\varDelta ^{-,0}\) resonances, the fractions of isospin multiplet of \(\varSigma ^{0,\pm }\) hyperons, n and p fractions, as well as \(\varXi ^-\) and \(\varXi ^0\) fractions coincide at that point. This property becomes evident from the \(\beta \)-equilibrium conditions (39)–(42). First, note that at high densities \(\mu _n^*-\mu _p^*\simeq \mu _n-\mu _p\) because the density scaling (34) implies that the contribution of the \(\rho \)-meson mean-field to the effective baryon chemical potentials (18) and (19) vanishes exponentially. Now, if at any ID point the neutron and proton fractions are equal, i.e., \(\mu _n^*=\mu _p^*\), then the charge chemical potential \(\mu _Q=\mu _p-\mu _n = 0\) and, therefore, \(\mu _b=\mu _B\). In this case, the effective chemical potentials within any given isospin-multiplet are equal and, therefore, their fractions are equal as well.

Fig. 7
figure 7

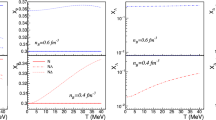
Effective chemical potentials with the effective mass subtracted as functions of the normalized baryon density \(n_B/n_\mathrm{sat}\). Each particles species are shown by the same lines as in Fig. 3 with temperature and lepton fraction fixed as indicated

Full size image
Fig. 8
figure 8

Same as in Fig. 7, but for constant entropy per baryon \(S/A = 1\)

Full size image
Fig. 9
figure 9

Effective Dirac masses of baryons as functions of normalized by saturation density baryonic density. The temperature is fixed at \(T=0.1\) MeV for \(\beta \)-equilibrated, neutrino-free matter. Note that the isospin multiplets have the same effective mass in the present model of CDF

Full size image

Returning to the chemical potentials, we show in Figs. 7 and 8 their effective values minus the respective effective masses for \(\varDelta \)-admixed hypernuclear matter in the cases of constant temperature and fixed entropy per baryon, respectively. The emergence of the isospin degeneracy point is seen in finite-temperature neutrino-trapped matter calculations in each isospin multiplet for all lepton number combinations considered. To the left from this point \(\mu _Q\le 0\) which according to Eqs. (39)–(42) implies that baryons with smaller charges are more abundant. To the right of this point \(\mu _Q\ge 0\), and the ordering of baryon fractions within each multiplet is reversed, as seen in Fig. 7. The same feature is observed also in the case of constant entropy (rather than constant temperature) case, see Refs. [43, 45].

Consider next the effective masses of the baryons, which are shown in Fig. 9 for \(\beta \)-equilibrium matter at fixed temperature \(T=0.1\) MeV as functions of density. The temperature dependence of the effective masses of baryons is very weak. The effective masses of isospin multiplets (n, p), \(\varSigma ^{0,\pm }\), \(\varXi ^{0,-}\) and \(\varDelta ^{0,-}\) are degenerate, which have important implications for degeneracies in chemical potentials.

Fig. 10
figure 10

Dependence of temperature on density for fixed \(S/A = 1\) in the cases of neutrino-transparent matter (\(\mu _{\nu } =0\)) with different compositions labeled as N, NY, and \(NY\varDelta \). The cases of neutrino-trapped matter with \(Y_e=Y_{\mu } = 0.1\) and \(Y_e=0.4, Y_{\mu }=0\) are shown shown by dash-dotted and dash-double-dotted curves

Full size image

The density dependence of the temperature for fixed \(S/A=1\) for the cases of \(\mu _\nu =0\) and neutrino-trapped regime with \(Y_e=Y_{\mu } = 0.1\) and \(Y_e=0.4, Y_{\mu }=0\) are shown in Fig. 10. The neutrino trapping occurs for temperatures (roughly) \(T\ge 5\) MeV [20,21,22]. It is seen that the temperature quickly rises above this limit as the density increases. This implies that most of the volume of an isentropic star with \(S/A=1\) will be in the neutrino-trapped regime. We, therefore, conclude that the upper panels in Figs. 4 and 7 do not refer to a realistic situation to be encountered in BNS or SN contexts.

4 Cold and hot, isentropic compact stars

Next, it is useful to use hot and cold EoS of \(\varDelta \)-admixed hyperonic matter presented in the previous sections to compute the spherical symmetrical static configurations of compact stars. The case of cold EoS can be confronted with the current astrophysical constraints. Such analysis in the case of \(\varDelta \)-admixed hyperonic matter can be found in Refs. [31, 32, 41, 43, 45]. The astrophysical constraints against which our EoS will be tested are as follows:

Fig. 11
figure 11

Gravitational mass versus radius for non-rotating spherically-symmetric stars. Three sequences are shown for \(\beta \)-equilibrated, neutrino-transparent stars with nucleonic (N), hypernuclear (NY) and \(\varDelta \)-admixed hypernuclear (\(NY \varDelta \)) composition for \(T=0.1\) MeV. In addition, we show sequences of fixed \(S/A=1\) neutrino-trapped, isentropic stars composed of \(NY \varDelta \) matter in two cases of constant lepton fractions \(Y_{Le}=Y_{L\mu }=0.1\) and \(Y_{Le}=0.4,\,Y_{L\mu }=0\). The ellipses show 90% CI regions for PSR J0030+0451, PSR J0740+6620 and gravitational wave event GW170817 (see the text for details)

Full size image
  1. (a)

    PSR J0030+0451 is the first object with highly accurate inferred mass and radius from X-ray observations [70, 71]. Both the mass and the radius were inferred by fitting to the data obtained by the NICER X-ray observatory. The modeling of the soft X-ray pulses emitted by hot spots of a rotating star leads to two (independent) predictions (\(68\%\) credible interval (CI)) \(M=1.34^{+0.15}_{-0.16} M_{\odot }\), \(R= 12.71^{+1.14}_{-1.19}\) km [70] and \(M = 1.44^{+0.15}_{-0.14}\, M_{\odot }\), \(R = 13.02^{+1.24}_{^-1.06}\) km [71].

  2. (b)

    PSR J0740+6620 is the second pulsar with a measured mass and radius again via observations and analysis of the NICER X-ray observatory data. Its radius estimates are \(12.39^{+1.30}_{-0.98}\) [72] and \(13.71^{+2.61}_{-1.50}\) km [73] and the mass estimates are \(2.07^{+0.07}_{-0.07}\,M_{\odot }\) and \(2.08^{+0.09}_{-0.09}\,M_{\odot }\) (\(68\%\) CI). Note that the mass of this pulsar was independently measured to be \(2.08^{+0.07}_{-0.07}\,M_\odot \) using the effect of Shapiro delay [74].

  3. (c)

    GW170817 is the first multimessenger gravitational wave event which among various observables in the gravitational and electromagnetic spectrum allowed an inference of the tidal deformability of a star involved by the LIGO-Virgo Collaboration [75]. The current upper limit of the (dimensionless) tidal deformability is \({\tilde{\varLambda }} \le 580\).

Table 3 Properties of non-rotating spherically symmetric cold \(\beta \)-equilibrated, neutrino-transparent, compact stars based on the EoS models considered in this work. The first three columns show the maximum gravitational mass (\(M_{G,\mathrm{max}}\)), and the corresponding radius \((R_\mathrm{max})\) and central baryon number density (\(n_{c,\mathrm{max}}\)) for the (cold) EoS with N, NY and \(NY\varDelta \) compositions. The remaining columns show the threshold densities of heavy baryon defined here by the condition \(n_{b,d}/n_\mathrm{sat}\ge 10^{-3}\). The radius of a canonical mass \(1.4M_{\odot }\) star for all cold EoS considered is \(R_{1.4M_{\odot }} = 13.13\) km and its (dimensionless) tidal deformability is \({\tilde{ \varLambda }}_{1.4M_{\odot }} = 707.3\)
Full size table

The 90% CI ellipses for the constraints in the M-R diagram are shown in Fig. 11. The static solutions of Einstein’s equations in spherical symmetry which are represented by the Tolman-Oppenheimer-Volkoff equations [76] were solved for input cold and finite-temperature isentropic EoS and the results are shown in Fig. 11. In the case of cold EoS we consider the three cases of purely nucleonic (N), hyperonic (YN) and \(\varDelta \)-resonance admixed hypernuclear matter (\(YN\varDelta \)). Our nucleonic model has a maximum gravitational mass of \(M_\mathrm{max}=2.48M_{\odot }\) and a radius of \(R = 12.1\) km. For cold YN and \(YN\varDelta \) matter the softening of the EoS results in a reduction of the maximum mass; for the \(YN\varDelta \) model \(M_\mathrm{max}=2.0M_{\odot }\) with the corresponding value of the radius \(R_\mathrm{max} = 11.6\) km. It is seen that the M-R values of the models are compatible with the NICER inferences for canonical (i.e. \(M\sim 1.4M_{\odot }\)) and massive (i.e. \(M\sim 2M_{\odot }\)) compact stars. Note that the radii of all models are the same as in the case of a canonical mass star, as the onsets of the hyperons and \(\varDelta \)-resonances are at densities that are beyond the central density of such a star. It is clearly seen that the bifurcation point of a heavy-baryon star from a purely nucleonic one lies at a higher mass \(\sim 1.55M_{\odot }\). The results for the radius are compatible with the GW170817, but lie at the upper edge of the allowed radius. Also, the (dimensionless) tidal deformability of 1.4\(M_{\odot }\) star turns out to be \({\tilde{\varLambda }}_{1.4M_{\odot }} = 707.3\), which is larger than the upper limit \({{\tilde{\varLambda }}} \le 580\) given above. However, note that larger values of \(\varDelta \)-resonance-mesons couplings, which imply an early onset of these particles, can lead to a reduction of the radius of the star by about \(15\%\) and a reduction in tidal deformability; for a discussion of this point see Ref. [32]. An alternative is a phase transition to quark matter phase at low densities [33].

The case of hot, isentropic stars is relevant for transient states of proto-neutron stars and BNS merger remnants. Fixing the value of the entropy per particle and the lepton fraction at a constant value throughout the entire star is clearly an approximation. These quantities are known to have variations along with the radial profile of the star. Nevertheless, such an assumption allows one to study (in a first approximation) the effects of trapped neutrinos and temperature on the configurations of stars. The sequences of isentropic stars composed of \(YN\varDelta \) matter are shown in Fig. 11. It is seen that in the trapped neutrino regime the maximum masses of the stars are shifted towards larger values. At the same time, the radii of the stars can be significantly larger than that of their cold counterparts. For example, for a massive \(M\sim 2M_{\odot }\) star this difference is about 2 km for \(Y_{Le}=0.4\).

5 Conclusions

We have extended our recent study of hypernuclear matter at finite temperature in the neutrino-free and neutrino-trapped regimes to include the non-strange \(\varDelta \)-resonances. Our work is based on the extension of the CDF formalism and numerical code of Ref. [30] with the extensions in the hypernuclear sector described previously in Ref. [29]. The zero-temperature counterpart of this CDF and its astrophysical consequences were already discussed extensively by Li et al. [31,32,33]. We have exposed two physical cases by adjusting the lepton fractions of electrons and \(\mu \)-ons to the conditions of BNS mergers and SN.

Firstly, we recovered the well-known features of the EoS that appear when hyperons and \(\varDelta \)-resonances are included in the composition of matter. The hyperonization softens the EoS compared to the nucleonic case. Secondly, the inclusion of \(\varDelta \)’s softens the EoS at intermediate densities and stiffens it at high densities compared to hypernuclear case (see Fig. 1).

Our conclusions can be summarized as follows:

  • \({\varDelta }\)-resonance thresholds The zero-temperature abrupt increase in the heavy baryon abundances, in particular \(\varDelta \)’s, at a given threshold is replaced by a much flatter increase at high temperatures with the low-density tail extending up to the lowest density value considered \(n = 0.5 n_\mathrm{sat}\), see Figs. 3, 5 and 6. This clearly indicates that at finite temperatures the \(\varDelta \)-resonances (in analogy to hyperons) extend further into the dilute gas regime of clustered nuclear matter.

  • Intermediate and large densities The dominant \(\varDelta \)-resonance is \(\varDelta ^-\) which has a threshold density close to that of \(\varLambda \) for the moderate values of \(\varDelta \)-couplings assumed in the present study. We find that \(\varDelta ^{-}\) is the dominant charged heavy baryon at intermediate densities (up to \(\sim 4n_\mathrm{sat}\)) and becomes sub-dominant (but not significantly) to \(\varXi ^{-}\) at higher densities. The only other resonances are \(\varDelta ^0\)s, which appear at very high densities in cold, \(\beta \)-equilibrated matter, but their fractions are comparable to \(\varDelta ^{-}\) if the matter is sufficiently hot, see Fig. 3. The effect of the \(\varDelta \)’s on the stiffening of the EoS of the hypernuclear matter at large densities, as seen in Figs.  1 and 2, results in the increase of maximum masses of compact stars with \(\varDelta \)’s compared to their hypernuclear counterparts, see Fig. 11.

  • Neutrino species In the two considered astrophysical scenarios – BNS mergers and SNs – the neutrino populations differ considerably. In the BNS merger scenario, the fractions of electron and \(\mu \)-on neutrinos are typically a few percent. The condition \(Y_{L,e}= Y_{L,\mu } = 0.1\) enforces almost equal numbers of electrons and \(\mu \)-ons. In SN scenario the condition \(Y_{L,\mu } = 0\) suppresses the \(\mu \)-ons leaving a negligible \(\mu \)-on fraction in the finite temperature neutrino-trapped regime due to a small amount of \(\mu \)-on antineutrinos. The matter is then dominated by electron neutrinos with a fraction \(\sim 10\%\). The \(\mu \)-on antineutrino fraction is negligible. The presence of \(\varDelta \) resonances will provide an additional source of interaction with neutrinos via direct Urca processes, e. g., \(\varDelta ^-\rightarrow \varLambda +e^- +{{\bar{\nu }}}\). Consequently, the neutrino opacities may be affected by their very efficient direct-Urca coupling to \(\varDelta \)’s (even in the absence of hyperons). Furthermore, the bulk viscous damping of density oscillations in BNS mergers can be affected by the \(\varDelta \)’s via non-equilibrium Urca processes involving \(\varDelta \)’s.

  • Stellar configurations The stellar sequences based on the cold EoS of \(NY\varDelta \) matter are consistent with the astrophysical constraints set by the analysis of the NICER data on the masses and radii of PSR J0030+0451 and PSR J0740+6620. They are also consistent with the radius determination in the gravitational wave event GW170817, although the radii are at the upper edge of 90% CI region. Hot isentropic sequences can support larger masses than their cold counterparts. They are also more extended than the cold ones, the difference in the radii ranging up to a few km depending on the values of the entropy and lepton fraction and the mass range considered.