1 Introduction

With the Large Hadron Collider entering its 13 TeV run phase, new phenomena will be investigated in previously inaccessible regions of phase space. Accurate calculations for background processes in the Standard Model (SM) thus have to be reliable when singling out phase space regions by applying intricate analysis techniques to the collider data. General Purpose Event Generators [1] that are combined with multi-parton fixed-order cross section calculations provide the most flexible assessments of SM backgrounds. The problems to address in these methods are to ensure that no momentum configurations are over- or under-counted, and that the perturbative accuracy of the fixed-order matrix-element calculation (ME) and parton-shower (PS) resummation merge without either being undermined. These obstacles were tackled in matching [2–14] and merging [15–25] methods, with next-to-next-to-leading order matching [26–31] and next-to-leading order merging [32–37] currently providing the most precise predictions.

It is crucial to note that these state-of-the art methods inherit both strengths and weaknesses from less precise methods, in particular from choices made in leading-order merging. These choices stem from uncontrolled or missing ingredients in the parton shower. More comprehensive parton showers will lead to less freedom and more precise predictions. This is also true for electroweak shower resummation [38, 39], which are shown to be important for the accurate modelling of jets at large transverse momenta. In this article, we discuss how to combine multi-jet calculations with QCD and weak parton showers in the context of W-boson production, which highlights that

  1. (a)

    processes that are disjoint at lowest-order need to be combined, yielding a “merging of mergings”, (e.g. Drell–Yan W-boson production and QCD \(2\rightarrow 2\) production both contribute to \({\mathrm p}{\mathrm p}\rightarrow \mathrm {jj{ W}}\)),

  2. (b)

    weak parton showers are necessary to describe weak bosons close to or inside jets, and to disentangle how a “merging of mergings” should proceed,

  3. (c)

    merging is necessary for an inclusive prediction, and to set starting conditions for the weak showers.

Note that if these points are not satisfactorily answered within a leading-order merging method, then the uncertainty due to the resulting choices can only partially be remedied by a more precise (e.g. NLO) merging method. Thus, to start with the simplest merging approach, we improve the CKKW-L leading-order merging prescription [24] in the Pythia  8 event generator [40] to address these issues. The improvements should then carry over when merging NLO calculations. We present results for both LHC and at a potential future 100 TeV proton collider.

In Sect. 2 we review the weak parton showers in Pythia, followed by a brief introduction to CKKW-L merging in Sect. 3. In these sections, we also highlight choices that have been made in both approaches. A merging of QCD and weak showers with multi-parton cross sections, which resolves these choices, is presented in Sect. 4. Validations of the implementation are presented in Sect. 5. We then move on to discuss results for LHC and a future 100 TeV collider in Sect. 6 and conclude in Sect. 7.

2 Weak parton-shower formalism

Scattering processes containing massless partons with very different transverse momenta exhibit logarithmic divergences that limit the applicability of perturbative calculations. Fortunately, it is possible to derive factorisation theorems and sum logarithmic terms to all orders in perturbation theory. This leads to a reliable, finite calculation with an extended range of validity. Leading-logarithmic contributions can be summed in a process- and observable-independent fashion by using PS programs.Footnote 1

Large scale hierarchies involving massless particles still lead to logarithmic enhancements that should, for a stable prediction, be summed to all orders in perturbation theory. The resummation of logarithmic electroweak enhancements becomes important when processes contain low transverse-momentum weak bosons and jets with transverse momentum much larger than the boson mass. It has been shown in fixed-order calculations that weak Sudakov corrections can indeed become relevant at LHC energies [43–48] and especially when considering potential future proton colliders [49]. Including all-order electroweak effects in flexible, commonly used programs facilitates realistic studies of these effects.

General purpose event generators include an approximation of all-order effects with the help of parton showers. Parton showers produce all-order (QCD or QED) results by resumming real-emission corrections into exponentiated no-emission probabilities. These no-emission probabilities are related to Sudakov form factors by application of DGLAP evolution [50–52]. Electroweak resummation is a natural extension to the QCD and QED showering. EW showers have, due to the dominance of QCD effects, only recently been investigated in event generators [38, 39]. The EW shower allows for an equal treatment of QCD, QED and weak radiation and naturally includes competition between emissions of gluons, photons or weak gauge bosons. In this section a short summary of the major issues are given, with a specific focus on aspects relevant for merging parton showers with matrix-element calculations.

There are two major differences between \(\gamma \) emission and \({W}^\pm \) emissions. First of all, the emission of a \({W}^\pm \) boson changes the flavour of the radiator, and second, the \({W}^\pm \) is massive. Flavour changes are handled according to the CKM matrix, with additional care needed for the evaluation of PDFs. A phase space mapping for emissions of massive particles was previously given in the context of a Hidden-Valley PS model [53], and the weak showers can directly reuse the corresponding structures in Pythia.

The massive phase space does not include the collinear and soft divergences, since the weak boson has to carry at least enough energy to be on its mass shell. The introduction of mass should also affect the PS splitting kernels. The normal massless collinear approximation in the PS is therefore not sensible for radiation of weak gauge bosons. Thus, a complicated assessment of mass effects seems necessary. However, this can be avoided if the full, massive matrix elements are used as splitting kernels. The weak parton shower in Pythia thus heavily relies on ME corrections [54–57]. All emissions are corrected with a fully massive \(2\rightarrow 3\) matrix element. The corrections vary depending on the type of process—an s-channel process will for example carry a different correction factor than a t-channel process. Different corrections are mandatory in order to obtain a reasonable agreement between the PS prediction and gauge-invariant subsets of the full ME calculations (including all interferences). Note, however, that the weak parton shower only recovers the \({\mathrm p}{\mathrm p}\rightarrow \mathrm {jj{ V}}\) matrix elements (where \({V}={W},{Z}\)). The weak shower further omits interference terms between different fermion lines. It is further only possible to choose the correct ME correction if the underlying type of process is known. Therefore the weak shower resorts to (artificial) choices if the evolution is not started from a \(2\rightarrow 1\) or a \(2\rightarrow 2\) process. As will be described in detail later, this problem is resolved through the introduction of PS histories.

Fig. 1
figure 1

Two examples of possible histories for a \({\mathrm p}{\mathrm p}\rightarrow {\mathrm g}{\mathrm g}{W}\) process. The two histories have different hard processes, either as a Drell–Yan process (left) or as a \(2\rightarrow 2\) QCD process (right)

Full size image

The introduction of weak parton showers leads to potential double counting in an inclusive event generation. If the desired process is dijet + \({W}^\pm \) it can be interpreted in two ways: either as a Drell–Yan-like \({W}^\pm \)-boson process followed by two QCD emissions, or as a \(2 \rightarrow 2\) QCD process radiating a \({W}^\pm \)-boson. Allowing these two possibilities to separately cover the full phase space results in double counting. Disallowing QCD emissions above the weak boson mass for Drell–Yan-like processes would ameliorate this double counting, yet result in an unconvincing data description of the pure PS result. Instead, a strategy using the \(k_\perp \) jet algorithm was adopted. If the jet separation between a \({W}^\pm \)-boson and a parton proves the minimal scale, then the events are removed from the Drell–Yan-like sample. Conversely, dijet states whose minimal jet separation is between partons are removed from the \(2\rightarrow 2\) QCD event sample. This artificial separation will be corrected upon merging weak and QCD showers with multi-parton matrix elements.

The weak coupling to a fermion depends on its spin. In the weak shower this is handled in a simplistic way, by assigning each fermion line a randomly chosen spin. The spin is then kept fixed through the whole PS. For a single weak emission it corresponds to using averaged spin results, but it introduces a slight enhancement for multiple weak gauge bosons to be emitted from the same fermion line.

The overall performance of the weak PS is surprisingly good. It is capable of describing a large number of measurements that earlier has only been possible to describe with merged samples. Notable the rate of \({W}+n\) jets could be described up to the highest measured (\(n=7\)) bin without using more than \({W}+2\) jet matrix elements. But the PS still does not provide a perfect description, and especially the description of angular distributions (e.g. \(\Delta \phi \) between leading and second leading jet) is poor. Merging is expected to significantly improve the results.

3 Merging

Many interesting multi-jet observables at a hadron collider are difficult to predict with calculations containing a fixed (or limited) number of outgoing partons in fixed-order perturbation theory. Parton showers are then necessary to spread the fixed-order calculation over a broader multi-jet phase space. Standard examples are jet rates, where fixed-order calculations become prohibitively expensive, or azimuthal separations between (reconstructed) heavy bosons and a hardest jet, which are naturally sensitive to momentum configurations with a variable number of hard jets [58]. To describe such genuine multi-jet observables, many multi-parton calculations need to be combined into an inclusive sample describing configurations with \(n \le N\) jets with fixed-order accuracy, where N should be as large as possible.

Matrix-element merging is a process-independent method that invokes the PS to facilitate this combination. The main steps in a merging procedure are:Footnote 2

  • choose a “history” of intermediate states through which a pre-calculated input multi-parton state has evolved from a lowest-multiplicity state (see e.g. Fig. 1),

  • use this history to make the state exclusive (i.e. additive) by calculating and applying the necessary no-emission probabilities (which are intimately linked to Sudakov form factors),

  • reweight the input state with additional factors (e.g. \(\alpha _{\mathrm {s}}(p_\perp ^2)\), PDF weights) that would have been applied by the PS, had it produced the input state by following the history of intermediate states (this is necessary to not impair the accuracy of the PS, or the event generator prediction more generally),

  • combine the result of all such post-processed input states for all parton multiplicities.

This immediately highlights that omissions in the shower lead to uncertainties in the merging prescription, which are commonly disposed of by judicious selection. Since we are interested in combining with weak parton showers, let us look at producing an inclusive sample of W-boson + N jets through CKKW-L merging, and assume \(N\le 3\) for simplicity.

In this example, the lowest-multiplicity state (W-boson production) should be used to describe very inclusive observables like e.g. the W-boson rapidity. The interface to the PS is straightforward since no partons are present initially—we only have to ensure that the PS does not produce hard jets, as such configurations should be covered by higher-multiplicity matrix elements. This leads to the introduction of a “merging scale” with arbitrary functional definition and value \(t_{\text {{{MS}}}}\). States that are classified as “below” \(t_{\text {{{MS}}}}\) will be produced by showering, while states “above” \(t_{\text {{{MS}}}}\) are governed by higher-order matrix elements. Any functional form of the merging scale should be allowed, as long as the function acts as a regularising cut on the fixed-order input calculations. Commonly used merging scale definitions are the minimum of all jet separations in the \(k_T\) algorithm [59], or the minimum of parton-shower evolution variables measured on the state. Merging methods have to ensure that the dependence of exclusive and inclusive observables on the merging scale are small. For inclusive jet observables, the merging scale dependence can be removed to reasonable accuracy.Footnote 3

Coming back to our example, the next calculation to be added is W-boson in association with one parton. As outlined above, a PS history has to be chosen for such states. These histories are well defined if the QCD parton shower can (at least in principle) cover the full single-emission phase space. In order to pick all histories in the proportion in which the PS would have produced the output state, the probability for a specific history is given by the product of splitting functions characterising each intermediate evolution step. This reduces the merging scale dependence of exclusive observables. Upon choosing a history, it is simple to reweight with no-QCD-emission probabilities (i.e. QCD Sudakov factors) and to account for the dynamic renormalisation and factorisation scales used in the PS evolution. Using the shower directly to produce the no-QCD-emission probabilities reduces the \(t_{\text {{{MS}}}}\) dependence. The starting conditions for PS emissions off the W + parton state are uniquely determined by the chosen history.

Including a W-boson in association with two partons uncovers further uncertainties, because no ordered PS will cover the full double-emission phase space. Thus, some states accessible to the fixed-order calculation will not yield any ordered PS history.Footnote 4 The reweighting of such a state is ambiguous due to ambiguous renormalisation and factorisation scale choices. Although this ambiguity has very small numerical impact for inclusive observables, it can have an uncomfortably large impact on more exclusive observables [24]. Furthermore, some flavour configurations are inaccessible to a QCD parton shower, meaning that no PS history can be reconstructed. Ambiguities in the treatment of such genuine non-shower (commonly called incomplete) states have vanishingly small impact on inclusive observables and yield only very minor variations of exclusive observables [24]. A precise method should, however, avoid having to make choices. The PS starting conditions are fixed once a history is chosen.

No new problems occur for higher-multiplicity processes. The issues related to unordered states outlined in the last paragraph can be aggravated in more exclusive observables, however, as the PS phase space coverage will be worse for higher multiplicities. It is still important to remember that merging offers a consistent way to set the PS starting conditions for multi-parton states—which is not the case in plain (QCD or EW) parton showers.

4 Weak showers and the merging of merged calculations

In the previous sections, we have seen that the construction of weak parton showers as well as multi-jet merging involves compromises. Summarising the most severe choices, we have addressed the following:

  • Weak showers are currently limited to dijet processes, while inclusive predictions require an ambiguous mixing with Drell–Yan-like configurations.

  • Matrix-element merging is ambiguous starting at W-boson + two partons, leading to uncomfortable compromises related to unordered states and incomplete histories.

The combination of weak parton showers and multi-jet merging remedies these deficiencies and should provide a more physical picture of multi-parton states. This will further mean that matrix element merging, which is usually regarded to realise corrections to one underlying process, is generalised to incorporate many underlying processes that mix at higher perturbative orders.

To explain the reasoning behind our new merging scheme, let us look at states including one weak boson and two final state partons for illustration. If the outgoing partons have very different transverse momenta, and if the \(p_\perp \) of the W-boson is thus comparable to the \(p_\perp \) of the harder parton, then it is natural to associate the partons with DGLAP evolution of the incoming beams. For a reliable perturbative prediction, a fixed-order calculation with large scale separation should then be supplemented with no-emission probabilities resumming unresolved QCD emissions. This W-boson + two parton state is an example for corrections to W-boson production.

If the state instead contains two partons with comparable and large \(p_\perp \) and a W-boson with small transverse momentum, it is prudent to resum large logarithms associated with the difference between the parton and W-boson transverse momenta. Then Sudakov form factors resumming the dominant weak virtual corrections need to be supplemented. Hence, the two parton + W-boson state is an example for corrections to dijet production. This correction can be approximated by weak parton showers.

Thus we find that, when going to \(\mathcal {O}\left( \alpha _{\mathrm {s}}^2\alpha _{\mathrm {w}}\right) \), it is not possible to disentangle QCD corrections to W-boson production and weak corrections to dijet production.Footnote 5 Beyond \(\mathcal {O}\left( \alpha _{\mathrm {s}}^2\alpha _{\mathrm {w}}\right) \), W-boson production and dijet production share a single evolution, so that only a combined treatment of these two processes (which are disjoint at lowest multiplicity) will yield a satisfactory prediction. This means that it is necessary to combine multi-jet merged corrections to W-boson production with multi-jet merged corrections for dijet production. These corrections then mix by virtue of weak showers.Footnote 6 This in a sense constitutes a “merging of mergings”.

Summarising, we have argued that a clean description of W + jets states necessitates a combination of QCD no-emission probability-reweighted corrections to W-boson production and weak no-emission probability-reweighted dijet production. Within this framework, it is possible to address and amend the choices in weak showering and merging that we have previously highlighted.

The first feature of the combined merging is the possibility to recombine W-boson radiation with other partons. As a natural consequence of this the lowest-multiplicity process is, as desired, no longer forced to be a colour-singlet Drell–Yan-like state if the input state contained W-bosons. The new clustering is illustrated in Fig. 1, where two very different possible histories are shown.Footnote 7 The decision which of these histories to choose should again ensure that the merging scale variation of exclusive observables is small. This means we should attempt to answer the question how would the (QCD+EW) parton shower have produced this state? The answer will minimise merging artefacts at the boundary between PS and fixed-order ME regions. With the parton shower probabilistically sampling all ways to evolve into a particular state, we again decide to pick histories with different underlying process probabilistically. For instance the two histories shown in Fig. 1 would have the following probabilities:

$$\begin{aligned}&\mathcal {P}_\text {left path} = \frac{ \mathcal {P}_{\text { QCD FSR}}^{(1)}\, \mathcal {P}_{\text { QCD ISR}}^{(2)}\, \mathcal {P}_{\text {weak { W} production}}^{(3)} }{{\sum \limits _{\text { all paths}}}~\,\, \prod \limits _{\begin{array}{c} \text { nodes j}\\ \text { in path i} \end{array}}\mathcal {P}^{(j)}_{\text { type}} }\nonumber \\&\mathcal {P}_\text {right path} = \frac{ \mathcal {P}_{\text {weak { ISR}}}^{(1)}\, \mathcal {P}_{\text {{ QCD} jet production}}^{(2)} }{{\sum \limits _{\text { all paths { i}}}}~\,\, \prod \limits _{\begin{array}{c} \text { nodes j}\\ \text { in path i} \end{array}}\mathcal {P}^{(j)}_{\text { type}} } \end{aligned}$$
(4.1)

where \(\mathcal {P}^{(j)}_{\text { type}}\) indicates probability associated to the jth clustering in the path, with “type” indicating what type of transition occurred.

The coupling between fermion and weak gauge bosons depends on the spin of the fermion. To capture this effect in the merging, histories for all possible spin assignments for fermions are considered. One improvement of spin treatment could be to use fully spin dependent input matrix elements. However, in order for this to be consistent, improvements in the spin handling within the PS would be required.

An additional constraint on the probabilities comes from insisting on \(p_\perp \)-ordered histories: clusterings of states with lower multiplicity have to have a larger \(p_\perp \) than clusterings of higher-multiplicity states. For instance, if the event consists of two hard jets and a soft W-boson, it is very unlikely to cluster it to a Drell–Yan hard process and obtain a \(p_\perp \)-ordered clustering sequence. Within a combined merging of dijet and W-boson production, the dominant scale hierarchies are correctly identified. Hence, the amount of unordered states is drastically reduced.

The necessity for weak clusterings and the weak showering effects introduces two new weights to the merging procedure: an \(\alpha _{\mathrm {w}}\) weight and the weak no-emission probability. The \(\alpha _{\mathrm {w}}\) weight is required because a dynamical scale setting is also assumed when evaluating \(\alpha _{\mathrm {w}}\).

The weak no-emission probability can be generated by trial showering. To treat QCD-like and electroweak emissions on equal footing, we include W-bosons in the merging scale definition, meaning that “soft” W-bosons will be generated by the PS, while “hard” W-bosons are generated with the help of a fixed-order matrix-element generator. This also means that in non-highest multiplicity states, any first PS response producing states with a hard W-boson (or, of course, hard QCD emissions) will lead to an event rejection. The impact of the weak no-emission probabilities can, due to the large W-boson mass and the small value of \(\alpha _{\mathrm {w}}\), be minor for many observables. However, for observables with large hierarchies between the scales associated to QCD emissions and scales of EW effects, larger effects are anticipated. An idealised observable highlighting weak resummation effects would be very inclusive over multi-parton states and fully exclusive for weak emissions (i.e. all weak bosons can be resolved). We will return to this in the result section, where the effect of the weak no-emission probabilities at a future 100 TeV collider is considered.

Fig. 2
figure 2

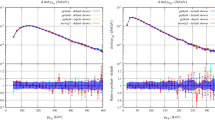
The figure shows the cross section for \({\mathrm u}\overline{\mathrm {u}}\rightarrow {\mathrm s}\overline{\mathrm {c}}{W}^+/\overline{\mathrm {s}}{\mathrm c}{W}^-\) as a function of respectively \(p_\perp \) of the \({W}^\pm \) (left) and \(p_\perp \) of leading jet (right). The cross section is calculated in two ways: Either through merging of \(2\rightarrow 2\) and \(2\rightarrow 3\) MEs, or as a \(2\rightarrow 2\) ME with weak shower

Full size image

While this new method leads to a more physical description of multi-parton states in association with W-bosons, it should be noted that the formal accuracy of neither QCD resummation nor fixed-order calculation is improved. However, this merging for the first time supplements arbitrary multi-jet states with weak resummation effects within a matrix-element-merged prediction. Thus, the electroweak all-order structure improves over previous results.

To round off this section, remember that merging methods allow the combination of different jet multiplicities. A combination is only possible because the inclusive fixed-order input states (describing N or more particles) are converted into exclusive calculations (describing exactly N resolved particles) by supplementing no-emission probabilities which resum logarithmic enhancements due to large scale hierarchies. It would thus at first glance seem that a state containing two soft QCD emissions at vastly different scales and a W-boson with transverse momentum commensurate with the larger jet scale is in some sense “more exclusive” than a dijet state with jets of similar \(p_\perp \) and a soft W-boson. In the former case two scale differences require resummation, while in the latter, only one hierarchy has to be considered. However, note that the dijet cross section is not well defined unless jet cuts are applied. These cuts make the cross section exclusive in the sense that at least two jets above a resolution scale are required. That the cross section contains exactly the desired number of jets (and no further resolved jets) is then again achieved by reweighting with no-emission probabilities. As an aside, note that multi-parton interaction (MPI) models [62–64] are derived from the condition that the dijet cross section needs to be regularised, and that this regularisation can be achieved in the same way that no-emission probabilities regularise parton-shower real-emission cross sections. The no-MPI-probabilities motivated by this argument should be correctly included in any merging scheme to ensure that the input states do not overlap with MPI, adding yet another layer of exclusivity. Our implementation in Pythia includes a consistent handling of interleaved MPI [65] as outlined in [24].

5 Validation

When developing an improved merging scheme, detailed tests validating the method and implementation are necessary. We have tested that the new implementation recovers the correct scales, probabilities and underlying states by directly comparing a reconstructed PS evolution history against the evolution as picked by the parton shower. Such technical comparisons are of course not particularly enlightening for the reader, so that below, we will focus on two hopefully convincing tests.

The weak PS relies on ME corrections for the process \(pp\rightarrow \mathrm {jj}{W}\). As such, an excellent agreement between merged and default weak PS results for such \(2\rightarrow 3\) processes is expected. We illustrate the agreement for the process \({\mathrm u}\overline{\mathrm {u}}\rightarrow {\mathrm s}\overline{\mathrm {c}}{W}^+/\overline{\mathrm {s}}{\mathrm c}{W}^-\), only including the \(\mathcal {O}\left( \alpha _s^2\alpha _{\mathrm {w}}\right) \) contributions as fixed-order inputs. This is an s-channel process, where only final state radiation is possible (assuming a diagonal CKM matrix). \(\alpha _{\mathrm {em}}\) was set to 0.1 to increase the statistics and the merging scale was 1000 GeV. The merged curve and the weak PS agree nicely over the whole kinematic range, as illustrated by both the W-boson \(p_\perp \) and the leading jet \(p_\perp \) distributions (Fig. 2). The merged result thus correctly applies all factors present in the weak PS resummation.

Fig. 3
figure 3

The figure shows the competition for either clustering a \({\mathrm p}{\mathrm p}\rightarrow \mathrm {jj}{W}\) process as a Drell–Yan process or a \(2\rightarrow 2\) QCD process. The probability is shown as a function of the fraction between either the second leading jet \(p_\perp \) divided by the leading jet \(p_\perp \) (left) or the fraction between the W \(p_\perp \) and the leading jet \(p_\perp \) (right). The minimum \(p_\perp \) for any jet is 5 GeV and the centre-of-mass energy is 7 TeV. The vertical lines indicate the statistical MC uncertainty and smooth curves have been added as a visual help

Full size image

To further validate the implementation, Fig. 3 shows the probability with which states are identified as corrections to a Drell–Yan-like or a \(2\rightarrow 2\) QCD hard scattering. Each path is expected to dominate in a specific region of phase-space. If the scales associated to jet production are low and exhibit a hierarchy, then a Drell–Yan-like underlying process should be expected. States with two hard jets at comparable scales should yield a \(2\rightarrow 2\) QCD underlying process. We investigate this expectation on the process \({\mathrm p}{\mathrm p}\rightarrow \mathrm {jjW}\), using different \(p_\perp \) cuts on the leading jet (Fig. 3). As expected, the lower the \(p_\perp ^{\text {leading jet}}\) cut is, the more likely states will lead to a Drell–Yan-like underlying process. Conversely, for a fixed leading jet \(p_\perp \), softer \({W}\) \(p_\perp \)’s and more back-to-back jet systems yield predominantly QCD \(2\rightarrow 2\) scatterings as underlying process.

6 Results

This section presents predictions of merging QCD+EW showers with multi-parton matrix elements. We begin by comparing with studies from both ATLAS and CMS and follow up by a study of the weak no-emission probability at 100 TeV.

6.1 Comparison with LHC data

In this section, we contrast results of the default CKKW-L merged prescription in Pythia and the new QCD+EW merging with LHC data.

To compare against LHC data, we merge five tree-level event samples for W-boson \(+\le 4\) jets, generated with MadGraph5\(\_\)aMC@NLO [14] using the CTEQ6m PDF set [68]. The merging scale was defined as the minimum of all Pythia transverse-momentum separations between partons, while no cut was applied to the W-boson. This means that the phase space for real weak parton showers is vanishing, thus making the inclusion of pure-QCD samples unnecessary.Footnote 8 Thus, this setup can be used in particular to check the impact of the “weak clustering” outlined in Sect. 4. The Monash tune [69] was used, but with \(\alpha _{\mathrm {s}}(M_Z)\) lowered to \(\alpha _{\mathrm {s}}(M_Z) = 0.118\).

Our results only contain tree-level normalisation, and an overall rescaling due to virtual corrections is missing. The results are therefore not expected to match the normalisation of the data. We choose to not rescale our results since we believe that presenting unnormalised experimental data adds additional information and should be encouraged. We do not want to undermine such efforts by rescaling tree-level results. The differential shape of the data should, however, be described by a tree-level merged prediction (i.e. the ratio between the data and the prediction should be flat for all distributions). All the data comparisons are done using the Rivet framework [70].

In the following, we will refer to the default CKKW-L implementation in Pythia as “default scheme”, while the new QCD+EW merging will be called “EW-improved” scheme. The EW-improved results are shown for three different merging scales, \(t_{\text {{{MS}}}}= 15\) GeV, \(t_{\text {{{MS}}}}= 25\) GeV and \(t_{\text {{{MS}}}}= 35\) GeV. The uncertainty due to this merging scale variation is very small for all observables we have investigated, and is nearly indistinguishable from statistical fluctuations for the observables below. The very small variation is a result of the PS both correctly recovering the \({W}+1\) j matrix element as well as hard (dijet-like) parts of the \({W}+2\) j matrix elements, thus pushing the merging scale dependence to yet higher orders.

Fig. 4
figure 4

Pythia predictions in comparison to ATLAS data [66] (left) and CMS data [67] (right) for W + jets as a function inclusive jet multiplicity. The yellow error band indicates the one sigma experimental uncertainty and the vertical line on the MC prediction is the statistical MC uncertainty

Full size image
Fig. 5
figure 5

Pythia predictions in comparison to ATLAS data [66] (left) and CMS data [67] (right) for W + jets as a function inclusive jet multiplicity. The yellow error band indicates the one sigma experimental uncertainty and the vertical line on the MC prediction is the statistical MC uncertainty. “\(\alpha _{\mathrm {s}}= 0.136\)” stands for the values of the Monash tune [69]

Full size image

The inclusive jet multiplicity in \({W}\)-boson events is well described by both the default and the EW-improved merging (Fig. 4). The EW-improved model predicts a slightly lower cross section for large jet multiplicities, but given the large experimental uncertainty it is difficult to distinguish between the models. Also, the value chosen for \(\alpha _{\mathrm {s}}(M_{Z})\) greatly influences the shape of the distribution (Fig. 5). The default value used in the Monash tune overshoots the tail, whereas the PDG best-fit value undershoots it. Choosing an in-between value leads to good agreement for all multiplicities. However, it should be noted that \(\alpha _{\mathrm {s}}(M_Z)\) in the parton shower is tuned to jet-shapes (in \({\mathrm e}^+{\mathrm e}^-\) and hadron-hadron collisions) and just changing the value on a process-by-process means a significant loss of predictivity. An optimal solution would be a full retuning of the merged event generator to observables that have been measured for the purpose of tuning. This would result in a sensible best-fit value of \(\alpha _{\mathrm {s}}(M_Z)\) that should be used for merged predictions of, say, the jet multiplicities. We refrain from providing a merged tune here, since distinguishing between the “uncertainties” and the “tunable parameters” of merged predictions is beyond the scope of this study. All observables presented below are not very sensitive to \(\alpha _{\mathrm {s}}(M_Z)\), up to overall normalisations. We thus use \(\alpha _{\mathrm {s}}(M_{Z}) = 0.118\) for all further studies.

Fig. 6
figure 6

Pythia predictions in comparison to ATLAS data [66] for W + jets as a function of the leading jet transverse momentum in inclusive n-jet events. The yellow error band indicates the one sigma experimental uncertainty and the vertical line on the MC prediction is the statistical MC uncertainty

Full size image
Fig. 7
figure 7

Pythia predictions in comparison to ATLAS data [66] for W + jets as a function of \(m_{12}\) and \(S_T\). The yellow error band indicates the one sigma experimental uncertainty and the vertical line on the MC prediction is the statistical MC uncertainty

Full size image

The \(p_\perp \) distributions of individual jets (Fig. 6) provide a better test of the default and EW-improved merging schemes. The fall-off observed in data is not captured by the default model, whereas the EW-improved model describes the shape of the data much better. This is the result of a more sensible scale setting, when the event is clustered to a \(2\rightarrow 2\) QCD process, and of the correct inclusion of the weak no-emission probability. The default merging scheme had to compromise to determine the no-emission probability for the unordered states. No such compromise is necessary now, since the EW-improved scheme will instead naturally yield an underlying \(2\rightarrow 2\) QCD process and reweight accordingly. This suggest that the “merging of mergings” scheme has beneficial features leading to a good shape description. However, an assessment simply based on one observable should not be overstated, since both the data and the leading-order-merged predictions will exhibit large (statistical or scale) uncertainties in the tails. Appropriate “scale setting” could thus be applied to the default scheme in order to ensure more satisfactory agreement—which is of course partly the motivation for the EW-improved scheme.

More inclusive hardness-measures like the scalar \(p_\perp \) sum of jets \(S_\text {T}\) (Fig. 7) encourage the same conclusion. The effect is even more pronounced for these observables. One of the observables that proved difficult to describe in the original experimental study was the invariant mass between the two leading jets, \(m_{12}\). Again, the EW-improved merging scheme describes this observable well.

Fig. 8
figure 8

Pythia predictions in comparison to ATLAS data [66] for W + jets as a function of \(\Delta \phi _{12}\) and \(\Delta y_{12}\). The yellow error band indicates the one sigma experimental uncertainty and the vertical line on the MC prediction is the statistical MC uncertainty

Full size image

Angular distributions are problematic for the weak parton showers. The inclusion of merging is expected to improve this. This is exactly what is seen for \(\Delta \phi _{12}\) and \(\Delta y_{12}\) distributions (Fig. 8). Both the default and the EW-improved merging schemes provide almost identical, and good, descriptions of the data.

6.2 Predictions at 100 TeV

When comparing with LHC data, we choose to highlight the importance of assigning the correct underlying process, and disregarded other weak resummation effects to not obscure the picture. In this section, we instead combine pure QCD multi-parton states with W-boson + jets states. We therefore include W-bosons in the merging scale cut: soft W-bosons will be produced by the shower, while states containing hard W-bosons will be given by the fixed-order result.

In order to assess the full effect of the merging QCD+EW showers with multi-parton matrix elements, it is preferable to consider 100 TeV pp collisions due to larger logarithmic enhancement with increasing energy. Observable that are commonly used to highlight weak resummation effects mostly relate to exclusive dijet production. However, in a combined resummation of QCD and EW logarithms, effects of weak resummation will be completely dwarfed by all-order QCD. We will therefore consider fully inclusive QCD and fully exclusive weak dijet production. Basically, whenever a weak boson is produced the event will not enter the histograms. This should of course not be regarded as experimentally feasible, since a perfect W / Z tagging is doubtful. However, the setup can provide valuable insight into the maximal size of effects related to the weak no-emission probability. As event selection, we require at least two jets with \(p_\perp > 500\) GeV and the leading jet above \(p_\perp > 1500\) GeV and no weak bosons.

The effects of the weak no-emission probability can seen in Fig. 9, where we compare the result of including/not including the weak PS when merging multi-jet with up to three outgoing partons. The merging scales value is \(t_{\text {{{MS}}}}=500\) GeV. As expected the weak no-emission probability becomes more important for higher \(p_\perp \) scales and reaches roughly 25 % for a leading jet \(p_\perp \) of 20 TeV. Even at lower energies it might become important for high precision measurements. This result is in agreement with the prediction from the stand-alone weak PS [38].

Fig. 9
figure 9

Predictions for 100 TeV, respectively, with and without including the weak PS for weak-exclusive dijet production (left) and weak-exclusive W + \(\ge 2\) jets (right). The yellow error band and the vertical lines indicate statistical MC uncertainty

Full size image

A similar observable is the exclusive weak production of a \({W}^\pm \) boson in association with at least two jets (Fig. 9). In addition to the multi-jet samples, this simulation also requires W + \(\le 2\) jets samples. As such, this simulation presents a fully inclusive merging of processes with vastly different cross sections. The event selection applies the jet selection outlined above, but additionally requires exactly one W with \(p_\perp > \) 500 GeV, and no further weak bosons. The interpretation in terms of resummation effects is not as straightforward for this observable. The inclusion of the weak PS both adds real radiation while simultaneously lowering the cross section due to the inclusion of no-emission probabilities. However, the real-emission enhancement is overwhelming and leads to a factor of 2–3 enhancement of the cross section. This clearly shows the need for including weak corrections, since the prediction from the ME alone is too low. If higher jet multiplicities (e.g. W + 4 jet) are included, this effect is expected to become milder.

An earlier study [49] of the electroweak corrections showed significantly larger effects, reaching up to \(\sim \) 80 % for lower jet energies. This earlier study calculates the full EW NLO and compares the differences between LO and NLO. The studies are not directly compatible, due to different treatment of multiple effects, including: handling of photons, competition between QCD and weak bosons, Bloch–Nordsieck violations [71] and different analysis conditions. Further studies to get a better handle on weak Sudakov effects would be of great interest.

7 Conclusions

We have presented a new consistent way of combining associated weak boson radiation in hard dijet production with hard QCD radiation in Drell–Yan-type events. It captures the strengths of both the merging technique and the weak PS, while removing issues intrinsic to either. More specifically, we provide a first matrix element merged prediction that consistently includes weak all-order effects. The combination of weak and QCD corrections leads to the concept of a “merging of mergings”: processes with vastly different lowest-order cross sections are combined into a single consistent sample. We have addressed the problem of unordered states in this context, and a dynamical solution based on the dominance of certain scale hierarchies (i.e. evolution histories) in certain phase-space regions has been presented. The novel prescription will be made available with the next release of Pythia 8.

The new merging scheme is compared to experimental data from ATLAS and CMS. For all considered distributions the new EW-improved merging scheme does as least as well as the old default merging. For a large fraction of the distributions related to multiple hard jets, the EW-improved scheme exhibits positive features that suggest improvements over the previous results. Especially for high \(S_\text {T}\), where the EW-improved merging predicts a lower production rate by a more physical scale setting, by including weak no-emission probabilities, and by identifying a \(2\rightarrow 2\) QCD scattering as underlying process.

The importance of the weak Sudakov for dijet production have been assessed in the EW-improved merging scheme. The effects are shown to be about \(25~\%\) at large jet \(p_\perp \) at a 100 TeV proton collider. Further studies comparing the predicted corrections in the EW-improved merging scheme with NLO EW calculation would be an interesting next step.

This study only includes the merging of \({W}\) bosons and jets, but the Sudakov coming from both \({W}^\pm \) and \({Z}^0\) bosons is accounted for. The implementation of \({Z}^0\) in the same merging framework is purely a technical, and is expected to simpler than that of the \({W}^\pm \).

In this study the weak merging scheme was only implemented for the CKKW-L merging of leading-order matrix elements, as this relatively simple merging method allows us to isolate and address generic problems without obscuring the discussion by irrelevant details. A natural, and intriguing, next step is to extend the novel prescription to the UMEPS and UNLOPS schemes implemented in Pythia. Especially the latter would be of great interest, since it would yield an event simulation that contains multiple NLO calculations for multiple processes consistently combined with both QCD and EW resummation. The challenge of such a generalisation is expected to be technical rather than conceptual.