Specificities of Electromagnetic Field Excitation in a Capacitive HF Discharge. III. Symmetric Discharge Partially Filling the Discharge Chamber

Abstract—

Electrodynamic characteristics of a low-pressure (electron collision frequency much lower than the field frequency) capacitive HF discharge maintained by an electromagnetic field with a frequency between 13 and 900 MHz are studied analytically and numerically. It is demonstrated that the field of both the fundamental mode (the field in the metal–space-charge sheath–plasma–space-charge sheath–metal structure) and the field of the higher-order evanescent modes must be taken into account for correct calculation of discharge characteristics under such conditions in a wide range of electron densities. Expressions governing the amplitudes of excited waves, along with expressions governing the discharge impedance in the presence of these waves, are derived by using field expansion in eigenwaves of an empty waveguide and eigenmodes of the three-layer structure. The case in which the size of plasma is smaller than the size of the electrodes is analyzed in detail. In this case, excitation of higher-order types of waves in the plasma column is generated by axial plasma inhomogeneity and is not related to electrodynamic effects near the electrode boundaries. It is demonstrated that the positions of current and voltage resonances related to propagation of surface waves along the three-layer structure becomes substantially modified due to excitation of higher-order field modes of the same structure. In addition, resonances caused by excitation of standing surface waves near the lateral surface (resonances of higher-order modes of the three-layer structure and an empty waveguide) can take place. Variation of relative position of resonances caused by changes in the discharge chamber geometry is investigated. Obtained results qualitatively agree with the results of numerical calculation of the discharge impedance and field propagation in the discharge by COMSOL Multiphysics^® software package.

Appendices

APPENDIX A

Calculation of Coefficients in Equations

Norms of eigenfunctions were calculated in [40]. Expressions governing coefficients in systems of equations (7) and (11) (the first index denotes the number of the wave in the three-layer system, while the second index denotes that in the empty space) have the form

$$\begin{gathered} {{C}_{{B00 + }}} = D_{{00 + }}^{E} = \left( {\frac{{\tanh \left( {{{a}_{{0 + }}}{{d}_{1}}} \right)}}{{{{a}_{{0 + }}}}} + \frac{{\tanh \left( {{{p}_{{0 + }}}{{L}_{2}}} \right)}}{{{{p}_{{0 + }}}}}} \right), \\ {{C}_{{Bj0 + }}} = D_{{0j + }}^{E} = \left( {\frac{{\tan \left( {{{{\tilde {a}}}_{{j + }}}{{d}_{1}}} \right)}}{{{{{\tilde {a}}}_{{j + }}}}} + \frac{{\tan \left( {{{{\tilde {p}}}_{{j + }}}{{L}_{2}}} \right)}}{{{{{\tilde {p}}}_{{j + }}}}}} \right), \\ \end{gathered} $$

$$\begin{gathered} {{C}_{{B0n + }}} = D_{{0n + }}^{E} = \left( {\frac{{{{a}_{{0 + }}}\tanh \left( {{{a}_{{0 + }}}{{d}_{1}}} \right) - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}\tan \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}{{d}_{1}}} \right)}}{{a_{{0 + }}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _{{n + }}^{2}}}} \right. \\ \, + \left. {\frac{{{{p}_{{0 + }}}\tanh \left( {{{p}_{{0 + }}}{{L}_{2}}} \right) + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}\tan \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}{{L}_{2}}} \right)}}{{p_{{0 + }}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _{{n + }}^{2}}}} \right), \\ \end{gathered} $$

$$\begin{gathered} {{C}_{{Bjn + }}} = D_{{nj + }}^{E} = \left( {\frac{1}{{\cos \left( {{{{\tilde {a}}}_{{j + }}}{{d}_{1}}} \right)}}} \right. \\ \times \;\left( {\frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {a}}}_{{j + }}}} \right){{d}_{1}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {a}}}_{{j + }}}} \right)}} + \frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {a}}}_{{j + }}}} \right){{d}_{1}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {a}}}_{{j + }}}} \right)}}} \right) \\ + \,\frac{1}{{\cos \left( {{{{\tilde {p}}}_{{j + }}}{{L}_{2}}} \right)}}\left( {\frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {p}}}_{{j + }}}} \right){{L}_{2}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {p}}}_{{j + }}}} \right)}}} \right. \\ \end{gathered} $$

$$\begin{gathered} \left. {\, + \left( {\frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {p}}}_{{j + }}}} \right){{L}_{2}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {p}}}_{{j + }}}} \right)}}} \right)} \right) \approx \left( {{{d}_{1}} + \frac{1}{{\cos \left( {{{{\tilde {p}}}_{{j + }}}{{L}_{2}}} \right)}}} \right. \\ \, \times \left. {\left( {\frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {p}}}_{{j + }}}} \right){{L}_{2}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {p}}}_{{j + }}}} \right)}} + \frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {p}}}_{{j + }}}} \right){{L}_{2}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {p}}}_{{j + }}}} \right)}}} \right)} \right), \\ \end{gathered} $$

$$\begin{gathered} {{C}_{{E00 + }}} = D_{{00 + }}^{B} = \left( {\frac{{\tanh \left( {{{a}_{{0 + }}}{{d}_{1}}} \right)}}{{{{a}_{{0 + }}}}} + \frac{{\tanh \left( {{{p}_{{0 + }}}{{L}_{2}}} \right)}}{{{{\varepsilon }_{P}}{{p}_{{0 + }}}}}} \right), \\ {{C}_{{Ej0 + }}} = D_{{0j + }}^{B} = \left( {\frac{{\tan \left( {{{{\tilde {a}}}_{{j + }}}{{d}_{1}}} \right)}}{{{{{\tilde {a}}}_{{j + }}}}} + \frac{{\tan \left( {{{{\tilde {p}}}_{{j + }}}{{L}_{2}}} \right)}}{{{{\varepsilon }_{P}}{{{\tilde {p}}}_{{j + }}}}}} \right), \\ \end{gathered} $$

$$\begin{gathered} {{C}_{{E0n + }}} = D_{{n0 + }}^{B} = \left( {\frac{{{{a}_{{0 + }}}\tanh \left( {{{a}_{{0 + }}}{{d}_{1}}} \right) - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}\tan \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}{{L}_{2}}} \right)}}{{a_{{0 + }}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _{{n + }}^{2}}}} \right. \\ \, + \left. {\frac{1}{{{{\varepsilon }_{p}}}}\frac{{{{p}_{{0 + }}}\tanh \left( {{{p}_{{0 + }}}{{L}_{2}}} \right) + {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}\tan \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}}{{L}_{2}}} \right)}}{{p_{{0 + }}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _{{n + }}^{2}}}} \right), \\ \end{gathered} $$

$$\begin{gathered} {{C}_{{Ejn + }}} = D_{{nj + }}^{B} = \left( {\frac{{{{\varepsilon }_{p}}}}{{\cos \left( {{{{\tilde {a}}}_{{j + }}}{{d}_{1}}} \right)}}} \right.\left( {\frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {a}}}_{{j + }}}} \right){{d}_{1}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {a}}}_{{j + }}}} \right)}}} \right. \\ \, + \left. {\frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {a}}}_{{j + }}}} \right){{d}_{1}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {p}}}_{{j + }}}} \right)}}} \right) + \frac{1}{{\cos \left( {{{{\tilde {p}}}_{{j + }}}{{L}_{2}}} \right)}} \\ \, \times \left. {\left( {\frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {p}}}_{{j + }}}} \right){{L}_{2}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} - {{{\tilde {p}}}_{{j + }}}} \right)}} + \frac{{\sin \left( {\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {p}}}_{{j + }}}} \right){{L}_{2}}} \right)}}{{2\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }}_{{n + }}} + {{{\tilde {p}}}_{{j + }}}} \right)}}} \right)} \right). \\ \end{gathered} $$

The following notations were used in the above expressions: ${{a}_{{0 + }}} = \sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{1}}}$; ${{p}_{{0 + }}} = \sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{P}}}$; ${{\tilde {a}}_{{n + }}} = \sqrt {{{k}^{2}}{{\varepsilon }_{1}} - h_{{n + }}^{2}}$; ${{\tilde {p}}_{{n + }}} = \sqrt {{{k}^{2}}{{\varepsilon }_{P}} - h_{{n + }}^{2}}$; ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }_{{n + }}} = {{n\pi } \mathord{\left/ {\vphantom {{n\pi } L}} \right. \kern-0em} L}$; ε_P and ε₁ are the dielectric permittivities of plasma and sheath, respectively. All coefficients (C, D) have the dimension of length. Note also that, for convenience of conducting numerical calculations, ${{\varepsilon }_{{\text{p}}}}$ enters in expressions for different coefficients in different ways.

APPENDIX B

Calculation of Amplitudes of Different Types of Waves in the Diagonal Representation. Expansion in Waveguide Modes

Using the assumption of predominant role played by the diagonal terms, we can write expressions governing different components of the electric field. The amplitudes of the fields of higher-order types of waves have the following form inside plasma (r < R)

$${{A}_{{j + }}} = - \frac{{{{A}_{{0 + }}}}}{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}\frac{{\left( {{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)\frac{{{{h}_{{0 + }}}}}{k}{{C}_{{E0j + }}} + {{J}_{1}}\left( {{{h}_{{0 + }}}R} \right){{C}_{{B0j + }}}\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}}}{k}\frac{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}} \right)}}{{\left( {\frac{{{{{\tilde {h}}}_{{j + }}}}}{{{{\varepsilon }_{P}}k}}\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}{{C}_{{Ejj + }}} + {{C}_{{Bjj + }}}\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}}}{k}\frac{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}} \right)}}\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}$$

(B.1)

and outside of plasma (r > R):

$${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }_{{j + }}} = {{A}_{{0 + }}}\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}\frac{{\left( {\frac{{{{{\tilde {h}}}_{{j + }}}}}{{{{\varepsilon }_{P}}k}}{{C}_{{Ejj + }}}{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right){{C}_{{B0j + }}}\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}} - {{C}_{{Bjj + }}}{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)\frac{{{{h}_{{0 + }}}}}{k}{{C}_{{E0j + }}}} \right)}}{{\left( {\frac{{{{{\tilde {h}}}_{{j + }}}}}{{{{\varepsilon }_{P}}k}}{{C}_{{Ejj + }}}\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}} + {{C}_{{Bjj + }}}\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}}}{k}\frac{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}} \right)}}\frac{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)}}.$$

The term in the denominator in the previous two expressions is the same, meaning that the fields of the higher-order modes grow simultaneously both outside and inside plasma, and plasma densities at which a resonance is observed are also the same. This resonance can be interpreted as the resonance related to excitation of surface waves at the plasma-column lateral surface. The amplitude of the surface wave propagating along the sheath can be calculated by using expression

$${{A}_{{0 + }}} = {{H}^{{{\text{ext}}}}}\left( {kR} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{0 + }}^{2}{{\left( {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right){{C}_{{B00 + }}} - \sum\limits_{n = 1}^K {\frac{{\left( {{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)\frac{{{{h}_{{0 + }}}}}{k}{{C}_{{E0n + }}} + \frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}}}{k}{{C}_{{B0n + }}}\frac{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)}}{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)}}{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)} \right)}}{{\left( {\frac{{{{{\tilde {h}}}_{{n + }}}}}{{{{\varepsilon }_{P}}k}}{{C}_{{Enn + }}}\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{n + }}}R} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}R} \right)}} + \frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}}}{k}{{C}_{{Bnn + }}}\frac{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)}}{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)}}} \right)}}} {{C}_{{Bn0 + }}}} \right)}^{{ - 1}}}.$$

APPENDIX C

Calculation of Amplitudes of Different Types of Waves in the Diagonal Approximation. Expansion in Modes of the Three-Layer Structure

Using general formulas, we find that the amplitude of the higher-order modes of the field in the diagonal approximation can be calculated by using the following expression:

$${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }_{{j + }}} = \frac{{\left( {\frac{{{{E}^{{{\text{ext}}}}}\left( {kR} \right)}}{{i\rho }}D_{{j0}}^{E}{{I}_{1}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right) - {{H}^{{{\text{ext}}}}}\left( {kR} \right)D_{{j0}}^{B}\frac{{{{{\tilde {h}}}_{{j + }}}}}{k}{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)} \right)}}{{\left( {\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}}}{k}{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)D_{{jj}}^{E}{{I}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right) + {{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)\frac{{D_{{jj}}^{B}}}{{{{\varepsilon }_{P}}}}\frac{{{{{\tilde {h}}}_{{j + }}}}}{k}{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)} \right)}},$$

where ${{E}^{{{\text{ext}}}}}\left( {kR} \right) = \rho {{H}^{{{\text{ext}}}}}\left( {kR} \right){{Z\pi R} \mathord{\left/ {\vphantom {{Z\pi R} L}} \right. \kern-0em} L}$. The amplitude of the surface wave propagating along the sheath satisfies expression

$${{A}_{{0 + }}} = \frac{{{{H}^{{{\text{ext}}}}}\left( {kR} \right)D_{{00}}^{B} - \sum\limits_{n = 1}^K {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}_{{n + }}}} {{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)D_{{0n}}^{B}}}{{{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}},$$

while the field of the higher-order modes inside plasma is given by

$${{A}_{{j + }}} = \frac{{{{H}^{{{\text{ext}}}}}\left( {kR} \right)D_{{j0}}^{B} - \sum\limits_{n = 1}^K {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}_{{n + }}}} {{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)D_{{jn}}^{B}}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)}}.$$

APPENDIX D

Calculation of Impedance Introduced by the Exterior Part of the Electrodes

Let the discharge impedance calculated according to any expression in (10)–(12) is equal to Z_D. Distribution of potential and current in the R < r < R₁ region satisfies the telegraph equations [37–39]:

$$U = \frac{1}{{ - i\omega \tilde {C}}}\frac{R}{r}\frac{{di}}{{dr}},\quad I = \frac{1}{{ - i\omega \tilde {L}}}\frac{r}{R}\frac{{dU}}{{dr}},$$

(D.1)

where ${{\tilde {C}r} \mathord{\left/ {\vphantom {{\tilde {C}r} R}} \right. \kern-0em} R}$ and ${{\tilde {L}R} \mathord{\left/ {\vphantom {{\tilde {L}R} r}} \right. \kern-0em} r}$ are the capacitance and inductance of the line per unit length, respectively; $\tilde {C} = {{{{\varepsilon }_{0}}2\pi R} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}2\pi R} L}} \right. \kern-0em} L}$; $\tilde {L} = {{{{\mu }_{0}}L} \mathord{\left/ {\vphantom {{{{\mu }_{0}}L} {\left( {2\pi R} \right)}}} \right. \kern-0em} {\left( {2\pi R} \right)}}$. Introducing resistance of the line $z = {{\rho L} \mathord{\left/ {\vphantom {{\rho L} {\left( {2\pi R} \right)}}} \right. \kern-0em} {\left( {2\pi R} \right)}}$ and substituting voltage and current in the form of a sum of Bessel and Neumann functions,

$$\left( {\begin{array}{*{20}{c}} U \\ I \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{Z}_{0}}} \\ 1 \end{array}} \right) = A\left( {\begin{array}{*{20}{c}} {z{{J}_{0}}\left( {kr} \right)} \\ {{{J}_{1}}\left( {kr} \right)} \end{array}} \right) + B\left( {\begin{array}{*{20}{c}} {z{{N}_{0}}\left( {kr} \right)} \\ {{{N}_{1}}\left( {kr} \right)} \end{array}} \right),$$

we find that the impedance at point r > R is given by

$${{Z}_{{D1}}}\left( r \right) = z\frac{{\left( {{{Z}_{D}}{{N}_{1}}\left( {kR} \right) - z{{N}_{0}}\left( {kR} \right)} \right){{J}_{0}}\left( {kr} \right) - \left( {{{Z}_{D}}{{J}_{1}}\left( {kR} \right) - z{{J}_{0}}\left( {kR} \right)} \right){{N}_{0}}\left( {kr} \right)}}{{\left( {{{Z}_{D}}{{N}_{1}}\left( {kR} \right) - z{{N}_{0}}\left( {kR} \right)} \right){{J}_{1}}\left( {kr} \right) - \left( {{{Z}_{D}}{{J}_{1}}\left( {kR} \right) - z{{J}_{0}}\left( {kR} \right)} \right){{N}_{1}}\left( {kr} \right)}}.$$

(D.2)

In the case of small difference of radii ($k(r-R) \ll 1$), it is easier to find the correction to the impedance directly from expression (D.1):

$${{Z}_{{D1}}}\left( r \right) = \frac{{{{Z}_{0}} - i\omega \tilde {L}\Delta r}}{{1 - i\omega \tilde {C}\Delta r{{Z}_{0}}}},$$

(D.3)

$\Delta r = r - R$. Under the conditions of the present study, the influence of inductance of the line can be neglected in most cases.

APPENDIX E

Calculation of Impedance Introduced by the Peripheral Region of the Working Chamber

The conditions of tangential components of the electric field being equal to each other at the surface at which external energy is deposited into the discharge leads to relation (${{U}_{{D1}}}$ is the voltage of the fundamental mode, and ${{Z}_{{D1}}}$ is the impedance of the interior transmission line at the electrode boundary calculated in the previous subsection)

$$\left( {\begin{array}{*{20}{c}} {{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{z0 + }}}{{U}_{{D1}}}} \mathord{\left/ {\vphantom {{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{z0 + }}}{{U}_{{D1}}}} L}} \right. \kern-0em} L}} \\ {{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{\varphi 0 + }}}{{U}_{{D1}}}} \mathord{\left/ {\vphantom {{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{\varphi 0 + }}}{{U}_{{D1}}}} {\left( {2\pi {{R}_{1}}{{Z}_{{D1}}}} \right)}}} \right. \kern-0em} {\left( {2\pi {{R}_{1}}{{Z}_{{D1}}}} \right)}}} \end{array}} \right)$$

$$\begin{gathered} \, + \sum\limits_{n = 1}^\infty {{{B}_{{n + }}}} \left( {\begin{array}{*{20}{c}} {i{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{zn + }}}\left( z \right)} \\ {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{\varphi n + }}}\left( z \right){{{{I}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{I}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)} {{{I}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}} \right. \kern-0em} {{{I}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}} \end{array}} \right) \hfill \\ \, - \sum\limits_{n = 1}^\infty {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }}_{{n + }}}} \left( {\begin{array}{*{20}{c}} { - i{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{zn + }}}} \\ {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{\varphi n + }}}\left( z \right){{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)} {{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}} \right. \kern-0em} {{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}} \end{array}} \right) \hfill \\ \end{gathered} $$

(E.1)

$$\, - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }_{{0 + }}}\left( {\begin{array}{*{20}{c}} {i{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{z0 + }}}} \\ {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{\varphi 0 + }}}{{{{Q}_{1}}\left( {k{{R}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{Q}_{1}}\left( {k{{R}_{1}}} \right)} {{{Q}_{0}}\left( {k{{R}_{1}}} \right)}}} \right. \kern-0em} {{{Q}_{0}}\left( {k{{R}_{1}}} \right)}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{E}^{S}}} \\ {{{H}^{S}}} \end{array}} \right).$$

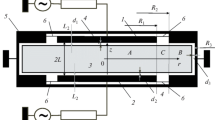
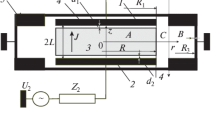
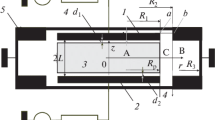
Here, the first term in the left-hand side corresponds to the field of the TEM wave in the interior region calculated in Appendix D; two sums correspond to the fields of the higher-order modes in the interior and exterior regions, respectively (${{B}_{{n + }}}$ and ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }_{{n + }}}$ are the wave amplitudes); the last term represents the field of the TEM wave with amplitude ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }_{{0 + }}}$ in the interior region representing a closed transmission line; the term in the right-hand side represents the external source of the field. Since the lateral surface of the chamber is made of metal, ${{Q}_{0}}\left( {k{{R}_{3}}} \right) = 0$. In the geometry under consideration (Fig. 1), we can write:

$$\left( {\begin{array}{*{20}{c}} {{{Q}_{0}}\left( r \right)} \\ {{{Q}_{1}}\left( r \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {H_{0}^{{\left( 1 \right)}}\left( {kr} \right)} \\ {H_{1}^{{\left( 1 \right)}}\left( {kr} \right)} \end{array}} \right) - \frac{{H_{0}^{{\left( 1 \right)}}\left( {k{{R}_{3}}} \right)}}{{H_{0}^{{\left( 2 \right)}}\left( {k{{R}_{3}}} \right)}}\left( {\begin{array}{*{20}{c}} {H_{0}^{{\left( 2 \right)}}\left( {kr} \right)} \\ {H_{1}^{{\left( 2 \right)}}\left( {kr} \right)} \end{array}} \right).$$

Similar to [36], we will assume that the region of energy deposition is small, so that ${{R}_{2}}-{{R}_{1}} \ll {{R}_{1}}$. The condition of currents at r = R₁ and r = R₂ being equal to each other means that H^S = 0. Voltage equal to U is applied at the boundary points z = ±L: ${{E}^{S}} =$ $- U\delta \left( {z - L} \right)$. Amplitudes of the fields can be calculated similar to [40] by replacing eigenwaves of the three-layer structure by eigenwaves of an empty waveguide. In the discussed case, (E.1) yields

$$\begin{gathered} {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }}_{{0 + }}} = \frac{{{{U}_{{D1}}}}}{{2\pi {{R}_{1}}{{Z}_{{D1}}}}}\frac{{{{Q}_{0}}\left( {k{{R}_{1}}} \right)}}{{{{Q}_{1}}\left( {k{{R}_{1}}} \right)}}, \\ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }}_{{n + }}} = {{B}_{{n + }}}\frac{{{{I}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right){{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}{{{{I}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right){{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}, \\ \end{gathered} $$

$$\frac{{{{U}_{{D1}}}}}{L} = {{U}_{{D2}}}\frac{{{{e}_{{z0 + }}}\left( L \right)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{0 + }}^{{E2}}}}{{\left( {1 - i\frac{L}{{2\pi {{R}_{1}}{{Z}_{{D1}}}}}\frac{{{{Q}_{0}}\left( {k{{R}_{1}}} \right)}}{{{{Q}_{1}}\left( {k{{R}_{1}}} \right)}}} \right)}^{{ - 1}}},$$

$${{B}_{{n + }}} = - i{{U}_{{D2}}}\frac{{{{e}_{{zn + }}}\left( L \right)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{n + }}^{{E2}}}}{{\left( {1 + \frac{{{{I}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right){{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}{{{{I}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right){{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}} \right)}^{{ - 1}}}.$$

Knowing amplitudes of all waves, we can find the source current (by using relation ${{i}_{n}} = 2\pi r{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_{{\varphi n + }}}(L)$):

$$\begin{gathered}{{I}_{{D2}}} = {{U}_{{D2}}}\left[ {\frac{{L{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{z0 + }}}(L){{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{\varphi 0 + }}}(L)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{0 + }}^{{E2}}}}{{{\left( {\frac{{{{Z}_{{D1}}}}}{\rho } - \frac{{iL}}{{2\pi {{R}_{1}}}}\frac{{{{Q}_{0}}\left( {k{{R}_{1}}} \right)}}{{{{Q}_{1}}\left( {k{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}}} \right. \\ \,\left. { - \;2\pi i{{R}_{1}}\sum\limits_{n = 1}^\infty {\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{zm + }}}(L){{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{\varphi n + }}}(L)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{n + }}^{{E2}}}}{{{\left( {\frac{{{{I}_{0}}{\kern 1pt} \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}{{{{I}_{1}}{\kern 1pt} \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}} + \frac{{{{K}_{0}}{\kern 1pt} \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}{{{{K}_{1}}{\kern 1pt} \left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}}} } \right] \\ \end{gathered} $$

and impedance at the point of excitation (16).