Skip to main content
SpringerLink
Log in

Existence and stability of a stationary solution of the system of diffusion equations in a medium with discontinuous characteristics under various quasimonotonicity conditions

  • Research Articles
  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

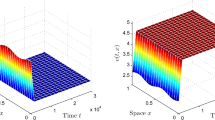
Asymptotic analysis is used to study the existence, local uniqueness, and asymptotic stability in the sense of Lyapunov of a solution of a one-dimensional nonlinear system of reaction–diffusion equations with various types of quasimonotonicity of the functions describing reactions. A feature of the problem is the discontinuities (jumps) of these functions at a single point on the segment on which the problem is posed. The solution with a large gradient in the vicinity of the discontinuity point is studied. Sufficient conditions for the existence of a stable stationary solution of systems with various quasimonotonicity conditions are given. The asymptotic method of differential inequalities is used to prove the existence and stability theorems. The main distinctive features of this method for various types of quasimonotonicity are listed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. N. Pavlenko and O. V. Ul’yanova, “The method of upper and lower solutions for elliptic-type equations with discontinuous nonlinearities,” Russian Math. (Iz. VUZ), 42, 65–72 (1998).

    MathSciNet  MATH  Google Scholar 

  2. V. N. Pavlenko and O. V. Ul’yanova, “Method of upper and lower solutions for parabolic-type equations with discontinuous nonlinearities,” Differ. Equ., 38, 520–527 (2002).

    Article  MathSciNet  Google Scholar 

  3. N. N. Nefedov and Minkang Ni, “Internal layers in the one-dimensional reaction–diffusion equation with a discontinuous reactive term,” Comput. Math. Math. Phys., 55, 2001–2007 (2015).

    Article  MathSciNet  Google Scholar 

  4. N. N. Nefedov, E. I. Nikulin, and A. O. Orlov, “On a periodic inner layer in the reaction–diffusion problem with a modular cubic source,” Comput. Math. Math. Phys., 60, 1461–1479 (2020).

    Article  MathSciNet  Google Scholar 

  5. N. N. Nefedov, E. I. Nikulin, and A. O. Orlov, “Contrast structures in the reaction- diffusion- advection problem in the case of a weak reaction discontinuity,” Russ. J. Math. Phys., 29, 81–90 (2022).

    Article  MathSciNet  Google Scholar 

  6. C. De Coster, F. Obersnel, and P. A. Omari, “A qualitative analysis via lower and upper solutions of first order periodic evolutionary equations with lack of uniqueness,” in: Handbook of Differential Equations: Ordinary Differential Equations, Vol. 3 (A. Cañada, R. Drábek, A. Fonda, and B. V. Elsevier, eds.), North-Holland, Amsterdam (2006), pp. 203–339.

    Chapter  Google Scholar 

  7. S. Carl and D. Motreanu, “Extremal solutions for nonvariational quasilinear elliptic systems via expanding trapping regions,” Monatsh. Math., 182, 801–821 (2017).

    Article  MathSciNet  Google Scholar 

  8. V. Bögelein, F. Duzaar, R. Korte, and C. Scheven, “The higher integrability of weak solutions of porous medium systems,” Adv. Nonlinear Anal., 8, 1004–1034 (2018).

    Article  MathSciNet  Google Scholar 

  9. N. T. Levashova and B. V. Tischenko, “Existence and stability of the solution to a system of two nonlinear diffusion equations in a medium with discontinuous characteristics,” Comput. Math. Math. Phys., 61, 1811–1833 (2021).

    Article  MathSciNet  Google Scholar 

  10. A. E. Sidorova, N. T. Levashova, A. E. Semina, and A. A. Melnikova, “The application of a distributed model of active media for the analysis of urban ecosystems development,” Math. Biol. Bioinf., 13, 454–465 (2018).

    Article  Google Scholar 

  11. N. T. Levashova, A. E. Sidorova, A. E. Semina, and Mingkang Ni, “A spatio-temporal autowave model of shanghai territory development,” Sustainability, 11, 3658, 13 pp. (2019).

    Article  Google Scholar 

  12. N. N. Nefedov, “Development of methods of asymptotic analysis of transition layers in reaction–diffusion–advection equations: theory and applications,” Comput. Math. Math. Phys., 61, 2068–2087 (2021).

    Article  MathSciNet  Google Scholar 

  13. C. V. Pao, Nonlinear Parabolic and Elliptic Equations, Plenum Press, New York, London (2004).

    Google Scholar 

  14. A. Melnikova, N. Levashova, and D. Lukyanenko, “Front dynamics in an activator-inhibitor system of equations,” in: Numerical Analysis and Its Applications (Lozenetz, Bulgaria, June 15–22, 2016, Lecture Notes in Computer Science, Vol. 10187, I. Dimov, I. Faragó, and L. Vulkov, eds.), Springer, Cham (2017), pp. 492–499.

    Chapter  Google Scholar 

  15. D. V. Lukyanenko and A. A. Melnikova, “Application of asymptotic analysis methods for solving a coefficient inverse problem for a system of nonlinear singularly perturbed reaction–diffusion equations with cubic nonlinearity [in Russian],” Numerical Methods and Programming (Vychislitel’nye Metody i Programmirovanie), 20, 363–377 (2019).

    Article  Google Scholar 

  16. D. V. Lukyanenko, A. A. Borzunov, and M. A. Shishlenin, “Solving coefficient inverse problems for nonlinear singularly perturbed equations of the reaction–diffusion–advection type with data on the position of a reaction front,” Commun. Nonlinear Sci. Numer. Simul., 99, 105824, 10 pp. (2021).

    Article  MathSciNet  Google Scholar 

  17. D. V. Lukyanenko, M. A. Shishlenin, and V. T. Volkov, “Asymptotic analysis of solving an inverse boundary value problem for a nonlinear singularly perturbed time-periodic reaction– diffusion–advection equation,” J. Inverse Ill-Posed Probl., 27, 745–758 (2019).

    Article  MathSciNet  Google Scholar 

  18. V. F. Butuzov, N. T. Levashova, and A. A. Mel’nikova, “Steplike contrast structure in a singularly perturbed system of equations with different powers of small parameter,” Comput. Math. Math. Phys., 52, 1526–1546 (2012).

    Article  MathSciNet  Google Scholar 

  19. A. B. Vasil’eva and V. F. Butuzov, Asymptotic Methods in the Theory of Singular Perturbations [in Russian], Vysshaja shkola, Moscow (1990).

    MATH  Google Scholar 

  20. P. C. Fife and J. B. MacLeod, “The approach of solutions of nonlinear diffusion equation to a travelling front solutions,” Arch. Rational Mech. Anal., 65, 335–361 (1977).

    Article  ADS  MathSciNet  Google Scholar 

  21. A. B. Vasil’eva and V. F. Butuzov, Asymptotic expansions of solutions of singularly perturbed equations [in Russian], Nauka, Moscow (1973).

    MATH  Google Scholar 

  22. B. V. Tishchenko, “The existence, local uniqueness, and asymptotic stability of the boundary layer type solution of the Neumann problem for a two-equation nonlinear system with different powers of a small parameter,” Moscow Univ. Phys. Bull., 76, 296–304 (2021).

    Article  ADS  Google Scholar 

  23. N. N. Nefedov and M. A. Davydova, “Contrast structures in multidimensional singularly perturbed reaction–diffusion–advection problems,” Differ. Equ., 48, 745–755 (2012).

    Article  MathSciNet  Google Scholar 

  24. M. A. Davydova, “Existence and stability of solutions with boundary layers in multidimensional singularly perturbed reaction–diffusion–advection problems,” Math. Notes, 98, 909–919 (2015).

    Article  MathSciNet  Google Scholar 

  25. A. Friedman, Partial Differential Equations of Parabolic Type, Dover Publ., Mineola, NY (2013).

    Google Scholar 

Download references

Funding

This paper was supported by the Russian Science Foundation (project No. 18-11-00042).

Author information

Authors and Affiliations

  1. Faculty of Physics, Lomonosov Moscow State University, Moscow, Russia

    N. T. Levashova & B. V. Tishchenko

Authors
  1. N. T. Levashova
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. V. Tishchenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. T. Levashova.

Ethics declarations

The authors declare no conflicts of interest.

Additional information

Translated from Teoreticheskaya i Matematicheskaya Fizika, 2022, Vol. 212, pp. 62–82 https://doi.org/10.4213/tmf10217.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Levashova, N.T., Tishchenko, B.V. Existence and stability of a stationary solution of the system of diffusion equations in a medium with discontinuous characteristics under various quasimonotonicity conditions. Theor Math Phys 212, 944–961 (2022). https://doi.org/10.1134/S0040577922070054

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040577922070054

Keywords

Search

Navigation