1 Introduction

Recently, duality concepts were successfully applied for minimizing nonsmooth and nonconvex functions appearing in certain applications in image and data processing. A frequently applied algorithm in this direction is the proximal alternating linearized minimization algorithm (PALM) by Bolte et al. [4] based on results in [1, 2]. Pock and Sabach [36] realized that the convergence speed of PALM can be considerably improved by inserting some nonexpensive inertial steps and called the accelerated algorithm iPALM. In many problems in imaging and machine learning, parts of the objective function can be often written as sum of a huge number of functions sharing the same structure. In general the computation of the gradient of these parts is too time and storage consuming so that stochastic gradient approximations were applied, see, e.g. [5] and the references therein. A combination of the simple stochastic gradient descent (SGD) estimator with PALM was first discussed by Xu and Yin in [46]. The authors refer to their method as block stochastic gradient iteration and do not mention the connection to PALM. Under rather hard assumptions on the objective function F, they proved that the sequence \((x^k)_k\) produced by their algorithm is such that \({\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x^k) \right) \) converges to zero as \(k \rightarrow \infty \). Another idea for a stochastic variant of PALM was proposed by Davis et al. [11]. The authors introduce an asynchronous variant of PALM with stochastic noise in the gradient and called it SAPALM. Assuming an explicit bound of the variance of the noise, they proved certain convergence results. Their approach requires an explicit bound on the noise, which is not fulfilled for the gradient estimators considered in this paper. Further, we like to mention that a stochastic variant of the primal-dual algorithm of Chambolle and Pock [9] for solving convex problems was developed in [8].

Replacing the simple stochastic gradient descent estimators by more sophisticated so-called variance-reduced gradient estimators, Driggs et al. [13] could weaken the assumptions on the objective function in [46] and improve the estimates on the convergence rate of a stochastic PALM algorithm. They called the corresponding algorithm SPRING. However, the convergence analysis within [13] is based on the so-called generalized gradient \({\mathscr {G}}F_{\tau _1,\tau _2}\). Within the first versions of the paper [13], when the preprint of this paper appeared, this generalized gradient was not even well-defined. Even if the definition was fixed over the time, the use of the generalized gradient is not satisfying at all, since it becomes not clear how this generalized gradient is related to the (sub)differential of the objective function in limit processes with varying \(\tau _1\) and \(\tau _2\). In particular, it is easy to find examples of F and sequences \((\tau _1^k)_k\) and \((\tau _2^k)_k\) such that the generalized gradient \({\mathscr {G}}F_{\tau _1^k,\tau _2^k}(x_1,x_2)\) is non-zero, but converges to zero for fixed \(x_1\) and \(x_2\). Note that the advantages of variance reduction to accelerate stochastic gradient methods were discussed by several authors, see, e.g. [24, 39].

In this paper, we merge a stochastic PALM algorithm with an inertial procedure to obtain a new iSPALM algorithm. The inertial parameters can also be viewed as a generalization of momentum parameters to nonsmooth problems. Momentum parameters are widely used to speed up and stabilize optimization algorithms based on (stochastic) gradient descent. In particular, for machine learning applications it is known that momentum algorithms [32, 37, 38, 41] as well as their stochastic modifications like the Adam optimizer [25] perform much better than a plain (stochastic) gradient descent, see e.g. [15, 43]. From this point of view, inertial or momentum parameters are one of the core ingredients for an efficient optimization algorithm to minimize the loss in data driven approaches. We examine the convergence behavior of iSPALM both theoretically and numerically. Under certain assumptions on the parameters of the algorithm which also appear in the iPALM algorithm, we show that iSPALM converges linearly. In particular, we have to modify the definition of variance-reduced gradient estimators to inertial ones. We clearly indicate the few lemmas which are somehow related e.g. to those in [13] and address the necessary technical adaptations in an extended preprint [21]. The proofs given in this paper are completely new. In the numerical part, we focus on two examples, namely (i) MNIST classification with proximal neural networks (PNNs), and (ii) parameter learning for Student-t mixture models (MMs).

PNNs basically replace the standard layer \(\sigma (Tx+b)\) of a feed-forward neural network by \(T^\mathrm {T}\sigma (Tx+b)\) and require that T is an element of the (compact) Stiefel manifold, i.e. has orthonormal columns, see [18, 20]. This implies that PNNs are 1-Lipschitz and hence more stable under adversarial attacks than a neural network of comparable size without the orthogonality constraints. While the PNNs were trained in [18] using a SGD on the Stiefel manifold, we train it in this paper by adding the characteristic function of the feasible weights to the loss for incorporating the orthogonality constraints and use PALM, iPALM, SPRING and iSPALM for the optimization.

Learned MMs provide a powerful tool in data and image processing. While Gaussian MMs are mostly used in the field, more robust methods can be achieved by using heavier tailed distributions, as, e.g. the Student-t distribution. In [44], it was shown that Student-t MMs are superior to Gaussian ones for modeling image patches and the authors proposed an application in image compression. Image denoising based on Student-t models was addressed in [27] and image deblurring in [12, 47]. Further applications include robust image segmentation [3, 34, 42] and superresolution [19] as well as registration [14, 48]. For learning MMs a maximizer of the corresponding log-likelihood has to be computed. Usually an expectation maximization (EM) algorithm [26, 30, 35] or certain of its acceleration [6, 31, 45] are applied for this purpose. However, if the MM has many components and we are given large data, a stochastic optimizat ion approach appears to be more efficient. Indeed, recently, also stochastic variants of the EM algorithm were proposed [7, 10], but show various disadvantages and we are not aware of a circumvent convergence result for these algorithms. In particular, one assumption on the stochastic EM algorithm is that the underlying distribution family is an exponential family, which is not the case for MMs. In this paper, we propose for the first time to use the (inertial) PALM algorithms as well as their stochastic variants for maximizing a modified version of the log-likelihood function.

This paper is organized as follows: In Sect. 2, we provide the notation used throughout the paper. To understand the differences of existing algorithms to our novel one, we discuss PALM and iPALM together with convergence results in Sect. 3. Section 4 introduces our iSPALM algorithm. We discuss the convergence behavior of iSPALM in Sect. 5. Finally, we compare the performance of our iSPALM with (inertial) PALM and stochastic PALM when applied to two nonconvex optimization problems in machine learning. We provide the code online.Footnote 1 Finally, conclusions are drawn and directions of further research are addressed in Sect. 7.

2 Preliminaries

In this section, we introduce the basic notation and results which we will use throughout this paper.

For an proper and lower semi-continuous function \(f:{\mathbb {R}}^d\rightarrow (-\infty ,\infty ]\) and \(\tau >0\) the proximal mapping \(\mathrm {prox}_\tau ^f:{\mathbb {R}}^d\rightarrow {\mathcal {P}}({\mathbb {R}}^d)\) is defined by

$$\begin{aligned} \mathrm {prox}_\tau ^f(x) :=\mathop {\text {argmin}}\limits _{y\in {\mathbb {R}}^d} \left\{ {\tfrac{\tau }{2}\Vert x-y\Vert ^2+f(y)} \right\} , \end{aligned}$$

where \({\mathcal {P}}({\mathbb {R}}^d)\) denotes the power set of \({\mathbb {R}}^d\). The proximal mapping admits the following properties, see e.g. [40].

Proposition 2.1

Let \(f:{\mathbb {R}}^d\rightarrow {\mathbb {R}}\cup \{\infty \}\) be proper and lower semi-continuous with \(\inf _{{\mathbb {R}}^d}f>-\infty \). Then, the following holds true.

  1. (i)

    The set \(\mathrm {prox}_\tau ^f(x)\) is nonempty and compact for any \(x\in {\mathbb {R}}^d\) and \(\tau >0\).

  2. (ii)

    If f is convex, then \(\mathrm {prox}_\tau ^f(x)\) contains exactly one value for any \(x\in {\mathbb {R}}^d\) and \(\tau >0\).

To describe critical points, we will need the definition of (general) subgradients, see e.g. [40].

Definition 2.2

Let \(f:{\mathbb {R}}^d\rightarrow (-\infty ,\infty ]\) be a proper and lower semi-continuous function and \(v\in {\mathbb {R}}^d\). Then we call

  1. (i)

    v a regular subgradient of f at \({{\bar{x}}}\), written \(v\in {{\hat{\partial }}} f({{\bar{x}}})\), if for all \(x \in {\mathbb {R}}^d\),

    $$\begin{aligned} f(x)\ge f({{\bar{x}}})+\langle v,x-{{\bar{x}}}\rangle +o(\Vert x-{{\bar{x}}}\Vert ). \end{aligned}$$
  2. (ii)

    v a (general) subgradient of f at \({{\bar{x}}}\), written \(v\in \partial f({{\bar{x}}})\), if there are sequences \(x^k \rightarrow {{\bar{x}}}\) and \(v^k\in {{\hat{\partial }}} f(x^k)\) with \(v^k\rightarrow v\) as \(k\rightarrow \infty \).

The following proposition lists useful properties of subgradients.

Proposition 2.3

(Properties of Subgradients) Let \(f:{\mathbb {R}}^{d_1}\rightarrow (-\infty ,\infty ]\) and \(g:{\mathbb {R}}^{d_2}\rightarrow (-\infty ,\infty ]\) be proper and lower semicontinuous and let \(h:{\mathbb {R}}^{d_1}\rightarrow {\mathbb {R}}\) be continuously differentiable. Then the following holds true.

  1. 1.

    For any \(x\in {\mathbb {R}}^{d_1}\), we have \({{\hat{\partial }}} f(x)\subseteq \partial f(x)\). If f is additionally convex, we have \({{\hat{\partial }}} f(x)=\partial f(x)\).

  2. 2.

    For \(x\in {\mathbb {R}}^{d_1}\) with \(f(x)<\infty \), it holds

    $$\begin{aligned} {{\hat{\partial }}} (f+h)(x)={{\hat{\partial }}} f(x)+\nabla h(x) \quad \text {and}\quad \partial (f+h)(x)=\partial f(x)+\nabla h(x). \end{aligned}$$
  3. 3.

    If \(\sigma (x_1,x_2)=f_1(x_1)+f_2(x_2)\), then

    $$\begin{aligned} \left( \begin{array}{c}{\hat{\partial }}_{x_1} f_1({{\bar{x}}}_1)\\ {\hat{\partial }}_{x_2} f_2({{\bar{x}}}_2)\end{array}\right) \subseteq {{\hat{\partial }}} \sigma ({{\bar{x}}}_1,{{\bar{x}}}_2) \quad \text {and}\quad \left( \begin{array}{c}\partial _{x_1} f_1({{\bar{x}}}_1)\\ \partial _{x_2} f_2({{\bar{x}}}_2)\end{array}\right) \subseteq \partial \sigma ({{\bar{x}}}_1,{{\bar{x}}}_2). \end{aligned}$$

Proof

Part (i) was proved in [40, Theorem 8.6 and Proposition 8.12] and part (ii) in [40, Exercise 8.8]. Concerning part (iii) we have for \(v_{x_i} \in {\hat{\partial }}_{x_i} f({{\bar{x}}}_i)\), \(i=1,2\) that for all \((x_1,x_2) \in {\mathbb {R}}^d \times {\mathbb {R}}^d\) it holds

$$\begin{aligned} \sigma (x_1,x_2)=f_1(x_1)+f_2(x_2) \ge \sum _{i=1}^2 f_i({\bar{x}}_i)+\langle v_{x_i},x_i-{{\bar{x}}}_i \rangle + o(\Vert x_i-{{\bar{x}}}_i\Vert ). \end{aligned}$$

This proves the claim for regular subgradients.

For general subgradients consider \(v_{x_i}\in \partial _{x_i} f_i(\bar{x}_i)\), \(i=1,2\) By definition there exist sequences \(x_i^k\rightarrow \bar{x}_i\) and \(v_{x_i}^k\rightarrow v_{x_i}\) with \(v_{x_i}^k \in {\hat{\partial }}_{x_i} f_i(x_i^k)\), \(i=1,2\). By the statement for regular subgradients we know that \((v_{x_1}^k,v_{x_2}^k)\in {\hat{\partial \sigma }}(x_1^k,x_2^k)\). Thus, it follows by definition of the general subgradient that \((v_{x_1},v_{x_2})\in \partial \sigma ({{\bar{x}}}_1,{{\bar{x}}}_2)\). \(\square \)

We call \((x_1,x_2)\in {\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\) a critical point of F if \(0\in \partial F(x_1,x_2)\). By [40, Theorem 10.1] we have that any local minimizer \({{\hat{x}}}\) of a proper and lower semi-continuous function \(f:{\mathbb {R}}^d\rightarrow (-\infty ,\infty ]\) fulfills

$$\begin{aligned} 0\in {{\hat{\partial }}} f({{\hat{x}}})\subseteq \partial f({{\hat{x}}}). \end{aligned}$$

In particular, it is a critical point of f. Further, we have by Proposition 2.3 that \( {{\hat{x}}} \in \mathrm {prox}_\tau ^f(x) \) implies

$$\begin{aligned} 0\in \tau ({{\hat{x}}} - x)+{{\hat{\partial }}} f(y)\subseteq \tau ({{\hat{x}}} - x)+\partial f(y). \end{aligned}$$
(1)

In this paper, we consider functions \(F:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\rightarrow (-\infty ,\infty ]\) of the form

$$\begin{aligned} F(x_1,x_2)=H(x_1,x_2)+f(x_1)+g(x_2) \end{aligned}$$
(2)

with proper, lower semicontinuous functions \(f:{\mathbb {R}}^{d_1}\rightarrow (-\infty ,\infty ]\) and \(g:{\mathbb {R}}^{d_2} \rightarrow (-\infty ,\infty ]\) bounded from below and a continuously differentiable function \(H:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\rightarrow {\mathbb {R}}\). Further, we assume throughout this paper that

$$\begin{aligned} \underline{F}:=\inf _{(x_1,x_2) \in {\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}} F (x_1,x_2) >-\infty . \end{aligned}$$

By Proposition 2.3 it holds

$$\begin{aligned} \left( \begin{array}{c}\partial _{x_1}F(x_1,x_2)\\ \partial _{x_2}F(x_1,x_2)\end{array}\right)&=\nabla H(x_1,x_2) +\left( \begin{array}{c}\partial _{x_1}f(x_1)\\ \partial _{x_2}g(x_2)\end{array}\right) \nonumber \\&\subseteq \nabla H(x_1,x_2) +\partial (f+g)(x_1,x_2)=\partial F(x_1,x_2). \end{aligned}$$
(3)

The generalized gradient of \(F:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\rightarrow (-\infty ,\infty ]\) was defined in [13] as set-valued function

$$\begin{aligned} {\mathscr {G}}F_{\tau _1,\tau _2}(x_1,x_2) := \left( \begin{array}{c}\tau _1(x_1-\mathrm {prox}^f_{\tau _1}(x_1-\tfrac{1}{\tau _1}\nabla _{x_1}H(x_1,x_2)))\\ \tau _2(x_2-\mathrm {prox}^g_{\tau _2}(x_2-\tfrac{1}{\tau _2}\nabla _{x_2}H(x_1,x_2)))\end{array}\right) . \end{aligned}$$

To motivate this definition, note that \(0\in {\mathscr {G}}F_{\tau _1,\tau _2}(x_1,x_2)\) is a sufficient criterion for \((x_1,x_2)\) being a critical point of F. This can be seen as follows: For \((x_1,x_2)\in {\mathscr {G}}F_{\tau _1,\tau _2}(x_1,x_2)\) we have

$$\begin{aligned} x_1\in \mathrm {prox}_{\tau _1}^f(x_1-\tfrac{1}{\tau _1}\nabla _{x_1}H(x_1,x_2)). \end{aligned}$$

Using (1), this implies

$$\begin{aligned} 0\in \tau _1(x_1-x_1+\tfrac{1}{\tau _1}\nabla _{x_1}H(x_1,x_2))+\partial f(x_1)=\nabla _{x_1}H(x_1,x_2)+\partial f(x_1). \end{aligned}$$

Similarly we get \( 0\in \nabla _{x_2}H(x_1,x_2)+\partial g(x_2) \). By (3) we conclude that \((x_1,x_2)\) is a critical point of F.

3 PALM and iPALM

In this section, we review PALM [4] and its inertial version iPALM [36].

3.1 PALM

The following Algorithm 3.1 for minimizing (2) was proposed in [4].

figure a

To prove convergence of PALM the following additional assumptions on H are needed:

Assumption 3.1

(Assumptions on H)

  1. (i)

    For any \(x_1\in {\mathbb {R}}^{d_1}\), the function \(\nabla _{x_2} H(x_1,\cdot )\) is globally Lipschitz continuous with Lipschitz constant \(L_2(x_1)\). Similarly, for any \(x_2\in {\mathbb {R}}^{d_2}\), the function \(\nabla _{x_2} H(\cdot ,x_2)\) is globally Lipschitz continuous with Lipschitz constant \(L_1(x_2)\).

  2. (ii)

    There exist \(\lambda _1^-,\lambda _2^-,\lambda _1^+,\lambda _2^+>0\) such that

    $$\begin{aligned} \inf \{L_1(x_2^{k}):k\in {\mathbb {N}}\}\ge \lambda _1^-\quad&\text {and}\quad \inf \{L_2(x_1^{k}):k\in {\mathbb {N}}\}\ge \lambda _2^-,\\ \sup \{L_1(x_2^{k}):k\in {\mathbb {N}}\}\le \lambda _1^+\quad&\text {and}\quad \sup \{L_2(x_1^{k}):k\in {\mathbb {N}}\}\le \lambda _2^+. \end{aligned}$$

Remark 3.2

Assume that \(H\in {\mathbb {C}}^2({\mathbb {R}}^{d_1\times d_2})\) fulfills Assumption 3.1(i). Then, the authors of [4] showed, that there are partial Lipschitz constants \(L_1(x_2)\) and \(L_2(x_1)\), such that Assumption 3.1(ii) is satisfied. \(\square \)

Convergence results rely on a Kurdyka-Łojasiewicz property of functions which is defined in Appendix A. The following theorem was proven in [4, Lemma 3, Theorem 1].

Theorem 3.3

(Convergence of PALM) Let \(F:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\rightarrow (-\infty ,\infty ]\) be given by (2). Further, assume that it fulfills Assumptions 3.1 and that \(\nabla H\) is Lipschitz continuous on bounded subsets of \({\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\). Let \((x_1^{k},x_2^{k})_k\) be the sequence generated by PALM, where the step size parameters fulfill

$$\begin{aligned} \tau _1^k \ge \gamma _1 L_1(x_2^k), \quad \tau _2^k \ge \gamma _2 L_2(x_1^{k+1}) \end{aligned}$$

for some \(\gamma _1,\gamma _2 >1\). Then, for \(\eta := \min \{(\gamma _1-1)\lambda _1^-,(\gamma _2-1)\lambda _2^-\}\), the sequence \((F(x_1^{k},x_2^{k}))_k\) is nonincreasing and

$$\begin{aligned} \tfrac{\eta }{2}\big \Vert (x_1^{k+1},x_2^{k+1})-(x_1^{k},x_2^{k})\big \Vert _2^2 \le F(x_1^{k},x_2^{k})-F(x_1^{k+1},x_2^{k+1}). \end{aligned}$$

If F is in addition a KL function and the sequence \((x_1^k,x_2^k)_k\) is bounded, then it converges to a critical point of F.

3.2 iPALM

To speed up the performance of PALM the inertial variant iPALM in Algorithm 3.2 was suggested in [36].

figure b

Remark 3.4

(Relation to Momentum Methods) The inertial parameters in iPALM can be viewed as a generalization of momentum parameters for nonsmooth functions. To see this, note that iPALM with one block, \(f=0\) and \(\beta ^k=0\) reads as

$$\begin{aligned} y^k&=x^k+\alpha ^k(x^k-x^{k-1}),\\ x^{k+1}&=y^k-\tfrac{1}{\tau ^k}\nabla H(x^k). \end{aligned}$$

By introducing \(g^k:= x^k-x^{k-1}\), this can be rewritten as

$$\begin{aligned} g^{k+1}&=\alpha ^k g^k - \tfrac{1}{\tau ^k} \nabla H(x^k),\\ x^{k+1}&=x^k+g^{k+1}. \end{aligned}$$

This is exactly the momentum method as introduced by Polyak in [37]. Similar, if \(f=0\) and \(\alpha ^k=\beta ^k\ne 0\), iPALM can be rewritten as

$$\begin{aligned} g^{k+1}&=\alpha ^k g^k - \tfrac{1}{\tau ^k} \nabla H(x^k+\alpha ^k g^k),\\ x^{k+1}&=x^k+g^{k+1}, \end{aligned}$$

which is known as Nesterov’s Accelerated Gradient (NAG) [32]. Consequently, iPALM can be viewed as a generalization of both the classical momentum method and NAG to the nonsmooth case. Even if there exists no proof of tighter convergence rates for iPALM than for PALM, this motivates that the inertial steps really accelerate PALM, since NAG has tighter convergence rates than a plain gradient descent algorithm provided that the objective function is convex. \(\square \)

To prove the convergence of iPALM the parameters of the algorithm must be carefully chosen.

Assumption 3.5

(Conditions on the Parameters of iPALM) Let \(\lambda _i^+\), \(i=1,2\) and \(L_1(x_2^k)\), \(L_2(x_1^k)\) be defined by Assumption 3.1. There exists some \(\epsilon >0\) such that for all \(k\in {\mathbb {N}}\) and \(i=1,2\) the following holds true:

  1. (i)

    There exist \(0<{{\bar{\alpha }}}_i<\tfrac{1-\epsilon }{2}\) such that \(0\le \alpha _i^{k}\le {{\bar{\alpha }}}_i\) and \(0< {{\bar{\beta }}}_i \le 1\) such that \(0\le \beta _i^{k}\le {{\bar{\beta }}}_i\).

  2. (ii)

    The parameters \(\tau _1^{k}\) and \(\tau _2^{k}\) are given by

    $$\begin{aligned} \tau _1^{k}:= \frac{(1+\epsilon )\delta _1+(1+{{\bar{\beta }}}_1)L_1(x_2^{k})}{1-\alpha _1^{k}} \quad \text {and}\quad \tau _2^{k}:= \frac{(1+\epsilon )\delta _2+(1+{{\bar{\beta }}}_2)L_2(x_1^ {k+1})}{1-\alpha _2^{k}}, \end{aligned}$$

    and for \(i=1,2\),

    $$\begin{aligned} \delta _i:= \frac{\bar{\alpha }_i+{{\bar{\beta }}}_i}{1-\epsilon -2{{\bar{\alpha }}}_i}\lambda _i^+ . \end{aligned}$$

The following theorem was proven in [36, Theorem 4.1].

Theorem 3.6

(Convergence of iPALM) Let \(F:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\rightarrow (-\infty ,\infty ]\) given by (2) be a KL function. Suppose that H fulfills the Assumptions 3.1 and that \(\nabla H\) is Lipschitz continuous on bounded subsets of \({\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\). Further, let the parameters of iPALM fulfill the parameter conditions of Assumption 3.5. If the sequence \((x_1^{k},x_2^{k})_k\) generated by iPALM is bounded, then it converges to a critical point of F.

Remark 3.7

Even though we cited PALM and iPALM just for two blocks \((x_1,x_2)\) of variables, the convergence proofs from [4] and [36] even work with more than two blocks. \(\Box \)

4 iSPALM

In many problems in imaging and machine learning the function \(H:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\rightarrow {\mathbb {R}}\) in (2) is of the form

$$\begin{aligned} H(x_1,x_2)=\frac{1}{n}\sum _{i=1}^n h_i(x_1,x_2), \end{aligned}$$
(4)

where n is large. Then the computation of the gradients in PALM and iPALM is very time consuming. The idea to combine stochastic gradient estimators with a PALM scheme was first discussed by Xu and Yin in [46]. The authors replaced the gradient in Algorithm 3.1 by the stochastic gradient descent (SGD) estimator

$$\begin{aligned} {{\tilde{\nabla }}}_{x_i} H(x_1,x_2) := \frac{1}{b}\sum _{j\in B}\nabla _{x_i}h_j(x_1,x_2), \end{aligned}$$

where \(B\subset \{1,\ldots ,n\}\) is a random subset (mini-batch) of fixed batch size \(b=|I|\). This gives Algorithm 4.1 which we call SPALM.

figure c

Xu and Yin showed in [46] under rather strong assumptions, in particular f, g have to be Lipschitz continuous and the variance of the SGD estimator has to be bounded, that there exists a subsequence \((x_1^k,x_2^k)_k\) of iterates generated by Algorithm 4.1 such that the sequence \({\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^k,x_2^k) \right) \) converges to zero as \(k \rightarrow \infty \). If F, f and g are strongly convex, the authors proved also convergence of the function values to the infimum of F.

Driggs et al. [13] could weaken the assumptions and improve the convergence rate by replacing the SGD estimator by so-called variance-reduced gradient estimators \({{\tilde{\nabla }}}\). They called their method SPRING.

However, in deep learning with nonsmooth functions, the combination of momentum-like methods and a stochastic gradient estimator turned out to be essential [15, 43]. To this end, we define inertial variance-reduced gradient estimators in a slightly different way as in [13].

Definition 4.1

(Inertial Variance-Reduced Gradient Estimator) A gradient estimator \({{\tilde{\nabla }}}\) is called inertial variance-reduced for a differentiable function \(H: {\mathbb {R}}^{d_1} \times {\mathbb {R}}^{d_2} \rightarrow {\mathbb {R}}\) with constants \(V_1,V_\Upsilon \ge 0\) and \(\rho \in (0,1]\), if for any sequence \((x^k)_k=(x_1^k,x_2^k)_{k \in {\mathbb {N}}_0}\), \(x^{-1} := x^0\) and any \(0 \le \beta _i^k < \bar{\beta }_i\), \(i=1,2\) there exists a sequence of random variables \((\Upsilon _k)_{k \in {\mathbb {N}}}\) with \({\mathbb {E}}(\Upsilon _1) < \infty \) such that following holds true:

  1. (i)

    For \(z_i^{k}:= x_i^{k}+\beta _i^{k}(x_i^{k}-x_i^{k-1})\), \(i=1,2\), we have

    $$\begin{aligned}&{\mathbb {E}}_k(\Vert {{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)-\nabla _{x_1}H(z_1^k,x_2^k)\Vert ^2+\Vert {{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^k)\\&\quad -\nabla _{x_2}H(x_1^{k+1},z_2^k)\Vert ^2) \\&\quad \le \Upsilon _k + V_1 \left( {\mathbb {E}}_k(\Vert x^{k+1}-x^k\Vert ^2)+\Vert x^k-x^{k-1}\Vert ^2+\Vert x^{k-1}-x^{k-2}\Vert ^2 \right) . \end{aligned}$$
  2. (ii)

    The sequence \((\Upsilon _k)_k\) decays geometrically, that is

    $$\begin{aligned}&{\mathbb {E}}_k(\Upsilon _{k+1})\le (1-\rho )\Upsilon _k+V_\Upsilon ({\mathbb {E}}_k(\Vert x^{k+1}\!-\!x^k\Vert ^2)\!+\!\Vert x^k\!-\!x^{k-1}\Vert ^2\\&\quad +\Vert x^{k-1}-x^{k-2}\Vert ^2). \end{aligned}$$
  3. (iii)

    If \(\lim _{k\rightarrow \infty }{\mathbb {E}}(\Vert x^k-x^{k-1}\Vert ^2)=0\), then \({\mathbb {E}}(\Upsilon _k)\rightarrow 0\) as \(k \rightarrow \infty \).

While the SGD estimator is not inertial variance-reduced, we will show that the SARAH [33] estimator has this property.

Definition 4.2

(SARAH Estimator) The SARAH estimator reads for \(k=0\) as

$$\begin{aligned} {{\tilde{\nabla }}}_{x_1} H(x_1^0,x_2^0)=\nabla _{x_1} H(x_1^0,x_2^0). \end{aligned}$$

For \(k=1,2,\ldots \) we define random variables \(p_i^k\in \{0,1\}\) with \(P(p_i^k=0)=\tfrac{1}{p}\) and \(P(p_i^k=1)=1-\tfrac{1}{p}\), where \(p\in (1,\infty )\) is a fixed chosen parameter. Further, we define \(B_i^k\) to be random subsets uniformly drawn from \(\{1,\ldots ,n\}\) of fixed batch size b. Then for \(k=1,2,\ldots \) the SARAH estimator reads as

$$\begin{aligned} {{\tilde{\nabla }}}_{x_1} H(x_1^k,x_2^k) = {\left\{ \begin{array}{ll} \nabla _{x_1} H(x_1^k,x_2^k),&{}\ \text {if}\ p_1^k=0,\\ \tfrac{1}{b} \sum \nolimits _{i\in B_i^k}\nabla _{x_1} h_i(x_1^k,x_2^k)-\nabla _{x_1} h_i(x_1^{k-1},x_2^{k-1}) + {{\tilde{\nabla }}}_{x_1}H(x_1^{k-1},x_2^{k-1}),&{}\text {if}\ p_1^k=1, \end{array}\right. } \end{aligned}$$

and analogously for \({{\tilde{\nabla }}}_{x_2} H\). In the sequel, we assume that the family of the random elements \(p_i^k\), \(B_i^k\) for \(i=1,2\) and \(k=1,2,\ldots \) is independent.

Indeed, we can show the desired property of the SARAH gradient estimator.

Proposition 4.3

Let \(H:{\mathbb {R}}^{d_1} \times {\mathbb {R}}^{d_2} \rightarrow {\mathbb {R}}\) be given by (4) with functions \(h_i:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\) having a globally M-Lipschitz continuous gradient. Then the SARAH estimator \({{\tilde{\nabla }}}\) is inertial variance-reduced with parameters \(\rho =\tfrac{1}{p}\) and

$$\begin{aligned} V_\Upsilon = 3(1-\tfrac{1}{p})M^2 \left( 1+\max \left( ({{\bar{\beta }}}_1)^2,({{\bar{\beta }}}_2)^2\right) \right) . \end{aligned}$$

Furthermore, we can choose

$$\begin{aligned} \Upsilon _{k+1} = \Vert {{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)-\nabla _{x_1}H(z_1^k,x_2^k)\Vert ^2 +\Vert {{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^k)-\nabla _{x_2}H(x_1^{k+1},z_2^k)\Vert ^2. \end{aligned}$$

For the proof which follows mainly the path of [13, Proposition 2.2], but must be nevertheless carefully adapted to the inertial setting, we refer to [21].

Finally, we can propose our inertial stochastic PALM (iSPALM) algorithm with SARAH estimator \({{\tilde{\nabla }}}\) in Algorithm 4.2.

figure d

Remark 4.4

Similarly as in Remark 3.4, iSPALM can be viewed as a generalization of the stochastic versions of the momentum method and NAG to the nonsmooth case. Note, that in the stochastic setting the theoretical error bounds of momentum methods are not tighter than for a plain gradient descent. An overview over these convergence results can be found in [15, 43]. Consequently, we are not able to show tighter convergence rates for iSPALM than for stochastic PALM. Nevertheless, stochastic momentum methods as the momentum SGD and the Adam optimizer [25] are widely used and have shown a better convergence behavior than a plain SGD in a huge number of applications. \(\Box \)

5 Convergence analysis of iSPALM

We assume that the parameters of iSPALM fulfill the following conditions.

Assumption 5.1

(Conditions on the Parameters of iSPALM) Let \(\lambda _i^+\), \(i=1,2\) and \(L_1(x_2^k)\), \(L_2(x_1^k)\) be defined by Assumption 3.1 and \(\rho , V_1,V_\Upsilon \) by Definition 4.1. Further, let \(H:{\mathbb {R}}^{d_1} \times {\mathbb {R}}^{d_2} \rightarrow {\mathbb {R}}\) be given by (4) with functions \(h_i:{\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}\) having a globally M-Lipschitz continuous gradient. There exist \(\epsilon ,\varepsilon >0\) such that for all \(k\in {\mathbb {N}}\) and \(i=1,2\) the following holds true:

  1. (i)

    There exist \(0<{{\bar{\alpha }}}_i<\tfrac{1-\epsilon }{2}\) such that \(0\le \alpha _i^{k}\le {{\bar{\alpha }}}_i\) and \(0<{{\bar{\beta }}}_i\le 1\) such that \(0\le \beta _i^{k}\le {{\bar{\beta }}}_i\)

  2. (ii)

    The parameters \(\tau _i^{k}\), \(i=1,2\) are given by

    $$\begin{aligned} \tau _1^{k} := \frac{(1+\epsilon )\delta _1+M+L_1(x_2^k)+S}{1-\alpha _1^k}, \quad \mathrm {and} \quad \tau _2^{k} := \frac{(1+\epsilon )\delta _2+M+L_2(x_1^{k+1})+S}{1-\alpha _2^k}, \end{aligned}$$

    where \(S := 4 \tfrac{\rho V_1+V_\Upsilon }{\rho M}+\varepsilon \) and for \(i=1,2\),

    $$\begin{aligned} \delta _i := \frac{(M+\lambda _i^+){{\bar{\alpha }}}_i+2\lambda _i^+{{\bar{\beta }}}_i^2+S}{1-2{{\bar{\alpha }}}_i-\epsilon }. \end{aligned}$$

To analyze the convergence behavior of iSPALM, we start with two auxiliary lemmas. The first one can be proven analogously to [36, Proposition 4.1].

Lemma 5.2

Let \((x_1^k,x_2^k)_k\) be an arbitrary sequence and \(\alpha _i^k,\beta _i^k\in {\mathbb {R}}\), \(i=1,2\). Further define

$$\begin{aligned} y_i^{k}:= x_i^{k}+\alpha _i^{k}(x_i^{k}-x_i^{k-1}),\quad z_i^{k}:= x_i^{k}+\beta _i^{k}(x_i^{k}-x_i^{k-1}), \quad i=1,2, \end{aligned}$$

and

$$\begin{aligned} \Delta _i^k := \tfrac{1}{2}\Vert x_i^k-x_i^{k-1}\Vert ^2, \qquad i=1,2. \end{aligned}$$

Then, for any \(k\in {\mathbb {N}}\) and \(i=1,2\), we have

  1. (i)

    \(\Vert x_i^k-y_i^k\Vert ^2=2(\alpha _i^k)^2\Delta _i^k\),

  2. (ii)

    \(\Vert x_i^k-z_i^k\Vert ^2=2(\beta _i^k)^2\Delta _i^k\),

  3. (iii)

    \(\Vert x_i^{k+1}-y_i^k\Vert ^2\ge 2(1-\alpha _i^k \Delta _i^{k+1}+2\alpha _i^k)(\alpha _i^k-1)\Delta _i^k\).

The second auxiliary lemma can be proven analogously to [36, Lemma 3.2].

Lemma 5.3

Let \(\psi =\sigma +h\), where \(h:{\mathbb {R}}^d\rightarrow {\mathbb {R}}\) is a continuously differentiable function with \(L_h\)-Lipschitz continuous gradient, and \(\sigma :{\mathbb {R}}^d\rightarrow (-\infty ,\infty ]\) is proper and lower semicontinuous with \(\inf _{{\mathbb {R}}^d}\sigma >-\infty \). Then it holds for any \(u,v,w\in {\mathbb {R}}^d\) and any \(u^+\in {\mathbb {R}}^d\) defined by

$$\begin{aligned} u^+\in \mathrm {prox}_t^\sigma (v-\tfrac{1}{t} {{\tilde{\nabla }}} h(w)),\quad t>0 \end{aligned}$$

that

$$\begin{aligned} \psi (u^+)\le & {} \psi (u)+\langle u^+-u,\nabla h(u)-{{\tilde{\nabla }}} h(w)\rangle + \frac{L_h}{2}^2 \Vert u - u^+\Vert ^2\\&+\frac{t}{2}\Vert u-v\Vert ^2-\frac{t}{2}\Vert u^+-v\Vert ^2. \end{aligned}$$

Now we can establish a result on the expectation of squared subsequent iterates. Note that equivalent results were shown for PALM, iPALM and SPRING. Here we use a function \(\Psi \), which not only contains the current function value, but also the distance of the iterates to the previous ones. A similar idea was used in the convergence proof of iPALM [36]. Nevertheless, incorporating the stochastic gradient estimator here makes the proof much more involved.

Theorem 5.4

Let \(F:{\mathbb {R}}^{d_1} \times {\mathbb {R}}^{d_2}\rightarrow (-\infty ,\infty ]\) be given by (2) and fulfill Assumption 3.1. Let \((x_1^k,x_2^k)_k\) be generated by iSPALM with parameters fulfilling Assumption 5.1, where we use an inertial variance-reduced gradient estimator \({{\tilde{\nabla }}}\). Then it holds for \(\Psi :({\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2})^3 \rightarrow {\mathbb {R}}\) defined for \(u = (u_{11},u_{12},u_{21},u_{22},u_{31},u_{32}) \in ({\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2})^3\) by

$$\begin{aligned} \Psi (u)&:= F(u_{11},u_{12})+\tfrac{\delta _1}{2}\Vert u_{11}-u_{21}\Vert ^2+\tfrac{\delta _2}{2}\Vert u_{12}-u_{22}\Vert ^2\\&\quad +\tfrac{S}{4} \left( \Vert u_{21}-u_{31}\Vert ^2+\Vert u_{22}-u_{32}\Vert ^2\right) \end{aligned}$$

that there exists \(\gamma >0\) such that

$$\begin{aligned} \Psi (u^1)-\inf _{u\in ({\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2})^2}\Psi (u)+\tfrac{1}{M\rho }{\mathbb {E}}(\Upsilon _1) \ge \gamma \sum _{k=0}^T{\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2), \end{aligned}$$

where \(u^k := (x_1^k,x_2^k,x_1^{k-1},x_2^{k-1},x_1^{k-2},x_2^{k-2} )\). In particular, we have

$$\begin{aligned} \sum _{k=0}^\infty {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)<\infty . \end{aligned}$$

Proof

By Lemma 5.3 with \(\psi := H(\cdot ,x_2) + f\), we obtain

$$\begin{aligned} H(x_1^{k+1},x_2^k)+f(x_1^{k+1})&\le H(x_1^k,x_2^k)+f(x_1^k)\nonumber \\&\quad + \left\langle x_1^{k+1}-x_1^k,\nabla _{x_1} H(x_1^k,x_2^k)-{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k) \right\rangle \nonumber \\&\quad + \tfrac{L_1(x_2^k)}{2} \Vert x_1^{k+1}-x_1^k\Vert ^2+\tfrac{\tau _1^k}{2}\Vert x_1^k-y_1^k\Vert ^2-\tfrac{\tau _1^k}{2}\Vert x_1^{k+1}-y_1^k\Vert ^2. \end{aligned}$$
(5)

Using \(ab \le \frac{s}{2} a^2 + \frac{1}{2s} b^2\) for \(s>0\) and \(\Vert a-c\Vert ^2\le 2\Vert a-b\Vert ^2+2\Vert b-c\Vert ^2\) the inner product is smaller or equal than

$$\begin{aligned}&\tfrac{s_1^k}{2}\Vert x_1^{k+1}-x_1^k\Vert ^2+\tfrac{1}{2s_1^k}\Vert \nabla _{x_1} H(x_1^k,x_2^k)-{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)\Vert ^2\\&\quad \le \tfrac{s_1^k}{2}\Vert x_1^{k+1}-x_1^k\Vert ^2+\tfrac{1}{s_1^k}\Vert \nabla _{x_1} H(z_1^k,x_2^k)-{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)\Vert ^2\\&\qquad +\tfrac{1}{s_1^k}\Vert \nabla _{x_1} H(x_1^k,x_2^k)-\nabla _{x_1} H(z_1^k,x_2^k)\Vert ^2 \\&\quad =\tfrac{s_1^k}{2}\Vert x_1^{k+1}-x_1^k\Vert ^2+\tfrac{1}{s_1^k}\Vert \nabla _{x_1} H(z_1^k,x_2^k) -{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)\Vert ^2+\tfrac{L_1(x_2^k)^2}{s_1^k}\Vert x_1^k - z_1^k\Vert ^2. \end{aligned}$$

Combined with (5) this becomes

$$\begin{aligned}&H(x_1^{k+1},x_2^k)+f(x_1^{k+1})\\&\quad \le H(x_1^k,x_2^k)+f(x_1^k) + \tfrac{L_1(x_2^k)}{2} \Vert x_1^{k+1}-x_1^k\Vert ^2+\tfrac{\tau _1^k}{2}\Vert x_1^k-y_1^k\Vert ^2-\tfrac{\tau _1^k}{2}\Vert x_1^{k+1}-y_1^k\Vert ^2\\&\qquad +\tfrac{s_1^k}{2}\Vert x_1^{k+1}-x_1^k\Vert ^2+\tfrac{1}{s_1^k}\Vert \nabla _{x_1} H(z_1^k,x_2^k)-{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)\Vert ^2 +\tfrac{L_1(x_2^k)^2}{s_1^k}\Vert x_1^k - z_1^k\Vert ^2. \end{aligned}$$

Using Lemma 5.2 we get

$$\begin{aligned}&H(x_1^{k+1},x_2^k)+f(x_1^{k+1})\\&\quad \le H(x_1^k,x_2^k)+f(x_1^k)+ \left( L_1(x_2^k)+s_1^k-\tau _1^k(1-\alpha _1^k) \right) \Delta _1^{k+1} \\&\qquad +\tfrac{1}{s_1^k} \left( 2L_1(x_2^k)^2(\beta _1^k)^2+s_1^k\tau _1^k\alpha _1^k \right) \Delta _1^k +\tfrac{1}{s_1^k}\Vert \nabla _{x_1} H(z_1^k,x_2^k)-{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)\Vert ^2. \end{aligned}$$

Analogously we conclude for \(\psi := H(x_1,\cdot ) + g\) that

$$\begin{aligned}&H(x_1^{k+1},x_2^{k+1})+g(x_2^{k+1})\\&\quad \le H(x_1^{k+1},x_2^k)+g(x_2^k)+ \left( L_2(x_1^{k+1})+s_2^k-\tau _2^k(1-\alpha _2^k) \right) \Delta _2^{k+1}\\&\qquad +\tfrac{1}{s_2^k} \left( 2L_2(x_1^{k+1})^2(\beta _2^k)^2+s_2^k\tau _2^k\alpha _2^k \right) \Delta _2^k +\tfrac{1}{s_2^k}\Vert \nabla _{x_2} H(x_1^{k+1},z_2^k)-{{\tilde{\nabla }}}_{x_2} H(x_1^{k+1},z_2^k)\Vert ^2. \end{aligned}$$

Adding the last two inequalities and using the abbreviation \(L_1^k := L_1(x_2^k)\) and \(L_2^k := L_2(x_1^{k+1})\), we obtain

$$\begin{aligned}&F(x_1^{k+1},x_2^{k+1}) \le F(x_1^k,x_2^k)\nonumber \\&\quad + \sum _{i=1}^2 \left( \left( L_i^k+s_i^k-\tau _i^k(1-\alpha _i^k)\right) \Delta _i^{k+1} +\tfrac{1}{s_i^k}\left( 2 (L_i^k)^2(\beta _i^k)^2+s_i^k\tau _i^k\alpha _i^k\right) \Delta _i^k \right) \nonumber \\&\quad +\tfrac{1}{s_1^k}\Vert \nabla _{x_1} H(z_1^k,x_2^k)-{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)\Vert ^2 +\tfrac{1}{s_2^k}\Vert \nabla _{x_2} H(x_1^{k+1},z_2^k)-{{\tilde{\nabla }}}_{x_2} H(x_1^{k+1},z_2^k)\Vert ^2 . \end{aligned}$$
(6)

Reformulating (6) in terms of

$$\begin{aligned} \Psi (u^k) = F(x_1^k,x_2^k)+\delta _1 \Delta _1^k+\delta _2\Delta _2^k+ \tfrac{S}{2}(\Delta _1^{k-1}+\Delta _2^{k-1}) \end{aligned}$$
(7)

leads to

$$\begin{aligned}&\Psi (u^k)-\Psi (u^{k+1}) =F(x_1^k,x_2^k)-F(x_1^{k+1},x_2^{k+1})+\delta _1\Delta _1^k+\delta _2\Delta _2^k-\delta _1\Delta _1^{k+1}-\delta _2\Delta _2^{k+1}\nonumber \\&\qquad + \tfrac{S}{2}\left( \Delta _1^{k-1} + \Delta _2^{k-1} - \Delta _1^k - \Delta _2^k\right) \nonumber \\&\quad \ge \sum _{i=1}^2 \left( \left( \tau ^k_i(1-\alpha _i^k)-s_i^k-L_i^k-\delta _i \right) \Delta _i^{k+1}\right) + \sum _{i=1}^2 \left( \left( \delta _i-\tfrac{2}{s_i^k} (L_i^k)^2 (\beta _i^k)^2-\tau _i^k\alpha _i^k\right) \Delta _i^k\right) \nonumber \\&\qquad - \tfrac{1}{s_1^k}\Vert \nabla _{x_1} H(z_1^k,x_2^k)-{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)\Vert ^2 - \tfrac{1}{s_2^k}\Vert \nabla _{x_2} H(x_1^{k+1},z_2^k)-{{\tilde{\nabla }}}_{x_2} H(x_1^{k+1},z_2^k)\Vert ^2\nonumber \\&\quad + \tfrac{S}{2}\left( \Delta _1^{k-1} + \Delta _2^{k-1} - \Delta _1^k - \Delta _2^k\right) . \end{aligned}$$
(8)

Now, we set \(s_1^k=s_2^k:= M\) use that \(L_i^k\le M\), take the conditional expectation \({\mathbb {E}}_k\) in (8) and use that \({{\tilde{\nabla }}}\) is an inertial variance-reduced estimator to get

$$\begin{aligned}&\Psi (u^k)-{\mathbb {E}}_k(\Psi (u^{k+1}))\nonumber \\&\quad \ge \sum _{i=1}^2 \left( \left( \tau ^k_i(1-\alpha _i^k)\!-\! M\!-\! L_i^k-\delta _i \right) {\mathbb {E}}_k(\Delta _i^{k+1}) + \left( \delta _i-\tfrac{2}{M} (L_i^k)^2(\beta _i^k)^2-\tau _i^k\alpha _i^k\right) \Delta _i^k \right) \nonumber \\&\qquad - \tfrac{2V_1}{M} \sum _{i=1}^2 \left( {\mathbb {E}}_k(\Delta _i^{k+1})+\Delta _i^k \right) - \tfrac{1}{M}\Upsilon _k + \tfrac{S}{2}\left( \Delta _1^{k-1} + \Delta _2^{k-1}- \Delta _1^k - \Delta _2^k\right) \nonumber \\&\quad \ge \sum _{i=1}^2 \left( \left( \tau ^k_i(1-\alpha _i^k)-M-L_i^k-\delta _i-\tfrac{2V_1}{M}\right) {\mathbb {E}}_k(\Delta _i^{k+1}) \right) \nonumber \\&\qquad + \sum _{i=1}^2 \left( \left( \delta _i-2 L_i^k(\beta _i^k)^2-\tau _i^k\alpha _i^k-\tfrac{2V_1}{M}\right) \Delta _i^k \right) \nonumber \\&\qquad - \tfrac{1}{M}\Upsilon _k + \tfrac{S}{2}\left( \Delta _1^{k-1} + \Delta _2^{k-1}- \Delta _1^k - \Delta _2^k\right) . \end{aligned}$$
(9)

Since \({{\tilde{\nabla }}}\) is inertial variance-reduced, we know from Definition 4.1 (ii) that

$$\begin{aligned} \rho \Upsilon _k \le \Upsilon _k-{\mathbb {E}}_k(\Upsilon _{k+1}) + 2V_\Upsilon \sum _{i=1}^2 \left( {\mathbb {E}}_k(\Delta _i^{k+1})+\Delta _i^k + \Delta _i^{k-1}\right) . \end{aligned}$$
(10)

Inserting this in (9) and using the definition of S yields

$$\begin{aligned}&\Psi (u^k)-{\mathbb {E}}_k\left( \Psi (u^{k+1}) \right) \ge \sum _{i=1}^2 \left( \left( \tau ^k_i (1-\alpha _i^k)-M-L_i^k)-\delta _i- \tfrac{S}{2} \right) {\mathbb {E}}_k(\Delta _i^{k+1}) \right) \nonumber \\&\qquad + \sum _{i=1}^2 \left( \left( \delta _i-2 L_i^k (\beta _i^k)^2-\tau _i^k\alpha _i^k-\tfrac{S}{2} \right) \Delta _i^k \right) \nonumber \\&\qquad - \frac{2 V_\Upsilon }{\rho M} (\Delta _1^{k-1} + \Delta _2^{k-1}) + \tfrac{1}{M\rho } \left( {\mathbb {E}}_k(\Upsilon _{k+1})-\Upsilon _k \right) + \tfrac{S}{2}\left( \Delta _1^{k-1} + \Delta _2^{k-1}- \Delta _1^k - \Delta _2^k\right) \nonumber \\&\quad \ge \sum _{i=1}^2 \Big ( \underbrace{ \left( \tau ^k_i (1-\alpha _i^k)-M-L_i^k -\delta _i- S \right) }_{a^k_i} {\mathbb {E}}_k(\Delta _i^{k+1}) \Big )\nonumber \\&\qquad + \sum _{i=1}^2 \Big ( \underbrace{ \left( \delta _i- 2 L_i^k(\beta _i^k)^2-\tau _i^k\alpha _i^k-S \right) }_{b^k_i} \Delta _i^k \Big )\nonumber \\&\qquad + \tfrac{1}{M\rho } \left( {\mathbb {E}}_k(\Upsilon _{k+1})-\Upsilon _k \right) + \left( \tfrac{S}{2} - \tfrac{2 V_\Upsilon }{\rho M}\right) \left( \Delta _1^{k-1} + \Delta _2^{k-1}\right) . \end{aligned}$$
(11)

Choosing \(\tau _i^k\), \(\delta _i\), \(i=1,2\) and \(\epsilon \) as in Assumption 5.1(ii), we obtain by straightforward computation for \(i=1,2\) and all \(k \in {\mathbb {N}}\) that \(a_i^k = \epsilon \delta _i\) and

$$\begin{aligned} b_i^k&= \tfrac{1}{1-\alpha _i^k} \left( (1- \epsilon - 2 \alpha _i^k) \delta _i - \alpha _i^k M - S - L_i^k \left( 2(\beta _i^k)^2(1-\alpha _i^k) + \alpha _i^k \right) \right) +\epsilon \delta _i\\&\ge \tfrac{1}{1-\alpha _i^k} \left( (1- \epsilon - 2 {{\bar{\alpha }}}_i) \delta _i - {{\bar{\alpha }}}_i M - S - \lambda _i^ + \left( 2(\bar{\beta }_i)^2(1-\alpha _i^k) + {{\bar{\alpha }}}_i \right) \right) +\epsilon \delta _i\\&= \epsilon \delta _i + 2 \frac{2 \lambda _i^+\alpha _i^k (\bar{\beta }_i)^2 }{1-\alpha _i^k} \ge \epsilon \delta _i. \end{aligned}$$

Applying this in (11), we get

$$\begin{aligned} \Psi (u^k)-{\mathbb {E}}_k\left( \Psi (u^{k+1}) \right)&\ge \epsilon \min (\delta _1,\delta _2) \sum _{i=1}^2 ({\mathbb {E}}_k(\Delta _i^{k+1})+\Delta _i^k)\\&\quad +\tfrac{1}{M\rho }({\mathbb {E}}_k(\Upsilon _{k+1})-\Upsilon _k) + \left( \tfrac{S}{2}- \tfrac{2 V_\Upsilon }{\rho M}\right) \left( \Delta _1^{k-1} + \Delta _2^{k-1}\right) . \end{aligned}$$

By definition of S it holds \(\left( \frac{2 V_\Upsilon }{\rho M}-\tfrac{S}{2}\right) \ge \varepsilon \). Thus, we get for \(\gamma := \tfrac{1}{2} \min (\epsilon \delta _1,\epsilon \delta _2,\varepsilon )\) that

$$\begin{aligned} \Psi (u^k)-{\mathbb {E}}_k\left( \Psi (u^{k+1}) \right)&\ge 2\gamma \sum _{i=1}^2 \left( {\mathbb {E}}_k(\Delta _i^{k+1})+\Delta _i^k+ \Delta _i^{k-1} \right) +\tfrac{1}{M\rho }({\mathbb {E}}_k(\Upsilon _{k+1})-\Upsilon _k). \end{aligned}$$

Taking the full expectation yields

$$\begin{aligned} {\mathbb {E}}(\Psi (u^k)-\Psi (u^{k+1}))&\ge \gamma {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)+\tfrac{1}{M\rho }{\mathbb {E}}(\Upsilon _{k+1}-\Upsilon _k), \end{aligned}$$
(12)

and summing up for \(k=1,\ldots ,T\),

$$\begin{aligned} {\mathbb {E}}(\Psi (u^1)-\Psi (u^{T+1}))&\ge \gamma \sum _{k=0}^T{\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)+\tfrac{1}{M\rho }{\mathbb {E}}(\Upsilon _{T+1}-\Upsilon _1). \end{aligned}$$

Since \(\Upsilon _k\ge 0\), this yields

$$\begin{aligned} \gamma \sum _{k=0}^T{\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2) \le \Psi (u^1)-\underbrace{\inf _{u\in ({\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2})^2}\Psi (u)}_{>-\infty }+\underbrace{\tfrac{1}{M\rho }{\mathbb {E}}(\Upsilon _1)}_{<\infty } < \infty . \end{aligned}$$

This finishes the proof. \(\square \)

Next, we want relate the sequence of iterates generated by iSPALM to the subgradient of the objective function. Such a relation was also established for the (inertial) PALM algorithm. However, due to the stochastic gradient estimator the proof differs significantly from its deterministic counterparts. Note that the convergence analysis of SPRING in [13] does not use the subdifferential but the so-called generalized gradient \({\mathscr {G}}F_{\tau _1,\tau _2}\). This is not satisfying at all, since it becomes not clear how this generalized gradient is related to the (sub)differential of the objective function in limit processes with varying \(\tau _1\) and \(\tau _2\). In particular, it is easy to find examples of F and sequences \((\tau _1^k)_k\) and \((\tau _2^k)_k\) such that the generalized gradient \({\mathscr {G}}F_{\tau _1^k,\tau _2^k}(x_1,x_2)\) is non-zero, but converges to zero for fixed \(x_1\) and \(x_2\).

Theorem 5.5

Under the assumptions of Theorem 5.4 there exists some \(C>0\) such that

$$\begin{aligned} {\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) \le C {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)+3{\mathbb {E}}(\Upsilon _k). \end{aligned}$$

In particular, it holds

$$\begin{aligned} {\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2 \right) \rightarrow 0\quad \text {as }k\rightarrow \infty . \end{aligned}$$

Proof

By definition of \(x_1^{k+1}\), and (1) as well as Proposition 2.3 it holds

$$\begin{aligned} 0\in \tau _1^k(x_1^{k+1}-y_1^k)+{{\tilde{\nabla }}}_{x_1} H(z_1^k,x_2^k)+\partial f(x_1^{k+1}). \end{aligned}$$

This is equivalent to

$$\begin{aligned}&\tau _1^k(y_1^k-x_1^{k+1})+\nabla _{x_1}H(x_1^{k+1},x_2^{k+1})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\\&\quad \in \nabla _{x_1} H(x_1^{k+1},x_2^{k+1})+\partial f(x_1^{k+1}) \in \partial _{x_1} F(x_1^{k+1},x_2^{k+1}). \end{aligned}$$

Analogously we get that

$$\begin{aligned}&\tau _2^k(y_2^k-x_2^{k+1})+\nabla _{x_2}H(x_1^{k+1},x_2^{k+1})-{{\tilde{\nabla }}}_{x_1}H(x_1^{k+1},z_2^k)\\&\quad \in \nabla _{x_2} H(x_1^{k+1},x_2^{k+1})+\partial g(x_2^{k+1}) \in \partial _{x_2} F(x_1^{k+1},x_2^{k+1}). \end{aligned}$$

Then we obtain by Proposition 2.3 that

$$\begin{aligned} v := \left( \begin{array}{c}\tau _1^k(y_1^k-x_1^{k+1})+\nabla _{x_1}H(x_1^{k+1},x_2^{k+1})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\\ \tau _2^k(y_2^k-x_2^{k+1})+\nabla _{x_2}H(x_1^{k+1},x_2^{k+1})-{{\tilde{\nabla }}}_{x_1}H(x_1^{k+1},z_2^k)\end{array}\right) \in \partial F(x_1^{k+1},x_2^{k+1}), \end{aligned}$$

and it remains to show that the squared norm of v is in expectation bounded by \(C {\mathbb {E}}( \Vert u^{k+1}-u^k\Vert ^2)+3{\mathbb {E}}(\Upsilon _k)\) for some \(C>0\). Using \((a+b+c)^2 \le 3(a^2+b^2+c^2)\) we estimate

$$\begin{aligned} \Vert v\Vert ^2&= \Vert \tau _1^k(y_1^k-x_1^{k+1})+\nabla _{x_1}H(x_1^{k+1},x_2^{k+1})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\Vert ^2\\&\quad +\Vert \tau _2^k(y_2^k-x_2^{k+1})+\nabla _{x_2}H(x_1^{k+1},x_2^{k+1})-{{\tilde{\nabla }}}_{x_1}H(x_1^{k+1},z_2^k)\Vert ^2\\&\le 3(\tau _1^k)^2\Vert y_1^k-x_1^{k+1}\Vert ^2+3\Vert \nabla _{x_1}H(x_1^{k+1},x_2^{k+1})-\nabla _{x_1}H(z_1^{k},x_2^{k})\Vert ^2\\&\quad +3\Vert \nabla _{x_1}H(z_1^{k},x_2^{k})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\Vert ^2+3(\tau _2^k)^2\Vert y_2^k-x_2^{k+1}\Vert ^2\\&\quad +3\Vert \nabla _{x_2}H(x_1^{k+1},x_2^{k+1})-\nabla _{x_2}H(x_1^{k+1},z_2^{k})\Vert ^2\\&\quad +3\Vert \nabla _{x_2}H(x_1^{k+1},z_2^{k})-{{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^{k})\Vert ^2. \end{aligned}$$

Since \(\nabla H\) is M-Lipschitz continuous and \((a+b)^2\le 2(a^2+b^2)\), we get further

$$\begin{aligned} \Vert v\Vert ^2&\le 12(\tau _1^k)^2\Delta _1^{k+1}+6(\tau _1^k)^2\Vert y_1^k-x_1^k\Vert ^2+12(\tau _2^k)^2\Delta _2^{k+1}+6(\tau _2^k)^2\Vert y_2^k-x_2^k\Vert ^2\\&\quad +3M^2\Vert x_1^{k+1}-z_1^k\Vert ^2+6M^2\Delta _2^{k+1}+3M^2\Vert x_2^{k+1}-z_2^k\Vert ^2\\&\quad +3 \left( \Vert \nabla _{x_1}H(z_1^{k},x_2^{k})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\Vert ^2+\Vert \nabla _{x_2}H(x_1^{k+1},z_2^{k}) -{{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^{k})\Vert ^2\right) . \end{aligned}$$

Using Lemma 5.2 and the fact that \({{\tilde{\nabla }}}\) is inertial variance-reduced, this implies

$$\begin{aligned} \Vert v\Vert ^2&\le 12(\tau _1^k)^2\Delta _1^{k+1}+12(\tau _1^k)^2(\alpha _1^k)^2\Delta _1^k+12(\tau _2^k)^2\Delta _2^{k+1}+12(\tau _2^k)^2(\alpha _2^k)^2\Delta _2^k\\&\quad +12M^2\Delta _1^{k+1}+6M^2\Vert x_1^{k}-z_1^k\Vert ^2+6M^2\Delta _2^{k+1}+12M^2\Delta _2^{k+1}+6M^2\Vert x_2^{k}-z_2^k\Vert ^2\\&\quad +3\left( \Vert \nabla _{x_1}H(z_1^{k},x_2^{k})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\Vert ^2+\Vert \nabla _{x_2}H(x_1^{k+1},z_2^{k}) -{{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^{k})\Vert ^2\right) \\&\le 12\left( (\tau _1^k)^2+M^2 \right) \Delta _1^{k+1} +12\left( (\tau _1^k)^2(\alpha _1^k)^2+M^2(\beta _1^k)^2\right) \Delta _1^k\\&\quad +\left( 12(\tau _2^k)^2+18M^2\right) \Delta _2^{k+1} + 12\left( (\tau _2^k)^2(\alpha _2^k)^2+M^2(\beta _2^k)^2\right) \Delta _2^k\\&\quad +3\left( \Vert \nabla _{x_1}H(z_1^{k},x_2^{k})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\Vert ^2+\Vert \nabla _{x_2}H(x_1^{k+1},z_2^{k}) -{{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^{k})\Vert ^2\right) \\&\le C_0 \Vert u^{k+1}-u^k\Vert ^2\\&\quad +3 (\Vert \nabla _{x_1}H(z_1^{k},x_2^{k})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\Vert ^2)\\&\quad +3 (\Vert \nabla _{x_2}H(x_1^{k+1},z_2^{k}) -{{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^{k})\Vert ^2 ), \end{aligned}$$

where

$$\begin{aligned} C_0=12 \max \left( (\tau _1^k)^2+M^2,(\tau _1^k)^2(\alpha _1^k)^2+M^2(\beta _1^k)^2,(\tau _2^k)^2+\frac{3}{2} M^2,(\tau _2^k)^2(\alpha _2^k)^2+M^2(\beta _2^k)^2\right) . \end{aligned}$$

Noting that \(\,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2 \le \Vert v\Vert ^2\), taking the conditional expectation \({\mathbb {E}}_k\) and using that \({{\tilde{\nabla }}}\) is inertial variance-reduced, we conclude

$$\begin{aligned}&{\mathbb {E}}_k\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) \\&\quad \le {\mathbb {E}}_k\left( C_0\Vert u^{k+1}-u^k\Vert ^2\right) \\&\qquad +3{\mathbb {E}}_k\left( \Vert \nabla _{x_1}H(z_1^{k},x_2^{k})-{{\tilde{\nabla }}}_{x_1}H(z_1^k,x_2^k)\Vert ^2+\Vert \nabla _{x_2}H(x_1^{k+1},z_2^{k})-{{\tilde{\nabla }}}_{x_2}H(x_1^{k+1},z_2^{k})\Vert ^2\right) \\&\quad \le {\mathbb {E}}_k\left( (C_0+3V_1)\Vert u^{k+1}-u^k\Vert ^2\right) +3\Upsilon _k. \end{aligned}$$

Taking the full expectation on both sides and setting \(C:= C_0+3V_1\) proves the claim. \(\square \)

Using Theorem 5.5, we can show the sub-linear decay of the expected squared distance of the subgradient to 0.

Theorem 5.6

(Convergence of iSPALM) Under the assumptions of Theorem 5.4 it holds for t drawn uniformly from \(\{2,\ldots ,T+1\}\) that there exists some \(0<\sigma <\gamma \) such that

$$\begin{aligned} {\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^t,x_2^t))^2\right)&\le \tfrac{C}{T (\gamma -\sigma )}\left( \Psi (u^1)-\inf _{u\in {\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2}}\Psi (u)+\left( \tfrac{3(\gamma -\sigma )}{\rho C}+\tfrac{1}{M\rho }\right) {\mathbb {E}}(\Upsilon _1)\right) . \end{aligned}$$

Proof

By (10), Theorem 5.5 and (12) it holds for \(0<\sigma <\gamma \) that

$$\begin{aligned} {\mathbb {E}}\left( \Psi (u^k)-\Psi (u^{k+1})\right)&\ge \gamma {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)+\tfrac{1}{M\rho }{\mathbb {E}}\left( \Upsilon _{k+1}-\Upsilon _k\right) \\&\ge \sigma {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)+\tfrac{\gamma -\sigma }{C}{\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) \\ {}&\quad -\tfrac{3(\gamma -\sigma )}{C}{\mathbb {E}}(\Upsilon _k)+\tfrac{1}{M\rho }{\mathbb {E}}\left( \Upsilon _{k+1}-\Upsilon _k\right) \\&\ge \sigma {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)+\tfrac{\gamma -\sigma }{C}{\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) \\ {}&\quad +\left( \tfrac{3(\gamma -\sigma )}{\rho C}+\tfrac{1}{M\rho }\right) {\mathbb {E}}\left( \Upsilon _{k+1}-\Upsilon _k\right) -\tfrac{3(\gamma -\sigma )V_\Upsilon }{C\rho }{\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2). \end{aligned}$$

Choosing \(\sigma := \tfrac{3(\gamma -\sigma )V_\Upsilon }{C\rho }\) yields

$$\begin{aligned} {\mathbb {E}}\left( \Psi (u^k)\!-\!\Psi (u^{k+1})\right) \ge \tfrac{\gamma -\sigma }{C}{\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) \!-\!\left( \tfrac{3(\gamma -\sigma )}{\rho C} \!+ \!\tfrac{1}{M\rho }\right) {\mathbb {E}}\left( \Upsilon _{k+1} \! -\! \Upsilon _k\right) . \end{aligned}$$

Adding this up for \(k=1,\ldots ,T\) we get

$$\begin{aligned} {\mathbb {E}}\left( \Psi (u^1) -\Psi (u^{T})\right)&\ge \tfrac{\gamma -\sigma }{C}\sum _{k=1}^{T}{\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) \\&\quad + \left( \tfrac{3(\gamma -\sigma )}{\rho C}+\tfrac{1}{M\rho }\right) {\mathbb {E}}\left( \Upsilon _{T}-\Upsilon _1\right) . \end{aligned}$$

Since \(\Upsilon _{T}\ge 0\) this yields for t drawn randomly from \(\{2,\ldots ,T+1\}\) that

$$\begin{aligned} {\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{t},x_2^{t}))^2\right)&=\tfrac{1}{T}\sum _{k=1}^{T}{\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) \\&\le \tfrac{C}{T(\gamma -\sigma )}\left( \Psi (u^1)-\inf _{u\in ({\mathbb {R}}^{d_1}\times {\mathbb {R}}^{d_2})^2}\Psi (u)+\left( \tfrac{3(\gamma -\sigma )}{\rho C}+\tfrac{1}{M\rho }\right) {\mathbb {E}}(\Upsilon _1)\right) . \end{aligned}$$

This finishes the proof. \(\square \)

In [13] the authors proved global convergence of the objective function evaluated at the iterates of SPRING in expectation if the global error bound

$$\begin{aligned} F(x_1,x_2)-\underline{F}\le \mu \,\mathrm {dist}(0,\partial F(x_1,x_2))^2,\quad \text {for all }x_1\in {\mathbb {R}}^{d_1},x_2\in {\mathbb {R}}^{d_2} \end{aligned}$$
(13)

is fulfilled for some \(\mu >0\). Using this error bound, we can also prove global convergence of iSPALM in expectation with a linear convergence rate. Note that the authors of [13] used the generalized gradient instead of the subgradient also for this error bound. Similar as before this seems to be unsuitable due to the heavy dependence on of the generalized gradient on the step size parameters.

Theorem 5.7

(Convergence of iSPALM) Let the assumptions of Theorem 5.4 hold true. If in addition (13) is fulfilled, then there exists some \(\Theta _0\in (0,1)\) and \(\Theta _1>0\) such that

$$\begin{aligned} {\mathbb {E}}\left( F(x_1^{T+1},x_2^{T+1})-\underline{F}\right) \le (\Theta _0)^T\left( \Psi (u^1)-\underline{F}+\Theta _1{\mathbb {E}}(\Upsilon _1)\right) . \end{aligned}$$

In particular, it holds \( \lim _{T\rightarrow \infty }{\mathbb {E}}(F(x_1^T,x_2^T)-\underline{F})=0. \)

Proof

By (12) and Theorem 5.5, we obtain for \(0<d<\min (\gamma ,\tfrac{C\rho \mu }{1-\rho })\) that

$$\begin{aligned} {\mathbb {E}}\left( \Psi (u^{k+1})-\underline{F}+\tfrac{1}{M\rho }\Upsilon _{k+1}\right)&\le {\mathbb {E}}\left( \Psi (u^k)-\underline{F}+\tfrac{1}{M\rho }\Upsilon _k\right) -\gamma {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2)\\&\le {\mathbb {E}}\left( \Psi (u^k)-\underline{F}+\tfrac{1}{M\rho }\Upsilon _k\right) \\&\quad -\tfrac{d}{C}{\mathbb {E}}\left( \,\mathrm {dist}(0,\partial F(x_1^{k+1},x_2^{k+1}))^2\right) +\tfrac{3d}{C}{\mathbb {E}}(\Upsilon _k) \\&\quad -\left( \gamma -d\right) {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2). \end{aligned}$$

Using (10) in combination with the global error bound (13), we get

$$\begin{aligned}&{\mathbb {E}}\left( \Psi (u^{k+1})-\underline{F}+\left( \tfrac{3d}{\rho C}+\tfrac{1}{M\rho }\right) \Upsilon _{k+1}\right) \le {\mathbb {E}}\left( \Psi (u^k)-\underline{F}+\left( \tfrac{3d}{\rho C}+\tfrac{1}{M\rho }\right) \Upsilon _k\right) \\&-\tfrac{d}{C\mu }{\mathbb {E}}\left( F(x_1^{k+1},x_2^{k+1})-\underline{F}\right) -\left( \gamma -d-\tfrac{3d V_\Upsilon }{\rho C}\right) {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2). \end{aligned}$$

Setting \(C_\Upsilon := \left( \tfrac{3d}{\rho C}+\tfrac{1}{M\rho }\right) \) and applying the definition (7) of \(\Psi \), this implies

$$\begin{aligned}&\left( 1+\tfrac{d}{C\mu }\right) {\mathbb {E}}\left( \Psi (u^{k+1})-\underline{F}\right) - \tfrac{d}{C\mu }{\mathbb {E}}(\delta _1\Delta _1^{k+1}+\delta _2\Delta _2^{k+1})+C_\Upsilon {\mathbb {E}}(\Upsilon _{k+1})\\&\quad \le {\mathbb {E}}\left( \Psi (u^k)-\underline{F}\right) +C_\Upsilon {\mathbb {E}}(\Upsilon _k)-\left( \gamma -d-\tfrac{3dV_\Upsilon }{\rho C}\right) {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2). \end{aligned}$$

With \(\delta := \max (\delta _1,\delta _2)\) and \(\Delta _1^{k+1}+\Delta _2^{k+1} \le \tfrac{1}{2}\Vert u^{k+1}-u^k\Vert ^2\) we get

$$\begin{aligned}&\left( 1+\tfrac{d}{C\mu }\right) {\mathbb {E}}\left( \Psi (u^{k+1})-\underline{F}\right) +C_\Upsilon {\mathbb {E}}(\Upsilon _{k+1})\\&\quad \le {\mathbb {E}}\left( \Psi (u^k)-\underline{F}\right) +C_\Upsilon {\mathbb {E}}(\Upsilon _k)-\left( \gamma -d-\tfrac{3dV_\Upsilon }{\rho C} - \tfrac{d\delta }{2 C\mu }\right) {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2). \end{aligned}$$

Multiplying by \(C_d := \tfrac{1}{1+\tfrac{d}{C\mu }}=\tfrac{C\mu }{C\mu +d}\) this becomes

$$\begin{aligned}&{\mathbb {E}}\left( \Psi (u^{k+1})-\underline{F}\right) + C_\Upsilon C_d {\mathbb {E}}(\Upsilon _{k+1}) \le \tfrac{C\mu }{C\mu +d}{\mathbb {E}}\left( \Psi (u^k)-\underline{F}\right) + C_\Upsilon C_d {\mathbb {E}}(\Upsilon _k)\nonumber \\&\quad -\tfrac{C\mu }{C\mu +d} \left( \gamma -d-\tfrac{3dV_\Upsilon }{\rho C}-\tfrac{d\delta }{ 2 C\mu }\right) {\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2). \end{aligned}$$
(14)

Since \(d<\tfrac{C\rho \mu }{1-\rho }\) we know that \(s:= \tfrac{1-C_d}{C_d+\rho -1} = \frac{d}{\rho C \mu + (\rho -1)d} > 0\). Thus, adding \(s C_\Upsilon C_d\) times equation Definition 4.1 (ii) to (14) gives

$$\begin{aligned}&{\mathbb {E}}\left( \Psi (u^{k+1})-\underline{F}\right) + (1+s) C_\Upsilon C_d {\mathbb {E}}(\Upsilon _{k+1}) \le C_d {\mathbb {E}}\left( \Psi (u^k)-\underline{F}+ (1+s) C_\Upsilon C_d {\mathbb {E}}(\Upsilon _k)\right) \\&\quad + C_d \underbrace{\left( V_\Upsilon s C_\Upsilon - \left( \gamma -d-\tfrac{3dV_\Upsilon }{\rho C} - \tfrac{d\delta }{2 C\mu }\right) \right) }_{=: h(d)}{\mathbb {E}}(\Vert u^{k+1}-u^k\Vert ^2), \end{aligned}$$

where we have used that \(1+(1-\rho )s=C_d(1+s)\). Since s converges to 0 as \(d\rightarrow 0\) we have that \(\lim _{d\rightarrow 0}h(d)=-\gamma \). Thus we can choose \(d>0\) small enough, such that \(h(d)<0\). Then we get

$$\begin{aligned} {\mathbb {E}}\left( \Psi (u^{k+1})-\underline{F}\right) + (1+s)C_\Upsilon C_d {\mathbb {E}}(\Upsilon _{k+1})&\le C_d {\mathbb {E}}\left( \Psi (u^k)-\underline{F}+ (1+s)C_\Upsilon C_d {\mathbb {E}}(\Upsilon _k)\right) . \end{aligned}$$

Finally, setting \(\Theta _0 := C_d\) and \(\Theta _1 := (1+s)C_\Upsilon C_d\) and applying the last equation iteratively, we obtain

$$\begin{aligned} {\mathbb {E}}\left( \Psi (u^{T+1})-\underline{F}+\Theta _1\Upsilon _{T+1}\right)&\le (\Theta _0)^T{\mathbb {E}}\left( \Psi (u^1)-\underline{F}+\Theta _1\Upsilon _1\right) . \end{aligned}$$

Note that \(\Psi (u^{T+1})\ge F(x_1^{T+1},x_2^{T+1})\) and that \(\Upsilon _{T+1}\ge 0\). This yields

$$\begin{aligned} {\mathbb {E}}\left( F(x_1^{T+1},x_2^{T+1})-\underline{F}\right)&\le (\Theta _0)^T{\mathbb {E}}\left( \Psi (u^1)-\underline{F}+\Theta _1\Upsilon _1\right) , \end{aligned}$$

and we are done. \(\square \)

6 Numerical results

In this section, we demonstrate the performance of iSPALM for two different applications, namely for learning (i) the parameters of Student-t MMs, and (ii) the weights of PNNs. In comparison with PALM, iPALM and SPRING, we will see that our algorithm increases the stability of SPRING and iSPALM if we enforce the evaluation of the full gradient at the beginning of each epoch. We will exclusively use the SARAH estimator.

We run all our experiments on a Lenovo ThinkStation with Intel i7-8700 processor, 32GB RAM and a NVIDIA GeForce GTX 2060 Super GPU. For the implementation we use Python and Tensorflow.

6.1 Parameter choice and implementation aspects

On the one hand, the algorithms based on PALM have many parameters which enables a high adaptivity of the algorithms to the specific problems. On the other hand, it is often hard to fit these parameters to ensure the optimal performance of the algorithms.

Based on approximations \({{\tilde{L}}}_1(x_2^k)\) and \(\tilde{L}_2(x_1^{k+1})\) of the partial Lipschitz constants \(L_1(x_2^k)\) and \(L_2(x_1^{k+1})\) outlined below, we use the following step size parameters \(\tau _i^k\), \(i=1,2\):

  • For PALM and iPALM, we choose \(\tau _1^k={{\tilde{L}}}_1(x_1^k,x_2^k)\) and \(\tau _2^k=\tilde{L}_2(x_1^{k+1},x_2^k)\) which was also suggested in [4, 36].

  • For SPRING and iSPALM, we choose \(\tau _1^k=s_1{{\tilde{L}}}_1(x_1^k,x_2^k)\) and \(\tau _2^k=s_1{{\tilde{L}}}_2(x_1^{k+1},x_2^k)\), where the manually chosen scalar \(s_1 > 0\) depends on the application. Note that the authors in [13] propose to take \(s_1=2\) which was not optimal in our examples.

Computation of Gradients and Approximative Lipschitz Constants Since the global and partial Lipschitz constants of the block-wise gradients of H are usually unknown, we estimate them locally using the second order derivative of H which exists in our examples. If H acts on a high dimensional space, it is often computationally to costly to compute the full Hessian matrix. Thus we compute a local Lipschitz constant only in the gradient direction, i.e. we compute

$$\begin{aligned} {{\tilde{L}}}_i(x_1,x_2) := \Vert \nabla _{x_i}^2 H(x_1,x_2)g\Vert , \quad g:= \frac{\nabla _{x_i} H(x_1,x_2)}{\Vert \nabla _{x_i}H(x_1,x_2)\Vert } \end{aligned}$$
(15)

For the stochastic algorithms we replace H by the approximated function \({{\tilde{H}}}(x_1,x_2):=\tfrac{1}{b}\sum _{i\in B_i^k}h_i(x_1,x_2)\), where \(B_i^k\) is the current mini-batch. The analytical computation of \({{\tilde{L}}}_i\) in (15) is still hard. Even computing the gradient of a complicated function H can be error prone and laborious. Therefore, we compute the (partial) gradients of H or \({{\tilde{H}}}\), respectively, using the reverse mode of algorithmic differentiation (also called backpropagation), see e.g. [16]. To this end, note that the chain rule yields that

$$\begin{aligned} \left\| \nabla _{x_i}\left( \Vert \nabla _{x_i}H(x_1,x_2)\Vert ^2\right) \right\|&=\left\| 2\Vert \nabla _{x_i}H(x_1,x_2)\Vert \nabla _{x_i}^2 H(x_1,x_2)\nabla _{x_i}H(x_1,x_2)\right\| \\&=2\Vert \nabla _{x_i}H(x_1,x_2)\Vert ^2{{\tilde{L}}}_i(x_1,x_2). \end{aligned}$$

Thus, we can compute \({{\tilde{L}}}_i(x_1,x_2)\) by applying two times the reverse mode. If we neglect the taping, the execution time of this procedure can provably be bounded by a constant times the execution time of H, see [16, Sect. 5.4]. Therefore, this procedure gives us an accurate and computationally very efficient estimation of the local partial Lipschitz constant.

Inertial Parameters For the iPALM and iSPALM we have to choose the inertial parameters \(\alpha _i^k\ge 0\) and \(\beta _i^k\ge 0\). With respect to our convergence results we have to assume that there exist \(\alpha _i^k\le {{\bar{\alpha }}}_i<\tfrac{1}{2}\) and \(\beta _i^k\le {{\bar{\beta }}}_i<1\), \(i=1,2\). Note that for convex functions f and g, the authors in [36] proved that the assumption on the \(\alpha \)’s can be lowered to \(\alpha _i^k\le {{\bar{\alpha }}}_i<1\) and suggested to use \(\alpha _i^k=\beta _i^k=\frac{k-1}{k+2}\). Unfortunately, we cannot show this for iSPALM and indeed we observe instability and divergence in iSPALM, if we choose \(\alpha _i^k>\frac{1}{2}\). Therefore, we choose for iSPALM the parameters

$$\begin{aligned} \alpha _i^k=\beta _i^k= s_2\frac{k-1}{k+2}, \end{aligned}$$

where the scalar \(0<s_2<1\) is manually chosen depending on the application.

Implementation We provide a general framework for implementing PALM, iPALM, SPRING and iSPALMFootnote 2 on a GPU. Using this framework, it suffice to provide an implementation for the functions H and \(\mathrm {prox}_{\tau _i}^{f_i}\) in order to use one of the above algorithms for the function \(F(x_1,\ldots ,x_K)=H(x_1,\ldots ,x_K)+\sum _{i=1}^K f_i(x_i)\). We provide also the code of our numerical examples below on this website.

6.2 Student-t mixture models

First, we apply the various PALM algorithms for estimating the parameters of d-dimensional Student-t MMs with K components. More precisely, we aim to find \(\alpha =(\alpha _1,\ldots ,\alpha _K)\in \Delta _K := \{(\alpha _k)_{k=1}^K: \sum _{k=1}^K \alpha _k = 1, \; \alpha _k \ge 0\}\), \(\nu = (\nu _1,\ldots ,\nu _K) \in {\mathbb {R}}_{>0}^K\), \(\mu = (\mu _1,\ldots ,\mu _K) \in {\mathbb {R}}^K\), and \(\Sigma = (\Sigma _1,\ldots ,\Sigma _K) \in {{\,\mathrm{SPD}\,}}(d)^K\) in the probability density function

$$\begin{aligned} p(x)=\sum _{k=1}^K \alpha _k f(x|\nu _k,\mu _k,\Sigma _k). \end{aligned}$$

Here \({{\,\mathrm{SPD}\,}}(d)\) denotes the symmetric positive definite \(d \times d\) matrices, and f is the density function of the Student-t distribution with \(\nu >0\) degrees of freedom, location parameter \(\mu \in {\mathbb {R}}^d\) and scatter matrix \(\Sigma \in {{\,\mathrm{SPD}\,}}(d)\) given by

$$\begin{aligned} f(x|\nu ,\mu ,\Sigma ) = \frac{\Gamma \left( \frac{d+\nu }{2}\right) }{\Gamma \left( \frac{\nu }{2}\right) \, \nu ^{\frac{d}{2}} \, \pi ^{\frac{d}{2}} \, {\left| \Sigma \right| }^{\frac{1}{2}}} \, \frac{1}{\left( 1 +\frac{1}{\nu }(x-\mu )^\mathrm {T}\Sigma ^{-1}(x-\mu ) \right) ^{\frac{d+\nu }{2}}} \end{aligned}$$

with the Gamma function \(\Gamma \).

For samples \({\mathcal {X}} = (x_1,\ldots ,x_n) \in {\mathbb {R}}^{d \times n}\), we want to minimize the negative log-likelihood function

$$\begin{aligned} {\mathcal {L}}(\alpha ,\nu ,\mu ,\Sigma |\mathcal X)=-\frac{1}{n}\sum _{i=1}^n\log \bigg (\sum _{k=1}^K\alpha _k f(x_i|\nu _k,\mu _k,\Sigma _k)\bigg ) \end{aligned}$$

subject to the parameter constraints. A first idea to rewrite this problem in the form (2) looks as

$$\begin{aligned} F(\alpha ,\nu ,\mu ,\Sigma )=H(\alpha ,\nu ,\mu ,\Sigma )+f_1(\alpha )+f_2(\nu )+f_3(\mu )+f_4(\Sigma ), \end{aligned}$$
(16)

where \(H := {\mathcal {L}}\), \(f_1 := \iota _{\Delta _K}\), \(f_2 := \iota _{{\mathbb {R}}^K_{>0}}\), \(f_3 := 0\), \(f_4 := \iota _{{{\,\mathrm{SPD}\,}}(d)^K}\), and \(\iota _{{\mathcal {S}}}\) denotes the indicator function of the set \({{\mathcal {S}}}\) defined by \(\iota _{{\mathcal {S}}}(x) := 0\) if \(x \in {\mathcal {S}}\) and \(\iota _{{\mathcal {S}}}(x) := \infty \) otherwise. Indeed one of the authors has applied PALM and iPALM to such a setting without any convergence guarantee in [19]. The problem is that \({\mathcal {L}}\) is not defined on the whole Euclidean space and since \({\mathcal {L}}(\alpha ,\nu ,\mu ,\Sigma )\rightarrow \infty \) as \(\Sigma _k\rightarrow 0\) for some k, the function can also not continuously extended to the whole \({\mathbb {R}}^K\times {\mathbb {R}}^K\times {\mathbb {R}}^{d\times K}\times {{\,\mathrm{Sym}\,}}(d)^K\), where \({{\,\mathrm{Sym}\,}}(d)\) denotes the space of symmetric \(d\times d\) matrices. Furthermore, the functions \(f_2\) and \(f_4\) are not lower semi-continuous. Consequently, the function (16) does not fulfill the assumptions required for the convergence of PALM and iPALM. Therefore we modify the above model as follows: Let \({{\,\mathrm{SPD}\,}}_\epsilon (d) := \{\Sigma \in {{\,\mathrm{SPD}\,}}(d): \Sigma \succeq \epsilon I_d\}\). Then we use the surjective mappings \(\varphi _1 :{\mathbb {R}}^K \rightarrow \Delta _K\), \(\varphi _2 :{\mathbb {R}}^K\rightarrow {\mathbb {R}}_{\ge \epsilon }^K\) and \(\varphi _3 :\mathrm {Sym}(d)^K \rightarrow {{\,\mathrm{SPD}\,}}_\varepsilon (d)^K\) defined by

$$\begin{aligned} \varphi _1(\alpha ) := \frac{\exp (\alpha )}{\sum _{j=1}^K\exp (\alpha _j)},\quad \varphi _2 (\nu ) := \nu ^2+\epsilon ,\quad \varphi _3(\Sigma ) := \left( \Sigma _k^T\Sigma _k+\epsilon I_d \right) _{k=1}^K \end{aligned}$$

to reshape problem (16) as the unconstrained optimization problem

$$\begin{aligned} \mathop {\text {argmin}}\limits _{\alpha \in {\mathbb {R}}^K,\nu \in {\mathbb {R}}^K,\mu \in {\mathbb {R}}^{d\times K},\Sigma \in {{\,\mathrm{Sym}\,}}(d)^{K}} H(\alpha , \nu ,\mu ,\Sigma ) := {{\mathcal {L}}}(\varphi _1(\alpha ),\varphi _2(\nu ),\mu ,\varphi _3 (\Sigma )|{\mathcal {X}}). \end{aligned}$$
(17)

For this problem, PALM and iPALM reduce basically to block gradient descent algorithms. In Appendix B, we verify that the above function H is indeed a KL function which is bounded from below, and satisfies the Assumption 3.1(i). Since \(H \in C^2({\mathbb {R}}^K\times {\mathbb {R}}^K\times {\mathbb {R}}^{d\times K} \times {{\,\mathrm{Sym}\,}}(d)^{K})\) , we know by Remark 3.2 that Assumption 3.1(ii) is also fulfilled. Further, \(\nabla H\) is continuous on bounded sets. Then, choosing the parameters of PALM, resp. iPALM as required by Theorem 3.3 resp. 3.6, we conclude that the sequences generated by both algorithms converge to a critical point of H supposed that they are bounded. Similarly, if we assume in addition that the stochastic gradient estimators are inertial variance-reduced, we can conclude that the iSPALM sequence converges as in Theorems 5.6 and 5.7, if the corresponding requirements on the parameters are fulfilled.

In our numerical examples, we generate the data by sampling from the Student-t MM, where the parameters of the ground truth MM are generate as follows:

  • We generate \(\alpha =\frac{{{\bar{\alpha }}}^2+1}{\Vert {{\bar{\alpha }}}^2+1\Vert _1}\), where the entries of \({{\bar{\alpha }}}\in {\mathbb {R}}^K\) are drawn independently from the standard normal distribution.

  • We generate \(\nu _i=\min ({{\bar{\nu }}}_i^2+1,100)\), where \({{\bar{\nu }}}_i\), \(i=1,\ldots ,n\) is drawn from a normal distribution with mean 0 and standard deviation 10.

  • The entries of \(\mu \in {\mathbb {R}}^{d\times K}\) are drawn independently from a normal distribution with mean 0 and standard deviation 2.

  • We generate \(\Sigma _i={{\bar{\Sigma }}}_i^T{{\bar{\Sigma }}}_i + I\), where the entries of \({{\bar{\Sigma }}}_i\in {\mathbb {R}}^{d\times d}\) are drawn independently from the standard normal distribution.

For the initialization of the algorithms, we assign to each sample \(x_i\) randomly a class \(c_i\in \{1,\ldots ,K\}\). Then we initialize the parameters \((\nu _k,\mu _k,\Sigma _k)\) by estimating the parameters of a Student-t distribution of all samples with \(c_i=k\) using a faster alternative of the EM algorithm called multivariate myriad filter, see [17]. Further we initialize \(\alpha \) by \(\alpha _k=\frac{|\{i\in \{1,\ldots ,N\}:c_i=k\}|}{N}\). We run the algorithm for \(n=200{,}000\) data points of dimension \(d=10\) and \(K=30\) components. We use a batch size of \(b=20{,}000\). To represent the randomness in SPRING and iSPALM, we repeat the experiment 10 times with the same samples and the same initialization. The resulting mean and standard deviation of the negative log-likelihood values versus the number of epochs and the execution times, respectively, are given in Fig. 1. Further, we visualize the mean squared norm of the gradient after each epoch. One epoch contains for SPRING and iSPALM 10 steps and for PALM and iPALM 1 step. We see that in terms of the number of epochs as well as in terms of the execution time the iSPALM is the fastest algorithm.

Fig. 1
figure 1

Objective function versus number of epochs and versus execution time for estimating the parameters of Student-t MMs

Full size image

6.3 Proximal neural networks (PNNs)

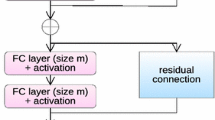
PNNs for MNIST classification In this example, we train a Proximal Neural Network as introduced in [18] for classification on the MNIST data set.Footnote 3 The training data consists of \(N=60{,}000\) images \(x_i\in {\mathbb {R}}^d\) of size \(d=28^2\) and labels \(y_i\in \{0,1\}^{10}\), where the jth entry of \(y_i\) is 1 if and only if \(x_i\) has the label j. A PNN with \(K-1\) layers and activation function \(\sigma \) is defined by

$$\begin{aligned} T_{K-1}^\mathrm {T}\sigma (T_{K-1} \cdots T_1^\mathrm {T}\sigma (T_1x+b_1) \cdots +b_{K-1}), \end{aligned}$$

where the \(T_i\) are contained in the (compact) Stiefel manifold \(\,\mathrm {St}(d,n_i)\) and \(b_i\in {\mathbb {R}}^{n_i}\) for \(i=1,\ldots ,K-1\). To get 10 output elements in (0, 1), we add similar as in [18] an additional layer

$$\begin{aligned} g(T_Kx),\quad T_K\in [-10,10]^{10,d}, b_K\in {\mathbb {R}}^{10} \end{aligned}$$

with the activation function \(g(x):=\tfrac{1}{1+\exp (-x)}\). Thus the full network is given by

$$\begin{aligned}&\Psi (x,u)=g(T_KT_{K-1}^\mathrm {T}\sigma (T_{K-1}\cdots T_1^\mathrm {T}\sigma (T_1x+b_1)+\cdots +b_{K-1}) +b_K),\\&\quad u=(T_1,\ldots ,T_K,b_1,\ldots ,b_K). \end{aligned}$$

It was demonstrated in [18] that this kind of network is more stable under adversarial attacks than the same network without the orthogonality constraints.

Training PNNs with iSPALM Now, we want to train a PNN with \(K-1=3\) layers and \(n_1=784\), \(n_2=400\) and \(n_3=200\) for MNIST classification. In order of applying our theory, we use the exponential linear unit (ELU)

$$\begin{aligned} \sigma (x)={\left\{ \begin{array}{ll}\exp (x)-1,&{}{ if}x<0,\\ x&{}{ if}x\ge 0,\end{array}\right. } \end{aligned}$$

as activation function, which is differentiable with a 1-Lipschitz gradient. Then, the loss function is given by

$$\begin{aligned} F(u)=H(u)+f(u),\quad u=(T_1,\ldots ,T_4,b_1,\ldots ,b_4) \end{aligned}$$

where \(T_i \in {\mathbb {R}}^{d,n_i}\), \(b_i \in {\mathbb {R}}^{n_i}\), \(i=1,2,3\), and \(T_4 \in [-10,10]^{10,d}\), \(b_4 \in {\mathbb {R}}^{10}\), and \(f(u)=\iota _{{\mathcal {U}}}\) with

$$\begin{aligned} {\mathcal {U}}:=\{(T_1,\ldots ,T_4,b_1,\ldots ,b_4):T_i\in \,\mathrm {St}(d,n_i), i=1,2,3, T_4\in [-10,10]^{10,d}\}. \end{aligned}$$

and

$$\begin{aligned} H(u):=\frac{1}{N}\sum _{i=1}^N \Vert \Psi (x_i,u) - y_i\Vert ^2. \end{aligned}$$
Fig. 2
figure 2

Loss function versus number of epochs and versus execution time for training a PNN for MNIST classification

Full size image

Since H is unfortunately not Lipschitz continuous, we propose a slight modification. Note that for any \(u=(T_1,\ldots ,T_4,b_1,\ldots ,b_4)\) which appears as \(x^k\), \(y^k\) or \(z^k\) in PALM, iPALM, SPRING or iSPALM we have that there exist \(v,w\in {\mathcal {U}}\) such that \(u=v+w\). In particular, we have that \(\Vert T_i\Vert _F\le 2\sqrt{d}\), \(i=1,2,3\) and \(\Vert T_4\Vert _F\le 20\sqrt{10 d}\) Therefore, we can replace H by

$$\begin{aligned} {{\tilde{H}}}(u)=\Pi _{i=1}^4\eta (\Vert T_i\Vert _F^2)\frac{1}{N}\sum _{i=1}^N \Vert \Psi (x_i,u)- y_i\Vert ^2, \end{aligned}$$

without changing the algorithm, where \(\eta \) is a smooth cutoff function of the interval \((-\infty ,4000 d]\). Now, simple calculations yield that the function \({{\tilde{H}}}\) is globally Lipschitz continuous. Since it is also bounded from below by 0 we can conclude that our convergence results of iSPALM are applicable.

Remark 6.1

For the implementation, we need to calculate \(\mathrm {prox}_{{{\tilde{f}}}}\), which is the orthogonal projection \(P_{{\mathcal {U}}}\) onto \(\mathcal U\). This includes the projection of the matrices \(T_i\), \(i=1,2,3\) onto the Stiefel manifold. In [23, Sect. 7.3,7.4] it is shown, that the projection of a matrix A onto the Stiefel manifold is given by the U-factor of the polar decomposition \(A=US\in {\mathbb {R}}^{d,n}\), where \(U\in \,\mathrm {St}(d,n)\) and S is symmetric and positive definite. Note that U is only unique, if A is non-singular. Several possibilities for the computing U are considered in [22, Chapter 8]. In particular, U is given by VW, where \(A=V\Sigma W\) is the singular value decomposition of A. For our numerical experiments we use the iteration

$$\begin{aligned} Y_{k+1}=2Y_k(I+Y_k^\mathrm {T}Y_k)^{-1} \end{aligned}$$

with \(Y_0=A\), which converges for any non-singular A to U, see [22]. \(\square \)

Now we run PALM, iPALM and SPRING, iSPRING for 200 epochs using a batch size of \(b=1500\). One epoch contains for SPRING and iSPALM 40 steps and for PALM and iPALM 1 step. As in the previous example we repeat the experiment 10 times with the same initialization and plot for the resulting loss functions mean and standard deviation to represent the randomness of the algorithms. Figure 2 shows the mean and standard deviation of the loss versus the number of epochs or the execution time as well as the squared norm of the Riemannian gradient for the iterates of iSPALM after each epoch. We observe that iSPALM performs much better than SPRING and that iPALM performs much better than PALM. Therefore this example demonstrates the importance of the inertial parameters in iPALM and iSPALM. Further, iSPALM and SPRING outperform their deterministic versions significantly. The resulting weights from iSPALM reach after 200 epochs an average accuracy of 0.985 on the test set.

7 Conclusions

We combined a stochastic variant of the PALM algorithm with the inertial PALM algorithm to a new algorithm, called iSPALM. We analyzed the convergence behavior of iSPALM and proved convergence results, if the gradient estimators are inertial variance-reduced. In particular, we showed that the expected distance of the subdifferential to zero converges to zero for the sequence of iterates generated by iSPALM. Additionally, the sequence of function values achieves linear convergence for functions satisfying a global error bound. We proved that a modified version of the negative log-likelihood function of Student-t MMs fulfills all necessary convergence assumption of PALM, iPALM. We demonstrated the performance of iSPALM for two quite different applications. In the numerical comparison, it turns out that iSPALM shows the best performance of all four algorithms. In particular, the example with the PNNs demonstrates the importance of combining inertial parameters and stochastic gradient estimators.

In future work, it would be interesting to compare the performance of the iSPALM algorithm with more classical algorithms for estimating the parameters of Student-t MMs, in particular with the EM algorithm and some of its accelerations. For first experiments in this direction we refer to our work [17, 19]. Further, we intend to apply iSPALM to other practical problems, e.g. in more sophisticated examples of deep learning.