Introduction

The predictive processing account is a key theoretical player in present-day cognitive neuroscience. The account postulates that our brains make sense of the world through a cycle of making predictions based on a hierarchical, generative model and updating its internal states to reduce prediction errors (Clark, 2013; Hohwy, 2013; Spratling, 2017; Walsh et al., 2020). While the account has been steadily growing in its explanatory scope, it also has its critics. For instance, some have argued that predictive processing presents old ideas under new labels (Cao, 2020), is not as unifying as proponents like to claim (Litwin & Miłkowski, 2020), or is difficult to falsify (Kogo & Trengove, 2015). Even those sympathetic of the approach, like ourselves, have posited substantive challenges. For instance, it has been shown that structured representations—needed to scale the account to higher-cognition (Griffiths et al., 2010; Kwisthout et al., 2017)—render the postulated (Bayesian) computations intractable and causes uncertainty about how they could be realized by resource-bounded wetware (Blokpoel et al., 2012; Kwisthout & van Rooij, 2020). Despite such critiques and challenges, proponents remain set on making the predictive processing account live up to its aspirations, i.e., to explain all of cognitive brain functioning.

The account’s explanatory and modelling successes—spanning domains like perception (Den Ouden et al., 2012; Kok et al., 2013), action (Yon et al., 2018), planning (Kaplan & Friston, 2018), communication (Friston & Penny, 2011) and learning (Da Costa et al., 2020; Friston et al., 2017; Smith et al., 2020)—seem to warrant optimism. While we share some of this optimism and see no reason in principle why predictive processing cannot ultimately deliver on its promise,Footnote 1 it may be premature to take these local successes as directly foreshadowing ultimate, global success. All successes to date have been limited to phenomena that can be mathematically cast as Bayesian inference of parameters of structurally predefined generative models. Even predictive processing proponents have become increasingly aware of the need to build explanations and mathematical models of how brains are able to learn the structure of their generative models (Friston et al., 2017; Smith et al., 2020; Da Costa et al., 2020). Recent attempts, by these same authors, draw inspiration from formalisms developed in engineering applications of Bayesian statistics and machine learning. We believe that when formalisms are adapted from one field to another in this way, it is good practice to evaluate whether or not the conceptual commitments that come along match the commitments the researchers are ready to make (cf. Guest & Martin 2021; van Rooij & Blokpoel 2020). Aspects of formalisms that work well for engineering applications can be inapplicable or misconceived for purposes of scientific explanation (cf. van Rooij & Wareham2008; van Rooij et al., 2012). In this paper, our focus is on scientific explanations as opposed to engineering applications.

In this theoretical paper, we evaluate the commitments of predictive processing models of (Bayesian) structure learning. We observe that these models make the contentious assumption that the generative model’s state space is fixed (i.e., pre-defined and immutable).Footnote 2 We show that this assumption generates a theoretical problem for this account of structure learning: agents that learn within the confines of a fixed state space inevitably will get stuck in one of two cognitive states that we refer to as cognitive blindness and category conflation, respectively. The only way out of these states is to allow for true structural changes to occur in generative models that can, in principle, expand the state space. This route will require the predictive processing account to tackle a set of new open questions that we will highlight.

Overview

The remainder of this paper is organized as follows. We first introduce formal concepts and notation from predictive processing and explain a predictive processing view of structure learning called model expansion. Next, we present a proof argument that this model predicts that predictive Bayesian brains inevitably get stuck in category conflation or cognitive blindness. Lastly, we present a way out of this conundrum by considering mathematical possibilities for structural changes in generative models, which we call structure learning proper.

Formal Definition of Predictive Processing

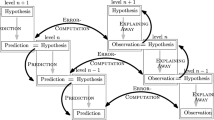
Predictive processing proposes that human (and other) brains make predictions about the world based on an internal, hierarchical, generative model. This generative model is taken to represent a person’s beliefs about concepts, relations, and transitions in the world (Clark, 2013; Friston et al., 2010). A generative model is defined as a hierarchy of prediction layers (see Fig. 1). Each such layer consists of a set of hypotheses H (or hidden states) with prior probability distribution P(H) and a distribution P(E∣H) that describes how these hypotheses relate to the sensory input E. Between layers, the predicted P(E) of a higher layer acts as the hypothesis distribution P(H) for the layer below it. By explicitly modelling the causal dynamics of the world, a generative model cannot only make sense of observations, but also make predictions about future observations.

Fig. 1
figure 1

A hierarchical generative model. Prediction layers at level n of the model act as hypothesis layers level n − 1. Beliefs of previous timesteps T − 1 influence the beliefs of future timesteps Tnow. Adapted with permission from Kwisthout et al. (2017)

Full size image

According to predictive processing, predictions form the basis of our interaction with the world. Due to the complexity and random nature of the world we live in, predictions made by a generative model are bound to have some degree of uncertainty. This is called prediction error (Den Ouden et al., 2012; Friston and Kiebel, 2009). It is assumed that brains reduce the uncertainty of their predictions as much as possible in order to reduce this prediction error over time (Clark, 2013; Friston et al., 2017). This prediction error reduction is important for a system to persist over time (Friston et al., 2012).

Structure Learning in Predictive Processing

In the predictive processing literature, learning typically refers to the process of optimizing the model parameters via the application of Bayes’ theorem. Here, we consider another form of learning referred to as structure learning. This type of learning is not concerned with parameter optimization but rather with learning the structure of the generative model. More specifically, structure learning pertains to learning the generative models’ variables and their functional dependencies (Smith et al., 2020; Da Costa et al., 2020).Footnote 3 Recently, the first attempts have been made towards a predictive processing formalization of structure learning. Specifically, model reduction (Friston and Penny, 2011) and model expansion (Smith et al., 2020) have been proposed as complementary methods for changing the structure of a generative model. In this paper, we will focus solely on model expansion. We will show how this formalism leads to conceptual problems. We omit discussion of model reduction as this method focusses on reducing the size of the generative model, while the conceptual problems we identify cannot be remedied by reducing the size of a generative model.

In model expansion, generative models have two distinct types of hypotheses: latent hypothesesu = {u1, ...,un} (also referred to as “spare slots”) and explicit hypotheses h = {h1, ...,hm}. The full hypothesis space is the union of the two types of hypotheses, i.e., H = u ∪h. Prior to learning all hypotheses are latent, i.e., h = ∅. Each hypothesis h ∈ H has a likelihood function P(E∣H = h). For latent hypotheses, this likelihood function is a noisy uniform distribution. For explicit hypotheses, the likelihood is developed over time based on observations as follows: when making an observation o, the agent determines which hypothesis h best explains that observation based on the posterior probability \(h = argmax_{h^{\prime }} P({H}=h^{\prime }\mid {E}=o)\). This posterior probability is computed by applying Bayes’ rule:

$$ P({H}\mid{E}=o) = \frac{P({E}=o\mid{H}) \times P({H})}{P({E}=o)} $$
(1)

Then, this most explanatory hypothesis is updated in two ways. First, the parameters that define the likelihood function are updated according to Bayes’ rule. Secondly, the distribution over the hypotheses is updated such that the prior probability P(H) of the next prediction cycle is set to the posterior probability of the current: Pt+ 1(H) = Pt(H∣o).Footnote 4

If the best hypothesis h was in u prior to this update, it is “moved” from u to h. It is this transition from a latent hypothesis u to an explicit hypothesis h that is referred to as “effectively expanding” the generative model. As such, a latent hypothesis u ∈u is made explicit when none of the explicit hypotheses h ∈h account better for the observation o than u. Note that the transition from latent to explicit is merely a verbal relabeling. Smith et al. (2020) refer to this kind of state space expansion as “effective” because the dimensions of the state space remain the same throughout. The only thing that changes is the number of explicit hypotheses used by the agent. Crucially, the total number of hypotheses, latent plus explicit, cannot be changed through learning. Consequently, the models that make use of model expansion have a fixed state space. That leaves one to wonder whether model expansion, or other models that similarly assume a fixed state space, can truly capture structure learning.

Problems Stemming from a Fixed State Space

We now describe two problems that emerge from a fixed-state space model of structure learning (such as model expansion). We define the problems formally, then provide a real-world example where the problem can occur. We prove that under a plausible assumption (that there are more categories in the world than hypotheses in a fixed state space) either of these two problems will inevitably occur (Fig. 2).

Fig. 2
figure 2

A visual representation of the two problems discussed in this paper. Hypotheses are indicated with a letter h, categories with a letter O, and dotted lines denote that a category is represented by a hypothesis (R(O,h)). In the situation on the left, categories O2 and O3 are both represented by h2. This is an example of category conflation. In the situation on the left, category O3 is not represented by any hypothesis. This is an example of cognitive blindness

Full size image

To explain the problems, we need to introduce some definitions. We define the world as a set of categories \(\boldsymbol {\mathcal {O}}\). Each element in this set is a specific category \(O \in \boldsymbol {\mathcal {O}}\). Furthermore, each such category is a set of instances o ∈ O. Making an observation is defined as evidencing the prediction variables with a particular instance of a category o ∈ O, such that P(E = o) = 1.

We define what it means for a category \({O} \in \boldsymbol {\mathcal {{O}}}\) to be represented by a concept h ∈ H as follows:

$$ R({O}, h) \equiv \forall_{o \in {O}} ( argmax_{h^{\prime}} P({H}=h^{\prime}\mid o) = h) $$
(2)

Thus, we say the hypothesis h represents a category O for an agent if for each instance of that category o ∈ O, the hypothesis h is the most probable given the evidence. That is, h is the maximum a posteriori (MAP) hypothesis for all o ∈ O. In real life, classification will never be this perfect and will instead be error prone. However, for ease of presentation we will work with this idealized error-free scenario; i.e., we assume that if h represents the category O, then h is the MAP hypothesis for all instances of category O. As will become clear, our conclusions do not rely on this assumption, even if it makes exposition easier.

Category Conflation

The first problem that we consider is category conflation. Category conflation is the cognitive phenomenon where an agent represents two distinct categories \({O}_{1}, {O}_{2} \in \boldsymbol {\mathcal {{O}}}\) in the world by one and the same hypothesis h ∈ H. In addition, there is no other hypothesis \(h^{\prime } \neq h\) that represents either of these categories. As such, the agent will classify instances of both (distinct) categories O1 and O2 as instances of h. In other words, for the agent the two categories are indistinguishable.

Given the definition in Eq. 2, we can formally define category conflation given hypotheses H and categories \({O}_{1}, {O}_{2} \in \boldsymbol {\mathcal {{O}}}\) as follows:

$$ Conf({O}_{1}, {O}_{2}, {H}) \equiv {O}_{1} \neq {O}_{2} \wedge \exists_{h \in {H}} (R({O}_{1}, h) \wedge R({O}_{2}, h)) $$
(3)

Let us illustrate the idea with a concrete example. Imagine an agent observing ducks and geese. Imagine further that due to the structure of its generative model, the agent believes that ducks and geese are different instances of the same category (we will call this combined category guck as opposed to the excellent alternative deese). It is not difficult to see how this situation may arise. Ducks and geese are quite similar to one another, especially visually. Furthermore, they can often be found in the same places, such as public parks, within the same general “group” of animals. Lastly, ducks and geese are strikingly different from, say, the plants, trees and decorations that tend to be near them. Whatever the exact reason for the confusion, the agent now has a problem. Whenever a duck or goose is seen, the agent infers that this is a guck. It has conflated two categories (ducks and geese) into a single hypothesis (gucks).

Cognitive Blindness

The second problem that we consider is cognitive blindness. Cognitive blindness is the cognitive phenomenon where a specific category \({O} \in \boldsymbol {\mathcal {{O}}}\) in the world is not represented by any hypothesis h ∈ H in the generative model of the agent. Therefore, the agent is blind to the category O. Using the definition of representation in Eq. 2, we formally define cognitive blindness with hypothesis variables H and a category \({O} \in \boldsymbol {\mathcal {{O}}}\) as follows:

$$ Blind({O}, {H}) \equiv \neg \exists_{h \in {H}} R({O}, h) $$
(4)

Let us again illustrate the idea with a concrete example. Imagine that an agent has three hypotheses, representing flamingos, geese and swans respectively. At some point, this agent encounters an ostrich. Now, the agent is confused. Because the ostrich shares some similarities with each of the agent’s hypotheses (such as colour, “kind”—they are all birds, and long shaped neck), it can be interpreted as belonging to any of these hypotheses. Which bird the ostrich is classified as will depend on the circumstances wherein the agent sees the ostrich (How far away is the agent? How clearly can be the colours be seen? Is only the neck visible?). Because these circumstances will inevitably vary, ostriches will sometimes be interpreted as a flamingo, sometimes as a goose and sometimes as a swan. Any one of the hypotheses that share enough features with the category ostrich can therefore be deemed the most likely hypothesis of an ostrich. As such, the agent is cognitively blind to the concept ostrich.

Proof

We will now prove that a generative model with a fixed state space will necessarily either conflate categories or be blind to categories if there are more categories in the world than the agent can represent in such a model. The assumption may seem bold, but we should consider the number of categories that we need to learn during our lifetime. All the animals, plants, tools, words, songs, types of food, faces, furniture and so much more need to be represented by a “spare slot.” Furthermore, even if evolution conveniently provided us with the right number of such slots for a particular time, we would be missing a means of representing all the new categories that are constantly being developed and discovered around us (e.g., the notions of a “neutrino,” “blockchain,” “tweet,” and “bitcoin” did not exist prior to 1930, 1998, 2006, and 2009 respectively).

  1. 1.

    Let \(\mid \boldsymbol {\mathcal {{O}}}\mid > \mid {H}\mid \)

  2. 2.

    By tautology, we have that: \((\forall _{{O} \in \boldsymbol {\mathcal {{O}}}} \exists _{h \in {H}} R({O}, h)) \vee \neg ( \forall _{O \in \boldsymbol {\mathcal {O}}} \exists _{h \in H} R(O, h))\)

  3. 3.

    For step 2, suppose that \(\neg ( \forall _{{O} \in \boldsymbol {\mathcal {{O}}}} \exists _{h \in {H}} R({O}, h))\)

  4. 4.

    From 3, it follows that \(\exists _{{O} \in \boldsymbol {\mathcal {{O}}}} \neg \exists _{h \in {H}} R({O}, h) \)

  5. 5.

    Step 4 is equivalent to \(\exists _{{O} \in \boldsymbol {\mathcal {{O}}}} Blind({O}, {H}) \). Therefore, supposing 3 under assumption 1 leads to cognitive blindness.

  6. 6.

    For step 2, suppose that \(\forall _{{O} \in \boldsymbol {\mathcal {{O}}}} \exists _{h \in {H}} R({O}, h)\)

  7. 7.

    From 1 and 6, it follows by pigeonhole principle that \(\exists _{{O}_{1}, {O}_{2} \in \boldsymbol {\mathcal {{O}}}} ({O}_{1} \neq {O}_{2} \wedge \exists _{h \in {H}}( R({O}_{1}, h) \wedge R(O_{2}, h) ) )\)

  8. 8.

    Step 7 is equivalent to \(\exists _{{O}_{1}, {O}_{2} \in \boldsymbol {\mathcal {{O}}}} (Conf({O}_{1}, {O}_{2}, {H}))\) Therefore, supposing 6 under assumption 1 leads to category conflation.

  9. 9.

    Combining steps 1, 2, 3, 5, 6, and 8, we conclude that every model must either suffer from category conflation or cognitive blindness, given that there are more categories in the world than there are concepts in the model.

Human Generative Models are Not Fixed

Our proof shows that structure learning on a fixed state space, as proposed by, e.g., model expansion (Smith et al., 2020), inevitably will end up conflating categories or be blind to categories in a world with ever-expanding number of categories.

Arguably, humans may also conflate categories from time to time, and they can at times be cognitively blind to certain features in the world. Be that as it may, unlike the fixed models adopted in the model expansion account of structure learning, humans certainly do not appear to be stuck indefinitely when these states arise. When humans find themselves with conflated categories, or when they come across something unfamiliar to them, they will often readily introduce new concepts to try and explain (i.e., resolve) the problem. For instance, while a child may indeed believe initially that ducks and geese are one and the same species guck, they will learn at some point that the animals are different species. Similarly, an explorer that first sees an ostrich might consider all other bird hypotheses to be insufficiently explanatory, and will introduce a new hypothesis “ostrich” instead. New hypotheses added in these situations are often wrong, perhaps most of the time so, but regardless of the verity of the new concept, the cognitive problem is actively being solved. In fact, humans continually hone their skills in structure learning through tools acquired through formal education, scientific training and explicit feedback from other people. For examples of successful structure learning, see the section below. So, if the predictive processing account aims to explain how the brain actually performs structure learning, we need to move beyond fixed models.

A Way Forward: Structure Learning Proper

In the previous section, we have argued that current attempts to model structure learning in predictive processing run into problems due to their reliance on a fixed state space. Therefore, predictive processing models will need to incorporate operations that allow for changing the structure of the generative models, if they want to avoid these problems. We refer to these types of operations as structure learning proper. We define structure learning proper as the process of going from a generative model G to a generative model G′ in a way that can not be explained by Bayesian (parameter) updating alone. Table 1 presents an overview of a number of changes that fall under structure learning proper. These changes are presented both verbally and formally. The verbal description gives an intuitive name for the type of change made to the generative model. In addition, Table 1 also gives intuitive real-world examples for each listed simple change. With these examples, we want to illustrate that our proposed changes are not just theoretical constructs, but also reflect aspects of human learning and how humans make changes to their generative models. In real life, some of these changes may occur simultaneously and some may happen more often than others. For ease of presentation, we illustrate the possible structural changes in isolation and in a minimal form.

Table 1 Options for structural changes to generative models formalized as Bayesian networks. Note that the possible preconditions mentioned here are mere suggestions. They should not be interpreted as a commitment to a particular stance
Full size table

The formal description takes the verbal description and translates it into a mathematical formalisation of the same change. To allow for these formal translations, we define the generative models postulated by the predictive processing account as Bayesian networks (see Fig. 3).Footnote 5 In the Bayesian networks that we consider we designate two types of variables: hypothesis variables H and prediction variables E. Hypothesis variables are equivalent to hidden states or concepts in predictive processing literature. Likewise, prediction variables are equivalent to outcomes. The values of a Bayesian variable X, which can either be a hypothesis or a prediction variable, are denoted with val(X) = {x1, ...,xn}, and a single value as x. The structure of the generative model is defined as a directed graph G = (V,A), where V is the set of vertices in G, and A is the set of arcs in G. Here, vertices are variables, and arcs indicate dependencies between those variables.

Fig. 3
figure 3

Example of a Bayesian network. The bubbles represent variables, and the arrows denote (causal) relations between those variables. Here, the variable “Diet” influences “Restaurant”: what kind of diet you are on limits the choice of restaurants you can go to. Both “Diet” and “Exercise” influence “Physical Health”: A healthy diet and more exercise lead to better physical health

Full size image

Lastly, the table lists a conceivable precondition for each simple change to occur (or for it to be justified to occur). These preconditions serve as an inspiration and illustration, and should not be interpreted as any definitive answer. The reason why we only provide an example is that for most of these changes these preconditions have not been both formally defined and empirically investigated. What the real preconditions are is therefore an open question. This paper does not aim to give answers to these questions, because each question would demand a research project to address, if not a body of research. This then is the challenge: In order for predictive processing to account for structure learning proper, it must investigate the formal and empirical underpinnings of the preconditions under which our proposed changes occur in human structure learning. We stress that the ultimate goal here is not to find statistical or engineering solutions, but to formulate an explanatory scientific account of structure learning proper at Marr’s (1982) computational level.

A Note on Bayesian Non-parametrics

Before we close, we reflect on the relationship between the challenge that we pose and an existing approach in computational cognitive science that takes inspiration from Bayesian non-parametrics. Readers familiar with that approach may believe that that method already addresses the challenge that we pose. Here, we briefly explain how and why it does not.

Bayesian non-parametrics is a method firmly rooted in Bayesian statistics that has found appreciation in modelling cognition (Griffiths et al., 2006; Perfors et al., 2011; Chater et al., 2010; Austerweil and Griffiths, 2013). A central tenet of Bayesian non-parametrics is that generative models can be defined without having to specify the number of values within a variable, the amount of layers in a belief model and other such parameters; hence the name “non-parametric” (see Gershman & Blei 2012; Griffiths & Ghahramani 2011, for reviews). In other words, this method allows modellers to define a generative model that is not fixed, but can flexibly expand and shrink. This property notwithstanding, the approach has some limitations relevant to the challenge that we pose.

The first limitation of Bayesian non-parametrics is that it only captures a proper subset of the possible structural changes listed in Table 1. Namely, to the best of our knowledge Bayesian non-parametrics is not (yet) capable of discovering new variables or establishing or removing causal connections between variables. Of course, one might argue that is it not necessary that our brains perform all the changes listed in Table 1. We can agree with this argument to some degree. However, the very structural changes missing in Bayesian non-parametrics are so central to our cognition that any account of human learning that cannot account for them is incomplete at best, and flawed at worst. Given that Bayesian non-parametrics is missing the capacity to enact some of the cognitively relevant structural changes, there will necessarily be situations where Bayesian non-parameterics predicts a structural change that does not match the structural change that actually occurs in human learning. Without a more complete account of structure learning we have no way of predicting which situations these could be.

The second, and arguably more important limitation of Bayesian non-parametrics is that it commits to a very particular stance of when and why values are changed in a generative model. This view, if considered at Marr’s computational level (Marr, 1982), postulates that generative models change in order to optimize the likelihood of future observations. This is indeed one possible precondition for a structural change to a generative model. It is, in fact, one formalisation of the precondition for adding a new value that we gave in Table 1, row 7. However, we can conceive of many other formalisations of “better explained” (column 4, row 7), that will lead to (very) different preconditions. Consider, for example, Kwisthout (2013), who proposes that in judging the quality of an explanation cognizers may weigh both informativeness and probability. This idea conflicts with the metric of likelihood alone used in Bayesian non-parametrics. Without knowing which preconditions most accurately describe structural changes as they apply to human learning, we should not treat Bayesian non-parametrics as the only possible answer.

To summarize, while we appreciate the perspective that Bayesian non-parametrics offers on a relevant subset of the changes that make up structure learning proper, we conclude that there are still important changes that are unaccounted for. Furthermore, we argue that there are other plausible preconditions possible that are not captured by Bayesian non-parametrics. Our challenge to predictive processing theorists, thus, remains to investigate which of these preconditions best explains human structure learning.

Conclusion

Learning in predictive processing has mostly been conceptualized as parameter learning. Recently, several developments have been made that aim to tackle the problem of structure learning. Structure learning is important as it can help explain why generative models have the structure that they do, as well as how this structure is learned over time. However, despite the name structure learning, these new developments in predictive processing are essentially a particular type of Bayesian parameter learning in a fixed state space.

We showed that generative models with a fixed state space will inevitably lead to at least one of the two conceptual problems. These problems are category conflation, where different categories in the world are interpreted as the same concept, and cognitive blindness, where a category in the world is not represented by any concept. Furthermore, we argued that when humans run into these problems, they have strategies that allow them to solve them. These strategies are best understood as structural changes to a generative model.

We presented an exhaustive set of minimal changes that can be made to a Bayesian generative model, defining structure learning proper (see Table 1). The idea that such changes are possible is not new: structure learning proper has been studied in the past, with or without a cognitive perspective (Tsamardinos et al., 2006; Piantadosi et al., 2016; Piantadosi, 2021; Perfors, 2012; Chickering, 1996; Chickering et al., 1994). Either this research has not provided a formal account of all possible and cognitive relevant structural changes or they have not explored the conditions under which these might occur in human learning. Given that we provide a formal characterisation of possible structural changes in this paper, our proposed way forward is to research cognitively plausible preconditions of when each change occurs.

We take the position that current theories of structure learning should integrate the proposed proper structural changes into their explanatory toolbox. The importance of structural changes, like the ones we suggest, cannot be understated as a means to explain the richness of human learning. If predictive processing wishes to live up to its ambition to explain all of learning, it needs to make the transition from its current formalisation of “effective” structure learning to structure learning proper.