Skip to main content
SpringerLink
Log in

Fractional Derivatives with Variable Memory

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions A: Science Aims and scope Submit manuscript

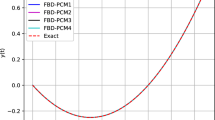
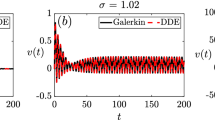
Abstract

Recently, fractional derivatives (FDs) and fractional differential equations are extensively used in modeling of most dynamic processes which generally involve memory factors. Normally, the dynamic models involving full memory effect can be solved with the help of global fractional derivatives, whereas those involves with local memory effect can be solved by using only fractional derivatives with short memory. The prime objective of this work is to define new fractional derivatives of Riemann–Liouville and Caputo types, which can be used for both short and global memory effects. Some general and dynamic properties of the proposed differential operators in comparison to existing formulas of FDs are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1

Similar content being viewed by others

Availability of data and material:

Not applicable.

Code availability:

Not applicable.

References

  • Bagley RL, Torvik J (1983) Fractional calculus-a different approach to the analysis of viscoelastically damped structures. AIAA J. 21(5):741–748

    Article  Google Scholar 

  • Baliarsingh P (2016) On a fractional difference operator. Alex. Eng. J. 55(2):1811–1816

    Article  Google Scholar 

  • Baliarsingh P, Nayak L (2018) A note on fractional difference operators. Alex. Eng. J. 57(2):1051–1054

    Article  Google Scholar 

  • Butera S, Di Paola M (2014) A physically based connection between fractional calculus and fractal geometry. Ann. Phys. 350:146–158

    Article  MathSciNet  Google Scholar 

  • Caputo M (1967) Linear models of dissipation whose q is almost frequency independent-ii. Geophys. J. Int. 13(5):529–539

    Article  Google Scholar 

  • Dai H, Zheng Z, Wang W (2017) A new fractional wavelet transform. Commun. Nonlinear Sci. Numer. Simul. 44:19–36

    Article  MathSciNet  Google Scholar 

  • Dokuyucu ML, Dutta H (2020) A fractional order model for Ebola virus with the new Caputo fractional derivative without singular kernel. Chao Soliton Fract. 134:109717

    Article  MathSciNet  Google Scholar 

  • Khanehgir M, Allahyari R, Mursaleen M, Kayvanloo HA (2020) On infinite system of Caputo fractional differential inclusions with boundary conditions for convex-compact multivalued mappings. Alex. Eng. J. 59(5):3233–3238

    Article  Google Scholar 

  • Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations. Elsevier, Amsterdam

    MATH  Google Scholar 

  • Kiryakova V (2008) A brief story about the operators of the generalized fractional calculus. Fract. Calc. Appl. Anal. 11(2):203–220

    MathSciNet  MATH  Google Scholar 

  • Liu C (2015) Counterexamples on Jumarie’s two basic fractional calculus formulae. Commun. Nonlinear Sci. Numer. Simul. 22:92–94

    Article  MathSciNet  Google Scholar 

  • Luchko Y (2021) Operational calculus for the general fractional derivative and its applications. Fract. Calc. Appl. Anal. 24(2):338–375

    Article  MathSciNet  Google Scholar 

  • Ortigueira MD, Trujillo JJ (2012) A unified approach to fractional derivatives. Commun. Nonlinear Sci. Numer. Simul. 17(12):5151–5157

    Article  MathSciNet  Google Scholar 

  • Rossikhin YA, Shitikova MV (2012) On fallacies in the decision between the Caputo and Riemann-Liouville fractional derivatives for the analysis of the dynamic response of a nonlinear viscoelastic oscillator. Mech. Res. Commun. 45:22–27

    Article  Google Scholar 

  • Rossikhin YA, Shitikova MV (2009) Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl Mech Rev 63(1):010801–01080152

    Article  Google Scholar 

  • Samko SG, Kilbas AA, Marichev OI (1993) Fractional integrals and derivatives theory and applications, vol 1993. Gordon and Breach, Yverdon

    MATH  Google Scholar 

  • Sneddon IN (1975) The use in mathematical analysis of Erdèlyi-Kober operators and some of their applications. In: Fractional calculus and its applications (Proc. Internat. Conf. Held in New Haven); Ross, B., Ed., Lecture Notes in Math. 457. Springer, New York, 37–79

  • Tarasov VE (2013) No violation of the Leibniz rule no fractional derivative. Commun Nonlinear Sci Numer Simul 18(11):2945–2948

    Article  MathSciNet  Google Scholar 

  • Wang J-L, Li H-F (2011) Surpassing the fractional derivative: concept of the memory dependent derivative. Comput Math Appl 62(3):1562–1567

    Article  MathSciNet  Google Scholar 

  • Wu GC, Baleanu D, Zeng SD, Deng ZG (2015) Discrete fractional diffusion equation. Nonlinear Dyn 80(1–2):281–286

    Article  MathSciNet  Google Scholar 

  • Wu GC, Luo M, Huang LL, Banerjee S (2020) Short memory fractional differential equations for new neural network and memristor design. Nonlinear Dyn 100:3611–3623

    Article  Google Scholar 

  • Xu J, Li J (2016) Stochastic dynamic response and reliability assessment of controlled structures with fractional derivative model of viscoelastic dampers. Mech. Syst. Signal Process. 72–73:865–896

    Article  Google Scholar 

  • Yang X-J, Srivastava HM, He J-H, Baleanu D (2013) Cantor-type cylindrical-coordinate method for differential equations with local fractional derivatives. Phys. Lett. A 377:1696–700

    Article  MathSciNet  Google Scholar 

  • Yu YJ, Zhao LJ (2020) Fractional thermoelasticity revisited with new definitions of fractional derivative. Eur J Mech A/Solids 84:104043

    Article  MathSciNet  Google Scholar 

  • Yu YJ, Deng ZC (2020) Fractional order theory of Cattaneo-type thermoelasticity using new fractional derivatives. Appl Math Model 87:731–751

    Article  MathSciNet  Google Scholar 

  • Yu YJ, Deng ZC (2021) Factional order thermoelasticity for pizeoelectric materials. Fractals 29(4):2150082–253

    Article  Google Scholar 

  • Zheng Z, Zhao W, Dai H (2019) A new definition of fractional derivative. Int J Non-Linear Mech 108:1–6

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the anonymous referees for their valuable suggestions that improved this paper remarkably. Present work is partially supported by NBHM, DAE, Mumbai, under the Grant No. 02011/7/2020/NBHM(RP)/R&D/6289.

Funding

Present submission is partially supported with NBHM, DAE, Mumbai, under the Grant No. 02011/7/2020/NBHM(RP)/R&D/6289.

Author information

Authors and Affiliations

  1. Institute of Mathematics and Applications, Bhubaneswar, Odisha, 751029, India

    P. Baliarsingh

  2. Department of Mathematics, School of Applied Sciences, Kalinga Institute of Industrial Technology, Bhubaneswar, 751024, India

    L. Nayak

Authors
  1. P. Baliarsingh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. Nayak
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Both the authors have contributed equally for preparing this submission.

Corresponding author

Correspondence to L. Nayak.

Ethics declarations

Conflict of interest

We have no conflicts of interest in- cluding any financial, personal or other relationships with other people or organiza- tions to disclose.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Baliarsingh, P., Nayak, L. Fractional Derivatives with Variable Memory. Iran J Sci Technol Trans Sci 46, 849–857 (2022). https://doi.org/10.1007/s40995-022-01296-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40995-022-01296-4

Keywords

Mathematics Subject Classification

Search

Navigation