An Optimal Crime Control Policy in a Dynamic Setting

Abstract

Existing literature does not capture efficiency losses on the dynamic adjustment path of crime control market from initial to final equilibrium after a shock in order to formulate an optimal crime control policy. Furthermore, number of public service units and crime control rate are major determinants of crimes controlled in a society, and a policy without taking into consideration such vital determinants cannot ensure adjustment of number of crimes controlled as a result of cost movement in desired time, which may lead to extra efficiency losses than those envisaged during policy formulation for an optimal level of crime control in a society. This article designs a comprehensive optimal crime control policy mechanism by modeling a three dimensional crime control system in society capturing number of public service units, crime control rate, and cost, while taking into account efficiency losses during adjustment of crime control market, crime control rate and number of public service units in addition to those which result due to movements from initial to final equilibriums.

Appendices

Appendix

Dynamic Problem of the Tax Policy Maker/Budget Allocator (TPM/BA)

This section discusses the dynamic problem of TPM/BA. Present discounted value of future stream of net social benefits are maximized in a dynamic environment, and the present value at time zero is given below:

$$\begin{aligned} V(0)= {\int \limits _{0}^{\infty }} \left[ U_{r}(r)-\varsigma _{B}(m_{B}(r,e_{B}))\right] e^{-\sigma t}dt, \end{aligned}$$

(66)

$\sigma$ denotes the discount rate. r(t) is the control variable and $m_{B}(t)$ the state variable. Maximization problem is as follows:

$$\begin{aligned} \underset{\left\{ r(t)\right\} }{Max}V(0)= {\int \limits _{0}^{\infty }} \left[ U_{r}(r)-\varsigma _{B}(m_{B}(r,e_{B}))\right] e^{-\sigma t}dt, \end{aligned}$$

subject to the constraints that

$\overset{.}{m_{B}}(t)=m_{B1}^{\prime }(r(t),e_{B}(r(t),z_{B}))\overset{.}{r} (t)+m_{B2}^{\prime }(r(t),e_{B}(r(t),z_{B}))e_{B1}^{\prime }(r(t),z_{B} )\overset{.}{r}(t)$ (state equation, describing how the state variable changes with time; $z_{B}$ are exogenous factors),

$m_{B}(0)=m_{Bs}$ (initial condition),

$m_{B}(t)\ge 0$ (non-negativity constraint on state variable),

$m_{B}(\infty )$ free (terminal condition).

The current-value Hamiltonian is as follows:

$$\begin{aligned} {\widetilde{H}}=\, & {} U_{r}(r\left( t\right) )-\varsigma _{B}(m_{B}(r(t),e_{B} (r(t),z_{B})))+\mu _{B}(t)\overset{.}{r}(t)\nonumber \\&\times \left[ \begin{array}{c} m_{B1}^{\prime }(r(t),e_{B}(r(t),z_{B}))+m_{B2}^{\prime }(r(t),e_{B} (r(t),z_{B}))*\\ e_{B1}^{\prime }(r(t),z_{B}) \end{array} \right] . \end{aligned}$$

(67)

Now the maximizing conditions are as follows:

• (i) $r^{*}(t)$ maximizes ${\widetilde{H}}$ for all t: $\frac{\partial {\widetilde{H}}}{\partial r}=0,$

• (ii) $\overset{.}{\mu _{B}}-\sigma \mu _{B}=-\frac{\partial {\widetilde{H}} }{\partial m_{B}},$

• (iii) $\overset{.}{m_{B}}^{*}=\frac{\partial {\widetilde{H}}}{\partial \mu _{B}}$ (this just gives back the state equation),

• (iv) $\lim _{t\rightarrow \infty }\mu _{B}(t)m_{B}(t)e^{-\sigma t}=0$ (the transversality condition).

The first two conditions are as follows:

$$\begin{aligned} \frac{\partial {\widetilde{H}}}{\partial r} =\,&U_{r}^{{\prime }}(r\left( t\right) )-\varsigma _{B}^{\prime }(m_{B}(r(t),e_{B}(r(t),z_{B})))\nonumber \\&\times \left\{ \begin{array}{c} m_{B1}^{\prime }(r(t),e_{B}(r(t),z_{B}))+m_{B2}^{\prime }(r(t),e_{B} (r(t),z_{B}))*\\ e_{B1}^{\prime }(r(t),z_{B}) \end{array} \right\} \nonumber \\&+\mu _{B}(t)\overset{.}{r}(t)*\nonumber \\&\times \left[ \begin{array}{c} m_{B11}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))+m_{B12}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))e_{B1}^{\prime }(r(t),z_{B})+\\ m_{B21}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))e_{B1}^{\prime }(r(t),z_{B} )+m_{B22}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))e_{B1}^{\prime 2} (r(t),z_{B})+\\ m_{B2}^{\prime }(r(t),e_{B}(r(t),z_{B}))e_{B11}^{\prime \prime }(r(t),z_{B}) \end{array} \right] \nonumber \\&=0, \end{aligned}$$

(68)

and

$$\begin{aligned} \overset{.}{\mu _{B}}-\sigma \mu _{B}=-\frac{\partial {\widetilde{H}}}{\partial m_{B}}=\varsigma _{B}^{\prime }(m_{B}(r(t),e_{B}(r(t),z_{B}))). \end{aligned}$$

(69)

In equilibrium, $\overset{.}{r}(t)=0,$ and the expression $\frac{\partial {\widetilde{H}}}{\partial r}$ boils down to the following:

$$\begin{aligned}&U_{r}^{\prime }(r\left( t\right) )-\varsigma _{B}^{\prime }(m_{B} (r(t),e_{B}(r(t),z_{B})))\\&\qquad \times \left\{ \begin{array}{c} m_{B1}^{\prime }(r(t),e_{B}(r(t),z_{B}))+m_{B2}^{\prime }(r(t),e_{B} (r(t),z_{B}))*\\ e_{B1}^{\prime }(r(t),z_{B}) \end{array} \right\} =0. \end{aligned}$$

If supply curve shifts to the right, then the number of crimes controlled is higher at the existing cost, and the term $\varsigma _{B}^{\prime } (m_{B}(r(t),e_{B}(r(t),z_{B})))$ is higher at the existing cost at that time. The term multiplying $\varsigma _{B}^{\prime }(m_{B}(r(t),e_{B}(r(t),z_{B})))$, i.e., $m_{B1}^{\prime }(r(t),e_{B}(r(t),z_{B}))+m_{B2}^{\prime }(r(t),e_{B} (r(t),z_{B}))e_{B1}^{\prime }(r(t),z_{B})$ is a function of cost and has not changed as the cost is the same as before. Therefore, the TPM/BA now faces the following inequality at the existing cost:

$$\begin{aligned} \frac{\partial {\widetilde{H}}}{\partial r} =\,&U_{r}^{{\prime }}(r\left( t\right) )-\varsigma _{B}^{\prime }(m_{B}(r(t),e_{B}(r(t),z_{B})))\\&\times \left\{ \begin{array}{c} m_{B1}^{\prime }(r(t),e_{B}(r(t),z_{B}))+m_{B2}^{\prime }(r(t),e_{B} (r(t),z_{B}))*\\ e_{B1}^{\prime }(r(t),z_{B}) \end{array} \right\} \\&+\mu _{B}(t)\overset{.}{r}(t)*\\&\times \left[ \begin{array}{c} m_{B11}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))+m_{B12}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))e_{B1}^{\prime }(r(t),z_{B})+\\ m_{B21}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))e_{B1}^{\prime }(r(t),z_{B} )+m_{B22}^{\prime \prime }(r(t),e_{B}(r(t),z_{B}))e_{B1}^{\prime 2} (r(t),z_{B})+\\ m_{B2}^{\prime }(r(t),e_{B}(r(t),z_{B}))e_{B11}^{\prime \prime }(r(t),z_{B}) \end{array} \right] \\&<0. \end{aligned}$$

The TPM/BA must decrease the cost for satisfying the net social benefit optimization condition after the shock. This implies that there is a negative relationship between the cumulative number of crimes controlled in society and the cost. If the rate of supply of public service in terms of number of crimes controlled is equal to the demand rate, the number of crimes controlled is in equilibrium. If a difference of a finite magnitude comes into force between the supply and demand rates, and the public and the private sector do not react to a change in the cost caused by a difference in the supply and demand rates, the cost will continue changing until the saturation point of society comes. The response of TPM/BA can be depicted by the following formulation:

$$\begin{aligned} \textit{Cost rate change}&\propto \textit{change in cumulative no. of controlled crime.}\\ R&=\textit{cost rate change.}\\ M_{B}&=m_{B}-m_{Bs}=\textit{change in cumulative no. of controlled crime,}\\ m_{B}&=\textit{cumulative no. of controlled crime at time t,}\\ m_{Bs}&=\textit{cumulative no. of controlled crime in steady state equilibrium.}\\ \textit{Input}-\textit{output}&=\frac{dm_{B}}{dt} =\frac{d(m_{B}-m_{Bs})}{dt}=\frac{dM_{B}}{dt},\\ \text{or }M_{B}&= {\int } \left( \textit{input}-\textit{output}\right) dt.\\ \textit{Cost rate change}&\propto {\int } \left( \textit{supply rate}-\textit{demand rate}\right) dt,\text{ or}\\ R&=-K_{m} {\int } \left( \textit{supply rate}-\textit{demand rate}\right) dt, \end{aligned}$$

where $K_{m}$ is the proportionality constant. A negative sign indicates that when $\left( \textit{supply rate}-\textit{demand rate}\right)$ is positive, R is negative, i.e., the cost decreases. The above expression can also be written as:

$$\begin{aligned}&{\int } \left( \textit{supply rate}-\textit{demand rate}\right) dt=-\frac{R}{K_{m}},\text{ or}\nonumber \\&{\int } \left( \textit{w}_{Bi}-\textit{w}_{B0}\right) dt=-\frac{R}{K_{m}}, \nonumber \\&w_{Bi} =\textit{supply rate},\nonumber \\&w_{B0} =demand\,rate,\nonumber \\&K_{m} =\textit{dimensional constant.} \end{aligned}$$

(70)

When $t=0$, supply rate = demand rate, i.e., public service market is in equilibrium and Eq. (70) can be expressed as:

$$\begin{aligned} {\int } \left( w_{Bis}-w_{B0s}\right) dt=0. \end{aligned}$$

(71)

The subscript s denotes steady state equilibrium and $R=0$ in steady state. Subtracting Eq. (71) from Eq. (70), we get:

$$\begin{aligned}&{\int } \left( w_{Bi}-w_{Bis}\right) dt- {\int } \left( w_{B0}-w_{B0s}\right) dt=-\frac{R}{K_{m}},\text{ or} \nonumber \\&{\int } \left( W_{Bi}-W_{B0}\right) dt=-\frac{R}{K_{m}}, \nonumber \\&\text{where }w_{Bi}-w_{Bis} =W_{Bi}=\textit{change in supply rate} ,\nonumber \\&w_{B0}-w_{B0s} =W_{B0}=\textit{change in demand rate.} \end{aligned}$$

(72)

R,  $W_{Bi}$ and $W_{B0}$ are deviation variables, i.e., deviation from steady state equilibrium and have zero initial values. Equation (72) can also be expressed as:

$$\begin{aligned} R=-K_{m} {\int } W_{B}dt=-K_{m}M_{B}, \end{aligned}$$

(73)

where $W_{B}=W_{Bi}-W_{B0}.$ If R gets a jump as a result of some factor other than a change in cumulative number of crimes controlled, that is another input which can be added to Eq. (73) as follows:

$$\begin{aligned} R=-K_{m} {\int } W_{B}dt+E_{B}=-K_{m}M_{B}+E_{B}. \end{aligned}$$

(73a)

There can also be an exogenous shock in cumulative number of crimes controlled other than the feedback of cost.

Solution of the Model-Panel B with a Crime Control Policy

Expressions from Eqs. (11a), (18), and (23) respectively along with $\tau _{d1}=0$ are as follows:

$$\begin{aligned} \frac{dR(t)}{dt}&=-K_{m}W_{B}(t),\\ W_{d}(t)&=-K_{d}R(t),\\ W_{m}&=-K_{s}\left( C_{c}-R\right) , \end{aligned}$$

and

$$\begin{aligned} W_{B}(t)=W_{m}(t)-W_{d}(t), \end{aligned}$$

if no exogenous demand or supply shock happens. $W_{m}(t)$ is number of crimes controlled. Combining the above expressions together, we can write:

$$\begin{aligned} W_{m}(t)=-K_{sp}\left[ C_{p}(t)-R(t)\right] -K_{sc}\left[ C_{c} (t)-R(t)\right] , \end{aligned}$$

(74)

where the p and c subscripts denote the private and the public sector respectively. Now, combining the above expressions together, we can write:

$$\begin{aligned} \frac{dR(t)}{dt}&=-K_{m}\left[ W_{m}(t)-W_{d}(t)\right] \\&=-K_{m}\left[ -K_{s}\left\{ C_{c}(t)-R(t)\right\} +K_{d}R(t)\right] \\&=-K_{m}\left[ -K_{s}C_{c}(t)+(K_{s}+K_{d})R(t)\right] . \end{aligned}$$

Rearranging the above expression gives:

$$\begin{aligned} \frac{dR(t)}{dt}+K_{m}(K_{s}+K_{d})R(t)=K_{m}K_{s}C_{c}(t). \end{aligned}$$

(75)

The Routh–Hurwitz stability criterion (which provides a necessary and sufficient condition for stability of a linear dynamical system) for the above differential equation’s stability is $K_{m}(K_{s}+K_{d})>0$; and as $K_{m}$,$K_{s}$, and $K_{d}$ are all defined as positive numbers, this criterion holds. This ensures that, away from a given initial equilibrium, every adjustment mechanism will lead to another equilibrium.

Suppose government reduces the per crime controlled cost of the public service provider by B, say through provision of some funds to buy an advanced technology for crime control, the above equation can be written as:

$$\begin{aligned} \frac{dR(t)}{dt}+K_{m}(K_{s}+K_{d})R(t)=-K_{m}K_{s}B. \end{aligned}$$

(76)

The solution is given by the following expression:

$$\begin{aligned} R(t)=-\frac{K_{s}B}{(K_{s}+K_{d})}+\frac{K_{s}B}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}. \end{aligned}$$

(77)

$R(0)=0$ (the initial condition), and $R(\infty )=$ $-\frac{K_{s}B}{(K_{s}+K_{d})}$ (the final steady state equilibrium value). In response to a policy, the per unit crime controlled cost dynamics depends on the parameters $K_{s},K_{d},$ $K_{m}$ and B.

A Dynamic Optimal Crime Control Policy-Panel B

After a crime control policy, there are efficiency gains in post policy equilibrium in comparison with the initial/pre-policy equilibrium. However, there are also some efficiency losses during the adjustment period of crime control market until new equilibrium arrives. As soon as crime control policy is implemented, supply of public service expands, whereas the demand remains the same at the initial per unit cost, pushing the crime control market out of equilibrium. Now the adjustment of per unit cost begins to equalize the supply and demand to bring the new crime control market equilibrium. The post policy equilibrium cost is a function of demand and supply elasticities. From the previous section, change in supply as a result of a crime control policy is as follows:

$$\begin{aligned} W_{m}(0)&=-K_{s}\left[ C_{c}(0)-R(0)\right] =K_{s}B,\nonumber \\ \text{as }R(0)&=0. \end{aligned}$$

(78)

As a result of crime control policy, supply of public service goes up by $K_{s}B.$ As demand does not change, therefore, cumulative number of crimes controlled also goes up by $K_{s}B$. Now the market is out of equilibrium, and the market forces push the crime control market toward a new equilibrium through the movement in per unit cost. As the per unit cost changes, the demand and supply of public service also change through feedback. If cumulative number of crime controlled goes up, it indicates a higher supply than demand and vice versa. There is no efficiency loss if crime control market is in equilibrium, and demand and supply are same. If market is out of equilibrium, either supply or demand is excessive at that point in time. Therefore, the total efficiency loss during the adjustment of crime control market is a sum of the differences in supply and demand at all points in time. Total efficiency loss for a crime control policy can be expressed as:

$$\begin{aligned} EL\,&= {\int \limits _{-\infty }^{0}} W_{m}(\infty )dt+ {\int \limits _{0}^{\infty }} \left[ W_{m}(t)-W_{d}(t)\right] dt\nonumber \\&= {\int \limits _{-\infty }^{0}} W_{m}(\infty )dt+M_{B}(t). \end{aligned}$$

(79)

Equation (73a) states the following:

$$\begin{aligned} R(t)=-K_{m}M_{B}(t)+E_{B}. \end{aligned}$$

By imposing the initial conditions, we can determine the value of $E_{B}$ as follows:

$$\begin{aligned} R(0)&=-K_{m}M_{B}(0)+E_{B},\\ 0&=-K_{m}K_{s}B+E_{B},\\ E_{B}&=K_{m}K_{s}B. \end{aligned}$$

After plugging in the above expression in Eq. (73a) it transforms to

$$\begin{aligned} R(t)&=-K_{m}M_{B}(t)+K_{m}K_{s}B,\text{ or}\\ M_{B}(t)&=-\frac{1}{K_{m}}\left[ R(t)-K_{m}K_{s}B\right] . \end{aligned}$$

With Crime Control Policy Cost Constraint:

According to Eq. (23), public service supply change due to change in per unit cost is:

$$\begin{aligned} W_{m}(t)=-K_{s}\left[ C_{c}(t)-R(t)\right] . \end{aligned}$$

It can also be written as:

$$\begin{aligned} w_{nm}(t)-w_{im}(0)=-K_{s}\left[ C_{c}(t)-R(t)\right] , \end{aligned}$$

where $w_{im}(0)$ is the initial public service supply, and $w_{nm}(t)$ is the new supply after government exercises crime control policy. $W_{m} (t)=w_{nm}(t)-w_{im}(0)$, as $W_{m}(t)$ is a deviation variable, i.e., deviation from the initial steady state equilibrium value. The crime control policy cost (CCPC) can be expressed as:

$$\begin{aligned} CCPC=B\left[ w_{im}(0)+K_{s}\left\{ B+R(t)\right\} \right] . \end{aligned}$$

(80)

Our problem of minimising efficiency loss subject to crime control policy cost constraint is as follows:

$$\begin{aligned} \min _{B}EL\text{ s.t. }CCPC\le G_{B}. \end{aligned}$$

$G_{B}$ is the government’s cost for exercising crime control policy. The choice variable is crime control policy, i.e., B, and the constraint is binding at $t=0$. The Lagrangian for the above problem can be written as follows:

$$\begin{aligned} {\mathcal {L}} =&{\int \limits _{-\infty }^{0}} W_{m}(\infty )dt+M_{B}(t)+\lambda \left[ G_{B}-B\left[ w_{im}(0)+K_{s}\left\{ B+R(t)\right\} \right] \right] \\ =&{\int \limits _{-\infty }^{0}} \left[ K_{s}B-\frac{K_{s}^{2}B}{(K_{s}+K_{d})}\right] dt\\&-\frac{1}{K_{m}}\left[ -\frac{K_{s}B}{(K_{s}+K_{d})}+\frac{K_{s}B}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}-K_{m}K_{s}B\right] \\&+\lambda \left[ G_{B}-B\left[ w_{im}(0)+K_{s}\left\{ B-\frac{K_{s} B}{(K_{s}+K_{d})}+\frac{K_{s}B}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}\right\} \right] \right] \\ =&{\int \limits _{-\infty }^{0}} \frac{K_{s}K_{d}B}{(K_{s}+K_{d})}dt-\frac{1}{K_{m}}\left[ -\frac{K_{s} B}{(K_{s}+K_{d})}+\frac{K_{s}B}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}-K_{m}K_{s}B\right] \\&+\lambda \left[ G_{B}-B\left[ w_{im}(0)+K_{s}\left\{ B-\frac{K_{s} B}{(K_{s}+K_{d})}+\frac{K_{s}B}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}\right\} \right] \right] . \end{aligned}$$

The first order condition with respect to B leads to the following:

$$\begin{aligned}&{\int \limits _{-\infty }^{0}} \frac{K_{s}K_{d}}{(K_{s}+K_{d})}dt-\frac{1}{K_{m}}\left[ -\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}-K_{m}K_{s}\right] \\&\quad -\lambda \left[ w_{im}(0)+K_{s}\left\{ B-\frac{K_{s}B}{(K_{s}+K_{d} )}+\frac{K_{s}B}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right\} \right] \\&\quad -\lambda BK_{s}\left[ 1-\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s} +K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right] =0. \end{aligned}$$

Rearranging this, we get:

$$\begin{aligned}&{\int \limits _{-\infty }^{0}} \frac{K_{s}K_{d}}{(K_{s}+K_{d})}dt-\frac{1}{K_{m}}\left[ -\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}-K_{m}K_{s}\right] \\&\qquad -2\lambda BK_{s}\left[ 1-\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right] \\&\quad =\lambda w_{im}(0), \end{aligned}$$

or

$$\begin{aligned} B=-\frac{\lambda w_{im}(0)-\left[ {\int \limits _{-\infty }^{0}} \frac{K_{s}K_{d}}{(K_{s}+K_{d})}dt-\frac{1}{K_{m}}\left[ -\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}-K_{m}K_{s}\right] \right] }{2\lambda K_{s}\left[ 1-\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right] }. \end{aligned}$$

(81)

The derivative with respect to $\lambda$, is as follows:

$$\begin{aligned} G_{B}-B\left[ w_{im}(0)+K_{s}\left\{ B-\frac{K_{s}B}{(K_{s}+K_{d})} +\frac{K_{s}B}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right\} \right] =0. \end{aligned}$$

(82)

Putting Eq. (81) into (82), we get:

$$\begin{aligned}&G_{B}= \\&\quad -w_{im}(0).\frac{\lambda w_{im}(0)-\left[ {\int \limits _{-\infty }^{0}} \frac{K_{s}K_{d}}{(K_{s}+K_{d})}dt-\frac{1}{K_{m}}\left[ -\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}-K_{m}K_{s}\right] \right] }{2\lambda K_{s}\left[ 1-\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right] } \\&\quad +K_{s}\left\{ 1-\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d} )}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right\} \\&\quad *\left[ -\frac{\lambda w_{im}(0)-\left[ {\int \limits _{-\infty }^{0}} \frac{K_{s}K_{d}}{(K_{s}+K_{d})}dt-\frac{1}{K_{m}}\left[ -\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}-K_{m}K_{s}\right] \right] }{2\lambda K_{s}\left[ 1-\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right] }\right] ^{2}, \\&\quad \text{or }4\lambda ^{2}Q_{B}G_{B}=-2\lambda ^{2}w_{im}^{2}(0)+2\lambda w_{im}(0)J_{B}+\lambda ^{2}w_{im}^{2}(0)+J_{B}^{2}-2\lambda w_{im}(0)J_{B}, \\&\quad \text{where }Q_{B}=K_{s}\left[ 1-\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s} }{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s}+K_{d})\right] t}\right] , \\&J_{B}= {\int \limits _{-\infty }^{0}} \frac{K_{s}K_{d}}{(K_{s}+K_{d})}dt-\frac{1}{K_{m}}\left[ -\frac{K_{s}}{(K_{s}+K_{d})}+\frac{K_{s}}{(K_{s}+K_{d})}e^{-\left[ K_{m}(K_{s} +K_{d})\right] t}-K_{m}K_{s}\right] , \end{aligned}$$

or

$$\begin{aligned}&\left\{ w_{im}^{2}(0)+4Q_{B}G_{B}\right\} \lambda ^{2}-J_{B}^{2}=0.\\&\lambda =\frac{J_{B}}{\sqrt{w_{im}^{2}(0)+4Q_{B}G_{B}}}. \end{aligned}$$

$\lambda$ is a positive number because when $G_{B}$ increases, the minimum efficiency loss also increases. From Eq. (81):

$$\begin{aligned} B=-\frac{\lambda w_{im}(0)-J_{B}}{2\lambda Q_{B}}. \end{aligned}$$

(83)

By replacing $\lambda$ with its value in the above expression, we get:

$$\begin{aligned} B&=-\frac{\frac{w_{im}(0)J_{B}}{\sqrt{w_{im}^{2}(0)+4Q_{B}G_{B}}}-J_{B} }{\frac{2Q_{B}J_{B}}{\sqrt{w_{im}^{2}(0)+4Q_{B}G_{B}}}},\nonumber \\ B&=-\frac{w_{im}(0)-\sqrt{w_{im}^{2}(0)+4Q_{B}G_{B}}}{2Q_{B}}. \end{aligned}$$

(84)

The second order condition for minimization can be checked as follows:

$$\begin{aligned} {\mathcal {L}} =J_{B}B+\lambda \left[ G_{B}-B\left( w_{im}(0)+Q_{B}B\right) \right] . \end{aligned}$$

Now we write the Bordered Hessian matrix of the Lagrange function as:

$$\begin{aligned} BH=\left[ \begin{array}{cc} 0 &{} w_{im}(0)+2Q_{B}B\\ w_{im}(0)+2Q_{B}B &{} \frac{-2Q_{B}J_{B}}{\sqrt{w_{im}^{2}(0)+4Q_{B}G_{B}}} \end{array} \right] . \end{aligned}$$

The determinant of the above matrix is negative as $-\left( w_{im} (0)+2Q_{B}B\right) ^{2}<0,$ and hence the efficiency loss got minimized.

A Dynamic Optimal Crime Control Policy-Panel A

The social damage due to inadequate/excessive crime control units includes the damage in the initial equilibrium, i.e., before the adoption of a crime control policy, plus the damage during the adjustment process from initial equilibrium to the final. After government adopts a policy to enhance/reduce the number of public service units, it shifts either the supply or the demand curve, e.g., it shifts the demand curve upward by a magnitude depending upon the size of the policy, which is taken as A in the solution of the model with a crime control policy. The crime control rate then adjusts over time to bring the new equilibrium rate which is higher than the previous equilibrium crime control rate and lower than that which existed at the time the policy was implemented depending on the elasticity of supply and demand curves. An excessive number of public service units in society implies that the number is higher on the supply curve than that on the demand curve, and a shortage in their number implies the opposite. When the number on the supply and the demand curve becomes equal, the new equilibrium has arrived. When the number is different on supply and demand curve, that difference is the social damage at that point in time. Furthermore, the number of crime control units in society was lower (in this example) in the previous equilibrium, which is also social damage in equilibrium. If we sum up either the number of excessive units on the supply curve or their number on the demand curve short of supply curve, we get the total social damage in terms of number of units as follows:

$$\begin{aligned} SD=M_{A}(t)+ {\int \limits _{-\infty }^{0}} W_{pr}(\infty )dt. \end{aligned}$$

(85)

From Eq. (55), the change in number of crime control units due to change in crime control rate after adoption of crime control policy is as under:

$$\begin{aligned} W_{pu}(t)&=K_{pu}\left[ A-C(t)\right] ,\\ \text{or }w_{npu}(t)-w_{ipu}(0)&=K_{pu}\left[ A-C(t)\right] , \end{aligned}$$

where $w_{ipu}(0)$ is the initial number of crime control units and $w_{npu}(t)$ is the new number after the implementation of crime control policy as $W_{pu}(t)$ is a deviation variable, i.e., deviation from the initial equilibrium value. An increase in number of crime control units per unit time is as follows:

$$\begin{aligned} INC=A\left[ w_{ipu}(0)+K_{pu}\left\{ A-C(t)\right\} \right] . \end{aligned}$$

(86)

If we want to minimize the social damage subject to the constraint that an increase in number of crimes controlled per unit time is greater than or equal to $G_{A}\left( \text{change in number of crimes controlled per unit time}=\frac{dM_{B}}{dt}\right)$, our problem is as follows:

$$\begin{aligned} \min _{A}SD\text{ s.t. }INC\ge G_{A}\left( =\frac{dM_{B}}{dt}\right) . \end{aligned}$$

The choice variable is A, i.e., an initial upward jump in the crime control rate chosen by government to shift the demand curve, and the constraint is binding. Lagrangian for the above problem is given below:

$$\begin{aligned} {\mathcal {L}} =M_{A}(t)+ {\int \limits _{-\infty }^{0}} W_{pr}(\infty )dt+\lambda \left[ G_{A}-A\left[ w_{ipu}(0)+K_{pu}\left\{ A-C(t)\right\} \right] \right] . \end{aligned}$$

From Eq. (44a), we have:

$$\begin{aligned} C(t)=-K_{c}M_{A}+E_{A}. \end{aligned}$$

The value of $E_{A}$ can be found by imposing the initial conditions as follows:

$$\begin{aligned} C(0)&=-K_{c}M_{A}(0)+E_{A},\\ A&=-K_{c}K_{pr}C(0)+E_{A},\\ E_{A}&=A\left[ 1+K_{c}K_{pr}\right] . \end{aligned}$$

This implies that

$$\begin{aligned} M_{A}(t)=-\frac{1}{K_{c}}\left[ C(t)-A\left\{ 1+K_{c}K_{pr}\right\} \right] . \end{aligned}$$

Therefore, the Lagrangian can now be written as:

$$\begin{aligned} {\mathcal {L}} =&-\frac{1}{K_{c}}\left[ C(t)-A\left\{ 1+K_{c}K_{pr}\right\} \right] + {\int \limits _{-\infty }^{0}} W_{pr}(\infty )dt\\&+\lambda \left[ G_{A}-A\left[ w_{ipu}(0)+K_{pu}\left\{ A-C(t)\right\} \right] \right] \\ =&-\frac{1}{K_{c}}\left[ \left\{ \frac{K_{pu}A}{K_{pr}+K_{pu}} +\frac{K_{pr}A}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} -A\left\{ 1+K_{c}K_{pr}\right\} \right] \\&+ {\int \limits _{-\infty }^{0}} W_{pr}(\infty )dt+\lambda \left[ G_{A}-A\left[ w_{ipu}(0)+K_{pu}\left\{ A-\frac{K_{pu}A}{K_{pr}+K_{pu}}-\frac{K_{pr}A}{{K}_{pr} +\,K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} \right] \right] . \end{aligned}$$

The first order condition with respect to A is as follows:

$$\begin{aligned}&-\frac{1}{K_{c}}\left[ \left\{ \frac{K_{pu}}{K_{pr}+K_{pu}}+\frac{K_{pr} }{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} -\left\{ 1+K_{c}K_{pr}\right\} \right] \\&\quad -\lambda \left[ w_{ipu}(0)+K_{pu}\left\{ A-\frac{K_{pu}A}{K_{pr}+K_{pu} }-\frac{K_{pr}A}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} \right] \\&\quad -\lambda AK_{pu}\left\{ 1-\frac{K_{pu}}{K_{pr}+K_{pu}}-\frac{K_{pr} }{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} , \end{aligned}$$

which implies that

$$\begin{aligned}&-\frac{1}{K_{c}}\left[ \left\{ \frac{K_{pu}}{K_{pr}+K_{pu}}+\frac{K_{pr} }{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} -\left\{ 1+K_{c}K_{pr}\right\} \right] \\&\qquad -2\lambda AK_{pu}\left\{ 1-\frac{K_{pu}}{K_{pr}+K_{pu}}-\frac{K_{pr} }{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} \\&\quad =\lambda w_{ipu}(0). \end{aligned}$$

or

$$\begin{aligned} A=\frac{\lambda w_{ipu}(0)-\frac{1}{K_{c}}\left[ \left\{ \frac{-K_{pu} }{K_{pr}+K_{pu}}-\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr} +K_{pu})\right] t}\right\} +\left\{ 1+K_{c}K_{pr}\right\} \right] }{-2\lambda K_{pu}\left\{ 1-\frac{K_{pu}}{K_{pr}+K_{pu}}-\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} }. \end{aligned}$$

(87)

The first order condition of the Lagrangian with respect to $\lambda$ is as follows:

$$\begin{aligned} G_{A}-A\left[ w_{ipu}(0)+K_{pu}\left\{ A-\frac{K_{pu}A}{K_{pr}+K_{pu}} -\frac{K_{pr}A}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} \right] =0. \end{aligned}$$

(88)

After substituting the value of A from Eq. (87) into (88), the later becomes as follows:

$$\begin{aligned}&G_{A} =w_{ipu}(0).\frac{\lambda w_{ipu}(0)-\frac{1}{K_{c}}\left[ \left\{ \frac{-K_{pu}}{K_{pr}+K_{pu}}-\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} +\left\{ 1+K_{c}K_{pr}\right\} \right] }{-2\lambda K_{pu}\left\{ 1-\frac{K_{pu}}{K_{pr}+K_{pu}} -\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} }\\&\qquad +K_{pu}\left\{ 1-\frac{K_{pu}}{K_{pr}+K_{pu}}-\frac{K_{pr}}{K_{pr}+K_{pu} }e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} \\&\qquad *\left[ \frac{\lambda w_{ipu}(0)-\frac{1}{K_{c}}\left[ \left\{ \frac{-K_{pu}}{K_{pr}+K_{pu}}-\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} +\left\{ 1+K_{c}K_{pr}\right\} \right] }{-2\lambda K_{pu}\left\{ 1-\frac{K_{pu}}{K_{pr}+K_{pu}} -\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} }\right] ^{2}.\\&\qquad \text{or }4\lambda ^{2}Q_{A}G_{A} =2\lambda ^{2}w_{ipu}^{2}(0)-2\lambda w_{ipu}(0)J_{A}-\lambda ^{2}w_{ipu}^{2}(0)-J_{A}^{2}+2\lambda w_{ipu} (0)J_{A},\\&\qquad \text{where }Q_{A} =-K_{pu}\left\{ 1-\frac{K_{pu}}{K_{pr}+K_{pu}} -\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} ,\\&J_{A} =\frac{1}{K_{c}}\left[ \left\{ \frac{-K_{pu}}{K_{pr}+K_{pu}} -\frac{K_{pr}}{K_{pr}+K_{pu}}e^{-\left[ K_{c}(K_{pr}+K_{pu})\right] t}\right\} +\left\{ 1+K_{c}K_{pr}\right\} \right] . \end{aligned}$$

This implies that

$$\begin{aligned}&\left\{ w_{ipu}^{2}(0)-4Q_{A}G_{A}\right\} \lambda ^{2}-J_{A}^{2}=0,\\&\lambda =\frac{J_{A}}{\sqrt{w_{ipu}^{2}(0)-4Q_{A}G_{A}}}. \end{aligned}$$

$\lambda$ must be positive as the social damage increases with an increase in $G_{A}$.

Equation (87) can also be written as

$$\begin{aligned} A=\frac{\lambda w_{ipu}(0)-J_{A}}{2\lambda Q_{A}}. \end{aligned}$$

(89)

Plugging the value of $\lambda$ into Eq. (89) leads to:

$$\begin{aligned} A&=\frac{\frac{w_{ipu}(0)J_{A}}{\sqrt{w_{ipu}^{2}(0)-4Q_{A}G_{A}}}-J_{A} }{\frac{2Q_{A}J_{A}}{\sqrt{w_{ipu}^{2}(0)-4Q_{A}G_{A}}}},\nonumber \\ A&=\frac{w_{ipu}(0)-\sqrt{w_{ipu}^{2}(0)-4Q_{A}G_{A}}}{2Q_{A}}. \end{aligned}$$

(90)

The second order condition for minimization is checked as follows:

$$\begin{aligned} {\mathcal {L}} =J_{A}A+ {\int \limits _{-\infty }^{0}} W_{pr}(\infty )dt+\lambda \left[ G_{A}-A\left[ w_{ipu}(0)-Q_{A}A\right] \right] . \end{aligned}$$

The Bordered Hessian matrix of the Lagrange function is as follows:

$$\begin{aligned} BH=\left[ \begin{array}{cc} 0 &{} w_{ipu}(0)-2Q_{A}A\\ w_{ipu}(0)-2Q_{A}A &{} \frac{2Q_{A}J_{A}}{\sqrt{w_{ipu}^{2}(0)-4Q_{A}G_{A}}} \end{array} \right] , \end{aligned}$$

which has a negative determinant as $-\left( w_{ipu}(0)-2Q_{A}A\right) ^{2}<0,$ therefore the social damage is minimized.

General Solution of Model-Panel A

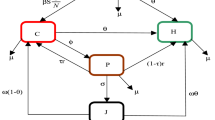
Figure 4 depicts a dynamic crime control model after joining together the blocks of inputs and outputs for various agents. Laplace transform is a convenient tool for solving differential equations. After Laplace transform, Fig. 4 gets transformed to Fig. 5. Let us first evaluate the transfer function relating C(s) to $W_{1}(s)$ in Fig. 5 (the part marked as A) as follows:

Fig. 4

A dynamic optimal crime control model for panel A

Fig. 5

A dynamic crime control model for panel A after Laplace transform

We have the following equations relating inputs to outputs for various blocks in A assuming that $\epsilon (s)=0$:

$$\begin{aligned} C(s)&=-\frac{K_{c}}{s}.W(s),\\ W_{pu}(s)&=-K_{pu}e^{-s\tau _{d2}}C(s),\\ W_{B}(s)&=W_{1}(s)-W_{pu}(s). \end{aligned}$$

We can solve the above equations simultaneously for C(s) in terms of $W_{1}(s)$ as follows:

$$\begin{aligned} C(s)&=-\frac{K_{c}}{s}\left[ W_{1}(s)-W_{pu}(s)\right] ,\\ C(s)&=-\frac{K_{c}}{s}\left[ W_{1}(s)+K_{pu}e^{-s\tau _{d2}}C(s)\right] ,\\ C(s)\left[ 1+\frac{K_{c}K_{pu}e^{-s\tau _{d2}}}{s}\right]&=-\frac{K_{c} }{s}W_{1}(s),\\ \frac{C(s)}{W_{1}(s)}&=\frac{-K_{c}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}}. \end{aligned}$$

Using the above expression to reduce part A in Fig. 5 to one block and shifting $W_{0}(s)$ in backward direction, results in Fig. 6, from which we can find the overall transfer function for D(s). We have the following equations:

$$\begin{aligned} C(s)&=\frac{-K_{c}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}}\left[ D(s)+W_{pr}(s)\right] ,\\ \text{where }D(s)&=W_{i}(s)-W_{0}(s),\\ W_{pr}(s)&=K_{pr}e^{-s\tau _{d1}}C(s). \end{aligned}$$

We can solve for C(s) in terms of D(s) as follows:

$$\begin{aligned} C(s)&=\frac{-K_{c}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}}\left[ D(s)+W_{pr}(s)\right] ,\nonumber \\ C(s)&=\frac{-K_{c}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}}\left[ D(s)+K_{pr} e^{-s\tau _{d1}}C(s)\right] ,\nonumber \\ C(s)\left[ 1+\frac{K_{c}K_{pr}e^{-s\tau _{d1}}}{s+K_{c}K_{pu}e^{-s\tau _{d2}} }\right]&=\frac{-K_{c}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}}D(s),\nonumber \\ \frac{C(s)}{D(s)}&=\frac{\frac{-K_{c}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}} }{1+\frac{K_{c}K_{pr}e^{-s\tau _{d1}}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}} },\nonumber \\ \frac{C(s)}{D(s)}&=\frac{-K_{c}}{s+K_{c}K_{pu}e^{-s\tau _{d2}}+K_{c} K_{pr}e^{-s\tau _{d1}}}. \end{aligned}$$

(91)

$K_{c},$ $K_{pu},$ $K_{pr},$ $\tau _{d1}$ and $\tau _{d2}$ are all positive numbers and the crime control rate depends on these five empirical parameters. Useful results and conclusions can be drawn by inversion and solution of Eq. (91). If inversion of Eq. (91) is to be done by partial fractions, then the following approximation has to be made:

$$\begin{aligned} e^{-\tau s}\approx 1-\tau s. \end{aligned}$$

(92)

Second better approximation is:

$$\begin{aligned} e^{-\tau s}\approx \frac{1-(\tau /2)s}{1+(\tau /2)s}. \end{aligned}$$

(93)

A third approximation (better than the above two) is as follows:

$$\begin{aligned} e^{-\tau s}\approx \frac{1-\tau s/2+\tau ^{2}s^{2}/12}{1+\tau s/2+\tau ^{2} s^{2}/12}. \end{aligned}$$

(94)

Equation (92) gives a crude approximation. One could possibly choose either Eq. (93) (which is simpler) or (94) (which is laborious but more accurate). If $D(t)=A$, a step input, i.e., an exogenous shift in either the number of public service units demanded, and/or a shift in supply, then after Laplace transform

$$\begin{aligned} D(s)=\frac{A}{s}. \end{aligned}$$

Using the final value theorem of Laplace transform we get:

$$\begin{aligned}&C(\infty )=\frac{-A}{K_{pu}+K_{pr}}, \nonumber \\&C(\infty )=C(t)\mid _{t=\infty }. \end{aligned}$$

(95)

Equation (93) can be rewritten as:

$$\begin{aligned} e^{-\tau s}\approx \frac{2-\tau s}{2+\tau s}. \end{aligned}$$

Using this approximation, Eq. (91) can be written as:

$$\begin{aligned}&\frac{C(s)}{D(s)}=\frac{-K_{c}}{s+K_{c}K_{pu}\left( \frac{2-s\tau _{d2} }{2+s\tau _{d2}}\right) +K_{c}K_{pr}\left( \frac{2-s\tau _{d1}}{2+s\tau _{d1} }\right) }, \\&\frac{C(s)}{D(s)}\\&\quad =\frac{-K_{c}\left( 2+s\tau _{d1}\right) \left( 2+s\tau _{d2}\right) }{s\left( 2+s\tau _{d1}\right) \left( 2+s\tau _{d2}\right) +K_{c}K_{pu}\left( 2+s\tau _{d1}\right) \left( 2-s\tau _{d2}\right) +K_{c}K_{pr}\left( 2-s\tau _{d1}\right) \left( 2+s\tau _{d2}\right) }, \\&\quad =\frac{-K_{c}\left\{ \tau _{d1}\tau _{d2}s^{2}+2\left( \tau _{d1}+\tau _{d2}\right) s+4\right\} }{\left[ \begin{array}{c} \tau _{d1}\tau _{d2}s^{3}+2\left( \tau _{d1}+\tau _{d2}\right) s^{2} +4s+K_{c}K_{pu}\left\{ -\tau _{d1}\tau _{d2}s^{2}+2\left( \tau _{d1}-\tau _{d2}\right) s+4\right\} \\ +K_{c}K_{pr}\left\{ -\tau _{d1}\tau _{d2}s^{2}+2\left( \tau _{d2}-\tau _{d1}\right) s+4\right\} \end{array} \right] },\\&\quad =\frac{-K_{c}\left\{ \tau _{d1}\tau _{d2}s^{2}+2\left( \tau _{d1}+\tau _{d2}\right) s+4\right\} }{\left[ \begin{array}{c} \tau _{d1}\tau _{d2}s^{3}+\left[ 2\left( \tau _{d1}+\tau _{d2}\right) -K_{c}K_{pu}\tau _{d1}\tau _{d2}-K_{c}K_{pr}\tau _{d1}\tau _{d2}\right] s^{2}+\\ \left[ 2K_{c}K_{pu}\left( \tau _{d1}-\tau _{d2}\right) +2K_{c}K_{pr}\left( \tau _{d2}-\tau _{d1}\right) +4\right] s+4K_{c}K_{pu}+4K_{c}K_{pr} \end{array} \right] }. \end{aligned}$$

The denominator of the above expression can be written as:

$$\begin{aligned} as^{3}+bs^{2}+cs+d, \end{aligned}$$

where

$$\begin{aligned} a&=\tau _{d1}\tau _{d2},\\ b&=2\left( \tau _{d1}+\tau _{d2}\right) -K_{c}\tau _{d1}\tau _{d2} (K_{pu}+K_{pr}),\\ c&=2\left[ K_{c}\left( \tau _{d1}-\tau _{d2}\right) (K_{pu} -K_{pr})+2\right] ,\\ d&=4K_{c}(K_{pu}+K_{pr}). \end{aligned}$$

This implies that

$$\begin{aligned} \frac{C(s)}{D(s)}=\frac{-K_{c}\left\{ as^{2}+2\left( \tau _{d1}+\tau _{d2}\right) s+4\right\} }{as^{3}+bs^{2}+cs+d}. \end{aligned}$$

(96)

The roots of the denominator of Eq. (96) depict the qualitative response of the crime control rate, therefore it will be convenient (for future reference) to write it as follows:

$$\begin{aligned} as^{3}+bs^{2}+cs+d=0. \end{aligned}$$

(97)

Now let us discuss the dimensions of the parameters involved. $\tau _{d1}$ and $\tau _{d2}$ and have the dimensions of time.

$$\begin{aligned} Dimensions\ of\ K_{c}&=(Dimensions\ of\ C)/(time\times Dimensions\ of\ W_{A})\\&=\frac{\textit{Number of new crimes controlled }}{time\ \times \ No.\ of \textit{ new } \textit{public service units}}\\ Dimensions\,of\,K_{pu}&=(Dimensions\,of\,W_{pu})/(Dimensions\,of\,C)\\&=\frac{No.\,of \textit{new } \textit{public service units } demanded}{\textit{Number} \,of\, \textit{new} \,crimes\, \textit{controlled}},\\ Dimensions\,of\,K_{pr}&=(Dimensions\,of\,W_{pr})/(Dimensions\,of\,C)\\&=\frac{No.\,of\,new \textit{ public service units supplied }}{\textit{Number} \,of\, \textit{new} \,crimes \,\textit{controlled}}. \end{aligned}$$

Therefore $K_{c}K_{pu}$ and $K_{c}K_{pr}$ have dimensions of 1/time. Using these facts, we can write: a has dimensions of $time^{2}$; b has dimensions of time; c is dimensionless and d has dimensions of 1/time. We can see that Eq. (97) is dimensionally consistent (as s has dimensions of 1/time).

Fig. 6

Crime control model in panel A after solution of block A in Fig. 5

Method to Solve Eq. (96):

Let a step input of magnitude A is given to D, then

$$\begin{aligned} D(s)=\frac{A}{s}. \end{aligned}$$

(98)

Putting this in Eq. (96), we get:

$$\begin{aligned} C(s)=\frac{-AK_{c}\left\{ as^{2}+2\left( \tau _{d1}+\tau _{d2}\right) s+4\right\} }{s(as^{3}+bs^{2}+cs+d)}. \end{aligned}$$

(99)

The parameters $K_{c},$ $K_{pr},$ $K_{pu},$ $\tau _{d1}$ and $\tau _{d2}$ are to be estimated empirically. This gives the values of a,  b,  c and d. Find roots of Eq. (97) and invert Eq. (99) to time function of C by using partial fractions and table of Laplace transform. Using the Final Value Theorem of Laplace transform on Eq. (99), we get:

$$\begin{aligned} C(\infty )=-AK_{c}\times \frac{4}{d}. \end{aligned}$$

(100)

Using the value of $d=4K_{c}(K_{pu}+K_{pr}),$ we get:

$$\begin{aligned} C(\infty )=\frac{-A}{K_{pu}+K_{pr}}. \end{aligned}$$

(101)

We get the same $C(\infty )$ from Eq. (99) as that from Eq. (91). Similarly using the Initial Value Theorem of Laplace transform on Eq. (99), we get:

$$\begin{aligned} C(0)=0. \end{aligned}$$

(102)

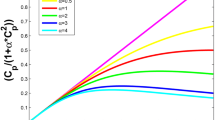
The qualitative nature of the solution C(t) is dependent on location of roots of the denominator of C(s) in the complex plane. Please look at Fig. 7 in which several roots are located. Table 1 gives the form of the terms in the expression for C(t) corresponding to these roots. $X1,X2,\ldots ,Y1,Y2,\ldots$ are all positive.

Table 1 Dynamic Response with respect to Location of Roots in Fig. 7

Fig. 7

Location of roots in a complex plane corresponding to Table 1

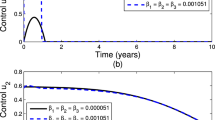
An optimal policy minimizing the social damage in terms of excessive/inadequate number of public service units in initial equilibrium, as well as the social loss in terms of excessive or inadequate number on dynamic adjustment path (when number of public service units demanded is not equal to supply) before arriving at final equilibrium, subject to a certain increase in number of crimes controlled per unit time can be derived on a case by case basis.

In equilibrium, the area under the demand curve is the social benefit in terms of number of crimes controlled per unit time. For estimating an optimal policy, the parameters $K_{c},$ $K_{pr},$ $K_{pu},$ $\tau _{d1}$ and $\tau _{d2}$ need to be estimated. The values of $K^{\prime }s$ can be estimated in the same manner as demand and supply elasticities. Time lags $\tau _{d1}$ and $\tau _{d2}$ can also be estimated through various techniques. As the optimal policy is a function of these parameters, Delta method can be used for confidence interval.