Practical workflow for assessment of seismic hazard in low enthalpy geothermal systems

Abstract

It is of vital importance to be able to determine the seismic hazard in advance of any geothermal operation in the subsurface, especially in a densely populated area such as The Netherlands. The author aims to arrive at a practical assessment of the seismic hazard in low-enthalpy geothermal doublet systems specifically designed for heat exchange in porous and permeable aquifers operated on a volume balance, at a depth range of 1800 to 3300 m having temperatures in the range of 60 °C to 100 °C. The article presents a practical workflow aiming to determine the probability distribution for mechanical re-activation along pre-existing weak faults. After presenting the tectonic structural setting the criticality criterion based on shear mobilisation is introduced. Existing stress models are reviewed and a practical manner to estimate and limit all geomechanical input parameters is presented, including fault mechanical properties. The workflow is demonstrated both for early period operation times and at final thermal breakthrough. The uncertainty is addressed through probabilistic logic tree analysis quantifying the variation of the four most uncertain input parameters: fault cohesion and friction coefficient, the thermal stress parameter and the initial minimum Earth stress. The probabilistic hazard assessment is characterised by four output parameters: the expected value, the probability that unity is exceeded and two more probabilities. In case unity is exceeded the range of fault dips prone to mechanical re-activation is shown. Exceedance of this first necessary condition requires the assessment of the other two necessary conditions: seismogeneity and moment magnitude.

Article highlights

• The article presents a practical workflow to assess the seismic hazard associated with geothermal operations.

• To be able to perform the necessary uncertainty analysis, four main input parameters are treated probabilistic.

• The first necessary condition for seismicity to occur is characterised by four probabilities: the expected probability, the probability that seismicity can occur and two higher probabilities.

1 Introduction

Climate-neutral heating and cooling is essential for the ambitious climate and energy targets for many European countries. Heating (and cooling) comprise about half the total end-use energy demand in Europe, of which about half is for industrial use and the other half for residential and commercial buildings. Geothermal energy has the potential to significantly contribute to the need of direct heat, globally and in The Netherlands (Limberger et al. 2018). The Netherlands has the ambition to accelerate the geothermal development and Van Wees et al. (2020) recognise several plays. Based on geothermal quality parameters such as temperature, porosity, permeability and thickness, attention is focussed on aquifers in the Lower Cretaceous, Upper Jurassic, Triassic and Permian, down to the Carboniferous (including the Dinantian fractured carbonates). Heijnen and Provoost (2021) emphasize the need for urgency to accelerate the Geothermal development in The Netherlands. In the public domain questions are raised about the risk of inducing earthquakes as a consequence of geothermal activities. Buijze et al. (2019) reviewed the induced seismicity in geothermal systems worldwide, clearly indicating the need for a new workflow to be able to build a practical, quantitative tool to quickly assess the induced seismicity potential in volume-balanced geothermal systems.

We focus on geothermal targets within a depth range of 1800 m to 3300 m, mainly aquifers of Cretaceous/Jurassic or Triassic age in the West Netherlands basin and Permian (Rotliegend) age aquifers in the Central Netherland basin and North-East Netherlands. Van Balen et al. (2005) and de Jager (2007) review the tectonics and basin evolution of The Netherlands. Kooi et al. (1989) have performed stratigraphic modelling based on the regional stress field to quantitatively understand the tectonic subsidence history of the southern North Sea Basin and Kooi et al. (1991) analysed the consequences of the changes in the intra-plate stresses during the Pliocene–Quaternary. Klein and Barr (1986) have analysed the maximum horizontal stress direction trends in Western Europe based on wellbore breakout analysis and suggested these are dominated by tectonic plate boundary forces. Houtgast and Van Balen (2000) demonstrate that at present the main tectonic structure in The Netherlands is the Lower Rhine Graben rift system, extending from Germany to the South-East Netherlands and Michon et al. (2003) show how Cenozoic evolution and stress field of the Roer Valley Rift System are linked to the Alpine chain. Prinz et al. (2017) show that the main tectonic active blocks are the Roer valley Graben, the Peel block and the Venlo block in The Netherlands and the Rur block, Erft block and Koln blocks in Germany. Olaiz et al. (2009) have produced a continuous tectonic strain–stress map for the western part of the Eurasian plate (Europe) based on the inversion of earthquake focal mechanisms. They have concluded that inside the European plate the dominant strain regime is extensional, close to strike-slip. The strain map shows in The Netherlands a clear NW–SE trend, consistent with the interpretation of the regional maximum horizontal stress patterns in the World Stress Map (Zoback 1992; Müller et al. 1992). The occurrence of natural seismicity can also be used to estimate the stresses. Natural seismicity is confined to the Roer Valley Rift System in the South-East of the Netherlands (de Crook 1996), mainly by normal faulting slip with a small strike-slip component (Dost and Haak 2007). Also, the 1992 Roermond earthquake near the Peel boundary fault with $M_{L} = 5.4$ was a natural normal dip-slip earthquake at a depth of 17 km. (Camelbeeck et al. 1994). All natural earthquakes registered from the year 1900 onwards with $M_{L} \ge 4$ had their origin assigned to depths ranging from 10 to 15 kms, while deep earthquakes south of the Feldbiss Fault (South Limburg) have attributed depths ranging from 20 to 23 kms. This is confirmed by Buijze et al. (2019), showing both the natural and induced earthquakes in The Netherlands. Excluding this south-east area of The Netherlands and considering only reservoirs/aquifers tens of kilometres away from large faults and diapirs, there are no indications of any other than the normal faulting stress regime at depths less than 3300 m. Here the normal-faulting stress regime is assumed to be present and we take $\sigma_{v} > \sigma_{H} > \sigma_{h} > p$. Verweij et al. (2012) reported large amount of pressure measurements and minimum stress indicators from leak-off tests for the Dutch subsurface. In the North-East Netherlands, based on analyses of sonic scanner and bore-hole breakout inversion data, a very low ambient stress ratio in the range of $\sigma_{H} /\sigma_{h} = 1 - 1.2$ has been reported by Van Eijs (2015). Also, in the West-Netherlands basin there are no indications of a strong tectonic stress component, neither from drilling experience nor from breakout analysis (Mechelse 2017) nor from observed seismicity. As pointed out by de Pater et al. (2020), induced seismicity was observed in the North-West Netherlands (e.g. Bergermeer area) and the area surrounding the Groningen reservoir in the North-East Netherlands, while the West-Netherlands Basin, the Central Netherlands Basin and the Friesland Platform have been seismically quiet. This indicates that outside the tectonic active South-East Netherlands (and possibly the Bergermeer area if those events also have a tectonic component), the dominant stress regime for large areas in the Netherlands down to depths of at least 3300 m is the normal faulting one, which is confirmed by drilling and production experience. It also seems that for the seismically very quiet West-Netherlands Basin and Central-Netherlands Basin the tectonic relaxed basin assumption applies, in which cases the expected horizontal stress anisotropy is low, $\sigma_{h} \cong \sigma_{H}$.

The aim of the article is to suggest a practical workflow and to show which data acquisition and what assumptions have to be made to arrive at a proper seismicity hazard prognosis. Note that the term “hazard” is used in the more strict sense in that it defines the chance of occurrence of a certain moment magnitude, without incorporating the GMPE (ground-motion prediction equation) necessary to determine the PGV (peak-ground velocity) or PGA (peak-ground acceleration) at the surface, as Bommer et al. (2017) developed for the Groningen area.

It also demonstrates how in a data-limited environment the uncertainty range of input parameters and sometimes the application of empirical correlations contribute to the uncertainty in the final prognosis. This also puts the value of early data collection in perspective. In anticipation of the new protocol to be initiated on a national level by the Dutch ministry of economic affairs and climate, this article aims to contribute in a constructive and scientific manner. To keep this workflow general and suitable for safety purposes, the results are presented in a scientific and open manner, clearly demonstrating the assumptions and choices made such that results can be presented including the uncertainties, allowing others to make final decisions based on metrics in line with regulations and public acceptance. Disclaimer: Although based on state-of-the art scientific knowledge, no legal claims whatsoever can be made based on any results derived using this workflow.

2 Materials and methods of the workflow

The aim of the workflow is to have a clear, standardised methodology that produces reproducible results independent of the operator. The presented workflow has been optimised through the application to several field cases of (planned) geothermal doublets in The Netherlands, using mainly input based on publicly available data. The workflow focusses on mechanical fault re-activation, the first necessary condition for seismicity to occur. The basis is the shear mobilisation criterion MR introduced in the next section. This parameter allows quantification of the criticality of the shear stress on any fault plane in the aquifer and the determination of exceedance. The criterion is written in terms of the Earth’s initial and changing stresses, the fault dip and its mechanical friction and cohesion parameters. In the presence of faults with a throw, (partially) sealing faults or boundary faults, differential compaction leads to an additional shear stress, resulting in an increase in the Mohr circle radius and a rotation of the principal stresses. The workflow is introduced stepwise:

• The first step is collect general input data, such as porosity, permeability, aquifer thickness, depth, pressure and temperature as well as the planned operational parameters, such as rate, injection temperature and inter-well distance.

• The second step is to select a key well, preferably located central in the structure, to build a one-dimensional geomechanics model to a) investigate the initial stress profile including practical applications of well-logs methods (see section “Stress models and initial stress state”) and b) develop a one-dimensional mechanical property model (see section “Approximation of the mechanical properties profile”). In case the model cannot be calibrated by local field stress measurements it is demonstrated how the model can be applied using calibrations from stress measurements of other nearby reservoirs/aquifers. The section also demonstrates the consequence of adding a tectonic plate strain to the (deep) stresses. The estimated mechanical properties profile is based on well log measurements preferably calibrated with core measurements. The influence of drainage on elastic properties is discussed and a criterion is derived to determine when this profile may be applied. In addition the application of certain empirical static-to-dynamic conversions of mechanical properties are suggested. This model serves not only as a basis for this workflow but can also be applied to safe drilling and completion operations.

• The next step is to determine the injection/production profile and the productivity index (see Appendix A) and the flooding and cooling extension for the early period, applying a mass balance and the first law of thermo-dynamics (see section “Extension of the flooding and cooling around the injector”). This allows determination of the injection-induced stress changes around the injector and producer, using the injection rate and the cumulative injected volume as independent variables, as shown in the section “Injection-induced stress changes”.

• The probabilities for fault re-activation for the “early period” of injection are assessed in the section “Assessment of probabilities for early period”, where the shear stress criticality is quantified through the shear mobilisation ratio MR. The uncertainty of the result is addressed through logic tree analysis quantifying the variation of four most uncertain input parameters including their probabilities. This is especially important for the ill-constrained fault parameters such as cohesion and friction coefficient, but also the thermal stress parameter and the initial Earth horizontal stresses. The section “Estimation and limitation of the fault mechanical parameters” gives practical methods to estimate and limit the very uncertain fault-mechanical parameters using tri-axial laboratory data, an empirical models and the initial stable Earth assumption. It is important to also report the probability tree of the input parameters, such that the final results can be evaluated by others in light of the chosen uncertainties. The probabilistic hazard assessment is presented as the cumulative probability distribution plot, which is characterised by four parameters: The expected value, the probability that unity is exceeded, P_95% and P_99%. In case $MR>1$ the range of fault dips prone to mechanical re-activation is presented. Finally, these probabilities together with the occurrence of faults with unfavourable dips and azimuths within the stress-changed zone form the basis for the assessment of the first necessary condition for seismicity to occur.

• For the assessment of the probabilities at thermal breakthrough first the cooled volume and time at thermal breakthrough are determined. As a consequence of the elliptical extension, the interior average thermo-elastic stress changes become dependent on the injector-producer direction. The results of the analysis are presented similar to the early-times assessment, but now for applying both for the direction of the well alignment as well as the direction perpendicular to that. As for the early-times assessment, these probabilities together with the occurrence of faults with unfavourable dips and azimuths within the stress-changed zone forms the basis for the assessment of the first necessary condition for seismicity to occur.

• If the first necessary but not sufficient condition for seismicity is satisfied, the other two necessary conditions for seismicity need to be investigated. The section “Seismogeneity and the maximum moment magnitude” shows that seismogeneity can be investigated by characterising the non-elastic deformation behaviour of the rock material, such as creep and ductility or by applying the dynamic friction model parameter $\left(a-b\right)$. Also, analogue field experience can be used, but the absence of seismicity can only be interpreted as proof for low seismogeneity if at the same time the other two necessary conditions are fulfilled. The section also presents three methods to determine the maximum seismic moment, expressed in terms of the stress drop and the active slip area of the fault plane.

2.1 The shear mobilisation ratio criterion

In this section a criterion is developed to quantify the criticality of the fault shear stress in relation to the Earth stresses modified by geothermal injection and production. The two-dimensional criterion applies to the initiation of re-activation along pre-existing fault planes of weakness. The Mohr–Coulomb criterion for shear failure initialisation and sliding along a plane of weakness reads (Jaeger et al. 2007, §3.5 & §4.7):

$$\left| {\tau_{f} } \right| = \mu \left( {\sigma_{n} - p} \right) + S_{0}$$

(1)

Here $\tau_{f}$ [MPa] is the shear stress acting on the fault plane, $\mu = \tan \phi$ [−] is the friction coefficient with $\phi$ [rad] being the friction angle of the fault plane, $S_{0}$ [MPa] is the cohesion (the intrinsic shear strength), $\sigma_{n}$ [MPa] is the normal stress acting on the fault plane and p [MPa] is the pore pressure inside the fully interconnected fault plane. Note that also here Terzaghi’s effective stress definition is used just as for rock yield failure (see also Zoback 2010, Ch. 4).

In a three-dimensional Mohr plot the three Mohr circles represent plane stresses in specific principal normal stress directions of ${\sigma }_{1}$ [MPa], ${\sigma }_{2}$ [MPa] and ${\sigma }_{3}$ [MPa] all perpendicular to one another. Jaeger et al. (2007, Ch. 2) have developed general fault plane solutions in terms of direction cosines while Zoback (2010, Ch. 5) shows the general matrix transformations in terms of fault dip, strike azimuth and rake. The solutions are simpler in case of a normal-faulting stress regime and if the vertical stress is the major principal stress ${\sigma }_{1}$ [MPa]. Figure 1 shows three-dimensional Mohr circles where the stress states are only possible inside the major Mohr circle (built-up by $\sigma_{1}$ and $\sigma_{3}$) and outside the minor Mohr circles (built-up by $\sigma_{1}$ and $\sigma_{2}$ and by $\sigma_{2}$ and $\sigma_{3}$, respectively). The next section shows the initial stress state in The Netherlands and the following two-dimensional analysis applies to the major Mohr circle, but for tectonic relaxed basins with a small contrast between the maximum horizontal stress $\sigma_{H}$ [MPa] and minimum horizontal stress $\sigma_{h}$ [MPa], the analysis applies to all fault azimuths. Hettema (2020) derives the relationships with respect to the Earth’s stresses which here will first be converted to principal stresses. The shear stress and the total normal stress acting on the fault plane whose normal is inclined by an angle $\theta$ [rad] to the $\sigma_{1}$ direction is given by (Fjear et al. 2008, §1.1.3):

$$\left| {\tau_{f} } \right| = \pm \left[ { - \frac{{\sigma_{v} - \sigma_{h} }}{2}\sin 2\theta + \tau_{vh} \cos 2\theta } \right]$$

(2)

$$\sigma_{n} = \frac{{\sigma_{v} + \sigma_{h} }}{2} + \frac{{\sigma_{v} - \sigma_{h} }}{2}\cos 2\theta + \tau_{vh} \sin 2\theta$$

(3)

Fig. 1

Three-dimensional Mohr’s representation including a fault-plane of weakness line, showing stress states prone to re-activation and those not prone to re-activation

The + sign applies to most normal dipping faults with $0 < \theta \le \pi /2$ while the – sign applies to most reverse dipping faults with $\pi /2 < \theta \le \pi$. Here $\tau_{vh}$ [MPa] is the induced shear stress, which will be explained in detail later. Application to criterion (1) allows it to be rewritten in terms of stresses as a slip criterion along any fault plane of weakness (see also Jaeger et al. 2007, §3.5):

$$\tau_{m} \sin \left( {2\theta - \phi } \right) = \left[ {\sigma_{m} - p + \frac{{S_{0} }}{\mu }} \right]\sin \phi$$

(4)

The maximum shear stress $\tau_{m}$ (or the Mohr circle radius) is defined in terms of principal stresses, which can also be related to the Earth’s stresses and the induced shear stress $\tau_{vh}$ by (Timoshenko and Goodier 1970, §10):

$$\tau_{m} \equiv \frac{{\sigma_{1} - \sigma_{3} }}{2} = \sqrt {\left( {\frac{{\sigma_{v} - \sigma_{h} }}{2}} \right)^{2} + \tau_{vh}^{2} }$$

(5)

Hettema (2020) has demonstrated that in depleting reservoirs the induced shear stress is the result of the presence of differential compaction, only occurring for three fault types: Intra-reservoir open faults with offset, (partially) sealing faults and boundary faults. The way pressure and temperature changes influence the induced shear stress will be demonstrated in the section “The injection-induced stress changes”. If the induced shear stress is present, $\tau_{m}$ becomes fault-specific and the principal stresses will rotate the Earth’s stresses near the fault plane (Timoshenko and Goodier 1970, §10), such that the angle θ is related to the fault dip $\delta$ [rad] by:

$$\theta = \delta - \frac{1}{2}\tan^{ - 1} \left( {\frac{{2\tau_{vh} }}{{\sigma_{v} - \sigma_{h} }}} \right)$$

(6)

The mean normal stress is invariant to stress rotation:

$$\sigma_{m} \equiv \frac{{\sigma_{1} + \sigma_{3} }}{2} = \frac{{\sigma_{v} + \sigma_{h} }}{2}$$

(7)

If none of the three previously mentioned fault types are present, differential compaction and thus the induced shear stress is absent $\tau_{vh} = 0$ and the near-fault stresses are not rotated, such that $\theta = \delta$. If differential compaction is present this has two consequences in the Mohr–Coulomb diagram: I) the Mohr-circle grows according to Eq. (5) and II) the angle θ is no longer equal to the fault dip $\delta$ according to Eq. (6). This is demonstrated in Fig. 2.

Fig. 2

Two-dimensional Mohr diagram, showing the initial stress state and the stress state after cold water injection in the absence of differential compaction and in the presence of differential compaction

The critical fault failure/slip angle $\theta_{c}$ [rad] is given by (Zoback 2010):

$$\theta_{c} = \frac{\pi }{4} + \frac{\phi }{2} = \tan^{ - 1} \left( {\mu + \sqrt {\mu^{2} + 1} } \right)$$

(8)

Note that $\sin \left( {2\theta_{c} - \phi } \right) = 1$. Applying this critical angle to criterion (4) gives the following criterion for fault shear failure, slip and/or re-activation in terms of the mean effective stress, the cohesion and the friction angle/coefficient:

$$\tau_{mf} \left( {\theta_{c} } \right) = \left( {\sigma_{m} - p + \frac{{S_{0} }}{\mu }} \right)\sin \phi$$

(9)

To quantify the hazard for shear re-activation, a shear mobilization angle $\phi_{mob}$[rad] is defined based on the common zero point $\sigma_{m} - p = - {{S_{0} } \mathord{\left/ {\vphantom {{S_{0} } \mu }} \right. \kern-\nulldelimiterspace} \mu }$ and the stress state under consideration. The fault re-activation hazard can be quantified in terms of the shear mobilization ratio MR defined as:

$$MR \equiv \frac{{\sin \phi_{mob} }}{\sin \phi } = \frac{{\tau_{m} }}{{\tau_{mf} }} = \frac{{\tau_{m} }}{{\left( {\sigma_{m} - p + \frac{{S_{0} }}{\mu }} \right)\sin \phi }}$$

(10)

If $MR < 1$ there is no hazard for fault re-activation for any fault dip. If $MR = 1$ only the critical oriented faults are prone to re-activation having a critical angle $\theta_{c}$ given by Eq. (8), which could be rotated according to Eq. (6). Figure 3 shows that for $MR > 1$, faults having a range of angles around the critical one prone to re-activation:

$$\theta_{re} = \theta_{c} \pm \Delta \theta_{re}$$

(11)

The range of fault dip-angles prone to re-activation as shown in Fig. 3 can be written as:

$$\begin{aligned} \Delta \theta _{{re}} & \cong \frac{1}{2}\cos ^{{ - 1}} \left( {\frac{{\tau _{{mf}} }}{{\tau _{m} }}} \right) = \frac{1}{2}\cos ^{{ - 1}} \left( {\frac{{\sin \phi }}{{\sin \phi _{{mob}} }}} \right) \\ & = \frac{1}{2}\cos ^{{ - 1}} \left( {\frac{1}{{MR}}} \right) \\ \end{aligned}$$

(12)

Fig. 3

Mohr diagram, showing the initial stress state and the stress state after cold water injection resulting in MR > 1 for a range of fault dips prone to re-activation

The parameter MR can be used to quantify the criticality for any stress state. In case $MR < 1$ there is no risk for fault rupture/slip and the seismic hazard is low. If $MR = 1$, only critical oriented fault planes having a dip given by Eq. (8) have slip potential. In case $MR > 1$ the slip hazard is limited to the range of angles given by Eq. (11) and Eq. (12), which are related to the (rotated) fault dips by Eq. (6). Figure 1 demonstrates that by first analysing the major Mohr circle $\left( {\sigma_{1} ;\sigma_{3} } \right)$ makes the results conservative. The injection-induced stress changes are discussed in the following section.

2.2 The injection-induced stress changes

We consider the thermo-poro-elastic Earth stress changes caused by the injection of cold water into a homogeneous, horizontally layered porous and permeable aquifer of constant thickness at some distance away from the wellbore. In order to be able to determine the mobility ratio from Eq. (10) it is necessary to quantify the effect of the injection-induced temperature and pressure changes resulting from cold water injection through the maximum shear stress from Eq. (5) and the mean normal stress from Eq. (7). Perkins and Gonzalez (1984; 1985) have developed theory to determine the total horizontal Earth stresses modified by the injection-induced thermal and pressure changes for cylindrical or elliptical disk-shaped regions:

$$\sigma_{h} \left( {\Delta T,\overline{\Delta p} ,W_{i} ,t_{D} } \right) - \sigma_{h,0} = \gamma_{u} G_{p} \left( {r_{eq} } \right)\overline{\Delta p} \left( {q_{i} } \right) + A_{T} G_{T} \left( {W_{i} ,t_{D} } \right)\Delta T$$

(13)

The running variables are the cumulative water volume injected $W_{i} = \int {q_{i} dt = \overline{{q_{i} }} t}$ [m³] and the dimensionless time defined in Eq. (26), both time-dependent. The independent variables are the average pressure change $\overline{\Delta p} \left( {q_{i} } \right)$ [MPa] (where $q_{i}$ [m³/s] is the injected flow rate) and the injection-induced change in water temperature $\Delta T = T_{i} - T_{0}$ [^oC], negative for cooling. Appendix A shows that for a doublet with an inter-well distance of D [m] the energy-based volume-averaged pressure change around the injector and producer equals half the drawdown. The extension of the pressure change is limited around the injector and producer by $r_{eq}$, as derived in Eq. (A8). Appendix B shows that $G_{p}$ and $G_{T}$ are the pressure- and temperature-controlled dimensionless geometrical functions, respectively. For constant injection rate $G_{p} \left( {r_{eq} } \right)$ is shown to be constant after a short transient time and while $G_{T} \left( {W_{i} ,t_{D} } \right)$ is shown to evolve with the running variables, all time-dependent.

The theory can also be used to determine the modified vertical stress:

$$\sigma_{v} \left( {\Delta T,\overline{\Delta p} ,W_{i} ,t_{D} } \right) - \sigma_{v,0} = \gamma_{u} G_{pv} \left( {r_{eq} } \right)\overline{\Delta p} \left( {q_{i} } \right) + A_{T} G_{Tv} \left( {W_{i} ,t_{D} } \right)\Delta T$$

(14)

Appendix B also shows how the vertical $G_{Tv}$ and $G_{pv}$ can be determined from their horizontal counterparts $G_{T}$ and $G_{p}$. Under isothermal conditions, the ratio of change of the horizontal stress to the pore pressure (the stress path) is given by:

$$\gamma_{h} \equiv \frac{{\Delta \sigma_{h} }}{\Delta p} = \gamma_{u} G_{p}$$

(15)

Here $\gamma_{u}$ [-] is the horizontal stress path under uniaxial strain conditions, defined by (Hettema et al. 2000):

$$\gamma_{u} \equiv \left[ {\frac{{\Delta \sigma_{h} }}{\Delta p}} \right]_{ust} = \alpha \left( {\frac{1 - 2\nu }{{1 - \nu }}} \right) = \left( {1 - \frac{{K_{b} }}{{K_{s} }}} \right)\left( {1 - K_{0} } \right)$$

(16)

The (isobaric) thermo-elastic parameter $A_{T}$ [MPa/ °C] is also defined under uniaxial strain conditions:

$$A_{T} \equiv \left[ {\frac{{\Delta \sigma_{h} }}{\Delta T}} \right]_{ust} = 3K_{b} \frac{1 - 2\nu }{{1 - \nu }}\beta = 2G\frac{1 + \nu }{{1 - \nu }}\beta = \frac{E}{1 - \nu }\beta$$

(17)

Here β [1/^oC] is the linear thermal expansion coefficient. Up-to this point only the changes in intra-reservoir Earth stresses are taken into account. However, Hettema (2020) has shown that an induced shear stress develops on a plane of weakness in case differential compaction occurs, resulting in $\tau_{vh} \ne 0$. This can be the case for three fault types, 1) Intra-reservoir faults with a throw, 2) (partly) sealing intra-reservoir faults and 3) boundary faults. For open intra-reservoir faults with a throw the controlling parameter is the throw $th < h$ [m] normalised by the aquifer thickness h, leading to an induced shear stress that can be approximated by:

$$\tau_{vh,th} \left( {\overline{\Delta p} ,\Delta T} \right) = \left[ {\gamma_{u} \overline{\Delta p} \left( {q_{i} } \right) + A_{T} \Delta T} \right]\left( \frac{th}{h} \right)f_{3} \left( {\frac{{r_{c} }}{h}} \right)$$

(18)

Applying the definition of the “driving stress” (Hettema 2020) to the injection-induced stress changes of Eq. (13) results in the term [between brackets] in Eq. (18), now depending on both pressure and temperature changes. The non-dimensional geometrical function $0 < f_{3} \left( {r_{c} /h} \right) < 1$ depend on the ratio of the extension radius of the cooled/depleted zone $r_{c}$[m] to the thickness of the aquifer h, see Hettema (2020, App. A). For boundary faults the maximum induced shear stress occurs at the top and amounts:

$$\tau_{vh,top} \left( {\overline{\Delta p} ,\Delta T} \right) = \left[ {\gamma_{u} \overline{\Delta p} \left( {q_{i} } \right) + A_{T} \Delta T\left( t \right)} \right]\left( {rc\left( {\frac{{r_{c} \left( t \right)}}{{D_{c} }}} \right) + \frac{{\overline{{f_{3} }} }}{2}} \right)$$

(19)

The non-dimensional geometrical function $0 < rc\left( {r_{c} \left( t \right)/D_{c} } \right) < 1$ depends on the ratio of the extension radius of the cooled/depleted zone, given by Eq. (31)/(72) respectively, to the central depth of the aquifer D_c[m] (see Hettema 2020; App. A). Note that for the (partially) sealing and boundary faults contrary to the pressure effect, the thermal factor $A_{T} \Delta T\left( t \right)$ becomes time-dependent as the temperature gradient over the fault plane will reduce over time due to heat conduction. Also, the cooling of the aquifer side of the fault plane by advection takes time, such that the entire fault plane will not be thermally loaded at once, which may cause partial slip release as the cooling front proceeds. Note that Hettema (2020) has shown that the induced shear stress profile has a sharp maximum at the top (and base) of the aquifer. Therefore, applying Eq. (19) and Eq. (20) to fault slip initiation and simply using the static $A_{T} \Delta T\left( t \right) = A_{T} \Delta T$ could seriously overestimate the seismicity hazard. The case of (partial) sealing intra-reservoir faults has also been solved, requiring depletion pressures and temperatures and geometrical functions for both sides of the fault plane, giving for the maximum induced shear stress at the top:

$$\tau_{vh,top} = \tau_{vh,top} \left( {\overline{\Delta p} ,\Delta T} \right)_{I} - \tau_{vh,top} \left( {\overline{\Delta p} ,\Delta T} \right)_{II}$$

(20)

Quantification requires an estimation of these geometric functions as suggested by Hettema (2020, App. A). However, as $r_{c} \left( t \right)$ increases, $f_{3} \to 1$, while for our target aquifers deeper than 1800 m, $rc\left( {{{r_{c} \left( t \right)} \mathord{\left/ {\vphantom {{r_{c} \left( t \right)} {D_{c} }}} \right. \kern-\nulldelimiterspace} {D_{c} }}} \right) \ll 1$. Applying these limits to solutions (18), (19) and (20) allows a more simplified estimation of the maximum effect of differential compaction for the initiation stress to slip. However, as will be shown in the section “Seismogeneity and maximum seismic moment”, care should be taken to apply these relationships to determine the maximum moment magnitude.

In relationships (13) and (14) the contributions from the thermo elastic and poro-elastic stresses are added independently, which is only allowed if there is no coupling between the two. Hettema et al. (1998) showed that this is the case if the following condition is satisfied: $C_{D} > \kappa$, where $C_{D}$[m²/s] is the consolidation coefficient and $\kappa$[m²/s] is the thermal diffusivity. Hettema et al. (2002) have determined the consolidation coefficient for several reservoirs worldwide using:

$$C_{D} = \frac{k}{{\eta \varphi \left( {c_{pf} + c_{pp} } \right)}}$$

(21)

Here k [m² ≈ 9.87*10^–16 mDarcy] is the permeability, η [Pa·s] is the viscosity, φ [−] is the porosity, $c_{pf}$ [1/Pa] is the pore-fill compressibility and $c_{pp}$ [1/Pa] is the pore volume compressibility with respect to pore pressure change (see Hettema et al. 2012). Applying the condition gives the following de-coupling permeability requirement: $k > \kappa \;\eta \;\varphi \left( {c_{pf} + c_{pp} } \right)$. The thermal diffusivity $\kappa = \lambda /\rho C_{p}$ [m²/s] (Carslaw and Jaeger 1959), where λ [W/mK] is the thermal conductivity, ρ [kg/m³] is the density and $C_{p}$ [J/kgK] is the specific heat capacity under constant pressure. Note that for many rock materials of interest $\kappa \le 10^{ - 6}$ [m²/s]. Hettema (2002) has analysed a wide range of oil and gas reservoirs worldwide which all comply with the decoupling condition, even the Venezuelan heavy oil reservoirs. When applying to a deep geothermal aquifer at 3300 m depth having a low porosity of 10% and a temperature of 100 °C and assuming a stiffness of 15 GPa, the requirement gives a minimum permeability of 1 microDarcy. It is concluded that unless the investigated aquifers have very low permeabilities (such as clay-rich sandstone, well-cemented siltstone or tight, non-fractured carbonates), the presented method can be applied with confidence. To apply this model, the initial stress state and the extension of the cooling front needs to be quantified.

2.3 Extension of the flooding and cooling around the injector

In this section the extension of the flooding and cooling fronts are determined in relation to the injected volume. Matrix injection will persist as long as the injection pressure satisfies none of conditions in Eq. (50), (51), (52) and (53), as shown in the Sect. “Assessment of probabilities for early period”. For matrix injection we consider piston-type displacement of water into a homogeneous, horizontal layered porous and permeable aquifer with constant bulk thickness h [m] from the base to the seal. In the absence of flow barriers between the injector-producer pair, for early period injection times there will be a cylindrical flooding front and eventually an elliptical flooding front will arise, following the flowlines of the doublet as long as matrix injection persists. Perkins and Gonzalez (1985) fully solved the thermally-fractured injection problem, showing that also in case of thermal fracturing elliptical flooding and cooling fronts will arise generated by thermal fracture growth, which in case of a normal-faulting stress regime will be in the maximum horizontal stress direction. Injection of a water volume ${W}_{i}$ [m³] can result in an elliptical water flooding front (from a mass balance becoming a volume balance when neglecting volume changes due to pressure changes of low-compressible water):

$$\overline{{r_{fl} }} = \sqrt {a_{fl} b_{fl} } = \sqrt {\frac{{W_{i} }}{{\pi h\varphi_{e} }}}$$

(22)

Here $\overline{{r_{fl} }}$ [m] is the volume-averaged flooding radius, $a_{fl}$ [m] is the major flooding axis, in the direction of the doublet wells in case of matrix injection and in the direction of the maximum horizontal stress in case of thermal fracturing. $b_{fl}$[m] is the minor flooding axis (perpendicular to the major axis) and the bulk effective porosity is defined as $\varphi_{e} \equiv \overline{\varphi }\cdot N/G$, where $\overline{\varphi }$ is the thickness-averaged net reservoir porosity and N/G is the net-over-gross volume ratio. The problem of thermal heat recovery was solved by Marx and Langenheim (1959) and Prats (1969), see also the monograph of Prats (1986) for an overview. The first law of thermodynamics can be written as (Wylen and Sonntag 1978):

$$\delta Q = dU + pdV = dH - Vdp$$

(23)

Here Q [J] is the heat, U [J] is the internal energy, thereby neglecting eventual contributions from potential and/or kinetic energy, which could be important in case of tilted reservoirs and/or high injection rates. This relationship is applied to semi-steady state injection in porous and permeable horizontal reservoirs with constant thickness. For heat transfer analysis in solids and fluids it is useful to analyse the enthalpy defined by $H\left( {T,p} \right) \equiv U + pV$ [J], which entered in the first law gives:

$$\delta Q = \left( {\frac{\partial H}{{\partial T}}} \right)_{p} dT + \left( {\frac{\partial H}{{\partial p}}} \right)_{T} dp - Vdp = \rho V\left[ {C_{p} dT + \left( {\frac{1}{m}\left( {\frac{\partial H}{{\partial p}}} \right)_{T} - \frac{1}{\rho }} \right)dp} \right]$$

(24)

Here $C_{p} = \frac{1}{m}\left( {\frac{\partial H}{{\partial T}}} \right)_{p}$ [J/kgK] is the specific heat capacity under constant pressure. From the steam tables (Wylen and Sonntag 1978) $C_{p} > 4$ [kJ/kgK], the pressure dependency of the specific enthalpy $\frac{1}{m}\left( {\frac{\partial H}{{\partial p}}} \right)_{T} < 0.9$ [kJ/kgMPa] and the density term (in the same units) is: ${1 \mathord{\left/ {\vphantom {1 \rho }} \right. \kern-\nulldelimiterspace} \rho } \approx 1$ [m³/Mg]. For our applications a typical geothermal doublet has temperature changes of a few tens of ^oC while the pressure changes are limited to a few MPa, such that the pressure terms in Eq. (24) may be neglected. By applying the first law as a rate equation, the downhole heat injection rate $\dot{Q}_{i}$ [J/s] becomes (see also Marx and Langenheim 1959):

$$\begin{aligned} \dot{Q}_{i} & = \left( {\rho C_{p} } \right)_{w} \left( {T_{{res}} - T_{i} } \right)q_{i} = \left( {\rho C_{p} } \right)_{g} \left( {T_{{res}} - T_{i} } \right)h\frac{{dA_{c} \left( t \right)}}{{dt}} \\ & \quad + \dot{Q}_{o} \left( {t_{D} } \right)_{{over,under}} \\ \end{aligned}$$

(25)

Here $\overline{{q_{i} }} = {{dW_{i} } \mathord{\left/ {\vphantom {{dW_{i} } {dt}}} \right. \kern-\nulldelimiterspace} {dt}}$ [m³/s] is the (average) injection rate, $T_{i}$ [^oC] is the (downhole) injection temperature and $\left( {\rho C_{p} } \right)_{w}$ [J/m³K] is the volumetric heat capacity for water. Since this parameter is slightly temperature- and pressure-dependent (Weast 1978), it is suggested to take the averages of the downhole injector and producer conditions of the doublet.$\left( {\rho C_{p} } \right)_{g} = \left( {1 - \varphi_{e} } \right)\left( {\rho C_{p} } \right)_{s} + \varphi_{e} \left( {\rho C_{p} } \right)_{w}$ [J/m³K] is the gross aquifer/reservoir volumetric heat capacity, where the subscript s refers to the solid rock material. The heat transport function between the aquifer and the over- and under-burden $\dot{Q}_{o} \left( {t_{D} } \right)$ is given by Pratts (1986, §5.2) and the controlling parameter is the non-dimensional time defined as:

$$t_{D} \left( t \right) \equiv \frac{{4\kappa_{s} }}{{h^{2} }}\left( {\frac{{\left( {\rho C_{p} } \right)_{s} }}{{\left( {\rho C_{p} } \right)_{g} }}} \right)^{2} t$$

(26)

Here ${\kappa }_{s}={\lambda }_{s}/{\left(\rho {C}_{p}\right)}_{s}$ [m²/s], the thermal diffusivity of the over- and under-burden bulk rock, which for low-porosity water-saturated clay-rich shale is assumed to be immobile, such that ${\left(\rho {C}_{p}\right)}_{s}=\left(1-{\varphi }_{s}\right){\left(\rho {C}_{p}\right)}_{s}+{\varphi }_{s}{\left(\rho {C}_{p}\right)}_{w}$. Note that even a low shale porosity ${\varphi }_{s}$ can significantly influence the heat capacity. The non-dimensional time controls the heat transport from the injected formation to the surrounding rock and it is proportional to its thermal conductivity ${\lambda }_{s}$ [W/mK] and inversely proportional to the layer thickness squared. Equation (25) represents the downhole geothermal power [W], which exceeds the geothermal power produced at the surface due to heat losses in the wells, pumps, etc. By solving Eq. (25) without heat transport to the over- and under-burden (subscript 0), the cooled volume inside the reservoir becomes (Hettema et al. 2004):

$$V_{c0} \left( t \right) = A_{c0} \left( t \right)h = \frac{{\left( {\rho C_{p} } \right)_{w} }}{{\left( {\rho C_{p} } \right)_{g} }}W_{i} \left( t \right)$$

(27)

Here ${A}_{c}$ [m²] is the cooled contact area between the aquifer and the over-/under-burden. Note that this coupling between water injection and cooling front implies thermal equilibrium of aquifer sand and shale layers, so this is only valid for relatively thin intra-reservoir shale layers compared to the injection rate. In case of conductive heat transport to the over- and under-burden, Marx and Langenheim (1959) found a solution for ${A}_{c}\left(t\right)$ by solving Eq. (25) and defining the cooling front at the volume-averaged temperature extension. A non-dimensional time-dependent parameter is defined as the ratio of areal extension of the cooled aquifer area to that without heat transport,

$$A_{D} \left( {t_{D} } \right) \equiv \frac{{A_{c} \left( t \right)}}{{A_{c0} \left( t \right)}} = \frac{2F}{{2F + \sqrt {t_{D} } }}$$

(28)

The location of the cooling front is based on the volume-averaged temperature, such that the parameter $F={erfc}^{-1}\left({T}_{D}=0.355\right)\cong 0.654$ (Koning 1985), consistent with the Marx and Langenheim (1959) solution. Besides the conductive heat transport to the over- and under-burden ${t}_{D}$ also controls the steepness of the temperature front inside the aquifer, being very steep if ${t}_{D}<0.05$ and gentle if ${t}_{D}>0.25$. The non-dimensional temperature profile becomes (Koning 1985, App D)):

$$T_{D} \left( {t_{D} } \right) \equiv \frac{{T - T_{res} }}{{T_{i} - T_{res} }} = erfc\left( {\sqrt {t_{D} } \frac{{A_{D} \left( {t_{D} } \right)}}{{2\left( {1 - A_{D} \left( {t_{D} } \right)} \right)}}} \right)$$

(29)

At the front the temperature is cooled by: $\Delta T_{cf} = 0.355\left( {T_{res} - T_{i} } \right)$. Finally, the solution of cooled volume inside the aquifer with heat conduction to over- and under-burden becomes:

$$V_{c} \left( t \right) = \pi a\left( t \right)b\left( t \right)h = A_{D} \left( {t_{D} } \right)\frac{{\left( {\rho C_{p} } \right)_{w} }}{{\left( {\rho C_{p} } \right)_{g} }}W_{i} \left( t \right)$$

(30)

The location of the elliptical flooding front is related to the injected water volume. The volume averaged cooling radius inside the aquifer becomes:

$$\overline{{r_{c} \left( t \right)}} = \sqrt {a\left( t \right)b\left( t \right)} = \sqrt {\frac{{V_{c} \left( t \right)}}{\pi h}}$$

(31)

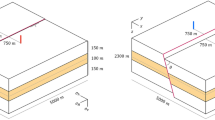
Figure 4 shows the location of the flooding front based on Eq. (22) and the location of the cooling front without heat transport to over- and under-burden based on Eq. (27) and with heat transport based on Eq. (30), applying Eq. (31) for the cylindrical model using the base-case reservoir with properties given in Table 3 (Appendix A).

Fig. 4

Location of the cooling and flooding fronts versus the injected volume for the cylindrical model up to the thermal breakthrough

These temperature profiles and cooling front extension are important input to calculate the thermal stress changes. Figure 5 shows results at the end of the early period, after 10.4 years of injection (${t}_{D}=0.04$) for the base-case reservoir with properties given in Table 3 (Appendix A).

Fig. 5

Temperature profile at the end of the early period, showing the methodology used to determine the front location

The thermal stress determination requires determination of the following parameter (re-writing Eq. 30):

$$\frac{b\left( t \right)}{h} = \sqrt {\frac{e}{{\pi h^{3} }}\frac{{\left( {\rho C_{p} } \right)_{w} }}{{\left( {\rho C_{p} } \right)_{g} }}A_{D} \left( {t_{D} } \right)W_{i} \left( t \right)}$$

(32)

Note that $e = {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a} \le 1$ (see Appendix B), the final ellipticity of the cooling region. The pre-injection stress state and stress models applicable to The Netherlands subsurface are discussed in the next section.

2.4 Stress models and the initial stress state

The initial, pre-production or -injection in-situ stress state is the result of a complex interaction of rock properties, fluid pressure, plate tectonic forces and burial history. The Netherlands is at present located at large distance from tectonic plate boundaries or orogenesis. Consequently, it is assumed that the sedimentary rocks resting upon the basement are free from tectonic shear stress loading, except possibly for the Lower Rhine Graben extension area in the South-East of The Netherlands, which presently displays natural seismicity. To the best of our present-day knowledge based on drilling and production experience there is a normal-faulting stress regime in the depth range of interest, down to 3300 m. If we in addition stay away from salt diapirs and major faults it is plausible that the vertical stress is the major principal stress, ${\sigma }_{v}={\sigma }_{1}$. Although both the major horizontal earth stress ${ }\sigma_{H}$ [Pa] and the minor horizontal earth stress ${\sigma }_{h}$ [Pa] are perpendicular in direction to each other and to the vertical, these are only principal stresses in case the shear stress is absent. If we consider a rock with an interconnected porosity-depth profile$\varphi \left(z\right)$, an equilibrium of body and surface forces and Archimedes’ law relates the vertical stress gradient $\rho_{b} g$ [kPa/m = MPa/km] to the solid grain density gradient $\rho_{s} g$ [kPa/m] and the pore-fill gradient $\rho_{f} g$ [kPa/m] as: $\rho_{b} \left( z \right)g = \left( {1 - \varphi \left( z \right)} \right)\rho_{s} g + \varphi \left( z \right)\rho_{f} g$. The vertical stress gradient at depth $z_{d}$ [m] can be determined from the average overburden density $\overline{\rho }_{b} \left( z \right)$ [g/cm³] by (Zoback 2010, Ch. 1; Zoback et al. 2003):

$$\frac{{\sigma_{v} \left( {z_{d} } \right)}}{{z_{d} }} = \frac{g}{{z_{d} }}\int\limits_{0}^{{z_{d} }} {\rho_{b} \left( z \right)dz \approx g\overline{\rho }_{b} \left( z \right)}$$

(33)

Here z [m] is the true vertical depth and in The Netherlands the gravity acceleration $g\cong 9.81$ [m/s²]. If density logs are not available it could be estimated from Verweij et al. (2016), who have evaluated the variation in lithostatic stresses in The Netherlands. They also concluded that the relatively low values found result from the low-density North Sea group, the Zechstein halite and local salt diapirs. At depth ranges where no density logging is present missing data can be added by a basin sediments trendline following an empirical exponential porosity-depth relation: $\varphi \left(z\right)={\varphi }_{0}{e}^{-cz}$ (Sclater and Christie 1980). For modelling of the North Sea basin Kooi et al. (1991) applied ${\varphi }_{0}=0.45$ and $c=0.4$ km⁻¹. The optimal values of these two parameters can be found for a specific basin through minimization of the sum of the least-squares differences of the model and the log measurements, excluding the non-porous evaporites such as halite and anhydrite, which are often present in the Zechstein. The density profile can then be determined from using for example a rock matrix density as free parameter or base it on the rock lithology using Carmichael (1984). Typical values for sedimentary basins are ${\rho }_{s}=2.70$ [g/cc] (depending on the rock type) and a brine density ${\rho }_{fl}=1.04$ [g/cc] (depending on salinity). Applying this method for locations in several basins in The Netherlands resulted in a range of trendline properties for the surface porosity in the range of $0.45 \le \varphi_{0} \le 0.7$ and for the compaction coefficient in the range of: $0.4 \le c \le 0.7$ [km⁻¹]. Figure 6 shows an example of a density log interpretation applying a basin trendline for the missing data depths based on the trendline parameters shown and $\rho_{s} = 2.7$ gr/cc and $\rho_{f} = 1.1$ gr/cc, giving an RMS deviation of 0.13 g/cc. Note that for modelling the evaporites (halite and anhydrite) are excluded as well as over-pressured reservoirs, which do not follow the normal basin compaction trend. The average overburden density is $\overline{{\rho_{b} }} = 2.19$ g/cc, strongly influenced by the overlying thick halite layer.

Fig. 6

Example of a density log including the compaction model for a typical Rotliegend reservoir situation, including the overlying evaporites

The minimum stress magnitude is preferably estimated from field measurements, interpreted from an extended leak-off test or a mini-fracture test (Zoback et al. 2003; Andrews et al. 2016). Adding a monitored flowback phase improves the precision of the minimum horizontal stress estimate (Raaen 2006). In the absence of such data the upper crust is modelled as a stack of thin poro-elastic plates under plane-strain loaded by a tectonic-induced strains at its boundaries. For a plate the following minimum horizontal Earth stress can be derived (Timoshenko and Goodier 1970, §20):

$$\sigma_{h} = K_{0} \sigma_{v} + \alpha_{1} \left( {1 - K_{0} } \right)p + E^{\prime } \left( {\varepsilon_{h} + \nu \varepsilon_{H} } \right)_{tec}$$

(34)

For the maximum horizontal stress, the model gives:

$$\sigma_{H} = K_{0} \sigma_{v} + \alpha_{1} \left( {1 - K_{0} } \right)p + E^{\prime } \left( {\varepsilon_{H} + \nu \varepsilon_{h} } \right)_{tec}$$

(35)

Note that all parameters and variables are depth-dependent. The right-most term shows the influence of the tectonic stress, consisting of the product of the tectonic strain and the plane-strain modulus ${E}^{^{\prime}}$ [MPa] given by:

$$E^{\prime } \left( z \right) = \frac{E\left( z \right)}{{1 - \nu \left( z \right)^{2} }} = \frac{2G\left( z \right)}{{1 - \nu \left( z \right)}}$$

(36)

Here E [MPa] is Young’s modulus, $\nu$ [-] is Poisson’s ratio, G [MPa] is the shear modulus. Here $\varepsilon_{h}$ [-] is the tectonic strain in the ${\sigma }_{h}$ direction and ${\varepsilon }_{H}$ [-] is the tectonic strain in the ${\sigma }_{H}$ direction. The parameter ${\alpha }_{1}$ depends on the effective stress definition to be used. When applied to intact porous rock deformation ${\alpha }_{1}=\alpha =1-{K}_{b}/{K}_{r}$ equals Biot’s parameter (Biot & Willis 1957), where $K_{r}$ [MPa] is the solid material bulk modulus and $K_{b}$ [MPa] is the rock bulk modulus (see also Addis et al. 1997). The main limitation of applying this model predictively to estimate the initial in-situ stress state is the fact that it is based on linear poro-elastic theory. The material properties have evolved during the geological compaction history due to for instance ductile creep processes. This could be taken into account by applying the averaged Biot’s parameter based on the pre-compaction and present-day bulk stiffnesses: $\alpha_{1} \left( z \right) = \overline{\alpha } = \left( {1 + \alpha \left( z \right)} \right)/2$. However, Jaeger et al. (2007) showed that both rock failure and slippage along fault planes can best be described by applying ${\alpha }_{1}=1$. Also, calibration of this model with minimum stresses estimated from mini-fractures and extended leak-off testing suggests that the Earth’s behaviour over large time- and length-scales could simply best be described by Terzaghi’s effective stress definition, $\alpha_{1} \left( z \right) = 1$. From the model the maximum horizontal stress can be determined from the minimum stress and the tectonic strain by:

$$\sigma_{H} \left( z \right) = \sigma_{h} \left( z \right) + \frac{{E_{h} \left( z \right)}}{{1 + \nu_{h} \left( z \right)}}\left( {\varepsilon_{H} - \varepsilon_{h} } \right)_{tec}$$

(37)

For a transverse isotropic material, the effective stress ratio under uniaxial strain conditions is (Thiercelin and Plumb 1991; Andrews and Lesquen 2019):

$$K_{0} \left( z \right) = \left. {\frac{{\sigma_{h} \left( z \right) - p\left( z \right)}}{{\sigma_{v} \left( z \right) - p\left( z \right)}}} \right]_{ust} = \frac{{E_{h} \left( z \right)}}{{E_{v} \left( z \right)}}\left( {\frac{{\nu_{v} \left( z \right)}}{{1 - \nu_{h} \left( z \right)}}} \right)$$

(38)

Here $E_{h}$ [MPa] and $E_{v}$ [MPa] are the horizontal and vertical Young’s moduli and $\nu_{h}$ [-] and $\nu_{h}$ [-] are the horizontal and vertical Poisson’s ratios, respectively. For a homogeneous isotropic material, $K_{0} \left( z \right) = {\nu \mathord{\left/ {\vphantom {\nu {\left( {1 - \nu } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - \nu } \right)}}$. Note that as a result of creep and ductility occurring when loading over geological time, Young’s modulus is always smaller and Poisson ratio is always larger than the laboratory-determined parameters under high loading rate. As a consequence, the $K_{0}$ based on laboratory testing time scale (days), but certainly when based on acoustic logging data (milliseconds) will give a lower limit estimate. In the presence of tectonic stresses, the plane-strain tectonic stress model (Eq. 34) gives a minimum effective stress ratio of:

$$K_{ps} \left( z \right) \equiv \left. {\frac{{\sigma_{h} \left( z \right) - p\left( z \right)}}{{\sigma_{v} \left( z \right) - p\left( z \right)}}} \right|_{ps} = K_{0} \left( z \right) + \frac{{E^{\prime}\left( z \right)}}{{\sigma_{v} \left( z \right) - p\left( z \right)}}\left( {\varepsilon_{h} + \nu \varepsilon_{H} } \right)_{tec}$$

(39)

Note that the tectonic stress component is controlled by the ratio of the plane-strain modulus (expected to increase with depth) and the effective vertical stress, strongly increasing with depth in a basin. The second model is based on the assumption that the Earth’s crust stresses are limited by the frictional strength of nearby faults (Addis et al. 1996; Addis 1997; Zoback et al. 2003; Zoback 2010; Dvory and Zoback 2021) or is in a self-organised critical state (Grasso and Sornette 1998). Re-arranging the Mohr–Coulomb relationship (Eq. 9) gives the following friction-based lower limit for the minimum stress:

$$\sigma_{h} \left( z \right) \ge K_{\phi } \sigma_{v} \left( z \right) + \left( {1 - K_{\phi } } \right)p\left( z \right) - 2S_{0} \sqrt {K_{\phi } }$$

(40)

Here the frictional effective stress ratio parameter is (Jaeger et al. 2007):

$$K_{\phi } = \frac{{\left( {1 - \sin \phi } \right)}}{{\left( {1 + \sin \phi } \right)}} = \left( {\mu + \sqrt {\mu^{2} + 1} } \right)^{ - 2}$$

(41)

This friction-based criterion limits the effective stress ratio by:

$$K_{fr} \left( z \right) \equiv \left. {\frac{{\sigma_{h} \left( z \right) - p\left( z \right)}}{{\sigma_{v} \left( z \right) - p\left( z \right)}}} \right|_{fr} \ge K_{\phi } - \frac{{2S_{0} }}{{\sigma_{v} \left( z \right) - p\left( z \right)}}\sqrt {K_{\phi } }$$

(42)

Note that in general the influence of the cohesive fault strength $S_{0}$ decreases with increasing depth as the vertical effective stress increases. The plane-strain model controls the minimum stress up to the point that the faults in the neighbourhood cannot sustain the differential stress any longer and starts slipping. The fault friction starts controlling the minimum stress as soon as the following criterion is met:

$$K_{fr} \le K_{ps}$$

(43)

Applying Eq. (42) and (39) shows that in a compressive tectonic environment and the presence of cohesive faults this criterion is easily satisfied. If we consider cohesionless faults ($S_{0} = 0$) in tectonic relaxed basins ($\varepsilon_{h} = \varepsilon_{H} = 0$) this criterion can be simplified to $K_{\phi } \le K_{0}$, showing that the fault friction will control the minimum stress if the friction angle is below:

$$\sin \phi \le \frac{{1 - k_{0} }}{{1 + k_{0} }} = 1 - 2\nu$$

(44)

This relationship shows that only critically stressed faults with a low friction angle can control the minimum stress. Table 1 shows typical example ranges of $K_{0}$ and $K_{\phi }$ for several sedimentary rocks.

Table 1 Typical ranges of rock properties for several sedimentary rocks (Barton 1976, his Table 1; Byerlee 1978; Jaeger et al. 2007, their Table 3.1)

In case the tectonic relaxed basin assumption applies the modelled Earth is in a state of uniaxial strain or limited by fault friction. For geothermal developments in the south-east of The Netherlands the presence of observed natural seismicity shows that a significant tectonic stress component is present at depth around 10 km. Because ultra-deep geothermal operations are also planned at depths below 3300 m where the stresses are largely unknown, we demonstrate how the tectonic stresses could be estimated by the model. The plane strain modulus in Eq. (36) is strongly depth-dependent. Combining an empirical model with a simple linear porosity dependence (based on a critical porosity ${\varphi }_{c}$ as suggested by Nur et al. (1995)) with the exponential porosity-depth relation used for the density log model from Sclater and Christie (1980) gives:

$$E^{\prime}\left( z \right) = E_{base}^{^{\prime}} \left( {1 - \frac{\varphi }{{\varphi_{c} }}} \right) = E_{base}^{^{\prime}} \left( {1 - e^{ - cz} } \right)$$

(45)

Mavko et al. (2007, §7.1) gives a table of critical porosities, ranging from 40% for sandstone and dolomite up to 65% for limestone and chalk. From the tectonic strain–stress map produced by Olaiz et al. (2009), we read tectonic strains of ${\varepsilon }_{h}=0$ and ${\varepsilon }_{H}=0.2$ mstrain in the NNW-SSE direction. Applying the compaction parameters from the density analysis shown in Fig. 6 and assuming a granite basement with a plane strain modulus of 53 GPa produces the results shown in Fig. 7. Note that despite the absence of a minimum tectonic strain (${\varepsilon }_{h,tec}=0$), Eq. (34) shows that if there is tectonic strain in the maximum direction (${\varepsilon }_{H,tec}\ne 0$), it can cause an increase in the modelled minimum stress due to the Poisson effect. As a consequence, the major Mohr circle $\left({\sigma }_{1};{\sigma }_{3}\right)$ becomes slightly smaller compared to the case of absence of tectonic stresses. On the other hand, the presence of a tectonic strain induces an increase of ${\sigma }_{H}$, causing the minor Mohr circle $\left({\sigma }_{2};{\sigma }_{3}\right)$ to increase and the major Mohr circle $\left({\sigma }_{1};{\sigma }_{3}\right)$ to decrease. As a result, for depth shallower than 4 km, more three-dimensional fault orientations are at hazard compared to the situation where tectonic strain-induced stresses are low, as sketched in Fig. 1.

Fig. 7

Result of plane strain stress model applying ${\varepsilon }_{h}=0$ and ${\varepsilon }_{H}=0.2$ mstrain

Note that in a compressive environment $K_{ps} > K_{0}$. In general, for both models the minimum stress gradient can be analysed from the overburden gradient and the pore pressure gradient by:

$$\frac{{\sigma_{h} \left( z \right)}}{z} = K\left( z \right)\frac{{\sigma_{v} \left( z \right)}}{z} + \left( {1 - K\left( z \right)} \right)\frac{p\left( z \right)}{z}$$

(46)

The next section will show that for the plain-strain model, $K_{0} \left( z \right) = 1 \to < 0.4$, the strong reduction caused by compaction of the highly porous water-saturated clays at shallow depths to the well-cemented sediments at larger depths. The application of this model and estimation $K_{0} \left( z \right)$ will be discussed in the next section.

Application of this model for prognosis requires determination of the vertical stress gradient from Eq. (33) and knowledge of the pressure gradient ${{p\left( z \right)} \mathord{\left/ {\vphantom {{p\left( z \right)} z}} \right. \kern-\nulldelimiterspace} z}$, which for a fully interconnected pore space, in the absence of any overpressure mechanisms, can simply be related to the average fluid density by: $p\left( z \right)/z = \overline{{\rho_{fl} }} g$. Note that the fluid density strongly dependent on its salinity (see Appendix A). In case criterion (43) is not fulfilled, the minimum stress is not controlled by friction and the plane-strain model applies with $K = K_{ps}$, given by Eq. (39). If condition (43) is fulfilled the friction limits the minimum stress such that $K = K_{fr}$ applies, given by Eq. (42). Finally the method can also be used to estimate the initial minimum stress at the geothermal target location of interest from field stress measurements from offset locations based on XLOT or minifracture testing. The field effective stress ratio $K\left( z \right)$ needs to be determined at the test location, preferably at similar depth range, formation and sedimentary basin. From Eq. (46):

$$K\left( z \right)_{field} = \left. {\frac{{\sigma_{h} - p}}{{\sigma_{v} - p}}} \right|_{field}$$

(47)

This methodology has successfully been applied by Hettema et al. (2009) to analyse the mini-frac measured depletion-induced stress changes within a HPHT reservoir, which in addition agreed with stress-path predictions based on a full-field geomechanical model. Applying this field-based $K\left( z \right)$ factor to the locally calibrated gradient model using Eq. (46) allows an estimation of the minimum stress for the investigated location based on field stress data from several nearby field locations in the same basin, properly corrected for local (small) depth and pore pressure differences. This requires the determination of the vertical stress gradient (Eq. 13) and the pore pressure gradient for all locations. If there are no field stress measurements available one could use drilling related data from nearby wells by using the drillers “wellbore stability plot”, containing the pore pressure prediction, a “fracture curve” and an overburden curve, usually verified and calibrated based on drilling events of borehole collapse, kicks, lost circulation, etc. However, if neither no offset stress data nor nearby drilling event data is available, one needs to rely on the predictive value of these models. The main assumptions are the linear elastic deformation behaviour and neglection of thermal stress effects, suggesting a systematic underestimation of the horizontal stress magnitude. The elastic material behaviour could be partially alleviated by performing proper laboratory experiments at low loading rates under the proper stress path conditions. Hettema et al. (2012) showed results for two shallow aquifers having porosities of 33% and 28%, respectively, giving for both: ${k}_{0}\approx 0.25$. In another study, great care was taken to reduce the core damage as much as possible (see Hettema et al. 2002) and to test the plugs as quickly as possible. Also, to restore the stress cautiously, Hettema et al. (2013) showed CAUST tests results (anisotropic consolidated and drained uniaxial strain loading) is probably the best way for the stress restauration, allowing proper determination of the ${k}_{0}$ during the strain-controlled uniaxial strain loading phase afterwards. Since some inelastic deformation is allowed to develop during these test performed at low rates, these measured ${K}_{0}\cong 0.28$ are regarded as being more representative than the log-based acoustically determined ones. More recently, Singh et al. (2021) present the concept of visco-elastic stress relaxation and apply their model to show how two laboratory-measured creep parameters can be used to limit the difference between the total vertical stress and the minimum stress, effectively increasing the modelled minimum stress (Ma and Zoback, 2020).

Although the basis for Eq. (46) is quite solid, it is not recommended to use these models predictively, especially since stress quantification is very sensitive to the often ill-constrained input such as Poisson’s ratio on a geological time scale, since in general, ${K}_{0d}\le {K}_{0}\le K$. Nevertheless, these models provide insight into the relative influence of material properties on the depth trends of the stress state and provide a lower limit of the minimum stress. Thiercelin and Plumb (1991) showed a reasonable success for stress predictions in a tectonic relaxed basin. Andrews et al. (2016) applied similar stress models to over 200 high-quality extended leak-off tests with several cycles in the Norwegian continental shelf and found these not in equilibrium state with the frictional strength. Andrews and Lesquen (2019) also found, based on sonic logs, to their own surprise a relatively good match to a large body of their high-quality extended leak-off data from the Norwegian continental shelf and concluded that, despite being physically flawed, their methodology allowed interrogation of the minimum stress.

2.5 Approximation of the mechanical properties profile.

To determine a geomechanical property model typically one would select a key well having a full petrophysical computer processed log interpretation (CPI), preferably calibrated with laboratory measurements on core data. In the absence of core data, a one-dimensional well-log based geomechanical model is constructed based mainly on the density log, the gamma-ray log and the sonic logs. The earth model is first simplified by four lithologies: 1) Clean sandstone or siltstone (aquifers or reservoirs), 2) Clay-rich siliciclastics (siltstone, claystone, mudstone), 3) Carbonate (limestone or dolostone), 4) Evaporates (Halite and Anhydrite). The dynamic Young’s modulus follows from $E_{d} = 2\rho V_{s}^{2} \left( {1 + \nu_{d} } \right)$ and the dynamic Poisson’s ratio is determined by (Mavko et al. 2009):

$$\nu_{d} = \frac{1}{2}\frac{{\left( {{{v_{p} } \mathord{\left/ {\vphantom {{v_{p} } {v_{s} }}} \right. \kern-\nulldelimiterspace} {v_{s} }}} \right)^{2} - 2}}{{\left( {{{v_{p} } \mathord{\left/ {\vphantom {{v_{p} } {v_{s} }}} \right. \kern-\nulldelimiterspace} {v_{s} }}} \right)^{2} - 1}}$$

(48)

The dynamic parameters are determined from acoustic waves at high frequencies and low amplitudes. They apply directly to solid materials and to undrained porous/fractured fluid-filled materials, so it seems appropriate to at least apply $K_{0,d} = {{\nu_{d} } \mathord{\left/ {\vphantom {{\nu_{d} } {\left( {1 - \nu_{d} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - \nu_{d} } \right)}}$ large parts of the overburden of lithologies 2) and 4). To determine the extent of the application of the dynamic parameters, Hettema et al. (2002) have applied the characteristic transient time for drainage on a field wide scale and the theory has also been demonstrated useful to determine the drainage of embedded layers (Hettema et al., 2009). A non-dimensional characteristic drainage time has been defined: $\tau_{c} = {{4C_{D} t} \mathord{\left/ {\vphantom {{4C_{D} t} {L^{2} }}} \right. \kern-\nulldelimiterspace} {L^{2} }}$, where $C_{D}$ [m²/s] is the consolidation coefficient defined in Eq. (21), t [s] is the time and L [m] is the layer thickness. If $\tau_{c} \gg 1$ the layer is regarded as being fully drained (on the timescale of one day), which for example for rock lithology 1) (or possibly 3)) of 100 m thickness would require a permeability of 4 mDarcy to drain, while a 10 m thick layer would require a permeability of 0.04 mDarcy. To be regarded as fully undrained (on a geological timescale of say 1000 years) requires $\tau_{c} \ll 1$, which for example for claystone rocks in category 2) of 200 m thickness would require a permeability of less than 50 nanoDarcy. In this case the pore pressure can no longer be regarded as being independent but could be determined by applying the consolidation theory as developed by Biot (1941) and demonstrated by Jaeger et al. (2007, §7.6).

In case the shear sonic log is not available it can be generated from the sonic log using empirical correlations as listed by Mavko et al. (2009; Ch 7) honouring the “assumptions and limitations”. Mavko et al. (2009, App. A.1) present $v_{p} /v_{s}$ ratios for several rock types in relation to porosity. We have reasonably good experience using Castagna et al. (1993): $v_{s} = 0.8042 \cdot v_{p} - 0.8559$ [km/s] for cleaner sandstone and for the clay-rich silicaclastics either the general “mudrock line” is used: $v_{s} = 0.8621 \cdot v_{p} - 1.1724$ [km/s] or in case the clay volume has been determined from petrophysical evaluation, there are two more specific empirical correlations separated by $V_{clay} = 0.25$ (Han et al. 1986). In some cases, these relationships could be calibrated using nearby analogue wells having full logging suites. Kruiver et al. (2017) analysed shallow $v_{p} /v_{s}$ ratios in the Groningen area and suggested several empirical relationships for the shallow subsurface (first 1000 m). They found for the depth range of 0 – 500 m a linear decrease of the ratio, resulting in a dynamic Poisson’s ratio decreasing from 0.48 at the surface to 0.4 at 500 m depth. High Poisson ratios are to be expected in loosely consolidated water-saturated sediments and result in ${K}_{0,d}=0.91$ at the surface and ${K}_{0,d}=0.66$ at 500 m depth. Figure 8 shows an example of a modelled minimum stress profile of a shallow pilot well drilled in the Central Netherlands basin, based on the model in Eq. (46). The shear wave velocities were empirically determined using the simplified lithologies suggested above. Although the North Sea Supergroup consists of both several sandstone layers as well as a clay-rich mudrock, very high average ${v}_{p}/{v}_{s}=4.55$ were found, resulting in $\overline{{K }_{0,d}}=0.88$ for the upper 536 m. The dynamic parameters were applied directly to the bulk of the overburden. Figure 8 shows an example the stress model applied to an onshore well in The Netherlands in the absence of tectonic stresses, assuming a passive basin. It is noted that the sharp transitions of the horizontal stresses between the various lithologies are regarded as being unrealistic, but no attempt was made to mitigate that.

Fig. 8

Example of a modelled minimum stress profile in the Central Netherlands basin based on the model presented in Eq. (46)

For porous and permeable sandstone aquifer layers, however, in case of the absence of core data for calibration, for the static-to-dynamic conversion of the stiffness we use the empirical models presented by Wang and Nur (2000) for soft sediments (E < 15 GPa): $E=0.41{E}_{d}-1.06$ [GPa] and for harder rocks (E > 15 GPa): $E=1.153{E}_{d}-15.2$ [GPa]. These models proved reasonable for the cases we could calibrate. For conversion of Poisson’s ratio, the drained Poisson ratio needs to be determined from the dynamic (undrained) Poisson ratio by (inverted from Jaeger et al. 2007, §7.5):

$$\nu = \frac{{\left( {3 - \alpha B} \right)\nu_{d} - \alpha B}}{{3 - 2\alpha B\left( {\nu_{d} + 1} \right)}}$$

(49)

Here $\varphi \le \alpha \le 1$ [-] is Biot’s parameter (Biot and Willis 1957) and B [-] is the Skempton parameter (Jaeger et al. 2007, §7.3). To determine the drained Poisson’s ratio requires interpreted logs for the porosity $\varphi$ and the bulk modulus of the rock frame ${K}_{b}$ [GPa], which is preferably determined from core measurements or overburden tests, but if not available can be approximated by ${K}_{b}=E/3\left(1-2{\nu }_{d}\right)$. The bulk modulus of the solid rock mineral ${K}_{s}$ [GPa] can be taken from Carmichael (1984) and the bulk modulus of the pore fill ${K}_{pf}={s}_{w}{K}_{w}+\left(1-{s}_{w}\right){K}_{g}$ [GPa], ${s}_{w}$[-] being the water saturation, ${K}_{w}$ [GPa] the bulk modulus of water and ${K}_{g}\approx p$ [GPa] the gas bulk modulus, which can be approximated by its pressure when regarded as an ideal gas. As an example, for an aquifer having ${K}_{0\mathrm{d}}=0.35\pm 0.02$ (average ± standard deviation), this technique resulted in ${K}_{0\mathrm{d}}=0.31\pm 0.06$, after filtering using a critical clay volume fraction and a critical porosity.

An important parameter for the thermal stress determination is the thermo-elastic constant ${A}_{T}$ [MPa/^oC] defined in Eq. (17). Applying a linear thermal expansion coefficient of 12 mstrain/^oC for a clean, quartz-rich sandstone gives the thermo-elastic constant profile shown in Fig. 9. The geological variation is captured by the standard deviation, giving in this case: ${A}_{T}=1.50\pm 0.22$ [Bar/^oC].

Fig. 9

Example of the log-determined thermo-elastic constant versus depth inside the sandstone aquifer

2.6 Assessment of probabilities for early period

The presented results apply to the stress situation of interest, as presented in the section “Stress models and the pre-injection stress state”. The first necessary condition for seismicity to occur is the mechanical re-activation along fault planes-of-weakness. By means of the shear mobilisation ratio the probability that mechanical re-activation along a fault plane of weakness can occur is determined. This requires the quantification of the shear mobilisation ratio MR defined in Eq. (12), which is determined without any geological pre-assumptions on the presence of any fault inside the cooled/pressurized zone. The analysis is performed at two stages: 1) Early period (matrix/fractured) injection with cylindrical flow- and cooling-patterns and 2) at the end of the doublet life, when thermal breakthrough occurs.

Firstly, it is established whether or not thermal fracturing occurs. For initiation/propagation of such fractures at a vertical wellbore inside the aquifer/reservoir Fjaer et al. (2008, §4.5) present the following solution for the critical well injection pressure:

$$p_{wf,I} \ge \frac{{2\sigma_{h,0} - \gamma_{u} p_{0} + A_{T} \Delta T + T_{0} }}{{2 - \gamma_{u} }}$$

(50)

Here $p_{0}$ [MPa] is the initial pressure and $T_{0}$ [MPa] is the tensile strength of the rock material. Around the wellbore, the stress concentration decreases rapidly by $\left( {{{r_{wb} } \mathord{\left/ {\vphantom {{r_{wb} } r}} \right. \kern-\nulldelimiterspace} r}} \right)^{2}$, where $r_{wb}$ [m] is the wellbore radius (see Fjaer et al. 2008, §4.3.4). It is shown in Eq. (65) (Appendix A) that for matrix injection that also the pore pressure diminishes rapidly with distance to the wellbore. Note that since $0 < \gamma_{u} < 1$ the wellbore fracture initiation pressures increase further consistent with Haimson and Fairhurst (1967), who found similar effects for near-wellbore hydraulic fracture initiation pressure. This also agrees with the operational observations for injection pressures required to be significantly above the (total) minimum stress to create a hydraulic fracture in porous and permeable formations. Although fracture initiation seems unlikely at the wellbore wall in case of prolonged injection, as in water flooding or geothermal operations, pressure and temperature changes will eventually extend far outside the near-wellbore stress concentration and pore-pressure penetration influence zone. In case condition (50) is met or there is a large pre-existing hydraulically open fracture/fault naturally present extending outside the wellbore stress influence zone, Perkins and Gonzalez (1985) applied the following downhole pressure injection criterion for mode I fracture extension, in our normal-faulting stress regime for vertical fractures growing in the major horizontal stress $\sigma_{H}$-direction:

$$p_{wf,I} - \Delta p_{fl} \left( {q_{i} } \right) \ge \sigma_{h} \left( {\Delta T,\overline{\Delta p} ,W_{i} ,t_{D} } \right) + \frac{{k_{Ic} }}{{\sqrt {\pi l_{f} } }}$$

(51)

Here $\Delta p_{fl} \left( {q_{i} } \right)$ [MPa] represents several pressure loss contributions from the flow of the well entry to the fracture tip due to the perforations, fracture debris, skin damage, fracture shape/roughness and flow loss depending on fluid viscosity, fracture width and injection rate. $l_{f}$[m] is the (pre-existing) fracture/fault length and $k_{Ic}$ [MPa $\sqrt m$] is the mode I critical stress intensity factor (Atkinson 1984). The fracture can grow in the maximum horizontal stress direction, causing elliptical cooling regions giving thermal stresses as described by Perkins and Gonzalez (1985) and also worked out by Koning (1985). If neither condition (50) is satisfied nor condition (51), sustained matrix injection will cause an extension of the cooling zone far outside the wellbore region, possibly leading to formation breakage within the influenced zone if:

$$\overline{\Delta p} \left( q \right) \ge \sigma_{h} \left( {\Delta T,\overline{\Delta p} ,W_{i} ,t_{D} } \right) - p_{0} + T_{0}$$

(52)

$T_{0}$ [MPa] is the tensile strength of the rock material unloaded in horizontal direction, perpendicular to a vertical plane. Applying the equivalent average pressure change defined in Eq. (71) and the minimum stress given in Eq. (13) gives after re-working:

$$\overline{\Delta p} \left( q \right) = \frac{{\left( {p_{wf} - p_{0} } \right)}}{2} \ge \frac{{\sigma_{h,0} - p_{0} + A_{T} G_{T,r} \Delta T + T_{0} }}{{1 - \gamma_{u} G_{p,r} }}$$

(53)

Note that as a consequence of the injection pressure causing the stress to increase (because the denominator in Eq. (53) is less than unity, since $0 < \gamma_{u} G_{p,r} < 1$), the critical injection pressure rises above the initial minimum stress, called “back stress” effect. Note that if at any point in time condition (52) is satisfied, the aquifer/reservoir could fracture spontaneously around the injector.

There are four moments of importance for the injection-induced stress determination shown in Table 2. First, using the base–base doublet parameters listed in Appendix A, it takes about one day for the semi-steady state pressure profile to establish. If the injection and production rates are kept constant, both the pressure profile shown in Fig. 16 and the geometric factor $G_{p,r}$ shown in Fig. 17 will also remain constant over time. From that moment onwards, the averaged near-wellbore pressures shown in Eq. (71) extends over the equivalent radius given by Eq. (72), causing a near-wellbore effect on the stresses. As injection proceeds, however, Appendix B show that thermally-induced stresses increase $G_{T,r} = 0.5 \to 1$, so criterion (52) could be fulfilled after a certain volume has been injected, possibly causing thermal fracturing. Matrix injection will sustain as long as neither criterion (50) nor criterion (32) are fulfilled and early period ends at the moment the cylindrical flooding front approaches the first flow barrier, caused either by a reservoir flow boundary or an impermeable fault. If no structural flow barriers are present surrounding the doublet wells, the second moment occurs when the extension of the cooling front reaches the extension of the averaged near-wellbore stresses, called the equivalent radius given by Eq. A8. At this point the near-wellbore stress changes are limited, since the thermal effect opposes the pressure effect. From that point in time onwards, however, the cooling front will extend beyond the pressure-induced stress changes, causing solely thermally-induced stress changes. To capture the early injection hazard, calculations are performed using the definition the early period at the moment the flooding front arrives halfway at the injector and producer distance as sketched in Fig. 10, which based on Eq. (22) will occur after injection of volume $W_{2}$ [m³] at time $t_{2}$ [s]:

$$W_{2} \left( {t_{2} } \right) = \overline{{q_{i} }} t_{2} = \pi \left( \frac{D}{2} \right)^{2} h\varphi_{e}$$

(54)

Fig. 10

Sketch of the layout of the circular flooding and cooling fronts defining the end of early period

Table 2 Pressure, temperature front and timings at four stages in the lifetime of a doublet

From this injected volume the cylindrical cooling parameter ${r}_{c2}/h$ can be determined from Eq. (32) for e = 1, from which the cylindrical geometrical function can be determined (${G}_{T}$ from Eq. 78). Now the thermal and pressure-induced changed horizontal stress and vertical stress can be determined by Eqs. (13) and (14), respectively. From the elastic properties the uniaxial strain stress path can be determined from Eq. (16) and the thermo-elastic constant from Eq. (17). The average pressure change given in Eq. (71) depends on the (planned) injection rate. To determine the shear mobilisation ratio MR and its variation, a sensitivity analysis applied to several case studies revealed that besides the initial stress state and stress change parameter A_T and γ_h, there are two parameters that have the largest uncertainty and impact: The fault friction angle and the fault cohesion. The determination of these parameters and their variation will be shown in the coming section “Estimation and limitation of the fault mechanical parameters”. We use a clear and user friendly method of a probabilistic logic tree to clearly show what input range has been chosen and with which uncertainty through the probabilities assigned to it. Each variable has three input values (low, expected, high) with a probability assigned to it, such that for each input variable separately: (for example for the friction angle) $\sum P_{\phi j} = 1$. The natural variation of thermal stress parameter $A_{T}$ (see example shown in Fig. 9) could be estimated using the expected value $E\left( {A_{T} } \right) = \overline{{A_{T} }}$ and the standard deviation of the data, giving the probabilities: $P\left[ { < \left( {E\left( {A_{T} } \right) - \sigma \left( {A_{T} } \right)} \right)} \right] = 16\%$, $P\left[ {E\left( {A_{T} } \right) \pm \sigma \left( {A_{T} } \right)} \right] = 68\%$ and $P\left[ { > \left( {E\left( {A_{T} } \right) + \sigma \left( {A_{T} } \right)} \right)} \right] = 16\%$. In case there are no stress measurements available, the value and variation of the minimum Earth stress could be obtained from the models presented in the section: “Stress models and the pre-injection stress state”, where the friction-based model shown in Eq. (40) poses a lower limit of the minimum stress. If there are analogue stress measurements available, it is suggested to calibrate $k\left( z \right)_{field}$ (and its variation) from Eq. (47) and apply the results to Eq. (46). In this methodology the four variables this will lead in total to $n = 3^{4} = 81$ possibilities. For each possibility the probability is given by: $P_{i} = P_{\phi } P_{c} P_{T} P_{s}$ and the sum of all possibilities has a likelihood of $\sum P_{i} = 1$. Figure 11 shows an example of a probabilistic logic tree diagram for four parameters.

Fig. 11

Example of a probabilistic logic tree input for four parameters including their probabilities

For each combination the shear mobilization ratio MR is determined and the probability of occurrence. In case $MR>1$ the range of critical dip angles is calculated according to Eq. 13 and Eq. 14. Figure 12 shows the calculated probabilities of occurrence of shear mobilisation ratios versus MR and the dip ranges in the cases when $MR > 1$.

Fig. 12

Shear mobilization ratio versus its probability of occurrence from 81 combinations of parameter values at end of early period. In cases MR > 1, the dip angle range is shown on the right axis

The resulting cumulative probability distribution is shown in Fig. 13, which can be used to determine any cumulative probability of occurrence $P\left( {MR} \right)$. The expected value is given by: $E\left( {MR} \right) = \sum P_{i} MR_{i}$. The probability that MR exceeds unity: $P\left( {MR > 1} \right) = 1 - P\left( 1 \right)$.

Fig. 13

Cumulative probability distribution of the shear mobilisation ratio, with expected value and probabilities of exceedance at the end of the early period

The results of this example can be characterised by four parameters: The expected value $E\left( {MR} \right) = 0.89$, meaning that the expected value predicts no mechanical re-activation for any fault orientation. Next, $P\left( 1 \right) = 91\%$, meaning there is a 9% probability that faults within a specific dip range within the cooled zone can mechanically re-activate. For the mobility ratios exceeding unity the range of fault dips prone to re-activation gradually increases. Since $P\left( {1.06} \right) = 95\%$, there is 5% probability that faults with dips in the range of 61 ± 10 degrees will re-activate. If a 99% certainty is required: $P\left( {1.31} \right) = 99\%$ and there is a 1% probability that faults with dips in the wide range of 61 ± 20 degrees will re-activate. The next step is to analyse the mapped faults with their dips and orientations located inside the cooled volume. If these probabilities together with the occurrence of faults with unfavourable dip and azimuth within the stress-changed zone are assessed unacceptable, work needs to be done on the assessment of the two other necessary conditions for seismicity: The seismogeneity of the rock material and the maximum seismic moment, which will be shown in the coming section “Seismogeneity and the maximum seismic moment”.

2.7 Assessment of probabilities at thermal breakthrough

To determine the thermal breakthrough time, it is assumed that during semi-steady state matrix injection the water flow will follow the streamlines around the injector and producer, causing an estimated elliptical cooled area as sketched in Fig. 14. The injection-cooled volume at thermal breakthrough can then be found from Eq. (30):

$$V_{c} \left( {t_{bt} } \right) = \pi r_{c2} \left( {\frac{D}{2} + r_{c2} } \right)h = A_{D} \left( {t_{D} } \right)\frac{{\left( {\rho C_{p} } \right)_{w} }}{{\left( {\rho C_{p} } \right)_{g} }}W_{bt}$$

(55)

Fig. 14

Estimated cooled elliptical area (top view) at thermal breakthrough

To solve $W_{bt}$ requires determination of the non-dimensional area $A_{D} \left( {t_{D} } \right)$ from Eq. (28), using the non-dimensional time at breakthrough $t_{D} \left( {t_{bt} } \right)$ defined in Eq. (26). Finally the thermal break-through time $t_{bt}$ [s] can be found by:

$$t_{bt} = \frac{{W_{bt} }}{{\overline{{q_{i} }} }}$$

(56)

Note that the term “thermal breakthrough” should not be used for commercial purposes, since this simple estimate is only used for seismic hazard assessment. At best, it estimates the moment some cooling reaches the producer, but at these large times the non-dimensional time from Eq. (26) is also large, resulting in a gentle temperature slope and consequently very slow cooling at the producer. The remaining analysis is similar to that described in the previous section, except that the ellipticity shown in Fig. 16 causes anisotropic stress changes with geometry functions shown in Appendix B. As a consequence of the elliptical extension, compared to the cylindrical-extension early-period assessment, Fig. 11 shows that the interior average thermo-elastic stress changes perpendicular to the injector—producer direction will reduce while the stress changes in the injector-producer direction will increase. Due to this anisotropy for this final stage two sets of result are reported, both for the probabilities of the shear mobilization ratio (comparable to Fig. 14) and for the cumulative distribution (comparable to Fig. 15), one valid for the injector-producer direction and the other one perpendicular to that. It is recommended to design injector-producer pairs in alignment with the major fault structure, both from an economic viewpoint (uncertainty of the fault conductivity) and from a safety viewpoint. Due to the stress anisotropy derived in Appendix B, the faults with a strike in the direction of the well alignment will experience lower stress changes, making these less prone to slip. Largest stress changes occur perpendicular to the well alignment showing that the most prone to re-activation are faults between the injector and producer with strike azimuths perpendicular to the well alignment direction. Moreover, if these faults are in addition (partially) sealing or have a throw, an additional induced shear stress component adds to the shear stress loading due to differential compaction. It is clear that this potential hazardous situation needs to be avoided when possible. Again, if these probabilities together with the occurrence of faults with unfavourable dip and azimuth within the stress-changed zone are assessed unacceptable, work needs to be done on the assessment of the two other necessary conditions for seismicity: The seismogeneity of the rock material and the maximum moment, which will be shown in the section “Seismogeneity and maximum seismic moment”.

Fig. 15

Failure strength and post-failure sliding stresses of four tri-axial experiments

2.8 Estimation and limitation of the fault mechanical parameters

The macroscopic fault mechanical properties cohesion and friction depend on the rock material on both sides of the fault plane. For example, for intra-aquifer cataclastic faults having mainly sandstone-to-sandstone contact it suffices to determine the sandstone properties. Hunfeld (2020) reported laboratory-measured friction coefficients for the basal Zechstein (0.63– 0.67), Ten Boer claystone (0.38–0.40), Slochteren sandstone (0.59 – 0.64) and one from the underlying Carboniferous shale/siltstone (0.45) for the Groningen field in the North-East of The Netherlands. For intra-reservoir normal faults having a large throw displacing several clay-rich layers, smearing has increased its sealing potential. Yielding et al. (1997) report several techniques to be able to quantify this effect, which has been extensively calibrated in the oil industry through fault-seal analyses (Yielding et al. 2010). To estimate the mechanical properties, it is suggested to use the shale-gouge-ratio, defined as: $SGR=\sum {V}_{clay}\Delta z/th$. To determine the SGR of the fault plane requires fault-geometrical knowledge from seismic interpretation to determine layer thicknesses $\Delta z$ [m] and the fault throw [m], in addition to the clay fraction ${V}_{clay}$ [−] determined from logging. To estimate the bulk mechanical fault friction coefficient, it is suggested to use $\mu _{{fault}} = SGR \cdot \mu _{{clay}} + \left( {1 - SGR} \right)\mu _{{sand}}$. In case no core material is available, typical ranges for the basic friction coefficients for various rock materials from literature are listed in Table 1. Note that if clay minerals are involved analogue fields should be selected with care, since the mechanical properties are strongly dependent on its consolidation history (age, stress- and temperature-history).

In case core material is available, the friction and cohesion of cataclastic faults can be limited from basic tri-axial laboratory experiments. Here results are shown of four one-inch diameter plug samples of a brittle dolomitic sandstone, tested under constant confining stress of 2, 3.5, 5 and 8 MPa, respectively. The samples were all loaded to failure and also the post-failure stable sliding was registered. The resulting failure stresses and the post-failure stable sliding stresses are presented in the maximum shear stress versus mean effective stress diagram shown in Fig. 15.

The friction angle and apparent cohesion follow from analysing the parameters from the trendlines interpreted based on Eq. (9). Two observations are made: 1) Both the primary and the residual friction angles of this dolomitic sandstone are comparable and relatively high and 2) the primary apparent cohesion applies to the intact rock and there is still significant amount of residual apparent cohesion during the post-failure sliding, probably caused by the slip-plane roughness. It is noted that the stress drop observer during these simple tri-axial experiments cannot be used quantitatively, since the boundary condition of constant confining stress causes a reduction of the mean normal stress after failure, while it is expected to remain constant or increase during seismicity. Nevertheless, the interpretation of this type of laboratory measurements could confine the friction angle and apparent cohesion of the cataclastic dolomitic sandstone faults in the field.

The fault friction and cohesion can also be estimated using the model developed by Barton (1976). The model was originally developed for stability of rock slopes and mining applications. The empirical, non-linear mobilized friction model for faults and joints includes the influence of surface roughness and variable rock strength:

$$\mu_{mob} = \tan \left[ {JRC\log \left( {\frac{JCS}{{\sigma_{n} - p}}} \right) + \phi_{r} } \right]$$

(57)

When applied at pre-peak shear strength, the static empirical joint roughness coefficient typically ranges $0 < JRC < 20$, being 0 for perfectly smooth joints and 20 for very rough, undulating joints. JRC can be estimated from the root-mean-square of the roughness profile (Jiang et al. 2006; Zhang et al. 2014) or can be estimated from the power spectral density (Unlusoy and Suzen 2020). After peak shear strength the coefficient becomes mobilised: $JRC \to JRC_{mob}$ (Barton et al. 1985) and is gradually destroyed as shear displacement continues (Barton 2013). The parameter JCS [MPa] is the joint-wall compressive strength representing the strength of the asperities and $JCS = UCS$ [MPa] the unconfined compressive strength (Barton 1976). Under relatively low effective normal stress, $\sigma_{n} - p < UCS$ [MPa] while if UCS is low or the normal effective stress is high, $JCS/\left( {\sigma_{n} - p} \right) \to 1$ and the mobilized friction theoretically approaches the basic friction angle (Byerlee 1978). At higher stress levels, Barton (1976) proposed $JCS = \sigma_{1} - \sigma_{3}$. The model can also be used to describe post-failure behaviour such that JRC becomes mobilized (see Barton (2013) for an overview). Barton et al. (1985) have characterized JRC from laboratory experiments in terms of tilt angles for dilatant surfaces and the residual friction angle and also describe the post-failure evolution of these parameters. After prolonged shearing flattening will cause $JRC_{mob} \to 0$, $\phi_{mob} \to \phi_{r}$ and the residual friction angle approaches $\phi_{r} \to \phi_{b}$ [degree], the basic friction angle of flat, non-dilatant rock surfaces which is regarded as a material property as reported in the cited literature. The review paper by Thirukumaran and Indraratna (2016) demonstrates the usefulness of this model for engineering practice and Lei et al. (2015) show how the models can be implemented in finite discrete element analyses.

If there are no local indications of an initially unstable Earth, such as registered seismicity, a stable Earth requires $MR_{0} \le 1$ in Eq. (10), giving the following minimum cohesion requirement:

$$S_{0,min} = \frac{{\tau_{m,0} }}{\cos \phi } - \mu \left( {\sigma_{m,0} - p_{0} } \right)$$

(58)

If on the other hand the cohesion is known, inversion gives the following minimum friction angle requirement (setting $\cos \phi = 1$, a good approximation for low friction angles):

$$\phi_{min} = \sin^{ - 1} \left( {\frac{{\tau_{m,0} - S_{0} }}{{\sigma_{m,0} - p_{0} }}} \right)$$

(59)

These requirements are useful to confine the cohesive strength and/or the friction angle in relation to the initial stress state assuming an initially stable Earth.

3 Seismogeneity and the maximum seismic moment

The previous assessment can lead to a cumulative probability distribution of the shear mobilisation ratio MR having unfavourable characteristic values together with the occurrence of faults with unfavourable dip and azimuth within the stress-changed zone (or they cannot be ruled out). In that case the second necessary condition for the occurrence of seismicity, namely the seismogeneity of the material needs to be assessed. To cause a significant seismic event, the post-failure rupture must be brittle and occurring at velocities of a significant portion of the rock’s shear wave velocity. From a material behaviour point of view, seismogeneity can be regarded as a material property related to contribution of ductility and creep processes e.g., Hettema 1996. These contributions are at least related to the mean effective stress, the temperature, the fluid type and the rock mineralogy (Jaeger et al. 2007). In the field, Zoback et al. (2012) demonstrated the importance of slow slip contributing to the effectiveness of the shale gas production. Seismogeneity can also be investigated using a rate- and state-dependent friction law (Ruina 1983) and slip weakening (Uenishi and Rice 2003), resulting in a dynamic friction becoming time and slip-rate dependent (Segall & Rice 1995; Scholz 1998; Chen and Spiers 2016). The rate-and-state friction law gives a velocity- and state-dependent friction:

$$\mu \left( {v,\vartheta } \right) - \mu_{0} = a\ln \left( {\frac{v}{{v_{0} }}} \right) + b\ln \left( {\frac{{v_{0} \vartheta }}{{D_{c} }}} \right)$$

(60)

Here v [m/s] is the slip rate, $\mu_{0}$ [-] is the steady-state friction at $v = v_{0}$, $\vartheta$ [s] is the state parameter, $D_{c}$ [m] is the characteristic slip distance and a and b are non-dimensional material parameters representing the frictional evolution. If $\left( {a - b} \right) < 0$, velocity-weakening occurs eventually leading to unstable stick–slip possibly causing seismic rupture (seismogenic), while if $\left( {a - b} \right) > 0$, velocity-strengthening occurs resulting in rupture arresting (non-seismogenic). Determination of these dynamic friction parameters requires extensive laboratory testing on the specific rock material under in-situ stress, temperature and loading-rate conditions. Typically, highly seismogenic rock materials are brittle behaving carbonates (such as limestone and dolostone), while more ductile behaving clay-rich shales tend to be less seismogenic. If the material is seismogenic (or cannot be ruled out), the (maximum) moment magnitude needs to be assessed.

Based on the energy budget of earthquakes, the energy available to seismic wave generation can be written as: $E_{s} = \Delta \tau_{s} \overline{{\Delta u_{f} }} A_{f} /2$ (Udias et al., 2014, §1.5; Scholz, 2001, §4.2), where $\Delta \tau_{s}$ [MN/m²] is the seismic stress drop, $\overline{{\Delta u_{f} }}$ [m] is the average fault slip over $A_{f}$ [m²], the active slipping fault plane. From this general equation the seismic moment $M_{0}$ [MNm] can be determined (see also Kostrov (1974); Kanamori (1977)), which for induced seismicity in a pure dip slip situation can be further specified in terms of practical fault dimensions as (Stein and Wysession, 2009):

$$M_{0,\max } = G_{f} \overline{{\Delta u_{f} }} A_{f} = \frac{3\pi }{8}W_{f}^{2} L_{f} \Delta \tau_{s}$$

(61)

Here $G_{f}$ [MPa] is the harmonic mean of the shear moduli bordering the fault plane (Hettema 2020), $L_{f}$ [m] is the length of the fault (cross section in the horizontal plane) and $W_{f}$ [m] is the width of the fault plane (in the dip and slip direction). Based on the dynamic energy balance and earthquake scaling relations, Scholz (2001; §4.3) showed the applicability of this relationship for a range of aspect ratio’s ${{1 < L_{f} } \mathord{\left/ {\vphantom {{1 < L_{f} } {W_{f} < 10}}} \right. \kern-\nulldelimiterspace} {W_{f} < 10}}$. The maximum moment magnitude is practically obtained by maximising all parameters. The active slip length of the cooled fault plane can be determined from its nearest distance to the injector $d_{f - inj}$ [m] by: $L_{f} = 2\sqrt {r_{c}^{2} - d_{f - inj}^{2} }$. For faults with a throw the induced shear stress determined in Eq. (18) also applies to the full displaced fault area. For the (partially) sealed faults and boundary faults, Eq. (19) and Eq. (20) give the maximum induced shear stresses at the top, which can be used to determine the slip initiation. However, in these cases only a portion will sustain slip, depending on the induced shear stress profile. Hettema (2020, Fig. 8) also showed that the poro-elastic and differential-compaction-induced slip tendencies counteract each-other at certain locations. More accurate quantification of the contribution of the induced shear stress component requires integration of the displacement profiles on both sides of the fault plane.

Quantification of the moment magnitude requires either the determination of the average slip distance or of the seismic stress drop. The average vertical aquifer displacement has been determined in relation to its geometry by Hettema (2020, appendix A). Extending this relationship for application to geothermal cases requires both pressure and temperature changes to be taken into account, each with its own geometric function rc, giving for the displacement of the aquifer:

$$\overline{\Delta u} = \left[ {C_{m} \Delta p \cdot rc\left( {r_{eq} /D_{c} } \right) - \left( {\frac{1 + \nu }{{1 - \nu }}} \right)\beta \Delta T \cdot rc\left( {r_{c} /D_{c} } \right)} \right]H$$

(62)

This relationship also forms the basis for differential compaction induced displacements $\overline{{\Delta u_{f} }}$ (see Hettema, 2020). Note that close to the injector $r_{c} < r_{eq}$ the pressure inflation effect counteracts the cooling-induced contraction while further away $r_{c} > r_{eq}$, the aquifer only contracts due to cooling. This methodology will result in the maximum possible seismic stress drop, since the entire differential displacement is assumed to relax during unloading. In case proper strain-controlled laboratory experiments (such as presented in Fig. 15) are carried out and interpreted with confidence, the stress drop is controlled by loss of cohesion and friction. However, there are several reasons this measured stress drop cannot be used directly: 1) These tri-axial tests determine failure and post slip under constant confinement, an unrealistic boundary condition for earthquakes, 2) the laboratory loading rates are very high and 3) the post-failure unloading is controlled by the rock- and loading-frame stiffness. Also, the irreversible post-failure loss of cohesion will cause entropy increase, not available to the strain energy to generate seismic waves. This is also recognised by Wassing et al. (2016) showing that, based on a simplified constitutive law for slip-dependent frictional weakening by applying the critical slip distance D_c, the post-breakdown stress drop starts after the peak stress has been reduced to a lower stress value. By making additional assumptions on the seismic stress drop depending only on slip weakening and the normal effective stress remaining constant during slip, the seismic stress drop can be estimated by:

$$\Delta \tau_{s} = \left( {\mu_{p} - \mu_{r} } \right)\left( {\sigma_{n} - p} \right)$$

(63)

Here the subscript p stands for primary and r for residual. Note that this stress drop will be further reduced if the unloading is not purely brittle but displays non-elastic (ductile or creep) behaviour. The normal effective stress on the fault plane can be determined by Eq. (3). Similarly, in case the empirical parameters of Barton’s mobilized friction model are determined the stress drop can be estimated by applying Barton’s model (Eq. (57)), applying $\mu_{p} = \mu_{mob}$. However, since the mobilised friction model describes the combined effects of cohesion loss (through the JRC degrading) and friction loss, this could seriously overestimate the seismic stress drop. In case rate-and-state friction laboratory experiments have been performed, Den Hartog and Spiers (2014) and Chen and Spiers (2016) demonstrate how microphysical models can be used to determine the dynamic friction parameters in Eq. (60) for porous, granular fault gauges. Considering steady-state, the seismic stress drop can be estimated by (Scholz (2002, §5.2.3)):

$$\Delta \tau_{ss} = \left( {a - b} \right)\ln \left( {\frac{{v_{cs} }}{{v_{0} }}} \right)\left( {\sigma_{n} - p} \right)$$

(64)

Here ${v}_{cs}$ [m/s] is the coseismic velocity, which has a significant portion of the shear wave velocity ${v}_{s}$ [m/s]. Hunfeld (2020) reports stress drops in the range of 0 to 5 MPa based on laboratory experiments on Groningen reservoir Slochteren sandstone and Basal Zechstein gauges. Note that the choice of the model, besides data availability, could also depend on which specific fault characteristic is deemed most appropriate. Note also that application of the models presented above assume the stress drop to be complete and occurring under constant normal effective stress, which are recognised to be huge assumptions but deemed necessary to determine the maximum stress drop. The advantage of these relatively simple Coulomb material based stress drop models is that it neither requires numerical modelling to determine the fault slip nor the shear modulus. Finally, the seismic moment $M_{0}$ can be converted to the seismic magnitude by applying Hanks & Kanamori (1979): $M_{w} = \frac{2}{3}\left[ {\log M_{0} } \right] - 6.07$.

4 Summary, conclusions and recommendations

The author presents a comprehensive analytical workflow to enable the determination of the seismic hazard of a geothermal doublet system operated on a volume balance in a porous and permeable aquifer up-front. There are many assumptions made as indicated in the text. The passive basin assumption allows interpretation of all fault azimuths, but in any case the results presented here are based on the major Mohr circle. Although common practise for conservative safety analyses, it does not allow ruling out potential safe fault orientations that require a full three-dimensional Mohr–Coulomb analysis. It is recommended to perform this initial assessment early in the project evaluation process, such that the decision to collect the necessary additional data can be planned. Data collection might also be more affordable early-on in the project and the early period assessment could show the value of data collection in terms of uncertainly reduction. The fault re-activation hazard has been quantified in terms of the shear mobilization ratio MR, which depends on the initial stress, the stress changes due to cooling and pressure changes as well as the fault mechanical properties cohesion and friction. In case of the presence of faults with a substantial throw, (partially) sealing faults or boundary faults, a more elaborate analysis is required to determine the induced shear stress, as elaborated by Hettema (2020), requiring more location-specific input such as the fault throw, dip and also aquifer geometric parameters as well as pressure/temperature differences in case of (partially) sealing faults. Also suggestions are made for simplification of input parameters to maximise the slip hazard. To determine the initial stress state and the influence of tectonics, two stress models have been combined and the possible consequences for the tectonic stress has been demonstrated. The preferred input for calibration of the material properties is laboratory-testing on core material, but also well-log based methods are presented, requiring static-to-dynamic conversions, especially important for the permeable/porous aquifer. The injection-induced stress changes have been derived in relation to the injected temperature, the injection rate and the cumulative injection volume. The elliptical extension of the cooling front is determined by applying a mass balance to the first law of thermodynamics as a rate equation. Important input are the fault mechanical parameters, which have been estimated from laboratory experiments. For field applications and upscaling, the empirical, non-linear mobilized friction model developed by Barton (1976) has proven useful, which includes the influence of surface roughness and variable rock strength. From the shear mobilisation ratio MR, the probability that mechanical re-activation along a fault plane of weakness can occur has been determined. The four main uncertain input parameters are the fault cohesion and friction, the thermal stress parameter and the initial minimum stress. To reduce the uncertainty in the fault parameters data collection and performance of core-laboratory experiments is recommended, as well as detailed fault geometrical seismic characterisation based on computer-aided fault identification and extraction tools, e.g., ant-tracking methodology. Laboratory experiments on core plugs are also recommended to determine the (unloading) Young’s modulus, Poisson’s ratio and the thermal expansion coefficient under proper stress and temperature conditions. Extended leak-off or mini-fracture testing is recommended to estimate the initial minimum stress in the overburden or aquifer, respectively. In the proposed workflow first the early period assessment is performed, defined by the flooding front reaching halfway the injector/producer distance. A criterion for thermal fracturing is given which if exceeded will cause a thermal fracture to grow in the direction of the maximum horizontal stress direction, as worked out be Perkins and Gonzales (1985) and demonstrated by Koning (1985). It is shown to be unlikely to initiate such a fracture near the pressurized geothermal injector due to “back-stress” effects. The workflow is demonstrated by a case example assessment of the probabilities for fault reactivation by assigning probabilities to each of the main four input parameters for matrix injection. The probabilistic hazard assessment is presented using two important output plots: The shear mobilization ratio versus its probability and the cumulative probability distribution, characterised by four important parameters: The expected value E(MR), the probability of exceeding unity $P\left( {MR > 1} \right) = 1 - P\left( 1 \right)$ and the exceeding probabilities: $1 - P_{95\% }$ and $1 - P_{99\% }$. The second moment of analysis is at thermal break-through. The calculations are similar to the early period, except that during undisturbed matrix injection the elliptical extension of the cooled zone results in higher stress changes in the injector-producer direction and lower stress changes in the perpendicular direction. If the first necessary condition for seismicity is met, the exceedance of the shear mobilisation criterion, methods to assess the other two are suggested: the seismogeneity of the rock material and the maximum seismic moment. It is suggested that only frictional loss contributes to the seismic stress drop, since cohesion loss will only lead to heat loss. The article presents a general applicable workflow in a scientific and open manner, clearly demonstrating the assumptions and choices made such that the uncertainties can also be reported, allowing others to make final decisions based on metrics in line with local regulations and public acceptance.

Appendices

Appendix A

1.1 Doublet pressure change around injectors and producers

In this appendix we determine the pressure drawdown and the average pressure changes around the injector and producer doublet well pair in relation to the injection and production rate (Golan and Whitson 1996, §2.6). For semi steady-state flow in a homogeneous reservoir with constant thickness the radial pressure profile becomes (Dake 1978, §6.2):

$$p\left( r \right) = p_{wf} + \left[ {\frac{{qB_{w} \eta }}{{2\pi kh^{\prime}}}} \right]\left( {\ln \left( {\frac{r}{{r_{w} }}} \right) - \frac{{r^{2} }}{{2r_{e}^{2} }}} \right)$$

(65)

Here $p_{wf}$[MPa] is the flowing well pressure, q [m³/s] is the production flow rate which is negative for injection, $q$ [Pa*s = 0.001 cPoise] is the viscosity, k [m² = mDarcy/9.87*10^–16] is the permeability, $r_{w}$[m] is the (effective) wellbore radius and $h\prime = h\left( {{N \mathord{\left/ {\vphantom {N G}} \right. \kern-\nulldelimiterspace} G}} \right)$ is the flow effective reservoir thickness, where h [m] is the gross reservoir thickness and $N/G$ is the net to gross ratio. The time to reach pseudo steady-state flow can be found from a dimensionless diffusion time requirement, giving for radial flow (Golan and Whitson 1996, §2.7): $t_{ps} = 0.1{{\pi r_{e}^{2} } \mathord{\left/ {\vphantom {{\pi r_{e}^{2} } {C_{D} }}} \right. \kern-\nulldelimiterspace} {C_{D} }}$, with the consolidation coefficient $C_{D}$ [m²/s] defined in Eq. (21). According to this criterion, it takes about one day for this pressure profile to be established using our base-case the input from Table 3. $B_{w}$ [-] is the volume factor of the fluid that converts the reference flow rate measured at surface pump to that under downhole reservoir pressure and temperature conditions:

$$B_{w} \equiv \frac{{V\left( {p,T} \right)}}{{V\left( {p,T} \right)_{ref} }} = \frac{{\rho \left( {p,T} \right)_{ref} }}{{\rho \left( {p,T} \right)}} = 1 + \alpha_{w} \left( {T - T_{ref} } \right) - C_{w} \left( {p - p_{ref} } \right)$$

(66)

Here $\alpha_{w}$ [1/K] is the volumetric expansion coefficient of water. Note that upon injection the thermal volumetric expansion counteracts the pressure compression. Also, since both the expansion coefficient and the compressibility of gas-free water are very low ($\alpha_{w} \cong 0.00064$ [1/K] and $C_{w} \cong 0.00046$ [1/MPa], both at 80 °C, Weast 1978), these volume effects can be neglected inside the reservoir, giving $B_{w} = 1$. However, if the injection and production flow rates are measured at surface installations or at the electrical submersible pump these volume factors might become relevant. At $r = r_{e}$, $p\left( {r_{e} } \right) = p_{0}$ [MPa] and solution (65) gives a drawdown of:

$$p_{0} - p_{wf} = \left[ {\frac{{qB_{w} \eta }}{{2\pi kh^{\prime}}}} \right]\left( {\ln \left( {\frac{{r_{e} }}{{r_{w} }}} \right) - \frac{1}{2} + S} \right)$$

(67)

The flow rate is the independent variable and for the injector $q = - q_{i}$. There are several processes that can cause skin S [-] (Golan and Whitson 1996, §3.5): The completion type (Screen, Slotted liner, Gravel packing, Perforations), the partial completion flow, the well deviation and formation damage, caused either by wellbore plugging or by internal formation plugging or by chemical reactions. Perforation completion could have skin due to the crushed zone reduced perforation permeability. If the drainage area is non-radial due to flow boundaries there will be a drainage area skin factor (Golan and Whitson 1996, §2.6). Note that skin factors for injectors and producers can be different and that the temperature-dependent viscosity is also different. To determine the effect of the pressure changes around the wellbore on the stress, a volume-averaged pressure drawdown within the drainage distance is given by:

$$\overline{{p\left( {r_{e} } \right)}} - p_{wf} = \left[ {\frac{{qB_{w} \eta }}{{2\pi kh^{\prime}}}} \right]\left( {\ln \left( {\frac{{r_{e} }}{{r_{w} }}} \right) - \frac{3}{4} + S} \right)$$

(68)

For a doublet operating semi-steady-state on a volume balance with (downhole) inter-well distance D [m] we assume the drainage distance $r_{e} = D/2$ [m]. Subtracting solutions Eq. (68) from Eq. (67) gives for the volume-averaged reservoir pressure change within the drainage radius:

$$\overline{{\Delta p\left( {r_{e} } \right)}} = \overline{{p\left( {r_{e} } \right)}} - p_{0} = - \frac{1}{4}\left[ {\frac{{qB_{w} \eta }}{{2\pi kh^{\prime } }}} \right]$$

(69)

To determine the pressure-induced stress changes, either the full drainage volume is considered or the equivalent cylindrical distance $r_{p}$[m] is determined for the near-wellbore stresses. Considering the equivalent change in work within a certain volume pressurised:

$$\int_{{r_{w} }}^{{{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left( {p\left( r \right) - p_{0} } \right)dV = \overline{{\Delta p\left( {r_{e} } \right)}} \pi \left( \frac{D}{2} \right)^{2} h\varphi = \overline{{\Delta p\left( {r_{eq} } \right)}} \pi r_{eq}^{2} h\varphi }$$

(70)

For full drainage distance the averaged pressure change is given by Eq. (69), while for the near-wellbore stress changes the half drawdown pressure applies given by Eq. (67):

$$\overline{{\Delta p\left( {r_{eq} } \right)}} \equiv \frac{{\left( {p_{wf} - p_{0} } \right)}}{2} = - \frac{1}{2}\left[ {\frac{{qB_{w} \eta }}{2\pi kh ^\prime }} \right]\left( {\ln \left( {\frac{{r_{e} }}{{r_{w} }}} \right) - \frac{1}{2} + S} \right)$$

(71)

The equivalent cylindrical influence distance $r_{eq}$ is found after introducing Eqs. (67) and (69) to relationship Eq. (70), after re-working:

$$r_{eq} = \frac{D}{{4\sqrt {\ln \left( {\frac{D}{{2r_{w} }}} \right) - \frac{1}{2} + S} }}$$

(72)

To arrive at semi-steady state pressure-induced stress changes around the doublet wells, it is suggested to use half the drawdown pressure from Eq. (71) with a cylindrical influence zone defined by Eq. (72). During injection, initially there will be cylindrical symmetric flow around the injector and producer, but eventually a pseudo-steady-state elliptic flooded area between the injector and producer will arise. Koning (1985) also presents the elliptical pressure solutions for fractured injection. The total pressure difference between injector (with subscript i) and producer (with subscript p) under downhole conditions can be found by applying Eq. (67), using $\Delta p_{doublet} = p_{wfi} - p_{wfp}$. The resulting system performance index PI [Nm/s = J/s] becomes:

$$PI_{doublet} = \frac{q}{{\Delta p_{doublet} }} = \frac{2\pi kh^\prime }{{\left( {\eta_{i} \;\;B_{wi} + \eta_{p} \;\;B_{wp} } \right)\left[ {\ln \left( {\frac{D}{{2r_{w} }}} \right) - \frac{1}{2} + S} \right]}}$$

(73)

Note that for the doublet, both the water volume factor as well as the viscosity are weakly pressure- but strongly temperature-dependent. When applied to the downhole reservoir conditions, $B_{wi} \cong B_{wp} \cong 1$. Batzle and Wang (1992) present empirical polynomial relations to determine the brine bulk modulus, density and viscosity in relation to its pressure, temperature and salinity. For the brine viscosity they also present a polynomial relation related to its temperature (up to 250 °C) and its salinity, neglecting the pressure effect. Figure 16 shows the semi steady-state pressure profile for the base-case doublet using the input from Table 3. The figure also shows the draw-down pressures at the injector and producer, their volume-averaged pressure changes and the doublet pressure difference.

Fig. 16

The semi steady-state pressure profile for the base-case doublet

This solution is valid as long as the matrix injection sustains. However, the injection well can be hydraulically and/or thermally stimulated (fracturing) or the well path has crossed a natural fracture with length $l_{fr}$[m]. Then most near-wellbore skin factors are removed and the injectivity index increases by applying an effective wellbore radius up to half the fracture length, $r_{w} \to l_{fr} /2$ (Golan and Whitson 1996, §4.6), resulting in a major increase in the system PI (see Eq. 73). Note that this is however the maximum effect since infinite fracture conductivity is assumed. Real injectors will create fractures with a finite width causing a pressure decline from the fracture mouth (at the wellbore) to its tip and can in addition experience plugging. For hydraulic fracture stimulation at high injection rates this pressure decline is important but for thermal fracturing induced by water flooding it is not so since at low to intermediate rates it is mainly controlled by the thermal stress reduction induced by formation cooling. Both Perkins and Gonzales (1985) and Koning (1985) present analytical expressions for full elliptical pressure and temperature distributions surrounding fractured water injectors allowing determination of dynamic thermal fracture propagation during the water injection.

Table 3 Base case input parameters of an imaginary aquifer

Appendix B

1.1 Geometrical functions

Perkins and Gonzalez (1985) have also developed approximate explicit solutions for thermal fractured injection, leading to elliptical inclusion solutions with $e \equiv b/a \le 1$ where b [m] is the minor axis and a [m] the major axis. For the average internal thermal stress perpendicular to each of the axes, Perkins and Gonzalez (1985) found approximate explicit solutions:

$$G_{T, \min } \left( {\frac{h}{2b},e} \right) = \frac{e}{1 + e} + \frac{1}{1 + e}\Delta f_{1}$$

(74)

Here:

$$f_{1} = 1/\left[ {1 + 0.5\left( {1.45\left( \frac{h}{2b} \right)^{0.9} + 0.35\left( \frac{h}{2b} \right)^{2} } \right)\left( {1 + e^{0.774} } \right)} \right]$$

(75)

For the average internal thermal stress parallel to the major axis, Perkins and Gonzalez (1985) also found approximate explicit solutions:

$$G_{T,\max } \left( {\frac{h}{2b},e} \right) = \frac{1}{1 + e} + \frac{e}{1 + e}\Delta f_{2}$$

(76)

Here:

$$f_{2} = 1/\left[ {\left( {1 + 1.45\left( \frac{h}{2b} \right)^{0.9} + 0.35\left( \frac{h}{2b} \right)^{2} } \right)\left( {1 + \left( {1 - e} \right)^{1.36} } \right)} \right]$$

(77)

During early period matrix injection there will be cylindrical-symmetric temperature profiles. Now e = 1 and $a = b = r_{c}$, the cooling radius. Both solutions collapse to the cylindrical one (Perkins and Gonzalez 1984):

$$G_{T,r} \left( {\frac{h}{{2r_{c} }}} \right) = 0.5\left( {1 + \frac{1}{{1 + 1.45\left( {\frac{h}{{2r_{c} }}} \right)^{0.9} + 0.35\left( {\frac{h}{{2r_{c} }}} \right)^{2} }}} \right)$$

(78)

ThiNote that $G_{T,r} = 0.5 \to 1$ increasing as injection proceeds. The normalized interior thermo-elastic stresses are plotted in Fig. 17. Perkins and Gonzalez (1984) also showed that the theory applies to pressure-induced stress changes, applying $G_{p,r} \left( {{h \mathord{\left/ {\vphantom {h {2r_{eq} }}} \right. \kern-\nulldelimiterspace} {2r_{eq} }}} \right)$ to Eq. (78), where $r_{eq}$ [m] is the equivalent radius of the volume averaged pressure change given by Eq. (71). The vertical stress path is given by $\gamma_{v} \equiv {{\Delta \sigma_{v} } \mathord{\left/ {\vphantom {{\Delta \sigma_{v} } {\overline{\Delta p} }}} \right. \kern-\nulldelimiterspace} {\overline{\Delta p} }} = \gamma_{u} G_{pv}$. As shown by Hettema et al. (2012) and Hettema (2020), the average stress path can be written as: $\overline{\gamma } = 2\gamma_{u} /3$, which is a material parameter independent of the reservoir geometry. This relationship allows the vertical stress path to be written as:

$$\gamma_{v} = 2\gamma_{u} - \left( {\gamma_{H} + \gamma_{h} } \right) = 2\gamma_{u} \left( {1 - \overline{{G_{p} }} } \right)$$

(79)

Fig. 17

Normalized average internal thermal stress change from equations (74–78)

s gives $G_{pv} = 2\left( {1 - \overline{{G_{p} }} } \right)$. A similar reasoning applies to the vertical thermal stress changes giving: $G_{Tv} = 2\left( {1 - \overline{{G_{T} }} } \right)$. Note that in case of ellipticity, $\overline{{G_{p} }} \cong G_{p,r}$ and $\overline{{G_{T} }} \cong G_{T,r}$.

Perkins and Gonzalez (1984, app. A & B) also present solutions for thermal and pressure-induced stress changes externally to the cooled/pressurized zone, showing that radially the stress changes quickly diminish:

$$\sigma_{h} \left( {r > r_{c} } \right) - \sigma_{h,0} = \left( {\overline{{\sigma_{h} \left( {r < r_{c} } \right) - \sigma_{h,0} }} } \right)\left( {\frac{{r_{c} }}{r}} \right)^{2}$$

(80)