The distribution of the tax burden and the income distribution: theory and empirical evidence

Abstract

We compare the tax burden distribution across incomes and the income share distribution, based on a stochastic dominance approach. We find conditions to assess the progressivity of different sources of taxes, given knowledge of the income share elasticities, which measure the relative marginal change in the income share accruing to each class of income, associated to a marginal increase in income. We first consider a simple setting with only indirect taxes and then extend it to savings and direct taxation. The progressivity of a given set of taxes depends on the correlation between the relative incidence of the different sources of taxation and the income elasticity of household net expenditure. We use this approach to test empirically for the progressivity of the fiscal system.

1 Introduction

The distributional impact of taxation on individual and household choices is an important issue for policy makers, which has become particularly prominent, given the recent trends of growing income inequality. Overall, the focus of the literature has been mainly on the distributional features of direct taxation (e.g., Seidl et al. 2013), while a much weaker emphasis has been laid on the theoretical and empirical assessment of the redistributive effects of other sources of taxation (for indirect taxation see e.g. Warren 2008). A general analysis on the distributional features of the taxation system as a whole is quite often lacking, as indeed the prevailing perspective is usually that of a tax-by-tax piecemeal approach.

On the one hand, the redistributive effects of direct taxation have been investigated using mainly local and global indices instead of dominance relationships among distributions.¹ On the other hand, in the case of indirect taxation there is not as yet a universal agreement on the most appropriate measure to assess its distributional effects, as several notions of (and measures for) income have been put forth for this purpose.² As is well known, the classical controversy is between adopting a regressive income-based vs a progressive expenditure-based approach.³ More recently, however, it has been shown that the regressivity arising from cross-sectional works based on current income is significantly reduced when a panel data analysis is performed on a lifetime perspective.⁴ As far as the payroll system is concerned, there is some debate on whether contributory pensions should be treated as a source of direct taxation, or just as savings providing deferred income once retired (Inchauste and Lustig 2017).

Although this piecemeal approach has been historically dominant, there has actually been recently a spate of works on the overall redistributive effect of the whole taxation system, including transfers (e.g. Bucheli et al. 2014; Jaramillo 2014; Lustig 2018, and all references cited therein). A notable analysis is Lambert (2001, ch. 11) who provides a distribution-based progressivity assessment of the ‘net fiscal system’ (which does not include indirect taxation). However, most of the works use global distributional measures,⁵ which—though they do provide synthetic information to compare different tax systems with different income distributions—typically suffer from of a series of drawbacks, due mainly to the aggregation procedure being in general sensitive to the weighting method used (e.g. Suits 1977). A recent overview of the topic is provided by Inchauste and Lustig (2017).

In this paper we do not use a global index approach, but instead we assess the distributional profile of the tax system on the basis of a first order stochastic dominance ordering of the tax burden distribution over the income share distribution. Our aim is to analyse the conditions for the progressivity of different types of taxes (e.g. tax on savings, income or on consumption) given knowledge of the income share elasticity (Esteban 1986). Ranking distributions using this approach leads to a general formula, based on income/expenditure elasticity and the incidence of the different sources of taxation, which allows us to identify whether or not a given set of taxes is progressive. The notion of income share elasticity lends itself quite naturally to analyzing progressivity issues: once the distributions of income and tax shares are both described in elasticity terms, assessing progressivity boils down to a convenient elasticity comparisons leading to stochastic dominance ranking.⁶ We use this approach to test for the progressivity of different taxes in the Italian system. We test our conditions using the Kolmogorov–Smirnov test for first order stochastic dominance on the Italian tax system. More generally, this approach may in principle help the tax authorities select the set of taxable goods to achieve a specific distributional profile of the taxation system when multiple taxes have to be chosen—e.g. by providing a measure of the progressivity trade-off involved in taxing savings.

We lay out the basic setting in the next Sect. 2, consider indirect taxation and savings in Sect. 3, and finally add direct taxation in Sect. 4 to model the distributional features of the overall taxation system for households. We provide an empirical assessment in Sect. 5 to test our main findings, and gather our concluding remarks in Sect. 6.

2 The basic setting

There are n commodities, such that $q_{i}\left( p,y\right)$ is the Marshallian demand for good $i=1,\ldots ,n$, where y is individual income and p the price vector. Income $y\in \mathcal {Y}$ is continuously distributed over $\left[ y_{\min },y_{\max }\right]$ $=\mathcal {Y}$, with $F:{\mathcal {Y}} \rightarrow \left[ 0,1\right]$ the associated distribution. We define the income density by $f(y)=\frac{dF}{dy}$, so that $\mu =\int _{\mathcal {Y} }yf(y)dy>0$ is aggregate (mean) income. Market demand for commodity i is accordingly

$$\begin{aligned} Q_{i}(p)=\int _{\mathcal {Y}}q_{i}(p,y)f(y)dy \end{aligned}$$

(1)

We also define for later reference the income share density h(y), such that the associated distribution $H:{\mathcal {Y}}\rightarrow \left[ 0,1\right]$ is

$$\begin{aligned} H\left( y\right) =\tfrac{1}{\mu }\int _{y_{\min }}^{y}xf(x)dx \end{aligned}$$

(2)

so that h gives the weight of the overall income accruing to income class y over total (mean) income $\mu$.

The overall tax paid by an individual whose income is y will be $\tau \left( \cdot ,y\right)$, so that overall government revenue will be

$$\begin{aligned} R=\int _{\mathcal {Y}}\tau \left( \cdot ,y\right) f\left( y\right) dy \end{aligned}$$

(3)

At this stage we do not specify the actual shape of $\tau$, apart from its link with the consumer’s income y. For example, if one considers indirect taxation only, one has $\tau \left( \cdot ,y\right) =\sum _{i}t_{i}q_{i}(p,y)$, $t=\left( t_{1}, \ldots ,t_{n}\right)$ the vector of tax rates; while if direct taxation is also included, one would have $\tau \left( \cdot ,y\right) =\sum _{i}t_{i}q^{i}(p,y)+\tau ^{d}(y)$, $\tau ^{d}$ being the income tax schedule. Whatever the actual content of $\tau$, there follows that the tax burden is distributed across income classes according to the density

$$\begin{aligned} g\left( y,\cdot \right) =\tfrac{1}{R}\tau \left( \cdot ,y\right) f\left( y\right) \end{aligned}$$

(4)

which gives the share of overall government revenue borne by those individuals whose income is y; the associated cumulative distribution will be $G\left( y,\cdot \right) =\int\nolimits_{y_{\min }}^{y}g\left( z,\cdot \right) dz$.

2.1 Income share elasticity and liability progression

One natural question is that of the relationship between the distributions F and H, and the distribution of the tax burden G. In this respect, we provide a new approach for evaluating the distributional impact of taxation, which links the stochastic ranking between the tax burden distribution and the income (share) distribution with the liability progression index. To do so, we use the elasticity framework for income distributions suggested by Esteban (1986). For any differentiable density $\phi \left( y\right)$ one can define the “income share elasticity” as a function $\pi ^{\phi }\left( y\right)$ such that

$$\begin{aligned} \pi ^{\phi }(y)=\lim _{h\rightarrow 0}\dfrac{d\log \left( \tfrac{1}{\mu }\int _{y}^{y+h}x\phi (x)dx\right) }{d\log y}=1+\frac{y}{\phi (y)}\frac{\partial \phi }{\partial y} \end{aligned}$$

(5)

which stands in a one-to-one relationship with the underlying $\phi$. The function $\pi$ is an elasticity giving the relative marginal change in the share of income accruing to class y, brought about by a marginal increase in y.

Using this definition, it easily established that

$$\begin{aligned} \pi ^{g}\left( y,\cdot \right)&=\pi ^{f}\left( y\right) +\ell (\cdot ,y)\nonumber \\&=\pi ^{h}\left( y\right) +\ell (\cdot ,y)-1 \end{aligned}$$

(6)

where

$$\begin{aligned} \ell (\cdot ,y)=\frac{\partial \tau }{\partial y}\frac{y}{\tau }\text { } \end{aligned}$$

(7)

is the income elasticity of the individual tax burden. The latter is the liability index standardly applied to direct taxation, which can in fact also cover the case of indirect taxation. If $\ell (\cdot ,y)>1$ taxation is “structurally” progressive, in the sense that it is characterized by a more than proportional rise in the tax revenue from individuals whose income is y, relative to the marginal increase of y (by the same token, $\ell <1$ identifies a regressive tax structure): $\ell$ gives information on how the individual tax burden reacts to changes in income.

This being said, the following result will be crucial for our analysis:

Background Result: Given any pair of distributions $F_{j}:{\mathcal {Y}}\rightarrow \left[ 0,1\right]$ with Esteban elasticities $\pi _{j}(y)$, $j=1,2$, if $\pi _{2}(y)\ge \pi _{1}(y)$ for all $y\in \mathcal {Y}$, then $F_{2}$ stochastically dominates $F_{1}$ in the first order sense, i.e. $F_{2}\le F_{1}$ for all $y\in \mathcal {Y}$ with the inequality holding strictly for some $y\in \mathcal {Y}$.⁷

Proof

(Benassi and Chirco 2006, p. 513). $\square$

The reason that this result is useful in our perspective is that it draws a link between comparing distributions and comparing the underlying elasticities,⁸ within a framework where one such elasticity is an individual measure of progressivity. One immediate implication of this is

Proposition 1

      (a) If $\ell (\cdot ,y)\ge 0$ for all $y\in \mathcal {Y}$, the burden distribution G stochastically dominates the income distribution F in the first order sense, i.e. $G\le F$ for all $y\in \mathcal {Y}$ (b) if $\ell (\cdot ,y)\ge 1$ for all $y\in \mathcal {Y}$, the burden distribution G stochastically dominates the income share distribution H in the first order sense, i.e. $G\le H$ for all $y\in \mathcal {Y}$ .

Proof

Both (a) and (b) follow from (6) and the Background Result above. $\square$

According to Proposition 1(a), the density of the tax burden to be skewed to the right with respect to that of income, cutting the latter from below: the tax burden distribution dominates the income distribution whenever individual taxation rises with individual income, which of course says nothing about progressivity. The latter is captured by Proposition 1(b), which compares the tax burden distribution with the income share distribution. Relying on the simple fact that $\pi ^{h}\left( y\right) =\pi ^{f}\left( y\right) +1$, if $\ell (\cdot ,y)\ge 1$ for all $y\in \mathcal {Y}$, the burden distribution G stochastically dominates the income share distribution H in the first order sense (and viceversa for $\ell (\cdot ,y)\le 1$ for all $y\in \mathcal {Y}$). This is relevant in our perspective, as we can define progressivity of the tax system in term of the dominance relationship between these distributions:

Definition 1

The tax system is progressive if G stochastically dominates H in the first order sense.

This seems to us a natural definition of progressivity: if the distribution of taxation shares by income dominates the distribution of income shares, for any income level y the overall taxation share borne by consumers whose income is below y is less than the overall income share accruing to those consumers.

Our Background Result establishes an elasticity-based general connection between distributions. In the next sections we are going to use it to compare H and G, where the latter includes specific taxation regimes. We start our analysis by specifying the function $\tau$ in terms of indirect taxation; we then include also savings and the case where savings are taxed.

3 The distribution of the tax burden: indirect taxation and savings

We start by taking up the case where $\tau \left( \cdot ,y\right) =\tau \left( t,y\right) =\sum _{i}t_{i}q_{i}(p,y)$, i.e. only indirect taxation is in place. Accordingly, p will denote the vector of gross prices, i.e. $p=\widetilde{p}+t$, with $\widetilde{p}=\left( \widetilde{p}_{1} ,\ldots ,\widetilde{p}_{n}\right)$ the given vector of net prices, and $t=\left( t_{1},\ldots ,t_{n}\right)$ the given vector of commodity tax rates. Definition (7) then becomes

$$\begin{aligned} \ell (t,y)=\frac{\partial \tau }{\partial y}\frac{y}{\tau }=\frac{y\sum _{i} t_{i}\frac{\partial q_{i}}{\partial y}}{\sum _{i}t_{i}q_{i}} \end{aligned}$$

In principle, this definition allows a direct comparison between the implied burden distribution G and the income share distribution H. Such an exercise would deliver that $\ell >1$ (and hence the vector t of indirect taxes is progressive according to the above Definition) if the consumption of luxuries weighs enough in the consumer’s budget. Given a set of tax rates t, the way consumption tax revenue will react to changes in income depends on the convexity/concavity of Engel curves and the way they are aggregated in the individual tax burden $\tau$.⁹

However, we prefer to assess the distributional features of indirect taxation by bringing in explicitly the role of savings from the outset. One of the main arguments for the regressivity of indirect taxation is based on the observation of decreasing consumption shares with income, which would imply that the income elasticity of saving is larger than one. We use a very simple framework and suppose that, given some intertemporal preferences, current savings for an individual with income y are given by $s(p,y)=y-\sum _{i} p_{i}q_{i}\left( p,y\right) \ge 0$, so that consumption expenditure $\sum _{i}p_{i}q_{i}\left( p,y\right) =c(p,y)\le y$ gives income net of savings.¹⁰ There follows that the distribution of consumption expenditure over total consumption is given by:

$$\begin{aligned} F^{c}\left( y\right) =\tfrac{1}{\mu ^{c}}\int _{y_{\min }}^{y}c(p,z)f(z)dz \end{aligned}$$

(8)

where $\mu ^{c}\left( p\right) =\int\nolimits_{\mathcal {Y}}c(p,y)f(y)dz=\mu -\int\nolimits_{\mathcal {Y}}s(p,y)f(y)dy$ is aggregate consumption. It is straightforward to obtain the corresponding Esteban elasticity $\pi ^{c}$, such that

$$\begin{aligned} \pi ^{c}\left( y;t\right) =\pi ^{f}\left( y\right) +\frac{1-\overline{s}\varepsilon ^{s}}{1-\overline{s}} \end{aligned}$$

(9)

where $\overline{s}(p,y)=s(p,y)/y$ is average saving at a given $y\in Y$, while $\varepsilon ^{s}=\varepsilon ^{s}\left( p,y\right)$ is the income elasticity of s at a given $y\in Y$. On the basis of the Background Result we have:

Proposition 2

(a) If $\partial s/\partial y\le 1$ for all $y\in \mathcal {Y}$, the distribution of expenditure $F^{c}$stochastically dominates the income distribution F in the first order sense, i.e. $F^{c}\le F$ for all $y\in \mathcal {Y}$ (b) If $\varepsilon ^{s}\left( p,y\right) \le 1$ for all $y\in \mathcal {Y}$, the distribution of expenditure $F^{c}$ stochastically dominates the income share distribution H in the first order sense, i.e. $F^{c}\le H$ for all $y\in \mathcal {Y}$.

Proof

Both results follow from the above Background Result, and by observing that (a) given (9), $\partial s/\partial y\le 1$ for all $y\in \mathcal {Y}$ implies $\pi ^{c}\left( y,t\right) -\pi ^{f}\left( y\right) \ge 0$ for all $y\in \mathcal {Y}$; (b) since $\pi ^{c}\left( y,t\right) -\pi ^{h}\left( y\right) =\frac{\overline{s}\left( 1-\varepsilon ^{s}\right) }{1-\overline{s}}$, $\varepsilon ^{s}\le 1$ implies $\pi ^{c}\left( y,t\right) -\pi ^{h}\left( y\right) \ge 0$ for all $y\in \mathcal {Y}$. $\square$

An implication of Proposition 2 is that the income elasticity of savings bears on the dominance relationship between $F^{c}$ and H. An income elasticity of savings less than one means that the distribution of consumption shares dominates that of income shares. This gives a perspective on the issue of assessing the progressivity of indirect taxation with respect to income or expenditure: in the former case the relevant comparison is between the distributions G and H; in the latter case, the relevant comparison is between G and $F^{c}$. Using again the Background Result, these comparisons amount to

$$\begin{aligned} \pi ^{g}\left( y,t\right) -\pi ^{h}\left( y\right)&=\ell (t,y)-1 \end{aligned}$$

(10)

$$\begin{aligned} \pi ^{g}\left( y,t\right) -\pi ^{c}\left( y\right)&=\ell (t,y)-\left( 1+\frac{\overline{s}\left( 1-\varepsilon ^{s}\right) }{1-\overline{s} }\right) \end{aligned}$$

(11)

Clearly, Proposition 2 implies that as $\varepsilon ^{s}\lesseqgtr 1$, $\pi ^{g}\left( y,t\right) -\pi ^{h}\left( y\right) \gtreqless \pi ^{g}\left( y,t\right) -\pi ^{c}\left( y\right)$. Roughly speaking, this would suggest that if e.g. $\varepsilon ^{s}>1$, the dominance of the taxation distribution over the distribution of income shares would be “weaker” than that over the distribution of consumptions shares (intuitively, if $G<H<F^{c}$ the “distance” between G and H is lower than that between G and $F^{c}$), which in turn would point to progressivity being stronger when assessed with respect to expenditure rather than income.

That this is so can be seen explicitly by defining the liability progression index in terms of consumption expenditure

$$\begin{aligned} \ell _{c}\left( t,y\right) =\frac{\partial \tau }{\partial c}\frac{c}{\tau } \end{aligned}$$

such that

$$\begin{aligned} \ell =\left( \frac{\overline{s}\left( 1-\varepsilon ^{s}\right) }{1-\overline{s}}+1\right) \ell _{c} \end{aligned}$$

to the effect that $\varepsilon ^{s}>1$ implies $\ell <\ell _{c}$.¹¹ Indeed, the connection between the ranking of distributions and the liability indices is apparent when one recasts (11) as

$$\begin{aligned} \pi ^{g}\left( y,t\right) -\pi ^{c}\left( y\right) =\ell (t,y)\left( 1-\frac{1}{\ell _{c}(t,y)}\right) \end{aligned}$$

(12)

so that the distribution of the tax burden will dominate that of expenditure if $\ell _{c}\left( t,y\right) \ge 1$ for all $y\in \mathcal {Y}$.

3.1 Taxing savings

Having set the basic framework for indirect taxation in the presence of savings, we now suppose that the latter also are taxed, at a rate $t_{s}>0$, such that an individual whose income is y will now face a tax system $\mathbf {t}=\left( t,t^{s}\right)$ and pay a saving tax $\tau ^{s}\left( \mathbf {t},y\right) =t^{s}s(p,y)$. Government revenue from this tax will be $R^{s}=\int\nolimits_{\mathcal {Y}}t^{s}s(p,y)f\left( y\right) dy$, where we recall that $s(p,y)=y-\sum _{i}p_{i}q_{i}\left( p,y\right)$ and $p=\widetilde{p}+t$ includes the commodity tax rates: clearly, the presence of a saving tax will affect consumption via its effect on the consumers’ intertemporal choices. The government will then be raising a revenue $R=R^{s}+\sum _{i} t_{i}Q_{i}\left( p\right)$. Overall, faced with a tax array $\mathbf {t}$, the individual with income y will pay taxes

$$\begin{aligned} \tau \left( \mathbf {t},y\right)&=\tau ^{s}\left( \mathbf {t},y\right) +\tau ^{c}\left( \mathbf {t},y\right) \nonumber \\&=t^{s}s(p,y)+\sum _{i}t_{i}q_{i}(p,y) \end{aligned}$$

(13)

while the distribution of the overall burden across income classes will have a density

$$\begin{aligned} \widehat{g}(y,\mathbf {t})=\tfrac{1}{R}\left[ \tau ^{s}\left( \mathbf {t} ,y\right) +\tau ^{c}\left( \mathbf {t},y\right) \right] f\left( y\right) \end{aligned}$$

the Esteban elasticity of which can be written as

$$\begin{aligned} \pi ^{\widehat{g}}\left( y,\mathbf {t}\right) =\pi ^{h}\left( y\right) +\ell \left( \mathbf {t},y\right) -1 \end{aligned}$$

(14)

where now $\ell \left( \mathbf {t},y\right) =$ $\alpha _{c}\ell ^{c}\left( \mathbf {t},y\right) +\alpha _{s}\ell ^{s}\left( \mathbf {t},y\right)$ with $\alpha _{k}=\tau ^{k}/\left( \tau ^{s}+\tau ^{c}\right)$, and liability progression $\ell ^{k}$ is defined as the income elasticity of $\tau ^{k}$, $k=c,s$. Indeed, the overall degree of progressivity is given by a weighted average of the degrees of progressivity of the taxes on consumption and savings.

Definition (14) and our Background Result clearly imply that the taxation structure $\mathbf {t}$ will be progressive if $\ell \left( \mathbf {t},y\right) >1$; in particular, writing out (13) as

$$\begin{aligned} \tau ^{s}\left( \mathbf {t},y\right) +\tau ^{c}\left( \mathbf {t},y\right) =t^{s}y+\sum _{i}\left( t_{i}-t^{s}p_{i}\right) q_{i}(p,y)=\tau (\mathbf {t},y) \end{aligned}$$

(15)

allows to enquire about the conditions for progressivity in terms of the relationship between consumption and savings taxation. Since in Sect. 5 the empirical part will be based on ad valorem indirect taxation, and we have direct evidence on net expenditure, we reformulate (15) by bringing out net prices explicitly, i.e. using $p_{i}=(1+t_{i}^{\prime })\widetilde{p}_{i}$, such that $t_{i}=t_{i}^{\prime }\widetilde{p}_{i}$. Thus (15) can be cast as

$$\begin{aligned} \tau (\mathbf {t},y)=t^{s}y+\sum _{i}\widehat{t}_{i}e_{i}(p,y) \end{aligned}$$

(16)

where $\widehat{t}_{i}=t_{i}^{\prime }-t^{s}\left( 1+t_{i}^{\prime }\right)$ is the “effective” consumption tax rate and $e_{i}=\widetilde{p}_{i} q_{i}(p,y)$ is net expenditure for commodity i. This allows to assess the progressivity of the overall burden in the following terms:

Proposition 3

Let $\varepsilon _{i}^{e} =\frac{\partial e_{i}}{\partial y}\frac{y}{e_{i}}$ denote the income elasticity of net expenditure for commodity i: the tax system $\mathbf {t}$ is progressive, i.e. $G\le H$ for all $y\in \mathcal {Y}$, if $\sum _{i}\widehat{t}_{i}e_{i}\left( \varepsilon _{i}^{e}-1\right) \ge 0$ for all $y\in \mathcal {Y}$.

Proof

It follows from (16) and the Background Result, since the overall liability progression index is given by

$$\begin{aligned} \ell (\mathbf {t},y)=\frac{\partial \tau }{\partial y}\frac{y}{\tau }=\frac{t^{s}y+\sum _{i}\widehat{t}_{i}\frac{\partial e_{i}}{\partial y}y}{t^{s} y+\sum _{i}\widehat{t}_{i}e_{i}(p,y)} \end{aligned}$$

such that $\ell (\mathbf {t},y)\lesseqgtr 1$ according as $\sum _{i}\widehat{t}_{i}\frac{\partial e_{i}}{\partial y}y\lesseqgtr \sum _{i}\widehat{t} _{i}e_{i}(p,y)$. $\square$

This points to the fact that the overall progressivity of the tax system (and hence the extent to which the distribution of the tax burden dominates that of the income shares) is given by the correlation between the relative incidence of saving taxation on indirect taxation (as summarized by $\widehat{t}_{i}$) and the income elasticity of household expenditure.

As a final remark to this section, one may observe that, though this paper focuses on comparing distributions, the condition for progressivity/regressivity can be easily extended to define an aggregate liability index

$$\begin{aligned} L\left( \mathbf {t}\right) = {\displaystyle \int _{\mathcal {Y}}} \ell (y,\mathbf {t})\widehat{g}\left( y,\mathbf {t}\right) dy \end{aligned}$$

(17)

such that if $L\left( \mathbf {t}\right) >1$ the “representative taxpayer” will face a progressive tax schedule.¹² It should be stressed that this aggregate index weighs individuals according to their share of tax payment by income classes. This we read as an aggregation procedure simply based on observed variables, which does not imply any social welfare function or ethical judgment. No optimality or normative considerations are involved in our framework, since we rely on a “positive” approach. When applied to our case, this boils down to

$$\begin{aligned} L(\mathbf {t})>1\text { if }t^{s}<\frac{ {\displaystyle \int _{\mathcal {Y}}} \sum _{i}t_{i}^{\prime }\left( \varepsilon _{i}^{e}-1\right) e_{i}f(y)dy}{ {\displaystyle \int _{\mathcal {Y}}} \sum _{i}\left( 1+t_{i}^{\prime }\right) \left( \varepsilon _{i}^{e}-1\right) e_{i}f(y)dy} \end{aligned}$$

The tractability of this formula may make it appealing for empirical applications. To fix ideas, suppose commodity taxation is uniform, $t_{i}^{\prime }=t^{\prime }$ for all i: then progressivity would follow from $t^{s}<t^{\prime }/\left( 1+t^{\prime }\right)$. By the same token, a saving tax rate high enough may make for a regressive system $\mathbf {t}$ for a given uniform tax rate $t^{\prime }$.

4 Direct taxation

The framework presented so far can easily be extended to cover the case where income taxation is also included. To do so, let $\tau ^{d}\left( y\right)$ be the direct component of taxes: the overall tax burden for an individual with income y is now given by

$$\begin{aligned} \tau \left( \mathbf {t}^{\prime },y\right) =t^{s}y+\sum _{i}\widehat{t}_{i} e_{i}(p,y)+\tau ^{d}\left( y\right) \end{aligned}$$

(18)

amounting to taxing expenditure on commodity i at a rate $\widehat{t}_{i}$, and income with a tax schedule $t^{s}y+\tau ^{d}\left( y\right)$. The distribution of the overall burden across income classes will now be $\widetilde{g}(y,\mathbf {t}^{\prime })=\tfrac{1}{R}\tau \left( \mathbf {t} ^{\prime },y\right) f\left( y\right)$, where revenue is now defined as $R=R^{d}+R^{e}+t^{s}\mu = {\displaystyle \int _{\mathcal {Y}}} \tau \left( \mathbf {t}^{\prime },y\right) f\left( y\right) dy$.¹³ The related Esteban elasticity is

$$\begin{aligned} \pi ^{\widetilde{g}}\left( y,\mathbf {t}^{\prime }\right) =\pi ^{f}\left( y\right) +\ell (\mathbf {t}^{\prime },y) \end{aligned}$$

(19)

where now $\ell (\mathbf {t}^{\prime },y)=$ $\alpha _{c}\ell ^{c}(\mathbf {t} ^{\prime },y)+\alpha _{s}\ell ^{s}(\mathbf {t}^{\prime },y)+\alpha _{d}\ell ^{d}(y)$ with $\alpha _{k}=\tau ^{k}/\tau$, where $k=c,s,d$; liability progression $\ell ^{k}$ is defined again as income elasticity – in particular, $\ell ^{d}$ is the income elasticity of $\tau ^{d}$, i.e, the ordinary (direct taxation) liability progression index. The same broad conclusions reached before will apply here. By using (18), one can easily assess also in this case the progressivity of the overall tax system.

Proposition 4

The overall tax burden distribution given by consumption and income taxation, plus a saving tax, is progressive, i.e. $G\le H$ for all $y\in \mathcal {Y}$, if $\sum _{i}\widehat{t}_{i}\left( \varepsilon _{i}^{e}-1\right) e_{i}\ge \tau ^{d}\left( 1-\ell ^{d}\right)$ for all $y\in \mathcal {Y}$.

Proof

It follows from definitions (18) and (19), and the Background Result, as $\sum _{i}\widehat{t}_{i}\left( \varepsilon _{i} ^{e}-1\right) e_{i}>\tau ^{d}\left( 1-\ell ^{d}\right)$ implies $\ell (\mathbf {t}^{\prime },y)>1$. $\square$

As was the case with Proposition 3, we can complement the comparison between distributions described in Proposition 4 by defining an aggregate progressivity index $L\left( \mathbf {t}^{\prime }\right) =\int _{\mathcal {Y} }\ell (t^{\prime },y)\widetilde{g}\left( y,\mathbf {t}^{\prime }\right) dy$ (obtained again by aggregating individual liability progression). In such a case,

$$\begin{aligned} L(\mathbf {t}^{\prime })>1\text { if }\int _{\mathcal {Y}}\sum _{i}\widehat{t} _{i}\left( \varepsilon _{i}^{e}-1\right) e_{i}f(y)dy>\int _{\mathcal {Y} }\left( 1-\ell ^{d}\right) \tau ^{d}\left( y\right) f(y)dy \end{aligned}$$

(20)

which can be given more compact form as

$$\begin{aligned} L(\mathbf {t}^{\prime })>1\text { if }\left( H^{e}-1\right) R^{e}>\left( 1-L^{d}\right) R^{d} \end{aligned}$$

(21)

where we recall that $R^{k}$ ($k=d,e$) are the revenues from direct and expenditure taxation, while $L^{d}$ and $H^{e}$ are their average income elasticities.¹⁴ In this aggregate perspective, progressivity is assessed on the basis of the correlation between expenditure tax revenue and its income elasticity, vs the correlation between direct tax revenue and its income elasticity.

5 Empirical evidence

In this section we provide an empirical application of the main theoretical findings shown above, merging the 2012 data set collected from the “Household Budget Survey (HBS)” by Istat—the National Institute of Statistics, with the Bank of Italy data on household disposable income gathered from “Survey on Household Income and Wealth (SHIW)”. The merge has been implemented via the propensity score method, using a number of relevant matching variables, such as the number of household members, workers in the household, job type, sex, education, etc. This allows us to have information on 18,483 households about socio-demographic characteristics, the net and gross yearly consumption expenditure as well as savings and net and gross disposable income (see the Appendix, Table 1, for descriptive statistics).¹⁵ We present our results following the order of our previous theoretical Propositions.

Proposition 1

Stochastic dominance of F and H vs G.

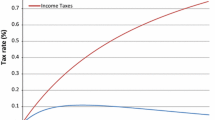
We start by estimating the first order stochastic dominance relationship of G vs F in Fig. 1, which shows the income distribution F and the distribution of taxation shares from different tax sources. F is dominated by the other distributions and, more generally, by the total tax burden distribution drawn in Fig. 2.

Fig. 1

Income distribution (F) dominated by each tax burden distribution G

Fig. 2

Income distribution (F) vs total tax burden distribution (G)

We confirm the intuition from Fig. 1 and Fig. 2 by explicitly testing for stochastic dominance, using the the Kolmogorov–Smirnov test (KS) for two samples (Smirnov 1933). As far as the comparison between the total tax burden distribution G and the income distribution F is concerned, the null hypothesis of KS is $H_{0}:G=F$ and the p value is defined as

$$\begin{aligned} KS_{p value}=1-\lim _{m,n\rightarrow \infty }\Pr \root 2 \of {\frac{mn}{(m+n)} }D_{m,n}\le z=2 {\displaystyle \sum \limits _{i=1}^{\infty }} (-1)^{i-1}\exp (-2i^{2}z^{2}) \end{aligned}$$

where $D_{m,n}=$ $\max _{y}\left| F^{i}-F^{h}\right|$ and $F^{i}$ and $F^{h}$ are the two empirical cumulative distributions that we want to compare. The first five terms give the $KS_{p value}$. In our sample, $m=n=18{,}483$ and $D_{m,n}^{tot}=0.94$ (i.e. $D_{m,n}^{tot}$ is the maximum difference between the cumulative distribution of the total tax burden and the income distribution), giving a $KS_{p value}=0$ which rejects the null hypothesis. We also find evidence of first order stochastic dominance of G over F for each single source of taxation, as the null hypothesis is rejected in each KS test between F and the cumulative distribution of each tax burden source (i.e. VAT, saving and personal income tax). We obtain $D_{m,n}^{VAT}=$ $\max _{y}\left| F-G\__{VAT}\right| =0.22$; $D_{m,n}^{saving}=\max _{y}\left| F-G\_saving\right| =0.36$; $D_{m,n}^{Income}=\max _{y}\left| F-G\_income\right| =0.39$— all of which give a null $KS_{p value}$ in each comparison. In Fig. 3 we confirm the prediction of Proposition 1 on the link between the liability progression index and the stochastic dominance relationship between F and G:

Fig. 3

Liability Index of the total tax burden distribution

We now compare the different specifications of G with the income share distribution (H). The main finding is that VAT is the only regressive source of taxation since its tax-burden distribution is dominated by H (Fig. 4). All other forms of taxation turn out to be progressive, since each cumulative tax burden distribution stochastically dominates H. Overall, the total tax burden distribution G dominates H (see Fig. 5), giving evidence of the progressivity of the overall taxation system.

Fig. 4

Income share distribution ($H$) dominated by the saving and income tax burden distribution

Fig. 5

Income share distribution (H) is stochastically dominated by the overall tax distribution (G)

The KS test confirms the stochastic dominance relationship of Fig. 5 of $G$ on H: in such a case $D_{m,n}=$ $\max _{y}\left| H-G\_totalburden\right| =0.094$, giving a null $KS_{p value}$. We also test for stochastic dominance with respect to all other taxes, obtaining that $D_{m,n}^{VAT}=\max _{y}\left| H-G\__{VAT}\right| =0.05$, $D_{m,n}^{inc}=\max _{y}\left| H-G\_income\_tax\right| =0.147$, and $D_{m,n}^{sav}=\max _{y}\left| H-G\_saving\right| =0.17$: such results allow us to reject the null in each KS test.¹⁶

Fig. 6

If $\partial s/\partial y\le 1$ for all $y\in \mathcal {Y}$, then $F^{c}\le F$ for all $y\in \mathcal {Y}$

Proposition 2

Stochastic dominance of F and H vs F$^{c}$.

Figure 6 gives a visual representation of Proposition 2: if $\partial s/\partial y\le 1$ for all $y\in \mathcal {Y}$, the distribution of expenditure $F^{c}$ stochastically dominates the income distribution F in the first order sense—the figure refers to the households with positive savings. Also in this case, the null of the KS is rejected ($D_{m,n}^{sav}=$ $\max _{y}\left| F-F^{c}\right| =0.36,$ giving a null $KS_{p value}$). We also provide evidence that if $\varepsilon ^{s}\left( p,y\right) \ge 1$ for all $y\in \mathcal {Y}$, then $H\le F^{c}$: Fig. 7 represents the behaviour of the saving income elasticity, and in Fig. 8 we show that $F^{c}$ is dominated by H. The KS test confirms this dominance relationship, as $D_{m,n}^{sav}=\max _{y}\left| H-F^{c} \right| =0.12$, giving a null $KS_{p value}$.¹⁷

Fig. 7

Saving income elasticity $\varepsilon ^{s}$ and income

Fig. 8

Stochastic dominance of the income share distribution (H) over the expenditure distribution ($F^{c}$)

Proposition 3

Stochastic Dominance of H vs G (savings plus VAT).

By Proposition 3, if $\sum _{i} \widehat{t}_{i}e_{i}\left( \varepsilon _{i}^{e}-1\right) \ge 0$ for all $y\in \mathcal {Y}$, then $G\le H$ (here G includes saving taxation and VAT: $G\_saving\_VAT$). The sufficient condition of Proposition 3 is equivalent to $\ell (\mathbf {t},y)\ge 1$ for all $y\in \mathcal {Y}$, where $\mathbf {t}$ includes VAT and saving taxation (see Fig. 9).

Fig. 9

Liability Progression of VAT and Saving tax

Using the KS, we find evidence of first order stochastic dominance of $G\_saving\_vat$ over H (also in this case the p value of the KS is null, as $D_{m,n}^{sav}=$ $\max _{y}H-G\_saving\_vat=0.48$, giving a null $KS_{p value}$: see Fig. 10).

Fig. 10

Stochastic dominance of the Income Share distribution (H) vs the tax burden distribution of savings plus VAT

Proposition 4

Progressivity in the aggregate.

We conclude by offering a measure of (21) for the sample of households with non-negative savings (total final observations are 13.327 observations), which gives evidence of progressivity of the overall taxation system: i.e. $L(\mathbf {t}^{\prime })>1$ since $H^{e}=0.641^{***}(0.004)$, $R^{e}=3089.615$, $L^{d}=1.697^{***}(.01)$, and $R^{d}=7540.174$ (see the Appendix).¹⁸ This can be confirmed using an equivalent expression:

$$\begin{aligned} \widehat{t}_{mean}\left( E^{e}-1\right) \overline{e}>\left( 1-L^{d}\right) R^{d} \end{aligned}$$

where $\widehat{t}_{mean}=-0.124$; $\overline{e}=25620$; $E^{e}=0.7^{***}(0.004)$ (see again the Appendix).

In addition, we compute (21) for the whole sample using a different notion of income, obtained by replacing income with the level of consumption for households with negative savings. This may arguably be considered as the ’true’ household income level, since negative savings can be conceived of as short run drops in financial resources (and hence a misleading measure of the true income capacity). Also in this case, the aggregate progressivity of the taxation system is confirmed, as $\overline{e}=27721.13$, $\widehat{t} _{mean}=$ $-0.123$; $E^{e}=0.75^{***}(0.0034)$, $L^{d}=1.65^{***}(0.01)$, and $R^{d}=6447.375$.

6 Concluding remarks

Several indices and approaches have been used to assess the distributional effects of taxation. In this paper, we use a methodology based on the income share elasticity that allows to assess the conditions for the progressivity of a given set of taxes looking at the stochastic dominance relationship of the income distribution and different specification of the tax burden distribution (VAT, personal income tax, saving tax, and the overall tax burden). Due to this approach, we find clear cut conditions based on the correlation among the incidence of the different source of taxes and the expenditure elasticity that allows us to rank the tax burden distribution relative to the different notion of income considered. We also find a condition based on the saving elasticity which allow us to rank the income distribution vs the expenditure distribution. Our approach might prove useful to the tax authorities aiming to reach a desired distributional profile of the taxation system, when multiple tax instruments have to be set.

The empirical analysis follows the order of the theoretical results. Using the Smirnov–Kolmogorov test on a large sample of Italian households, we test for the stochastic ranking of the income distribution vs the tax burden distribution across different income specifications and sources of revenue. Firstly, we find that all the tax burden distributions dominate the income distribution. Secondly, only the VAT tax burden is dominated by the income share distribution, giving evidence of regressivity: all the other types of tax burden distributions dominate the income share distribution, giving evidence of progressivity. Moreover, we find that for households with positive savings, the income distribution is dominated by the expenditure distribution, but the latter is dominated by the income share distribution, since the saving elasticity is greater than one.

Our analysis adopts a snapshot approach based on cross-sectional data. The first natural future extension is to insert benefits and transfers and to analyse the distributional impact of the net tax system. Secondly, the “income share elasticity” might be used to analyse the impact of the taxation system in a lifetime prospective. In addition, we can enrich the analysis with more behavioral insights and responses adding more structure in term of markets and individual features. We leave these suggestions to future research.

Appendix

Table 1 Descriptive statistics of income and revenue variables ($n=18{,}483$)

Proposition 1

Computing $L^{d}$, $H^{e}$ and $E^{e}$.

We recall that $L^{d}=\int\nolimits_{\mathcal {Y}}\ell ^{d}g^{d}\left( y\right) dy$, with $g^{d}=\tau ^{d}\left( y\right) f(y)/R^{d}$, $H^{e}=\int\nolimits_{\mathcal {Y}}\sum _{i}\varepsilon _{i} ^{e}g^{e}dy$, with $g^{e}=\sum _{i}\widehat{t}_{i}e_{i}f(y)/R^{e}$, and $E^{e}=\int\nolimits_{\mathcal {Y}}\sum _{i}\varepsilon _{i}^{e}f^{e}dy$ with $f^{e} =\sum _{i}e_{i}f(y)/E^{e}$. Estimates of $L^{d}$, $H^{e}$ and $E^{e}$ are obtained by running the following regressions:

$$\begin{aligned} \ln (\tau ^{d}\left( y\right) )&=\alpha _{d}+L^{d}\ln (y)\\ \ln \left( \sum _{i}\left( \left| \widehat{t}_{i}\right| e_{i}(y)\right) \right)&=\alpha _{e}+H^{e}\ln (y)\\ \ln \left( \sum _{i}e_{i}(y)\right)&=\alpha +E^{e}\ln (y) \end{aligned}$$

giving: $\alpha _{d}=$ $-9.700(0.103)$, $L^{d}=1.697^{***}(0.01)$; $\alpha _{e}=1.111^{***}(0.0435278)$, $H^{e}=0.641^{***}(0.004)$; and $\alpha =2.045^{***}(0.039)$ $E^{e}=0.75^{***}(0.0037)$ (Robust SE in parentheses; P values:***1%).