Forecasting performance of Bayesian VEC-MSF models for financial data in the presence of long-run relationships

Abstract

The paper is focused on comparing the forecasting performance of two relatively new types of Vector Error Correction - Multiplicative Stochastic Factor (VEC-MSF) specifications: VEC-MSF with constant conditional correlations, and VEC-MSF-SBEKK with time-varying conditional correlations. For the sake of comparison, random walks, vector autoregressions (VAR) with constant conditional covariance matrix, and VAR-SBEKK models are also considered. Based on daily quotations on three exchange rates: PLN/EUR, PLN/USD, and EUR/USD, where the cointegrating vector may be assumed to be known a priori, we show that in econometric models it can be more important to allow for cointegration relationships than for time-varying conditional covariance matrix.

1 Introduction

Widely-used models for financial time series are based on conditional heteroscedasticity processes. The most popular ones are the Generalized Autoregressive Conditional Heteroskedastic (GARCH) and the Stochastic Volatility (SV) processes. The latter are less often used, though (for a review see, e.g., Silvennoinen & Teräsvirta, 2009; Asai et al., 2006; Shephard & Andersen, 2009; Chib et al., 2009; Eratalay, 2016). However, some research has shown that apart from the fact that the variability of financial time series (measured, for example, by the conditional covariance matrix) varies over time, on financial markets there can also exist long-term relationships. Therefore, it appears essential to construct such models in which the possible presence of long-run relationships and time-variable volatility are simultaneously taken into account. As the vector autoregression (VAR) models underlie the cointegration analysis, the efforts have been focused on suitably tailoring the vector error correction (VEC) representation of VAR so as to accommodate for time-varying conditional covariances, see, e.g., Seo (2007), Herwartz and Lütkepohl (2011), Koop et al. (2011), Osiewalski and Osiewalski (2013), Osiewalski and Osiewalski (2016), Cavaliere et al. (2015), Pajor and Wróblewska (2017), Cavaliere et al. (2018).

Although there exists a growing number of publications discussing the forecast accuracy of Bayesian VAR models with time-varying parameters or with the time-varying covariance structure (see, e.g., Clark, 2011; D’Agostino et al., 2013; Rossi & Skhposyan, 2014; Clark & Ravazzolo, 2015; Berg, 2017; Abbate & Marcellino, 2018; Chan & Eisenstat, 2018; Vardar et al., 2018; Huber et al., 2020; Kastner & Huber, 2021), one can find rather few publications in which different vector error correction models are compared in respect to their forecasting potential (see, e.g., Anderson et al., 2002; Swanson, 2002; Kuo, 2016; Huber & Zörner, 2019). The main conclusion of the papers mentioned above is that VAR models with time-varying parameters and with time-varying covariance structure are often found to have better forecasting performance than their constant coefficient variants. On the other hand, Kuo (2016) showed that VEC models outperform VAR models in forecasting stock prices on Taiwan markets.

Our research is focused on Bayesian Vector Error Correction - Multiplicative Stochastic Factor (VEC-MSF) models, proposed by Pajor and Wróblewska (2017). These models integrate the VEC representation of a VAR structure with stochastic volatility. In consequence, the VEC-MSF models enable us to capture long-run relationships among processes. Also, they make it possible to formally examine the presence of time-variation in the conditional covariances. In the VEC-MSF models proposed by Pajor and Wróblewska (2017), conditional heteroskedasticity is taken into account by the Multiplicative Stochastic Factor (MSF) process, or, alternatively, by one of its generalizations, namely, by the hybrid Multiplicative Stochastic Factor - Scalar BEKK (MSF-SBEKK) specification. It is worth mentioning that, in the VEC-GMSF-SBEKK models proposed by Osiewalski and Osiewalski (2016), the authors consider only two cases of reduced rank long-run multiplier matrix, ${\varvec{\Pi }}$. In their paper only three partial and one global relationships are analyzed. In our paper, by contrast, all possible cases of the long-run multiplier matrix ${\varvec{\Pi }}$ are considered.

The main purpose of this paper is to discuss properties of Bayesian VEC-MSF models in the context of modeling financial time series. Another purpose is to compare the forecasting performance of three types of model specifications: the VEC-MSF model with constant conditional correlations, the VEC-MSF-SBEKK and VEC-SBEKK models with varying conditional correlations, and the VEC model with constant conditional covariance matrix.

Based on daily quotations on three exchange rates: PLN/EUR, PLN/USD and EUR/USD, the predictive capacity of the models under consideration is compared. By modeling the exchange rates (where, as arbitrage opportunities are lacking, the cointegrating vector may be assumed to be known a priori, see Osiewalski and Pipień, 2016), it will be possible to show how important for prediction it is to incorporate a long-run relationship in financial data. It is important to stress that our attention is focused on pure time-series specifications for daily data, without applying any extra variables suggested by economic or financial theory. The fundamentals of exchange rate modeling are explained in Kębłowski et al. (2020), where the classical VEC model with constant conditional covariance matrix is used for monthly data spanning a period from January 2000 to June 2017.

The main criterion used in this study for drawing this comparison is the predictive Bayes factor. The Probability Integral Transform (PIT) of Rosenblatt (1952) is also applied. As it is pointed out by Geweke and Amisano (2010, p. 229) “the two approaches can be complementary, each identifying strengths and weaknesses in the models”. A popular measure of forecasting performance is the so-called continuous ranked probability score (CRPS). The definition of CRPS and its generalization to energy score can be found in Gneiting and Raftery (2007). As the analysis conducted here is mainly Bayesian, the predictive Bayes factor will be used as the main criterion applied for evaluating the forecast performance of models under consideration.

The paper is organized as follows. In Sect. 2 Bayesian VEC-MSF models are presented. Sections 3 and 4 are devoted to the predictive Bayes factor and to the PIT in the context of predictive performance of models. Section 5 contains empirical results, and Sect. 6 concludes the paper.

2 Bayesian VEC models with stochastic volatility

Let us start with a linear n-variate and kth-order vector autoregressive (VAR) process:

$$\begin{aligned} \mathbf{x} _{t} = \mathbf{A} _{1} \mathbf{x} _{t-1} + \mathbf{A} _{2} \mathbf{x} _{t-2} +...+ \mathbf{A}_{k} \mathbf{x}_{t-k} + \mathbf{\Phi D}_{t} + {\varvec{\varepsilon }}_{t}, \quad t=1,2,...,T+h, \end{aligned}$$

(1)

where $\mathbf{x} _{t}$ is an $n \times 1$ random vector, $\{ {\varvec{\varepsilon }}_{t} \}$ is a vector white noise process with the covariance matrix ${\varvec{\Sigma }}$ (i.e. $\{ {\varvec{\varepsilon }}_{t} \} \sim \textit{WN}(0,{\varvec{\Sigma }} ))$, $\mathbf{A}_{i}$ is an $n \times n$ matrix of real coefficients ($i = 1, 2, ..., k$), matrix $\mathbf{D}_{t}$ is comprised of deterministic variables, ${\varvec{\Phi }}$ is a parameter matrix, T is the number of observations, h is the forecasting horizon, and $\mathbf{x}_{1-k}, \mathbf{x}_{2-k},\ldots , \mathbf{x}_{0}$ are the initial conditions. The $\{\mathbf{x}_{t} \}$ process takes on the following VEC representation:

$$\begin{aligned} \Delta \mathbf{x}_{t} =\tilde{{\varvec{\Pi }}} \mathbf{x}_{t-1} +\sum \limits _{i=1}^{k-1} {{\varvec{\Gamma }}_{i} \Delta \mathbf{x}_{t-i} +{\varvec{\Phi }} \mathbf{D}_{t} + {\varvec{\varepsilon }}_{t} }, \end{aligned}$$

(2)

where $\Delta \mathbf{x}_{t} = \mathbf{x}_{t}-\mathbf{x}_{t-1}$, $\tilde{{\varvec{\Pi }}}=\sum \nolimits _{i=1}^k {\mathbf{A}_{i}} -\mathbf{I},\,\,\,\,\ {{\varvec{\Gamma }}}_{i} = -\sum \nolimits _{j=i+1}^k {\mathbf{A}_{j} }$. Moreover, $\tilde{{{\varvec{\Pi }} }}= {\varvec{\alpha }} \tilde{{{\varvec{\beta }} }}'$, with ${\varvec{\alpha }}$ and $\tilde{{{\varvec{\beta }} }}'$ being some $(n \times r)$ - sized matrices, and $r < n$ is the number of cointegration relationships (if they exist).

The definition of $\{ \mathbf{x}_{t} \}$ provided in (2), has been generalized in Pajor and Wróblewska (2017) by introducing random-variability into elements of ${\varvec{\Sigma }}$:

$$\begin{aligned}&\Delta \mathbf{x}_{t} ={\varvec{\alpha }} \tilde{{{\varvec{\beta }} }}'{} \mathbf{x}_{t-1} +\sum \limits _{i=1}^{k-1} {{\varvec{\Gamma }}_{i} \Delta \mathbf{x}_{t-i} + {\varvec{\Phi }} \mathbf{D}_{t} + {\varvec{\varepsilon }}_{t} }, \quad t=1,2,...,T+h, \end{aligned}$$

(3)

$$\begin{aligned}&{\varvec{\varepsilon }}_{t} \vert \psi _{t-1} ,\mathbf{D}_{t} ,q_{t} , {\varvec{\theta }} \sim N( \mathbf{0}, {\varvec{\Sigma }}_{t} ), \end{aligned}$$

(4)

where $\psi _{t-1}$ denotes the past of the process $\{\mathbf{x}_{t}\}$ up to time $t-1$, $q_{t}$ is a latent variable, ${\varvec{\theta }}$ is a vector of parameters, and ${\varvec{\Sigma }}_{t} = {\varvec{\Sigma }} (q_{t}, \psi _{t-1}, \mathbf{D}_{t}, {\varvec{\theta }} )$.

In order to investigate the influence of assumptions (pertaining to the conditional covariance matrix) on the predictive abilities of the models we consider four structures for matrix ${\varvec{\Sigma }}_{t}$: constant, Multiplicative Stochastic Factor (MSF), SBEKK, and hybrid MSF-SBEKK [type I; see, e.g., Osiewalski (2009); Osiewalski and Pajor (2009); Pajor and Wróblewska (2017)].

The Multiplicative Stochastic Factor structure for matrix ${\varvec{\Sigma }}_{t}$ is as follows:

$$\begin{aligned} {\varvec{\Sigma }}_{t} =q_{t} {\varvec{\Sigma }}, \end{aligned}$$

(5)

where $\ln q_{t} =\;\varphi \ln q_{t-1} +\sigma _{q} \eta _{t}$, $|\varphi | < 1$, $\{\eta _{t} \}\sim iiN(0,\;1),$ and ${\varvec{\varepsilon }}_{t} \bot \eta _{s}$, for $t, s \in \{ 1,2, \ldots , T+h\}$.

Although the VEC-MSF process features non-zero time-variable conditional covariances, conditional correlations remain constant in time. Such a result is attributable to the fact that the very same $q_{t}$ factor drives the dynamics of each element of ${\varvec{\Sigma }}_{t}$. The process has been employed in, e.g., Osiewalski and Pajor (2009) and Pajor and Osiewalski (2012).

The type I hybrid MSF-SBEKK structure for matrix ${\varvec{\Sigma }}_{t}$ proposed by Osiewalski (2009) and Osiewalski and Pajor (2009) is the following:

$$\begin{aligned}&{\varvec{\Sigma }}_{t} = q_{t} \tilde{{{\varvec{\Sigma }}}}_{t} , \end{aligned}$$

(6)

$$\begin{aligned}&\tilde{{{\varvec{\Sigma }}}}_{t} =(1-a-b){\varvec{\Sigma }} +b\left( {{\varvec{\varepsilon }}_{t-1} {\varvec{\varepsilon }}_{t-1} '} \right) +a\tilde{{{\varvec{\Sigma }}}}_{t-1} , \end{aligned}$$

(7)

with $\ln q_{t} = \varphi \ln q_{t-1} + \sigma _{q} \eta _{t}$, $|\varphi | < 1$, $\{\eta _{t} \}\sim iiN(0,\;1),$ and $\varvec{\varepsilon} _{t} \bot \eta _{s}\,$, for $t, s\in \{ 1, 2, \ldots , T+h \},\; a, b \in [0,1],\; a + b < 1$.

As regards the initial conditions for $\tilde{{{\varvec{\Sigma }}}}_{t}$, we assume ${\varvec{\varepsilon }}_{0}=\mathbf{0}$, $\tilde{{{\varvec{\Sigma }}}}_{0} =s_{0,{\varvec{\Sigma }}} \mathbf{I}_{n}$, where $s_{0,{\varvec{\Sigma }} } > 0$, and $\mathbf{I}_{n}$ denotes identity matrix of size n. The presence of the scalar BEKK(1,1) structure in the conditional covariance matrix allows to model time-varying conditional correlations without introducing more latent processes. The hybrid model defined by (3, 4) and (6, 7) nests two simple basic structures. For $b = 0$ and $a = 0$ we obtain the VEC-MSF model. In the limiting case when $\sigma _{q} \rightarrow 0$ and $\varphi ~= 0$, the VEC-MSF-SBEKK model becomes the VEC-SBEKK one.

Equation (3) can be decomposed and expressed as follows:

$$\begin{aligned} \Delta \mathbf{x}_{t} ={\varvec{\alpha }} [\tilde{{{\varvec{\beta }}}}',{\varvec{\Phi }}_{1} ']\left[ {\begin{array}{l} \mathbf{x}_{t-1} \\ \mathbf{D}_{t}^{(1)} \\ \end{array}} \right] +\sum \limits _{i=1}^{k-1} {{\varvec{\Gamma }}_{i} \Delta \mathbf{x}_{t-i} + {\varvec{\Phi }}_{2} \mathbf{D}_{t}^{(2)} +{\varvec{\varepsilon }}_{t} } \nonumber \\ ={\varvec{\alpha }} {\varvec{\beta }} '{} \mathbf{z}_{1,t} +{\varvec{\Gamma }} '{} \mathbf{z}_{2,t} + {\varvec{\Gamma }}_{s} '{} \mathbf{z}_{3,t} + {\varvec{\varepsilon }}_{t}, \end{aligned}$$

(8)

where ${\varvec{\beta }}'=[\tilde{{{\varvec{\beta }}}}',{\varvec{\Phi }}_{1}']$, $\mathbf{z}_{1,t} = [\mathbf{x}_{t-1}',\mathbf{D}_{t}^{(1)}]'$, $\mathbf{z}_{2,t} =(\Delta \mathbf{x}_{t-1}',\Delta \mathbf{x}_{t-2}',\ldots ,\Delta \mathbf{x}_{t-k+1}')'$, $\mathbf{z}_{3,t} =\mathbf{D}_{t}^{(2)}$, ${\varvec{\Gamma }} =[{\varvec{\Gamma }}_{1} ,{\varvec{\Gamma }}_{2},\ldots ,{\varvec{\Gamma }}_{k-1} ]'$, ${\varvec{\Gamma }}_{s} ={\varvec{\Phi }}_{2}'$, and ${\varvec{\alpha }} \; {\varvec{\Phi }}_{1} '{} \mathbf{D}_{t}^{(1)} + {\varvec{\Phi }}_{2} \mathbf{D}_{t}^{(2)} ={\varvec{\Phi }} \mathbf{D}_{t}$.

The conditional distribution of $\mathbf{x}_{t}$ (given the past of the process, $\psi _{t-1}$, the deterministic variables, $\mathbf{D}_{t}$, the parameters and the latent variable, $q_{t})$ is n-variate Normal with the mean ${\varvec{\mu }}_{t} = \mathbf{x}_{t-1} +{\varvec{\Pi }} \mathbf{z}_{1,t} +{\varvec{\Gamma }} '\mathbf{z}_{2,t} + {\varvec{\Gamma }}_{s} '{} \mathbf{z}_{3,t}$ and the covariance matrix ${\varvec{\Sigma }}_{t}$:

$$\begin{aligned} p(\mathbf{x}_{t} \vert \psi _{t-1} ,\mathbf{D}_{t} ,{\varvec{\alpha }} ,{\varvec{\beta }} ,{\varvec{\Gamma }} ,{\varvec{\Gamma }}_{s} ,q_{t},{\varvec{\Sigma }} ,{\varvec{\theta }}_{{\varvec{\Sigma }} } ,q_{0,{\varvec{\Sigma }}})=f_{N,n} (\mathbf{x}_{t} \vert {\varvec{\mu }}_{t},{\varvec{\Sigma }}_{t}), \end{aligned}$$

(9)

where ${\varvec{\Pi }} = {\varvec{\alpha }} {\varvec{\beta }}',{\varvec{\theta }}_{{\varvec{\Sigma }}}$ and $q_{0,{\varvec{\Sigma }}}$ are the vectors of the stochastic volatility parameters: in the VEC-MSF model ${\varvec{\theta }}_{{\varvec{\Sigma }}} =(\varphi ,\sigma _{q}^{2} )'$ and $q_{0,{\varvec{\Sigma }}} =\ln q_{0}$, in the VEC-MSF-SBEKK model we have $\theta _{{\varvec{\Sigma }}} =(\varphi ,\sigma _{q}^{2} ,a,b)'$ and $\mathbf{q}_{0,{\varvec{\Sigma }}} =(\ln q_{0} ,s_{0,{\varvec{\Sigma }} } )'$, whereas in the VEC-SBEKK specification ${\varvec{\theta }}_{{\varvec{\Sigma }}} =(a,b)'$ and $\mathbf{q}_{0,{\varvec{\Sigma }}} =s_{0,{\varvec{\Sigma }}}$.

2.1 Predictive distribution

Let us adopt the following symbols:

${\varvec{\theta }} =(vec~{\varvec{\alpha }}', vec~{\varvec{\beta }}', vec~{\varvec{\Gamma }}', vec~{\varvec{\Gamma }}_{s}', vech~{\varvec{\Sigma }}',{\varvec{\theta }}_{{\varvec{\Sigma }}}',q_{0,{\varvec{\Sigma }} })'$ – the parameter vector,

$\mathbf{x}_{t}, \quad t=1,2,\ldots ,T$ – the observable random vectors,

$\mathbf{x}_{.T}=[\mathbf{x}_{1} \mathbf{x}_{2} \ldots \mathbf{x}_{T}]$ – the matrix of observables,

$\mathbf{x}_{f}=[\mathbf{x}_{T+1} \mathbf{x}_{T+2} \ldots \mathbf{x}_{T+h}]$ – the matrix of future observables,

$\mathbf{q}_{.T} = (q_{1}, q_{2},\ldots , q_{T})'$ – the vector of latent variables for the first T observations,

$\mathbf{q}_{f} = (q_{T+1}, q_{T+2},\ldots ,q_{T+h})'$ – the vector of future latent variables,

$\mathbf{D} = [\mathbf{D}_{1} \mathbf{D}_{2} \ldots \mathbf{D}_{T+h}]$ – the matrix of deterministic variables.

Inference on all unknown and unobserved quantities (parameters, latent variables and future observables) can be based on the joint posterior – predictive density function. The joint density function of the observed data, h forecasted values of the data and forecasted latent variables (given the parameters and latent variables up to time T) is as follows:

$$\begin{aligned}&p(\mathbf{x}_{.T} ,\mathbf{x}_{f} ,\mathbf{q}_{f} \vert \mathbf{D},{\varvec{\theta }},\mathbf{q}_{.T})\nonumber \\&\quad =\prod \limits _{t=1}^{T+h} f_{N,n} (\mathbf{x}_{t} \vert {\varvec{\mu }}_{t} ,{\varvec{\Sigma }}_{t} )\prod \limits _{t=1}^{T+h} {q_{t}^{-1} } f_{N,1} (\ln q_{t} \vert \varphi \ln q_{t-1} ,\sigma _{q}^{2} ). \end{aligned}$$

(10)

This density depends on some initial values, which are not shown in our notation. The out-of-sample predictive density of h future values of observations and of latent variables is obtained through averaging the sampling predictive densities over the parameters and latent variables space, with the use of the posterior density as a weight function:

$$\begin{aligned} p(\mathbf{x}_{f} ,\mathbf{q}_{f} \vert \mathbf{x}_{.T}^{o} ,\mathbf{D})=\int {p(\mathbf{x}_{f} ,\mathbf{q}_{f} \vert \mathbf{x}_{.T}^{o} ,\mathbf{D},\mathbf{q}_{.T} ,{\varvec{\theta }} )p(\mathbf{q}_{.T} ,{\varvec{\theta }} \vert \mathbf{x}_{.T}^{o} ,\mathbf{D})\;d \mathbf{q}_{.T} d {\varvec{\theta }}}, \end{aligned}$$

(11)

where

$$\begin{aligned}&p(\mathbf{x}_{f} ,\mathbf{q}_{f} \vert \mathbf{x}_{.T}^{o} ,\mathbf{D},\mathbf{q},{\varvec{\theta }} )\nonumber \\&\quad =\prod \limits _{t=T+1}^{T+h} f_{N,n} (\mathbf{x}_{t} \vert {\varvec{\mu }}_{t} ,{\varvec{\Sigma }}_{t} )\prod \limits _{t=T+1}^{T+h} {q_{t}^{-1} } f_{N,1} (\ln q_{t} \vert \varphi \ln q_{t-1} ,\sigma _{q}^{2}), \end{aligned}$$

(12)

$\mathbf{x}_{.T}^{o} =[\mathbf{x}_{1}^{o} ... \mathbf{x}_{T}^{o} ]$ denotes the ex post, observed, value of $\mathbf{x}_{.T}$.

The main advantage of the Bayesian approach is that it provides a probability distribution for future observables (or any function of them). If we are interested only in prediction of future observables, we can use the following Bayesian predictive distribution:

$$\begin{aligned} p(\mathbf{x}_{f} \vert \mathbf{x}_{.T}^{o} ,\mathbf{D})=\int {p(\mathbf{x}_{f} ,\mathbf{q}_{f} \vert \mathbf{x}_{.T}^{o} ,\mathbf{D},\mathbf{q}_{.T},{\varvec{\theta }} )p(\mathbf{q}_{.T} ,{\varvec{\theta }} \vert \mathbf{x}_{.T}^{o} ,\mathbf{D})\;d\mathbf{q}_{.T} \;d {\varvec{\theta }} } \;d \mathbf{q}_{f}, \end{aligned}$$

(13)

which takes into account uncertainty regarding parameters and latent variables, given the data, sampling model and a prior distribution.

2.2 Prior distribution and sampling scheme

It remains to formulate the prior distribution of the parameter vector $\varvec{\theta}$. We assume independence among certain blocks of parameters, and we use the same prior distributions as in Pajor and Wróblewska (2017):

$$\begin{aligned} p({\varvec{\theta }})=p({\varvec{\alpha }} \vert {\varvec{\beta }} )p({\varvec{\beta }} )p({\varvec{\Gamma }} )p({\varvec{\Gamma }}_{s} )p({\varvec{\Sigma }})p({\varvec{\theta }}_{{\varvec{\Sigma }} } )p(\mathbf{q}_{0,{\varvec{\Sigma }} } )I_{[0,1]} (\vert {\varvec{\lambda }} \vert _{\max } ), \end{aligned}$$

(14)

where $I_{[0, 1]}$(.) denotes the indicator function of the interval [0, 1], and ${\varvec{\lambda }}$ is the vector of eigenvalues of the companion matrix, connected with the VAR form.

For matrix ${\varvec{\Pi }}$ we use the parameterization which has been proposed by Koop et al. (2010):

$$\begin{aligned} {\varvec{\alpha }} {\varvec{\beta }}'=({\varvec{\alpha }} \mathbf{M}_{\Pi } )({\varvec{\beta }} \mathbf{M}_{\Pi }^{-1})'\equiv \mathbf{A} \mathbf{B}', \end{aligned}$$

where $\mathbf{M}_{\Pi }$ is an $r\times r$ symmetric positive-definite matrix, and $\mathbf{A}$ and $\mathbf{B}$ are unrestricted matrices. It can be shown that ${\varvec{\alpha }} = \mathbf{A} (\mathbf{B}'\mathbf{B})^{\frac{1}{2}}$, ${\varvec{\beta }} = \mathbf{B} (\mathbf{B}'\mathbf{B})^{-\frac{1}{2}}$. The prior distributions for matrices $\mathbf{A}$ and $\mathbf{B}$ imply the prior distributions for ${\varvec{\alpha }}$ and ${\varvec{\beta }}$. They are assumed to be as follows:

• for matrix $\mathbf{B}$ the matrix normal distribution is used: $p(\mathbf{B}\vert r)=f_{mN} (\mathbf{B} \vert \mathbf{0},\mathbf{I}_{r} ,\mathbf{I}_{n} ),$ which leads to the matrix angular central Gaussian (MACG) distribution for ${\varvec{\beta }}$: $p({\varvec{\beta }})=f_{MACG} ({\varvec{\beta }} \vert \mathbf{I}_{n} )$. By imposing MACG distribution with identity matrix we set uniform prior for $\beta$, (see, e.g., Chikuse, 2002).

• on matrix $\mathbf{A}$ we also impose the matrix normal distribution: $p(\mathbf{A}\vert \nu ,r)=f_{mN} (\mathbf{A}\vert \mathbf{0},\nu \mathbf{I}_{r}, \; \mathbf{I}_{n} ),$ where parameter $\nu$ has the inverse-gamma distribution: $p(v)=f_{IG} (\nu \vert 2,\;3)$.

The priors for the remaining parameters are as follows:

• $p({\varvec{\Gamma }} \vert h)=f_{mN} ({\varvec{\Gamma }} \vert \mathbf{0},\mathbf{I}_{n} ,h\mathbf{I}_{l} ),$ where $l=n(k-1)$,

• $p({\varvec{\Gamma }}_{s} \vert h_{s} )=f_{mN} ({\varvec{\Gamma }}_{s} \vert \mathbf{0},\mathbf{I}_{n} ,h_{s} \mathbf{I}_{l_{s} } ),$ where $l_{s}$ is the number of deterministic terms in $\mathbf{D}_{t}$, moreover, $p(h)=f_{IG} (h \vert 2,\;3)$ and $p(h_{s} )=f_{IG} (h_{s} \vert 2,\;3)$;

• $p(\varphi ) \propto f_{N,1}(\varphi \mid 0,\; 100) I_{(-1,1)}(\varphi )$, – the normal density with mean zero and variance 100, truncated by the restriction $\mid \varphi \mid < 1$;

• $p(\sigma _{q}^{2} ) = f_{IG}(\sigma _{q}^{2} \mid 1,\; 0.005)$ – the density of the inverted gamma distribution, it is assumed that $E(\sigma _{q}^{-2} )=200, Var(\sigma _{q}^{-2} )=200^{2}$ (see Jacquier et al., 2004);

• $p({\varvec{\Sigma }} ) = f_{IW}({\varvec{\Sigma }} \mid \mathbf{I}_{n}, n+2, n)$ – the inverted Wishart distribution with mean $I_{n}$;

• $p(a,b) \propto I_{(0,1)}(a+b)$ – the uniform distribution over the unit simplex;

• $p(lnq_{0}) = f_{N,1}(lnq_{0} \mid 0,\; 100)$;

• $p(s_{0,{\varvec{\Sigma }} } ) = f_{Exp}(s_{0,{\varvec{\Sigma }} } \mid 1)$ – the exponential distribution with mean 1.

In order to estimate our VAR-MSF models, which contain as many latent variables as the number of observations, we resort to MCMC methods which allow for generating a pseudorandom sample from the posterior distribution. The MCMC methods adapted to our models are presented in Pajor and Wróblewska (2017). Simulation from the predictive distribution is performed by generating pseudorandom values from posterior distribution of parameters and latent variables, and by inserting them into the sampling distributions of future observables and latent variables. In other words, at each step of Gibbs algorithm (for each simulated vector of parameters and latent variables) $\mathbf{x}_{f}$ and $\mathbf{q}_{f}$ are drawn from the sampling predictive distributions. The resulting sequence of future observables and latent variables is a simulation from the predictive distribution (expressed in 11). The sampling scheme is the following:

• Step 1. Set $i=0$ and get starting values for the vector of parameters ${\varvec{\theta }} ^{(i)}$ and for the vector of latent variables $\mathbf{q}_{.T}^{(i)}$;

• Step 2. Generate ${\varvec{\theta }}_{1}^{(i+1)}=(a,b,s_{0,{\varvec{\Sigma }}},vec({\varvec{\Sigma }})')'^{(i+1)}$ from the full conditional posterior distribution of the parameter, using the sequential Metropolis-Hastings algorithm. The proposal distribution used to simulate ${\varvec{\theta }}_{1}^{(i+1)}$ is a truncated Student t distribution with 3 degrees of freedom, centered at previous values of the chain. The covariance matrix of the Student t distribution is determined by initial draws of the algorithm;

• Step 3. Draw $\varphi ^{(i+1)}$ from a truncated normal distribution;

• Step 4. Draw $(\sigma _{q}^{2})^{(i+1)}$ from an inverted gamma distribution;

• Step 5. Draw $\ln q_{0}^{(i+1)}$ from a normal distribution;

• Step 6. Generate ${\varvec{\theta }}_{2}^{(i+1)}=(vec(\mathbf{A})', vec(\mathbf{B})', vec({\varvec{\Gamma }})',vec({\varvec{\Gamma }}_{s})', h,h_{s}, v)'^{(i+1)}$ from the full conditional posterior distribution of the vector of parameters, using the sequential Metropolis-Hastings algorithm. The proposal distribution used to simulate ${\varvec{\theta }}_{2}^{(i+1)}$ is a truncated normal distribution;

• Step 7. For $t=1, \ldots , T$ generate $q_{t}^{(i+1)}$ from the full conditional posterior distribution of this latent variable, using the independence Metropolis - Hastings algorithm. The proposal distribution used to simulate $q_{t}$ is an inverted gamma distribution;

• Step 8. For $j=1, \ldots , h$ draw $q_{T+j}^{(i+1)}$ from the sampling predictive distribution whose density is a product of log-normal densities;

• Step 9. For $j=1, \ldots , h$ draw $\mathbf{x}_{T+j}^{(i+1)}$ from the conditional (given $q_{T+j}^{(i+1)}$) sampling predictive distribution whose density is a product of multivariate normal densities;

• Step 10. Set $i=i+1$ and return to Step 2 until convergence is achieved.

Details on the full conditionals of parameters and the latent variables, as well as proposals distributions can be found in Pajor and Wróblewska (2017).

3 Predictive Bayes factor

Comparing and evaluating the predictive performance of models requires the use of inference methods for predictive accuracy. The Bayesian approach delivers the concept related to the marginal likelihood and predictive likelihood, which are relevant for the context of the comparison of models. Because “there is no distinction between a model’s adequacy and its out of sample prediction record.” (see Geweke, 2005, p. 23), we can start with the model comparison. Let us assume that $M_{1}, \ldots , M_{m}$ are mutually exclusive (non-nested) and jointly exhaustive models. The posterior probability of model $M_{i}$ is

$$\begin{aligned} p(M_{i} \vert \mathbf{x}_{.T}^{o} )=\frac{p(\mathbf{x}_{.T}^{o} \vert M_{i} )p(M_{i} )}{\sum \limits _{j=1}^m {p(\mathbf{x}_{.T}^{o} \vert M_{i} )p(M_{i} )} }, \quad i = 1, 2, ..., m, \end{aligned}$$

(15)

where $p(M_{i} )$ and $p(\mathbf{x}_{.T}^{o} \vert M_{i} )$ denote a prior probability of model $M_{i}$ and the marginal likelihood, respectively. The marginal likelihood is defined as a value of the marginal probability density function for $\mathbf{x}_{.T}$ in observed data, $\mathbf{x}_{.T}^{o}$, and thus it is a real number (see Geweke, 2005). The marginal probability density function for $\mathbf{x}_{.T}$ is

$$\begin{aligned} p(\mathbf{x}_{.T} \vert M_{i} )=\int {p(\mathbf{x}_{.T} \vert {\varvec{\theta }}_{i} ,\mathbf{q}_{.Ti} ,M_{i} )p(\theta _{i} ,\mathbf{q}_{.Ti} \vert M_{i} )\;d{\varvec{\theta }}_{i} \;d\mathbf{q}_{.Ti} } , \end{aligned}$$

(16)

where ${\varvec{\theta }}_{i}$ and $\mathbf{q}_{.Ti}$ denote the vector of parameters and the vector of latent variables, respectively, in the model $M_{i}$. As it is pointed out by Geweke (2005, p. 23), the marginal density “is a prediction of what the data will be, before they are observed”.

To compare two econometric models, their ratio of posterior probabilities (called the posterior odds ratio) can be used. For any pair of competing models, $M_{i}$ and $M_{j}$, the posterior odds ratio in favor of the model $M_{i}$ is given by the following:

$$\begin{aligned} \frac{p(M_{i} \vert \mathbf{x}_{.T}^{o} )}{p(M_{j} \vert \mathbf{x}_{.T}^{o} )}=\frac{p(\mathbf{x}_{.T}^{o} \vert M_{i} )}{p(\mathbf{x}_{.T}^{o} \vert M_{j} )}\times \frac{p(M_{i} )}{p(M_{j} )}, \end{aligned}$$

(17)

where $p(M_{i} )/p(M_{j} )$ is the prior odds ratio, and $p(\mathbf{x}_{.T}^{o} \vert M_{i} )/p(\mathbf{x}_{.T}^{o} \vert M_{j} )$ is the ratio of the marginal data density, called the Bayes factor. Thus the posterior odds ratio relating to models $M_{i}$ and $M_{j}$ is the product of the Bayes factor pertaining to models $M_{i}$ and $M_{j}$ and of the prior odds ratio. In turn, the marginal probability density function for $\mathbf{x}_{.T}$ in model $M_{i}$ can be expressed as the product of conditional distributions:

$$\begin{aligned} p(\mathbf{x}_{.T} \vert M_{i} )=\prod \limits _{t=1}^T {p(\mathbf{x}_{t} \vert \mathbf{x}_{.t-1} ,M_{i} )} . \end{aligned}$$

(18)

Thus the Bayes factor in favor of the model $M_{i}$ versus model $M_{j}$ can be expressed as follows (Geweke and Amisano, 2010, p. 229):

$$\begin{aligned} \frac{p(\mathbf{x}_{.T}^{o} \vert M_{i} )}{p(\mathbf{x}_{.T}^{o} \vert M_{j} )}=\frac{\prod \limits _{t=1}^T {p(\mathbf{x}_{t}^{o} \vert \mathbf{x}_{.t-1}^{o} ,M_{i} )} }{\prod \limits _{t=1}^T {p(\mathbf{x}_{t}^{o} \vert \mathbf{x}_{.t-1}^{o} ,M_{j} )} }=\prod \limits _{t=1}^T {\frac{PL_{M_{i} } (t)}{PL_{M_{j} } (t)}} , \end{aligned}$$

(19)

where $PL_{M_{i} } (t)=p(\mathbf{x}_{t}^{o} \vert \mathbf{x}_{.t-1}^{o} ,M_{i} )$ denotes the one-step-ahead predictive likelihood in model $M_{i}$, $\mathbf{x}_{.t-1}^{o} =[\mathbf{x}_{1}^{o} ,\ldots ,\mathbf{x}_{t-1}^{o} ]$. The one-step-ahead predictive likelihood, which is a real number, can be calculated as follows:

$$\begin{aligned} PL_{M_{i} } (t)=\int {p(\mathbf{x}_{t}^{o} \vert \mathbf{x}_{.t-1}^{o} ,{\varvec{\theta }}_{i} ,\mathbf{q}_{.ti} ,M_{i} )p({\varvec{\theta }}_{i} ,\mathbf{q}_{.ti} \vert \mathbf{x}_{.t-1}^{o} ,M_{i} )\;d {\varvec{\theta }}_{i} \;d\mathbf{q}_{.ti} }, \end{aligned}$$

(20)

where $\mathbf{q}_{.ti} =(q_{1i} ,\ldots , q_{ti} )'$. The approximation of $PL_{M_{i} } (t)$ is:

$$\begin{aligned} P\hat{{L}}_{M_{i} } (t)=\frac{1}{M}\sum \limits _{d=1}^M {p(\mathbf{x}_{t}^{o} \vert \mathbf{x}_{.t-1}^{o} ,{\varvec{\theta }}_{i}^{(d)},\mathbf{q}_{.ti}^{(d)},M_{i} )} , \end{aligned}$$

(21)

where $\{{\varvec{\theta }}_{i}^{(d)},\mathbf{q}_{.ti}^{(d)}\}_{d=1}^{M}$ are drawn from $p({\varvec{\theta }}_{i} ,\mathbf{q}_{.ti} \vert \mathbf{x}_{.t-1}^{o} ,M_{i})$, see also Pajor (2021). $PL_{M_{i} } (t)$ constitutes a measure of how well model $M_{i}$ predicts the observation $\mathbf{x}_{t}^{o}$ conditional on $\mathbf{x}_{.t-1}^{o}$. To compare how well alternative models predict the same set of observations, the predictive Bayes factor can be applied. The predictive Bayes factor in favor of $M_{i}$ over $M_{j}$ for observation t is defined as a ratio of the predictive likelihoods: $PL_{M_{i} } (t)/PL_{M_{j} } (t)$. From equation (19) it can be seen that the Bayes factor can be expressed in terms of predictive Bayes factors.

Let us assume that $T < S$. Then, the predictive likelihood, $p(\mathbf{x}_{.S}^{o,T+1} \vert \mathbf{x}_{.T}^{o} ,M_{i})=\prod \limits _{t=T+1}^S {PL_{M_{i} } (t)}$, is a measure of how well the model $M_{i}$ predicts the data $\mathbf{x}_{.S}^{o, T+1} =[\mathbf{x}_{T+1}^{o} ,\ldots ,\mathbf{x}_{S}^{o}]$ conditional on $\mathbf{x}_{.T}^{o}$. For two models we obtain the following:

$$\begin{aligned} \frac{p(\mathbf{x}_{.S}^{o,T+1} \vert \mathbf{x}_{.T}^{o} ,M_{i} )}{p(\mathbf{x}_{.S}^{o,T+1} \vert \mathbf{x}_{.T}^{o} ,M_{j})}=\prod \limits _{t=T+1}^S {\frac{PL_{M_{i} } (t)}{PL_{M_{j} } (t)}} , \end{aligned}$$

(22)

and consequently the cumulative log predictive Bayes factor for period $T+1$ through S can be calculated as follows:

$$\begin{aligned} \log \left[ {\frac{p(\mathbf{x}_{.S}^{o,T+1} \vert \mathbf{x}_{.T}^{o} ,M_{i} )}{p(\mathbf{x}_{.S}^{o,T+1} \vert \mathbf{x}_{.T}^{o} ,M_{j} )}} \right] =\sum \limits _{t=T+1}^S {\log \left[ {\frac{PL_{M_{i} } (t)}{PL_{M_{j} } (t)}} \right] }. \end{aligned}$$

(23)

The formula (22) shows that the predictive Bayes factor is a multiplicative updating factor applied to the predictive likelihood, after the individual observation that produces the new predictive likelihood. Each individual observation contributes to the evidence of superiority of one model over another. In equations (22) and (23) the accumulation of this evidence starts at $t=T+1$, and thus, if we were to regard $p({\varvec{\theta }}_{i} ,\mathbf{q}_{.Si} \vert \mathbf{x}_{.T}^{o} ,M_{i} )$ as the prior distribution for ${\varvec{\theta }}_{i},\mathbf{q}_{.Si}$ (that is, if $\mathbf{x}_{.T}^{o}$ were to be treated as a training sample), then the ratio (22) would have the same interpretation as the Bayes factor. In other words, the first T observations are used to update the prior distribution, whereas the remaining ones are used to compare the models. Further details can be found in Geweke (2005) and Geweke and Amisano (2010).

It is worth mentioning that the use of the logarithm of the Bayes factor is equivalent to the use of the so-called ignorance or logarithmic score (see Gneiting & Raftery, 2007). The logarithm of the Bayes factor is the difference of the logarithmic scores for corresponding two models. Thus, the predictive Bayes factor is equivalent to the difference in the logarithmic score.

4 Forecast evaluation with probability integral transformations

The predictive Bayes factor measures the relative predictive performances of models. It depends only on the predictive probability densities evaluated at the observed values of the future data. An alternative, but non-Bayesian, assessment of the predictive performance of a model is provided by the probability integral transformation (PIT) of Rosenblatt (1952). The idea based on the PIT derives from the fact that, if a random variable z has the cumulative distribution function F, then F(z) has the uniform distribution over the interval [0, 1]. Let $\left\{ {x_{j;t-1+h}^{o} } \right\} _{t=T+1}^{T+N}$ be the realized values of $x_{j;t-1+h}$ at time $t=T+1,\ldots ,T+N$, and let $\hat{{p}}_{j} (u\vert \mathbf{x}_{.t-1}^{o} ,M_{i} )$ be the assessment of the conditional predictive density for the j-th component of vector $\mathbf{x}_{t-1+h}$ in the model $M_{i}$. The PIT corresponding to model $M_{i}$ as well as to the sequence $\left\{ {x_{j;t-1+h}^{o} } \right\} _{t=T+1}^{T+N}$ is a sequence of values of the cumulative density function:

$$\begin{aligned}&z_{j;t-1+h} =\int \limits _{-\infty }^{x_{j;t-1+h}^{o} } {\hat{{p}}_{j} (u\vert \mathbf{x}_{.t-1}^{o} ,M_{i} )} \;du\nonumber \\&\quad \equiv \hat{{F}}_{j} (x_{j;t-1+h}^{o} \vert \mathbf{x}_{.t-1}^{o} ,M_{i} ), j=1, \ldots , n. \end{aligned}$$

(24)

Under some regularity conditions (see Diebold et al., 1998) and if the realized values $\left\{ {x_{j;t-1+h}^{o} } \right\} _{t=T+1}^{T+N}$ are generated by the predictive distribution $p_{j} (u\vert \mathbf{x}_{.t-1}^{o}, M_{i} )$, then $\hat{{F}}_{j} (x_{j;t-1+h}^{o} \vert \mathbf{x}_{.t-1}^{o}, M_{i})$ has a uniform distribution over the interval [0, 1]. Moreover, if $h=1$, then the sequence $\left\{ {z_{j;t-1+h} } \right\} _{t=T+1}^{T+N}$ is distributed i.i.d. uniform [0, 1] ex ante (see Geweke & Amisano, 2010). The uniformity of the PIT can be tested, e.g., using the Kolmogorov-Smirnov or Anderson–Darling tests (see Rossi & Skhposyan, 2014). The test statistics are as follows:

• Kolmogorov-Smirnov test (KS, Kolmogorov, 1933; Smirnov, 1948):

  $$\begin{aligned} KS_{j} =\sqrt{N} \max _{t=1,2,\ldots ,N} {\max } \left\{ {\left| {z_{j,t}^{*} -t {/} N} \right| ,\left| {z_{j,t}^{*} -{\left( {t-1} \right) } {/} N} \right| } \right\} \end{aligned}$$

• Anderson-Darling test (AD, Anderson & Darling, 1952, 1954):

  $$\begin{aligned} AD_{j} =-N-\frac{1}{N}\sum \limits _{t=1}^N {(2t-1)\ln \left( {z_{j,t}^{*} \left( {1-z_{j,N+1-t}^{*} } \right) } \right) } \end{aligned}$$

where $\left\{ {z_{j;t-1+h}^{*} } \right\} _{t=T+1}^{T+N}$ denotes the values of $\left\{ {z_{j;t-1+h} } \right\} _{t=T+1}^{T+N}$ in ascending order.

5 Empirical results

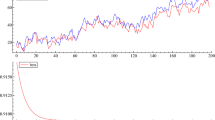
In this part of the paper we analyze financial data of daily quotations on two major Polish exchange rates, PLN/EUR and PLN/USD, and on EUR/USD (see Fig. 1). We consider the exchange rates, where the cointegrating vector may be assumed to be known a priori, in order to compare the forecast performance of our models in the presence of the long-run relationship and time-varying volatility.

Fig. 1

The Polish official exchange rates (left axis) and the euro value of the US dollar (right axis), expressed in logarithms (in hundreds). Source of the data: https://www.nbp.pl/home.aspx?f=/kursy/arch_a.html in the case of the Polish official exchange rates; https://stooq.com/ in the case of the EUR/USD exchange rate

Following Pajor and Wróblewska (2017), we consider two average daily Polish official exchange rates downloaded from the website of the National Bank of Poland: the zloty (PLN) values of the euro (EUR/PLN, $y_{2,t}$), and the zloty values of the US dollar (USD/PLN, $y_{3,t}$), over the period from January 2, 2013 to February 3, 2017. Due to the fact that the Polish official exchange rates are linked to the exchange rates quoted on Forex, we introduce the euro value of the US dollar, downloaded from http://stooq.com: EUR/USD ($y_{1,t}$). The dataset of hundreds of logarithms of exchange rates consists of 1032 observations (for each series). The first five observations are treated as an initial condition, thus $T = 1027$. We consider one-step-ahead predictions during the period beginning on February 3, 2017 and ending on August 8, 2017, thus $S = T+N = 1027 + 130 = 1157$. We calculate predictive distributions of $\mathbf{x}_{t}$ based on the whole dataset available at time $T + i$ for each $i = 0, 1, \ldots , N$ (up to $T+N=1162$). Thus, we obtained 130 predictive distributions for a 1-day forecast horizon. The computations are based on the 30000 Markov chain Monte Carlo posterior samples (after having burnt 30000 cycles) in each model. Due to the typical properties of daily growth rates of exchange rates and the relationship: (EUR/PLN)/(USD/PLN) $\approx$ EUR/USD, we consider VEC-MSF, VEC-SBEKK, and VEC-MSF-SBEKK models with one and two cointegrating vectors ($r = 1, 2$), containing an unrestricted vector of constants ($d = 3$), and the number of lags equal to 2 ($k=2$). The above approximate relation among exchange rates (in logarithmic terms) yields the cointegrating vector $(1,-1,1)$ and the long-run relationship: $100 \ln y_{1,t}= 100 \ln y_{2,t}- 100 \ln y_{3,t}$, i.e., $x_{1,t}=x_{2,t}-x_{3,t}$. For the sake of comparison, we also consider random walk with drift processes ($k=1, r = 0$), VEC models with constant conditional covariance matrix, VAR-SBEKK, and the VAR-MSF-SBEKK model for the levels of these processes ($r=3$). The latter model is inadequate for the type of the data considered, but we use it to check the relative forecasting performance of the ”wrong” model.

5.1 A comparison of models with the predictive Bayes factor

The overall ranking of the compared models $M_{i}$ as well as $log(p(\mathbf{x}_{f}|\mathbf{x}_{.T}, M))$, and also the decimal logarithms of the predictive Bayes factors in favor of the VEC-MSF-SBEKK specification ($log(B_{1,i})$) are shown in Table 1.

Table 1 Decimal logs of predictive Bayes factors in favor of VEC-MSF-SBEKK (d = 3, N = 130)

Table 1 provides the log predictive likelihoods and the log predictive Bayes factors in favor of the VEC-MSF-SBEKK model over thirteen selected specifications of the VEC model. As expected, the highest log predictive likelihood is in VEC-MSF-SBEKK with two cointegrating vectors ($r=2$). The random walk model with drift and with constant conditional covariance matrix has the lowest predictive likelihood, rounding out the ranking. Models with time-varying condition covariance matrix and with one or two cointegrating vectors occupy four of the top positions. Using the VEC process together with the MSF-SBEKK covariance structure seems to be a powerful modeling strategy. Models with one or two cointegrating vectors have more explanatory power than models with $r=0$. Even the VEC specification with constant conditional covariance matrix, but with one cointegrating vector, prevails over the VEC-SBEKK, the VEC-MSF and over the VEC-MSF-SBEKK structures without any cointegration relationship in terms of the predictive data density value (a natural Bayesian measure of fit). Capturing the long-run relationship (if one exists) turned out to be more important from a predictive point of view than allowing the conditional covariance matrix to be time-variable (stochastic). In other words, if the long-run relationships exist, allowing for the cointegration relationships in econometric models is more important than allowing conditional covariances to vary over time. It is worth mentioning that in the case of the Polish macroeconomic data the most important feature for the predictive ability of the vector autoregression models is allowing for changing covariance matrices, while the number of long-run relationships is of lesser importance, see Wróblewska and Pajor (2019).

Fig. 2

Cumulative log predictive Bayes factors in favor of the VEC-MSF-SBEKK model over selected ones, and quantiles of predictive distributions

Fig. 3

Quantiles of predictive distributions and “future” observations

It is no surprise that the VEC-SBEKK models fit the data much worse (in terms of the predictive Bayes factors) than their alternative variants with multiplicative stochastic factors, but still better than the VEC specifications with constant conditional covariance matrix. The VEC-MSF specification uses one latent process common to all conditional variances and covariances. This assumption of common dynamics leads to constant conditional correlations. Nevertheless, the VEC-SBEKK models, which do not use any latent processes and therefore are less flexible in dealing with outliers, appear still worse in term of the predictive Bayes factor.

The plots of cumulative log predictive Bayes factors for $t=T+1,\ldots ,T+S$ are presented in Fig. 2. The sequence of cumulative log predictive Bayes factors in favor of the VEC-MSF-SBEKK structure with $k=2$, $d=3$, $r=1$ (called MSF-SBEKK231) over the one with $k=2$, $d=3$, $r=0$ (called MSF-SBEKK230) tends to increase with the rise of the number of predictions. The log predictive Bayes factors in favor of the MSF-SBEKK231 specification over the MSF-SBEKK232 one are less than 1 each. According to the scale presented by Kass and Raftery (1995), it is a negligible strength of evidence against the MSF-SBEKK232 model. Furthermore, the cumulative log predictive Bayes factors in favor of the MSF-SBEKK231 model over the VAR-MSF with $k=2$, $d=3$, $r=1$ (MSF231) indicate strong but not very strong (decisive) evidence against the latter. The right panels of Fig. 2 depict quantiles of predictive distributions obtained in the VEC-MSF-SBEKK model with $r=1$ (very similar results were obtained for $r=2$). Black points represent the real returns. As can be seen, the realized returns (out-of-sample data) lie in areas of high values of predictive densities. As expected, a very small value of each predictive Bayes factor in favor of VAR-MSF-SBEKK for the levels of the exchange rates (with $r=3$) indicates poor predictive potential of the model. As can be seen from the Fig. 3, the predictive distributions obtained in VEC-MSF-SBEKK model with $r=3$ are more diffused than those obtained in the same specification of the model, but with $r=1$. This unsuitable specification leads to more diffuse predictive distributions and large predictive Bayes factors in favor of the VEC-MSF models. It is worth noting that, for the median of the 1-day ahead predictive distribution as a point predictor the root mean square forecast errors (RMSFE) obtained in both models are almost the same. As a by-product, our results show that the RMSFE is not a good indicator of predictive performance of models.

5.2 Forecast evaluation with PITs

An alternative, but non-Bayesian, assessment of the predictive performance of a model is provided by the probability integral transformation (PIT). The PIT is the inverse of the sequence of ex ante predictive cumulative distribution functions evaluated on the sequence of “realized” observation (ex post). Figures 4, 5, 6 provide a further comparison of the predictive performances of the VEC-MSF-SBEKK, VEC-MSF, and VEC models with the use of PIT values. Histograms of PIT values allow for an informal assessment of their uniformity.

Fig. 4

PIT for selected VEC-MSF-SBEKK models with $r = 1$ and $r =2$. The histograms depict the empirical distributions of the PITs. Solid lines represent the numbers of draws that are expected to fall into each bin under an U(0, 1) distribution

Fig. 5

PIT for selected VEC-MSF and VEC models. Meaning of symbols used the same as in Fig. 4

Fig. 6

PIT for selected VEC-MSF-SBEKK models with $r = 0$ and $r =3$. Meaning of symbols used the same as in Fig. 4

In all models (excluding the VAR-MSF-SBEKK one with $r=3$), the histograms of the PITs for the EUR/USD exchange rates show that more realizations fall in the right tail of the predictive distribution than would be expected if the PITs were uniformly distributed. Overall, there is a lack of uniformity for density forecasts of the EUR/USD exchange rates. The correct specification of the predictive distributions of the EUR/USD exchange rates is rejected in all cases. The figures also provide a visual presentation of the misspecification in the PITs: future realizations of the EUR/USD exchange rates are under-predicts. The evident inadequacy of the predictive densities for EUR/USD in the right tail can be explained by the unexpected depreciation of the US dollar to the euro in the forecasting period. In Kębłowski et al. (2020) it has been shown that in the long-run the exchange rates of the EUR/USD and EUR/PLN are driven by crude oil prices, by the European Central Bank’s monetary policy and by the monetary policy decisions of the Federal Reserve System (see also Ghalayini, 2017).

The histograms of the PITs in the VAR-MSF-SBEKK (with $r=3$) show that more ”future” observations/realizations fall in the middle of the distribution than would be expected if the PITs had the uniform distributions.

To test the correctness of the specification of the predictive densities (more specifically: whether the PIT is uniform) the Kolmogorov-Smirnov and Anderson-Darling tests are used. Figures 4, 5, 6 provide results for the Kolmogorov-Smirnov (labelled ”KS”) and Anderson-Darling (labeld ”AD”) tests of uniformity of the distribution of the PITs. In all models, the uniformity of PITs for the EUR/USD exchange rates is rejected. Both the Kolmogorov-Smirnov and Anderson-Darling tests manifest empirical evidence against the correct specification of the VAR-MSF-SBEKK (with $r=3$).

Table 2 p -value for autocorrelation test of PIT and $PIT^{2}$ for selected models (lags: 10, k = 2, d = 3)

Regarding the independence of the PITs, the Ljung–Box test of no autocorrelation in the PITs and in the squares of the PITs has been used. Table 2 reports the p-values of the LB tests for serial correlation of PITs as well as of their squares. No such autocorrelation has been detected.

6 Conclusion

This paper evaluates the predictive performance of VEC-SV models in the context of modeling financial time series and in the presence of long-run relationships. Financial data of daily quotations on three exchange rates: PLN/EUR, PLN/USD, and EUR/USD was analyzed. As there exists at least one long-run relationship among the exchange rates (which is known a priori), we could check whether these models which account for long-run relationships perform better than those without the relationships. The empirical findings indicate that, overall, the VAR models with one or two cointegration relationships perform better than those without cointegration relationship. The VAR models with constant conditional covariance matrix are dominated by those with time-varying conditional covariances. However, if the long-run relationships exist, allowing for the cointegration relationships in econometric models is more important than allowing for conditional covariance matrix to vary over time. The analysis of PITs also shows that the predictive distributions are not perfectly fitted. In all models, the uniformity of PITs for the EUR/USD exchange rates is rejected. More ”realized” observations fall in the right tail of the predictive distribution than would be expected if the PITs were uniformly distributed. The lack of uniformity of the distribution of the PIT suggests that the VEC-SV models considered should be modified by allowing for asymmetries of conditional distributions. This can be achieved by using, e.g., copulas or skew normal distributions.