A Fuzzy Multi Objective Inventory Model with Production Cost and Set-up-Cost Dependent on Population

Abstract

In this paper, I have developed a multi item production inventory model for the non-deteriorating items with constant demand rate under the limitation on set up cost. The production price and set-up price are the most vital problem within the inventory system of the marketplace in international. Here the production cost is dependent on the demand as well as populations. Set up cost is dependent on the average inventory level. Holding cost is the most challenging issue in the business world. In order to reduce the holding cost, the holding cost function has been considered as on the number of peoples. Due to uncertainty all the cost parameters are taken as the generalized triangular fuzzy number. Multi objective fuzzy inventory model has been solved by various techniques like Fuzzy programming technique with hyperbolic membership function, Fuzzy non-linear programming technique and Fuzzy additive goal programming technique. Numerical example is given to illustrate the inventory model. Sensitivity analysis and the graphical representations have been shown to illustrate the reality of the inventory model.

1 Introduction

An inventory model deals with decisions that minimize the total average cost or maximize the total average profit. In that way to construct a real life mathematical inventory model we use various assumptions and notations and approximations.

In the ordinary inventory system inventory cost i.e. set-up cost, holding cost, deterioration cost, etc. are taken fixed amounts but in real life inventory systems these costs are not always fixed. So consideration of fuzzy variables is more realistic and interesting.

Harris [1] first developed the inventory model in 1913. Ghare and Schrader [2] developed a model for exponentially decaying inventory systems. Philip [3] considered a generalized EOQ model for items with Weibull distribution. Sana [4] presented a deterministic EOQ model with delay in payments and time varying deterioration rate. Sarkar [5] studied a finite replenishment model with increasing demand under inflation. Sarkar [6] discussed an EOQ model with delay in payments and stock dependent demand in the presence of imperfect production. Khanra, et al. [7] presented an inventory model with time dependent demand and shortages under trade-credit policy. Sarkar, Saren and Wee [8] studied an inventory model with variable demand, component cost and selling price for deteriorating items. Sarkar [9] developed an EOQ model with delay in payments and time varying deterioration rate. Sarkar and Sarkar [10] presented variable deterioration and demand-an inventory model. Sarkar, Saren and Leopoldo [11] discussed an inventory model with trade-credit policy and variable deterioration for fixed lifetime products. Mishra and Singh [12] considered computational approach to an inventory model with ramp-type demand and linear deterioration. Ghosh, Sarkar and Chaudhuri [13] considered a multi-item inventory model for deteriorating items in limited storage space with stock-dependent demand. Alfares and Ghaithan [14] developed the inventory and pricing model with price-dependent demand, time-varying holding cost, and quantity discounts. Das et al. [15] discussed the preservation technology in inventory control system with price dependent demand and partial backlogging. Liuxin et al. [16] presented optimal pricing and replenishment policy for deteriorating inventory under stock-level-dependent, time-varying and price-dependent demand. Chakraborty et al. [17] developed multi-warehouse partial backlogging inventory system with inflation for non-instantaneous deteriorating multi-item under imprecise environment. Shaikh et al. [18] studied price discount facility in an EOQ model for deteriorating items with stock-dependent demand and partial backlogging. Sarkar, Mandal and Sarkar [19] studied on preservation of deteriorating seasonal products with stock-dependent consumption rate and shortages. Singh et al. [20] developed on partially backlogged EPQ model with demand dependent production and non-instantaneous deterioration. Pandoet al. [21] discussed optimal lot-size policy for deteriorating items with stock-dependent demand considering profit maximization. Mondal et al. [22] studied optimization of generalized order-level inventory system under fully permissible delay in payment. Das [23] has developed a fuzzy multi objective inventory model of demand dependent deterioration including lead time. Poswal et al. [24] have preddsented the investigation and analysis of fuzzy EOQ model for price sensitive and stock dependent demand under shortages.

In the real life system, any project costs more or less than the amount of exact allocated. So fuzzy system is very important. The concept of fuzzy set theory was first introduced by Zadeh [25] in 1965. Afterward Zimmermann [26] applied the fuzzy set theory concept with some useful membership functions to solve the linear programming problem with some objective functions. Roy and Maity [27] developed a fuzzy inventory model with constraints. Multi item is also interesting in real life in the inventory system. Roy and Maiti [28] discussed the multi-objective inventory models of deteriorating items with some constraints in a fuzzy environment. Maity [29] presented fuzzy inventory model with two warehouses under possibility measure in fuzzy goal. Garai et al. [30] discussed expected Value of exponential fuzzy number and its application to multi-item deterministic inventory model for deteriorating items. Garai et al. [31] developed a multi-item inventory model with fuzzy rough coefficients via fuzzy rough expectation. Das and Islam [32] studied multi-objective two echelon supply chain inventory model with customer demand dependent purchase cost and production rate dependent production cost. Das and Islam [33] considered multi objective fuzzy inventory model with deterioration, price and time dependent demand and time dependent holding cost, also Das and Islam [34] discussed production cost and set-up-cost dependent fuzzy multi objective inventory model under space constraints in the fuzzy environment. Tayyab et al. [35] worked on the sustainable development framework for a cleaner multi-item multi-stage textile production system with a process improvement initiative. Malik and Sarkar [36] considered disruption management in a constrained multi-product imperfect production system. Garai, Chakraborty and Roy [37] presented multi-objective inventory model with both stock-dependent demand rate and holding cost rate under fuzzy random environment. Soni and Suthar [38] considered EOQ model of deteriorating items for fuzzy demand and learning in fuzziness with finite horizon. Bera et al. [39] discussed two-phase multi-criteria fuzzy group decision making approach for supplier evaluation and order allocation considering multi-objective, multi-product and multi-period. Mandal [40] has developed bipolar pythagorean fuzzy sets and their application in multi-attribute decision making problems. Das [41] has developed multi item inventory model include lead time with demand dependent production cost and set-up-cost in fuzzy environment. De and Roy and Bhattacharya [42] have presented solving an EPQ model with doubt fuzzy set in a robust intelligent decision-making approach. Further we study the references [43,44,45,46,47].

The remaining portion of this research work is organized as follows: Sect. 2 presents notation, assumption, and formulation of the inventory model as a nonlinear constraint optimization problem. Section 3 develops the fuzzy model, due to uncertainty all the cost parameters. Section 4 for the solution procedure is shown. Section 5 solves a numerical example to verify the inventory model. In Sect. 6, sensitivity analysis and the graphical representations have been shown to illustrate the inventory model. Finally, Sect. 7 provides conclusions and some opportunities for future research.

2 Notation, Assumption and Formulation of the Inventory Model

2.1 Notation

$S_{i}$: Set-up cost per order for ith item.

$h_{i}$: Holding cost per unit per unit time for ith item.

$M$: Total expected set-up-cost.

$P$: Population in the neighborhood of sell center.

$T_{i}$: The length of cycle time for $i$th item, $T_{i} > 0.$

$D_{i}$: Demand rate per unit time for the ith item.

$I_{i} \left( t \right)$: Inventory level of the ith item at time t.

$Q_{i}$: The order quantity for the duration of a cycle of length $T_{i}$ for ith item.

$C_{p}^{i}$: Unit production cost of the ith item.

$TAC_{i} (Q_{i} ,D_{i} )$: Total average profit per unit for the ith item.

$\widetilde{{TAC_{i} }}(Q_{i,} D_{i} )$: Fuzzy total average profit per unit for the ith item.

2.2 Assumptions

• 1. The inventory system with multi item.

• 2. The replenishment occurs instantaneously at infinite rate.

• 3. The lead time is negligible.

• 4. Shortages are not allowed.

• 5. Demand rate is constant.

• 6. The unit production cost $C_{p}^{i}$ is inversely related to the demand rate $D_{i}$ and $P$. So we take the following form $C_{p}^{i} \left( {{ }D_{i} , P} \right) = \delta_{i} D_{i}^{{ - a_{i} }} P^{{ - b_{i} }}$, where $\delta_{i} > 0,$ ${ }0 < b_{i} < 1$ and $a_{i} > 1$ are constant real numbers.

• 7. The set-up-cost $S_{i}$ is proportionally related to the average inventory level. So we take the form $S_{i} \left( {Q_{i} } \right) = { }\alpha_{i} \left( {\frac{{Q_{i,} }}{2}} \right)^{{{ }\beta_{i} }}$ where $0 < { }\beta_{i} <1,\left\langle { { }\alpha_{i} }>0 \right\rangle$ are constant real numbers.

• 8. $h_{i} \left( P \right) = \mu_{i} P^{{ - d_{i} t}}$, where $\mu_{i} > 0,$ and ${ }0 < d_{i} < < 1$ are constant real numbers.

2.3 Model Formation in Crisp Model of ith Item

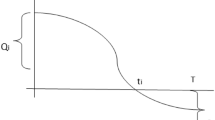
The inventory level for ith item is shown in Fig. 1. During the time period $[0,{T}_{i}]$ the stock reduces due to only demand rate. In that time period, the inventory level is defined by the governing differential equation-

$$ \frac{{dI_{i} \left( t \right)}}{dt} = - D_{i} ,\;0 \le t \le T_{i} $$

(1)

Fig. 1

Inventory level for ith item

With boundary condition, $I_{i} \left( 0 \right) = Q_{i}$, $I_{i} \left( {T_{i} } \right) = 0$.

Solving the above differential Eq. (1), we get

$$ I_{i} \left( t \right) = D_{i} \left( {T_{i} - t} \right), \;0 \le t \le T_{i} $$

(2)

$$ {\text{and}}\;\;Q_{i} = D_{i} T_{i} . $$

(3)

The model related the various cost as following.

• 1. Average production cost $\begin{aligned} & = \frac{{Q_{i} \delta_{i} D_{i}^{{ - a_{i} }} P^{{ - b_{i} }} }}{{T_{i} }} \\ & = \delta_{i} D_{i}^{{1 - a_{i} }} P^{{ - b_{i} }} \\ \end{aligned}$

• 2. Average holding cost $\begin{aligned} & = \frac{1}{{T_{i} }}\mathop \smallint \limits_{0}^{{T_{i} }} h_{i} \left( P \right)I_{i} \left( t \right)dt \\ & = \frac{{\mu_{i} D_{i}^{2} }}{{Q_{i} }}\left[ {\frac{{Q_{i} }}{{D_{i} d_{i} logP}} + \frac{1}{{\left( {d_{i} logP} \right)^{2} }}\left( {P^{{ - \left( {{\raise0.7ex\hbox{${d_{i} Q_{i} }$} \!\mathord{\left/ {\vphantom {{d_{i} Q_{i} } {D_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{i} }$}}} \right)}} - 1} \right)} \right] \\ \end{aligned}$

• 3. Average set-up-cost $\begin{aligned} & = \frac{{S_{i} }}{{T_{i} }} \\ & = \frac{{\alpha_{i} Q_{i}^{{\beta_{i} - 1}} D_{i} }}{{2^{{\beta_{i} }} }} \\ \end{aligned}$

Total average cost in this inventory model is given by

$$ \begin{aligned}TAC_{i} (Q_{i} ,D_{i} ) &= \delta_{i} D_{i}^{{1 - a_{i} }} P^{{ - b_{i} }} \\ &+ \frac{{\mu_{i} D_{i}^{2} }}{{Q_{i} }}\left[ {\frac{{Q_{i} }}{{D_{i} d_{i} logP}} + \frac{1}{{\left( {d_{i} logP} \right)^{2} }}\left( {P^{{ - \left( {{\raise0.7ex\hbox{${d_{i} Q_{i} }$} \!\mathord{\left/ {\vphantom {{d_{i} Q_{i} } {D_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{i} }$}}} \right)}} - 1} \right)} \right] \\ &+ \frac{{\alpha_{i} Q_{i}^{{\beta_{i} - 1}} D_{i} }}{{2^{{\beta_{i} }} }} \end{aligned}$$

(4)

Therefore the multi objective optimization problem in this inventory model is

$$ \begin{aligned} & {\text{Minimize}}\;\;TAC_{i} (Q_{i} ,D_{i} ) = \delta_{i} D_{i}^{{1 - a_{i} }} P^{{ - b_{i} }}\\&\quad + \frac{{\mu_{i} D_{i}^{2} }}{{Q_{i} }}\left[ {\frac{{Q_{i} }}{{D_{i} d_{i} logP}} + \frac{1}{{\left( {d_{i} logP} \right)^{2} }}\left( {P^{{ - \left( {{\raise0.7ex\hbox{${d_{i} Q_{i} }$} \!\mathord{\left/ {\vphantom {{d_{i} Q_{i} } {D_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{i} }$}}} \right)}} - 1} \right)} \right] + \frac{{\alpha_{i} Q_{i}^{{\beta_{i} - 1}} D_{i} }}{{2^{{\beta_{i} }} }} \\ & {\text{Subject}}\;{\text{to}},\;\;\sum \frac{{\alpha_{i} Q_{i}^{{\beta_{i} - 1}} D_{i} }}{{2^{{\beta_{i} }} }} \le M , Q_{i} > 0,D_{i} > 0, i = 1,2, \ldots \ldots \ldots .n \\ \end{aligned} $$

(5)

3 Fuzzy Model

Generally the parameters for holding cost, unit production cost, and set-up cost are not particularly known to us. Due to uncertainty, we assume all the parameters $\left( {\alpha_{i} ,\beta_{i} ,a_{i} ,b_{i} ,\mu_{i} ,\delta_{i} ,d_{i} ,P} \right)$ as generalized triangular fuzzy number (GTFN) $\left( {\widetilde{{\alpha_{i} }},\widetilde{{\beta_{i} }},\widetilde{{a_{i} }},\widetilde{{b_{i} }},\widetilde{{\mu_{i} }},\widetilde{{\delta_{i} }},\widetilde{{d_{i} }},\tilde{P}} \right)$ as following

$$ \widetilde{{\alpha_{i} }} = \left( {\alpha_{i}^{1} ,\alpha_{i}^{2} ,\alpha_{i}^{3} ;\omega_{{\alpha_{i} }} } \right), 0 < \omega_{{\alpha_{i} }} \le 1;\;\;\widetilde{{a_{i} }} = \left( {a_{i}^{1} ,a_{i}^{2} ,a_{i}^{3} ;\omega_{{a_{i} }} } \right), 0 < \omega_{{a_{i} }} \le 1; $$

$$ \widetilde{{\beta_{i} }} = \left( {\beta_{i}^{1} ,\beta_{i}^{2} ,\beta_{i}^{3} ;\omega_{{\beta_{i} }} } \right), 0 < \omega_{{\beta_{i} }} \le 1;\;\;\widetilde{{b_{i} }} = \left( {b_{i}^{1} ,b_{i}^{2} ,b_{i}^{3} ;\omega_{{b_{i} }} } \right), 0 < \omega_{{b_{i} }} \le 1; $$

$$ \widetilde{{\mu_{i} }} = \left( {\mu_{i}^{1} ,\mu_{i}^{2} ,\mu_{i}^{3} ;\omega_{{\mu_{i} }} } \right), 0 < \omega_{{\mu_{i} }} \le 1;\;\;\widetilde{{d_{i} }} = \left( {d_{i}^{1} ,d_{i}^{2} ,d_{i}^{3} ;\omega_{{d_{i} }} } \right), 0 < \omega_{{d_{i} }} \le 1; $$

$$ \widetilde{{\delta_{i} }} = \left( {\delta_{i}^{1} ,\delta_{i}^{2} ,\delta_{i}^{3} ;\omega_{{\delta_{i} }} } \right), 0 < \omega_{{\delta_{i} }} \le 1;\;\;\tilde{P} = \left( {P^{1} ,P^{2} ,P^{3} ;\omega_{P} } \right), 0 < \omega_{P} \le 1\;\; \left( {i = 1,2, \ldots \ldots \ldots ,n} \right) $$

Then the above crisp inventory model (5) becomes the fuzzy model as

$$ \begin{aligned} & {\text{Minimize}}\;\;\widetilde{{TAC_{i} \left( {Q_{i} ,D_{i} } \right)}} = \widetilde{{\delta_{i} }}D_{i}^{{1 - \widetilde{{a_{i} }}}} \tilde{P}^{{ - \widetilde{{b_{i} }}}}\\&\quad + \frac{{\widetilde{{\mu_{i} }}D_{i}^{2} }}{{Q_{i} }}\left[ {\frac{{Q_{i} }}{{D_{i} \widetilde{{d_{i} }}log\tilde{P}}} + \frac{1}{{\left( {\widetilde{{d_{i} }}log\tilde{P}} \right)^{2} }}\left( {\tilde{P}^{{ - \left( {{\raise0.7ex\hbox{${d_{i} Q_{i} }$} \!\mathord{\left/ {\vphantom {{d_{i} Q_{i} } {D_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{i} }$}}} \right)}} - 1} \right)} \right] + \frac{{\widetilde{{\alpha_{i} }}Q_{i}^{{\widetilde{{\beta_{i} }} - 1}} D_{i} }}{{2^{{\widetilde{{\beta_{i} }}}} }} \\ & {\text{Subject}}\;{\text{to}}\;\;\sum \frac{{\widetilde{{\alpha_{i} }}Q_{i}^{{\widetilde{{\beta_{i} }} - 1}} D_{i} }}{{2^{{\widetilde{{\beta_{i} }}}} }} \le M , Q_{i} > 0,D_{i} > 0, i = 1,2, \ldots \ldots \ldots .n \\ \end{aligned} $$

(6)

In defuzzification of fuzzy number technique, if we consider a GTFN $\tilde{A} = \left( {a,b,c;\omega } \right)$, then the total $\lambda$- integer value of $\tilde{A} = \left( {a,b,c;\omega } \right)$ is

$$ I_{\lambda }^{w} \left( {\tilde{A}} \right) = \lambda \omega \frac{c + b}{2} + \left( {1 - \lambda } \right)\omega \frac{a + b}{2} $$

Therefore we get approximated value of a GTFN $\tilde{A} = \left( {a,b,c;\omega } \right)$ is $\omega \left( {\frac{a + 2b + c}{4}} \right)$ by taking $\lambda = 0.5.$

So we have the approximated values $\left( {\widehat{{\alpha_{i} }},\widehat{{\beta_{i} }},\widehat{{a_{i} }},\widehat{{b_{i} }},\widehat{{\mu_{i} }},\widehat{{\delta_{i} }},\widehat{{d_{i} }},\hat{P}} \right)$ of the GTFN parameters. So the above model $\left( 6 \right)$ reduces to the multi objective inventory model (MOIM) as following

$$ \begin{aligned} & {\text{Minimize}}\;\;\widehat{{TAC_{i} \left( {Q_{i} ,D_{i} } \right)}} = \widehat{{\delta_{i} }}D_{i}^{{1 - \widehat{{a_{i} }}}} \hat{P}^{{ - \widehat{{b_{i} }}}} \\&\quad+ \frac{{\widehat{{\mu_{i} }}D_{i}^{2} }}{{Q_{i} }}\left[ {\frac{{Q_{i} }}{{D_{i} \widehat{{d_{i} }}log\hat{P}}} + \frac{1}{{\left( {\widetilde{{d_{i} }}log\hat{P}} \right)^{2} }}\left( {\tilde{P}^{{ - \left( {{\raise0.7ex\hbox{${d_{i} Q_{i} }$} \!\mathord{\left/ {\vphantom {{d_{i} Q_{i} } {D_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{i} }$}}} \right)}} - 1} \right)} \right] + \frac{{\widehat{{\alpha_{i} }}Q_{i}^{{\widehat{{\beta_{i} }} - 1}} D_{i} }}{{2^{{\widehat{{\beta_{i} }}}} }} \\ & {\text{Subject}}\;{\text{to}}\;\;\sum \frac{{\widehat{{\alpha_{i} }}Q_{i}^{{\widehat{{\beta_{i} }} - 1}} D_{i} }}{{2^{{\widehat{{\beta_{i} }}}} }} \le M , Q_{i} > 0,D_{i} > 0, i = 1,2, \ldots \ldots \ldots .n \\ \end{aligned} $$

(7)

4 Solution Procedure

4.1 Fuzzy Programming Technique with Hyperbolic Membership Function (FPTHMF) for Solving MOIM

Solve the MOIM $(7)$ as a single objective NLP using only one objective at a time and ignoring the others. So we get the ideal solutions. Using the ideal solutions the pay-off matrix is defined as follows:

$$ \begin{array}{*{20}l} {} \hfill \\ {\left( {Q_{1}^{1} ,D_{1}^{1} } \right)} \hfill \\ {\left( {Q_{2}^{2} ,D_{2}^{2} } \right)} \hfill \\ {} \hfill \\ {} \hfill \\ {(Q_{n}^{n} ,D_{n}^{n} )} \hfill \\ \end{array} \left[ {\begin{array}{*{20}l} {TAC_{1} \left( {Q_{1} ,D_{1} } \right)} \hfill & {TAC_{2} \left( {Q_{2} ,D_{2} } \right)} \hfill & \ldots \hfill & {TAC_{n} \left( {Q_{n} ,D_{n} } \right)} \hfill \\ {TAC_{1}^{*} \left( {Q_{1}^{1} ,D_{1}^{1} } \right)} \hfill & {TAC_{2} \left( {Q_{1}^{1} ,D_{1}^{1} } \right)} \hfill & \ldots \hfill & {TAC_{n} \left( {Q_{1}^{1} ,D_{1}^{1} } \right) } \hfill \\ {TAC_{1} \left( {Q_{2}^{2} ,D_{2}^{2} } \right)} \hfill & {TAC_{2}^{*} \left( {Q_{2}^{2} ,D_{2}^{2} } \right)} \hfill & \ldots \hfill & {TAC_{n} \left( {Q_{2}^{2} ,D_{2}^{2} } \right)} \hfill \\ {} \hfill & {} \hfill & \ldots \hfill & \ldots \hfill \\ {} \hfill & {} \hfill & \ldots \hfill & \ldots \hfill \\ {TAC_{1} \left( {Q_{n}^{n} ,D_{n}^{n} } \right)} \hfill & {TAC_{2} \left( {Q_{n}^{n} ,D_{n}^{n} } \right)} \hfill & \ldots \hfill & {TAC_{n}^{*} \left( {Q_{n}^{n} ,D_{n}^{n} } \right)} \hfill \\ \end{array} } \right] $$

${\text{Let}}\;\;U^{k} = {\text{max}}\left\{ {TAC_{k} \left( {Q_{i}^{i} ,D_{i}^{i} } \right),{ }i = 1,2, \ldots .,n} \right\}\; for\;k = 1,2, \ldots .,n$ and $L^{k} = TAC_{k}^{*} \left( {Q_{k}^{k} ,D_{k}^{k} } \right)for k = 1,2, \ldots .,n.$

$$ {\text{Hence}}\;\;U^{k} , L^{k} \;{\text{are}}\;{\text{identified}},\;\;L^{k} \le TAC_{k} \left( {Q_{i}^{i} ,D_{i}^{i} } \right) \le U^{k} , for i = 1,2, \ldots .,n ;k = 1,2, \ldots .,n. $$

(8)

Now objective functions of the problem (7) are considered as fuzzy constraints. Therefore fuzzy non-linear hyperbolic membership functions $\mu_{{TAC_{k} }}^{H} \left( {TAC_{k} \left( {Q_{k} ,D_{k} } \right)} \right)$ for the k^th objective functions $TAC_{k} \left( {Q_{k} ,D_{k} } \right)$ respectively for $k = 1,2, \ldots .,n$ are defined as follows:

$$ \mu_{{TAC_{k} }}^{H} \left( {TAC_{k} \left( {Q_{k} ,D_{k} } \right)} \right) = \frac{1}{2}tanh\left( {\left( {\frac{{U^{k} + L^{k} }}{2} - TAC_{k} \left( {Q_{k} ,D_{k} } \right)} \right)\sigma_{k} } \right) + \frac{1}{2} $$

(9)

here $\alpha_{k}$ are the parameters, $\sigma_{k} = \frac{3}{{{\raise0.7ex\hbox{${\left( {U^{k} - L^{k} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {U^{k} - L^{k} } \right)} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} = \frac{6}{{U^{k} - L^{k} }}$, $k = 1,2, \ldots .,n.$

Using the above membership function, fuzzy non-linear programming problems are formulated as follows:

$$ \begin{aligned} & Max\quad \lambda \\ & {\text{Subject}}\;{\text{to}}\; \frac{1}{2}tanh\left( {\left( {\frac{{U^{k} + L^{k} }}{2} - TAC_{k} \left( {Q_{k} ,D_{k} } \right)} \right)\sigma_{k} } \right) + \frac{1}{2} \ge \lambda ,\;\lambda \ge 0 \\ \end{aligned} $$

(10)

And same constraints and restrictions as the problem (7).

The above non-linear programming problem after simplification we can be formulated as

$$ \begin{aligned} & Max\, y \\ & {\text{Subject}}\;{\text{to}}\;y + \sigma_{k} TAC_{k} \left( {Q_{k} ,D_{k} } \right) \le \frac{{U^{k} + L^{k} }}{2}\sigma_{k} ,y \ge 0 \\ \end{aligned} $$

(11)

And same constraints and restrictions as the problem (7).

The programming problems (11) can be solved by a suitable mathematical programming algorithm and we get the solution of the MOIM (7).

4.2 Fuzzy Programming Technique (Multi-Objective on Max–Min and Additive Operators)

In this technique for solving MOIM (7), first we have to reach equation no. (8) which has been shown in the above. In this technique fuzzy membership functions $\mu_{{TAC_{k} }} \left( {TAC_{k} \left( {Q_{k} ,D_{k} } \right)} \right)$ for the k^th objective functions $TAC_{k} \left( {Q_{k} ,D_{k} } \right)$ respectively for $k = 1,2, \ldots .,n$ are defined as follows:

$$ \mu_{{TAC_{k} }} \left( {TAC_{k} \left( {Q_{k} ,D_{k} } \right)} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\text{for}\;\;TAC_{k} \left( {Q_{k} ,D_{k} } \right) < L^{k} } \hfill \\ {\frac{{U^{k} - TAC_{k} \left( {Q_{k,} D_{k} } \right)}}{{U^{k} - L^{k} }}} \hfill & {\text{for}\;\;L^{k} \le TAC_{k} \left( {Q_{k} ,D_{k} } \right) \le U^{k} } \hfill \\ 0 \hfill & {\text{for}\;\;TAC_{k} \left( {Q_{k} ,D_{k} } \right) > U^{k} } \hfill \\ \end{array} } \right. $$

(12)

4.2.1 Fuzzy Non-linear Programming Technique (FNLP) Based on Max–Min Operator

Using the above membership function, fuzzy non-linear programming problems are formulated as follows:

$$ \begin{aligned} & {\text{Max}}\;\alpha^{\prime} \\ & {\text{Subject}}\;{\text{to}} \\ & TAC_{k} \left( {Q_{k} ,D_{k} } \right) + \alpha^{\prime}\left( {U^{k} - L^{k} } \right) \le U^{k} ,\;\;\text{for}\;\;k = 1,2, \ldots .,n. \\ & 0 \le \alpha^{\prime} \le 1, \\ \end{aligned} $$

(13)

And same constraints and restrictions as the problem (7).

The non-linear programming problems (13) can be solved by a suitable mathematical programming algorithm and we get the solution of MOIM (7).

4.2.2 Fuzzy Additive Goal Programming Technique (FAGP) Based on Additive Operator

In this technique, using (12) membership function, fuzzy non-linear programming problems are formulated as follows:

$$ \begin{aligned} & {\text{Max}}\mathop \sum \limits_{k = 1}^{n} \frac{{U^{k} - TAC_{k} \left( {Q_{k,} D_{k} } \right)}}{{U^{k} - L^{k} }} \\ & {\text{Subject}}\;{\text{to}} \;U^{k} - TAC_{k} \left( {Q_{k,} D_{k} } \right) \le U^{k} - L^{k} ,\;\;for\;k = 1,2, \ldots .,n \\ \end{aligned} $$

(14)

And same constraints and restrictions as the problem (7).

The non-linear programming problems (14) can be solved by a suitable mathematical programming algorithm and we get the solution of MOIM (7).

5 Numerical Example

Let us consider an inventory model which consist two items and $M=Rs.\mathrm{10,000}$ (Tables 1, 2).

Table 1 Input imprecise data for shape parameters

Table 2 Optimal solutions of MOIM using different methods

Approximate value of the above parameter is.

Items	Parameters
	$\widehat{{\alpha_{i} }}$	$\widehat{{\beta_{i} }}$	$\widehat{{d_{i} }}$	$\widehat{{\mu_{i} }}$	$\widehat{{\delta_{i} }}$	$\widehat{{a_{i} }}$	$\widetilde{{b_{i} }}$	$\hat{P}$
I	7000	0.54	0.0045	540	6400	4.8	0.027	94,500
II	6547.5	0.63	0.0024	640	9600	5.2	0.042	94,500

6 Sensitivity Analysis

In the sensitivity analysis optimal solutions have been found by using FNLP and FAGP methods (Table 3).

Table 3 Optimal solutions of MOIM by FNLP and FAGP methods for different values of ${b}_{1},{b}_{2}$

From the above Figs. 2 and 3 shows that minimum cost of the both item is decreased when values of ${b}_{1}$, ${b}_{2}$ are increased (Table 4).

Fig. 2

optimal cost of 1st item using different methods for different values of $b_{1}$

Fig. 3

optimal cost of 2nd item using different methods for different values of $b_{2}$

Table 4 Optimal solutions of MOIM by FNLP and FAGP methods for different values of ${a}_{1},{a}_{2}$

From the above Figs. 4 and 5 shows that minimum cost of the both item is decreased when values of ${a}_{1}$,${a}_{2}$ are increased (Table 5).

Fig. 4

minimizing cost of 1st item using different methods for different values of $a_{1}$

Fig. 5

minimizing cost of 2nd item using different methods for different values of $a_{2}$

Table 5 Optimal solutions of MOIM by FNLP and FAGP methods for different values of ${\delta }_{1},{\delta }_{2}$

From the above Figs. 6 and 7 shows that minimum cost of the both item is increased when values of ${{\varvec{\delta}}}_{1}$,${{\varvec{\delta}}}_{2}$ are increased (Table 6).

Fig. 6

minimizing cost of 1st item using different methods for different values of $\delta_{1}$

Fig. 7

minimizing cost of 2nd item using different methods for different values of $\delta_{2}$

Table 6 Optimal solutions of MOIM by FNLP and FAGP methods for different values of ${\mu }_{1},{\mu }_{2}$

From the above Figs. 8 and 9 shows that minimum cost of the both item is increased when values of ${{\varvec{\mu}}}_{1}$,${{\varvec{\mu}}}_{2}$ are increased (Table 7).

Fig. 8

minimizing cost of 1st item using different methods for different values of $\mu_{1}$

Fig. 9

minimizing cost of 2nd item using different methods for different values of $\mu_{2}$

Table 7 Optimal solutions of MOIM by FNLP and FAGP methods for different values of ${d}_{1},{d}_{2}$

From the above Figs. 10 and 11 shows that minimum cost of the both item is decreased when values of ${{\varvec{d}}}_{1}$,${{\varvec{d}}}_{2}$ are increased.

Fig. 10

minimizing cost of 1st item using different methods for different values of $d_{1}$

Fig. 11

minimizing cost of 2nd item using different methods for different values of $d_{2}$

7 Conclusion

In this article, I have considered a multi item production inventory model for the non-deteriorating items with constant demand and the restriction on set up cost. I think shops in more populated places sell more goods than shops in less populated places. Therefore some inventory costs (like as holding cost, deterioration etc.) are always dependent on the number of population. Here the production cost in dependent on the demand as well as populations. Set up cost is dependent on the average inventory level. Holding cost is considered on depend on the number of population. I first formed crisp inventory model and then using fuzzy number, form fuzzy model. Multi objective fuzzy inventory model has been solved by various techniques like as FPTHMF, FNLP and FAGP methods. Numerical example is given for two items to illustrate the inventory model. Numerical example is solved by using LINGO13 software.

In the future study, it is hoped to further incorporate the proposed model into more realistic assumptions, such as probabilistic demand, introduce shortages etc. In the future this inventory problem can be solved in different techniques.