Abstract
This article studies the problem of statistical estimation and optimal censoring from three-parameter inverted generalized linear exponential distribution under progressive first failure censored samples. The maximum likelihood estimation is presented to estimate the unknown parameters. Approximate confidence interval is constructed to compute the interval estimation for the parameters and the delta method is used to compute the interval estimation for survival, hazard rate, and reversed hazard rate functions. The Gibbs sampler with the Metropolis-Hastings algorithm is applied to generate the Markov chain Monte Carlo samples from the posterior functions to approximate the Bayes estimation using several loss functions and to establish the symmetric credible interval for the parameters. A two real data sets are used to study the suggested censoring schemes and the optimal censoring is used to show the performance of the censoring schemes using maximum likelihood estimator and Bayes estimator. Also, a new vision is studied to obtain the optimal censoring using Bayes estimator under varying loss functions. Finally, a simulation study is presented to compare the different estimation methods based on mean square error and average absolute bias.


Similar content being viewed by others
References
Zheng G (2002) On the Fisher information matrix in type-II censored data from the exponentiated exponential family. Biom J 44(3):353–357
Singh U, Gupta PK, Upadhyay SK (2005) Estimation of parameters for exponentiated-Weibull family under type-II censoring scheme. Comput Stat Data Anal 48:509–523
Balakrishnan N, Han D (2008) Exact inference for a simple step-stress model with competing risks for failure from exponential distribution under type-II censoring. J Stat Plan Inference 138:4172–4186
Sultan KS, Alsadat NH, Kundu D (2014) Bayesian and maximum likelihood estimations of the inverse Weibull parameters under progressive type-II censoring. J Stat Comput Simul 84(10):2248–2265
Khorram E, Farahani ZSM (2014) Statistical inference of weighted exponential lifetimes under progressive type-II censoring scheme. Qual Technol Quant Manag 11(4):433–451
Rezaei S, Noughabi RA, Nadarajah S (2015) Estimation of stress-strength reliability for the generalized Pareto distribution based on progressively censored samples. Ann Data Sci 2:83–101
Deya S, Singh S, Tripathi YM, Asgharzadeh A (2016) Estimation and prediction for a progressively censored generalized inverted exponential distribution. Stat Methodol 32:185–202
Mahmoud MAW, Yhiea NM, El-Said SM (2016) Estimation of parameters for the exponentiated Pareto distribution based on progressively type-II right censored data. J Egypt Math Soc 24:431–436
Lee K, Cho Y (2017) Bayesian and maximum likelihood estimations of the inverted exponentiated half logistic distribution under progressive type-II censoring. J Appl Stat 44(5):811–832
Gunasekera S (2018) Inference for the Burr-XII reliability under progressive censoring with random removals. Math Comput Simul 144:182–195
Salemi UH, Rezaei S, Si Y, Nadarajah S (2018) On optimal progressive censoring schemes for normal distribution. Ann Data Sci 5:637–658
Kumar M, Pathak A, Soni S (2019) Bayesian inference for Rayleigh distribution under step-stress partially accelerated test with progressive type-II censoring with binomial removal. Ann Data Sci 6:117–152
Balasooriya U (1995) Failure-censored reliability sampling plans for the exponential distribution. J Stat Comput Simul 52:337–349
Wu J-W, Hung W-L, Tsai C-H (2003) Estimation of the parameters of the Gompertz distribution under the first failure-censored sampling plan. Statistics 37:517–525
Wu J-W, Yu H-Y (2005) Statistical inference about the shape parameter of the Burr type-XII distribution under the failure-censored sampling plan. Appl Math Comput 163:443–482
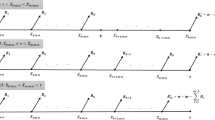
Wu S-J, Kus C (2009) On estimation based on progressive first-failure-censored sampling. Comput Stat Data Anal 53:3659–3670
Dube M, Krishna H, Garg R (2016) Generalized inverted exponential distribution under progressive first-failure censoring. J Stat Comput Simul 86(6):1095–1114
Dube M, Garg R, Krishna H (2016) On progressively first failure fensored Lindley distribution. Comput Stat 31:139–163
Ahmed EA (2017) Estimation and prediction for the generalized inverted exponential distribution based on progressively first-failure-censored data with application. J Appl Stat 44(9):1576–1608
Maurya RK, Tripathi YM, Rastogi MK (2019) Estimation and prediction for a progressively first-failure censored inverted exponentiated Rayleigh distribution. J Stat Theory Pract 13:39
Kayal T, Tripathi YM, Wang L (2019) Inference for the Chen distribution under progressive first-failure censoring. J Stat Theory Pract 13:52
Sarhan AM, Kundu D (2009) Generalized linear failure rate distribution. Commun Stat Theory Methods 38:642–660
Tian Y, Tian M, Zhu Q (2014) Transmuted linear exponential distribution: a new generalization of the linear exponential distribution. Commun Stat Simul Comput 43:2661–2677
Mahmoud MAW, Alam FMA (2010) The generalized linear exponential distribution. Stat Probab Lett 80:1005–1014
Mahmoud MAW, Ghazal MGM, Radwan HMM (2017) Inverted generalized linear exponential distribution as a lifetime model. Appl Math Inf Sci 11(6):1747–1765
Hassan AS, Abd-Allah M (2019) On the inverse power Lomax distribution. Ann Data Sci 6:259–278
Eliwa MS, El-Morshedy M, Ibrahim M (2019) Inverted inverse Gompertz distribution: properties and different estimation methods with application to complete and censored data. Ann Data Sci 6:321–339
Yadav AS, Maiti SS, Saha M (2019) The inverse Xgamma distribution: statistical properties and different methods of estimation. Ann Data Sci
Cohen AC (1965) Maximum likelihood estimation in the Weibull distribution based on complete and censored samples. Technometric 7(4):579–588
Greene WH (2000) Econometric analysis, 4th edn. Prentice-Hall, New York
Barot DR, Patel MN (2017) Posterior analysis of the compound Rayleigh distribution under balanced loss functions for censored data. Commun Stat Theory Method 46(3):1317–1336
Peng X, Yan Z (2014) Estimation and application for a new extended Weibull distribution. Reliab Eng Syst Saf 121:34–42
Devroye L (1984) A simple algorithm for generating random variates with a log-concave density function. Computing 33:247–257
Jia X, Guo B (2015) Analysis of non-repairable cold-standby systems in Bayes theory. J Stat Comput Simul 86:2089–2112
Chen MH, Shao QM (1999) Monte Carlo estimation of Bayesian credible and HPD intervals. J Comput Graph Stat 8:69–92
Galea M, Leiva V, Paula GA (2004) Influence diagnostics in log-Birnbaum–Saunders regression models. J Appl Stat 31(9):1049–1064
Leiva V, Barros M, Paula GA (2009) Generalized Birnbaum–Saunders models using R. Brazilian Statistical Association, Brazil
Kang MS, Goo JH, Song I, Chun JA, Her YG, Hwang SW, Park SW (2013) Estimating design floods based on the critical storm duration for small watersheds. J Hydro-environ Res 7:209–218
Ng HKT, Chan PS, Balakrishnan N (2004) Optimal progressive censoring plans for the Weibull distribution. Technometrics 46:470–481
Zhang Y, Meeker WQ (2005) Bayesian life test planning for the Weibull distribution with given shape parameter. Metrika 61:237–249
Kundu D (2008) Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Technometrics 50(2):144–154
Balakrishnan N, Sandhu RA (1995) A simple algorithm for generating progressively type-II generated samples. Am Stat 49:229–230
Acknowledgements
All calculations were performed on the High-Performance Computer (HPC) maintained by Computational Chemistry Laboratory, Faculty of Science, Minia University, Egypt. This HPC was funded through grants from the Science and Technology Development Fund, STDF, Egypt (Grant Nos. 5480 & 7972).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
To prove Lemma 1, we want to prove that \(\frac{\partial ^2 \log {(\delta _{1}(\lambda |\mu ,\theta ,\mathbf{x} ))}}{\partial \lambda ^2}\) and \(\frac{\partial ^2 \log {(\delta _{2}(\mu |\lambda ,\theta ,\mathbf{x} ))}}{\partial \mu ^2}\) are negative. The second derivative of \(\log {(\delta _{1}(\lambda |\mu ,\theta ,\mathbf{x} ))}\) w.r.t. \(\lambda\) can be written as
and the second derivative of \(\log {(\delta _{2}(\mu |\lambda ,\theta ,\mathbf{x} ))}\) w.r.t. \(\mu\) can be written as
Since \(\Biggr (\ e^{-\left( \frac{\lambda }{x_{i}}+\frac{\mu }{2 \ x_{i}^2}\right) ^{\theta }} +\left( \frac{\lambda }{x_{i}}+\frac{\mu }{2 \ x_{i}^2}\right) ^{\theta } \Biggr )\ > 1\), for \(\lambda >0\), \(\mu >0\), \(\theta >0\) and \(x_{i}>0,i=1,,m\), then the result is satisfied.
Appendix 2
To prove Lemma 2, we want to prove that \(\frac{\partial ^2 \log {(\delta _{3}(\theta |\mu ,\lambda ,\mathbf{x} ))}}{\partial \theta ^2}\) is negative. The second derivative of \(\log {(\delta _{3}(\theta |\mu ,\lambda ,\mathbf{x} ))}\) w.r.t. \(\theta\) can be written as
Since \(\Biggr (\ e^{-\left( \frac{\lambda }{x_{i}}+\frac{\mu }{2 \ x_{i}^2}\right) ^{\theta }} +\left( \frac{\lambda }{x_{i}}+\frac{\mu }{2 \ x_{i}^2}\right) ^{\theta } \Biggr )\ > 1\), for \(\lambda >0\), \(\mu >0\), \(\theta >0\) and \(x_{i}>0,i=1,,m\), then the result is satisfied.
Rights and permissions
About this article
Cite this article
Mahmoud, M.A.W., Ghazal, M.G.M. & Radwan, H.M.M. Bayesian Estimation and Optimal Censoring of Inverted Generalized Linear Exponential Distribution Using Progressive First Failure Censoring. Ann. Data. Sci. 10, 527–554 (2023). https://doi.org/10.1007/s40745-020-00259-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40745-020-00259-z