Modified Beta Linear Exponential Distribution with Hydrologic Applications

Abstract

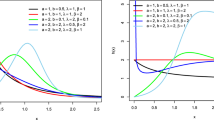
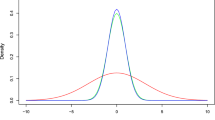
In this paper, we introduce a flexible modified beta linear exponential (MBLE) distribution. Our motivation, besides others are there, dues to its ability in hydrology applications. We investigate a set of its statistical properties for supporting such applications, like moments, moment generating function, conditional moments, mean deviations, entropy, mean and variance (reversed) residual life and maximum likelihood estimators with observed information matrix. The distribution can accommodate both decreasing and increasing hazard rates as well as upside down bathtub and bathtub shaped hazard rates. Moreover, several distributions arise as special cases of the distribution. The MBLE distribution with others are fitted to two hydrology data sets. It is shown that, the MBLE distribution is the best fit among the compared distributions based on nine goodness-of-fit statistics among them the Corrected Akaike information criterion, Hannan–Quinn information criterion, Anderson–Darling and Kolmogorov–Smirnov p value. Consequently, some parameters of these data are obtained such as return level, conditional mean, mean deviation about the return level, risk of failure for designing hydraulic structures. Finally, we hope that this model will be able to attract wider applicability in hydrology and other life areas.

Appendix A. Meijer G-function

The symbol $G_{p,q}^{m,n}( \cdot |\, \cdot )$ denotes Meijer’s G-function [21] defined in terms of the Mellin–Barnes integral as

$$\begin{aligned}&G_{p,q}^{m,n}\Big ( z \,\Big | \begin{array}{c} a_1, \ldots , a_p\\ b_1, \ldots , b_q \end{array}\Big ) = \frac{1}{2\pi \mathrm{i}}\oint _{{\mathfrak {C}}}\frac{\prod _{j=1}^{m}\Gamma (b_j-s) \prod _{j=1}^{n}\Gamma ( 1-a_j + s)}{\prod _{j=m+1}^q \Gamma ( 1-b_j + s) \prod _{j=n+1}^{p}\Gamma (a_j - s)} z^s \mathrm {d}s, \end{aligned}$$

where $0\le m\le q,\, 0\le n\le p$ and the poles $a_j, b_j$ are such that no pole of $\Gamma (b_j - s), j=\overline{1,m}$ coincides with any pole of $\Gamma (1-a_j+s), j=\overline{1,n}$; i.e. $a_k-b_j \not \in {\mathbb {N}}$, while $z \ne 0$. ${\mathfrak {C}}$ is a suitable integration contour, see [20, p. 143] and [21] for more details.

The G function’s Mathematica code reads

$$\begin{aligned} \texttt {MeijerG[}\{\{a_1,\ldots ,a_n\}, \{a_{n+1},\ldots ,a_p\}\}, \{\{b_1,\ldots ,b_m\}, \{b_{m+1},\ldots ,b_q\}\}, z\texttt {]}. \end{aligned}$$

$\psi ^{(1)}(.)$ is the polygamma fucntion, noting that the polygamma function of order m is defined as: $\psi ^{(m)}(z)=\frac{d^{m+1}}{dz^{m+1}} \ln \Gamma (z).$