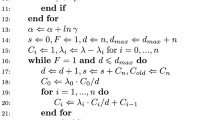Abstract
The Weibull distribution has been generalized by many authors in recent years. Here, we introduce a new generalization, called alpha-power transformed Weibull distribution that provides better fits than the Weibull distribution and some of its known generalizations. The distribution contains alpha-power transformed exponential and alpha-power transformed Rayleigh distributions as special cases. Various properties of the proposed distribution, including explicit expressions for the quantiles, mode, moments, conditional moments, mean residual lifetime, stochastic ordering, Bonferroni and Lorenz curve, stress–strength reliability and order statistics are derived. The distribution is capable of modeling monotonically increasing, decreasing, constant, bathtub, upside-down bathtub and increasing–decreasing–increasing hazard rates. The maximum likelihood estimators of unknown parameters cannot be obtained in explicit forms, and they have to be obtained by solving non-linear equations only. Two data sets have been analyzed to show how the proposed models work in practice. Further, a bivariate extension based on Marshall–Olkin and copula concept of the proposed model are developed but the properties of the distribution not considered in detail in this paper that can be addressed in future research.











Similar content being viewed by others
References
Aarset MV (1987) How to identify bathtub hazard rate. IEEE Trans Reliab 36:106–108
Alexander C, Cordeiro GM, Ortega EMM, Sarabia JM (2012) Generalized beta-generated distributions. Comput Stat Data Anal 56:1880–1897
Alzaatreh A, Famoye F, Lee C (2013) A new method for generating families of continuous distributions. Metron 71(1):63–79
Andrews DF, Herzberg AM (2012) Data: a collection of problems from many fields for the student and research worker. Springer, Berlin
Azzalini A (1985) A class of distributions which includes the normal ones. Scand J Stat 12:171–178
Azzalini A (1986) Further results on a class of distributions which includes the normal ones. Statistica 46:199–208
Azzalini A, Capitanio A (2003) Distribution generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J R Stat Soc Ser B 65:367–389
Barlow RE, Proschan F (1975) Statistical theory of reliability and life testing probability models. Holt, Rinehart and Winston, New York
Barlow RE, Toland RH, Freeman T (1984) A Bayesian analysis of stress rupture life of kevlar 49/epoxy spherical pressure vessels. In: Proceedings of the conference on applications of statistics. Marcel Dekker, New York
Barreto-Souza W, de Morais AL, Cordeiro GM (2011) The Weibull geometric distribution. J Stat Comput Simul 81:645–657
Barreto-Souza W, Santos AHS, Cordeiro GM (2010) The beta generalized exponential distribution. J Stat Comput Simul 80:159–172
Bebbington M, Lai CD, Zitikis R (2007) A flexible Weibull extension. Reliab Eng Syst Saf 92:719–726
Burr IW (1942) Cumulative frequency functions. Ann Math Stat 13:215–232
Cooray K, Ananda MMA (2005) Modeling actuarial data with a composite lognormal-pareto model. Scand Actuar J 5:321–334
Cordeiro GM, Ortega EM, Nadarajah S (2010) The Kumaraswamy Weibull distribution with application to failure data. J Frankl Inst 347(8):1399–1429
Cordeiro GM, Silva RB (2014) The complementary extended Weibull power series class of distributions. Cincia Nat 36:1–13
Eugene N, Lee C, Famoye F (2002) The beta-normal distribution and its applications. Commun Stat Theory Methods 31:497–512
Famoye F, Lee C, Olumolade O (2005) The beta-Weibull distribution. J Stat Theory Appl 4:121–136
Ferreira JTAS, Steel MFJ (2006) A constructive representation of univariate skewed distributions. J Am Stat Assoc 101:823–829
Genest C, Remillard B, Beaudoin D (2009) Goodness-of-fit tests for copulas: a review and a power study. Insur Math Econ 44:199–213
Gupta R, Kirmani S (1990) The role of weighted distribution in stochastic modeling. Commun Stat Theory Methods 19:3147–3162
Gupta RC, Keating JP (1985) Relations for reliability measures under length biased sampling. Scan J Stat 13:49–56
Gupta RD, Kundu D (1999) Generalized exponential distribution. Aust NZ J Stat 41:173–188
Hansen BE (1994) Autoregressive conditional density estimation. Int Econ Rev 35:705–730
Hastings JC, Mosteller F, Tukey JW, Windsor C (1947) Low moments for small samples: a comparative study of order statistics. Ann Stat 18:413–426
Johnson NL (1949) Systems of frequency curves generated by methods of translation. Biometrika 36:149–176
Kotz S, Vicari D (2005) Survey of developments in the theory of continuous skewed distributions. Metron LXIII:225–261
Lai CD, Xie M, Murthy DNP (2009) A modified Weibull distribution. IEEE Trans Reliab 52:33–37
Lee ET, Wang JW (2013) Statistical methods for survival data analysis, 3rd edn. Wiley, Hoboken
Mahdavi A, Kundu D (2016) A new method for generating distributions with an application to exponential distribution. Commun Stat Theory Methods. doi:10.1080/03610926.2015.1130839
Marshall AW, Olkin I (1967) A multivariate exponential distribution. J Am Stat Assoc 62:30–44
Marshall AW, Olkin I (1997) A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 84:641–652
Morais AL, Barreto-Souza W (2011) A compound class of Weibull and power series distributions. Comput Stat Data Anal 55:14101425
Mudholkar GS, Srivastava DK (1993) Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans Reliab 42:299–302
Nelsen RB (2006) An introduction to copulas, 2nd edn. Springer, New York
Oluyede BO (1999) On inequalities and selection of experiments for length-biased distributions. Probab Eng Inf Sci 13:169–185
Patil GP (2002) Weighted distributions. Encyclopedia of Environmetics, vol 4. pp 2369–2377
Patil GP, Rao CR (1978) Weighted distributions and size-biased sampling with application to wildlife populations and human families. Biometrics 34:179–189
Patil GP, Rao CR, Ratnaparkhi MV (1986) On discrete weighted distributions and their use in model choice for observed data. Commun Stat Theory Methods 15:907–918
Pearson K (1895) Contributions to the mathematical theory of evolution. II. Skew variation in homogeneous material. Philos Trans R Soc Lond A 186:343–414
Rao CR (1965) On discrete distributions arising out of methods of ascertainment. In: Patil GP (ed) Classical and contagious discrete distributions. Pergamon Press and Statistical Publishing Society, Calcutta, pp 320–332
Renyi A (1961) On measures of entropy and information. In: Proceedings of the 4th Berkeley symposium on mathematical statistics and probability. University of California Press, Berkeley, pp 547–561
Sarhan AM, Apaloo J (2013) Exponentiated modified Weibull extension distribution. Reliab Eng Syst Saf 112:137–144
Sarhan AM, Zaindin M (2009) Modified Weibull distribution. Appl Sci 11:2336
Shannon CE (1951) Prediction and entropy of printed English. Bell Syst Tech J 30:50–64
Silva GO, Ortega EMM, Cordeiro GM (2010) The beta modified Weibull distribution. Lifetime Data Anal 16:409–430
Singh H, Misra N (1994) On redundancy allocations in systems. J Appl Probab 31:10041014
Singla N, Jain K, Sharma SK (2012) The beta generalized Weibull distribution: properties and applications. Reliab Eng Syst Saf 102:5–15
Sklar A (1959) Fonctions de répartition à \(n\) dimensions et leurs marges. Publ Inst Stat Univ Paris 8:229–233
Smith RL, Naylor JC (1987) A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. Appl Stat 36:358–369
Tukey JW (1960) The Practical Relationship Between the Common Transformations of Percentages of Counts and Amounts, Technical Report, 36. Statistical Techniques Research Group, Princeton University, Princeton, NJ
Wanbo L, Daimin S (2012) A new compounding life distribution: the Weibull–Poisson distribution. J Appl Stat 39:21–38
Weibull WA (1951) Statistical distribution function of wide applicability. J Appl Mech 18:293296
Xie M, Lai CD (1996) Reliability analysis using an additive Weibull modelwith bathtub-shaped failure rate function. Reliab Eng Syst Saf 52:87–93
Xie M, Tang Y, Goh TN (2002) A modified Weibull extension with bathtub-shaped failure rate function. Reliab Eng Syst Saf 76:279–285
Zhang T, Xie M (2011) On the upper truncated Weibull distribution and its reliability implications. Reliab Eng Syst Saf 96:194–200
Acknowledgements
The authors are thankful to the Editorial Board and to the reviewers for their valuable comments and suggestions which led to this improved version. Mhamed Mesfioui acknowledges the financial support of the Natural Sciences and Engineering Research Council of Canada No 261968-2013.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The elements of the observed information matrix \(J(\varvec{\theta })\) for the three parameters \((\alpha ,\beta ,\lambda )\) are given by
whose elements are
Rights and permissions
About this article
Cite this article
Dey, S., Sharma, V.K. & Mesfioui, M. A New Extension of Weibull Distribution with Application to Lifetime Data. Ann. Data. Sci. 4, 31–61 (2017). https://doi.org/10.1007/s40745-016-0094-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40745-016-0094-8
Keywords
- Weibull distribution
- Weighted distribution
- Moments
- Quantile function
- Stochastic ordering
- Entropy
- Stress–strength reliability
- Maximum likelihood estimation