Failures in discrete-event systems and dealing with them by means of Petri nets

Abstract

An approach based on Petri nets pointing to the manner how to deal with failures in discrete-event systems is presented. It uses the reachability tree and/or reachability graph of the Petri net-based model of the real system as well as the synthesis of a supervisor to remove the possible deadlock(s). To illustrate the applicability of the approach to the detection and recovery of failures in DES modelled by Petri nets the case study on a railroad crossing is introduced.

1 Introduction

A failure can be defined [2, 3, 10] as a deviation of a system from its intended (normal) behaviour. The process of detecting a potential failure in the system behaviour followed by isolating the cause or the source of the failure, is called the system diagnosis. In the discrete-event systems (DES) diagnosis, faults may correspond to any discrete event. Unfortunately, the predisposition of systems to fail increases with their complexity. The research effort has been spent in the development of diagnostic systems. It is necessary to distinguish (according to the manner in which faults are reset after they occur) [2, 14] between permanent and intermittent faults. In case of the permanent fault the recovery event occurs only due to repairing the controllable and observable fault. In case of the intermittent fault the recovery event occurs either spontaneously or due to repairing, and such event has a tendency to be uncontrollable and unobservable. The fault diagnosability [27] is interested in whether the system is diagnosable or not—i.e., in the fact whether the system can detect the occurrence of the fault in a finite number of steps or not.

Error recovery is [12, 19, 25] the set of actions that must be performed in order to return the system to its normal state. At least one sequence of actions should exist in order to bring the system into its normal operation. When there exist more sequences, the best one is chosen with respect to a prescribed criterion. Usually it is the sequence of actions which minimally disorganizes the system.

For systems without failures usage of Petri nets (PN) is very useful for modelling, analysing and control synthesis. However, practically any system is not failure-free. Failures can emerge in any device or software. It is gratifying that PN can be used [3, 7, 10, 11, 15,16,17, 19, 21,22,23, 26] also for systems where failures occur. There failures can be categorized into hardware failures and software ones. To minimize the hardware failures of devices, it is necessary to timely execute maintenance of devices, test and/or check as well as timely replace their components.

To decrease occurrence of software failures, fault-tolerant software techniques are necessary. Error recovery is possible only for the so called soft failures [6]. Hard (catastrophic) failures in systems are classified as functional and/or structural failures.

Strategies and forms for detection and recovery of system soft failures are based on the so called error treatment and failure treatment. The error treatment contains error detection, damage assessment and error recovery. The failure treatment includes localization, identification, system repair and continued service. However, the hard failures can be overcome in most systems by means of redundancy [1].

Here, in this paper, failures in DES and their recovery will be examined by means of utilizing Petri nets (PN). DES are systems discrete by nature. They persist in a steady state until the occurrence of a discrete event which will cause their transition into another state. Typical representatives of DES are discrete manufacturing systems, transport systems, communication systems, etc. PN are frequently used for DES modelling, analysing and control synthesizing.

1.1 Preliminaries about Petri nets

Petri nets (PN) [8, 18, 20] are (as to their structure) bipartite directed graphs—i.e., graphs with two kinds of nodes (places and transitions) and two kinds of edges (arcs directed from places to transitions and arcs directed contrary)— $\left\langle P, T, F, G \right\rangle$ with $P \cap T = \varnothing$ and $P \cup T \ne \varnothing$ ($\varnothing$ is the empty set), where P, $|P| = n$, is a finite set of places and T, $|T| = m$, is a finite set of transitions; $F \subseteq P \times T$, $G \subseteq T \times P$ are subsets of the directed arcs. The set $B = F \cup G$ contains all directed arcs. The so called preset (a set of input places) of a transition t is defined as ${}^{(p)}t= \{p|(p, t) \in B\}$, while the so called postset (a set of output places) of t is defined as $t^{(p)}= \{p|(t, p) \in B\}$. On the contrary, the preset of a place p (a set of input transitions) is defined as ${}^{(t)}p= \{t|(t, p) \in B\}$ while the postset (a set of output transitions) of p is defined as $p^{(t)}= \{t|(p, t) \in B\}$. P/T PN is said to be pure if no self-loops occur in it, i.e., if for $p \in P,\, t \in T$, $\{(p, t) \in B) \Rightarrow (t,p) \notin B\}$.

Places model some particular activities or operations of a modelled DES being a real object (plant). This is expressed by putting tokens inside the places. Such a marking m is a vector $m\,{:} \,P \rightarrow {{\mathbb {Z}}}_{\ge 0}$ (${{\mathbb {Z}}}_{\ge 0}$ represents positive integers including 0). The marking enables a set of transitions $\tau \subseteq T$. Namely, $\forall p \in P,\, m(p) \ge |p^{(t)} \cap \tau |$ (i.e., m(p) is greater than the number of transitions in $\tau$ for which p is the input place or equal to this number). The enabled transitions may be (but need not be) fired. After their firing the PN marking is changed.

As to the marking development (marking propagation can be understood to be PN dynamics), the PN can be formally defined as $\left\langle X, U, \delta , \mathbf{x}_0 \right\rangle$, where X is a set of PN states, U is a set of discrete events; $\delta : X \times U \rightarrow X$ symbolizes the fact that the new state of marking depends on existing state and an occurred discrete event; $\mathbf{x}_0 \in X$ is the initial state of marking. The state equation (PN model of DES) is as follows:

$$\begin{aligned}&x_{k+1} = x_k + \mathbf{B} \cdot \mathbf{u}_k,\; k =0,\;1,\;\ldots ,\;N ,\end{aligned}$$

(1)

$$\begin{aligned}&{} \mathbf{F} \cdot \mathbf{u}_k \le \mathbf{x}_k, \end{aligned}$$

(2)

where $\mathbf{B} =\mathbf{G}^T-\mathbf{F}$. It expresses the PN dynamics. Here, $\mathbf{x}_k=(\sigma ^k_{p_1},\ldots ,\,\sigma ^k_{p_n})^T$ with entries $\sigma ^k_{p_i} \in \{0, 1,\ldots ,\,\infty \}$, representing the states of particular places, is the PN state vector in the k-th step of the dynamics development; $\mathbf{u}_k=(\gamma ^k_{t_1},\ldots ,\,\gamma ^k_{t_m})^T$ with entries $\gamma ^k_{p_i} \in \{0, 1\}$, representing the states of particular transitions (either enable—when 1, or disable—when 0) is the control vector; $\mathbf{F}$, $\mathbf{G}^T$ are incidence matrices of arcs corresponding, respectively, to the sets F, G mentioned above.

A firing sequence from the initial state $\mathbf{x}_0$ (i.e., from the initial marking $m_0$) is a sequence of transition sets ${{{\mathcal {T}}}} = \{\tau _1\,\tau _2\,\ldots \,\tau _k\}$ such that $\mathbf{x}_0\,[\,{\tau _1}>\,\mathbf{x}_1\,[\,\,{\tau _2}>\,\mathbf{x}_2>\,\cdots \,\,{\tau _{k}}>\,\mathbf{x}_{k-1}\,[\,\tau _k>\,\mathbf{x}_k$. The set may be also empty, of course. The notation $\mathbf{x}_0\,[\,{{\mathcal {T}}}$ denotes that the sequence ${{\mathcal {T}}}$ can be fired at $\mathbf{x}_0$ and the notation $\mathbf{x}_0 \, [ \, {{\mathcal {T}}} \,> \, \mathbf{x}_k$ denotes that the firing of ${{\mathcal {T}}}$ yields $\mathbf{x}_k$.

More than one transition can be fired at any instant. Thus there are two possibilities (i) to fire more than one transition at any instant (concurrency assumption); (ii) to fire only one of them at any instant [no concurrency (NC) assumption]. Under the NC assumption, each $\tau _i$ is a singleton set, and ${{\mathcal {T}}}$ is a sequence of transitions. It can also be written that $\mathbf{x}_0 \, [ \,{{\mathcal {T}}} >\, \mathbf{x}_k$ to denote that firing of ${{\mathcal {T}}}$ the state $\mathbf{x}_k$ can be reached from $\mathbf{x}_0$. In general, the state $\mathbf{x}_k$ is reachable from $\mathbf{x}_0$ if there exists a firing sequence ${{\mathcal {T}}}$ such that $\mathbf{x}_0\, [\, {{\mathcal {T}}}\, > \mathbf{x}_k$. For PN the set of reachable state vectors is $R(\text{ PN },\mathbf{x}_0)$. All these vectors create columns of the matrix $\mathbf{X}_{\mathrm{{reach}}}$.

Fig. 1

The illustrative examples of such accidents

The PN reachability tree (RT) expresses all states reachable from $\mathbf{x}_0$ as well as how (by means of firing which transitions) they can be reached. Thus, the nodes of the RT are labelled with the actual PN marking (state vectors) and the arcs are labelled with the transitions between the states. The RT root is represented by the initial state $\mathbf{x}_0$ and the RT leafs are expressed by the states reachable from $\mathbf{x}_0$. Connecting the leafs with the same name the reachability graph (RG) arises.

The PN T-invariants and P-invariants [9, 13, 18] are important too, respectively, at diagnosability [16] and supervision [4] (and subsequently for deadlocks elimination). While T-invariants restore an initial state, P-invariants ensure the token preservation. A T-invariant $\mathbf{v}$ is a solution of the equation $\mathbf{B}{} \mathbf{v} = \mathbf{0}$. A P-invariant $\mathbf{y}$ is a solution of the equation $\mathbf{B}^T\mathbf{y} = \mathbf{0}$. For any state $\mathbf{x}$ reachable from $\mathbf{x}_0$ the relation $\mathbf{y}^T \cdot \mathbf{x}=\mathbf{y}^T \cdot \mathbf{x}_0$ is valid. This fact was utilized at the supervisor synthesis [4] based on P-invariants.

To express time, we can use timed Petri nets (TPN), where time is assigned to the transitions as their duration function $D: T \rightarrow {\mathbb {Q}}_{\ge 0}$, where ${\mathbb {Q}}_{\ge 0}$ symbolizes non-negative rational numbers.

To illustrate the PN-based approach to the detection and recovery of failures in DES modelled by PN let us introduce the following case study.

This paper is an expanded version of the paper [5] presented at the conference ACIIDS 2017. In comparison with the conference paper, the part concerning the safety of technical systems in general was added. Because the introduced Case Study concerns the accident on a railroad crossing, certain illustrations of formidable effects of such accidents were introduced. Also the passage concerning the supervisor synthesis was modified, to be more comprehensible to readers.

Fig. 2

The PN model of the failure-free case together with its RT (left) and the PN model with three potential failures (right)

2 Safety of technical systems

The safety of different kind of technical systems is very important. Especially, in case of the systems where the human life is endangered. From this point of view the transport systems belong to the systems where the human life is often endangered. At present, man is directly endangered at the contact with the transport systems during whole day. The mass transport is dangerous not only for the road user(s) who are crossing a road as pedestrian(s) but also for car drivers and their travel companion. For example the car collisions occur very frequently. Likewise, collisions on railroad crossings are not unusual. Only in such small country like Slovakia, tragic collisions between cars and/or trucks with trains occur practically every month—see e.g., Fig. 1. The train having a many times bigger mass, speed and consequently, also dynamics, destroys not only human lives (being inside of the road vehicles and the train) but also the vehicles and some times also the train itself ends completely destroyed.

During last several years such collisions caused many casualties—130 human lives and huge material damages. Consequently, it is necessary to be concerned with such problems and to find possibilities how to improve security in that area. Also PN can help along this line. Of course, it is impossible to anticipate failures caused by people themselves. The failures due to the human behaviour like the absent-mindedness, willful and wanton acts of law breaking, infringement of traffic regulations, etc., cannot be removed simply. To prevent the bad habits the education or training, in extreme cases a punishment, are necessary. Only right way to the improvement of the safety of systems is to increase the reliability of the software and equipment. The following simple case study on railroad crossing offers the approach how to do this in such a case.

2.1 Case study on simple railroad crossing

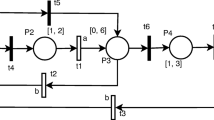
Consider the simple railroad crossing where the railroad crossing gate prevents a direct contact of vehicles on the road with trains. The PN model of such system consists of three cooperating sub-models expressing in Fig. 2(left) the behaviour of the train, crossing gate and control system. Here, the sense of the places in the failure-free case is the following: (i) the train has the states: $p_1$ = approaching to the crossing, $p_2$ = being before the crossing, $p_3$ = being within the crossing, $p_4$ = being after the crossing; (ii) the barrier of the crossing gate has the states: $p_{11}$ = it is up, $p_{12}$ = it is down. The transitions $t_6$ and $t_7$ model, respectively, the events of raising and lowering the barrier; (iii) the control system has the states: $p_5$, $p_6$, $p_7$, $p_8$, $p_9$, $p_{10}$; (iv) the place $p_{13}$ represents the interlock giving the warning signal for the train that the barrier is still up. The reachable states $\mathbf{x}_i, i=0,\ldots ,7$ (RT/RG nodes $N_{i+1}$), of the failure-free system are expressed as the rows of the following matrix

$$\begin{aligned} \mathbf{X}^T_{\mathrm{{reach}}}=\left( \begin{array}{ccccccccccccc} 1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ 0&{}1&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}1\\ 0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}1&{}0\\ 0&{}0&{}0&{}1&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0\end{array}\right) \end{aligned}$$

(3)

The RT is displayed just by the failure-free PN model in Fig. 2. It is simple, without any branching.

However, there can occur three potential failures, one in each subsystem. They are expressed by means of the failure transitions $t_{f_2}$, $t_{f_5}$, $t_{f_6}$ given in Fig. 2 (right). The transition $t_{f_2}$ takes a token from $p_2$ and puts a token into $p_3$ out of the correct sequence, $t_{f_6}$ does the same for $p_{12}$ and $p_{11}$, and $t_{f_5}$ involves an erroneous generation of a token in $p_{l0}$ which directly influences the position of the barrier. Thus, $t_{f_2}$ represents a human failure (when the engine-driver omits or ignores the warning signal), $t_{f_6}$ expresses the failure of the crossing gate (when a premature gate raising occurs or the gate is mechanically damaged), and $t_{f_5}$ represents a control system failure (when an illegitimate signal occurs).

It is practically impossible to recover the human failure of the engine-driver. Likewise, the technical problem in the crossing gate caused by a wrong function of the barrier raising/lowering can be hardly recovered. However, the erroneous function of the control system can be detected and recovered. Consequently, let us consider in Fig. 2(right) only the failure represented by $t_{f_5}$ and neglect the failures represented by the transitions $t_{f_2}$ and $t_{f_6}$. Then the coverability tree and graph are given in Fig. 3. The reachable states of this model (nodes of the RT/RG) are given as the columns of the following matrix, where

$$\begin{aligned} \mathbf{X}_{\mathrm{{reach}}}=\left( \begin{array}{cccccccccccccccccccccc} 1&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}1&{}0&{}1&{}1&{}1&{}1\\ 0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}1&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}1\\ 0&{}0&{}0&{}1&{}0&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}1&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}\omega &{}1&{}\omega &{}1&{}\omega &{}1&{}0&{}\omega &{}1&{}0&{}\omega &{}\omega &{}2&{}0&{}\omega &{}\omega &{}1&{}\omega &{}\omega &{}\omega \\ 1&{}1&{}1&{}1&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}1&{}0&{}1&{}1\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\end{array}\right) \end{aligned}$$

(4)

Fig. 3

The coverability tree (left) and coverability graph (right) of the PN model with $t_{f_5}$ at the infinite number of possible occurrences of the failure

It can be seen that at the infinity number of $t_{f_5}$ occurrences, one half of the 22 states have the self-loops (see Fig. 3 right) which are expressed by the symbol $\omega$.

In order to generate only the finite number of the failure $t_{f_5}$ occurrences, the place $p_{14}$ was added to the previous 13 places—see Fig. 4. In general, the failure can occur more times. The more times the failure occurs, the more complicated will be the structure and dimensionality of RT (RG). Therefore, here we will suppose its occurrence only once as displayed in Fig. 4 in order to demonstrate how to deal with the failure. In case of more failures such process will be more complicated. The model parameters are

Fig. 4

The PN model of the system with the failure represented by $t_{f_5}$

Fig. 5

The RT of the system with the finite number (namely only once in this case) of possible occurrences of the failure represented by $t_{f_5}$ (left) and the corresponding RG (right)

$$\begin{aligned} \mathbf{F}= & {} \left( \begin{array}{cccccccccc} 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}1&{}1\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0\end{array}\right) ; \nonumber \\ \mathbf{G}^T= & {} \left( \begin{array}{cccccccccc} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\end{array}\right) ;\; \mathbf{x}_0=\left( \begin{array}{c} 1\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 1\end{array}\right) . \end{aligned}$$

(5)

Then, RT and RG of the failed system are given in Fig. 5. It can be seen that the number of states as well as the RT/RG structure are completely different in comparison with RT of the failure-free system in Fig. 2. Namely, the branching occurs here. The states (nodes of the RT/RG) are the columns of the matrix $\mathbf{X}_{\mathrm{{reach}}}$.

$$\begin{aligned} \mathbf{X}_{reach}=\left( \begin{array}{ccccccccccccccccccc} 1&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}1&{}1&{}1&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}1&{}1&{}1&{}1\\ 0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}1&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}1\\ 0&{}0&{}0&{}1&{}0&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}1&{}0&{}0&{}2&{}0&{}1\\ 1&{}1&{}1&{}1&{}1&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}1&{}1\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0\end{array}\right) \end{aligned}$$

(6)

The RT has 19 nodes. However, with the accruing number of occurrences of the failure, the RT/RG dimensionality and complexity escalate. When $\sigma _{p_{14}}=2$ RT has 30 nodes, when $\sigma _{p_{14}}=5$ RT has 63 nodes, when $\sigma _{p_{14}}=10$ RT has 118 nodes, etc. Although the procedure of RT computation is the same, computational time correspondingly increases.

To detect and recover the failure(s) we have to distinguish whether the barrier is down or up. When the train is approaching, in the standard situation (without any failure) the barrier is down. However, in the non-standard situation (when the failure $t_{f_5}$ occurs) the barrier is going up. This is very dangerous situation, critical as to safety. To detect the failure it is necessary to have redundant information. It must be contained in the control system itself. Because $p_6$ and $p_7$ in the control system correspond to $p_{11}$ and $p_{12}$ in the real crossing gate, the failure is detected by checking if $p_7$ and $p_{11}$ are active simultaneously. If yes, there exists a contradiction between the real (i.e., fault) situation and standard one. After detecting the failure a kind of recovery can be applied. It depends on which case is accepted as the true state. When it is supposed that the barrier is up and drops down the recovery is realized by means of $t_{r_1}$. The PN model of the recovered system is given in Fig. 6.

More detailed analysis is possible by means of the RT and/or RG in Fig. 7 using information about the nodes given in the matrix given by the relation (7). When the barrier is up and none train is approaching, the situation is considerably simpler. Namely, by virtue of $t_{r_2}$ the fail signal $p_{10}$ from the control system and the activity of $p_{11}$ guarantee that the fail signal can be practically ignored.

Fig. 6

The PN model of the final recovered system

Fig. 7

The RT of the recovered system (left) and the corresponding RG (right)

It has 30 states being the columns of the following matrix:

$$\begin{aligned} \mathbf{X}_{reach}{=}\left( \begin{array}{cccccccccccccccccccccccccccccc} 1&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}1&{}1&{}0&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}1&{}0&{}0&{}1&{}1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}1&{}1&{}1&{}1&{}1&{}1&{}1\\ 0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}1&{}0&{}1&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}1&{}1&{}1\\ 0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}1&{}0&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}1&{}0&{}0&{}1&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}2&{}0&{}0&{}1&{}1&{}0\\ 1&{}1&{}1&{}1&{}1&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}1&{}1&{}0&{}1&{}1&{}0&{}1&{}1&{}1&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0\end{array}\right) \end{aligned}$$

(7)

The RT and RG of the recovered system are given in Fig. 7. But the deadlock $N_{19}$ ($\mathbf{x}_{18}$) occurs there.

2.2 Supervisor synthesis for deadlock(s) elimination

A general approach to the supervisor synthesis based on P-invariants of PN was presented in [4]. Suitable linear combinations of entries of the state vector $\mathbf{x}$ (i.e., $\mathbf{L}.\mathbf{x}$) are restricted by means of entries of the constant vector $\mathbf{b}$, i.e., $\mathbf{L}.\mathbf{x} \le \mathbf{b}$, $\mathbf{L} \in {{\mathbb {Z}}}_{\ge 0}^{n_s \times n}$, $\mathbf{b} \in {{\mathbb {Z}}}_{\ge 0}^{n_s \times 1}$. Then, in a nutshell, the supervisor synthesis is as follows. Remove the inequality by adding the vector $\mathbf{x}_s$ of the so called slacks, i.e.,

$$\begin{aligned}&{} \mathbf{L}.\mathbf{x} \le \mathbf{b}, \end{aligned}$$

(8)

$$\begin{aligned}&{} \mathbf{L}.\mathbf{x}+\mathbf{I}_s.\mathbf{x}_s=\mathbf{b}, \end{aligned}$$

(9)

where $\mathbf{I}_s$ is the $(s \times s)$-dimensional identity matrix. Now suppose that $\mathbf{Y}$ is a matrix of invariants of the extended PN model (the model of the plant and the supervisor together). Then

$$\begin{aligned} \mathbf{Y}^T.(\mathbf{B}^T\;\mathbf{B}_s^T)^T=\mathbf{0}. \end{aligned}$$

(10)

Let us define

$$\begin{aligned} \mathbf{Y}^T \triangleq (\mathbf{L}\;\mathbf{I}_s). \end{aligned}$$

(11)

After multiplying the matrices in (10), we obtain

$$\begin{aligned}&{} \mathbf{L}.\mathbf{B} + \mathbf{I}_s\cdot \mathbf{B}_s=\mathbf{0}, \end{aligned}$$

(12)

$$\begin{aligned}&{} \mathbf{B}_s= - \,\mathbf{L}\cdot \mathbf{B} = \mathbf{G}^T_s - \mathbf{F}_s. \end{aligned}$$

(13)

The initial state vector of the supervisor follows from (9) in the form

$$\begin{aligned} \mathbf{x}^s_0=\mathbf{b}-\mathbf{L}.\mathbf{x}_0. \end{aligned}$$

(14)

$\mathbf{B}_s$ is the supervisor structure and $\mathbf{x}^s_0$ is its initial state, $\mathbf{F}_s$, $\mathbf{G}_s$ are the incidence matrices of the supervisor. Consequently, ${}^s\mathbf{B}=(\mathbf{B}^T\;\mathbf{B}_s^T)^T$ is the structure of the supervised system (i.e., original system plus supervisor) and ${}^s\mathbf{x}_0=(\mathbf{x}_0^T\;(\mathbf{x}_0^s)^T)^T$ is its initial state.

Fig. 8

The PN model of the system with the recovered failure and the deadlock removed by means of the supervisor

Fig. 9

The RT of the recovered system with removed deadlock by means of the supervisor (left) and the corresponding RG (right)

Let us deal with the deadlock state $\mathbf{x}_{18}$ by means of synthesizing a suitable supervisor. Because the deadlock state is $N_{19}$, i.e., $\mathbf{x}_{18}=(0,\,1,\,0,\,0,\,0,\,0,\,1,\,0,\,1,\,0,\,0,\,1,\,0,\,0)^T$, we have to avoid its activation.

Consider $\mathbf{L}=(0,\,1,\,0,\,0,\,0,\,0,\,1,\,0,\,1,\,0,\,0,\,1,\,0,\,0)$ and $\mathbf{b} = 3$, i.e., at most three of $p_2,\,p_7,\,p_9,\,p_{12}$ can be active together. Then, the supervisor structure is given as $\mathbf{B}_s= (-\,1,\,1,\,0,\,-\,2,\,1,\,1,\,0,\,0,\,0,\,-\,1)$. After the break-up of $\mathbf{B}_s$ the incidence matrices of arcs are acquired. $\mathbf{F}_s=(1,\,0,\,0,\,2,\,0,\,0,\,0,\,0,\,0,\,1)$ and $\mathbf{G}^T_s=(0,\,1,\,0,\,0,\,1,\,1,0,\,0,\,0,\,0)$. The initial state of the supervisor is ${}^s\mathbf{x}_0 = 3 - 0 = 3$. The supervisor is incorporated into the PN model of the recovered system given in Fig. 6. Consequently, the form of the PN model is changed into the form given in Fig. 8. Its RT and RG are in Fig. 9. The reachable states of the deadlock-free recovered system are given as the columns of the matrix:

$$\begin{aligned} \mathbf{X}^s_{\mathrm{{reach}}}=\left( \begin{array}{ccccccccccccccccccccccccccc} 1&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}1&{}1&{}0&{}1&{}1&{}1&{}0&{}1&{}1&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}1&{}1&{}1&{}1&{}1&{}1&{}1\\ 0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}1&{}0&{}1&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}1&{}1&{}1\\ 0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}1&{}1&{}1&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}1&{}0&{}0&{}1&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}2&{}0&{}0&{}1&{}1&{}0\\ 1&{}1&{}1&{}1&{}1&{}1&{}0&{}1&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}1&{}1&{}0&{}1&{}1&{}0&{}1&{}1&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1&{}1&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ 3&{}2&{}3&{}0&{}2&{}3&{}0&{}0&{}2&{}1&{}0&{}0&{}1&{}1&{}1&{}0&{}2&{}1&{}2&{}1&{}3&{}2&{}2&{}1&{}3&{}2&{}3\end{array}\right) \end{aligned}$$

(15)

Fig. 10

The courses of marking the places $p_1 - p_4$ wrt. (with respect to) time

Fig. 11

The courses of marking the places $p_5 - p_{12}$ wrt. time. The marking of $p_{10}$ is directly influenced by $t_{f_5}$ (i.e., by a failure)

Fig. 12

The courses of marking the places $p_{13} - p_{15}$ wrt. time. The place $p_{15}$ expresses the state (marking) of the supervisor

Fig. 13

The courses of marking the place $p_{10}$ in the case (i) the left picture, and in the case (ii) the right picture

2.3 Time views on results

To give an image about time relations let us use TPN with time parameters of the transitions (delays in a time unit) defined by $D = 0.2\times (1,\,1,\,1,\,1,\,1,\,2,\,2,\,0.1,\,0.05,\,0.05)$, where first 7 parameters concerns transitions $t_1 - t_7$, 8-th parameter is assigned to $t_{f_5}$, 9-th parameter concerns $t_{r_2}$ and finally 10-th parameter concerns $t_{r_1}$. Simulation in Matlab by means of the tool HYPENS [24] brings the results given in Figs. 10, 11 and 12. Till now the deterministic timing of all transitions was used, including $t_{f_5}$. To make sure that non-deterministic timing of $t_{f_5}$ does not affect the results, consider for $t_{f_5}$ the discrete uniform probability distribution of timing: ${}^u f_x=1/(b-a)$ if $x \in (a,b)$, otherwise $x=0$. Test two cases: (i) $a=0.1,\;b=1.2$; (ii) $a=0.3,\;b=0.7$. The results are introduced in Fig.13.

As it can be seen, only the time instant of the failure incidence represented by $t_{f_5}$ manifests itself in marking of $p_{10}$—compare both pictures in Fig.13 each other and both of them with the corresponding part Fig.11 containing $p_{10}$. Courses of marking of all other places stay unchanged.

3 Conclusion

The PN-based approach to dealing with failures in DES was presented. It is based on utilizing RT/RG of the PN-based model of DES. Moreover, the elimination of deadlock(s) by means of supervision (synthesizing of the suitable supervisor) based on P-invariants of PN, introduced in [4], was utilized.

The presented approach consists of the following steps: (i) creating the PN model of the investigated kind of DES; (ii) finding its behaviour in the standard (failure-free) situation; (iii) analysing the model with respect to possible failures (in general, each system has its specificity and it is practically impossible to find a unified approach for all systems); (iv) selecting the failures which can be successfully recovered (because there are different kinds of failures and some of them cannot be recovered—e.g., human failures of the engine-driver or a mechanical problem in the crossing gate); (v) finding the structure of the recovered PN model; (vi) testing its behaviour with respect to deadlocks; (vii) removing deadlocks and finding the deadlock-free PN model.

PN were used in all of the steps. They make possible to create the uniform model of a system and compute its RT/RG. However, in different systems different states can fail. Hence, the model recovering process is individual. As to the computational complexity of the approach, it corresponds especially to that of computing RT, that depends on the structure of the PN model in question.

To illustrate the soundness of the procedure, the case study on the simple railroad crossing was introduced. Finally, the deadlock-free recovery model was found. It is necessary to emphasize that there are also the failures in DES which cannot be recovered by means of the procedure. They depend on human failures, bad properties and mistakes and/or on bad technical state of devices. They must be precluded either by means of the better preparation of human operators and/or by means of better executing maintenance of devices, their routine testing and/or checking, early replacing their components, etc.

In future a possibility of generalization of the recovery process by means of PN will be investigated.