The many facets of the Estrada indices of graphs and networks

Abstract

The Estrada index of a graph/network is defined as the trace of the adjacency matrix exponential. It has been extended to other graph-theoretic matrices, such as the Laplacian, distance, Seidel adjacency, Harary, etc. Here, we describe many of these extensions, including new ones, such as Gaussian, Mittag–Leffler and Onsager ones. More importantly, we contextualize all of these indices in physico-mathematical frameworks which allow their interpretations and facilitate their extensions and further studies. We also describe several of the bounds and estimations of these indices reported in the literature and analyze many of them computationally for small graphs as well as large complex networks. This article is intended to formalize many of the Estrada indices proposed and studied in the mathematical literature serving as a guide for their further studies.

1 Introduction

At the dawn of the XXI century the current author proposed an index to quantify the “degree of folding” of a linear chain in a three-dimensional space [70]. The motivation of this work came from the fact that many scientific articles make claims like that the structure A “is more folded than” the structure B (see examples at: [44, 67, 128, 237]), or that certain structure is “highly folded” (see for instance: [42, 129, 142, 246]), etc. These expressions could be referring to protein or polymer structures, but also to brain regions or even geological structures (see previous refs.). However, in neither of these works there was an index that quantifies how folded a linear chain is. Thus, the author proposed the index $I_{3}=\sum _{j=1}^{n}\exp \left( \lambda _{j}\left( W\right) \right)$, where $\lambda _{j}\left( W\right)$ are the eigenvalues of certain tridiagonal matrix W whose diagonal entries are related to the cosines of the dihedral angles between adjacent planes and $W_{i,i+1}$ and $W_{i+1,i}$ are equal to one. This index characterizes very well the degree of folding of a geometric chain and it has been mainly applied to the study of the degree of folding of proteins (see for instance [71, 73, 211]), although it can be applied to the folding of any linear chain.

Five years after the publication of the “folding degree” paper, the authors of [88] proposed the “subgraph centrality” as a way to characterize the importance of the nodes in a complex network. “Complex networks” are large graphs representing the skeleton of complex systems in social, ecological, cellular, molecular, infrastructural, semantic and other scenarios [78]. The subgraph centrality of a node v in a network is defined as $SC_{v}=\sum _{j=1}^{n}\psi _{jv}^{2}\exp \left( \lambda _{j}\left( A\right) \right)$, where $\lambda _{j}=\lambda _{j}\left( A\right)$ are the eigenvalues of the adjacency matrix of the graph and $\psi _{jv}$ is the vth entry of its jth normalized eigenvector. Then, the so-called subgraph centralization of the network is $\sum _{v}SC_{v}=\sum _{j=1}^{n}\exp \left( \lambda _{j}\left( A\right) \right)$ [88], which is similar to the folding degree $I_{3}$.

In June 2005 the current author presented the lecture “Topological characterization of complex networks” at the International Academy of Mathematical Chemistry in Dubrovnik, Croatia. As a consequence Ivan Gutman proposed to organize a small seminar at a park near the port of Dubrovnik to discuss some of the mathematical aspects of the index $\sum _{v}SC_{v}=\sum _{j=1}^{n}\exp \left( \lambda _{j}\right)$ for general graphs. As a result, a paper was published in 2006 in Croatica Chemica Acta introducing $\sum _{v}SC_{v}$ as a molecular structure descriptor [113]. A year later the paper “Estimating the Estrada index” was published, where the authors proposed to call $EE\left( G\right) =\sum _{j=1}^{n}\exp \left( \lambda _{j}\right)$ the Estrada index [54]. The same year a statistical mechanics interpretation of $EE\left( G\right)$ as the partition function of a graph [83] appeared. A year later, in 2008, there were more than 30 papers published in the mathematical literature containing “Estrada index” in the title.

It seems a priori that $EE\left( G\right)$ has emerged in different, apparently unrelated, scenarios: folding of linear chains, subgraphs in networks, and partition function in statistical mechanics. This reminds us the story told by Eugene Wigner in the first paragraph of his paper “The unreasonable effectiveness of mathematics in the natural sciences” [233] where a fellow asked a former classmate, now a statistician, about a symbol in a paper dealing with population trends. The statistician replied that the symbol was “$\pi$” and to clarify the skepticism of the other he added that it is “the ratio of the circumference of the circle to its diameter.” The fellow then replied more skeptical: “Well, now you are pushing your joke too far, surely the population has nothing to do with the circumference of the circle.” The situation of the Estrada index seems murkier than the one in that story, particularly after the ad hoc definition of several other variations of the index based not on the eigenvalues of the adjacency matrix, but of the graph Laplacian, distance matrix, resolvent of the adjacency matrix, Hadamard pseudo-inverse of the distance matrix (a.k.a. Harary matrix), Mittag–Leffler matrix functions of A, etc.

The goal of this paper is to make an account of the different facets of the Estrada indices. In doing so we will provide contextualization of several of these indices, many of which have been proposed in an ad hoc way. Therefore, we will provide a physical and/or mathematical context and interpretation of these indices. They include a combinatorial interpretation based on counting subgraphs, a statistical mechanics approach, a probabilistic interpretation in the context of walk-regular graphs, an interpretation on the basis of oscillations in (quantum and classical) systems of ball-and-springs, a contextualization on the basis of epidemiological models (normal and fractional) on graphs, diffusive processes with negative diffusiveness, nonlocal processes on graphs, quantification of graph radius of gyration. Although this paper does not intend to describe all the results published in the literature on this topic we make an account of many of the different bounds and estimations of the Estrada, Seidel Estrada, Harary Estrada, Laplacian Estrada, resolvent Estrada, Mittag–Leffler Estrada, and distance Estrada indices. For this purpose we include some numerical analysis of these bounds in the set of 11,117 connected graphs with 8 nodes and in five real-world networks representing a variety of complex system scenarios. The paper is written in a way that intend to be self-contained and make the necessary definitions for understanding the concepts used in it. The paper is then intended as a guide for further studies and developments in this area of spectral graph theory.

2 General definitions

Here we present some definitions which are used across the paper and settle down the notation. We consider here simple, connected graphs $G=(V,E)$ with n nodes (vertices) and m edges.

Definition 1

A walk of length k in G is a set of nodes and edges $v_{1},e_{1,2},v_{2}\cdots v_{k-1},e_{k-1,k},v_{k}$ such that for all $1\le l\le k$, $(v_{l},v_{l+1})\in E$. A closed walk is a walk for which $v_{1}=v_{k+1}$.

Definition 2

A path of length k in G is a walk in which neither vertices nor edges are repeated. A cycle is a closed path. The length of the shortest path connecting two vertices v and w is the (topological) shortest path distance $d_{vw}$ between the two nodes. The diameter of G is the longest distance between two vertices of G.

Definition 3

A subgraph $G'=(V',E')$ of G is a graph such that $V'\subseteq V$ and $E'\subseteq E\cap \left( V'\times V'\right)$. An induced subgraph is a subgraph formed by a subset of the vertices of the graph and all of the edges connecting pairs of vertices in that subset.

Definition 4

A graph $G=\left( V,E\right)$ is connected if there is a path between every pair of nodes $v,w\in V$. If the graph is directed we said that it is strongly connected if there is a directed path between every pair of nodes $v,w\in V$. A (strongly) connected component in a (directed) graph is a subgraph in which any two vertices are connected to each other by (directed) paths, and which is connected to no additional vertices in the rest of the graph.

Definition 5

The degree of a node v is the number $k_{v}$ of edges incident with that node. A graph is regular if the degree of all its nodes is the same.

The following matrices will be considered (Table 1):

Table 1 Definition of some matrices used in this paper

Other matrices such as the Seidel adjacency matrix and Harary matrix, are defined in situ in the corresponding sections of the paper. The following types of graphs are used in this work.

• Complete graph of n vertices $K_{n}$: the graph having an edge between every pair of vertices.

• Empty graph of n vertices ${\bar{K}}_{n}$: the graph having n vertices and no edges.

• Complete bipartite graph $K_{n_{1},n_{2}}$: the graph with $n=n_{1}+n_{2}$ vertices in which the vertex set is partitioned into two disjoint subsets of cardinalities $n_{1}$ and $n_{2},$ respectively, such that every vertex in one set is connected to every vertex in the other set.

• Star graph $S_{n}$: the particular case of $K_{n_{1},n_{2}}$ in which $n_{1}=1$ and $n_{2}=n-1.$

• Path graph of n vertices $P_{n}$: the connected graph in which every vertex has degree 2, except two vertices which have degree one.

• Cycle $C_{n}$: a connected graph in which every vertex has degree 2.

Finally we consider two kinds of random graphs.

• Erdős–Rényi (ER) $G\left( n,p\right)$ [68] graph with n nodes: constructed by connecting nodes randomly in such a way that each edge is included in $G\left( n,p\right)$ with probability p independent from every other edge.

• Barabási and Albert (BA) one [21]: created on the basis of a preferential attachment process. The graph is constructed from an initial seed of $m_{0}$ vertices connected randomly like in an Erdős–Rényi $G\left( n,p\right)$. Then, new nodes are added to the network in such a way that each new node is connected to $c\le m_{0}$ of the existing ones with a probability that is proportional to the degree of these existing nodes.

3 Estrada index and subgraph centralization

The main goal in proposing the Estrada index was for the structural characterization of networks. This index corresponds to the “centralization”, a global structural index, derived from the node centrality known as “subgraph centrality. In network theory a centrality measure (see [78] Chapter 7 and refs. therein) is any graph-theoretic quantity that captures the relative “importance” of a node in the network. Here “importance” means a relevant–mainly from applications point of view–structural feature such as connectivity, closeness to the rest of the nodes, position of a node in relation to the shortest paths connecting other others, etc. The simplest of these centrality measures is the degree of a node, which counts the number of connections that a node has. Let us first introduce the following result.

Theorem 1

Let $G=\left( V,E\right)$ be a simple graph with adjacency matrix A. Let $v,w\in V$, then the number of walks of length k between the nodes v and w is given by $\left( A^{k}\right) _{vw}.$

Remark 1

The roots of Theorem 1 can be traced back to the paper “The analysis of sociograms by matrix algebra” by Leo Festinger in 1949 [93], although Festinger mentioned it only for the case of walks of length three. Then, Leo Katz in his seminal paper “A new status index derived from sociometric analysis” extended it to longer walks in 1953 [141]. The result appeared formally in the book of Claude Berge in 1962 in the form of Corollary 1 on page 131 [29].

Then, from a walks perspective, the degree is defined as the number of closed walks of length two starting at the given node. That is, let $v\in V$, then the degree of v is given by:

$$\begin{aligned} k_{v}=\left( A^{2}\right) _{vv}. \end{aligned}$$

(3.1)

The degree of a node can be seen as a first order approximation of centrality measures that accounts for the walks of all length in the graph. That is, in a graph without self-loops the following measures can be defined

$$\begin{aligned} C_{v}-1=\sum _{k=2}^{\infty }c_{k}\left( A^{k}\right) _{vv}, \end{aligned}$$

(3.2)

where $c_{k}$ are coefficients which give more weight to the shorter than to the longer walks. Then, if $c_{k}=\left( k!\right) ^{-1}$:

$$\begin{aligned} EE_{v}-1=\sum _{k=2}^{\infty }\left( k!\right) ^{-1}\left( A^{k}\right) _{vv}=\left( \exp \left( A\right) \right) _{vv}-1, \end{aligned}$$

(3.3)

where $EE_{v}$ is known as the “subgraph centrality” of the node v [88]. The term “subgraph” in the name of this centrality is due to the following.

Lemma 1

Let G be a (directed) graph. Then, every closed walk of length k starting at the node $v\in V$ encloses one (strongly) connected subgraph having at most k (directed) edges and at most k vertices including v.

Proof

A (directed) graph G is (strongly) connected if there is a (directed) path connecting every pair of vertices G. By the definition of walk it is clear that a walk of length k between two nodes v and w cannot visit more than $k+1$ vertices. Therefore, a closed walk, where the initial and final nodes coincide, can visit no more than k nodes. In a closed walk of length k without backtracking the number of edges visited is k, i.e., in a cycle. For a given length k, backtracking reduces the number of edges that can be visited. Therefore, a closed walk of length k cannot visit more than k edges. Obviously, the nodes and edges visited by the closed walk form the sets $V'\subseteq V$ and $E'\subseteq E\cap \left( V'\times V'\right) ,$ which implies that $G'=\left( V',E'\right)$ is a subgraph of $G=\left( V,E\right)$. Finally, because the walk of length k is a sequence $v_{v},e_{v,v+1},v_{v+1}\cdots v_{v-1},e_{v-1,i},v_{v}$ there is a (directed) path connecting every pair of nodes in the subgraph, which means that $G'$ is (strongly) connected. $\square$

The previous result implies that we can express $EE_{v}$ as a weighted sum of subgraphs, which gives the index its name. However, as we are focused here on the Estrada index let us move to the fact that the Estrada index is the sum of the subgraph centralities of all nodes in the graph:

$$\begin{aligned} EE\left( G\right) =\sum _{v=1}^{n}EE_{v}. \end{aligned}$$

(3.4)

The sum of node centralities in a graph is known as the corresponding centralization of the graph, or simply as a graph-theoretic invariant. Therefore, the Estrada index of the graph can be seen as its subgraph centralization.

Theorem 2

Let G be a (directed) graph and let ${{\mathscr {F}}}$ be the set of all (strongly) connected subgraphs of G, and let us designate the cardinality of the set ${{\mathscr {F}}}$ by $\eta$. Then,

$$\begin{aligned} EE\left( G\right) =\sum _{l=1}^{\eta }c_{l}F_{l}, \end{aligned}$$

(3.5)

where $F_{l}\in {\mathscr {F}}$ and $c_{l}\in {\mathbb {Q}}$.

Proof

Using Lemma 1 we can show that that $M_{k}=\text {tr}\left( A^{k}\right)$ can be expressed as a weighted sum of (strongly) connected subgraphs. The weight of each subgraph is given by the number of closed walks of length k in the given subgraph. Then, grouping together all identical subgraphs and summing their weights we obtain the final result. $\square$

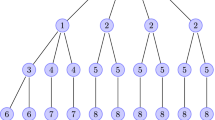
For instance, let us consider the first seven powers of the adjacency matrix. Then,

$$\begin{aligned} \text {tr}\left( A^{2}\right)= & {} 2F_{2}, \end{aligned}$$

(3.6)

$$\begin{aligned} \text {tr}\left( A^{3}\right)= & {} 6F_{4}, \end{aligned}$$

(3.7)

$$\begin{aligned} \text {tr}\left( A^{4}\right)= & {} 2F_{2}+4F_{3}+8F_{7}, \end{aligned}$$

(3.8)

$$\begin{aligned} \text {tr}\left( A^{5}\right)= & {} 30F_{4}+10F_{8}+10F_{10}, \end{aligned}$$

(3.9)

$$\begin{aligned} \text {tr}\left( A^{6}\right)= & {} 2F_{2}+12F_{3}+24F_{4}+6F_{5}+12F_{6}+48F_{7}\nonumber \\&+36F_{9}+12F_{12}+12F_{16}, \end{aligned}$$

(3.10)

$$\begin{aligned} \text {tr}\left( A^{7}\right)= & {} 126F_{4}+84F_{8}+112F_{9}+70F_{10}+28F_{11}+14F_{13}\nonumber \\&+14F_{14}+56F_{15}+14F_{17}+84F_{18}+28F_{19}+14F_{20}, \end{aligned}$$

(3.11)

where the subgraphs are illustrated in Fig. 1.

Fig. 1

Illustration of the small subgraphs appearing in the first seven spectral moments of the adjacency matrix of simple graphs

Then, we have the following result.

Lemma 2

Let G be a simple graph. Then, the Estrada index of G is bounded as

$$\begin{aligned} \begin{aligned} EE\left( G\right)&\ge F_{1}+\dfrac{391}{360}F_{2}+\dfrac{11}{60}F_{3}+\dfrac{157}{126}F_{4}+\dfrac{1}{120}F_{5}+\dfrac{1}{60}F_{6}+\dfrac{2}{5}F_{7}+\dfrac{1}{10}F_{8}\\&\quad +\dfrac{13}{180}F_{9}+\dfrac{7}{72}F_{10}+\dfrac{1}{180}F_{11}+\dfrac{1}{60}F_{12}+\dfrac{1}{360}F_{13}+\dfrac{1}{360}F_{14}\\&\quad +\dfrac{1}{90}F_{15}+\dfrac{1}{60}F_{16}+\dfrac{1}{360}F_{17}+\dfrac{1}{60}F_{18}+\dfrac{1}{180}F_{19}+\dfrac{1}{360}F_{20}. \end{aligned}\nonumber \\ \end{aligned}$$

(3.12)

Proof

Based on the relations shown before for $\text {tr}\left( A^{k}\right)$ for $k\le 7$ and calling $F_{1}=n$ we have that the right-hand-side part of Eq. (3.12) is $\sum _{k=0}^{7}\tfrac{\text {tr}\left( A^{k}\right) }{k!}$ from which the inequality follows. $\square$

The expressions for calculating these subgraphs are given in the Appendix as adapted from [9]. The formula for $F_{20}$ is given here by the first time.

3.1 Some elementary properties of the Estrada index

Before proceeding to more complex properties of the Estrada index let us state a few elementary ones that could be helpful in understanding the structural nature of this index. The reader is referred to the following references [54, 57, 112, 116] for details and references.

Lemma 3

Let G be a simple graph and let $G-e$ the same graph from which edge e has been removed. Then

$$\begin{aligned} EE\left( G-e\right) \le EE\left( G\right) . \end{aligned}$$

(3.13)

Corollary 1

Let G be a simple graph and let T be a tree with the same number of nodes as G. Then

$$\begin{aligned} EE\left( T\right) \le EE\left( G\right) . \end{aligned}$$

(3.14)

Theorem 3

[53, 56] Let G be a simple connected graph with n nodes. Then

$$\begin{aligned} EE\left( P_{n}\right) \le EE\left( G\right) \le EE\left( K_{n}\right) . \end{aligned}$$

(3.15)

Theorem 4

Let G be a simple graph with n nodes. Then

$$\begin{aligned} EE\left( {\bar{K}}_{n}\right) \le EE\left( G\right) \le EE\left( K_{n}\right) . \end{aligned}$$

(3.16)

The Estrada indices of some elementary graphs are given below.

• $EE\left( K_{n}\right) =e^{n-1}+\left( n-1\right) e^{-1};$

• $EE\left( K_{n_{1},n_{2}}\right) =n_{1}+n_{2}-2+2\cosh \left( \sqrt{n_{1}n_{2}}\right) ;$

• $EE\left( S_{n}\right) =n-2+2\cosh \left( \sqrt{n-1}\right) ;$

• $\lim _{n\rightarrow \infty }EE\left( C_{n}\right) =nI_{0}$, where $I_{0}=\dfrac{1}{\pi }\int _{0}^{\pi }e^{2\cos x}dx$;

• $\lim _{n\rightarrow \infty }EE\left( P_{n}\right) =\left( n-1\right) -2\cosh \left( 2\right)$.

3.2 Numerical analysis

We consider here two datasets which will be used in the rest of the paper for the numerical evaluation of the different indices and bounds. The first one consists of the 11,117 connected graphs with 8 nodes. The second one is formed by five real-world networks, which correspond to a food web at Stony stream, a network of the neurons in the worm C. elegans, the protein–protein interaction network of yeast, a representation of the Internet at the autonomous system (AS) level, and a network of the USA western power grid system. The number of nodes n, of edges m, the maximum degree of the nodes $k_{max}$, and the diameter $d_{max}$ of each network are given in Table 2.

Table 2 General characteristics, number of nodes n, of edges m, the maximum degree of the nodes $k_{max}$, and the diameter $d_{max}$, of the five real-world networks analyzed in this paper

The main goal of these numerical experiments is to show how close the bounds reported in the literature are to the actual values of the Estrada index. This is done because in most of the papers where these bounds are proposed there are no numerical experiments to illustrate this relation. When possible we will find some connection between structural characteristics of the networks studied and the corresponding bounds analyzed to understand why are they close or far away the actual values of the Estrada index.

First, we consider the deviation of the bound from the actual value as $\left| EE_{\text {exact}}-EE_{\text {bound}}\right| /EE_{\text {exact}}$ expressed as percentage. We do this calculation considering the bound given in Lemma 2 for all the connected graphs with 8 nodes. The histogram illustrating the number of graphs having a given relative deviation (frequency) among the 11,117 connected graphs with 8 nodes is illustrated in Fig. 2. We should remark that we use here the terms “good bound” or refer to a bound as “better than” another just on the basis of the deviation of this bound relative to the actual value of the index. This is used only as a guide as for many cases there is large room for improvement as some of the bounds reported are orders of magnitude further from the real values of the indices.

The mean deviation is $5.768\pm 4.169$, which indicates that this bound is a good estimation of the Estrada index for these small graphs. The largest deviation is 40.352 obtained for the complete graph $K_{8}$. In general, the most densely connected graphs are richer in small subgraphs than the poorly dense ones, which increases the relative deviation of this bound for these graphs.

Fig. 2

Histogram of the relative deviation of the bound given in Lemma 2 for all 11,117 connected graphs with 8 nodes

In Table 3 we illustrate the results for the five real-world networks. The largest deviation occurs for the Internet at AS indicating that in this network there are many larger subgraphs with important contribution to the Estrada index. On the other hand, the bound is very close to the actual value for the power grid of western USA, which points out that the Estrada index of this network is well approximated by counting the number of the 21 subgraphs described by Lemma 2. These differences point out clearly to the differences in the subgraph richness contained in different networks, which is what the Estrada index characterizes at the structural level.

Table 3 Values of the bound for the Estrada index in Lemma 2 and the actual values calculated with Matlab function “expm” for the five real-world networks considered in this work

4 Estrada index and matrix functions

Soon after the definition of the Estrada index and the subgraph centrality several authors started to be interested in these indices due to their clear relation to functions of the adjacency matrix. The study of matrix functions is an active area of research in (numerical) linear algebra [25, 97, 127, 222]. The topic of matrix functions in network theory has been recently reviewed by the authors of [28]. Therefore, we will not give too many details here and the interested reader is directed to the excellent review [28]. The goal of this section is then to establish the connection between the Estrada indices and functions of the corresponding matrices which pave the way for further sections of the article. Here we will follow the book [127].

Let M be any graph-theoretic matrix, e.g., adjacency, Laplacian, distance, etc. Then, its Jordan canonical form is given by

$$\begin{aligned} Z^{-1}MZ=J=\text {diag}\left( J_{1},J_{2},\ldots ,J_{p}\right) , \end{aligned}$$

(4.1)

where

$$\begin{aligned} J_{k}=J_{k}\left( \lambda _{k}\right) =\left[ \begin{array}{cccc} \lambda _{k} &{}\quad 1\\ &{}\quad \lambda _{k} &{}\quad \ddots \\ &{} &{}\quad \ddots &{}\quad 1\\ &{} &{} &{}\quad \lambda _{k} \end{array}\right] \in {\mathbb {C}}^{m_{k}\times m_{k}}, \end{aligned}$$

(4.2)

where Z is nonsingular and $m_{1}+m_{2}+\cdot \cdot \cdot +m_{p}=n$.

Definition 6

Let $\lambda _{1},\ldots ,\lambda _{s}$ be the distinct eigenvalues of M and let and let $n_{i}$ be the order of the largest Jordan block in which $\lambda _{i}$ appears, which is called the index of $\lambda _{i}$. The function f is defined on the spectrum of M if the values

$$\begin{aligned} f^{\left( j\right) }\left( \lambda _{i}\right) ,\quad j=0,\ldots ,n_{i}-1,i=1,\ldots ,s \end{aligned}$$

(4.3)

exist, which are called the values of the function f on the spectrum of M. Here $f^{\left( j\right) }$ represents the jth derivative of f.

Then we have a definition of matrix function via the Jordan canonical form.

Definition 7

Let f be defined on the spectrum of M and let M have the Jordan canonical form given before. Then, the matrix function $f\left( M\right)$ is given by

$$\begin{aligned} f\left( M\right) \,{:}{=}\,Zf\left( J\right) Z^{-1}=Z\text {diag}\left( f\left( J_{k}\right) \right) Z^{-1}, \end{aligned}$$

(4.4)

where

$$\begin{aligned} f\left( J_{k}\right) \,{:}{=}\,\left[ \begin{array}{cccc} f\left( \lambda _{k}\right) &{}\quad f'\left( \lambda _{k}\right) &{}\quad \cdots &{}\quad \dfrac{f^{\left( m_{k}-1\right) }\left( \lambda _{k}\right) }{\left( m_{k}-1\right) !}\\ &{}\quad f\left( \lambda _{k}\right) &{}\quad \ddots &{}\quad \vdots \\ &{} &{}\quad \ddots &{}\quad f'\left( \lambda _{k}\right) \\ &{} &{} &{}\quad f\left( \lambda _{k}\right) \end{array}\right] . \end{aligned}$$

(4.5)

Another, equivalent, definition is given via the Cauchy integral.

Definition 8

Let $M\in {\mathbb {C}}^{n\times n}$, then

$$\begin{aligned} f\left( M\right) \,{:}{=}\,\dfrac{1}{2\pi i}\int _{\varGamma }f\left( z\right) \left( zI-M\right) ^{-1}dz, \end{aligned}$$

(4.6)

here f is analytic on and inside a closed contour $\varGamma$ that encloses the spectrum of M.

5 Estrada index and spectral graph theory

An obvious connection exists between the Estrada index and the area of algebraic graph theory. Algebraic graph theory [24, 30, 105] deals with the use of algebraic methods to solve problems about graphs. Of particular interest is the use of the spectra of graph theoretic matrices to understand the structure of graphs, which is known as spectral graph theory [46, 50,51,52, 213, 214]. This area of research started in an applied context when Collatz and Sinogowitz published their paper entitled: “Spektren endlicher grafen” motivated by application problems such as the vibrations of a membrane [223]. Let us consider a simple example of the connections between structural properties of graphs and their spectra: counting triangles in a graph. The number of triangles, which is a combinatorial property of the graph, can be obtained from the spectrum of the adjacency matrix as: $\dfrac{1}{6}\sum _{j=1}^{n}\lambda _{j}^{3}$, where $\lambda _{j}$ are the eigenvalues of the adjacency matrix. The field of spectral graph theory had a tremendous impulse in the 1970s due to its connection with electronic properties of conjugated molecules [59, 95, 124, 215, 216, 219].

The relation between the trace of a matrix and its eigenvalues immediately implies that the Estrada index of a graph can be expressed in terms of the eigenvalues of A as follows:

$$\begin{aligned} EE\left( G\right) =\sum _{j=1}^{n}\exp \left( \lambda _{j}\right) . \end{aligned}$$

(5.1)

In general, the exponentiation of A enlarges the spectral gap $\lambda _{1}-\lambda _{2}$ and contracts the negative part of the spectrum. On the contrary, $\exp \left( -A\right)$ largely contracts the positive part of the spectrum and enlarges its negative part. These simple dilation/contraction effects of the main parts of the spectrum of A have important consequences on the Estrada index of a graph as we will see in the next parts of this review.

The analysis of the relation between the spectrum of a graph, i.e., the eigenvalues of its adjacency matrix, and the structure of the graph is the main goal of spectral graph theory. One of the first results on spectral graph theory related to the Estrada index was the following bounds obtained by the authors of [54].

Theorem 5

Let G be a simple graph with n nodes and m edges. Then, the Estrada index of G is bounded as

$$\begin{aligned} \sqrt{n^{2}+4m}\le EE\left( G\right) \le n-1+\exp \left( \sqrt{2m}\right) , \end{aligned}$$

(5.2)

with equality attained if and only if $G\cong {\bar{K}}_{n}$.

These bounds were further improved in [166] where the following was proved.

Theorem 6

Let G be a simple graph with n nodes and $m\ge 1$ edges. Then, the Estrada index of G is bounded as

$$\begin{aligned} \sqrt{n^{2}+\dfrac{5}{3}m}<EE\left( G\right) <n-1+\exp \left( \sqrt{m}\right) . \end{aligned}$$

(5.3)

Based on Gauss–Radau quadrature rule the authors of [27] obtained the following bounds.

Theorem 7

Let G be a simple graph and let $a,b\in {\mathbb {R}}$ be such that the spectrum of A is contained in $\left[ a,b\right]$. Then, the Estrada index of G is bounded as

$$\begin{aligned} \sum _{i=1}^{n}\dfrac{b^{2}\exp \left( k_{i}/b\right) +k_{i}\exp \left( -b\right) }{b^{2}+k_{i}}\le EE\left( G\right) \le \sum _{i=1}^{n}\dfrac{a^{2}\exp \left( k_{i}/a\right) +k_{i}\exp \left( -a\right) }{a^{2}+k_{i}}, \end{aligned}$$

(5.4)

where $k_{i}$ is the degree of the node i.

Remark 2

Two examples of the use of this bound are (i) considering $a=-\lambda _{1}$ and $b=-\lambda _{n}$; (b) considering $a=-k_{max}$ and $b=k_{max}$.

Another set of bounds was obtained in 2016 [156] by using the number of triangles t and $\text {tr}\left( A^{4}\right)$ in addition to the number of nodes and edges of the graph.

Theorem 8

Let G be a simple graph with n nodes, m edges, t triangles and let $Q=\text {tr} \left( A^{4}\right)$. Then, the Estrada index of G is bounded as

$$\begin{aligned} m+n\le \sqrt{n^{2}+mn+2nt+\dfrac{1}{12}nQ+m^{2}}\le EE\left( G\right) \le n-1+\exp \left( \root 4 \of {Q}\right) , \end{aligned}$$

(5.5)

with equality attained if and only if $G\cong {\bar{K}}_{n}$.

Other bounds have been proposed, specially lower bounds, for the Estrada index. Some examples are given below.

Theorem 9

[247] Let G be a simple graph with n nodes and let $Z=\sum _{i=1}^{n}k_{i}^{2}$. Then, the Estrada index of G is bounded as

$$\begin{aligned} EE\left( G\right) \ge \exp \left( \sqrt{Z/n}\right) +\left( n-1\right) \exp \left( -\left( \sqrt{Z/n}\right) /\left( n-1\right) \right) , \end{aligned}$$

(5.6)

with equality attained if and only if $G\cong K_{n}$ or $G\cong {\bar{K}}_{n}$.

Theorem 10

[110] Let G be a simple graph with n nodes and m edges either without isolated vertices or having the property $2m/n>1$, then, the Estrada index of G is bounded as

$$\begin{aligned} EE\left( G\right) \ge n\cosh \left( \sqrt{2m/n}\right) , \end{aligned}$$

(5.7)

with equality if and only if G is a regular graph of degree 1.

Theorem 11

[110] Let G be a simple graph with n nodes and m edges, such that $2m/n<1$. Then, the Estrada index of G is bounded as

$$\begin{aligned} EE\left( G\right) \ge n-2m+2m\cosh \left( 1\right) , \end{aligned}$$

(5.8)

where equality holds if and only if G consists of $n-2m$ isolated vertices and m copies of $K_{2}$.

Theorem 12

[110, 119] Let G be a simple graph with n nodes, m edges and graph nullity $\eta _{0}$. Then, the Estrada index of G is bounded as

$$\begin{aligned} EE\left( G\right) \ge \eta _{0}+\left( n-\eta _{0}\right) \cosh \left( \dfrac{2m}{n-\eta _{0}}\right) , \end{aligned}$$

(5.9)

where equality is attained if and only if $n-\eta _{0}$ is even, and if G consists of copies of complete bipartite graphs $K_{r_{i},s_{i}},i=1,\ldots ,\left( n-\eta _{0}\right) /2$, such that all products $r_{i}\cdot s_{i}$ are mutually equal.

Theorem 13

[190] Let G be a simple graph with n nodes, m edges and minimum degree $k_{min}$. Then, the Estrada index of G is bounded as

$$\begin{aligned} EE\left( G\right) \ge 2\cosh \left( \dfrac{2\left( m-k_{min}\right) }{n-1}\right) +n-2, \end{aligned}$$

(5.10)

with equality if and only if $G\cong K_{p,p}\cup K_{1}$ with $n=2p+1.$

Theorem 14

[190] Let G be a simple graph with n nodes, m edges and minimum degree $k_{min}$. Then, the Estrada index of G is bounded as

$$\begin{aligned} EE\left( G\right) \ge 2\cosh \left( 2\cos \left( \dfrac{\pi }{n+1}\right) \right) +n-2, \end{aligned}$$

(5.11)

with equality if and only if $G\cong P_{2}$ or $G\cong P_{4}.$

Theorem 15

[19] Let G be a simple graph with n nodes, m edges and t triangles. Then, the Estrada index of G is bounded as

$$\begin{aligned} EE\left( G\right) \ge \sqrt{n^{2}+mn+2nt}, \end{aligned}$$

(5.12)

with equality if and only if $G\cong {\bar{K}}_{n}$.

Other bounds reported in the literature are based on different graph-theoretic indices and properties or for specific classes of graphs. A non-exhaustive resume is provided in Table 4.

Table 4 Examples of studies reported in the literature for some classes of graphs

5.1 Numerical analysis

We now do some calculations to show how close to the actual values of the Estrada index are some of the bounds studied in the previous sections. In particular, we consider the following five bounds: Bound 1 (Theorem 5); Bound 2 (Theorem 6; Bound 3 (Theorem 7 using $a=-\lambda _{1}$ and $b=-\lambda _{n}$); Bound 4 (Theorem 7 using $a=-k_{max}$ and $b=k_{max}$); Bound 5 (Theorem 8). First, we study these bounds for the 11,117 connected graphs with 8 nodes. The histograms of the relative deviations of these bounds are illustrated in Fig. 3, where the lower bound is always drawn in blue and the upper one in red. The means and standard deviations of the lower, upper bounds are as follow: Bound 1 ($79.672\pm 9.485$, $259.948\pm 44.555$); Bound 2 ($82.588\pm 8.499$, $19.205\pm 14.198$); Bound 3 ($57.915\pm 13.701$, $30.466\pm 5.860$); Bound 4 ($73.741\pm 12.359$, $239.249\pm 156.52$); Bound 5 ($54.629\pm 14.214$, $18.276\pm 8.812$). Therefore, the best lower and upper bounds are Bound 5 (Theorem 8) for these small graphs.

Fig. 3

Histograms of the relative deviations in percentage for: a Bound 1 (Theorem 5), b Bound 2 (Theorem 6, c Bound 3 (Theorem 7 using $a=-\lambda _{1}$ and $b=-\lambda _{n}$), d Bound 4 (Theorem 7 using $a=-k_{max}$ and $b=k_{max}$), e Bound 5 (Theorem 8). In blue we illustrate the histogram for the lower and in red for the upper bounds. As usual for histograms, frequency stands for the number of graphs in each bin

In Fig. 4 we illustrate the results for the five real-world networks considered in this work. In general, with the exception of Bound 3, which is based on eigenvalues, and Bound 5, which uses $\text {tr}\left( A^{4}\right)$, the rest of the bounds are very far from the actual values for these four networks. With these two exceptions, the upper bounds exaggerate dramatically the estimation, in particular the Bound 1. Bound 4, performs very badly when the maximum degree of the network is very high and not close to the spectral radius, which is the case for instance of Internet, but also of many real-world networks. All in all, these results point out to the necessity of improving the bounds for the Estrada index of large graphs.

Fig. 4

Plot of the estimates of the lower (blue circles) and upper (red squares) for the bounds: (1) (Theorem 5), (2) (Theorem 6, (3) (Theorem 7 using $a=-\lambda _{1}$ and $b=-\lambda _{n}$), (4) (Theorem 7 using $a=-k_{max}$ and $b=k_{max}$), (5) (Theorem 8). The results are for (a) Stony, (b) neurons, (c) yeast, (d) internet and (e) powergrid. The dashed lines represents the “exact” value of the Estrada index for the networks. Very large values are obtained by using variable-precision floating-point arithmetic (vpa) in Matlab

We then consider simple bounds based on the spectral radius of the adjacency matrix $\lambda _{1}$. That is,

$$\begin{aligned} e^{\lambda _{1}}<EE\left( G\right) <ne^{\lambda _{1}}. \end{aligned}$$

(5.13)

The results are given in Table 5. As can be seen the bounds are very close to the actual values of the Estrada index. This is a consequence of the relatively large values of the spectral radius and of the spectral gap observed in most of the real-world networks, which when exponentiated are significantly enlarged. Notice that the largest deviation is obtained for powergrid, where the spectral radius is significantly smaller than in the rest of the networks and the spectral gap is very small.

Table 5 Naive bounds based on the spectral radius of the adjacency matrix for the Estrada index of real-world networks

5.2 Random graphs

In the study of real-world networks it is desired to investigate how unique are their structural and dynamical properties in relation to some null model. For instance, suppose that we have found that certain network displays relatively large Estrada index in relation to other networks of the same size. Is this a characteristic feature of the topological organization of this network or just an artifact emerging from a random interconnection of their nodes? A way to investigate this is by comparing the Estrada index of these networks with those of random realizations of such networks with the same number of nodes and edges. Then, the use of random graphs is frequent in the analysis of real-world networks [220]. Two classical models, although not the only ones, to do such studies are the Erdős–Rényi random graphs [68] and the Barabási–Albert preferential attachment model [21]. For instance, the Estrada index of the network “neurons” studied here is $EE\left( G_{\text {real}}\right) \approx 1.3062\times 10^{10}$ and that of an Erdős–Rényi random graph with the same number of nodes and edges is $EE\left( G_{\text {ER}}\right) \approx 3.4688\times 10^{6}$, which indicates that the large Estrada index of this network is not due to a random interconnection of the neurons of C. elegans. However, the consideration of a Barabási–Albert network with the same number of nodes and edges than those in the network “neurons” gives $EE\left( G_{\text {BA}}\right) \approx 1.2131\times 10^{10}$, which clearly points out that the relatively large Estrada index of this network may be explained by its skewed degree distribution.

For the Estrada index of random graphs, only the Erdős–Rényi model has been considered so far, indicating the necessity of extending these studied to other classes of random graphs such as the Barabási–Albert one. The following estimates were found for Erdős–Rényi random graphs based on the number of nodes and the probability of connection.

Lemma 4

[196] Let $G_{n,p}$ be an Erdős–Rényi random graph with n nodes and probability

$$\begin{aligned} \dfrac{\ln n}{n}\ll p<1-\dfrac{\ln n}{n}. \end{aligned}$$

(5.14)

Then, the Estrada index is

$$\begin{aligned} EE\left( G_{n,p}\right) =\left( 1+o\left( 1\right) \right) e^{np}, \end{aligned}$$

(5.15)

almost surely as $n\rightarrow \infty .$

Theorem 16

[43] Let $G_{n,p}$ be e an Erdős–Rényi random graph with n nodes and probability p. Then, the Estrada index is

$$\begin{aligned} EE\left( G_{n,p}\right) =\left( e^{O\left( \sqrt{n}\right) }+o\left( 1\right) \right) e^{np}, \end{aligned}$$

(5.16)

almost surely (a.s.) if and only if $\lim _{n\rightarrow \infty }n_{2}/n_{1}=1$.

In the case of Erdős–Rényi random bipartite graphs the author of [206] proved the following bounds for the Estrada index.

Theorem 17

Let $G_{n_{1},n_{2},p}$ be an Erdős–Rényi random bipartite graph with $n=n_{1}+n_{2}$ nodes, such that $\lim _{n\rightarrow \infty }n_{2}/n_{1}\,{:}{=}\,y\in \left( 0,1\right]$, and probability p. Then, the Estrada index is bounded as

$$\begin{aligned} \left( e^{O\left( \sqrt{n}\right) }+o\left( 1\right) \right) e^{n_{2}p}\le EE\left( G_{n,p}\right) \le \left( e^{O\left( \sqrt{n}\right) }+O\left( 1\right) \right) e^{n_{1}p},a.s. \end{aligned}$$

(5.17)

provided that $y=1$.

6 Estrada index and statistical mechanics

The analogy of the Estrada index $EE\left( G\right) =tr\left( e^{A}\right)$ with the partition function of a quantum system $Z=tr\left( e^{-\hat{\tau \mathcal {H}}}\right)$ (see further for definitions) is remarkable, and was noticed soon after the definition of this index [83]. The importance of establishing this connection is twofold. On the one hand, the index can be interpreted in a physical context which at the same time facilitates its interpretation in other contexts where it is applied. On the other hand, new tools and techniques from statistical mechanics can be used to enrich the theory behind this index. Here, we will describe the statistical mechanics interpretation of the Estrada index.

Let us consider a physical system ${\mathcal {S}}$ that can be represented by a graph G, such that the total energy E of ${\mathcal {S}}$ can be obtained by the time-independent Schrödinger equation: $\hat{{\mathcal {H}}}\varPsi =E\varPsi$, where $\varPsi$ is the wavefunction and $\hat{{\mathcal {H}}}$ is the Hamiltonian describing the interactions between the elements of ${\mathcal {S}}$. In certain approaches in physics and chemistry, it is customary to use an effective Hamiltonian which describes the interaction between nearest-neighbors (NN) in the system

$$\begin{aligned} {\hat{\mathcal {H}}}_{NN}=\alpha I+t_{NN}A, \end{aligned}$$

(6.1)

where $\alpha$ is a self-energy parameter for the elements of ${\mathcal {S}}$ and $t_{NN}$ is the energy of the interaction between pairs of adjacent elements. In Chemistry this model is known as the Hückel Molecular Orbital (HMO) method [154, 239], while in Physics it is better known as the tight-binding approach [184]. The parameter $t_{NN}$ is negative as it is supposed to be an attractive interaction. Therefore, it is common to set $\alpha =0$ and $t_{NN}=-1,$ such that ${\hat{\mathcal {H}}}=-A.$ Therefore, the energy levels of the system are $E_{j}=-\lambda _{j}$ and the wavefunctions correspond to the eigenvectors associated to the eigenvalues of A.

In the statistical mechanics framework [23, 69], the Boltzmann probability $p_{j}\left( \tau \right)$ of finding the system in a state with energy $E_{j}$ when the inverse temperature of the system is $\tau =\left( k_{B}T\right) ^{-1}>0$ with $k_{B}$ being a constant and T being the temperature¹ is

$$\begin{aligned} p_{j}\left( \tau \right) =\dfrac{e^{-\tau E_{j}}}{Z}, \end{aligned}$$

(6.2)

where $Z=\text {tr}\left( e^{-\tau {\hat{\mathcal {H}}}_{NN}}\right)$. Therefore, the Boltzmann probability of the system is given by

$$\begin{aligned} p_{j}\left( \tau \right) =\dfrac{e^{\tau \lambda _{j}}}{EE\left( G,\tau \right) }, \end{aligned}$$

(6.3)

where the Estrada index plays the role of the partition function of the graph.

We now can define the entropy of the graph as [83]

$$\begin{aligned} S\left( G,\tau \right) =-k_{B}\sum _{j}p_{j}\left( \tau \right) \ln p_{j}\left( \tau \right) =-\dfrac{1}{T}\sum _{j}\left( p_{j}\left( \tau \right) \lambda _{j}\right) +k_{B}\ln EE\left( G,\tau \right) , \end{aligned}$$

(6.4)

which in general is bounded as follows.

Lemma 5

Let G be a simple graph. Then, the free energy of G is bounded as

$$\begin{aligned} 0\le \left( \ln \left( \exp \left( n\right) +n-1\right) -\dfrac{n\exp \left( n\right) }{\exp \left( n\right) +n-1}\right) \le S\left( G,\tau \right) \le \ln n, \end{aligned}$$

(6.5)

where the upper bound is attained for the null graph ${\overline{K}}_{n}$ and the lower bound is reached for the complete graph $K_{n}$.

From the general expression of the entropy one can obtain the graph “enthalpy” $H\left( G,\tau \right) =-\sum _{j}p_{j}\lambda _{j}$ and the graph free energy, which is sometimes named the natural connectivity of the network [83]:

$$\begin{aligned} F\left( G,\tau \right) =-\tau ^{-1}\ln EE\left( G,\tau \right) . \end{aligned}$$

(6.6)

We can write the logarithm of the Estrada index as follows,

$$\begin{aligned} \ln EE\left( G,\tau \right) =\tau \lambda _{1}+\ln \sum _{j}e^{\tau \left( \lambda _{j}-\lambda _{1}\right) }, \end{aligned}$$

(6.7)

which implies that

$$\begin{aligned} \ln EE\left( G,\tau \right) \le \tau \lambda _{1}+\ln \left( 1+e^{-\tau \triangle }\right) , \end{aligned}$$

(6.8)

where $\triangle =\lambda _{1}-\lambda _{2}$ is the spectral gap. Therefore, we have proved the following.

Lemma 6

Let G be a simple graph. Then, the free energy of G is bounded as

$$\begin{aligned} F\left( G,\tau \right) \le -\left[ \lambda _{1}+\tau ^{-1}\ln \left( 1+e^{-\tau \triangle }\right) \right] . \end{aligned}$$

(6.9)

More generally, the free energy of a graph can be bounded by using the many bounds obtained for the Estrada index which have been previously reported in the literature. One important example is the following [83].

Lemma 7

Let G be a simple graph. Then, the free energy of G is bounded as

$$\begin{aligned} \left( n-1\right) <1-\tau ^{-1}\ln \left( e^{\tau n}+n-1\right) \le F\left( G,\tau \right) \le -\tau ^{-1}\ln n, \end{aligned}$$

(6.10)

where the lower bound is obtained for the complete graph $K_{n}$ and the upper bound for the null graph ${\overline{K}}_{n}$.

6.1 Numerical analysis

We consider here numerical experiments to illustrate some general characteristics of the indices described in the previous section. We report the change of the entropy, enthalpy and free energy of all connected graphs with the increase of the number of edges in the connected graphs with 8 nodes, i.e., its edge density. It can be seen in Fig. 5, as expected, that the three parameters decay with the increase in the edge density. However, it should be noticed that for graphs with exactly the same number of edges there is a wide variability in these parameters, particularly for the entropy. The readers interested in more details about the implications of these parameters on the structure of graphs are referred to [83].

Fig. 5

Plots of the entropy (a), enthalpy (b) and free energy (c) versus the number of edges in all connected graphs with 8 nodes

We then computed the three statistical mechanics parameters for the five networks studied here. The results are in Table 6 where we also give the values of the edge density of these graphs: $\delta \left( G\right) =2m/\left( n\left( n-1\right) \right)$ where n and m are the number of nodes and edges of the graph. The most densely connected network, Stony, displays the lowest entropy and the least dense, powergrid, displays the largest one. However, as can be seen for the intermediate values of $\delta \left( G\right)$ this trend is not always followed as there are other structural factors influencing these statistical mechanics parameters. For instance, the network of Internet at AS displays the second smaller entropy of all the networks and the lowest free energy of all, although it is not very dense.

Table 6 Values of the entropy, enthalpy and free energy of the five real-world networks analyzed here

7 Marginal probability, walk entropy and walk regularity

Having in mind the importance that the probability $p_{j}\left( \tau \right)$ has in the definition of statistical mechanics properties of networks we propose to explore it further in this section. That is, we consider here the role of the Estrada index in defining some probability-based measures for graphs. Let us start with two definitions from basic statistics (see for instance [49, Ch. 2]).

Definition 9

The conditional probability $P\left( A\left| B\right. \right)$ is the probability that the event A occurs given that the event B occurs.

Definition 10

The marginal probability is the unconditional probability of one event A. That is, the probability that A occurs regardless of whether B occurs or not.

To obtain the marginal probability of an event A one should sum all possible configurations of the other event to obtain a weighted average probability

$$\begin{aligned} P\left( A\right) =\sum _{B}P\left( A\left| B\right. \right) \cdot P\left( B\right) . \end{aligned}$$

(7.1)

Let us then return to the time-independent Schrödinger equation:

$$\begin{aligned} {\hat{\mathcal {H}}}\psi _{j}=E_{j}\psi _{j}, \end{aligned}$$

(7.2)

where $E_{j}$ are the energy levels of the system and $\psi _{j}$ are the corresponding eigenfunctions. As usual, $\left| \psi _{j,v}\right| ^{2}$ represents the probability of finding a quantum particle at a given vertex v and time conditional to the system to be at the energy level described by the wave function $\psi _{j}$. That is, $\left| \psi _{j,v}\right| ^{2}=P\left( v\left| j\right. \right)$ using the notation defined before.

On the other hand, $p_{j}\left( \tau \right)$ which was defined in the previous section accounts for the probability that the system is at the jth energy level for a given $\tau$. Then, fixing $\tau$, $p_{j}\left( \tau \right) =P\left( j\right) .$ Therefore, the marginal probability that the node v is occupied by the quantum particle independently of the energy level in which the system is, is given by:

$$\begin{aligned} P\left( v\right) =\sum _{j}P\left( v\left| j\right. \right) \cdot P\left( j\right) =\sum _{j}\left| \psi _{j,v}\right| ^{2}\cdot p_{j}\left( \tau \right) , \end{aligned}$$

(7.3)

which can be expressed as [86]:

$$\begin{aligned} P\left( v,\tau \right) =\dfrac{\sum _{j}\psi _{j,v}^{2}e^{\tau \lambda _{j}}}{EE\left( G,\tau \right) }=\dfrac{EE_{v}\left( \tau \right) }{EE\left( G,\tau \right) }. \end{aligned}$$

(7.4)

The corresponding entropy, known as the walk-entropy of the graph [86], is defined using Shannon formula:

$$\begin{aligned} S^{w}\left( \tau \right) =-\sum _{v}P\left( v,\tau \right) \ln P\left( v,\tau \right) . \end{aligned}$$

(7.5)

We now consider a graph property known as walk-regularity and the role that the walk entropy play in its characterization. Let us introduce the concept of walk regularity first (see for instance [106]).

Definition 11

A graph is walk-regular if $\forall i,j\in V$ and for every nonnegative integer r, $[A^{r}]_{ii}=[A^{r}]_{jj}$.

The following conjecture was formulated in [86] as an extension of the conjecture related to the subgraph centrality which had been previously stated in [88].

Conjecture 1

A graph is walk-regular if and only if $S^{w}\left( \tau \right) =\ln n$ for all $\tau >0.$

Let us then introduce some necessary concepts for the further developments in the proof of this conjecture.

Definition 12

Two vertices i, j of G are $\tau$-subgraph equivalent if $[e^{\tau A}]_{ii}=[e^{\tau A}]_{jj}$.

Definition 13

A graph is $\tau$-subgraph regular if all pairs of vertices are $\tau$-subgraph equivalent.

The following result was a step forwards the proof of Conjecture 1.

Theorem 18

[26] A graph G is walk-regular if and only if G is $\tau$-subgraph regular for all $\tau \in \mathscr {{\mathcal {I}}}\subseteq {\mathbb {R}}$, where ${\mathcal {I}}$ is any set of real numbers containing an accumulation point.

In the saga, in [151] the authors found some counterexamples to a new conjecture proposed in [26] and stated a new conjecture. The final proof of Conjecture 1 came from an elegant Theorem in 2021 [18] where the authors used results from the Lindemann–Weierstrass Theorem.

Theorem 19

[18] Let $\tau >0$ be an algebraic number and let G be a connected undirected graph with adjacency matrix A.

• 1. G is $\tau$-subgraph regular if and only if G is walk-regular.

• 2. If two vertices i, j are $\tau$-subgraph equivalent, then the degree and eigenvector centralities of i and j are equal.

• 3. If G is $\tau$-subgraph regular, then the degree and eigenvector centralities are also identical for all nodes.

Walk regular graphs can be constructed by using Kronecker product of the adjacency matrices of two walk-regular graphs [106]. That is, if $G_{1}$ and $G_{2}$ are walk regular graphs, then $G_{1}\otimes G_{2}$ is also walk regular. Therefore, we have the following result.

Proposition 1

[86] Let $G_{1}$ and $G_{2}$ be two simple graphs with $n_{1}$ and $n_{2}$ vertices, respectively. Then,

$$\begin{aligned} S^{w}\left( G_{1}\otimes G_{2},\tau \right) =\ln n_{1}+\ln n_{2}, \end{aligned}$$

(7.6)

for all $\tau >0$ if $G_{1}$ and $G_{2}$ are walk-regular.

8 Bipartivity, signed graphs and Seidel Estrada index

A graph $G=\left( V,E\right)$ is bipartite if its set of nodes V can be split into two subsets $V_{1}$ and $V_{2}$ such that there are edges only between the two sets but no edge connects vertices in neither $V_{1}$ nor $V_{2}$ . Therefore, a graph is or is not bipartite. However, in certain real-world situations a graph can be “close to bipartite”, meaning that by removing very few edges the graph become bipartite. This is the case, for instance, of human sexual contact networks and human romance or partnership networks as remarked in [130]. In 2003 the authors of [130] proposed to quantify the “bipartivity” of a graph. The first of their measures is defined by

$$\begin{aligned} b_{H}=1-\dfrac{m_{f}}{m}, \end{aligned}$$

(8.1)

where $m_{f}$ is the number of edges that if removed the network becomes bipartite.² The calculation of this index is computationally intractable as it is NP complete. The authors [130] then proposed another index in which $m_{f}$ is assessed computationally. Here we will show how the use of the Estrada index of graphs allows the calculation of an index of bipartivity which depends only on the eigenvalues of the graph. The first of these approaches was published in [87] and will not be discussed here. Instead we will consider the index studied in [82]. Another measure of bipartivity was also proposed in [180]. We will start with some basic definitions for the sake of completeness of this section.

A bipartite graph is characterized by the following result proved by Konig in 1916 [153] (see also [15]).

Theorem 20

A graph is bipartite if and only if G has no cycles of odd length.

Corollary 2

A graph G is bipartite if and only if it contains no closed walks of odd length.

The Estrada index of a graph can be expressed in terms of the hyperbolic matrix functions as

$$\begin{aligned} EE\left( G\right) =\text {tr}\left( \cosh \left( A\right) \right) +\text {tr}\left( \sinh \left( A\right) \right) . \end{aligned}$$

(8.2)

The $\text {tr}\left( \sinh \left( A\right) \right)$ counts the odd-length closed walks in the graph:

$$\begin{aligned} \text {tr}\left( \sinh \left( A\right) \right) =\sum _{k=0}^{\infty }\dfrac{1}{\left( 2k+1\right) !}\text {tr}\left( A^{2k+1}\right) . \end{aligned}$$

(8.3)

Similarly, $\text {tr}\left( \cosh \left( A\right) \right)$ counts the even-length closed walks. An odd closed walk of any length in the graph exists if and only if the graph contains at least one odd-length cycle. Therefore, we can reformulate the previous Corollary as.

Corollary 3

A graph G is bipartite if and only if $\text {tr} \left( \sinh \left( A\right) \right) =0$.

Based on this result the authors of [82] proposed the following.

Definition 14

The bipartivity of a graph is defined as the relative difference between the number of closed walks of even and odd length,

$$\begin{aligned} b\left( G\right) =\dfrac{\text {tr}\left( \cosh \left( A\right) \right) -\text {tr}\left( \sinh \left( A\right) \right) }{\text {tr}\left( \cosh \left( A\right) \right) +\text {tr}\left( \sinh \left( A\right) \right) }=\dfrac{\text {tr}\left( \exp \left( -A\right) \right) }{\text {tr}\left( \exp \left( A\right) \right) }=\dfrac{EE\left( G^{-}\right) }{EE\left( G\right) }, \end{aligned}$$

(8.4)

where $G^{-}$ is the graph in which all the edges are weighted by $-1$.

It is easy to see that $\text {tr}\left( \exp \left( -A\right) \right)$ reaches its minimum for the complete graph, which is also the graph for which $EE\left( G\right)$ is maximum (see an example in Fig. 6). In this figure the reader can also visualize how the bipartivity index changes monotonically with the increase of the number of edges “frustrating” the bipartition.

Fig. 6

Illustration of the change in the bipartivity index with the increase in the number of edges in a complete bipartite graph

Then, we have the following result.

Lemma 8

Let G be a simple graph. Then, its bipartivity is bounded as

$$\begin{aligned} e^{2-n}\left( \dfrac{ne^{n}-e^{n}+1}{e^{n}+n-1}\right) \le b\left( G\right) \le 1, \end{aligned}$$

(8.5)

where the upper bound is attained for any bipartite graph and the lower bound is reached for $G\cong K_{n}.$

Therefore, we have that

$$\begin{aligned} \lim _{n\rightarrow \infty }b\left( K_{n}\right) =0. \end{aligned}$$

(8.6)

8.1 Signed graphs

In order to understand why the index $b\left( G\right)$ quantifies the bipartivity of a graph we should start by recognizing that the numerator of $b\left( G\right)$ is the trace of the adjacency matrix of a fully-negative signed graph. For an exhaustive compilation of mathematical results about signed graphs the reader is referred to [241]. Let us introduce here the necessary concepts for understanding the connections between bipartivity and signed graphs. We will start with the following.

Definition 15

A signed graph is the 4-tuple $G^{+-}=\left( V,E,\varSigma ,\varphi \right)$, where $V=\left\{ v_{1},\ldots ,v_{n}\right\}$ is the set of nodes or vertices representing individual social entities, $E\subseteq V\times V$ is the set of edges formed by (ordered or unordered) pairs of nodes, $\varSigma =\left\{ +,-\right\}$ is a set of signs, positive and negative relations,³ and $\varphi :E\rightarrow \varSigma$ is a mapping assigning one sign to each edge.

Therefore, the numerator of $b\left( G\right)$ counts the number of negative cycles in G, where a negative cycle is any cycle in which the product of the sign of its edges is negative. In a fully-negative graph, the negative cycles are the odd-length cycles, which are indeed those that break the bipartivity of the graph. In the theory of signed graphs we have the following important concept (for a list of references and some critical account see [79]).

Definition 16

A signed graph $G^{+-}$ is balanced if all its cycles are positive.

Then, it is obvious that a fully-negative graph is balanced if and only if it is bipartite. In the general case of any signed graph the following result is well-known.

Theorem 21

A signed graph $G^{+-}$ is balanced if and only if its nodes can be separated into two mutually disjoint sets, such that positive edges joint nodes only inside the subsets and negative edges joint nodes from different subsets.

The adjacency matrix of a signed graph can be expressed as: $A=A^{+}-A^{-},$ where $A^{+}$ represents the adjacency between pairs of nodes connected by positive edges, and $A^{-}$ represents the adjacency between pairs of nodes connected by negative edges.

Definition 17

[79, 81] The balance of a signed network with adjacency matrix $A=A^{+}-A^{-}$ can be quantified by

$$\begin{aligned} K\left( G^{+-}\right) =\dfrac{\text {tr}\left( \exp \left( A^{+}-A^{-}\right) \right) }{\text {tr}\left( \exp \left( \left| A^{+}-A^{-}\right| \right) \right) }=\dfrac{EE\left( G^{+-}\right) }{EE\left( \left| G^{+-}\right| \right) }, \end{aligned}$$

(8.7)

where $\left| \cdot \right|$ represents the entrywise absolute of the corresponding matrix.

The following result was proved in 1980 [2].

Theorem 22

For any signed graph, the matrices $A^{+}-A^{-}$ and $\left| A^{+}-A^{-}\right|$ are isospectral (cospectral) if and only if the signed graph is balanced.

Then, we have the following.

Theorem 23

Let $G^{+-}$ be a signed graph with adjacency matrix $A^{+}-A^{-}$. Then,

$$\begin{aligned} e^{2-n}\left( \dfrac{ne^{n}-e^{n}+1}{e^{n}+n-1}\right) \le K\left( G^{+-}\right) \le 1, \end{aligned}$$

(8.8)

where the upper bound is attained for any balanced graph and the lower bound is reached for a fully-negative complete graph.

Then, we also have that

$$\begin{aligned} \lim _{n\rightarrow \infty }K\left( K_{n}^{-}\right) =0, \end{aligned}$$

(8.9)

which is a maximally unbalanced graph.

8.2 Seidel Estrada index

Let us focus now on a particular kind of signed graph. Let J and I be the all-ones and identity matrices, respectively. The following matrix was introduced in [221] and it is nowadays known as the Seidel matrix.

Definition 18

The Seidel matrix of a simple graph G with adjacency matrix A is defined as

$$\begin{aligned} S\left( G\right) =J-I-2A. \end{aligned}$$

(8.10)

Obviously, $S\left( G\right) =A^{+}-A^{-}$ is the adjacency matrix of a signed graph $G^{+-}$, where $A^{+}\text {=}J-I-A$ and $A^{-}\text {=}-A$. Therefore, we have the following result.

Theorem 24

Let $G^{+-}$ be a signed graph with adjacency matrix $S\left( G\right)$. Then, G is balanced if and only if $S\left( G\right)$ is isospectral to $A\left( K_{n}\right)$.

Proof

The balance index of a signed graph with adjacency matrix $S\left( G\right)$ is

$$\begin{aligned} K\left( G^{+-}\right) =\dfrac{\text {tr}\left( \exp \left( J-I-2A\right) \right) }{\text {tr}\left( \exp \left( J-I\right) \right) }=\dfrac{\text {tr}\left( \exp \left( S\left( G\right) \right) \right) }{EE\left( K_{n}\right) }, \end{aligned}$$

(8.11)

which immediately implies the result. $\square$

Remark 3

The term $\text {tr}\left( \exp \left( S\left( G\right) \right) \right) \,{=:}\,SEE\left( G\right)$ was denoted in [122] as the Seidel Estrada index of the graph. The name Seidel honors mathematician Johan Jacob Seidel (1919–2001).⁴

We can prove here the following result.

Theorem 25

Let $K_{n_{1},n_{2}}$ be a complete bipartite graph. Let $S\left( K_{n_{1},n_{2}}\right)$ be the Seidel matrix of $K_{n_{1},n_{2}}$. Then, $S\left( K_{n_{1},n_{2}}\right)$ and $A\left( K_{n_{1}+n_{2}}\right)$ are cospectral.

Proof Using the structural balance theorem we can show that the signed graph whose adjacency matrix is $S\left( K_{n_{1},n_{2}}\right)$ is balanced. That is, we can split the set of nodes into two disjoint sets containing $n_{1}$ and $n_{2}$ nodes, respectively, in which the inter-set edges are negative and all intra-set edges are positive. Then, using Theorem 24 we prove the result. $\square$

Remark 4

The previous result implies that any signed graph with adjacency matrix

$$\begin{aligned} A=\left( \begin{array}{cc} A\left( K_{n_{1}}\right) &{}\quad -J\\ -J &{}\quad A\left( K_{n_{1}}\right) \end{array}\right) , \end{aligned}$$

(8.12)

is balanced. Also that $SEE\left( K_{n_{1},n_{2}}\right) =EE\left( K_{n_{1}+n_{2}}\right) =\exp \left( n\right) +\left( n-1\right) e^{-1}.$

In [122] it was proved the following results for the Seidel Estrada index.

Theorem 26

Let G be a simple graph with $n\ge 2$ nodes, m edges, t triangles and $Z=\sum _{i}k_{i}^{2}$. Then,

$$\begin{aligned} SEE\left( G\right) >\sqrt{\dfrac{n}{3}\left( n^{3}-n+12\left( Z+4t-nm+\dfrac{1}{2}\right) \right) }. \end{aligned}$$

(8.13)

Theorem 27

Let G be a simple k-regular graph. Then,

$$\begin{aligned} SEE\left( G\right) \ge e^{n-1-2k}+\left( n-1\right) \exp \left( \dfrac{2k}{n-1}-1\right) . \end{aligned}$$

(8.14)

Theorem 28

Let G be a simple k-regular bipartite graph. Then,

$$\begin{aligned} SEE\left( G\right) <e^{n-1-2k}+\dfrac{1}{e}\left( EE\left( G\right) -e^{-k}\right) ^{2}. \end{aligned}$$

(8.15)

In this subsection we have shown that although the so-called Seidel Estrada index was proposed and studied in a completely ad hoc way, it can be connected with the theory of signed graphs. This may facilitate further studies of this index, its extension to consider statistical mechanics parameters and its applications to the study of real-world signed graphs.

8.3 Negative absolute temperatures and the Onsager Estrada index

In the definition of the bipartivity index we have considered in the numerator of Eq. (8.4) the term $EE\left( G^{-}\right) =\text {tr}\left( \exp \left( -A\right) \right) .$ In the context of statistical mechanics which we have analyzed in Sect. 6 this corresponds to consider the inverse temperature $\tau =-1$. So far, we have considered the inverse temperature $\tau$ to be positive. So, what a negative inverse temperature could mean? Let us first analyze what is the physical definition of $\tau$. Let S be the statistical entropy, which is a function of the possible microstates of the system, and let E be the system’s energy. Then, the absolute temperature is defined as:

$$\begin{aligned} \tau \,{:}{=}\,\dfrac{1}{T}\dfrac{dS}{dE}. \end{aligned}$$

(8.16)

Graphically, it corresponds to the slope of the curve of entropy versus energy at a given point. Therefore, as can be seen in Fig. 7 the inverse temperature can be negative. In a system at negative temperature the high-energy states are more occupied than low-energy states. Such systems have been created by physicists in the real-world [35].

Fig. 7

Sketch of the plot of entropy versus energy used to illustrate the definition of the inverse temperature which is given by the slope of the curve in a given point. The scale of inverse temperature is given on top of this plot

From a graph-theory perspective what it means that “the high-energy states are more occupied than low-energy states”? In the Sect. 6 we have considered that the Hamiltonian describing the graph as a quantum system is given by the negative of the adjacency matrix ${\hat{\mathcal {H}}}_{NN}=-A$, such that the energy levels of the system are $E_{j}=-\lambda _{j}$ and the wavefunctions are the eigenvectors associated to the eigenvalues of A. In this case the partition function of the graph is given by $Z=\sum _{j=1}^{n}\left( e^{\tau \lambda _{j}}\right)$ with $\tau >0$. Therefore, for $\tau \rightarrow \infty$, we have that $Z=e^{\tau \lambda _{1}}.$ In the current case, where $\tau <0$, we have that when $\tau \rightarrow -\infty$, the partition function is: $Z=e^{\tau \lambda _{n}}.$ This means that we have changed the “importance” given to the different eigenvalues in the Estrada index, giving now more weight to the contributions of the smallest ones. Because Lars Onsager (1903-1976) was the scientist who first study the negative absolute temperatures in [178] we propose to name the following index in his honor.⁵

Definition 19

The Onsager Estrada index of G is defined as

$$\begin{aligned} OEE\left( G\right) =\text {tr}\left[ \exp \left( -A\right) \right] . \end{aligned}$$

(8.17)

First let us consider some elementary results, which are presented here by the first time. First, because $\text {tr}\left[ \exp \left( -A\right) \right] =\text {tr}\left[ \cosh \left( A\right) \right] -\text {tr}\left[ \sinh \left( A\right) \right] ,$ and due to the fact that a graph is bipartite if and only if it has no odd cycles, we have the following result.

Lemma 9

Let G be a simple graph. Then, $OEE\left( G\right) =\text {tr} \left[ \cosh \left( A\right) \right]$ if and only if G is bipartite. In this case $OEE\left( G\right) =EE\left( G\right)$.

Remark 5

Some graphs for which $OEE\left( G\right) =EE\left( G\right)$ for which we can write explicitly the indices are

• $OEE\left( K_{n_{1},n_{2}}\right) =EE\left( K_{n_{1},n_{2}}\right) =n_{1}+n_{2}-2+2\cosh \left( \sqrt{n_{1}n_{2}}\right)$;

• $OEE\left( S_{n}\right) =EE\left( S_{n}\right) =n-2+2\cosh \left( \sqrt{n-1}\right)$;

• $\lim _{n\rightarrow \infty }EE\left( C_{n}\right) =nI_{0}$, n even, where $I_{0}=\dfrac{1}{\pi }\int _{0}^{\pi }e^{2\cos x}dx$;

• $\lim _{n\rightarrow \infty }EE\left( P_{n}\right) =\left( n-1\right) -2\cosh \left( 2\right)$.

Lemma 10

Let G be a simple graph and let $\lambda _{n}$ be the least eigenvalue of A. Then,

$$\begin{aligned} e^{-\lambda _{n}}\le OEE\left( G\right) \le ne^{-\lambda _{n}}. \end{aligned}$$

(8.18)

The following result allows us to compare $OEE\left( G\right)$ with $EE\left( G\right)$ using Eq. (3.12).

Lemma 11

Let G be a simple graph. Then, the Onsager Estrada index of G is bounded as

$$\begin{aligned} \begin{aligned}OEE\left( G\right)&\ge F_{1}+\dfrac{391}{360}F_{2}+\dfrac{11}{60}F_{3}+\dfrac{1}{120}F_{5}+\dfrac{1}{60}F_{6}+\dfrac{2}{5}F_{7}+\dfrac{1}{36}F_{9}+\dfrac{1}{60}F_{12}+\dfrac{1}{60}F_{16}\\&\quad -\left( \dfrac{149}{120}F_{4}+\dfrac{1}{10}F_{8}+\dfrac{7}{72}F_{10}+\dfrac{1}{180}F_{11}+\dfrac{1}{360}F_{13}+\dfrac{1}{360}F_{14}\right. \\&\quad \left. +\dfrac{1}{90}F_{15}+\dfrac{1}{360}F_{17}+\dfrac{1}{60}F_{18}+\dfrac{1}{180}F_{19}+\dfrac{1}{360}F_{20}\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(8.19)

As we can see only bipartite subgraphs make a positive contribution to the Onsager Estrada index.

8.4 Numerical analysis

Here we compute the bipartivity index for all connected graphs with 8 nodes. We select two other network parameters to compare with the bipartivity. The first is the edge density $\delta \left( G\right) =2m/\left( n\left( n-1\right) \right)$ where m is the number of edges. The reason for selecting this parameter is that as the density of the graph increases the number of cycles of any length will also increase. For instance, in Erdős–Rényi random graphs we can find that the number of triangles $F_{4}$ (see Fig. 1) is bounded as

$$\begin{aligned} F_{4}\ge \dfrac{1}{6}\lambda _{1}^{3}\ge \dfrac{1}{6}\left( np\right) ^{3}=\dfrac{1}{6}n^{3}\delta ^{3}. \end{aligned}$$

(8.20)

The second parameter is the clustering coefficient $C\left( G\right)$, which is defined as $C\left( G\right) =3F_{4}/F_{3}$, where $F_{3}$ is the number of paths of length 2 in the graph (see [78]). Here again we would expect that the bipartivity and the clustering coefficient are negatively correlated due to the fact that the increase in clustering means the relative increase in the number of triangles. However, bipartivity is also related to other odd-cycles in the graphs and we want to investigate their influence of this network parameter.

In Fig. 8 we plot the results of the bipartivity vs. the clustering coefficient where the points are colored according to the number of edges that the graph has. As can be seen the most dense graphs also have the highest clustering and lowest bipartivity, as expected. Although there is a decaying trend between the bipartivity and the clustering coefficient, it is clear that even for these small graphs, the contribution of longer cycles to the bipartivity is very important.

Fig. 8

Scatter plot of the bipartivity and the clustering coefficient of all connected graphs with 8 nodes. The points in the plot are colored by the number of edges that the corresponding graph has

In Table 7 we give the values of the bipartivity for the five networks studied in this work. The networks of Stony and powergrid have significant bipartivity, while neurons and yeast are highly non-bipartite. As can be seen in the Table there is not a clear trend between bipartivity and edge density nor to the clustering coefficient of these graphs.

Table 7 Values of the bipartivity, clustering coefficient and edge density of the five real-world networks studied in this paper

In the case of Stony we have obtained a bipartition of the network using a technique also based on matrix exponentials. The result is illustrated in Fig. 9 where the edges colored in red or in blue are those that frustrate the bipartition of the network, i.e., those that, if removed, make the graph bipartite.

Fig. 9

Illustration of a bipartition of the network of Stony stream using the method developed by [82]. The dotted lines joints the two partitions and continuous lines connect vertices inside the same partition, i.e., they frustrate the bipartition of the network

9 Gaussian Estrada indices

As we have seen in the previous analysis there are situations in which the Estrada index of a graph is mainly determined by the spectral radius of the adjacency matrix. That is, when $\lambda _{1}\gg \lambda _{2}\gg 1$ the sum $\sum _{j}\exp \left( \lambda _{j}\right)$ is approximated very well by $\exp \left( \lambda _{1}\right) .$ From the structural point of view, this means that most of the information contained in the eigenvalues $\lambda _{j}$ for $j>1$ is making almost no contribution to the Estrada index. It is well-known that structural information encoded by some other eigenvalues other than $\lambda _{1}$ is very important for several kinds of problems [46, 50,51,52, 213, 214]. For instance, the nullity of the graph (see [111] for a review), i.e., the multiplicity of the zero eigenvalue of the adjacency matrix, plays a fundamental role in explaining magnetic properties of materials [230]. In general, many real-world networks have large multiplicity of $\lambda _{j}=0$ (nullity) and of $\lambda _{j}=-1$ which points to the fact that some important structural information on these networks is encoded in eigenvalues different from $\lambda _{1}$ .

In this section we investigate Estrada indices that give higher weights to the contribution of eigenvalues other than the spectral radius. In particular we use here a technique known as spectral folding [36, 229] to produce Gaussian Estrada indices [5, 80]. In the following let ${\tilde{\lambda }}$ be a given reference eigenvalue, $I\left( z\right)$ be the modified Bessel function of the first kinds, $\text {erf}\left( z\right)$ be the error function and $\text {erfc}\left( z\right) =1-\text {erf}\left( z\right)$ be the complimentary error function [5, 80].

Definition 20

The Gaussian Estrada index of G is defined as

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( G\right) =\text {tr}\left\{ \exp \left[ -\left( {\tilde{\lambda }}I-A\right) ^{2}\right] \right\} . \end{aligned}$$

(9.1)

The idea behind this Gaussian Estrada index is explained graphically in Fig. 10. The name Gaussian honors Carl Friedrich Gauss (1777–1855).⁶

Fig. 10

Illustration of the gaussianized spectrum method. The eigenvalues of the adjacency matrix of the network are folded at ${\tilde{\lambda }}$ into the spectrum of $\left( {\tilde{\lambda }}I-A\right) ^{2}$. Then they are exponentiated to give more weight to $\lambda _{\text {ref}}$

First we give a few general results for the Gaussian Estrada index (see [5, 80]).

Lemma 12

Let G be any graph. Then,

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( G\right) =\text {tr} \left( e^{-{\tilde{\lambda }}^{2}}e^{2{\tilde{\lambda }}A}e^{-A^{2}}\right) ={{e^{-{\tilde{\lambda }}^{2}}}tr}\left( e^{2{\tilde{\lambda }}A}e^{-A^{2}}\right) . \end{aligned}$$

(9.2)

Theorem 29

Let G be a graph with n nodes and m edges. Then,

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( G\right) \le \left\{ \begin{array}{cc} EE\left( K_{n},{\tilde{\lambda }}\right) &{} \quad \text {if } \lambda _{\text {ref} }=0,\\ \\ EE\left( K_{1,n-1},{\tilde{\lambda }}\right) &{} \quad \text {if } \lambda _{\text {ref} }=-1, \end{array}\right. \end{aligned}$$

(9.3)

where $k_{i}$ is the degree of the node i in the graph G .

Lemma 13

Let $K_{n}$ be the complete graph of n nodes. Then

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( K_{n}\right) =\left\{ \begin{array}{ll} e^{-(n-1)^{2}}+\frac{n-1}{e} &{} \quad \text {if } {\tilde{\lambda }}=0,\\ \\ e^{-n^{2}}+n-1 &{} \quad \text {if } {\tilde{\lambda }}=-1. \end{array}\right. \end{aligned}$$

(9.4)

Lemma 14

Let $P_{n}$ be a path having n nodes. Then, asymptotically as $n\rightarrow \infty$ and for some $c\in (0,\pi )$

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( P_{n}\right) =\left\{ \begin{array}{ll} e^{-2}I_{0}\left( 2\right) \left( n+1\right) -e^{-4} &{} \quad \text {if } {\tilde{\lambda }}=0,\\ \\ e^{-3}e^{-4\cos c}\left( \left( n+1\right) I_{0}\left( 2\right) -e^{-2}\right) &{} \quad \text {if } {\tilde{\lambda }}=-1. \end{array}\right. \end{aligned}$$

(9.5)

Lemma 15

Let $C_{n}$ be a cycle having n nodes. Then, asymptotically as $n\rightarrow \infty$ and for some $c\in (0,\pi )$

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( C_{n}\right) =\left\{ \begin{array}{ll} e^{-2}nI_{0}\left( -2\right) &{} \quad \text {if } {\tilde{\lambda }}=0,\\ \\ ne^{-3}e^{-4\cos c}I_{0}\left( -2\right) &{} \quad \text {if } {\tilde{\lambda }}=-1. \end{array}\right. \end{aligned}$$

(9.6)

Lemma 16

Let $K_{n_{1},n_{2}}$ be the complete bipartite graph of $n_{1}+n_{2}$ nodes. Then

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( K_{n_{1},n_{2}}\right) =\left\{ \begin{array}{ll} 2e^{-n_{1}n_{2}}+n_{1}+n_{2}-2 &{} \quad \text {if } {\tilde{\lambda }}=0,\\ \\ e^{-1}\left( e^{-n_{1}n_{2}}\cosh (2\sqrt{n_{1}n_{2}})+n_{1}+n_{2}-2\right) &{} \quad \text {if } {\tilde{\lambda }}=-1. \end{array}\right. \end{aligned}$$

(9.7)

Corollary 4

Let $K_{1,n-1}$ be the star graph of n nodes. Then

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( K_{1,n-1}\right) =\left\{ \begin{array}{ll} 2e^{1-n}+n-2 &{} \ \text {if } {\tilde{\lambda }}=0,\\ \\ e^{-1}\left( e^{1-n}\cosh (2\sqrt{n-1})+n-2\right) &{} \ \text {if } {\tilde{\lambda }}=-1. \end{array}\right. \end{aligned}$$

(9.8)

In [210] the authors studied several bounds for the Gaussian Estrada index when ${\tilde{\lambda }}=0$ which are resumed below.

Theorem 30

Let G be a simple graph with n nodes and $m\le \dfrac{n}{2}$ edges and let ${\tilde{\lambda }}=0$. Then,

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( G\right) \ge n/2m, \end{aligned}$$

(9.9)

with equality if and only if $G\cong {\bar{K}}_{n}$.

Theorem 31

Let G be a simple graph with n nodes and $m\le \dfrac{n}{4}+\dfrac{n\left( n-1\right) }{4}\exp \left( -4m/n\right)$ edges and let ${\tilde{\lambda }}=0$. Then,

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( G\right) \ge \sqrt{n-4m+n\left( n-1\right) \exp \left( -4m/n\right) }, \end{aligned}$$

(9.10)

with equality if and only if $G\cong {\bar{K}}_{n}$.

Remark 6

The previous bound can only be applied for very sparse networks where the density $\delta \left( G\right) =2m/\left( n\left( n-1\right) \right)$ is bounded as

$$\begin{aligned} \delta \left( G\right) \le \dfrac{1}{2\left( n-1\right) }+e^{-4m/n}. \end{aligned}$$

(9.11)

Theorem 32

Let G be a simple graph with $n\ge 2$ nodes and $m\le \dfrac{n}{2}$ edges. Let $M=\sum _{i}k_{i}^{2}$, then,

$$\begin{aligned} GEE_{0}\left( G\right) \ge \exp \left( -M/n\right) +\left( n-1\right) \exp \left( \left( M/n-2m\right) /\left( n-1\right) \right) , \end{aligned}$$

(9.12)

with equality attained if and only if G admits $\lambda _{1}=\sqrt{M/n}$ , $\lambda _{2}=\cdots =\lambda _{k}=\left( n-2k+1\right) ^{-1}\sqrt{M/n}$ and $\lambda _{k+1}=\cdots =\lambda _{n}=-\left( n-2k+1\right) ^{-1}\sqrt{M/n}$ for some $1\le k\le \left\lfloor \dfrac{n}{2}\right\rfloor$.

9.1 Random graphs

In this subsection we consider the estimation of the Gaussian Estrada indices of random graphs. The reasons for studying random graphs have been explained in Sect. 5.2. Here we will consider both Erdős–Rényi and Barabási–Albert random graphs.

Theorem 33

[5, 80] For an Erdős–Rényi random graph $G_{n,p}$ with $\frac{\ln n}{n}\ll p$ for significantly large $r=2\sqrt{np\left( 1-p\right) }$, we have

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( G_{n,p}\right) =n\exp \left( \frac{-r^{2}}{2}\right) \left( I_{0}\left( \frac{r^{2}}{2}\right) +I_{1}\left( \frac{r^{2}}{2}\right) \right) , \end{aligned}$$

(9.13)

if ${\tilde{\lambda }}=0,$ and

$$\begin{aligned} \begin{aligned} GEE_{{\tilde{\lambda }}}\left( G_{n,p}\right)&=\frac{2n\sqrt{r^{2}-1}}{r}e^{r^{2}}\text {erfc} \left( r\right) \end{aligned} \end{aligned}$$

(9.14)

if ${\tilde{\lambda }}=-1,$ as $n\rightarrow \infty$.

Theorem 34

[5, 80] Let $G_{BA}$ be a Barabási–Albert random graph and let $r=2\sqrt{np\left( 1-p\right) }$. Then, when $n\rightarrow \infty$,

$$\begin{aligned} GEE_{{\tilde{\lambda }}}\left( G_{BA}\right) =\dfrac{n}{r^{2}}\left( \sqrt{\pi }r\text {erf} \left( r\right) +e^{-r^{2}}-1\right) , \end{aligned}$$

(9.15)

if ${\tilde{\lambda }}=0,$ and

$$\begin{aligned} \begin{aligned} GEE_{{\tilde{\lambda }}}\left( G_{BA}\right)&=\frac{\sqrt{\pi }}{2}\left( \left( 1-r\right) \text {erf} \left( 1-r\right) +\left( 1+r\right) \text {erf} \left( 1+r\right) \right) \\&\quad \left. -\sqrt{\pi }\text {erf} \left( 1\right) -e^{-1}\right) \end{aligned} \end{aligned}$$

(9.16)

if ${\tilde{\lambda }}=-1$.

9.2 Double Gaussian Estrada index

Another important situation appearing in many molecular systems is the existence of two reference eigenvalues, typically located around the mid part of the spectrum, which are of great relevance for understanding the behavior of these systems. In 1952, Fukui et al. [99] calculated the chemical reactivity of molecules by using molecular orbital theory, but their method neglects all molecular orbitals except two, the occupied one of higher energy (HOMO) and the vacant one of lowest energy (LUMO). According to Fukui the HOMO gives a molecule a character of electron donor, whereas the LUMO acts as an electron acceptor. The theory was further applied by Woodward and Hoffmann [234] in the interpretation of the stereochemistry of electrocyclic organic reactions. Both, the Frontiers Molecular Orbital (FMO) theory of Fukui and the Woodward-Hoffmann rules are paradigmatic examples of success of theoretical approaches in Chemistry. Both Fukui and Hoffmann won the Nobel Prize in Chemistry for such works. Since then [98], FMO is widely applied for studying chemical reactivity [176].

Let us consider here, for instance, molecular systems ${\mathcal {S}}$ where the energy E is obtained by the time-independent Schrödinger equation: $\left( \alpha I+t_{NN}A\right) \varPsi =E\varPsi$, as described before. Then, when $\alpha =0$ and $t_{NN}=-1,$ the energy levels of the system are $E_{j}=-\lambda _{j}$. Typically, the states with energy levels $E_{j}<0$ are occupied by electrons, while those with energy $E_{j}\ge 0$ are empty. Then, the energy level just below $E_{j}=0$ is known as the highest occupied molecular orbital (HOMO) and the one just over $E_{j}=0$ is the lowest unoccuppied molecular orbital (LUMO). These two molecular orbitals are fundamental in understanding the chemical reactivity of these molecular systems [182]. They can be described in the current approach by the negative of two references eigenvalues ${\tilde{\lambda }}_{1}$ and ${\tilde{\lambda }}_{2}$ of the adjacency matrix. Then, we have the following [6] (Fig. 11).

Definition 21

The double-Gaussianized Estrada index of G is defined as

$$\begin{aligned} DGEE_{{\tilde{\lambda }}_{1},{\tilde{\lambda }}_{2}}\left( G\right) =\text {tr}\left\{ \exp \left[ -\left( {\tilde{\lambda }}_{1}I-A\right) ^{2}\left( {\tilde{\lambda }}_{2}I-A\right) ^{2}\right] \right\} . \end{aligned}$$

(9.17)

Fig. 11

Schematic illustration of the double Gaussianization of the graph spectra. The eigenvalues of the adjacency matrix are folded at two different reference eigenvalues and then exponentiated as illustrated in the right part of the figure

Lemma 17

Let G be any graph. Then,

$$\begin{aligned} \begin{aligned} DGEE_{{\tilde{\lambda }}_{1},{\tilde{\lambda }}_{2}}\left( G\right)&={{e^{-{\tilde{\lambda }}_{1}^{2}{\tilde{\lambda }}_{2}^{2}}}tr}\left( e^{2\left( {\tilde{\lambda }}_{1}^{2}{\tilde{\lambda }}_{2}+{\tilde{\lambda }}_{1}{\tilde{\lambda }}_{2}^{2}\right) A}e^{-\left( {\tilde{\lambda }}_{1}^{2}+{\tilde{\lambda }}_{2}^{2}+4{\tilde{\lambda }}_{1}{\tilde{\lambda }}_{2}\right) A^{2}}\left. e^{2\left( {\tilde{\lambda }}_{1}+{\tilde{\lambda }}_{2}\right) A^{3}}e^{-A^{4}}\right) .\right. \end{aligned}\nonumber \\ \end{aligned}$$

(9.18)

Lemma 18

Let ${\tilde{\lambda }}_{1}=-1$ and ${\tilde{\lambda }}_{2}=1$, such that $EE\left( G,-1,1\right) =\text {tr} \left( \exp \left[ -\left( A^{2}-I\right) ^{2}\right] \right) .$ Let $K_{n}$, $K_{n_{1},n_{2}}$ and $K_{1,n-1}$ be the complete, bicomplete and star graphs of n nodes, respectively. Then

$$\begin{aligned} DGEE_{-1,1}\left( K_{n}\right)= & {} n-1+e^{-n^{2}\left( n-2\right) {}^{2}}, \end{aligned}$$

(9.19)

$$\begin{aligned} DGEE_{-1,1}\left( K_{n_{1},n_{2}}\right)= & {} \frac{n_{1}+n_{2}-2}{e}+2e^{-\left( n_{1}n_{2}-1\right) {}^{2}}, \end{aligned}$$

(9.20)

$$\begin{aligned} DGEE_{-1,1}\left( K_{1,n-1}\right)= & {} \frac{n-2}{e}+2e^{-(n-2)^{2}}. \end{aligned}$$

(9.21)

Lemma 19

Let $G_{b}$ be connected bipartite graph of n nodes, then

$$\begin{aligned} DGEE_{-1,1}\left( G_{b}\right) \le DGEE_{-1,1}\left( K_{n}\right) . \end{aligned}$$

(9.22)

Conjecture 2

Let G be any connected graph of n nodes, then

$$\begin{aligned} DGEE_{-1,1}\left( G\right) \le DGEE_{-1,1}\left( K_{n}\right) . \end{aligned}$$

(9.23)

Claim 1

The double-Gaussianized Estrada index of a simple graph has the following Taylor series expansion:

$$\begin{aligned} \begin{aligned}DGEE_{-1,1}&=\frac{1}{e}\left( \sum _{k=0}^{\infty }a_{k}\text {tr}A^{2k}\right) \\&=\frac{1}{e}\left( \text {tr}I+2\text {tr}A^{2}+\text {tr}A^{4}-\frac{2}{3}\text {tr}A^{6}-\frac{5}{6}\text {tr}A^{8}\right. \\&\quad \left. -\frac{1}{15}\text {tr}A^{10}+\frac{23}{90}\text {tr}A^{12}+\ldots \right) . \end{aligned}\nonumber \\ \end{aligned}$$

(9.24)

where $a_{k}={\sum }_{4a+2b=2k}(-1)^{a}\frac{2^{b}}{a!b!}$, and a, b are non negative integers.

9.3 Numerical analysis

We consider here the bounds given in Theorem 30 and in Theorem 32 for all connected graphs with 8 nodes. The bound given in Theorem 31 is not applicable in all the cases and we do not considered it for this general case. We show in Fig. 12 the histogram of the relative deviations for these two bounds in these small graphs. The mean relative deviations (in %) of the two bounds are, respectively $89.84\pm 2.51$ and $66.51\pm 6.55$, which points to the fact that the second bound is a better approximation than the first one to the Gaussian Estrada index.

Fig. 12

Histograms of the relative deviations in percentage of the bounds given in Theorem 30 and in Theorem 32 for all connected graphs with 8 nodes

In Table 8 we give the values of the three bounds for the five networks studied here as well as the values of the actual Gaussian Estrada index for ${\tilde{\lambda }}=0$. The bound given in Theorem 30 is extremely far away from the actual values and practically says the same as the trivial bound $GEE_{0}\left( G\right) >0.$ The same happens for Theorem 32 in the cases of Stony and neurons, but it gives more decent estimations for the cases of the bigger networks of Internet and powergrid.

Table 8 Values of the bounds given in Theorems 30, 31 and in 32 for the Gaussian Estrada index $GEE_{0}\left( G\right)$ of the five real-world networks studied here. The bound given in Theorem 31 is not applicable (NA) for most of the networks as they do not fulfill the necessary condition on the edge density

10 Mittag–Leffler Estrada indices

As we have seen in previous sections of this paper, the Estrada indices of a graph may arise as the solution of the linear dynamical system

$$\begin{aligned} \dfrac{d}{dt}u\left( t\right) =Mu\left( t\right) , \end{aligned}$$

(10.1)

where M is a given graph matrix, with initial condition $u\left( 0\right) =u_{0}$. The solution of this system is given by $u\left( t\right) =\exp \left( tM\right) u_{0}$. The case in which $M=A$ is the adjacency matrix of the graph has been analyzed in the paper [172].

Let us consider that, instead of using the first derivative of $u\left( t\right)$ respect to time, we use a fractional derivative. Then we have a system of the form:

$$\begin{aligned} D_{t}^{\alpha }u\left( t\right) =Mu\left( t\right) , \end{aligned}$$

(10.2)

for $0<\alpha <1$, where the Caputo fractional derivative [37] is given by

$$\begin{aligned} D_{t}^{\alpha }u\left( t\right) =\dfrac{1}{\varGamma \left( \left\lceil \alpha \right\rceil -\alpha \right) }\int _{0}^{t}\dfrac{u^{\left( \left\lceil \alpha \right\rceil \right) }\left( \tau \right) }{\left( t-\tau \right) ^{\alpha +1-\left\lceil \alpha \right\rceil }}d\tau , \end{aligned}$$

(10.3)

where $f^{\left( k\right) }$ represents the kth derivative of f and $\varGamma \left( z\right)$ is the Euler gamma function:

$$\begin{aligned} \varGamma \left( z\right) =\int x^{z-1}e^{-x}dx,\text {Re}\left( z\right) >0. \end{aligned}$$

(10.4)

The solution of this system is given by

$$\begin{aligned} u\left( t\right) =E_{\alpha ,1}\left( t^{\alpha }M\right) u_{0}, \end{aligned}$$

(10.5)

where

$$\begin{aligned} E_{\alpha ,1}\left( t^{\alpha }M\right) =\left( \sum _{k=0}^{\infty }\dfrac{\left( t^{\alpha }M\right) ^{k}}{\varGamma \left( \alpha k+\beta \right) }\right) , \end{aligned}$$

(10.6)

which are the Mittag–Leffler matrix functions (for properties of Mittag–Leffler matrix function the reader is referred to [102, 183]).

To catch the analogy with the standard Estrada index of a graph we can write is as

$$\begin{aligned} EE\left( G\right) =\text {tr}\left( \sum _{k=0}^{\infty }\dfrac{A^{k}}{\varGamma \left( k+1\right) }\right) =\text {tr}\left( \exp \left( A\right) \right) , \end{aligned}$$

(10.7)

due to the fact that $\varGamma \left( k+1\right) =k!$,

Therefore we can generalize the Estrada index to account for a wider class of penalization functions, such that we write

$$\begin{aligned} EE_{\alpha ,\beta }\left( G\right) =\text {tr}\left( \sum _{k=0}^{\infty }\dfrac{A^{k}}{\varGamma \left( \alpha k+\beta \right) }\right) . \end{aligned}$$

(10.8)

At the same time we keep in mind that $EE_{\alpha ,\beta }\left( G\right)$ is the solution of a system of equations of the form $D_{t}^{\alpha }u\left( t\right) =Au\left( t\right)$ as we will explore later. We propose the name Mittag–Leffler Estrada index for $EE_{\alpha ,\beta }\left( G\right)$ in honor to the mathematician Gösta Mittag–Leffler (1846–1927).⁷ Some examples of closed formulas are illustrated in Table 9.

Table 9 Examples of Mittag–Leffler functions of the adjacency matrix

One important aspect of these functions in general is that by controlling the parameters $\alpha$ and $\beta$ we can penalize the walks of k length in different ways. For instance, if $\left( \left( \alpha -1\right) k+\beta \right) <0$ for all k, then the walks of any length are penalized less than in $EE_{1,1}\left( G\right)$. This is for instance, the case of $EE_{1/2,1}\left( G\right)$ (see Table 9). In those cases where $\left( \left( \alpha -1\right) k+\beta \right) >0$ for all k, the penalization of all walks is heavier than in the exponential, which are for instance the cases of $EE_{\alpha >1,\beta }\left( G\right)$. There is a third case which occurs when $\left( \alpha -1\right) k+\beta$ is negative for $0\le k\le k_{c}$ and positive for $k>k_{c}$, where $k_{c}$ is a given integer. This is the case, for instance, of the matrix functions where $k_{c}<-\left( \dfrac{\beta }{\alpha -1}\right)$.

Let us first consider the Estrada index $EE_{1/2,1}\left( G\right) =\text {tr}\left( \exp \left( A^{2}\right) {{\left( I+\text {erf}\left( A\right) \right) }}\right)$. A similar index was defined and studied in the paper [89] in the following form:

$$\begin{aligned} \sum _{k=0}^{\infty }\dfrac{A^{k}}{k!!}=\text {tr}\left( \tfrac{1}{2}\exp \left( \tfrac{A^{2}}{2}\right) {{\left( 2I+\sqrt{2\pi }\text {erf}\left( \tfrac{A}{\sqrt{2}}\right) \right) }}\right) , \end{aligned}$$

(10.9)

where k!! is the double factorial of k. The goal of defining such index was to account for less penalization of longer walks, which may play an important role in several applications (for some examples see [1, 89]) . For instance, if we compare the subgraph expansion of $EE_{1/2,1}\left( G\right)$ with that of $EE_{1,1}\left( G\right)$ (see Eq. (3.12)) we can clearly observe the differences in the penalization of bigger subgraphs made by both indices. In the case of $EE_{1/2,1}\left( G\right)$ we have:

$$\begin{aligned} \begin{aligned}EE_{1/2,1}\left( G\right)&\approx F_{1}+\dfrac{10}{3}F_{2}+4F_{3}+\dfrac{1674}{59}F_{4}+F_{5}+2F_{6}+12F_{7}+\dfrac{5944}{581}F_{8}\\&\quad +\dfrac{1516}{97}F_{9}+\dfrac{334}{37}F_{10}+\dfrac{467}{194}F_{11}+2F_{12}+\dfrac{65}{54}F_{13}+\dfrac{65}{54}F_{14}\\&\quad +4F_{15}+\dfrac{467}{97}F_{16}+2F_{17}+\dfrac{65}{54}F_{18}+\dfrac{1336}{185}F_{19}+\dfrac{467}{194}F_{20}+\dfrac{65}{54}F_{21}, \end{aligned}\nonumber \\ \end{aligned}$$

(10.10)

which points out that triangles are more than 20 times less penalized by this function that by the exponential, squares are penalized 30 times less, pentagons, hexagons and heptagons are penalized 93, 120 and 433 times less by $EE_{1/2,1}\left( G\right)$ than by $EE_{1,1}\left( G\right)$. Let us show a practical example on how these different penalizations influence the Estrada indices of cycle graphs. In Fig. 13 we illustrate three graphs with 8 nodes but having different length of their main cycles. In $G_{I}$ there is a triangle and an heptagon, in $G_{II}$ a square and a hexagon, and in $G_{III}$ two pentagons. The index $EE_{1,1}\left( G\right)$ of the three graphs are: 21.68, 20.64 and 20.38, respectively. That is, there is a difference of 4.8% between $G_{I}$ and $G_{II}$ and of 1.25% between $G_{II}$ and $G_{III}$. On the other hand, the index $EE_{1/2,1}\left( G\right)$ is 672.24, 540.58 and 507.13 for $G_{I}$, $G_{II}$ and $G_{III}$, respectively, which represent 19.6% of difference between the first pair and 6.2% between the second one.

Fig. 13

Examples of three graphs with 8 nodes and chordless cycles of different lengths: $G_{I}$ has a triangle and an heptagon; $G_{II}$ has a square and a hexagon; $G_{III}$ has two pentagons

Finally, we consider the Mittag–Leffler Estrada indices defined as follow:

$$\begin{aligned} MTEE_{1,\beta +1}\left( G\right) =\text {tr}\left( \sum _{k=0}^{\infty }\dfrac{A^{k}}{\varGamma \left( k+\beta +1\right) }\right) =\text {tr}\left( \sum _{k=0}^{\infty }\dfrac{A^{k}}{\left( k+\beta \right) !}\right) ,\beta =1,2,3,\ldots .\nonumber \\ \end{aligned}$$

(10.11)

These indices were developed and studied in 2010 in the paper [75], as a way to penalize more heavily the longer walks than in the matrix exponential. The indices $EE_{1,\beta +1}\left( G\right)$ are also the trace of the so-called matrix $\varPsi$ functions:

$$\begin{aligned} MTEE_{1,\beta +1}\left( G\right) =\text {tr}\varPsi _{\beta }\left( A\right) , \end{aligned}$$

(10.12)

where

$$\begin{aligned} \varPsi _{\gamma }\left( A\right) \,{:}{=}\,\dfrac{1}{\left( \beta -1\right) !}\int _{0}^{1}e^{\left( 1-t\right) A}x^{t-1}dt, \end{aligned}$$

(10.13)

which obey the following recurrence formula:

$$\begin{aligned} \varPsi _{\beta }\left( A\right) =A\varPsi _{\beta +1}\left( A\right) +\dfrac{1}{\beta !}I. \end{aligned}$$

(10.14)

When the adjacency matrix is not singular we can represent these Estrada indices as follow

$$\begin{aligned} MTEE_{1,2}\left( G\right)= & {} \text {tr}\left( \varPsi _{1}\left( A\right) \right) , \end{aligned}$$

(10.15)

$$\begin{aligned} MTEE_{1,3}\left( G\right)= & {} \text {tr}\left( \varPsi _{2}\left( A\right) \right) , \end{aligned}$$

(10.16)

and so forth. Other Mittag–Leffler matrix functions in the context of network theory have been recently studied in [13].

10.1 Resolvent Estrada index

The context of Mittag–Leffler Estrada indices also allow the consideration of other indices that were previously proposed in the literature. This is the case of an index proposed in 2010 in [85]. The goal of introducing this index was to change the penalization of the different powers of the adjacency matrix from k! to $\left( n-1\right) ^{k}$ to increase the contribution of walks of longer lengths. The index proposed in [85] corresponds to the trace of the resolvent of the adjacency matrix:

$$\begin{aligned} REE\left( G\right) =\text {tr}\left( \sum _{k=0}^{\infty }\dfrac{A^{k}}{\left( n-1\right) ^{k}}\right) =\text {tr}\left( \left( I-\dfrac{1}{n-1}A\right) ^{-1}\right) , \end{aligned}$$

(10.17)

which eventually was proposed in [27] to be named as the resolvent Estrada index of the graph. It can be seen that the resolvent Estrada index is a particular case of Mittag–Leffler Estrada index:

$$\begin{aligned} REE\left( G\right) =MTEE_{0,1}\left( G\right) =\text {tr}\left( \sum _{k=0}^{\infty }\dfrac{\left( A/n\right) ^{k}}{\varGamma \left( \alpha k+\beta \right) }\right) =\text {tr}\left( \left( I-\dfrac{A}{n}\right) ^{-1}\right) . \end{aligned}$$

(10.18)

Remark 7

The use of the normalization $c_{k}=1/\left( n-1\right)$ in $\left( c_{k}A\right) ^{k}$ is just one of the many possibilities that exist. In reality this normalization is not a good one, because the corresponding Estrada index is very close to the number of nodes of the graph, as can be inferred from the bounds presented before. Then, other general choices of the type $\left( \varrho A\right) ^{k}$ where $\varrho <\left( \lambda _{1}\right) ^{-1}$ are more appropriate here.

A nice result relating the resolvent Estrada index and the characteristic polynomial of the adjacency matrix was proved by in [41] and is given below.

Theorem 35

Let G any graph with n nodes and let $P\left( G,x\right)$ be the characteristic polynomial of the adjacency matrix of G, aka its characteristic polynomial. Then,

$$\begin{aligned} EE_{0,1}\left( G\right) =\left( n\right) \dfrac{P'\left( G,n\right) }{P\left( G,n\right) }, \end{aligned}$$

(10.19)

where $P'\left( G,n\right)$ is the first derivative of $P\left( G,x\right)$ evaluated at $x=n$.

To illustrate the previous result let us consider the three graphs in Fig. 13. Their characteristic polynomials are, respectively:

$$\begin{aligned} P\left( G_{I},x\right)= & {} x^{8}-9x^{6}-2x^{5}+24x^{4}+8x^{3}-19x^{2}-8x, \end{aligned}$$

(10.20)

$$\begin{aligned} P\left( G_{II},x\right)= & {} x^{8}-9x^{6}+22x^{4}-16x^{2}+1, \end{aligned}$$

(10.21)

$$\begin{aligned} P\left( G_{III},x\right)= & {} x^{8}-9x^{6}+24x^{4}-4x^{3}-20x^{2}+8x, \end{aligned}$$

(10.22)

which give $EE_{0,1}\left( G_{I}\right) =4023/484,$ $EE_{0,1}\left( G_{II}\right) =2980/359,$ and $EE_{0,1}\left( G_{III}\right) =2191/264.$ That is, the difference between the first pair of graphs is only 0.13% and between the second pair is only 0.02%. This is a direct consequence of penalizing more heavily the longer walks than in the exponential matrix function.

Some other inequalities have been reported for the resolvent Estrada index in terms of the number of nodes, edges, maximum degree, etc.

Lemma 20

[41] Let G be a simple graph with n nodes and m edges. Then,

$$\begin{aligned} REE\left( G\right) \ge \dfrac{n^{2}\left( n-1\right) ^{2}}{n\left( n-1\right) ^{2}-2m}, \end{aligned}$$

(10.23)

with equality if and only if $G\cong {\bar{K}}_{n}.$

Lemma 21

[114] Let G be a simple noncomplete graph with $n>3$ nodes and m edges. Then,

$$\begin{aligned} REE\left( G\right) \le n+\dfrac{4m}{\left( n-1\right) ^{2}-2m}, \end{aligned}$$

(10.24)

with equality if and only if $G\cong {\bar{K}}_{n}.$

Lemma 22

[175] Let G be a simple graph with n nodes, m edges and maximum degree $k_{max}\ne n-1$. Then,

$$\begin{aligned} REE\left( G\right)< & {} n\left( 1+\dfrac{k_{max}}{\left( n-1\right) \left( n-1-k_{max}\right) }\right) , \end{aligned}$$

(10.25)

$$\begin{aligned} REE\left( G\right)< & {} n+\dfrac{2m}{\left( n-1\right) \left( n-1-k_{max}\right) }. \end{aligned}$$

(10.26)

11 Estrada indices and network of oscillators

The study of vibrations on regular graphs, known as lattices, is standard in solid-state physics (see for instance Chapter 4 in [144]). The techniques of classical as well as of quantum mechanics are used in the analysis of such vibrational problems. In 2003 this analysis was extended to consider non-regular networks [146] where the vibrations where analyzed in the context of a quantum system. Here we investigate the connections existing between some of the Estrada indices and the network vibrations, used in a metaphorical sense. That is, although some physical systems represented by non-regular graphs can be analyzed using the techniques developed here we consider the current approach as an appropriate tool for giving a physical meaning to the indices involved.

Let us consider a system ${\mathcal {S}}$ consisting of ball of mass M which are connected by springs with the spring constant $M\omega ^{2}$. Let us consider that the ball-spring system is submerged into a thermal bath at the temperature $\tau$. Then the balls in the complex network oscillate under thermal disturbances. We will consider that every ball is tied to the ground by a spring which has spring constant satisfying $K\gg \max _{v}k_{v}$ (see Fig. 14). This guarantees that the system can oscillates but do not translate from a fixed position. In this way we can analyze how a given ball can transmit small oscillations to the rest of the balls of the system.

Fig. 14

Illustration of a system formed by three balls of mass M tied to the ground with springs of constant K connected by springs of constant $M\omega ^{2}$

The general Hamiltonian of this system is written as

$$\begin{aligned} H=\sum _{v}\left[ \dfrac{p_{v}^{2}}{2M}+\left( K-k_{v}\right) \dfrac{M\omega ^{2}x_{v}^{2}}{2}\right] +\dfrac{M\omega ^{2}}{2}\sum _{i<j}A_{vw}\left( x_{v}-x_{w}\right) ^{2}, \end{aligned}$$

(11.1)

where the first term represents the kinetic energy of the corresponding balls and the second term represents the potential energy of the system, with $p_{v}$ being the momentum and $x_{v}$ the coordinate of the ball v.

11.1 Quantum oscillators

In this setup we consider that the system obeys the laws of quantum mechanics. Then, the momenta $p_{w}$ and the coordinates $x_{v}$ are not independent variables but they are operators that satisfy the commutation relation: $\left[ x_{v},p_{w}\right] =i\hbar \delta _{vw},$where $i=\sqrt{-1}$, $\hbar$ is the Dirac constant and $\delta _{vw}$ is Dirac delta. Additionally we will use second quantization to express the creation and annihilation of oscillations at the given balls of the system. That is, we use the boson creation and annihilation operators defined by [184]

$$\begin{aligned} a_{v}^{\mathrm{\dagger }}= & {} \frac{1}{\sqrt{2\hbar }}\left( x_{v}\sqrt{M\varOmega }-\frac{i}{\sqrt{{{M}}\varOmega }}p_{v}\right) , \end{aligned}$$

(11.2)

$$\begin{aligned} a_{v}= & {} \frac{1}{\sqrt{2\hbar }}\left( x_{v}\sqrt{M\varOmega }+\frac{i}{\sqrt{M\varOmega }}p_{v}\right) . \end{aligned}$$

(11.3)

With the use of these operators, the Hamiltonian of a network of quantum harmonic oscillators is given by [84]

$$\begin{aligned} {\hat{\mathscr {H}}}\left( {\mathcal {S}}\right) =\sum _{v}\hbar \varOmega \left( a_{v}^{\mathrm{\dagger }}a_{v}+\frac{1}{2}\right) -\frac{\hbar \omega ^{2}}{4\varOmega }\sum _{v,w}\left( a_{v}^{\dagger }+a_{v}\right) A_{vw}\left( a_{w}^{\dagger }+a_{w}\right) . \end{aligned}$$

(11.4)

where $\varOmega =\sqrt{K/M\omega }$ and K is a constant such that $K\gg \max _{v}k_{v}$.

Since A is symmetric, we can diagonalize it by means of an orthogonal matrix O as in

$$\begin{aligned} \varLambda =O\left( KI-A\right) O^{T}, \end{aligned}$$

(11.5)

where $\varLambda$ is the diagonal matrix with the eigenvalues $\lambda _{\mu }$ of $\left( KI-A\right)$ on the diagonal. This generates a new set of boson creation and annihilation operators as

$$\begin{aligned} b_{\mu }= & {} \sum _{v}O_{\mu v}a_{v}=\sum _{v}a_{v}\left( O^{T}\right) _{v\mu }, \end{aligned}$$

(11.6)

$$\begin{aligned} b_{\mu }^{\mathrm{\mathrm{\dagger }}}= & {} \sum _{v}O_{\mu v}a_{v}^{\mathrm{\mathrm{\dagger }}}=\sum _{i}a_{v}^{\mathrm{\mathrm{\dagger }}}\left( O^{T}\right) _{v\mu }, \end{aligned}$$

(11.7)

We can then decouple the Hamiltonian as

$$\begin{aligned} \mathscr {{\hat{H}}}\left( {\mathcal {S}}\right) =\sum _{\mu }H_{\mu }\left( {\mathcal {S}}\right) , \end{aligned}$$

(11.8)

with

$$\begin{aligned} \begin{aligned}H_{\mu }\left( {\mathcal {S}}\right)&\equiv \hbar \varOmega \left( b_{\mu }^{\mathrm{\dagger }}b_{\mu }+\frac{1}{2}\right) +\frac{\hbar \omega ^{2}}{4\varOmega }\left( \lambda _{\mu }-K\right) \left( b_{\mu }^{\mathrm{\mathrm{\dagger }}}+b_{\mu }\right) ^{2}\\&=\hbar \varOmega \left[ 1+\dfrac{\omega ^{2}}{2\varOmega ^{2}}\left( \lambda _{\mu }-K\right) \right] \left( b_{\mu }^{\mathrm{\dagger }}b_{\mu }+\frac{1}{2}\right) +\frac{\hbar \omega ^{2}}{4\varOmega }\left( \lambda _{\mu }-K\right) \left[ \left( b_{\mu }^{\mathrm{\mathrm{\dagger }}}\right) ^{2}+\left( b_{\mu }\right) ^{2}\right] . \end{aligned}\nonumber \\ \end{aligned}$$

(11.9)

We now introduce an approximation in which each mode of oscillation does not get excited beyond the first excited state. In other words, we restrict ourselves to the space spanned by the ground state (the vacuum) $\left| \mathrm{vac}\right\rangle$ and the first excited states $b_{\mu }^{\dagger }\left| \mathrm{vac}\right\rangle$. Then the second term in the last line of the Hamiltonian (11.9) equals zero and we have

$$\begin{aligned} H_{\mu }\left( {\mathcal {S}}\right) =\hbar \varOmega \left[ 1+\frac{\omega ^{2}}{2\varOmega ^{2}}\left( \lambda _{\mu }-K\right) \right] \left( b_{\mu }^{\mathrm{\dagger }}b_{\mu }+\frac{1}{2}\right) . \end{aligned}$$

(11.10)

Remark 8

This approximation is justified when the energy level spacing $\hbar \varOmega$ is much greater than the energy scale of external disturbances, (specifically the temperature fluctuation $k_{B}T=1/\tau$), as well as than the energy of the network springs $\hbar \omega$, i.e. $\tau \hbar \varOmega>>1$ and $\varOmega>>\omega$. This happens when the mass of each oscillator is small, when the springs to the ground, $M\varOmega ^{2}$, are strong, and when the network springs $M\omega ^{2}$ are weak. Then an oscillation of tiny amplitude propagates over the network.

We are going to work in this limit hereafter. The thermal bath represents here an ’external situation’ which affects all the links in the network at the same time, e.g., economic crisis, social agitation, extreme physiological conditions, etc. After equilibration, all links in the network are weighted by the parameter $\tau =\left( k_{B}T\right) ^{-1}$.

Let us now compute how much an excitation at the node p propagates throughout the network before coming back to the same node and being annihilated. This information is obtained through the diagonal thermal Green’s function, which is given in the framework of quantum mechanics by

$$\begin{aligned} G_{vv}\left( {\mathcal {S}},\tau \right) =\frac{1}{Z}\left\langle \mathrm{vac}\right| a_{v}e^{-\tau \mathscr {{\hat{H}}}\left( {\mathcal {S}}\right) }a_{v}^{\mathrm{\dagger }}\left| \mathrm{vac}\right\rangle , \end{aligned}$$

(11.11)

where the partition function is given by

$$\begin{aligned} \begin{aligned}Z&\left( {\mathcal {S}}\right) =\prod _{\mu }\exp \left\{ -\dfrac{\tau \hbar \varOmega }{2}\left[ 1+\dfrac{\omega ^{2}}{2\varOmega ^{2}}\left( \lambda _{\mu }-K\right) \right] \right\} .\end{aligned} \end{aligned}$$

(11.12)

The diagonal thermal Green’s function can then be obtained as [84]

$$\begin{aligned} \begin{aligned}G_{vv}\left( {\mathcal {S}},\tau \right)&=\frac{1}{Z}\sum _{\mu ,\nu }\left( O^{T}\right) _{v\mu }\left\langle \mathrm{vac}\right| b_{\mu }e^{-\tau \mathscr {{\hat{H}}}\left( {\mathcal {S}}\right) }b_{\nu }^{\mathrm{\dagger }}\left| \mathrm{vac}\right\rangle O_{\nu v}\\&=\frac{1}{Z^{A}}\sum _{\mu }\left[ \left( O^{T}\right) _{v\mu }\left( O^{T}\right) _{v\mu }\left\langle \mathrm{vac}\right| b_{\mu }e^{-\tau H_{\mu }}b_{\mu }^{\mathrm{\dagger }}\left| \mathrm{vac}\right\rangle O_{\mu v}\prod _{\nu \left( \ne \mu \right) }\left\langle \mathrm{vac}\right| e^{-\tau H_{\nu }}\left| \mathrm{vac}\right\rangle \right] \\&=\sum _{\mu }\left( O^{T}\right) _{v\mu }\dfrac{\left\langle \mathrm{vac}\right| b_{\mu }e^{-\tau H_{\mu }}b_{\mu }^{\mathrm{\dagger }}\left| \mathrm{vac}\right\rangle }{\left\langle \mathrm{vac}\right| e^{-\tau H_{\mu }}\left| \mathrm{vac}\right\rangle }O_{\mu v}\\&=\sum _{\mu }\left( O^{T}\right) _{v\mu }\exp \left\{ -\tau \hbar \varOmega \left[ 1+\dfrac{\omega ^{2}}{2\varOmega ^{2}}\left( \lambda _{\mu }-K\right) \right] \right\} O_{\mu v}\\&=e^{-\beta \hbar \varOmega }\left( \exp \left[ \dfrac{\tau \hbar \omega ^{2}}{2\varOmega ^{2}}A\right] \right) _{vv} \end{aligned}\nonumber \\ \end{aligned}$$

(11.13)

where we have used the spectral decomposition of A in the last line.

Let us consider $\hbar =1$ and $K=\dfrac{1}{2}M\omega ^{3}$. Then, [84]

$$\begin{aligned} G_{vv}\left( {\mathcal {S}},\tau \right) =e^{-\tau \sqrt{2}\omega }\left( \exp \left[ \tau A\right] \right) _{vv}=e^{-\tau \sqrt{2}\omega }G_{vv}\left( G,\tau \right) . \end{aligned}$$

(11.14)

Remark 9

In [84] it is remarked that

$$\begin{aligned} EE\left( G,\tau \right) =\sum _{v}G_{vv}\left( G,\tau \right) =e^{\tau \sqrt{2}\omega }\sum _{v}G_{vv}\left( S,\tau \right) , \end{aligned}$$

(11.15)

which indicates that the Estrada index represents the sum of the excitations started at every node of a graph, which propagate throughout the network before coming back to the same node and being annihilated in a network of quantum harmonic oscillators.

11.2 Classical oscillators

Here we consider a system S like the one described before but obeying the laws of classical mechanics. In this case we can write the Hamiltonian of the system by considering only the potential energy (for justification see [84]):

$$\begin{aligned} \begin{aligned}{\mathscr {H}}&=\frac{KM\omega ^{2}}{2}\sum _{v}x_{v}^{2}-\frac{M\omega ^{2}}{2}\sum _{v,w}x_{v}A_{vw}x_{w}\\&=\frac{M\omega ^{2}}{2}x^{T}\left( KI-A\right) x, \end{aligned}\nonumber \\ \end{aligned}$$

(11.16)

where $x=\left( x_{1},x_{2},\ldots ,x_{n}\right) ^{T}$ and I is the $n\times n$ identity matrix.

We can now diagonalize A as before and by taking a sufficiently large value of the constant K, we can make all eigenvalues $\lambda _{\mu }$ positive. By defining a new set of variables $y_{\mu }$ as $y=Ox$ and $x=O^{T}y$, we can transform the Hamiltonian in the form

$$\begin{aligned} {\mathscr {H}}=\frac{M\omega ^{2}}{2}y^{T}\varLambda y=\frac{M\omega ^{2}}{2}\sum _{\mu }y_{\mu }^{2}+\frac{M\omega ^{2}}{2}\sum _{\mu }\lambda _{\mu }y_{\mu }^{2}. \end{aligned}$$

(11.17)

Here again we focus of the quantification of those oscillations that start at a given ball of the system, navigates the whole system and return to the corresponding ball. Namely,

$$\begin{aligned} \varGamma _{vv}\left( {\mathcal {S}},\beta \right) =\left\langle x_{v}^{2}\right\rangle =\frac{1}{Z}\int x_{v}^{2}e^{-\tau {\mathscr {H}}}\prod _{w}dx_{w}, \end{aligned}$$

(11.18)

where the partition function is given by

$$\begin{aligned} Z\left( {\mathcal {S}}\right) =\int e^{-\tau {\mathscr {H}}}\prod _{v}dx_{v}=\int dx\exp \left( -\frac{\tau M\omega ^{2}}{2}x^{T}\left( KI-A\right) x\right) , \end{aligned}$$

(11.19)

where the integral is n-fold.

Now, because the Jacobian of the orthogonal matrix O is unity we have $\prod _{i}dx_{i}=\prod _{\mu }dy_{\mu }.$ Therefore, the multi-fold integration in the partition function is decoupled to give

$$\begin{aligned} \begin{aligned}Z\left( {\mathcal {S}}\right)&=\prod _{\mu }\left[ \int \exp \left( -\frac{\tau M\omega ^{2}}{2}\lambda _{\mu }y_{\mu }^{2}\right) dy_{\mu }\right] \\&=\prod _{\mu }\sqrt{\frac{2\pi }{\tau M\omega ^{2}\lambda _{\mu }}}, \end{aligned}\nonumber \\ \end{aligned}$$

(11.20)

which can be written in matrix form as

$$\begin{aligned} Z\left( {\mathcal {S}}\right) =\left( \frac{2\pi }{\tau M}\omega ^{2}\right) ^{n/2}\frac{1}{\sqrt{\det \left( KI-A\right) }}. \end{aligned}$$

(11.21)

Since we have made all the eigenvalues of $\left( KI-A\right)$ positive, its determinant is positive. Similarly, we have

$$\begin{aligned} \varGamma _{vv}\left( {\mathcal {S}},\tau \right) =\frac{1}{Z}\int \left[ \sum _{\sigma }\left( O^{T}\right) _{v\sigma }y_{\sigma }\right] ^{2}e^{-\tau {\mathscr {H}}}\prod _{\mu }dy_{\mu }. \end{aligned}$$

(11.22)

In the integrand, odd functions with respect to $y_{\mu }$ vanish. Therefore, only the terms of $y_{\sigma }^{2}$ survive after integration in the expansion of the square parentheses in the integrand. This gives

$$\begin{aligned} \begin{aligned}\varGamma _{vv}\left( {\mathcal {S}},\tau \right)&=\frac{1}{Z}\int \left[ \sum _{\sigma }\left( O_{\sigma v}y_{\sigma }\right) ^{2}\right] \exp \left( -\frac{\tau M\omega ^{2}}{2}\sum _{\nu }\lambda _{\nu }y_{\nu }^{2}\right) \prod _{\mu }dy_{\mu }\\&=\frac{1}{Z}\sum _{\sigma }O_{\sigma v}\int y_{\sigma }^{2}\exp \left( -\frac{\tau M\omega ^{2}}{2}\lambda _{\sigma }y_{\sigma }^{2}\right) dy_{\sigma }\\&=\prod _{\mu \left( \ne \sigma \right) }\left( \int \exp \left( -\frac{\tau M\omega ^{2}}{2}\lambda _{\mu }y_{\mu }^{2}\right) dy_{\mu }\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(11.23)

Comparing this expression with that of the partition function we have [84]

$$\begin{aligned} \begin{aligned}\varGamma _{vv}\left( {\mathcal {S}},\tau \right)&=\sum _{\sigma }O_{\sigma v}^{2}\left( \frac{\int y_{\sigma }^{2}e^{-\tau M\omega ^{2}\lambda _{\sigma }y_{\sigma }^{2}/2}dy_{\sigma }}{\int e^{-\tau M\omega ^{2}\lambda _{\sigma }y_{\sigma }^{2}/2}dy_{\sigma }}\right) =\sum _{\sigma }O_{\sigma v}^{2}\frac{\sqrt{\frac{2\pi }{\left[ \tau M\omega ^{2}\lambda _{\sigma }\right] ^{3}}}}{\sqrt{\frac{2\pi }{\tau M\omega ^{2}\lambda _{\sigma }}}}\\&=\sum _{\sigma }\dfrac{O_{\sigma v}^{2}}{\tau M\omega ^{2}\lambda _{\sigma }}\\&=\dfrac{1}{\tau M\omega ^{2}}\left[ \left( KI-A\right) ^{-1}\right] _{vv}\\&=\frac{1}{\tau KM\omega ^{2}}\left[ \left( I-\dfrac{A}{K}\right) ^{-1}\right] _{vv}. \end{aligned} \end{aligned}$$

(11.24)

Remark 10

In [84] it is remarked that if $K=n-1$ then we have

$$\begin{aligned} REE\left( G,\tau \right) =\sum _{v}\left[ \left( I-\dfrac{A}{n-1}\right) ^{-1}\right] _{vv}=\tau \left( n-1\right) M\omega ^{2}\sum _{v}\varGamma _{vv}\left( S,\tau \right) , \end{aligned}$$

(11.25)

which indicates that the resolvent Estrada index represents the sum of the excitations started at every node of a graph, which propagate throughout the network before coming back to the same node in a network of classical harmonic oscillators.

12 Estrada indices and epidemics on networks

In continuation with the previous line of research in which the Estrada index is derived from a given dynamical systems context we analyze here its connection with epidemiological models on networks. The field of mathematical epidemiology has a long tradition in applied mathematics (see for instance [7, 34, 169]. In 2001, the authors of the seminal work [179] discovered the tremendous influence of network topology on epidemic spreadings. Since then, the use of network-theoretic approaches together with epidemiological models have become a necessary combination [143, 149]. Here we will show that such networked epidemiological models have a clear connection with the Estrada index of a graph.

For that we will briefly introduce the Susceptible/Infected (SI) model on networks. The reader should be aware that this is a generalist model that can be used in many different scenarios, not only on the analysis of diseases propagating on a network. Let G be a graphs whose nodes can be in either of two states: either susceptible or infected one. An infected node can transmit the infection to any other node in the graph to which it interacts with. Then, if $\zeta$ is the rate at which such infection is transmitted between nodes, and if $s_{v}\left( t\right)$ and $x_{v}\left( t\right)$ are the probabilities that the node v is susceptible or get perturbed at time t, respectively, we can write the dynamics [170]:

$$\begin{aligned} \dfrac{dx_{v}\left( t\right) }{dt}=\zeta \left( 1-x_{v}\left( t\right) \right) \sum _{w\in {\mathcal {N}}}A_{vw}x_{w}\left( t\right) ,t\ge t_{0}, \end{aligned}$$

(12.1)

where $A_{vw}$ are the entries of the adjacency matrix of the graph for the pair of nodes v and w, and ${\mathcal {N}}$ is the set of nearest neighbors of v. In matrix-vector form becomes [170]:

$$\begin{aligned} \dfrac{dx\left( t\right) }{dt}=\zeta \left[ I_{N}-\text {diag}\left( x\left( t\right) \right) \right] Ax\left( t\right) , \end{aligned}$$

(12.2)

with initial condition $x\left( 0\right) =x_{0}.$

The SI model can be rewritten as

$$\begin{aligned} \dfrac{1}{1-x_{v}(t)}\dfrac{dx_{v}\left( t\right) }{dt}=\zeta \sum _{w\in {\mathcal {N}}}A_{vw}\left( 1-e^{-\left( -\log \left( 1-x_{w}\left( t\right) \right) \right) }\right) , \end{aligned}$$

(12.3)

which is equivalent to

$$\begin{aligned} \dfrac{dy_{v}\left( t\right) }{dt}=\zeta \sum _{w\in {\mathcal {N}}}A_{vw}f\left( y_{w}\left( t\right) \right) , \end{aligned}$$

(12.4)

where $y_{v}\left( t\right) \,{:}{=}\,g\left( x_{v}\left( t\right) \right) =-\log \left( 1-x_{v}\left( t\right) \right) \in \left[ 0,\infty \right]$, $f\left( y\right) \,{:}{=}\,1-e^{-y}=g^{-1}\left( y\right)$.

Lee et al. [155] have considered the following linearized version of the previous nonlinear equation

$$\begin{aligned} \dfrac{d{\hat{y}}\left( t\right) }{dt}=\zeta A\text {diag}\left( 1-x\left( t_{0}\right) \right) {\hat{y}}\left( t\right) +\zeta b\left( x\left( t_{0}\right) \right) , \end{aligned}$$

(12.5)

where ${\hat{x}}\left( t\right) =f\left( {\hat{y}}\left( t\right) \right)$ in which ${\hat{x}}\left( t\right)$ is the approximate solution to the SI model, ${\hat{y}}\left( t_{0}\right) =g\left( x\left( t_{0}\right) \right)$ and $b\left( x\right) \,{:}{=}\,x+\left( 1-x\right) \log \left( 1-x\right) .$ They have found that the solution to this linearized model is [155]:

$$\begin{aligned} \begin{aligned}{\hat{y}}\left( t\right)&=e^{\zeta \left( t-t_{0}\right) A\text {diag}\left( 1-x\left( t_{0}\right) \right) }g\left( x\left( t_{0}\right) \right) \\&\quad +\sum _{k=0}^{\infty }\dfrac{\left( \zeta \left( t-t_{0}\right) \right) ^{k+1}}{\left( k+1\right) !}\left[ A\text {diag}\left( 1-x\left( t_{0}\right) \right) \right] ^{k}Ab\left( x\left( t_{0}\right) \right) . \end{aligned} \end{aligned}$$

(12.6)

When $t_{0}=0$, $x_{i}\left( 0\right) =c/N$, $i=1,2,\ldots ,N$ for some c, the previous equation is transformed to

$$\begin{aligned} {\hat{y}}\left( t\right) =\left( 1/\gamma -1\right) e^{\gamma \zeta tA}\mathbf {1}-\left( 1/\gamma -1+\log \left( \gamma \right) \right) \mathbf {1}, \end{aligned}$$

(12.7)

where $\gamma =1-c/N$ and $\mathbf {1}$ is the all-ones vector. In [155] the authors proved that this solution is an upper bound to the exact solution of the SI model.

Therefore, if we take the sum of the entries of ${\hat{y}}\left( t\right)$ at a given t we have

$$\begin{aligned} \sum _{v=1}^{n}\hat{y_{v}}\left( t\right) =C_{1}\left[ \text {tr}\left( e^{\gamma \zeta tA}\right) +\text {tr}\left( \left( J-I\right) \left( e^{\gamma \zeta tA}\right) \right) \right] -nC_{2}, \end{aligned}$$

(12.8)

where $C_{1}=\left( 1/\gamma -1\right)$ and $C_{2}=\left( 1/\gamma -1+\log \left( \gamma \right) \right) .$ Obviously the first term in the square bracket is the Estrada index of the graph in which edges are weighted by $\gamma \zeta t$. This term represents the circulability of the infection around the nodes of the graph, while the term $\text {tr}\left( \left( J-I\right) \left( e^{\gamma \zeta tA}\right) \right)$, where J is the all-ones matrix, accounts for the transmissibility of the disease between the nodes.

12.1 Fractional SI model on networks

In recent years there have been an explosion of works in which the classical derivatives used in the epidemiological models have been substituted by fractional ones [8, 11, 12, 133, 192]. There have been several reasons for adopting fractional epidemiological models. They include for instance

• 1. the fact that the fractional parameter can be tuned to adjust the output of the model to real data [8] and so they can be more accurate that models using standard derivatives;

• 2. the fact that a fractional differential operators may be derived from epidemiological models whenever the recovery time from the disease is power-law distributed [11];

• 3. the fact that fractional derivatives capture the history of the variable, that is, they have memory, and the effect of recent memory is more important than the effect of older memory [12, 192].

In general, fractional derivatives are nowadays widely used to model biological processes [136] to incorporate different aspects of the dynamics in such systems. Here, we will describe a model which naturally gives rise to the Mittag–Leffler Estrada index in the context of epidemiological models.

We proceed by considering fractional time-derivatives in the modified SI model proposed in [155]. That is, in [1] the authors considered the following linearized fractional SI equation

$$\begin{aligned} D_{t}^{\alpha }{\hat{y}}\left( t\right) =\zeta ^{\alpha }A\text {diag}\left( 1-x_{0}\right) {\hat{y}}\left( t\right) +\zeta ^{\alpha }Ab\left( x\left( 0\right) \right) , \end{aligned}$$

(12.9)

where ${\hat{x}}\left( t\right) =f\left( {\hat{y}}\left( t\right) \right)$ in which ${\hat{x}}\left( t\right)$ is an approximate solution to the fractional SI model, ${\hat{y}}$ is the solution of (12.9) with initial condition ${\hat{y}}\left( 0\right) =g\left( x\left( 0\right) \right)$ and $b\left( x\right) :=x+\left( 1-x\right) \log \left( 1-x\right) .$ Here $D_{t}^{\alpha }f\left( t\right)$ is the fractional time derivative in the Caputo formulation [37], which was previously given in Eq. (10.3).

For convenience, we write $\varOmega :=\text {diag}\left( 1-x_{0}\right) ,$ and ${\hat{A}}=A\varOmega .$ It was then proved that this solution is an upper bound to the exact fractional SI model.

Let us fix the following notation. Let x and y be two vectors of the same length n. Then, we say that $x\preceq y$ is $x_{i}\le y_{i}$ for all $i=1,\ldots n$. Let ${\tilde{x}}(t)$ be the solution of the linearized fractional models of the form: $D_{t}^{\alpha }{\tilde{x}}(t)=\zeta A{\tilde{x}}(t)$, which is exponential unstable.

Theorem 36

[1] For any $t\ge 0$, we have

$$\begin{aligned} x(t)\preceq {\hat{x}}(t)=f({\hat{y}}(t))\preceq {\tilde{x}}(t), \end{aligned}$$

under the same initial conditions $x_{0}:=x(0)={\hat{x}}(0)={\tilde{x}}(0),$ where the solution ${\hat{y}}$ of (12.9) is given by

$$\begin{aligned} {\hat{y}}\left( t\right) =E_{\alpha ,1}\left( (\zeta t)^{\alpha }{\hat{A}}\right) g\left( x_{0}\right) +\sum _{n=0}^{\infty }\frac{(\zeta t)^{\alpha \left( n+1\right) }{\hat{A}}^{n}Ab\left( x_{0}\right) }{\varGamma \left( \alpha \left( n+1\right) +1\right) }. \end{aligned}$$

(12.10)

Furthermore, $\Vert {\hat{x}}(t)-x(t)\Vert \rightarrow 0$ and $\Vert {\tilde{x}}(t)-x(t)\Vert \rightarrow \infty$ as t goes to infinity.

Corollary 5

[1] Let $x_{0}\preceq 1$, $x_{0}=\frac{c}{N}$ where $c\in {\mathbb {R}}^{+},$ let $\gamma =1-x_{0}.$ Then

$$\begin{aligned} {\hat{y}}\left( t\right)&=\left( \frac{1-\gamma }{\gamma }\right) E_{\alpha ,1}\Bigl (t^{\alpha }\zeta ^{\alpha }\gamma A\Bigr )\mathbf {1}-\left( \frac{1-\gamma }{\gamma }+\log \gamma \right) \mathbf {1}, \end{aligned}$$

(12.11)

where $E_{\alpha ,1}\Bigl (.\Bigr )$ is the Mittag–Leffler matrix function of the corresponding matrix.

Therefore, here again if we take the sum of the entries of ${\hat{y}}\left( t\right)$ at a given t we have

$$\begin{aligned} \sum _{v=1}^{n}\hat{y_{v}}\left( t\right) =C_{1}\left[ \text {tr}\left( E_{\alpha ,1}\Bigl (t^{\alpha }\zeta ^{\alpha }\gamma A\Bigr )\right) +\text {tr}\left( \left( J-I\right) \left( E_{\alpha ,1}\Bigl (t^{\alpha }\zeta ^{\alpha }\gamma A\Bigr )\right) \right) \right] -nC_{2},\nonumber \\ \end{aligned}$$

(12.12)

Thus, again the Mittag–Leffler Estrada index, which is the first term in the squared bracket, represents the circulability of the infection around the nodes of the graph in the fractional SI model, while the second term represents the transmissibility of the disease between the nodes.

13 Estrada indices from piecewise walk penalization

In the same work [75] in which the author proposed the use of the matrix $\varPsi$ functions as a way to increase the penalization of longer walks in graphs, a different strategy was proposed to drop such penalization relative to the exponential matrix function. This strategy can be formulated as a piecewise penalization as follows. Suppose that we do not want to penalize the walks of lengths smaller than certain value $t\in {\mathbb {Z}}$. Then, we define the following stepwise function:

$$\begin{aligned} f_{t}\left( k\right) =\left\{ \begin{array}{cc} 1 &{}\quad \text {if } k<t,\\ k! &{}\quad \text {if } k\ge t, \end{array}\right. \end{aligned}$$

(13.1)

such that the piecewise Estrada index of the graph G is defined as:

$$\begin{aligned} EE_{t}\left( G\right) =\text {tr}\left( \sum _{k=0}^{\infty }\dfrac{A^{k}}{f_{t}\left( k\right) }\right) =\text {tr}\left( \sum _{k=0}^{t-1}A^{k}+\sum _{k=t}^{\infty }\dfrac{A^{k}}{k!}\right) . \end{aligned}$$

(13.2)

In the case that the adjacency matrix has no unity eigenvalue we can write this Estrada index as [75]:

$$\begin{aligned} EE_{t}\left( G\right) =\text {tr}\left[ \left( I-A\right) ^{-1}\left( I-A^{t}\left( I+e^{A}-Ae^{A}\right) \right) \right] . \end{aligned}$$

(13.3)

For computational purposes this expression can be adapted for any network as follows. Let r be a constant sufficiently close to one, such that $r\ne 1/\lambda$ for all $\lambda$, which are the eigenvalues of A. Then,

$$\begin{aligned} EE_{t}\left( G\right) \approx \text {tr}\left[ \left( I-rA\right) ^{-1}\left( I-\left( rA\right) ^{t}\left( I+e^{rA}-rAe^{rA}\right) \right) \right] . \end{aligned}$$

(13.4)

14 Nonlocal adjacency, Harary Estrada index and beyond

There are physical situations in which the entities of a system not only interact if they are nearest neighbors, but also through nonlocal interactions. These long-range interactions have been documented in physical, chemical and biological systems [3, 39, 148, 164, 177, 194, 195, 235, 240]. In a physical context, like the tight-binding kind of models described before, these nonlocal interactions corresponds to the case where the Hamiltonian of the system describes not only NN interactions but also next-nearest-neighbor (NNN) and other interactions beyond them [31, 168, 174, 193]:

$$\begin{aligned} {\hat{\mathcal {H}}}={\hat{\mathcal {H}}}_{NN}+{\hat{\mathcal {H}}}_{NNN}+\cdots . \end{aligned}$$

(14.1)

In this framework we have that the system can be described by the weighted sum of higher-order adjacency matrices:

$$\begin{aligned} {\hat{\mathcal {H}}}=\alpha I+t_{NN}A+t_{NNN}A_{2}+\cdots , \end{aligned}$$

(14.2)

where $A_{2}$ is a matrix with entries $\left( A_{2}\right) _{ij}$ equal to one if i and j are not adjacent and are separated by two edges or zero otherwise. We can extend this concept to any other separation, such that [77]

$$\begin{aligned} \left( A_{d}\right) _{ij}=\left\{ \begin{array}{cc} 1 &{}\quad \text {if } d_{ij}=d,\\ 0 &{}\quad \text {otherwise,} \end{array}\right. \end{aligned}$$

(14.3)

where $d_{ij}$ is the length of the shortest path between the two nodes. The parameters $t_{NN}$, $t_{NNN}$, etc. are expected to decay with the length of the separation between the corresponding entities. That is, the strength of the interaction decays with a given law of their separation d, i.e., $f\left( d\right)$. In this way we can write [72, 218]

$$\begin{aligned} {\hat{\mathcal {H}}}=\alpha I+t_{NN}A+t_{NNN}A_{2}+\cdots =\alpha I+\sum _{d=1}^{diam}f\left( d\right) A_{d}, \end{aligned}$$

(14.4)

where diam is the diameter of the graph. Let us see how we can construct ${\hat{\mathcal {H}}}$.

Here we will use a min-plus algebra to define what otherwise is the shortest path distance matrix of the graph. We do that because it is a mathematically elegant approach, which may also open some possibilities for studying other kinds of functions for graphs.

Let $\left( {\mathbb {R}}\cup \left\{ +\infty \right\} ,\oplus ,\otimes \right)$ be the min tropical semiring with the operations [32, 131, 139]:

$$\begin{aligned} \begin{aligned}x\oplus y&\,{:}{=}\,\min \left\{ x,y\right\} ,\\ x\otimes y&\,{:}{=}\,x+y. \end{aligned} \end{aligned}$$

(14.5)

The identity element for $\oplus$ is $+\infty$ and that for $\otimes$ is 0. Then, we can define the tropical adjacency matrix power as

$$\begin{aligned} A^{\otimes k+1}=A^{\otimes k}\otimes A, \end{aligned}$$

(14.6)

where $A^{\otimes 0}={\hat{I}}$, which is the tropical identity matrix, i.e., a matrix with zeros in the main diagonal and $\infty$ outside it.

Let us fix any $\alpha$ with $0<\alpha \le \infty$ and let us define the matrix $M=\left[ m_{ij}\right] :m_{ij}\in \left( -\alpha ,\alpha \right)$ for all $i,j=1,\ldots ,n$. Let ${\tilde{f}}$ be a real function on the open interval $\left( -\alpha ,\alpha \right) .$ We define the pseudo-entrywise (pseudo-Hadamard) matrix function ${\tilde{f}}\left( M\right)$ as

$$\begin{aligned} \left( {\tilde{f}}\left( M\right) \right) _{ij}\,{:}{=}\,\left\{ \begin{array}{cc} f\left( m_{ij}\right) &{}\quad \text { if }m_{ij}\ne 0\\ 0 &{}\quad \text { if }m_{ij}=0 \end{array}\right. . \end{aligned}$$

(14.7)

Here, the function f could be an exponential, a trigonometric function or simply the power function. Let us hereafter focus only on the negative power function, such that $\left( -s\right)$ represents the entrywise power. We can now write:

$$\begin{aligned} {\hat{\mathcal {H}}}=\mathscr {{\mathcal {A}}}_{s}=\left( \bigoplus _{k=0}^{\infty }A^{\otimes k}\right) ^{\left( -s\right) }. \end{aligned}$$

(14.8)

The tropical sum is carried out up to infinity as it converges in all cases where there are no negative cycles in the graph. A negative cycle is a cycle where the product of the weights of all its edges is negative. Typically, except for signed graphs, we consider positive edge weights, which always avoid such negative cycles. The infinite sum $\bigoplus _{k=0}^{\infty }A^{\otimes k}$ is known as the Kleene star operator of A [32, 131, 139]. Obviously, $\mathscr {{\mathcal {A}}}_{s}=\left[ {\mathcal {A}}_{ij}\left( s\right) \right]$, where [72, 218]

$$\begin{aligned} {\mathcal {A}}_{ij}\left( s\right) \,{:}{=}\,\left\{ \begin{array}{cc} d_{ij}^{-s} &{}\quad \text {if } i\ne j,\\ 0 &{}\quad \text {if } i=j, \end{array}\right. \end{aligned}$$

(14.9)

which are the entry-wise powers of all nondiagonal entries of the shortest path distance matrix of the graph. The parameter s accounts for the strength of the nonlocal interaction. Notice that

$$\begin{aligned} \lim _{s\rightarrow 0}{{\mathcal {A}}}_{s}=A\left( K_{n}\right) . \end{aligned}$$

Here again, in the statistical physics context, the partition function of the system containing nonlocal interactions is:

$$\begin{aligned} Z=\text {tr}\left( e^{-\tau {\hat{\mathcal {H}}}}\right) , \end{aligned}$$

(14.10)

where $\tau$ is the inverse temperature as before. Because the parameters $t_{NN},$ $t_{NNN},$ etc., are negative we have that

$$\begin{aligned} Z=\text {tr}\left( e^{\tau {{\mathcal {A}}}_{s}}\right) \,{=:}\,EE\left( \mathscr {{\mathcal {A}}}_{s},\beta \right) , \end{aligned}$$

(14.11)

Then, using the same definitions as the ones given before we can define the entropy, enthalpy and free energy of the system having local and nonlocal interactions.

It is important to notice that

$$\begin{aligned} {{\mathcal {A}}}_{s}=A+\sum _{d=2}^{diam}d^{-s}A_{d}, \end{aligned}$$

(14.12)

which implies that

$$\begin{aligned} \lim _{s\rightarrow \infty }{{\mathcal {A}}}_{s}=A\left( G\right) . \end{aligned}$$

(14.13)

Let ${{\tilde{\mathcal {A}}}}_{s}\,{:}{=}\,\sum _{d=2}^{diam}d^{-s}A_{d}$. Then, because A and ${{\tilde{\mathcal {A}}}}_{s}$ do not commute in general, we have according to the Golden-Thompson inequality that

$$\begin{aligned} EE\left( \mathscr {{\mathcal {A}}}_{s},\tau \right) =\text {tr}\left( e^{\tau \left( A+{{\tilde{\mathcal {A}}}}_{s}\right) }\right) \le \text {tr}\left( e^{\tau A}e^{\tau {{\tilde{\mathcal {A}}}}_{s}}\right) . \end{aligned}$$

(14.14)

When $s=1$, the corresponding matrix $\mathscr {{\mathcal {A}}}_{s=1}$ is known in mathematical chemistry as the Harary matrix [137, 167, 181] in honor to mathematician Frank Harary (1921–2005).⁸

Nowadays there are not many results about the HEE index. Hereafter we collect some of the existing ones for simple graphs [109], $HEE\left( G\right) =EE\left( \mathscr {{\mathcal {A}}}_{s=1},\tau =1\right) .$

Theorem 37

[109] Let G be a simple graph with n vertices and m edges. Then, the Harary Estrada index of G is bounded as

$$\begin{aligned} \sqrt{n^{2}+2\left( \dfrac{3m}{2}+\dfrac{n\left( n-1\right) }{4}\right) }\le HEE\left( G\right) \le n-1+\exp \left( \sqrt{\dfrac{3m}{2}+\dfrac{n\left( n-1\right) }{4}}\right) \nonumber \\ \end{aligned}$$

(14.15)

with equalities attained if and only if $G\cong {\bar{K}}_{1}$.

Theorem 38

[138] Let G be a simple graph with $n\ge 2$ vertices and let $\kappa =\tfrac{1}{2}\text {tr} \left( \mathscr {{\mathcal {A}}}_{s=1}^{2}\right)$. Then, the Harary Estrada index is bounded as

$$\begin{aligned} HEE\left( G\right) \ge \exp \left( \sqrt{\dfrac{2\kappa }{n\left( n-1\right) }}\right) +\left( n-1\right) \exp \left( -\sqrt{\dfrac{2\kappa }{n\left( n-1\right) }}\right) . \end{aligned}$$

(14.16)

14.1 Numerical analysis

In Fig. 15 we illustrate the histograms of the relative deviations of the lower bounds given in Theorem 37 and in Theorem 38 as well as of the upper bound given in Theorem 37. We consider all connected graphs with 8 nodes.

For both lower bounds, the values obtained with these bounds are about 20–40 times smaller than the actual values. The mean relative deviations are, respectively $93.16\pm 2.19$ and $96.591\pm 1.52$. The upper bound is as average $10^{19}$ times bigger than the actual $HEE\left( G\right)$ indices for these small graphs, which is an extremely poor performance of this bound.

Fig. 15

Histogram of the relative deviations for the lower bounds Theorems 37 and 38 (in %) as well as of the upper bound Theorem 37 (as logarithm) for all 11,117 connected graphs with 8 nodes

In Table 10 we give the values of the bounds previously considered for the five real-world networks analyzed here as well as the actual values of $HEE\left( G\right)$. As can be seen both lower and upper bounds are extremely far from the actual values of the Harary Estrada indices of these real-world networks. In particular, the upper bound is extremely higher than the actual values.

Table 10 Values of the lower bounds Theorems 37 and 38 as well as the upper bound Theorem 37 for the Harary Estrada index of the five real-world networks analyzed in this paper. The actual values of $HEE\left( G\right)$ of these networks are also given. We have used “very precise arithmetic” (vpa) in Matlab for these calculations

15 Laplacian Estrada index and backward diffusion

In the study of graph properties, the function ${\mathscr {K}}\left( G\right) =\left( e^{-tL}\right)$, where L is the graph Laplacian, has found many applications [22, 45, 150, 236]. The name “Laplacian” honors mathematician Pierre–Simon Laplace (1749–1827).⁹ The function ${\mathscr {K}}\left( G\right)$ is known as the heat kernel of the graph [125, 191] and appears naturally in the solution $u\left( t\right) =\exp \left( -t{\mathscr {D}}L\right) u_{0}$ of the diffusion equation on graphs:

$$\begin{aligned} \dfrac{du\left( t\right) }{dt}=-{\mathscr {D}}Lu\left( t\right) ,\qquad u\left( 0\right) =u_{0}, \end{aligned}$$

(15.1)

where ${\mathscr {D}}$ is the diffusivity (see Sect. 16). Therefore, the trace of the heat kernel would correspond to a sort of diffusion Estrada index. However, in [92] the following index was proposed and named “the Laplacian Estrada index” of the graph

$$\begin{aligned} LEE\left( G\right) =\text {tr}\left( e^{L}\right) =\sum _{j=1}^{n}e^{\mu _{j}}, \end{aligned}$$

(15.2)

where $\mu _{j}$ are the corresponding eigenvalues of L. Therefore, what the authors of [92] have proposed can be though as an index related to the solution of the backward diffusion equation, i.e., negative time, or as a diffusion equation with negative diffusivity ${\mathscr {D}}<0$ [65]. There are physical situations in which such negative diffusivity appears [48, 140, 173, 225, 226]. For instance, in the simultaneous diffusion of boron and point defect in silicon, the diffusivities of interstitial could be negative [225]. That is, the diffusion process of interstitial or vacancy could be a backward diffusion in silicon. In other scenarios, a backward diffusive model is used to detect the potential location of sources in spreading processes.

In [92] the authors proved the following result.

Proposition 2

Let G be a simple graph with n nodes and m edges. Let $Z=\sum _{i}k_{i}^{2}$ be the first Zagreb index of G. Then,

$$\begin{aligned} \sqrt{n\left( n-1\right) e^{4m/n}+n+8m+2Z}\le LEE\left( G\right) \le n-1+e^{2m}+m-2m^{2}+\dfrac{1}{2}Z,\nonumber \\ \end{aligned}$$

(15.3)

with equality if and only if $G\cong {\bar{K}}_{n}$.

Further, in [249] the authors proved the following results.

Proposition 3

Let G be a simple graph with n nodes and m edges. Let $Z=\sum _{i}k_{i}^{2}$ be the first Zagreb index of G. Then,

$$\begin{aligned} LEE\left( G\right) \le n-1+2m-\sqrt{Z+2m}+\exp \left( \sqrt{Z+2m}\right) , \end{aligned}$$

(15.4)

with equality if and only if $G\cong K_{2}\cup {\bar{K}}_{n-2}$ or $G\cong {\bar{K}}_{n}$.

Proposition 4

Let G be a simple graph with n nodes and m edges. Then,

$$\begin{aligned} LEE\left( G\right) \ge 2+\sqrt{n\left( n-1\right) e^{4m}+4-3n-4m}, \end{aligned}$$

(15.5)

with equality if and only if $G\cong {\bar{K}}_{n}$.

Other bounds were obtained in [248] on the basis of the degree sequence of a graph.

Proposition 5

Let G be a simple graph with n nodes and m edges. Let $k_{max},k_{2},\ldots ,k_{min}$ be the nonincreasing ordering of the node degrees of G. Then,

$$\begin{aligned} LEE\left( G\right) \ge e^{k_{max}+1}+\sum _{i=2}^{n-1}e^{k_{i}}+e^{k_{min}-1}, \end{aligned}$$

(15.6)

with equality if and only if $G\cong S_{n}$.

Proposition 6

Let G be a simple graph with n nodes and m edges. Let $k_{max},k_{2},\ldots ,k_{min}$ be the nonincreasing ordering of the node degrees of G. Then,

$$\begin{aligned} LEE\left( G\right) \ge n+\sum \dfrac{k_{i}}{k_{i}+1}\left( e^{k_{i}+1}-1\right) , \end{aligned}$$

(15.7)

with equality if and only if G is a vertex disjoint union of complete subgraphs.

Several bounds have been proposed on the basis of the maximum and minimum degrees of a graph. We resume some of them here.

Theorem 39

[160] Let G be a simple graph with n nodes and m edges. Let $k_{max}$ and $k_{min}$ be the maximum and minimum node degrees of G. Then,

$$\begin{aligned} LEE\left( G\right) \ge e^{k_{max}+1-2m/n}+\left( n-2\right) \left( e^{4m/n-k_{max}-1}\right) ^{1/\left( n-2\right) }+e^{-2m/n}, \end{aligned}$$

(15.8)

with equality if and only if $G\cong K_{n}$ or $G\cong S_{n}$.

Theorem 40

[40] Let G be a simple graph with n nodes and m edges. Let $k_{max}$ and $k_{min}$ be the maximum and minimum node degrees of G. Then,

$$\begin{aligned} LEE\left( G\right) \ge 1+e^{k_{max}+1}+e^{k_{min}}+\left( n-3\right) e^{\left( 2m-k_{max}-k_{min}-1\right) /\left( n-3\right) }, \end{aligned}$$

(15.9)

with equality if and only if $G\cong 2K_{1}\vee K_{n-2}$ or $G\cong K_{1,n-1}$ or $G\cong K_{\left( n-1\right) /2}\cup K_{\left( n-1\right) /2}$ (n is odd).

Theorem 41

[161] Let G be a simple graph with n nodes and m edges. Let $k_{max}$ and $k_{min}$ be the maximum and minimum node degrees of G. Then,

$$\begin{aligned} \sqrt{n^{2}+4m}\le LEE\left( G\right) \le n-1+\exp \left( \sqrt{2m\left( k_{max}+k_{min}+1-2m/n\right) -nk_{min}k_{max}}\right) ,\nonumber \\ \end{aligned}$$

(15.10)

with equality if and only if $G\cong {\bar{K}}_{n}$.

The following is an upper bound found in [163].

Theorem 42

Let G be a simple graph with n nodes and m edges. Then,

$$\begin{aligned} LEE\left( G\right) \le \left\lfloor \dfrac{2m}{n}\right\rfloor e^{n}+n-\left\lfloor \dfrac{2m}{n}\right\rfloor -1+\exp \left( \sqrt{2m-n\left\lfloor \dfrac{2m}{n}\right\rfloor }\right) , \end{aligned}$$

(15.11)

with equality if and only if $G\cong K_{n}$ or $G\cong K_{n}-e$.

Finally, we present the estimation made in [100] for the Laplacian Estrada index of Erdős–Rényi random graphs.

Theorem 43

Let $G_{n,p}$ be an Erdős–Rényi random graph with n nodes and probability p. Then, the Laplacian Estrada index is given by

$$\begin{aligned} LEE\left( G_{n,p}\right) =e^{np}\left( \left( n-1\right) e^{o\left( 1\right) n}+o\left( 1\right) \right) ,a.s. \end{aligned}$$

(15.12)

In [132] the authors find estimations for the Laplacian Estrada index of random multipartite graphs.

Remark 11

Other bounds and estimations have been reported for the Laplacian Estrada index of specific graphs, or based on other graph parameters not considered here. Some non-exhaustive examples are: [20, 58, 60, 61, 117, 135, 145, 162, 207, 242, 243, 251].

Remark 12

The normalized Laplacian Estrada index defined as

$$\begin{aligned} NLEE\left( G\right) =\text {tr}\left( e^{K^{-1/2}LK^{-1/2}}\right) , \end{aligned}$$

(15.13)

where K is the diagonal matrix of node degree has been studied in [47, 123, 158, 203, 207].

Remark 13

The signless Laplacian Estrada index defined as

$$\begin{aligned} SLEE\left( G\right) =\text {tr}\left( e^{K+A}\right) , \end{aligned}$$

(15.14)

has been also studied in [16, 117, 227].

15.1 Numerical analysis

In Fig. 16 we illustrate the histograms of the relative deviations (in %) of the lower bounds (Proposition 2), (Proposition 4) (Proposition 5), (Proposition 6), (Theorem 40) and (Theorem 41) for all connected graphs with 8 nodes. The best performance is obtained from the bound (Proposition 6) followed by (Proposition 5).

Fig. 16

Relative deviations (in %) of the lower bounds (Proposition 2), (Proposition 4) (Proposition 5), (Proposition 6), (Theorem 40) and (Theorem 41) for all connected graphs with 8 nodes

We also analyzed the upper bounds given in Proposition 2, Proposition 3, Theorem 41 and Theorem 42 for the same set of graphs. In these cases the best performances were obtained for Theorem 41 and Theorem 42, while 2 give very high upper bounds (Fig. 17).

Fig. 17

Relative deviation (in logarithmic scale) of the upper bounds given in Propositiosns 2, 3, Theorems 41 and 42 for all connected graphs with 8 nodes

In Table 11 we give the lower bounds for the Laplacian Estrada index of five real-world networks. In general, the bounds (Proposition 5), (Proposition 6) and (Theorem 40) perform very well, while (Proposition 2), (Proposition 4) and (Proposition 41) are several orders of magnitude below the actual values of the Laplacian Estrada indices of these networks.

Table 11 Values of the lower bounds (Proposition 2), (Proposition 4) (Proposition 5), (Proposition 6), (Theorem 40) and (Theorem 41) for the five real-world networks analyzed and well their actual values of $LEE\left( G\right)$

The case of the upper bound is much more contrasting with values several orders of magnitude over the actual values of the Laplacian Estrada indices of these five networks. We have used variable-precision floating-point arithmetic” (VPA) to evaluate each element of the symbolic input in Matlab for these calculations. It is used to evaluate symbolic inputs with variable-precision floating-point arithmetic, calculating values to 32 significant digits.

The results are given in Table 12.

Table 12 Values of the upper bounds given in Propositions 2, 3, Theorem 41 and Theorem 42 for all connected graphs with 8 nodes for the five real-world networks analyzed and well their actual values of $LEE\left( G\right)$

The following bounds based on the largest Laplacian eigenvalue $\mu _{1}$ perform very well for the four real-world networks analyzed as can be seen in Table 13. The reason is that the largest eigenvalue of the Laplacian matrix dominates the spectrum of this matrix, i.e., it is very large and separated from the second largest eigenvalue.

Table 13 Values of lower and upper bounds based on $\mu _{1}$for $LEE\left( G\right)$ of the five real-world networks analyzed based on the spectral radius of the Laplacian matrix

16 Radius of gyration and distance Estrada index

When presenting the diffusion equation on graphs, Eq. (15.1), we mentioned in passing the diffusion coefficient ${\mathscr {D}}$, which appears in the equation and in its solution. The diffusion coefficient is related to the radius r of the spherical particle diffusing on a medium of viscosity $\eta$ by the Stokes-Einstein equation [66]:

$$\begin{aligned} {\mathscr {D}}=\dfrac{1}{6\tau \pi \eta r}, \end{aligned}$$

(16.1)

where $\tau$ is the inverse temperature. In the case of small molecules like drugs, or macromolecular systems like proteins, the particles cannot longer be considered spherical. In these cases it is customary to replace the radius of the spherical particle by the radius of gyration of the corresponding molecule [94, 107, 126, 152, 171]. The radius of gyration is defined as follows. Let ${\mathcal {S}}=\left( p_{1},\ldots ,p_{n}\right)$ be a system formed by n particles or points $p_{i}$, which are located in a given region of the three-dimensional Euclidean space. Let $r_{ij}$ be the Euclidean distance between the particles $p_{i}$ and $p_{j}$. Then, the radius of gyration of ${\mathcal {S}}$ is defined as $R_{{\mathcal {S}}}^{2}=\dfrac{1}{2n^{2}}\sum _{i,j}r_{ij}^{2}$ [94]. However, it has been shown that even when the radius of gyration based on Euclidean distances is used, there are cases of undesired degeneration of the index for pairs of clusters [74]. That is, there are pairs of nonisomorphic clusters which have the same radius of gyration. Some examples in 2- and in 3-dimensions are given in Fig. 18.

Fig. 18

Examples of Euclidean objects in 2- (a, b) and 3-dimensions (c, d), which have the same radius of gyration: (a, b) $R_{{\mathcal {S}}}^{2}=\tfrac{1}{4}$, (c, d) $R_{{\mathcal {S}}}^{2}=\tfrac{3}{16}$. Every edge has length equal to one in each of the objects

The radius of gyration is widely used in organic chemistry, polymer sciences, proteins, and RNA, in general, for the study of their compactness. Most of these molecular systems can be represented as graphs. For instance, molecules are typically represented by molecular graphs [217], proteins can be represented by “protein residue networks” [76, 212], and the secondary structure of RNA is also represented by graphs [147]. Then, it is important to extend the concept of “radius of gyration” to graphs.

Definition 22

Let G be a simple graph. Let $d_{ij}$ be the shortest path distance between the nodes i and j. The graph radius of gyration is defined as

$$\begin{aligned} R_{G}^{2}=\dfrac{1}{2n^{2}}\sum _{i,j}d_{ij}^{2}. \end{aligned}$$

(16.2)

Let D be the shortest path distance matrix of G. Then, it is straightforward to realize that

$$\begin{aligned} \text {tr}\left( D^{2}\right) =2\sum _{i,j}d_{ij}^{2}=4n^{2}R_{G}^{2}. \end{aligned}$$

(16.3)

Then, if $\sigma _{1}\ge \sigma _{2}\ge \cdots \ge \sigma _{n}$ are the eigenvalues of D, the graph radius of gyration is the second spectral moment of D, i.e.,

$$\begin{aligned} R_{G}^{2}=\dfrac{1}{4n^{2}}\sum _{j=1}^{n}\sigma _{j}^{2}. \end{aligned}$$

(16.4)

Therefore, we can say that the second moment of the shortest path distance matrix is a measure of the packing of the graph. In the case of the graph we can have a similar degeneracy of the index $R_{G}^{2}$ for nonisomorphic graphs. For instance in Fig. 19 we give an example of four nonisomorphic graphs with the same value of $R_{G}^{2}=\frac{9}{50}.$

Fig. 19

Example of four nonisomorphic graphs with the same value of $R_{G}^{2}$

In order to ameliorate this degeneracy problem we can think on extending the packing measure to higher moments of D as

$$\begin{aligned} P\left( G\right) =c_{2}\text {tr}\left( D^{2}\right) +c_{3}\text {tr}\left( D^{3}\right) +\cdots . \end{aligned}$$

(16.5)

Let us include the term $c_{0}\text {tr}\left( D^{0}\right) +c_{1}\text {tr}\left( D^{1}\right)$ (the first is the weighted number of vertices and the second is zero in simple graphs) and let us consider $c_{k}=\left( k!\right) ^{-1}$. Then, we get the following index, first defined in [108].

Definition 23

Let G be a simple graph. Let D be the shortest path distance matrix of G with eigenvalues $\sigma _{1}\ge \sigma _{2}\ge \cdots \ge \sigma _{n}$. Then the distance Estrada index of the graph is

$$\begin{aligned} DEE\left( G\right) =\text {tr}\left( \exp \left( D\right) \right) =\sum _{j=1}^{n}e^{\sigma _{j}}, \end{aligned}$$

(16.6)

which is an index of the packing of the graph.

For instance, for the graphs in Fig. 19 we obtain the following values: $DEE\left( a\right) \approx 318.467$, $DEE\left( b\right) \approx 300.616,$ $DEE\left( c\right) \approx 284.917$, and $DEE\left( d\right) \approx 281.697$. This means that among the graphs in Fig. 19, (d) is the most “packed” one in terms of its shortest path distance and the one in (a) is the least packed.

Several bound have been obtained for the distance Estrada index, some of which are resumed below.

Theorem 44

[108] Let G be a simple graph with n nodes and m edges. Then, if the diameter is $d_{max}$, the distance Estrada index is bounded as

$$\begin{aligned} \sqrt{n^{2}+4m}\le DEE\left( G\right) \le \left( n-1\right) \exp \left( d_{max}\sqrt{n\left( n-1\right) }\right) , \end{aligned}$$

(16.7)

where equalities are attained if and only if $G\cong K_{1}$.

Theorem 45

[202] Let G be a simple graph with n nodes and m edges. Then, if $d_{max}$, $\mathscr {{\mathcal {G}}}=\left( \prod _{i}D_{i}\right) ^{1/n}$ and $W=\sum _{ij}d_{ij}$ stand for the diameter, the geometric mean of the graph distances and the Wiener index of G, the distance Estrada index is bounded as

$$\begin{aligned} \left( \sqrt{\dfrac{4W^{2}-n{\mathcal {G}}^{2}}{n\left( n-1\right) }}\right) +\dfrac{n-1}{\exp \left( \dfrac{1}{n-1}\sqrt{\dfrac{4W^{2}-n{\mathcal {G}}^{2}}{n\left( n-1\right) }}\right) }\le DEE\left( G\right) \le \left( n-1\right) +e^{\sqrt{2d_{max}W}},\nonumber \\ \end{aligned}$$

(16.8)

where upper bound is attained if and only if $G\cong K_{1}$ and the lower one if and only if $G\cong K_{n}.$

Theorem 46

[204] Let G be a simple graph with n nodes with maximum and second maximum degress $k_{max}$ and $k_{max_{2}}$ and diameter $d_{max}$. Then, the distance Estrada index is bounded as

$$\begin{aligned} DEE\left( G\right)\ge & {} e^{\sqrt{\left( 2n-2-k_{max}\right) \left( 2n-2-k_{max_{2}}\right) }}+\left( n-1\right) e^{-\sqrt{\left( 2-\dfrac{k_{max}}{n-1}\right) \left( 2-\dfrac{k_{max_{2}}}{n-2}\right) }}, \end{aligned}$$

(16.9)

$$\begin{aligned} DEE\left( G\right)< & {} \left( n-1\right) +e^{\sqrt{n\left( n-1\right) d_{max}^{2}-1}}, \end{aligned}$$

(16.10)

where equality is attained if and only if $G\cong K_{2}$.

Theorem 47

[204] Let G be a simple graph with n nodes and m edges, the distance Estrada index is bounded as

$$\begin{aligned} DEE\left( G\right) \ge e^{2\left( n-1\right) -2m/n}+e^{-\left( 2\left( n-1\right) -2m/n\right) }+n-2 \end{aligned}$$

(16.11)

where equality is attained if and only if $G\cong K_{2}$.

16.1 Random graphs

The distance Estrada index has been studied for random graphs where some bounds have been reported in [205, 209].

Theorem 48

Let $G_{n,p}$ be an Erdős–Rényi random graph with n nodes and probability p. Then, the distance Estrada index is bounded as

$$\begin{aligned} \left( 1+o\left( 1\right) \right) +e^{2\left( n-1\right) -np-O\left( \sqrt{n}\right) }\le DEE\left( G_{n,p}\right) \le \left( 1+o\left( 1\right) \right) +e^{\left( n-1\right) \sqrt{4-3p}},\nonumber \\ \end{aligned}$$

(16.12)

almost surely (a.s).

Theorem 49

Let $G_{n_{1},n_{2},p}$ be an Erdős–Rényi random bipartite graph with $n=n_{1}+n_{2}$ nodes and probability p. If $n_{1}=\varTheta \left( n_{2}\right) ,$ then the distance Estrada index is bounded as

$$\begin{aligned} \left( 1+o\left( 1\right) \right) +e^{5n_{2}-2np-O\left( \sqrt{n}\right) }\le DEE\left( G_{n,p}\right) \le \left( 1+o\left( 1\right) \right) +e^{5n_{1}+2n_{1}p-O\left( \sqrt{n}\right) },\nonumber \\ \end{aligned}$$

(16.13)

asymptotically almost surely (a.a.s.) which, when $n_{1}=n_{2}$ becomes

$$\begin{aligned} \left( 1+o\left( 1\right) \right) +e^{n\left( 5/2-p\right) -O\left( \sqrt{n}\right) }\le DEE\left( G_{n,p}\right) \le \left( 1+o\left( 1\right) \right) +e^{n\left( 5/2+p\right) -O\left( \sqrt{n}\right) },a.a.s.\nonumber \\ \end{aligned}$$

(16.14)

16.2 Numerical analysis

We analyze here the lower bounds in Theorems 44, 45, 46 and 47. The relative deviations (in %) are illustrated in Fig. 20. As can be seen the closest values are obtained by the bound given in Theorem 45. The distributions of the relative deviations for Theorems 46 and 47 appears to show some dependencies with the structure of the graphs, which produce the multi-peak structures observed in the histograms.

Fig. 20

Relative deviations of the lower bounds in Theorems 44, 45, 46 and 47 for all connected graphs with 8 nodes

We also considered the upper bounds given in Theorems 44, 45 and 46 were we observe that these bounds are several order of magnitude over the actual values of $DEE\left( G\right)$ even for small graphs like the ones studied here (Fig. 21).

Fig. 21

Relative deviations (in logarithmic scale) of the upper bounds given in Theorems 44, 45 and 46 for all connected graphs with 8 nodes

In Table 14 we give the values of the lower and upper bounds as well as the actual values calculated with very precise arithmetic (vpa) in Matlab for the five real-world networks studied. As can be seen in the Table 14 the bound given in Theorem 45 gives the best lower and upper estimates of the distance Estrada index. It is also interesting to remark that the network of the western USA power grid displays an extremely large value of $DEE\left( G\right)$, indicating that it is a very poorly packed network. Indeed, this network is planar as the power stations are embedded in the landscape of the western USA

Table 14 Values of the lower and upper bounds for $DEE\left( G\right)$ in the five real-world networks analyzed in this paper

The results obtained for Erdős–Rényi random graphs $G_{n,p}$ with $1000\le n\le 4000$ and $p=0.5$ are illustrated in Table 15, showing good agreement between the actual values and those predicted by Theorem 48. The values were computed in [209] using variable-precision floating-point arithmetic (VPA) in Matlab.

Table 15 Actual values for Erdős–Rényi random graphs $G_{n,p}$ as well as the lower and upper bounds found in [209]

17 Conclusions

We presented an account of the many different facets of the Estrada indices of graphs. Starting from the “classical” Estrada index we give several interpretations of the index based on (i) combinatorics of subgraphs, (ii) statistical mechanics, (iii) marginal probability in a quantum system, (iv) oscillations models on networks, and (v) epidemiological models on networks. Then we move forward to the analysis of other kinds of Estrada indices. First we contextualize these indices originally introduced in an ad hoc way in the mathematical literature. For instance, the Seidel Estrada index is placed in the context of signed graphs, the theory of balance and the concept of network bipartivity. The resolvent Estrada index is analyzed as a case of Mittag–Leffler Estrada indices which appear in the context of fractional epidemiological models on graphs. The Harary Estrada index is understood as a particular case of nonlocal operator on graphs. The Laplacian Estrada index is now pondered on the basis of the diffusion equation with negative diffusivity or a backward diffusive process. Finally, the distance Estrada index is considered in the context of the radius of gyration of a graph, which can be connected to the diffusion coefficient of graphs via the Stokes-Einstein equation. In all cases we have provided numerical analysis of several of the bounds and estimations made for these indices. Such results have revealed the necessity of investigating more robust bounds, particularly upper bounds, for most of the indices studied. In many cases the bounds, although correct, are very far away from the actual values of the indices, which leaves large rooms for improvements. We encourage authors searching for new bounds to compare them with the existing ones with the challenge of improving them for general classes of graphs.

Finally, we have not considered many of the results obtained in the literature for specific classes of graphs, which would make this paper too long to be digested. We advice the reader that such bounds exist for several of the indices described in this paper and for several classes of graphs of importance in specific areas of applications.

Appendix

The following result allows the calculation of the 21 different subgraphs which are used in the expressions of spectral moments of the adjacency matrix.

Theorem 50

Let $k_{i}$ and $t_{i}$ be the degree and the number of triangles at the node i. Then, the number of subgraphs illustrated in Fig. 1 are obtained as follow:

$$\begin{aligned} F_{2}= & {} \frac{1}{2}\sum _{i}k_{i}, \end{aligned}$$

(17.1)

$$\begin{aligned} F_{3}= & {} \frac{1}{2}\sum _{i}k_{i}\left( k_{i}-1\right) , \end{aligned}$$

(17.2)

$$\begin{aligned} F_{4}= & {} \frac{1}{6}\text {tr} \left( A^{3}\right) , \end{aligned}$$

(17.3)

$$\begin{aligned} F_{5}= & {} \sum _{(i,j)\in E}\left( k_{i}-1\right) \left( k_{j}-1\right) -3F_{4}, \end{aligned}$$

(17.4)

$$\begin{aligned} F_{6}= & {} \frac{1}{6}\sum _{k_{i}\ge 3}k_{i}\left( k_{i}-1\right) \left( k_{i}-2\right) , \end{aligned}$$

(17.5)

$$\begin{aligned} F_{7}= & {} \frac{1}{8}\left( \text {tr} \left( A^{4}\right) -4F_{3}-2F_{2}\right) , \end{aligned}$$

(17.6)

$$\begin{aligned} F_{8}= & {} \sum _{k_{i}>2}t_{i}\left( k_{i}-2\right) , \end{aligned}$$

(17.7)

$$\begin{aligned} F_{9}= & {} \frac{1}{4}\sum _{i,j}\Big (\left( A^{2}\right) {}_{ij}A_{ij}\Big )\Big (\left( A^{2}\right) {}_{ij}\cdot A_{ij}-1\Big ), \end{aligned}$$

(17.8)

$$\begin{aligned} F_{10}= & {} \frac{1}{10}\left( \text {tr} \left( A^{5}\right) -30F_{4}-10F_{8}\right) , \end{aligned}$$

(17.9)

$$\begin{aligned} F_{11}= & {} \frac{1}{2}\sum _{k_{i}\ge 4}t_{i}\left( k_{i}-2\right) \left( k_{i}-3\right) , \end{aligned}$$

(17.10)

$$\begin{aligned} F_{12}= & {} \frac{1}{2}\sum _{k_{i}>2}\left( k_{i}-2\right) \times \sum _{i,j}{\left( A^{2}\right) {}_{ij} \atopwithdelims ()2}-2F_{9}, \end{aligned}$$

(17.11)

$$\begin{aligned} F_{13}= & {} \sum _{(i,j)\in E}\left( A^{2}\right) {}_{ij}\left( k_{i}-2\right) \left( k_{j}-2\right) -2F_{9}, \end{aligned}$$

(17.12)

$$\begin{aligned} F_{14}= & {} \sum _{i}t_{i}\left( \sum _{i\ne j}(A^{2})_{ij}\right) -6F_{4}-2F_{8}-4F_{9}, \end{aligned}$$

(17.13)

$$\begin{aligned} F_{15}= & {} \sum _{(i,j)\in E}\left( A^{3}\right) {}_{ij}\left( A^{2}\right) {}_{ij}-9F_{4}-2F_{8}-4F_{9}, \end{aligned}$$

(17.14)

$$\begin{aligned} F_{16}= & {} \frac{1}{12}\left( \text {tr} \left( A^{6}\right) -2m-12F_{3}-24F_{4}-6F_{5}-12F_{6}\right. \nonumber \\&\left. -48F_{7}-36F_{9}-12F_{12}-24F_{15}\right) , \end{aligned}$$

(17.15)

$$\begin{aligned} F_{17}= & {} \frac{1}{2}\sum _{k_{i}>2}\left( k_{i}-2\right) B_{i}-2F_{16}, \end{aligned}$$

(17.16)

where

$$\begin{aligned} B_{i}= & {} \left( A^{5}\right) {}_{ii}-20t_{i}-8t_{i}\left( k_{i}-2\right) -2\sum _{(i,j)\in E}\left( A^{2}\right) {}_{ij}\left( k_{j}-2\right) -2\sum _{(i,j)\in E}\left( t_{j}-\left( A^{2}\right) {}_{ij}\right) ,\nonumber \\ \end{aligned}$$

(17.17)

$$\begin{aligned} F_{18}= & {} \sum _{(i,j)\in E}{\left( A^{2}\right) {}_{ij} \atopwithdelims ()3}, \end{aligned}$$

(17.18)

$$\begin{aligned} F_{19}= & {} \sum _{i}t_{i}\cdot \sum _{i\ne j}{\left( A^{2}\right) {}_{ij} \atopwithdelims ()2}-6F_{9}-2F_{16}-6F_{19}, \end{aligned}$$

(17.19)

$$\begin{aligned} F_{20}= & {} \frac{1}{14}\left( \text {tr} \left( A^{7}\right) -126F_{4}-84F_{8}-112F_{9}-70F_{10}-28F_{11}-14F_{13}\right. \nonumber \\&\left. -14F_{14}-56F_{16}-14F_{18}-84F_{19}-28F_{20}\right) . \end{aligned}$$

(17.20)