A digitization method of subspaces of the Euclidean $n$D space associated with the Khalimsky adjacency structure

Abstract

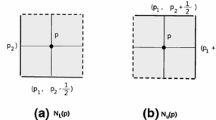
To digitize subspaces of the Euclidean $n$D space, the present paper uses the Khalimsky (for short $K$-, if there is no danger of ambiguity) topology, $K$-adjacency and $K$-localized neighborhoods of points in $\mathbf{Z}^n$, where $\mathbf{Z}^n$ represents the set of points in the Euclidean $n$D space with integer coordinates. Namely, given a point $p \in \mathbf{Z}^n$, the paper first develops a $K$-localized neighborhood of $p \in \mathbf{Z}^n$, denoted by $N_K(p)$ in $\mathbf{R}^n$, which is substantially used in digitizing subspaces of the Euclidean $n$D space. The recent paper Han and Sostak in (Comput Appl Math 32(3):521–536, 2013) proposes a connectedness preserving map (for short CP-map, e.g., an $A$-map in this paper) which need not be a continuous map under $K$-topology and further, develops a certain CP-isomorphism, e.g., an $A$-isomorphism in this paper. It turns out that an $A$-map overcomes some limitations of both a $K$-continuous map and a Khalimsky adjacency map (for brevity $KA$-map) so that both an $A$-map and an $A$-isomorphism can substantially contribute to applied topology including both digital topology and digital geometry Han and Sostak in (Comput Appl Math 32(3):521–536, 2013). Using both an $A$-map and a $K$-localized neighborhood, we further develop the notions of a lattice-based $A$-map (for short $LA$-map) and a lattice-based $A$-isomorphism (for brevity $LA$-isomorphism) which are used for digitizing subspaces of the Euclidean $n$D space in the $K$-topological approach. Thus, this approach can contribute to certain branches of applied topology and computer science such as image analysis, image processing, and mathematical morphology.