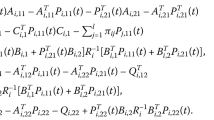Linear Quadratic Nash Differential Games of Stochastic Singular Systems with Markovian Jumps

Abstract

This paper investigates Nash games for stochastic singular systems with Markovian jumps. Based on the generalized Itô’s formula, the corresponding linear quadratic optimal control problem is studied for the first time. Then, we establish the existence of Nash strategies by means of generalized coupled Riccati algebraic equations. As an application, the stochastic H₂/H_∞ control with state, control, and external disturbance-dependent noise is discussed.

1 Introduction

Nash differential games have gained considerable attention due to their widespread applications in a variety of fields such as economics, ecology. A great deal of research has been devoted to it (see, for example, [3,4,5] and the references therein). Recent advances in stochastic linear quadratic (LQ) control problems have motivated us to expand the study on Nash games for stochastic (singular) systems with state- and control-dependent noise ([7, 8]).

On the other hand, the Markov jump parameter system model represents a convenient mathematical model to describe system dynamics in situation when the system experiences frequent unpredictable parameter variations. In view of Nash games for Markov jump stochastic differential systems, we refer readers to [6, 9,10,11] and the references therein. However, to the best of our knowledge, the work on Nash games for stochastic singular systems with Markovian jumps is yet to be initiated. Even for the particular case, i.e., the LQ optimal control problem for Markov jump stochastic singular systems, there is no relevant result.

Being directly inspired by the works mentioned above, the purpose of this paper is to study the Nash differential games for stochastic singular systems with Markovian jumps. The main contributions of this paper are as follows. We investigate the LQ problem of stochastic singular systems with Markovian jumps for the first time. Then the existence of Nash strategies can be established, which is characterized by a system of coupled generalized stochastic Riccati algebraic equations (GCSRAEs). Meanwhile, we discuss their solvability. What’s more, our results directly enrich the contents about mixed H₂/H_∞ control theory, which is one of the most important robust control methods, and we do not need to look for other approaches to solve this problem exclusively.

The rest of this paper is organized as follows. Preliminaries are in Section 2. Then in Section 3, the main results are given, which generalize the existing results. Section 4 is devoted to establish the solvability of the GCSRAEs. Section 5 discusses the stochastic H₂/H_∞ control with (x,u,v)-dependent noise by applying the obtained results.

2 Preliminaries

Throughout this paper, let (${\Omega }, \mathcal {F}, \{\mathcal {F}_{t}\}_{t\geq 0}, \mathcal {P}$) be a given filtered probability space where there exists a standard one-dimensional Wiener process {w(t)}_t≥ 0, and a right continuous homogeneous Markov chain {r_t}_t≥ 0 with state space ψ = {1,2,…,l}. We assume that {r_t} is independent of {w(t)} and has the transition probabilities given by

$$\text{Pr}\left\{r_{t+\triangle}=j|r_{t}=i\right\}=\left\{\begin{array}{lll} \pi_{ij}\triangle+o(\triangle),&& i\neq j, \\ 1+\pi_{ii}\triangle+o(\triangle),&& i=j, \end{array}\right. $$

where π_ij ≥ 0 for i≠j and $\pi _{ii}=-{\sum }_{j = 1, j\neq i}^{l}\pi _{ij}$. $\mathcal {F}_{t}$ stands for the smallest σ-algebra generated by process w(s),r_s,0 ≤ s ≤ t, i.e., $\mathcal {F}_{t}=\sigma \{w(s), r_{s} | 0\leq s\leq t\}$.

Consider the following linear stochastic singular system with Markovian jumps

$$ \left\{\begin{array}{lll} Edx(t)& =&\left[A(r_{t})x(t)+B_{1}(r_{t})u_{1}(t)+B_{2}(r_{t})u_{2}(t)\right]dt\\ & &+~\left[C(r_{t})x(t)+D_{1}(r_{t})u_{1}(t)+D_{2}(r_{t})u_{2}(t)\right]dw(t), \\ x(0)&=&x_{0}\in R^{n}, \end{array}\right. $$

(2.1)

where x(t) ∈ Rⁿ is the state variable, $u_{k}(t)\in R^{m_{k}}$ is control strategy taken by player P_k,k = 1,2. E is a known singular matrix with rank(E) = r ≤ n. Let U_k[0,∞),k = 1,2, be the admissible control set of the $R^{m_{k}}$-valued, $\mathcal {F}_{t}$-adapted, square integrable processes on [0,∞).

For each initial condition (0,x₀) and control (u₁,u₂) ∈ U[0,∞) ≡ U₁[0,∞) × U₂[0,∞), the associated cost is

$$ J_{k}(u_{1}, u_{2}; x_{0}, i)=\mathbb{E}\left\{{\int}_{0}^{\infty} \left( x^{T}(t) \ \ {u_{1}^{T}}(t) \ \ {u_{2}^{T}}(t)\right)M_{k}(r_{t})\left( \begin{array}{c} x(t) \\ u_{1}(t) \\ u_{2}(t) \end{array} \right)dt|r_{0}=i\right\}, $$

(2.2)

where

$$M_{k}(r_{t})=\left( \begin{array}{ccc} Q_{k}(r_{t}) & L_{k1}(r_{t}) & L_{k2}(r_{t}) \\ L_{k1}^{T}(r_{t}) & R_{k1}(r_{t}) & 0 \\ L_{k2}^{T}(r_{t}) & 0 & R_{k2}(r_{t}) \end{array}\right), \ \ k = 1, 2. $$

In (2.1) and (2.2), A(r_t) = A(i),M_k(r_t) = M_k(i), etc. whenever r_t = i, whereas the matrices mentioned above are given real matrices of suitable sizes, k = 1,2, i ∈ ψ. The value function V_k(x₀,i) is defined as

$$V_{k}(x_{0}, i)=\inf_{u_{k}\in U_{k}}J_{k}\left( u_{k}, u_{\tau}^{*}; x_{0}, i\right), \ \ k, \tau= 1, 2, \ \ k\neq \tau, \ \ i\in \psi, $$

Remark 2.1

Since the symmetric matrices M_k(i),k = 1,2, are allowed to be indefinite, the above problem is referred as indefinite stochastic Nash games.

Definition 2.1

The indefinite stochastic Nash games (2.1)–(2.2) are well-posed if

$$-\infty <V_{k}(x_{0}, i)< +\infty, \ \ \forall \ x_{0}\in R^{n}, \ \ k = 1,2, \ \ i\in \psi. $$

An admissible triple $\left (x^{*}, u_{1}^{*}, u_{2}^{*}\right )$ is called optimal with respect to the initial condition (0,x₀,i) if $u_{1}^{*}$ achieves the infimum of $J_{1}(u_{1}, u_{2}^{*}; 0, x_{0}, i)$ and $u_{2}^{*}$ achieves the infimum of $J_{2}\left (u_{1}^{*}, u_{2}; 0, x_{0}, i\right )$.

Definition 2.2

The stochastic Nash equilibrium strategy pair $(u_{1}^{*}, u_{2}^{*})\in U[0, \infty )$ is defined as satisfying the following conditions:

$$\left\{\begin{array}{l} J_{1}\left( u_{1}^{*}, u_{2}^{*}; x_{0}, i\right)\leq J_{1}\left( u_{1}, u_{2}^{*}; x_{0}, i\right), \\ J_{2}\left( u_{1}^{*}, u_{2}^{*}; x_{0}, i\right)\leq J_{2}\left( u_{1}^{*}, u_{2}; x_{0}, i\right), \end{array}\right. $$

where u_τ(t) is restricted to be composed of linear feedback strategies of the form u_τ(t) = K_τ(r_t)x(t),τ = 1,2 for all (x₀,i) ∈ Rⁿ × ψ, and K_τ are matrix-valued functions in this paper.

In order to guarantee the well-posedness of (2.1) with u₁ = u₂ = 0 (denoted as (2.1a)), we introduce the following lemmas and definitions, which are slight generation of previous ones.

Lemma 2.1

System (2.1a) has a unique solution if there exist nonsingular matricesM(i), N(i) ∈ R^n×n for the triple (E,A(i),C(i)) such that the following conditions are satisfied fori ∈ ψ:

$$\begin{array}{@{}rcl@{}} &&M(i)EN(i)=\left( \begin{array}{cc} I_{r} & 0 \\ 0 & 0 \end{array} \right),\quad M(i)A(i)N(i)=\left( \begin{array}{cc} A_{11}(i) & A_{12}(i) \\ 0 & A_{22}(i) \end{array}\right),\\ &&\qquad \qquad \qquad M(i)C(i)N(i)=\left( \begin{array}{cc} C_{11}(i) & 0 \\ 0 & I_{n-r} \end{array} \right), \end{array} $$

where A₁₁(i) ∈ R^n×n,A₁₂(i) ∈ R^r×(n−r),C₁₁(i) ∈ R^n×n,A₂₂(i) ∈ R^{(n−r)×(n−r)}.

Proof

Its proof can be proceed with the paper [7] similarly, so here we omit it. This completes the proof. □

Definition 2.3

The system (2.1a) is said to be

• (i) Regular and impulse-free if the pair (E,A(i)) is regular and impulse-free for each i ∈ ψ;

• (ii) Stochastically mean-square stable if for any x₀ ∈ Rⁿ and r₀ ∈ ψ, there exists a positive scalar Γ(x₀,r₀) such that $\lim _{t\rightarrow \infty }\mathbb {E}{{\int }_{0}^{t}}[||x(s, x_{0}, r_{0})||^{2}|(x_{0}, r_{0})]\leq {\Gamma }(x_{0}, r_{0})$;

• (iii) Stochastically admissible, if it is regular, impulse-free and stochastically mean-square stable.

Lemma 2.2

([1]) System (2.1a) is said to be stochastically admissible if there exists a nonsingular matrix G(i) such that the following conditions hold for eachi ∈ ψ:

$$\left\{\begin{array}{l} E^{T}G(i)=G^{T}(i)E\geq 0, \\ A^{T}(i)G(i)+G^{T}(i)A(i)+C^{T}(i)E^{T}G(i)C(i)+\sum\limits_{j = 1}^{l}\pi_{ij}E^{T}G(j)<0. \end{array}\right. $$

3 Main Results

Firstly, one-player case, i.e., LQ optimal control for stochastic singular system with Markovian jumps is discussed, which is the basis for the derivation of the results later.

The optimization problem can be stated as follows:

$$ V(x_{0}, i)=\min_{u_{1}\in U_{1}}\mathbb{E}\left\{{\int}_{0}^{\infty}\left( \begin{array}{c} x(t) \\ u_{1}(t) \end{array} \right)^{T}\left( \begin{array}{cc} Q_{1}(r_{t}) & L_{1}(r_{t}) \\ {L_{1}^{T}}(r_{t}) & R_{1}(r_{t}) \end{array} \right) \left( \begin{array}{c} x(t) \\ u_{1}(t) \end{array} \right)dt|r_{0}=i\right\}, $$

(3.1)

where x(t) follows from

$$ \left\{\begin{array}{l} Edx(t)=[A(r_{t})x(t)+B_{1}(r_{t})u_{1}(t)]dt+[C(r_{t})x(t)+D_{1}(r_{t})u_{1}(t)]dw(t), \\ x(0)=x_{0}. \end{array}\right. $$

(3.2)

Definition 3.1

The following system of constrained differential equations

$$ \left\{\begin{array}{l} E^{T}P(i)A(i)+A^{T}(i)P(i)E+C^{T}(i)P(i)C(i)+Q_{1}(i)+\sum\limits_{j = 1}^{l}\pi_{ij}E^{T}P(j)E\\ +~(E^{T}P(i)B_{1}(i)+C^{T}(i)P(i)D_{1}(i)+L_{1}(i))K(i)= 0, \\ K(i)=-(R_{1}(i)+{D_{1}^{T}}(i)P(i)D_{1}(i))^{-1}({B_{1}^{T}}(i)P(i)E+{D_{1}^{T}}(i)P(i)C(i)+{L_{1}^{T}}(i)), \\ R_{1}(i)+{D_{1}^{T}}(i)P(i)D_{1}(i)>0, \ \ i\in \psi \end{array}\right. $$

(3.3)

is called a system of coupled generalized stochastic Riccati algebraic equations (GCSRAEs).

Definition 3.2

The stochastic singular system with Markovian jumps is called stochastically mean-square stabilizable, if there exist feedback laws such that the closed-loop system is stochastically mean-square stable.

Theorem 3.1

Assuming that for any u₁(t), the closed-loop system is stochastically stabilizable. Suppose GCSRAEs (3.3) admit a solution $P_{1}=(P_{1}(1), P_{1}(2), \ldots , P_{1}(l))\in {S_{n}^{l}}$(components are all n × n symmetric matrices), then the LQ problem (3.1)–(3.2) is well-posed with respect to any initial valuex₀ ∈ Rⁿ, and there exists an optimal control in the form of state feedback

$$ u_{1}^{*}(t)=\sum\limits_{i = 1}^{l}K(i)x(t)\chi_{r_{t}=i}, \ \ i\in \psi. $$

(3.4)

Further, the optimal value is given by $V(x_{0}, i)={x_{0}^{T}}E^{T}P(i)Ex_{0}$.

Proof

Let $P_{1}\in {S_{n}^{l}}$ be a solution of the GCSRAEs (3.3). Setting φ(t,x,i) = x^TE^TP(i)Ex and applying the generalized Itô’s formula to (3.2), we have

$$ \mathbb{E}\left[x^{T}(T)E^{T}P(r_{T})Ex(T)-{x_{0}^{T}}E^{T}P(r_{0})Ex_{0}|r_{0} = i\right] = \mathbb{E}\left\{{{\int}_{0}^{T}}\nabla\varphi(t, x(t), r_{t})dt|r_{0}=i\right\}, $$

(3.5)

where $\nabla \varphi (t, x, i)=x^{T}\left [E^{T}P(i)A(i)+A^{T}(i)P(i)E+C^{T}(i)P(i)C(i)+{\sum }_{j = 1}^{l} \pi _{ij}\right .$$\left .E^{T}P(j)E \vphantom {{\sum }_{j = 1}^{l}}\right ]x + 2{u_{1}^{T}}\left [{B_{1}^{T}}(i)P(i)E+{D_{1}^{T}}(i)P(i)C(i)\right ]x+{u_{1}^{T}}{D_{1}^{T}}(i)P(i)D_{1}(i)u_{1}$.

Substituting (3.5) back into (3.1), we get

$$\begin{array}{@{}rcl@{}} J(u_{1}; x_{0}, i)&=&\mathbb{E}\left\{{{\int}_{0}^{T}}\nabla\varphi(t, x(t), r_{t})+x^{T}Q_{1}(r_{t})x + 2{u_{1}^{T}}{L_{1}^{T}}(r_{t})x\right.\\ &&\left.+~{u_{1}^{T}}R_{1}(r_{t})u_{1}dt|r_{0}=i\vphantom{{{\int}_{0}^{T}}}\right\}\\ &&+~{x_{0}^{T}}E^{T}P(r_{0})Ex_{0}-\mathbb{E}\left[x^{T}(T)E^{T}P(r_{T})Ex(T)|r_{0}=i\right]. \end{array} $$

(3.6)

From the definition of the GCSRAEs and the square completion technique, we have

$$\begin{array}{@{}rcl@{}} &&\nabla\varphi(t, x, i)+x^{T}Q_{1}(i)x + 2{u_{1}^{T}}{L_{1}^{T}}(i)+{u_{1}^{T}}R_{1}(i)u_{1}\\ &=&x^{T}\left[E^{T}P(i)A(i)+A^{T}(t)P(i)E+C^{T}(i)P(i)C(i)+Q_{1}(i)+\sum\limits_{j = 1}^{l}\pi_{ij}E^{T}P(j)E\right]x\\ &&+~2{u^{T}_{1}}\left[{B_{1}^{T}}(i)P(i)E+{D_{1}^{T}}(i)P(i)C(i)+{L_{1}^{T}}(i)\right]x\\ &&+~{u^{T}_{1}}\left[R_{1}(i)+{D_{1}^{T}}(i)P(i)D_{1}(i)\right]u_{1}\\ &=&\left[u_{1}-K(i)x\right]^{T}\left[R_{1}(i)+{D_{1}^{T}}(i)P(i)D_{1}(i)\right][u_{1}-K(i)x]. \end{array} $$

Then (3.6) can be expressed as

$$\begin{array}{@{}rcl@{}} J(u_{1}; x_{0}, i)&=&{x_{0}^{T}}E^{T}P(i)Ex_{0}-\mathbb{E}\left[x^{T}(T)E^{T}P(r_{T})Ex(T)|r_{0}=i\right]\\ &&+~\mathbb{E}\left\{{{\int}_{0}^{T}}[u_{1}-K(r_{t})x]^{T}\left[R_{1}(r_{t})+{D_{1}^{T}}(r_{t})P(r_{t})D_{1}(r_{t})\right]\right.\\ &&~~~~~\left.[u_{1}-K(r_{t})x]dt|r_{0}=i\vphantom{{{\int}_{0}^{T}}}\right\}. \end{array} $$

(3.7)

Letting T → +∞ and in view of the stochastically mean-square stabilizability, from (3.7) we can see that J(u₁;x₀,i) is minimized by the control given by (3.4) with the optimal value ${x_{0}^{T}}E^{T}P(i)Ex_{0}$. This completes the proof. □

The solution of the stochastic Nash games is given below.

Theorem 3.2

Assuming there exist u_k(t),k = 1,2, the closed-loop system is stochastically mean-square admissible. Suppose there exists a solution $P=(P_{1}, P_{2})\in {S_{n}^{l}}\times {S_{n}^{l}}$satisfying the following GCSRAEs for τ = 1,2 (i,j ∈ ψ)

$$\left\{\begin{array}{l} E^{T}P_{\tau}(i)A_{\tau}(i)+A^{T}_{\tau}(t)P_{\tau}(i)E+C^{T}_{\tau}(i)P_{\tau}(i)C_{\tau}(i)+\bar{Q}_{\tau}(i)+\sum\limits_{j = 1}^{l}\pi_{ij}E^{T}P_{\tau}(j)E\\ +\left( E^{T}P_{\tau}(i)B_{\tau}(i)+C_{\tau}^{T}(i)P_{\tau}(i)D_{\tau}(i)+L_{\tau\tau}(i)\right)K_{\tau}(i)= 0, \\ K_{\tau}(i)=-(R_{\tau\tau}(i)+D_{\tau}^{T}(i)P_{\tau}(i)D_{\tau}(i))^{-1}(B_{\tau}^{T}(i)P_{\tau}(i)E\\ +~D_{\tau}^{T}(i)P_{\tau}(i)C_{\tau}(i)+L_{\tau\tau}^{T}(i)), \\ R_{\tau\tau}(i)+D_{\tau}^{T}(i)P_{\tau}(i)D_{\tau}(i)>0, \ \ i\in \psi, \end{array}\right. $$

where

$$\begin{array}{@{}rcl@{}} A_{1}&=&A+B_{2}K_{2}, \quad C_{1}=C+D_{2}K_{2}, \quad \bar{Q}_{1}=Q_{1}+L_{12}K_{2}+{K_{2}^{T}}L_{12}^{T}+{K_{2}^{T}}R_{12}K_{2}, \\ A_{2}&=&A+B_{1}K_{1}, \quad C_{2}=C+D_{1}K_{1}, \quad \bar{Q}_{2}=Q_{2}+L_{21}K_{1}+{K_{1}^{T}}L_{21}^{T}+{K_{1}^{T}}R_{21}K_{1}. \end{array} $$

Denote $F_{1}^{*}(i)=K_{1}(i), F_{2}^{*}(i)=K_{2}(i)$, then the stochastic Nash equilibrium strategy $(u_{1}^{*}, u_{2}^{*})$ can be represented by

$$u_{1}^{*}(t)=\sum\limits_{i = 1}^{l}F_{1}^{*}(i)x(t)\chi_{r_{t}=i}, \ \ u_{2}^{*}(t)=\sum\limits_{i = 1}^{l}F_{2}^{*}(i)x(t)\chi_{r_{t}=i}. $$

Furthermore, the Nash games are well-posed with respect to (x₀,i), and the optimal value is determined by $V_{k}(x_{0}, i)={x_{0}^{T}}E^{T}P_{k}(i)Ex_{0}, \ \ k = 1,2, \ \ i\in \psi$.

Proof

These results can be proved by using the concept of Nash equilibrium described in Definition 2.2 as follows. Given that $u_{2}^{*}=F_{2}^{*}(r_{t})x(t)$ is the optimal control strategy implemented by player P₂, player P₁ facing the following optimization problem in which the following cost function is minimal at $u_{1}^{*}=F_{1}^{*}(r_{t})x(t)$.

$$\begin{array}{@{}rcl@{}} && \min_{F_{1}(r_{t})\in U_{1}}\mathbb{E}\left\{{\int}_{0}^{\infty}(x^{T}(t) \ \ {u^{T}_{1}}(t)) \left( \begin{array}{cc} \bar{Q}_{1}(r_{t}) & L_{11}(r_{t}) \\ L_{11}^{T}(r_{t}) & R_{11}(r_{t}) \end{array} \right)\left( \begin{array}{c} x(t) \\ u_{1}(t) \end{array}\right)dt|r_{0}=i\right\},\\ &&\left\{\begin{array}{l} Edx(t)=\left[\bar{A}(r_{t})x(t)+B_{1}(r_{t})u_{1}(t)\right]dt+\left[\bar{C}(r_{t})x(t)+D_{1}(r_{t})u_{1}(t)\right]dw(t), \\ x(0)=x_{0}\in R^{n}, \end{array}\right. \end{array} $$

(3.8)

here $\bar {Q}_{1}=Q_{1}+\left (F_{2}^{*}\right )^{T}L_{12}^{T}+L_{12}F_{2}^{*}+\left (F_{2}^{*}\right )^{T}R_{12}F_{2}^{*}, \bar {A}=A+B_{2}F_{2}^{*}, \bar {C}=C+D_{2}F_{2}^{*}$. Note that the above optimization problem defined in (3.8) is a standard indefinite stochastic LQ problem. Applying Theorem 3.1 to this optimization problem as

$$\left( \begin{array}{cc} \bar{Q}_{1} & L_{11} \\ L_{11}^{T} & R_{11} \end{array} \right)\Rightarrow\left( \begin{array}{cc} Q_{1} & L_{1} \\ L_{1} & R_{1} \end{array} \right), \ \ \bar{A}\Rightarrow A, \ \ \bar{C}\Rightarrow C, $$

we can easily get the optimal control $u_{1}^{*}(t)=F_{1}^{*}(r_{t})x(t)$, and the optimal value function $V_{1}(x_{0}, i)={x_{0}^{T}}E^{T}P_{1}(i)Ex_{0}, \ i\in \psi$.

Similarly, we can prove that $u_{2}^{*}=F_{2}^{*}(r_{t})x(t)$ is the optimal control strategy of player P₂. This completes the proof. □

Remark 3.1

A more general problem with multiple decision makers could also be considered in finite-time and infinite-time horizon, but for simplicity we analyze the problem stated above.

Remark 3.2

In particular, if the matrix E = I or there is no Markovian jump, the result in this section can be reduced to the ones before.

4 Solvability of GCSRAEs

In this section, we will give some conditions under which the GCSRAEs are solvable. With the limit of our knowledge, we only deal with the case in the following:

$$ \left\{\begin{array}{l} E^{T}P(i)A(i)+A^{T}(i)P(i)E+C^{T}(i)P(i)C(i)+Q_{1}(i)+\sum\limits_{j = 1}^{l}\pi_{ij}E^{T}P(j)E\\ +\left( E^{T}P(i)B_{1}(i)+L_{1}(i)\right)R_{1}^{-1}(i)\left( {B_{1}^{T}}(i)P(i)E+{L_{1}^{T}}(i)\right)= 0, \\ R_{1}(i)>0, i\in \psi. \end{array}\right. $$

(4.1)

First, we state some transformations which will be used later,

$$\begin{array}{@{}rcl@{}} M^{-T}(i)P(i)M(i)&=&\left( \begin{array}{cc} P_{11}(i) & P_{12}(i) \\ P_{12}^{T}(i) & P_{22}(i) \end{array}\right), \quad N^{T}(i)Q_{1}(i)N(i)=\left( \begin{array}{cc} Q_{11}(i) & Q_{12}(i) \\ Q_{12}^{T}(i) & Q_{22}(i) \end{array}\right),\\ M(i)B_{1}(i)&=&\left( \begin{array}{c} B_{11}(i) \\ B_{12}(i) \end{array}\right), \qquad\qquad \qquad N^{T}(i)L_{1}(i)=\left( \begin{array}{c} L_{11}(i) \\ L_{12}(i) \end{array} \right). \end{array} $$

Then we directly use the above transformations and Lemma 2.1 to (4.1), it can be partitioned into

$$\begin{array}{@{}rcl@{}} &&\left( \begin{array}{cc} I_{r} & 0 \\ 0 & 0 \end{array}\right)\left( \begin{array}{cc} P_{11}(i) & P_{12}(i) \\ P_{12}^{T}(i) & P_{22}(i) \end{array}\right)\left( \begin{array}{cc} A_{11}(i) & A_{12}(i) \\ 0 & A_{22}(i) \end{array}\right)+\left( \begin{array}{cc} Q_{11}(i) & Q_{12}(i) \\ Q_{12}^{T}(i) & Q_{22}(i) \end{array}\right)\\ &&+~\left( \begin{array}{cc} A_{11}^{T}(i) & 0 \\ A_{12}^{T}(i) & A_{22}^{T}(i) \end{array}\right)\left( \begin{array}{cc} P_{11}(i) & P_{12}(i) \\ P_{12}^{T}(i) & P_{22}(i) \end{array}\right)\left( \begin{array}{cc} I_{r} & 0 \\ 0 & 0 \end{array}\right)+\sum\limits_{j = 1}^{l}\pi_{ij}\left( \begin{array}{cc} P_{11}(i) & P_{12}(i) \\ P_{12}^{T}(i) & P_{22}(i) \end{array}\right)\\ &&+\left( \begin{array}{cc} C_{11}^{T}(i) & 0 \\ 0 & I_{n-r} \end{array}\right)\left( \begin{array}{cc} P_{11}(i) & P_{12}(i) \\ P_{12}^{T}(i) & P_{22}(i) \end{array}\right)\left( \begin{array}{cc} C_{11}(i) & 0 \\ 0 & I_{n-r} \end{array}\right)\\ &&-\left( \begin{array}{c} P_{11}(i)B_{11}(i)+P_{12}(i)B_{12}(i)+L_{11}(i) \\ L_{12}(i) \end{array}\right)R^{-1}(i)\\ &&\times\left( B_{11}^{T}(i)P_{11}(i)+B_{12}^{T}(i)P_{12}^{T}(i)+L_{11}^{T}(i) L_{12}^{T}(i)\right)= 0. \end{array} $$

Now we give an assumption as follows:$(\mathcal {H}.4.1)$B₁₂(i) = 0 and A₂₂(i) = 0 for every i ∈ ψ. Then, let us write the above matrix functions separately, we obtain the following equations:

$$ \left\{\begin{array}{l} P_{11}(i)A_{11}(i)+A_{11}^{T}(i)P_{11}(i)+C_{11}^{T}(i)P_{11}(i)C_{11}(i)+Q_{11}(i)+\sum\limits_{j = 1}^{l}\pi_{ij}P_{11}(i)\\ -\left( P_{11}(i)B_{11}(i)+L_{11}(i)\right)R^{-1}_{1}(i)\left( B_{11}^{T}(i)P_{11}(i)+L_{11}^{T}(i)\right)= 0\\ P_{11}(i)A_{12}(i)+P_{12}(i)A_{22}(i)+A_{12}^{T}(i)P_{11}(i)+A_{22}^{T}(i)P_{12}^{T}(i)\\ +C_{11}^{T}(i)P_{12}(i)+Q_{12}(i) -(P_{11}(i)B_{11}(i)+L_{11}(i))R^{-1}_{1}(i)L_{12}^{T}(i)= 0,\\ P_{22}(i)+Q_{22}(i)-L_{12}(i)R^{-1}_{1}(i)L^{T}_{12}(i)= 0. \end{array}\right. $$

(4.2)

Obviously, the third equation in (4.2) gives

$$P_{22}(i)=-Q_{22}(i)+L_{12}(i)R^{-1}_{1}(i)L^{T}_{12}(i), $$

and after some calculation, from the second equation we can also get that

$$\begin{array}{@{}rcl@{}} P_{12}(i) &=&-~C_{11}^{-T}(i)\left[P_{11}(i)A_{12}(i)+A_{12}^{T}(i)P_{11}(i)+Q_{12}(i)\right.\\ &&-~\left.(P_{11}(i)B_{11}(i)+L_{11}(i))R^{-1}_{1}(i)L_{12}^{T}(i)\right]. \end{array} $$

And then the only thing we have to do is that the solvability of the first equation in (4.2), so we can substitute it into the above equation to get the explicit expression of P₁₂(i). To do this, we give the following assumptions:$(\mathcal {H}.4.2)$$(B^{T}_{11}(i), D_{11}^{T}(i), A^{T}_{11}(i), C_{11}^{T}(i); Q)$ is detectable for every i ∈ ψ, where Q = (q_ij)_i,j∈ψ.$(\mathcal {H}.4.3)$ There exists $\hat {P}_{11}=(\hat {P}_{11}(1),\ldots ,\hat {P}_{11}(l))\in {S_{n}^{l}}$ satisfying $\tilde {\mathcal {N}}(\hat {P}_{11})>0$, where

$$\begin{array}{@{}rcl@{}} &&\qquad \qquad \qquad\qquad\qquad \tilde{\mathcal{N}}(P_{11})=(\tilde{\mathcal{N}}_{1}(P_{11}),\ldots,\tilde{\mathcal{N}}_{l}(P_{11})), \\ &&\tilde{N_{i}}\left( P_{11}\right)\\ &&=\left( \begin{array}{cc} \left( A_{11}^{T}P_{11}+P_{11}A_{11}+C_{11}^{T}P_{11}C_{11}+Q_{11}\right)(i)+\sum\limits_{j = 1}^{l}q_{ij}P_{11}(j) & \left( P_{11}B_{11}+L_{11}\right)(i) \\ \left( B_{11}^{T}P_{11}+L_{11}^{T}\right)(i) & R^{-1}_{1}(i) \end{array}\right). \end{array} $$

By means of [2, Theorem 5.7.1], we can easily know that the first equation in (4.2) has a stabilizing solution $\tilde {P}$. Thus, the solvability of the GCSRAEs (4.1) has been established.

5 Application

By means of the above developed theory, we solve some problems related to stochastic H₂/H_∞ control in this section.

Consider the following stochastic singular system with state- and control-dependent noise:

$$ \left\{ \begin{array}{lll} Edx(t)& =&[A(r_{t})x(t)+B_{2}(r_{t})u(t)+B_{1}(r_{t})v(t)]dt\\ & &+~[C(r_{t})x(t)+D_{2}(r_{t})u(t)+D_{1}(r_{t})v(t)]dw(t),\\ z(t)& =&\left( \begin{array}{c} F(r_{t})x(t) \\ u(t) \end{array} \right), \ \ x(0)=x_{0}\in R^{n}, \end{array}\right. $$

(5.1)

where x(t),u(t),v(t),z(t) are respectively the system state, control input, external disturbance and controlled output.

Define two associated performance functions

$$J_{1}(u, v; x_{0}, i)=\mathbb{E}\left\{{\int}_{0}^{\infty}\left[||z(t)||^{2}-\gamma^{2}||v(t)||^{2}\right]dt|r_{0}=i\right\}, $$

and

$$J_{2}(u, v; x_{0}, i)=\mathbb{E}\left\{{\int}_{0}^{\infty}||z(t)||^{2}dt|r_{0}=i\right\}, \ \ i\in \psi. $$

The stochastic H₂/H_∞ control of (5.1) can be stated as follows.

Definition 5.1

For given disturbance attenuation level γ > 0, if we can find v^∗(t) × u^∗(t) ∈ U[0,∞), such that(1) u^∗(t) makes (5.1) stochastically admissible.(2) $|L_{u^{*}}|_{\infty }< \gamma$ with

$$|L_{u^{*}}|_{\infty}=\sup_{v\in U_{1}[0, \infty), v\neq 0, u=u^{*}, x_{0}= 0}\frac{\left\{{\sum}_{i = 1}^{l}\mathbb{E}\left[{\int}_{0}^{\infty}z^{T}(t)z(t)dt|r_{0}=i\right]\right\}^{\frac{1}{2}}}{\left\{{\sum}_{i = 1}^{l}\mathbb{E}\left[{\int}_{0}^{\infty}v^{T}(t)v(t)dt|r_{0}=i\right]\right\}^{\frac{1}{2}}}. $$

(3) When the worst case disturbance v^∗(t) ∈ U₁[0,∞), if existing, is applied to (5.1), u^∗(t) minimizes the output energy J₂(u,v^∗;x₀,i).Then we say that the infinite-time horizon stochastic H₂/H_∞ control problem is solvable. Obviously, (u^∗,v^∗) is the Nash equilibrium strategies, such that

$$\left\{\begin{array}{l} J_{1}(u^{*}, v^{*}; x_{0}, i)\leq J_{1}(u^{*}, v; x_{0}, i), \\ J_{2}(u^{*}, v^{*}; x_{0}, i)\leq J_{2}(u, v^{*}, x_{0}, i), \ \ i\in \psi. \end{array}\right. $$

According to Theorem 3.2, the following results can be obtained straightly.

Theorem 5.1

Assuming there exist u_k(t),k = 1,2, the closed-loop system is stochastically admissible. Suppose there exists a solution $P=(P_{1}, P_{2})\in {S_{n}^{l}}\times {S_{n}^{l}}$satisfying the following GCSRAEs (i,j ∈ ψ):

$$\begin{array}{@{}rcl@{}} &&\left\{\begin{array}{l} E^{T}P_{1}(i)A_{1}(i)+{A_{1}^{T}}(t)P_{1}(i)E+{C_{1}^{T}}(i)P_{1}(i)C_{1}(i)+\bar{Q}(i)\\ +\sum\limits_{j = 1}^{l}\pi_{ij}E^{T}P_{1}(j)E+(E^{T}P_{1}(i)B_{1}(i)+{C_{1}^{T}}(i)P_{1}(i)D_{1}(i))K_{1}(i)= 0, \\ K_{1}(i)=-\left( -\gamma^{2}I+{D_{1}^{T}}(i)P_{1}(i)D_{1}(i)\right)^{-1}\left( {B_{1}^{T}}(i)P_{1}(i)E+{D_{1}^{T}}(i)P_{1}(i)C_{1}(i)\right), \\ -~\gamma^{2}I+{D_{1}^{T}}(i)P_{1}(i)D_{1}(i)>0, \ \ i\in \psi, \end{array}\right.\\ &&\left\{\begin{array}{l} E^{T}P_{2}(j)A_{2}(j)+{A_{2}^{T}}(j)P_{2}(j)E+{C_{2}^{T}}(j)P_{2}(j)C_{2}(j)\\ +~F^{T}(j)F(j)+\sum\limits_{k = 1}^{l}\pi_{jk}E^{T}P_{2}(k)E\\ +~\left( E^{T}P_{2}(j)B_{1}(j)+{C_{2}^{T}}(j)P_{2}(j)D_{1}(j)\right)K_{2}(j)= 0, \\ K_{2}(j)=-\left( I+{D_{2}^{T}}(j)P_{2}(j)D_{2}(j)\right)^{-1}\left( {B^{T}_{2}}(j)P_{2}(j)E+{D_{2}^{T}}(j)P_{2}(j)C_{2}(j)\right), \\ I+{D_{2}^{T}}(j)P_{2}(j)D_{2}(j)>0, \ \ j\in \psi, \end{array}\right. \end{array} $$

where $\bar {Q}=F^{T}F+{K_{2}^{T}}K_{2}$,and the others are defined as before.

Then the stochastic H₂/H_∞ control has a pair of solutions (u^∗,v^∗) with the feedback form

$$u^{*}(t)=K_{2}(r_{t})x(t), \ \ v^{*}(t)=K_{1}(r_{t})x(t). $$

In this case, u^∗(t) is a solution to the stochastic H₂/H_∞ control of (5.1), and v^∗(t) is the corresponding worst case disturbance.

6 Conclusion

In the present paper, we have dealt with the Nash games of stochastic singular systems with Markovian jumps in infinite-time horizon. The Nash strategies can be calculated by solving GCADEs. Further, the obtained results have been applied to stochastic H₂/H_∞ control for Markov jump singular systems with (x,u,v)-dependent noises. More specific practical applications, such as in the engineering and economics, need our future research.