Identification and Estimation of Generalized Additive Partial Linear Models with Nonignorable Missing Response

Abstract

The generalized additive partial linear models (GAPLM) have been widely used for flexible modeling of various types of response. In practice, missing data usually occurs in studies of economics, medicine, and public health. We address the problem of identifying and estimating GAPLM when the response variable is nonignorably missing. Three types of monotone missing data mechanism are assumed, including logistic model, probit model and complementary log-log model. In this situation, likelihood based on observed data may not be identifiable. In this article, we show that the parameters of interest are identifiable under very mild conditions, and then construct the estimators of the unknown parameters and unknown functions based on a likelihood-based approach by expanding the unknown functions as a linear combination of polynomial spline functions. We establish asymptotic normality for the estimators of the parametric components. Simulation studies demonstrate that the proposed inference procedure performs well in many settings. We apply the proposed method to the household income dataset from the Chinese Household Income Project Survey 2013.

Appendix

In this section the proof of Theorems 2.3–2.1 and corollary will be provided. We introduce some notation and regularity conditions for our results. The following conditions are needed for the results:

• (A) The functions defined in (2.1) satisfy the following assumptions

  • a(x) is a known one-to-one function;

  • $\lambda (x)$ is a known one-to-one, twice differential function;

  • b(x) is a known, strictly convex and twice differentiable function;

  • $g_k(z_k)$ has the first derivative $g'_k(z_k)$ and the second derivative $g''_k(z_k)\ne 0.$

• (B) When response variable Y is discrete and takes on at least three values, besides (A), we assume that

  • $a(x)\equiv C>0$ for any $x\in {\mathbb {R}}$;

  • b(x) is a strictly increasing function;

  • $c(y,\phi )\equiv c(y)$ for any $y,\phi \in {\mathbb {R}}$.

• (C) The distribution of each element of ${\textbf{Z}}$ is absolutely continuous and its density is bounded away from zero and infinity on [0, 1].

• (D) The second derivative function $g''_{k}(\cdot )$ is continuous and $g_{k}(\cdot ) \in \mathcal {H} (p), k=1,\ldots ,d_2$, where $p=v+k>2$ for some positive integer $\upsilon$ and $\kappa \in (0,1].$ Here, $\mathcal {H}(p)$ is the collection of functions g on [0, 1] whose $\upsilon$th derivative, $g^{(\upsilon )}$, exists and satisfies a Lipschitz condition of order $\kappa$, $|g^{(\upsilon )}(m^*)-g^{(\upsilon )}(m)|\le C|m^*-m|^{\kappa }$, for $0\le m^*, m \le 1$, where C is a positive constant.

• (E) The terms $q_{1,i}(\varvec{\beta },g,\phi ),q_{2,i}(\varvec{\beta },g,\phi ),\partial q_{1,i}(\varvec{\beta },g,\phi )/\partial \eta ,\partial q_{2,i}(\varvec{\beta },g,\phi )/\partial \eta ,\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },g)/\partial \eta$, ${\textbf{o}}_{i}(\alpha ,\varvec{\theta })$ and $\partial ^3l_{ni}(\varvec{\zeta },g)/\partial ^{s_1}\varvec{\zeta }\partial ^{s_2}\varvec{\gamma }$ with $s_1,s_2=1,2$ satisfying that $s_1+s_2=3,$ are bounded in probability. The eigenvalues of $E\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)/\partial \varvec{\zeta }$ are bounded away from zero and infinity in probability.

• (F) The number of knots $n^{1/(2p)}\ll N_n \ll n^{1/4}.$

• (G) The matrix $\Sigma (\varvec{\zeta }_0,g_0)$ is positive definite, and $A_n(\varvec{\zeta }_0,{\widetilde{g}})\rightarrow A(\varvec{\zeta }_0,g_0),$ $G_n(\varvec{\zeta }_0,{\widetilde{g}})\rightarrow G(\varvec{\zeta }_0,g_0)$ in probability, where

  $$\begin{aligned} A_n(\varvec{\zeta }_0,{\widetilde{g}})= n^{-1}\sum \limits _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\zeta }-G_n(\varvec{\zeta }_0,{\widetilde{g}}) n^{-1}\sum _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\zeta } \end{aligned}$$

  and

  $$\begin{aligned} G_n(\varvec{\zeta }_0,{\widetilde{g}})=n^{-1}\sum _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\gamma } \left\{ n^{-1}\sum _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\gamma }\right\} ^{-1}. \end{aligned}$$

Conditions (A)–(B) are essential for the identifiability of the observed likelihood which is defined in (2.4). Condition (A) is common for used generalized additive partial linear models. Condition (B) is mild enough to include most of commonly used generalized additive partial linear models regression models if Y is discrete, for example binomial/Poisson/negative binomial regression. Condition (C) requires a boundedness condition on the covariates, which is often assumed in asymptotic analysis of nonparametric regression problems. Condition (D) describes a requirement on the best rate of convergence that the functions $g'_{0k}(\cdot )s$ can be approximated by functions in the spline spaces. Condition (F) keeps the number of distinct knots increasing with n at an appropriate rate for asymptotic consistency. Conditions (E) and (G) imply that the eigenvalues of $\{E\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)/\partial \varvec{\zeta }\}$ and $\Sigma (\varvec{\zeta }_0,g_0)$ are bounded away from 0 and $\infty$.

Let

$$\begin{aligned} F_1({\textbf{x}})=\text{ expit }({\textbf{x}}),\quad F_2({\textbf{x}})=\Phi ({\textbf{x}}),\quad F_3({\textbf{x}})=1-\exp \{-\exp ({\textbf{x}})\}. \end{aligned}$$

(7.1)

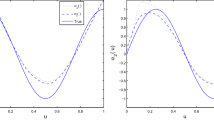
The functions $\log F_i(x), F'_i(x)/F_i(x)$ and $F'_i(x)/\{1-F_i(x)\}$ are graphed in Fig. 6. This graph illustrates that

$$\begin{aligned}&\log F_i({\textbf{x}})\le 0 \quad \text{ and } \text{ is } \text{ strictly } \text{ increasing } \text{ on } \,\,R,\nonumber \\&F'_i({\textbf{x}})/F_i({\textbf{x}})\ge 0 \quad \text{ and } \text{ is } \text{ strictly } \text{ decreasing } \text{ on }\,\, R,\nonumber \\&F'_i({\textbf{x}})/\{1-F_i({\textbf{x}})\}\ge 0 \quad \text{ and } \text{ is } \text{ strictly } \text{ increasing } \text{ on }\,\, R. \end{aligned}$$

(7.2)

Now, we proceed to the proof of Theorem 2.3, Corollary 2.6 and Theorem 2.1.

Proof of Theorem 2.3

Let us consider three cases: Y is binary, Y is discrete and take on at least three values, Y is continuous. A linear transformation of $g_{k}(z_k)$ gives that

$$\begin{aligned} \sum \limits _{k=1}^{d_2} g_{k}(z_k)=\sum \limits _{k=1}^{d_2} f_{k}(z_k)+h, \end{aligned}$$

where $f_{k}(\cdot )$ satisfies that $f_{k}(0)=0, 1\le k\le d_2.$ And the parameter vector $\varvec{\beta }$ can be rewritten as $(\beta _0+h,\beta _1,\ldots ,\beta _{d-1})^{\top }.$ Without loss of generality, throughout this proof, we assume that $g_{k}(0)=0, 1\le k\le d_2.$ We will prove that $\pi (y,{\textbf{x}},{\textbf{z}};\alpha ,\varvec{\theta })p(y|{\textbf{x}},{\textbf{z}};\varvec{\beta },g,\phi ) = \pi (y,{\textbf{x}},{\textbf{z}};\alpha ^*,\varvec{\theta }^*)p(y|{\textbf{x}},{\textbf{z}};\varvec{\beta }^*,g^*,\phi ^*)$ implies that

$$\begin{aligned} \alpha =\alpha ^*,\quad \varvec{\theta }=\varvec{\theta }^*, \quad \varvec{\beta }=\varvec{\beta }^*,\quad g=g^*, \quad \phi =\phi ^*, \end{aligned}$$

for two different sets of parameters $(\alpha ,\varvec{\theta },\varvec{\beta },g,\phi )$ and $(\alpha ^*,\varvec{\theta }^*,\varvec{\beta }^*,g^*,\phi ^*).$

For simplicity of notation, let covariates $\{X_1,X_2,\ldots ,X_{d_1-1}\}$ and $\{Z_2,Z_3,\ldots ,Z_{d_2}\}$ are omitted , since we can view $\{X_1,X_2,\ldots ,X_{d_1-1}\}$ and $\{Z_2,Z_3,\ldots ,Z_{d_2}\}$ as fixed while varying $Z_1$. Suppose $Z_1$ can take any real values. Because the proof for the case $\theta _1=0$ can be obtained by mimicking the following process, here we consider the case $\theta _1\ne 0$.

(i) When Y is a discrete variable.

(i.1). In the first case that Y is binary, we consider three commonly used types of missing mechanism probability which are defined in (7.1), $i=1,2,3,$

$$\begin{aligned} \pi (y,z_1;\alpha ,\theta _0,\theta _1)=F_i(\alpha y+\theta _0+\theta _1z_1). \end{aligned}$$

The probability of Y given $Z_1$ also takes three forms, $j=1,2,3,$

$$\begin{aligned} P(Y=1|Z_1=z_1;\beta ,g,\phi ) = F_j(\beta _0+g_1(z_1)) . \end{aligned}$$

Specially, denote $\log F_i(\cdot )$ by $h_i(\cdot )$ and then equality (2.5) reduces to

$$\begin{aligned}{} & {} h_i(\alpha y+\theta _0+\theta _1 z_1)+y\log F_j(\beta _0+g_1(z_1))+(1-y)\log \{1-F_j(\beta _0+g_1(z_1))\} \nonumber \\{} & {} \quad =h_i(\alpha ^* y+\theta _0^*+\theta _1^* z_1)+y\log F_j(\beta _0^*+g_1^*(z_1))\nonumber \\{} & {} \qquad +(1-y)\log \{1-F_j(\beta _0^*+g_1^*(z_1))\}. \end{aligned}$$

(7.3)

(i.1.1). Considering $\theta _1=\theta _1^*.$ When $y=0$, the condition in (7.3) reduces to

$$\begin{aligned}{} & {} h_i(\theta _0+\theta _1 z_1)-h_i(\theta _0^*+\theta _1 z_1) \nonumber \\{} & {} \quad =\log \{1-F_j(\beta _0^*+g_1(z_1))\}-\log \{1-F_j(\beta _0+g_1(z_1))\}, \end{aligned}$$

(7.4)

and $y=1$ results in

$$\begin{aligned}{} & {} h_i(\alpha +\theta _0+\theta _1 z_1)-h_i(\alpha ^* +\theta _0^*+\theta _1 z_1) \nonumber \\{} & {} \quad =\log F_j(\beta _0^*+g_1(z_1))-\log F_j(\beta _0+g_1(z_1)). \end{aligned}$$

(7.5)

If $\theta _0=\theta _0^*$, from (7.4) it follows that $\log \{1-F_j(\beta _0^*+g_1(z_1))\}=\log \{1-F_j(\beta _0+g_1(z_1))\}$, hence $\beta _0=\beta _0^*$ and then $\alpha =\alpha ^*$ according to (7.5). If $\beta _0=\beta _0^*$, it can similarly show that $\theta _0=\theta _0^*$ and $\alpha =\alpha ^*.$

Now we suppose that $\theta _0\ne \theta _0^*$ and $\beta _0\ne \beta _0^*.$ Without loss of generality, we assume that $\theta _0>\theta _0^*.$ From (7.2) and (7.4), we obtain that $\beta _0>\beta _0^*.$ Combining this and (7.5), we have that $\alpha +\theta _0<\alpha ^*+\theta _0^*.$ Taking the first derivative in both sides of (7.4) and (7.5) with respect to $z_1$ at zero yields

$$\begin{aligned} \left\{ \frac{F'_i(\theta _0)}{F_i(\theta _0)}-\frac{F'_i(\theta _0^*)}{F_i(\theta _0^*)} \right\} \theta _1= \left\{ \frac{F'_j(\beta _0)}{1-F_j(\beta _0)}-\frac{F'_j(\beta _0^*)}{1-F_j(\beta _0^*)} \right\} g'_1(0) \end{aligned}$$

(7.6)

and

$$\begin{aligned} \left\{ \frac{F'_i(\alpha +\theta _0)}{F_i(\alpha +\theta _0)} -\frac{F'_i(\alpha ^*+\theta _0^*)}{F_i(\alpha ^*+\theta _0^*)}\right\} \theta _1= \left\{ \frac{F'_j(\beta _0^*)}{F_j(\beta _0^*)} -\frac{F'_j(\beta _0)}{F_j(\beta _0)}\right\} {g^*_1}'(0). \end{aligned}$$

(7.7)

Note that $F'_i(x)/F_i(x)$ is decreasing and $F'_i(x)/\{1-F_i(x)\}$ is increasing. From $\theta _0>\theta _0^*$ and $\beta _0>\beta _0^*$, it follows that $F'_i(\theta _0)/F_i(\theta _0)<F'_i(\theta _0^*)/F_i(\theta _0^*)$ and $F'_j(\beta _0)/\{1-F_j(\beta _0)\}>F'_j(\beta _0^*)/\{1-F_j(\beta _0^*)\}.$ From equality (7.6), we have that $\theta _1$ and $g'_1(0)$ have different sign. Combining $\alpha +\theta _0<\alpha ^*+\theta _0^*$, $\beta _0>\beta _0^*$ and that $F'_i(x)/F_i(x)$ is decreasing, we have that $\theta _1$ and ${g^*_1}'(0)$ have the same sign in equality (7.7). This leads to a contradiction since the condition of (i) of Theorem 2.3 implies that $g'_1(0)$ and ${g^*_1}'(0)$ have the same sign.

This contradiction shows that either $\theta _0=\theta _0^*$ or $\beta _0=\beta _0^*$ holds. We finally conclude that $\theta _0=\theta _0^*, \beta _0=\beta _0^*$ and $\alpha =\alpha ^*,$ that is, the observed likelihood (2.4) is identifiable.

(i.1.2). Considering $\theta _1\ne \theta _1^*$. Assume the line $\theta _0+\theta _1z_1$ intersects with $\theta _0^*+\theta _1^*z_1$ at ${\widetilde{z}}_1$. On one hand, let $y=0, z_1={\widetilde{z}}_1$ in (7.3), we have

$$\begin{aligned} \log \{1-F_j(\beta _0+g_1({\widetilde{z}}_1))\} =\log \{1-F_j(\beta _0^*+g^*_1({\widetilde{z}}_1))\}, \end{aligned}$$

and hence $\beta _0+g_1({\widetilde{z}}_1))=\beta _0^*+g^*_1({\widetilde{z}}_1)$. This means that $\beta _0+g_1({\widetilde{z}}_1)$ has to intersect with $\beta _0^*+g^*_1({\widetilde{z}}_1)$ at the same ${\widetilde{z}}_1.$ On the other hand, combining this and letting $y=1, z_1={\widetilde{z}}_1$ in (7.3) yields

$$\begin{aligned} h_i(\alpha +\theta _0+\theta _1{\widetilde{z}}_1) =h_i(\alpha ^*+\theta _0^*+\theta _1^* {\widetilde{z}}_1), \end{aligned}$$

which means that $\alpha +\theta _0+\theta _1{\widetilde{z}}_1=\alpha ^*+\theta _0^*+\theta _1^* {\widetilde{z}}_1.$ Recall that $\theta _0+\theta _1{\widetilde{z}}_1=\theta _0^*+\theta _1^* {\widetilde{z}}_1,$ and hence $\alpha =\alpha ^*.$ Letting $y=0, z_1=0$ in (7.3), we have that

$$\begin{aligned} h_i(\theta _0)-h_i(\theta _0^*)=\log \{1-F_j(\beta _0^*)\}-\log \{1-F_j(\beta _0)\}, \end{aligned}$$

and $y=1, z_1=0$ leads to

$$\begin{aligned} h_i(\alpha +\theta _0)-h_i(\alpha +\theta _0^*)=\log F_j(\beta _0^*)-\log F_j(\beta _0). \end{aligned}$$

If $\beta _0>\beta _0^*$, the above first equality means $\theta _0>\theta _0^*$ while the above second equality means $\theta _0<\theta _0^*$. This is a contradiction. Similarly, $\beta _0<\beta _0^*$ also leads to a contradiction on the sign of $\theta _0-\theta _0^*$. Hence $\beta _0=\beta _0^*$ and $\theta _0=\theta _0^*$. Substitute $\alpha =\alpha ^*,\beta _0=\beta _0^*$ and $\theta _0=\theta _0^*$ into (7.3) and let $y=0,z_1=1$, we have

$$\begin{aligned} h_i(\theta _0+\theta _1)-h_i(\theta _0+\theta ^*_1)=\log \{1-F_j(\beta _0+f^*_1(1)\}-\log \{1-F_j(\beta _0+f_1(1))\}, \end{aligned}$$

and $y=1, z_1=1$ leads to

$$\begin{aligned} h_i(\alpha +\theta _0+\theta _1)-h_i(\alpha +\theta _0+\theta ^*_1)=\log F_j(\beta _0+f^*_1(1))-\log F_j(\beta _0+f_1(1)). \end{aligned}$$

Similar to the process of above proof, it can reduce to that $\theta _1=\theta _1^*$. Similar to (i.1.2), the results of identifiability can be achieved.

(i.2). In the second case that Y is discrete and take on at least three values, without loss of generality we assume Y takes values $\{0,1,2\}$. By condition (B), without loss of generality we take $a(\phi )=1$. Equality (2.5) reduces to

$$\begin{aligned}{} & {} h_i(\alpha y+\theta _0+\theta _1 z_1)+y\lambda (\beta _0+g_1(z_1))-b\{\lambda (\beta _0+g_1(z_1))\} \nonumber \\{} & {} \quad =h_i(\alpha ^* y+\theta _0^*+\theta _1^* z_1)+y\lambda (\beta _0^*+g_1^*(z_1))-b\{\lambda (\beta _0^*+g_1^*(z_1))\}. \end{aligned}$$

(7.8)

By subtracting (7.8) with $y=0$ from (7.8) with $y=1$, we have

$$\begin{aligned}{} & {} h_i(\alpha +\theta _0+\theta _1 z_1)-h_i(\theta _0+\theta _1z_1)+\lambda (\beta _0+g_1(z_1)) \nonumber \\{} & {} \quad =h_i(\alpha ^* +\theta _0^*+\theta _1^* z_1)-h_i(\theta _0^*+\theta _1^* z_1)+\lambda (\beta _0^*+g_1^*(z_1)). \end{aligned}$$

(7.9)

Subtracting (7.9) from the equality which is obtained by subtracting (7.8) with $y=1$ from (7.8) with $y=2$, we can get

$$\begin{aligned}{} & {} h_i(2\alpha +\theta _0+\theta _1 z_1)+h_i(\theta _0+\theta _1 z_1)-2h_i(\alpha +\theta _0+\theta _1 z_1)\nonumber \\{} & {} \quad =h_i(2\alpha ^* +\theta _0^*+\theta _1^* z_1)+h_i(\theta _0^*+\theta _1^* z_1)-2h_i(\alpha ^*+\theta _0^*+\theta _1^* z_1). \end{aligned}$$

(7.10)

(i.2.1). Considering $\theta _1=\theta _1^*$. Let $H(s)=h_i(s+c)+h_i(s-c)-2h_i(s)$ for some constant $c\in {\mathbb {R}}$. When $h_i(x)=\log \text{ expit }(x)$ or $h_i(x)=\log (1-\exp (-\exp (x)))$, H(s) has one unique minimum value. In the case that $h_i(x)=\log \Phi (x)$, $H'(s)$ has one unique maximum value. Let $H_l(s_l)=h_i(s_l+\alpha )+h_i(s_l-\alpha )-2h_i(s_l)$ with $s_l=\alpha +\theta _0+\theta _1 z_1$ and $H_r(s_r)=h_i(s_r+\alpha ^*)+h_i(s_r-\alpha ^*)-2h_i(s_r)$ with $s_r=\alpha ^*+\theta _0^*+\theta _1 z_1.$ Then, we have $H_l(s_l)=H_r(s_r)$ and $H'_l(s_l)=H'_r(s_r).$ When $h_i(x)=\log \text{ expit }(x)$ or $h_i(x)=\log (1-\exp (-\exp (x))),$ there is a point ${\widetilde{s}}$ so that $H_l(\cdot )$ and $H_r(\cdot )$ attain the minimum, that is, $H_l({\widetilde{s}})=H_r({\widetilde{s}}).$ Then,

$$\begin{aligned} h_i({\widetilde{s}}+\alpha )+h_i({\widetilde{s}}-\alpha )=h_i({\widetilde{s}}+\alpha ^*) +h_i({\widetilde{s}}-\alpha ^*), \end{aligned}$$

which leads to that $|\alpha |=|\alpha ^*|$ in terms of that $h_i$ is an increasing function. When $h_i(x)=\log \Phi (x),$ $H'_l(\cdot )$ and $H'_r(\cdot )$ can attain the maximum at $\widetilde{{\widetilde{s}}}.$ Then,

$$\begin{aligned} h'_i(\widetilde{{\widetilde{s}}}+\alpha )+h'_i(\widetilde{{\widetilde{s}}}-\alpha )=h'_i (\widetilde{{\widetilde{s}}}+\alpha ^*)+h'_i(\widetilde{{\widetilde{s}}}-\alpha ^*). \end{aligned}$$

Since $h'(\cdot )$ is a monotone function, we have that $|\alpha |=|\alpha ^*|.$ If $\alpha =\alpha ^*,$ note that there is a point ${\widetilde{z}}_1$ so that $\alpha +\theta _0+\theta _1 {\widetilde{z}}_1=\alpha ^*+\theta _0^*+\theta _1 {\widetilde{z}}_1={\widetilde{s}} \,\,(\text{ or }\,\,\widetilde{{\widetilde{s}}}),$ then $\theta _0=\theta _0^*.$ If $\alpha =-\alpha ^*,$ $\alpha +\theta _0+\theta _1 {\widetilde{z}}_1=\alpha ^*+\theta _0^*+\theta _1 {\widetilde{z}}_1$ implies that $\alpha ^*+\theta _0^*=\alpha +\theta _0.$ Then, (7.8) for $y=1$ leads to

$$\begin{aligned} b\{\lambda (\beta ^*_0+g^*_1(z_1))\}-b\{\lambda (\beta _0+g_1(z_1))\}= \lambda (\beta ^*_0+g^*_1(z_1))-\lambda (\beta _0+g_1(z_1)). \end{aligned}$$

Applying the mean value theorem to left side for $z_1=z_1^1,z_1^2$ yields

$$\begin{aligned} b'(\xi _k)\{\lambda (\beta ^*_0+g^*_1(z_1^k))-\lambda (\beta _0+g_1(z_1^k))\}= \lambda (\beta ^*_0+g^*_1(z_1^k))-\lambda (\beta _0+g_1(z_1^k)), \end{aligned}$$

where $\xi _k$ is one point between $\lambda (\beta ^*_0+g^*_1(z_1^k))$ and $\lambda (\beta _0+g_1(z_1^k))$, and $b'(\xi _k)=1$. It contradicts with Condition (A) in which b(x) is a strictly convex, hence $b'(x)$ is a strictly increasing function. Therefore, $\alpha =\alpha ^*$ and $\theta _0=\theta _0^*.$

Substituting $\alpha =\alpha ^*, \theta _0=\theta _0^*$ and $\theta _1=\theta _1^*$ into (7.9), we have

$$\begin{aligned} \lambda (\beta ^*_0+g^*_1(z_1))=\lambda (\beta _0+g_1(z_1)). \end{aligned}$$

Recall that $g^*_1(0)=g_1(0)=0,$ so we have $\beta ^*_0=\beta _0$ by condition (b) that $\lambda (\cdot )$ is a one-to-one function. Then, $g^*_1(z_1)=g_1(z_1).$

(i.2.2). $\theta _1\ne \theta _1^*$. Assume that $\theta _0+\theta _1z_1$ intersects with $\theta _0^*+\theta _1^*z_1$ at ${\widetilde{z}}_1$, then

$$\begin{aligned} h_i(2\alpha +\theta _0+\theta _1 {\widetilde{z}}_1)+h_i(\theta _0+\theta _1 {\widetilde{z}}_1) =h_i(2\alpha ^* +\theta _0^*+\theta _1^* {\widetilde{z}}_1)+h_i(\theta _0^*+\theta _1^* {\widetilde{z}}_1). \end{aligned}$$

Note that $h_i(\cdot )$ is an increasing function, we can get that $\alpha =\alpha ^*.$ Taking first derivative of both sides of (7.10) with respect to $z_1$ at ${\widetilde{z}}_1$, we can get that

$$\begin{aligned} \theta _1=\theta _1^*. \end{aligned}$$

It is a contradiction. Therefore, this case reduces to $\theta _1=\theta _1^*$. $\square$

(ii). When Y is a continuous variable and $h(x)=\log {\textbf{expit}}(x).$

Equality (2.5) reduces to

$$\begin{aligned}&h_i(\alpha y+\theta _0+\theta _1 z_1)+\frac{y\lambda (\beta _0+g_1(z_1))-b\{\lambda (\beta _0+g_1(z_1))\}}{a(\phi )}+c(y;\phi )\nonumber \\&\quad =h_i(\alpha ^* y+\theta _0^*+\theta _1^* z_1)+\frac{y\lambda (\beta _0^*+{g^*_1}(z_1))-b\{\lambda (\beta _0^*+{g^*_1}(z_1))\}}{a(\phi ^*)}+c(y;\phi ^*). \end{aligned}$$

(7.11)

Applying operation $\partial /\partial z_1$, $\partial ^2/\partial z_1\partial y$ and $\partial ^3/\partial z_1\partial y^2$ on both sides of (7.11) yields

$$\begin{aligned}{} & {} h'_i(\alpha y+\theta _0+\theta _1 z_1)\theta _1+\frac{y\lambda '(\beta _0+g_1(z_1))-b'\{\lambda (\beta _0+g_1(z_1))\} \lambda '(\beta _0+g_1(z_1))}{a(\phi )}g'_1(z_1) \\{} & {} \quad =h'_i(\alpha ^* y+\theta _0^*+\theta _1^* z_1)\theta _1^*\\{} & {} \qquad +\frac{y\lambda '(\beta _0^*+{g^*_1}(z_1)) -b'\{\lambda (\beta _0^*+{g^*_1}(z_1))\}\lambda '(\beta _0^*+{g^*_1}(z_1))}{a(\phi ^*)}{g^*_1}'(z_1), \\{} & {} h^{(2)}_i(\alpha y+\theta _0+\theta _1 z_1)\theta _1\alpha +\frac{\lambda '(\beta _0+g_1(z_1))}{a(\phi )}g'_1(z_1)\\{} & {} \quad =h^{(2)}_i(\alpha ^* y+\theta _0^*+\theta _1^* z_1)\theta _1^*\alpha ^*+\frac{\lambda '(\beta _0^*+{g^*_1}(z_1))}{a(\phi ^*)}{g^*_1}'(z_1) \end{aligned}$$

and

$$\begin{aligned} h^{(3)}_i(\alpha y+\theta _0+\theta _1 z_1)\theta _1\alpha ^2 =h^{(3)}_i(\alpha ^* y+\theta _0^*+\theta _1^* z_1)\theta _1^*\alpha ^{*2}, \end{aligned}$$

(7.12)

respectively.

If $\theta _1^*=0$ or $\alpha ^*=0$, (7.12) reduces to $h^{(3)}_i(\alpha y+\theta _0+\theta _1 z_1)\theta _1\alpha ^2=0$ and hence $\theta _1\alpha ^2=0$, which contradicts the assumption $\theta _1\ne 0$ and $\alpha \ne 0.$ So we consider the case $\theta _1^*\ne 0$ and $\alpha ^*\ne 0.$

When $i=1$, that is $h_1(x)=\log \text{ expit }(x).$ In this case, the roots of derivatives of $h_1(x)$ are as follows,

$$\begin{aligned} \left\{ \begin{array}{ll} h'_1(x), &{}\quad \text{ has } \text{ no } \text{ roots, }\\ h''_1(x), &{}\quad \text{ has } \text{ no } \text{ roots, }\\ h_1^{(3)}(x), &{}\quad \text{ has } \text{ one } \text{ root }\,\,0,\\ h_1^{(4)}(x), &{}\quad \text{ has } \text{ two } \text{ roots }\,\, \log (2+\sqrt{3}), \log (2-\sqrt{3}) ,\\ h_1^{(5)}(x), &{}\quad \text{ has } \text{ three } \text{ roots }\,\, 0,\log (5+2\sqrt{6}),\log (5-2\sqrt{6}). \end{array} \right. \end{aligned}$$

(ii.1). If $\theta _1\alpha ^*\ne \theta _1^*\alpha$, we show that this assumption leads to a contradiction. Assume that the line $\alpha y + \theta _0 +\theta _1z_1$ intersects with $\alpha ^* y + \theta _0^* +\theta _1^*z_1$ at $({\dot{z}}_1,{\dot{y}})$, and $\alpha {\dot{y}} + \theta _0 +\theta _1{\dot{z}}_1=\alpha ^* {\dot{y}} + \theta _0^* +\theta _1^*{\dot{z}}_1=x$. If $x=0,$ by applying operation $\partial /\partial y$ and $\partial /\partial z_1$ in both sides of (7.12) at $({\dot{x}}_1,{\dot{y}})$, we can obtain $\theta _1\alpha ^3=\theta _1^*\alpha ^{*3}$ and $\theta _1^2\alpha ^2=\theta _1^{*2}\alpha ^{*2}$, then $\theta _1\alpha ^*=\theta _1^*\alpha$, it is a contradiction. If x is equal to $\log (2+\sqrt{3})$ or $\log (2-\sqrt{3})$, by (7.12) and by applying operation $\partial ^2/\partial z_1\partial y$ in both sides of (7.12) at $({\dot{z}}_1,{\dot{y}})$, we can get that $\theta _1\alpha ^2=\theta _1^*\alpha ^{*2}$ and $\theta _1^2\alpha ^3=\theta _1^{*2}\alpha ^{*3}$, then $\theta _1\alpha ^*=\theta _1^*\alpha$, it is also a contradiction. If $x\ne a, a\in \{0,\log (2+\sqrt{3}), \log (2-\sqrt{3})\},$ by (7.12) and by applying operation $\partial /\partial y$ in both sides of (7.12) at $({\dot{z}}_1,{\dot{y}})$, we can get that $\theta _1\alpha ^2=\theta _1^*\alpha ^{*2}$, $\theta _1\alpha ^3=\theta _1^{*}\alpha ^{*3}$, which implies that $\{\theta _1=\theta _1^*, \alpha =\alpha ^*\}$, then $\theta _1\alpha ^*=\theta _1^*\alpha$, it is also a contradiction. Therefore, $\theta _1\alpha ^*=\theta _1^*\alpha .$

(ii.2). Now we will complete the remainder part under $\theta _1\alpha ^*=\theta _1^*\alpha$. Denote by $\theta _1/\theta _1^*=\alpha /\alpha ^*=k,$ (7.12) reduces to

$$\begin{aligned} h^{(3)}_1(k t+\theta _0)k^3 =h^{(3)}_1(t+\theta _0^*), \end{aligned}$$

(7.13)

with $t=\alpha ^*y+\theta _1^*z_1.$ If $k\ne 1,$ assume that the line $k t+\theta _0$ intersects with $t+\theta _0^*$ at ${\dot{t}}$, and $k {\dot{t}}+\theta _0={\dot{t}}+\theta _0^*=x$. If $x\ne 0,$ let $t={\dot{t}}$ in (7.13), we can get that $k=1$, it is a contradiction. If $x=0,$ by applying operation $\partial /\partial t$ in both sides of (7.13) at ${\dot{t}}$, we can obtain $k^4=1$, that is $k=1$ or $k=-1$. If $k=-1,$ then $\alpha =-\alpha ^*, \theta _1=-\theta _1^*$ and $-{\dot{t}}+\theta _0={\dot{t}}+\theta _0^*=0$ means that $\theta _0=-\theta _0^*,$ that is $(\alpha ^*,\theta _0^*,\theta _1^*)=-(\alpha ,\theta _0,\theta _1).$ Recall that when $h(x)=\text{ expit }(x)$, the condition that the sign of any element of $(\alpha ,\theta _0,\theta _1)$ is assumed to be known. So the case that $x=0$ and $k=-1$ is impossible. Therefore, we have $k=1,$ then (7.13) reduces to

$$\begin{aligned} h^{(3)}_1(t+\theta _0)=h^{(3)}_1(t+\theta _0^*), \end{aligned}$$

which implies that $\theta _0=\theta _0^*$ because $h_1^{(3)}(\cdot )$ has only one maximum point. Now we have $(\alpha ^*,\theta _0^*,\theta _1^*)=(\alpha ,\theta _0,\theta _1).$

(ii.3). If $(\alpha ^*,\theta _0^*,\theta _1^*)=(\alpha ,\theta _0,\theta _1),$ (7.11) implies that

$$\begin{aligned}{} & {} \frac{y\lambda (\beta _0+g_1(z_1))-b\{\lambda (\beta _0+g_1(z_1))\}}{a(\phi )}+c(y;\phi )\\{} & {} \quad =\frac{y\lambda (\beta _0^*+{g^*_1}(z_1))-b\{\lambda (\beta _0^*+{g^*_1}(z_1))\}}{a(\phi ^*)}+c(y;\phi ^*). \end{aligned}$$

By applying operation $\partial /\partial z_1$ and $\partial ^2/\partial z_1\partial y$ in both sides, we have

$$\begin{aligned}{} & {} \frac{y\lambda '(\beta _0+g_1(z_1))-b'\{\lambda (\beta _0+g_1(z_1))\}\lambda '(\beta _0+g_1(z_1))}{a(\phi )}g'_1(z_1)\\{} & {} \quad =\frac{y\lambda '(\beta _0^*+g^*_1(z_1))-b'\{\lambda (\beta _0^*+g^*_1(z_1))\}\lambda '(\beta _0^*+g^*_1(z_1))}{a(\phi ^*)}{g^*_1}'(z_1) \end{aligned}$$

and

$$\begin{aligned} \frac{\lambda '(\beta _0+g_1(z_1))}{a(\phi )}g'_1(z_1) = \frac{\lambda '(\beta _0^*+g^*_1(z_1))}{a(\phi ^*)}{g^*_1}'(z_1). \end{aligned}$$

(7.14)

Combining these two identities, we have for any $z_1,$

$$\begin{aligned} b'\{\lambda (\beta _0+g_1(z_1))\}=b'\{\lambda (\beta _0^*+g^*_1(z_1))\}. \end{aligned}$$

Because $b'(\cdot )$ is strictly monotone and $\lambda (\cdot )$ is a one-to-one function, we must have $\beta _0=\beta _0^*$ and $g_1(z_1)=g_1^*(z_1)$. Substituting this into (7.14), we have $a(\phi )=a(\phi ^*)$ and then by Condition (A), $\phi =\phi ^*.$ $\square$

(iii). When Y is a continuous random variable and $h_i(x)=\log \Phi (x)$ or $\log [1-\exp \{-\exp (x)\}].$

(iii.1). When $h_i(x)=\log \Phi (x),$ the third derivative of $h_i(x)$ has no root, the fourth derivative has one root $x_0$ and the fifth derivative has roots different from $x_0$. If $\theta _1\alpha ^*\ne \theta _1^*\alpha$, we can show that this assumption leads to a contradiction. Assume that the line $\alpha y + \theta _0 +\theta _1z_1$ intersects with $\alpha ^* y + \theta _0^* +\theta _1^*z_1$ at $({\dot{z}}_1,{\dot{y}})$, and $\alpha {\dot{y}} + \theta _0 +\theta _1{\dot{z}}_1=\alpha ^* {\dot{y}} + \theta _0^* +\theta _1^*{\dot{z}}_1=x$. If $x\ne x_0,$ by (7.12) and its partial derivative with respect to y at $({\dot{z}}_1,{\dot{y}})$, we can obtain $\theta _1\alpha ^2=\theta _1^*\alpha ^{*2}$ and $\theta _1\alpha ^3=\theta _1^{*}\alpha ^{*3}$, then $\theta _1\alpha ^*=\theta _1^*\alpha$, it is a contradiction. If $x= x_0,$ by (7.12) and its second-order partial derivative with respect to $z_1,y$ at $({\dot{z}}_1,{\dot{y}})$, we can obtain $\theta _1\alpha ^2=\theta _1^*\alpha ^{*2}$ and $\theta _1^2\alpha ^3=\theta _1^{*2}\alpha ^{*3}$, then $\theta _1\alpha ^*=\theta _1^*\alpha$, it is a contradiction.

If $\theta _1\alpha ^*=\theta _1^*\alpha$, denote by $\theta _1/\theta _1^*=\alpha /\alpha ^*=k,$ (7.12) reduces to

$$\begin{aligned} h^{(3)}_2(k t+\theta _0)k^3 =h^{(3)}_2(t+\theta _0^*), \end{aligned}$$

(7.15)

with $t=\alpha ^*y+\theta _1^*z_1.$ If $k\ne 1,$ assume that the line $k t+\theta _0$ intersects with $t+\theta _0^*$ at ${\dot{t}}$. Let $t={\dot{t}}$ in above identity, we can get that $k=1$, it is a contradiction. Therefore, we have $k=1,$ then (7.15) reduces to

$$\begin{aligned} h^{(3)}_2(t+\theta _0)=h^{(3)}_2(t+\theta _0^*), \end{aligned}$$

which implies that $\theta _0=\theta _0^*$ because $h^{(3)}_2(\cdot )$ has only one maximum. Now we have $(\alpha ^*,\theta _0^*,\theta _1^*)=(\alpha ,\theta _0,\theta _1).$

The proof of $(\beta _0^*,g_1^*(z_1),\phi ^*)=(\beta _0,g_1(z_1),\phi )$ is similar to (ii.3), so we omitted here.

(iii.2). When $h_3(x)=\log [1-\exp \{-\exp (x)\}],$ its third, fourth and fifth derivatives have roots, however, all roots are different. Assume $h^{(3)}_3(x_0)=0,$ and after some calculation we can get that $h^{(5)}_3(x_0)\ne 0$.

By the similar arguments of (ii.1), we have $\theta _1\alpha ^*=\theta _1^*\alpha .$ Let $\theta _1/\theta _1^*=\alpha /\alpha ^*=k,$ (7.12) reduces to

$$\begin{aligned} h^{(3)}_3(k t+\theta _0)k^3 =h^{(3)}_3(t+\theta _0^*), \end{aligned}$$

(7.16)

with $t=\alpha ^*y+\theta _1^*z_1.$ If $k\ne 1,$ assume that the line $k t+\theta _0$ intersects with $t+\theta _0^*$ at ${\dot{t}}$ and $k {\dot{t}}+\theta _0={\dot{t}}+\theta _0^*=x$. If $x\ne x_0,$ let $t={\dot{t}}$ in (7.16), we can get that $k=1$, it is a contradiction. If $x=x_0,$ by applying operation $\partial ^2/\partial t^2$ in both sides of (7.16) at ${\dot{t}}$, we can obtain $k^5=1$, that is $k=1$. Therefore, we have $k=1,$ then (7.16) reduces to

$$\begin{aligned} h^{(3)}_3(t+\theta _0)=h^{(3)}_3(t+\theta _0^*), \end{aligned}$$

which implies that $\theta _0=\theta _0^*$ because $h_3^{(3)}(\cdot )$ has only one maximum point. Now we have $(\alpha ^*,\theta _0^*,\theta _1^*)=(\alpha ,\theta _0,\theta _1).$

The proof of $(\beta _0^*,g_1^*(z_1),\phi ^*)=(\beta _0,g_1(z_1),\phi )$ is similar to (ii.3) , so we omitted here. $\square$

Therefore, the parameters of Eq. (2.4) are identifiability.

Proof of Corollary 2.6

When $h_i(x)=\log \Phi (x)$ or $\log [1-\exp \{-\exp (x)\}],$ it holds by a similar argument of (iii) in the proof of Theorem 2.3. Now, we consider the situation, where Y is a continuous variable and $h_i(x)=\log \text{ expit }(x)$. Assume covariates $\{X_2,\ldots ,X_{d_1-1}\}$ and $\{Z_2,Z_3,\ldots ,Z_{d_2}\}$ are omitted , since we can view $\{X_2,X_3,\ldots ,X_{d_1-1}\}$ and $\{Z_2,Z_3,\ldots ,Z_{d_2}\}$ as fixed while varying $X_1$ and $Z_1$, then Eq. (2.5) can be converted to

$$\begin{aligned}{} & {} h_i(\alpha y+\theta _0+\theta _1 x_1+\theta _2 z_1)+\frac{y\lambda (\eta ) - b\{\lambda (\eta \}}{a(\phi )} + c(y;\phi )\\{} & {} \quad =h_i(\alpha ^* y+\theta _0^*+\theta _1^* x_1+\theta _2^* z_1)+\frac{y\lambda (\eta ^*)- b\{\lambda (\eta ^*)\}}{a(\phi ^*)} + c(y;\phi ^*), \end{aligned}$$

where $\eta =\beta _0+\beta _1 x_1+g_1(z_1)$ and $\eta ^*=\beta ^*_0+\beta ^*_1 x_1+g^*_1(z_1)$.

By mimicking (ii.2) of the proof of Theorem 2.3, we can get that $\alpha /\alpha ^*=\theta _1/\theta _1^*=\theta _2/\theta _2^*=\pm 1$, where $k=1$ means the parameters of Eq. (2.4) are identifiable. Now we will prove that $k=-1$ leads to a contradiction. Eq. (2.5) can be written as

$$\begin{aligned}{} & {} \alpha y+\theta _0+\theta _1 x_1+\theta _2 z_1+\frac{y\lambda (\eta ) - b\{\lambda (\eta )\}}{a(\phi )} + c(y;\phi )\nonumber \\{} & {} \quad =\frac{y\lambda (\eta ^*)- b\{\lambda (\eta ^*)\}}{a(\phi ^*)} + c(y;\phi ^*). \end{aligned}$$

(7.17)

Applying operation $\partial /\partial x_1$ and $\partial ^2/\partial x_1\partial y$ in both sides of (7.17) yields

$$\begin{aligned} \theta _1 +\frac{y\lambda '(\eta ) - b'\{\lambda (\eta )\}\lambda '(\eta )}{a(\phi )}\beta _1 =\frac{y\lambda '(\eta ^*) - b'\{\lambda (\eta ^*)\}\lambda '(\eta ^*)}{a(\phi ^*)}\beta ^*_1 \end{aligned}$$

and

$$\begin{aligned} \frac{\lambda '(\eta )}{a(\phi )}\beta _1 =\frac{\lambda '(\eta ^*)}{a(\phi ^*)}\beta ^*_1. \end{aligned}$$

Combining the above two equalities, we have for any $x_1\in R,$

$$\begin{aligned} \theta _1 -\frac{ b'\{\lambda (\eta )\}\lambda '(\eta )}{a(\phi )}\beta _1 =-\frac{b'\{\lambda (\eta ^*)\}\lambda '(\eta )}{a(\phi )}\beta _1. \end{aligned}$$

(7.18)

Applying operation $\partial /\partial z_1$ and $\partial ^2/\partial z_1\partial y$ in both sides of (7.17) yields

$$\begin{aligned} \theta _2 +\frac{y\lambda '(\eta ) - b'\{\lambda (\eta )\}\lambda '(\eta )}{a(\phi )}g'_1(z_1) =\frac{y\lambda '(\eta ^*) - b'\{\lambda (\eta ^*)\}\lambda '(\eta ^*)}{a(\phi ^*)}{g^*_1}'(z_1) \end{aligned}$$

and

$$\begin{aligned} \frac{\lambda '(\eta )}{a(\phi )}g'_1(z_1) =\frac{\lambda '(\eta ^*)}{a(\phi ^*)} {g^*_1}'(z_1). \end{aligned}$$

Combining the above two equalities, we have for any $z_1\in R,$

$$\begin{aligned} \theta _2 -\frac{ b'\{\lambda (\eta )\}\lambda '(\eta )}{a(\phi )}g'_1(z_1) =-\frac{b'\{\lambda (\eta ^*)\}\lambda '(\eta )}{a(\phi )}g'_1(z_1). \end{aligned}$$

(7.19)

Combining (7.18) and (7.19), we have

$$\begin{aligned} g'_1(z_1)=\frac{\beta _1 \theta _2}{\theta _1}, \end{aligned}$$

which contradicts with the fact that $g_1(z_1)$ is not a linear function of $z_1.$

Therefore, the parameters of Eq. (2.4) are identifiable.

To prove Theorem 2.1, we need Lemmas 7.1, 7.2 and 7.3. $\square$

In the following, let $\Vert \cdot \Vert$ be the Euclidean norm and $\Vert g\Vert _\infty = \sup _x |g(x)|$ be the supremum norm of a function g on [0, 1]. According to a result of De Boor [7], for any function $g\in \mathcal {H}(p)$ with $p<q-1$, there exists a function ${\widetilde{g}}\in \mathcal {S}_n^0$, where $\mathcal {S}_n^0$ is defined in Section 3, such that $\Vert {\widetilde{g}}-g\Vert _\infty \le CN_n^{-p}$, where C is some fixed positive constant. For $g_0$ satisfying (D), we can find ${\widetilde{\varvec{\gamma }}}=\{{\widetilde{\gamma }}_{j,k},j=1,\ldots ,N_n,k=1,\ldots ,d_2\}^T$ and an additive spline function ${\widetilde{g}}={\widetilde{\varvec{\gamma }}}^\top {\textbf{B}}\in \mathcal {G}_n$, the collection of functions g with additive form $g({\textbf{Z}})=\sum _{k=1}^{d_2}g_k(Z_k)$ such that

$$\begin{aligned} \Vert {\widetilde{g}}-g_0\Vert _\infty =O(N_n^{-p}). \end{aligned}$$

(7.20)

Lemma 7.1

Under conditions (A)–(F), for any unit vector $\varvec{\omega }\in {\mathbb {R}}^{2d_1+d_2+2+N_nd_2},$ there exist positive constants $C>c>0$ such that

$$\begin{aligned} c\le n^{-1}\sum _{i=1}^n \varvec{\omega }^\top \frac{\partial {\textbf{U}}_{i}(\varvec{\zeta },{\widetilde{g}})}{\partial (\varvec{\zeta },\varvec{\gamma })}\varvec{\omega } \le C,\,\,\text{ almost } \text{ surely. } \end{aligned}$$

Proof

Suppose $\varvec{\omega }$ has the partition that $\varvec{\omega }=(\varvec{\omega }_1^\top ,\varvec{\omega }_2^\top )^\top$ with $\varvec{\omega }_1\in {\mathbb {R}}^{2d_1+d_2+2}$ and $\varvec{\omega }_2=\{\omega _{j,k}=1\ldots ,N_n,k=1,\ldots ,d_2\}\in {\mathbb {R}}^{N_n\times d_2}.$ By (3.4), we have that

$$\begin{aligned} n^{-1}\sum _{i=1}^n \varvec{\omega }^\top \frac{\partial {\textbf{U}}_{i}(\varvec{\zeta },{\widetilde{g}})}{\partial (\varvec{\zeta },\varvec{\gamma })}\varvec{\omega }&= n^{-1}\sum _{i=1}^n\varvec{\omega }_1^\top \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\zeta }} \varvec{\omega }_1+ n^{-1}\sum _{i=1}^n\varvec{\omega }_2^\top \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\gamma }}\varvec{\omega }_2 \nonumber \\&\quad + n^{-1}\sum _{i=1}^n\varvec{\omega }_1^\top \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\gamma }}\varvec{\omega }_2 +n^{-1}\sum _{i=1}^n\varvec{\omega }_2^\top \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\zeta }}\varvec{\omega }_1. \end{aligned}$$

(7.21)

Observing that

$$\begin{aligned} n^{-1}\sum _{i=1}^n\varvec{\omega }_1^\top \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\zeta }}\varvec{\omega }_1&=\varvec{\omega }_1^\top E\left\{ \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },g_0)}{\partial \varvec{\zeta }}\right\} \varvec{\omega }_1\\&\quad +n^{-1}\sum _{i=1}^n\varvec{\omega }_1^\top \frac{\partial ^2{\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },{\bar{g}})}{\partial \varvec{\zeta }\partial \eta }\left\{ \sum _{k=1}^{d_2}{\widetilde{g}}_k(Z_{ki})-\sum _{k=1}^{d_2}g_{0k}(Z_{ki})\right\} \varvec{\omega }_1\\&\quad +n^{-1}\sum _{i=1}^n\varvec{\omega }_1^\top \left[ \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },g_0)}{\partial \varvec{\zeta }}- E\left\{ \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },g_0)}{\partial \varvec{\zeta }}\right\} \right] \varvec{\omega }_1, \end{aligned}$$

with ${\bar{g}}$ between $\sum _{k=1}^{d_2}g_{0k}(Z_{ki})$ and $\sum _{k=1}^{d_2}{\widetilde{g}}_k(Z_{ki}).$ According to Condition (E) and that $\Vert {\widetilde{g}}-g_0\Vert _\infty =o(1),$ we have that

$$\begin{aligned} c\Vert \varvec{\omega }_1\Vert ^2\le \varvec{\omega }_1^\top n^{-1}\sum _{i=1}^n\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },{\widetilde{g}})/\partial \varvec{\zeta }\varvec{\omega }_1\le C\Vert \varvec{\omega }_1\Vert ^2, \end{aligned}$$

(7.22)

almost surely.

Now we will consider the second term of (7.21),

$$\begin{aligned} n^{-1}\sum _{i=1}^n\varvec{\omega }_2^\top \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\gamma }}\varvec{\omega }_2 = n^{-1}\sum _{i=1}^n \varpi _i\varvec{\omega }_2^\top {\textbf{B}}_i{\textbf{B}}_i^\top \varvec{\omega }_2 \end{aligned}$$

with

$$\begin{aligned} \varpi _i&= r_i \partial q_{1,i}(\varvec{\beta },{\widetilde{g}},\phi )/\partial {\widetilde{\eta }}\\&\quad +(1-r_i) \frac{\int \{1-\pi _i(\alpha ,\varvec{\theta })\}\partial q_{1,i}(\varvec{\beta },{\widetilde{g}},\phi )/\partial {\widetilde{\eta }} \,\,p_i(\varvec{\beta },{\widetilde{g}},\phi )d Y_i}{\int \{1-\pi _i(\alpha ,\varvec{\theta })\}p_i(\varvec{\beta },{\widetilde{g}},\phi )d Y_i} \\&\quad +(1-r_i) \frac{\int \{1-\pi _i(\alpha ,\varvec{\theta })\} q_{1,i}^2(\varvec{\beta },{\widetilde{g}},\phi ) p_i(\varvec{\beta },{\widetilde{g}},\phi )d Y_i}{\int \{1-\pi _i(\alpha ,\varvec{\theta })\}p_i(\varvec{\beta },{\widetilde{g}},\phi )d Y_i}\\&\quad -(1-r_i) \frac{\{\int \{1-\pi _i(\alpha ,\varvec{\theta })\} q_{1,i}(\varvec{\beta },{\widetilde{g}},\phi ) p_i(\varvec{\beta },{\widetilde{g}},\phi )d Y_i\}^2}{\{\int \{1-\pi _i(\alpha ,\varvec{\theta })\}p_i(\varvec{\beta },{\widetilde{g}},\phi )d Y_i\}^2}. \end{aligned}$$

In terms of Condition (E), it holds that $|\varpi _i|$ is bounded, that is ${\widetilde{c}}\le |\varpi _i|\le {\widetilde{C}}$ for some positive constant ${\widetilde{c}}$ and ${\widetilde{C}}$ and then

$$\begin{aligned} \frac{{\widetilde{c}}}{n}\sum _{i=1}^n \varvec{\omega }_2^\top {\textbf{B}}_i{\textbf{B}}_i^\top \varvec{\omega }_2\le n^{-1}\sum _{i=1}^n\varvec{\omega }_2^\top \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\gamma }}\varvec{\omega }_2\le \frac{{\widetilde{C}}}{n}\sum _{i=1}^n \varvec{\omega }_2^\top {\textbf{B}}_i{\textbf{B}}_i^\top \varvec{\omega }_2. \end{aligned}$$

Next we will bound the term $n^{-1}\sum _{i=1}^n \varvec{\omega }_2^\top {\textbf{B}}_i{\textbf{B}}_i^\top \varvec{\omega }_2.$

Lemma 1 of Stone [30] provides a constant $c>0$ such that

$$\begin{aligned} \left\| \sum \limits _{k=1}^{d_2}\sum \limits _{j=1}^{N_n} \omega _{j,k}B_{j,k}\right\| ^2 \ge c \sum \limits _{k=1}^{d_2}\left\| \sum \limits _{j=1}^{N_n}\omega _{j,k}B_{j,k}\right\| ^2. \end{aligned}$$

According to Theorem 5.4.2 of DeVore and Lorentz [8], Condition (D) and the definition of $B_{j,k}$ in (3.1), there exist constants $C'_k>c'_k>0$ such that for any $k=1,\ldots ,d_2$,

$$\begin{aligned} c'_k\sum \limits _{j=1}^{N_n}\omega _{j,k}^2\le \left\| \sum \limits _{i=1}^{N_n}\omega _{j,k}B_{j,k}\right\| ^2\le C'_k\sum \limits _{j=1}^{N_n}\omega _{j,k}^2. \end{aligned}$$

Thus, there exist constants $C_0>c_0>0$ such that

$$\begin{aligned} c_0\Vert \varvec{\omega }_2\Vert ^2\le \left\| \sum \limits _{k=1}^{d_2}\sum \limits _{j=1}^{N_n} \omega _{j,k}B_{j,k}\right\| ^2 \le C_0\Vert \varvec{\omega }_2\Vert ^2. \end{aligned}$$

By Lemma A.8 in Li and Yang [21], we have

$$\begin{aligned} A_n\equiv \sup \limits _{g_1,g_2\in \mathcal {G}_n}\left| \frac{<g_1,g_2>_n-<g_1,g_2>}{\parallel g_1\parallel \parallel g_2\parallel }\right| =O_p\Big \{(N_n\log n/ n)^{1/2}\Big \}, \,\,\text{ a.s. } \end{aligned}$$

It is clear to see that

$$\begin{aligned} (1-A_n)\left\| \sum \limits _{k=1}^{d_2}\sum \limits _{j=1}^{N_n} \omega _{j,k}B_{j,k}\right\| ^2&\le n^{-1}\sum \limits _{i=1}^n \varvec{\omega }_2^\top {\textbf{B}}_i {\textbf{B}}_i^\top \varvec{\omega }_2\\&\le (1+A_n)\left\| \sum \limits _{k=1}^{d_2}\sum \limits _{j=1}^{N_n} \omega _{j,k}B_{j,k}\right\| ^2. \end{aligned}$$

Therefore,

$$\begin{aligned} c\Vert \varvec{\omega }_2\Vert ^2\le n^{-1}\sum _{i=1}^n\varvec{\omega }_2^\top \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\gamma }}\varvec{\omega }_2 \le C\Vert \varvec{\omega }_2\Vert ^2,\,\,\text{ a.s. } \end{aligned}$$

(7.23)

For the third term and the fourth term of (7.21), combining Condition (E) we have that

$$\begin{aligned} n^{-1}\sum _{i=1}^n\left| \varvec{\omega }_1^\top \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\gamma }}\varvec{\omega }_2\right|\le & {} C n^{-1}\sum _{i=1}^n\left| \varvec{\omega }_1^\top (1,{\textbf{X}}_i^\top ,{\textbf{Z}}_i^\top ,{\textbf{X}}_i^\top ,1)^\top {\textbf{B}}_i^\top \varvec{\omega }_2\right| \\= & {} o(\Vert \varvec{\omega }_1\Vert ,\Vert \varvec{\omega }_2\Vert ),\,\,\text{ a.s. }, \end{aligned}$$

and

$$\begin{aligned} n^{-1}\sum _{i=1}^n\left| \varvec{\omega }_2^\top \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta },{\widetilde{g}})}{\partial \varvec{\zeta }}\varvec{\omega }_1\right|\le & {} C n^{-1}\sum _{i=1}^n\Big |\varvec{\omega }_1^\top (1,{\textbf{X}}_i^\top ,{\textbf{Z}}_i^\top ,{\textbf{X}}_i^\top ,1)^\top {\textbf{B}}_i^\top \varvec{\omega }_2\Big |\\= & {} o(\Vert \varvec{\omega }_1\Vert ,\Vert \varvec{\omega }_2\Vert ),\,\,\text{ a.s. } \end{aligned}$$

The conclusion of Lemma 7.1 follows.

When $\varvec{\gamma }={\widetilde{\varvec{\gamma }}},$ the log-likelihood $l_{ni}(\varvec{\beta },{\widetilde{g}},\phi ,\alpha ,\varvec{\theta })$ can be rewritten as $l_{ni}(\varvec{\zeta },\widetilde{\varvec{\gamma }}),$ and define

$$\begin{aligned} \widetilde{\varvec{\zeta }}=\arg \max \limits _{\varvec{\zeta }} n^{-1}\sum \limits _{i=1}^n l_{ni}(\varvec{\zeta },\widetilde{\varvec{\gamma }}). \end{aligned}$$

(7.24)

Lemma 7.2

Under conditions (A)–(F), $\sqrt{n}(\widetilde{\varvec{\zeta }}-\varvec{\zeta }_0)\rightarrow N(0,{\widetilde{A}}^{-1}{\widetilde{\Sigma }} {\widetilde{A}}^{-1}),$ where $\widetilde{\varvec{\zeta }}$ is given in (7.24), ${\widetilde{A}}=E\{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)/\partial \varvec{\zeta }\}$ and ${\widetilde{\Sigma }}=E\{{\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0){\textbf{U}}_{\varvec{\zeta },i}^\top (\varvec{\zeta }_0,g_0)\}.$

Proof

Let $\widetilde{\varvec{\upsilon }}=\sqrt{n}(\widetilde{\varvec{\zeta }}-\varvec{\zeta }_0)$. Since $\widetilde{\varvec{\zeta }}$ maximizes the $n^{-1}\sum _{i=1}^n l_{ni}(\varvec{\zeta },\widetilde{\varvec{\gamma }})$, $\widetilde{\varvec{\upsilon }}$ maximizes

$$\begin{aligned} \widetilde{l_n}(\varvec{\upsilon })=\sum _{i=1}^n \Big \{ l_{ni}(\varvec{\zeta }_0+n^{-1/2}{\varvec{\upsilon }},\widetilde{\varvec{\gamma }})-l_{ni}(\varvec{\zeta }_0,\widetilde{\varvec{\gamma }})\Big \}. \end{aligned}$$

By Taylor expansion,

$$\begin{aligned} \widetilde{l_n}(\widetilde{\varvec{\upsilon }})=n^{-1/2}\sum \limits _{i=1}^n \widetilde{\varvec{\upsilon }}^\top {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})+ n^{-1}\sum \limits _{i=1}^n \widetilde{\varvec{\upsilon }}^\top \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\overline{\varvec{\zeta }},g_0)}{\partial \varvec{\zeta }} \widetilde{\varvec{\upsilon }}, \end{aligned}$$

with $\overline{\varvec{\zeta }}$ between $\varvec{\zeta }_0$ and $\widetilde{\varvec{\zeta }}$. From the conclusions of Carroll et al. [4],

$$\begin{aligned} \left\| n^{-1}\sum \limits _{i=1}^n\frac{\partial {\textbf{U}}_{\varvec{\zeta },i} (\overline{\varvec{\zeta }},g_0)}{\partial \varvec{\zeta }} -n^{-1}\sum \limits _{i=1}^n\frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)}{\partial \varvec{\zeta }}\right\| =o_p(1) \end{aligned}$$

and

$$\begin{aligned} n^{-1}\sum \limits _{i=1}^n\frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)}{\partial \varvec{\zeta }}= E\left\{ \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)}{\partial \varvec{\zeta }}\right\} +op(1)={\widetilde{A}}+o_p(1). \end{aligned}$$

As in Carroll et al. [4],

$$\begin{aligned} n^{-1/2}\sum \limits _{i=1}^n {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})=n^{-1/2}\sum \limits _{i=1}^n {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0) +O_p(n^{1/2}\Vert {\widetilde{g}}-g_0\Vert _\infty ){.} \end{aligned}$$

By Condition (F) and (7.20), we have

$$\begin{aligned} n^{-1/2}\sum \limits _{i=1}^n {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}}) =n^{-1/2}\sum \limits _{i=1}^n {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)+o_p(1). \end{aligned}$$

By the convexity lemma of Pollard [25], $\widetilde{\varvec{\upsilon }}={\widetilde{A}}^{-1}n^{-1/2}\sum _{i=1}^n{\textbf{U}}_{\varvec{\zeta },i} (\varvec{\zeta }_0,g_0)+o_p(1)$, from which the result follows. $\square$

Lemma 7.3

Under conditions (A)–(F), we have

$$\begin{aligned} \Vert \widehat{\varvec{\zeta }}-\widetilde{\varvec{\zeta }}\Vert +\Vert \widehat{\varvec{\gamma }}- \widetilde{\varvec{\gamma }}\Vert =O_p\{(N_n/n)^{1/2}\}. \end{aligned}$$

Proof

Note that

$$\begin{aligned} n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{i}({\widehat{\varvec{\zeta }}},{\widehat{g}})-n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{i}({\widetilde{\varvec{\zeta }}},{\widetilde{g}})= n^{-1}\sum \limits _{i=1}^{n} \frac{\partial {\textbf{U}}_{i}({\overline{\varvec{\zeta }}},{\overline{g}})}{\partial (\varvec{\zeta }^\top ,\varvec{\gamma }^\top )^\top }\left( \begin{array}{c} {\widehat{\varvec{\zeta }}}-{\widetilde{\varvec{\zeta }}} \\ {\widehat{\varvec{\gamma }}}-{\widetilde{\varvec{\gamma }}} \\ \end{array} \right) , \end{aligned}$$

with $({\overline{\varvec{\zeta }}}^\top ,{\overline{g}})=t({\widehat{\varvec{\zeta }}}^\top ,{\widehat{g}}) +(1-t)({\widetilde{\varvec{\zeta }}}^\top ,{\widetilde{g}}),$ for $t\in [0,1]$. So

$$\begin{aligned} \left( \begin{array}{c} {\widehat{\varvec{\zeta }}}-{\widetilde{\varvec{\zeta }}} \\ {\widehat{\varvec{\gamma }}}-{\widetilde{\varvec{\gamma }}} \\ \end{array} \right) =-\left\{ n^{-1}\sum \limits _{i=1}^n\frac{\partial {\textbf{U}}_{i}({\overline{\varvec{\zeta }}},{\overline{g}})}{\partial (\varvec{\zeta }^\top ,\varvec{\gamma }^\top )^\top }\right\} ^{-1}n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{i} ({\widetilde{\varvec{\zeta }}},{\widetilde{g}}). \end{aligned}$$

Recall that ${\textbf{U}}_{i}({\widetilde{\varvec{\zeta }}},{\widetilde{g}})=({\textbf{U}}_{\varvec{\zeta },i}^\top ({\widetilde{\varvec{\zeta }}},{\widetilde{g}}),{\textbf{U}}_{\varvec{\gamma },i}^\top ({\widetilde{\varvec{\zeta }}},{\widetilde{g}}))^\top .$ Let $\eta _{0i}=\varvec{\beta }_0^\top {\textbf{X}}_i+g_0({\textbf{Z}}_i)$, ${\widetilde{\eta }}_i=\widetilde{\varvec{\beta }}^\top {\textbf{X}}_i+{\widetilde{g}}({\textbf{Z}}_i)$ Then,

$$\begin{aligned} n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\gamma },i}({\widetilde{\varvec{\zeta }}},{\widetilde{g}})&=n^{-1}\sum \limits _{i=1}^n\frac{\partial l_{ni}(\varvec{\zeta }_0,g_0)}{\partial \eta }{\textbf{B}}_i+n^{-1}\sum \limits _{i=1}^n \frac{\partial ^2l_{ni}(\overline{\overline{\varvec{\zeta }}},\overline{{\overline{g}}})}{\partial \varvec{\zeta }\partial \eta }({\widetilde{\varvec{\zeta }}}-\varvec{\zeta }_0){\textbf{B}}_i\\&\quad +n^{-1}\sum \limits _{i=1}^n \frac{\partial ^2l_{ni}(\overline{\overline{\varvec{\zeta }}},\overline{{\overline{g}}})}{\partial \eta ^2}({\widetilde{\eta }}_i-\eta _{0i}){\textbf{B}}_i \end{aligned}$$

and

$$\begin{aligned} n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\zeta },i}({\widetilde{\varvec{\zeta }}},{\widetilde{g}})&=n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)+n^{-1}\sum \limits _{i=1}^n \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\overline{\overline{\varvec{\zeta }}},\overline{{\overline{g}}})}{\partial \varvec{\zeta }}({\widetilde{\varvec{\zeta }}}-\varvec{\zeta }_0)\\&\quad +n^{-1}\sum \limits _{i=1}^n \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\overline{\overline{\varvec{\zeta }}},\overline{{\overline{g}}})}{\partial \eta }({\widetilde{\eta }}_i-\eta _{0i}), \end{aligned}$$

with $\overline{\overline{\varvec{\zeta }}}=t\varvec{\zeta }_0+(1-t)\widetilde{\varvec{\zeta }}, (t\in [0,1])$ and $\overline{{\overline{g}}}$ is between ${\widetilde{g}}$ and $g_0,$

Observing that

$$\begin{aligned} \left\| n^{-1}\sum \limits _{i=1}^n\frac{\partial l_{ni}(\varvec{\zeta },g_0)}{\partial \eta }{\textbf{B}}_i\right\| =\left[ \sum \limits _{k=1}^{d_2}\sum \limits _{j=1}^{N_n}\left\{ \frac{1}{n}\sum \limits _{i=1}^{n}\frac{\partial l_{ni}(\varvec{\zeta },g_0)}{\partial \eta }B_{j,k}(Z_{ik})\right\} ^2\right] ^{1/2} \end{aligned}$$

and

$$\begin{aligned} E\left[ \sum \limits _{k=1}^{d_2}\sum \limits _{j=1}^{N_n}\left\{ \frac{1}{n}\sum \limits _{i=1}^{n}\frac{\partial l_{ni}(\varvec{\zeta },g_0)}{\partial \eta }B_{j,k}(Z_{ik})\right\} ^2\right] = O_p(N_n/n), \end{aligned}$$

because of $E\{\partial l_{ni}(\varvec{\zeta }_0,g_0)/\partial \eta |Y_i,{\textbf{X}}_i,{\textbf{Z}}_i\}=0.$ We have that $\Vert n^{-1}\sum \limits _{i=1}^n\partial l_{ni}(\varvec{\zeta },g_0)/\partial \eta {\textbf{B}}_i\Vert = O_p\{(N_n/n)^{1/2}\}.$ In addition, (7.20) and Lemma 2 imply that

$$\begin{aligned}&\left\| n^{-1}\sum \limits _{i=1}^n \frac{\partial ^2l_{ni}(\overline{\overline{\varvec{\zeta }}}, \overline{{\overline{g}}})}{\partial \eta ^2}({\widetilde{\eta }}_i-\eta _{0i}){\textbf{B}}_i\right\| \\&\quad \le \left\| n^{-1}\sum \limits _{i=1}^n \frac{\partial ^2l_{ni}(\overline{\overline{\varvec{\varrho }}})}{\partial \eta ^2}\{{\widetilde{g}}({\textbf{Z}}_i)-g_0({\textbf{Z}}_i)\}{\textbf{B}}_i\right\| \\&\qquad +\left\| n^{-1}\sum \limits _{i=1}^n \frac{\partial ^2l_{ni}(\overline{\overline{\varvec{\varrho }}})}{\partial \eta ^2}\{{\textbf{X}}_i^\top (\widetilde{\varvec{\beta }}-\varvec{\beta }_0)\} {\textbf{B}}_i\right\| \\&\quad =O_p\{N_n^{1/2-p}+(N_n/n)^{1/2}\}=O_p\{(N_n/n)^{1/2}\}. \end{aligned}$$

The last equation holds because of condition (F). Therefore,

$$\begin{aligned} \left\| n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\gamma },i}({\widetilde{\varvec{\zeta }}},{\widetilde{g}})\right\| =O_p\{(N_n/n)^{1/2}\}. \end{aligned}$$

Similarly,

$$\begin{aligned} \left\| n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\zeta },i}({\widetilde{\varvec{\zeta }}},{\widetilde{g}})\right\| =O_p\{N_n^{-p}+(N_n/n)^{1/2}\}=O_p\{(N_n/n)^{1/2}\}. \end{aligned}$$

Thus,

$$\begin{aligned} \left\| n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{i}({\widetilde{\varvec{\zeta }}},{\widetilde{g}}) \right\| =O_p\{(N_n/n)^{1/2}\}. \end{aligned}$$

By Lemma 7.1, we have

$$\begin{aligned} \lambda _{\text{ min }}\left\{ n^{-1}\sum \limits _{i=1}^n\frac{\partial {\textbf{U}}_{i}({\overline{\varvec{\zeta }}},{\overline{g}})}{\partial (\varvec{\zeta }^\top ,\varvec{\gamma }^\top )^\top }\right\} =O(1),\quad \mathrm{a.s.}, \end{aligned}$$

thus

$$\begin{aligned} \Vert \widehat{\varvec{\zeta }}-\widetilde{\varvec{\zeta }}\Vert +\Vert \widehat{\varvec{\gamma }} -\widetilde{\varvec{\gamma }}\Vert\le & {} \sqrt{2}\lambda _{\text{ min }}^{-1}\left\{ n^{-1}\sum \limits _{i=1}^n\frac{\partial {\textbf{U}}_{i}({\overline{\varvec{\zeta }}},{\overline{g}})}{\partial (\varvec{\zeta }^\top ,\varvec{\gamma }^\top )^\top }\right\} \left\| n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{i} ({\widetilde{\varvec{\zeta }}},{\widetilde{g}})\right\| \\ {}= & {} O_p\{(N_n/n)^{1/2}\}. \end{aligned}$$

$\square$

Proof of Theorem 2.1

• (i) According to Lemmas 7.1 and 7.3,

  $$\begin{aligned} \Vert {\widehat{g}}-{\widetilde{g}}\Vert ^2= & {} \Vert ({\widehat{\varvec{\gamma }}}-{\widetilde{\varvec{\gamma }}})^\top {\textbf{B}}\Vert ^2=({\widehat{\varvec{\gamma }}}-{\widetilde{\varvec{\gamma }}})^\top \left\{ n^{-1}\sum \limits _{i=1}^{n}{\textbf{B}}_i{\textbf{B}}_i^\top \right\} ({\widehat{\varvec{\gamma }}}-{\widetilde{\varvec{\gamma }}})\\\le & {} C\Vert ({\widehat{\varvec{\gamma }}}-{\widetilde{\varvec{\gamma }}})\Vert ^2, \end{aligned}$$

  thus $\Vert {\widehat{g}}-{\widetilde{g}}\Vert =O_p\{(N_n/n)^{1/2}\}$ and

  $$\begin{aligned} \Vert {\widehat{g}}-g_0\Vert \le \Vert {\widehat{g}}-{\widetilde{g}}\Vert +\Vert {\widetilde{g}}-g_0\Vert= & {} O_p\{(N_n/n)^{1/2}\}+O_p(N_n^{-p})\\ {}= & {} O_p\{(N_n/n)^{1/2}\}. \end{aligned}$$

• (ii) By Taylor expansion and Condition (E), we have

  $$\begin{aligned} 0&\equiv \begin{pmatrix} n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\zeta },i}({\widehat{\varvec{\zeta }}},{\widehat{g}})\\ n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\gamma },i}({\widehat{\varvec{\zeta }}},{\widehat{g}}) \end{pmatrix} = \begin{pmatrix} n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})\\ n^{-1}\sum \limits _{i=1}^n{\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}}) \end{pmatrix} \\&\quad + \begin{pmatrix} n^{-1}\sum \limits _{i=1}^{n} \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})}{\partial \varvec{\zeta }^\top } &{} n^{-1}\sum \limits _{i=1}^{n} \frac{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})}{\partial \varvec{\gamma }^\top } \\ n^{-1}\sum \limits _{i=1}^{n} \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})}{\partial \varvec{\zeta }^\top } &{} n^{-1}\sum \limits _{i=1}^{n} \frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})}{\partial \varvec{\gamma }^\top } \\ \end{pmatrix} \begin{pmatrix} \widehat{\varvec{\zeta }}-\varvec{\zeta }_0 \\ \widehat{\varvec{\gamma }}- {\widetilde{\varvec{\gamma }}}\\ \end{pmatrix} \\&\quad +O_p(\Vert \widehat{\varvec{\zeta }}-\varvec{\zeta }_0\Vert ^2+\Vert \widehat{\varvec{\gamma }}- {\widetilde{\varvec{\gamma }}}\Vert ^2). \end{aligned}$$

  Lemmas 7.2 and 7.3 imply that $\Vert \widehat{\varvec{\zeta }}-\varvec{\zeta }_0\Vert ^2\le \Vert \widehat{\varvec{\zeta }}-\widetilde{\varvec{\zeta }}\Vert ^2+\Vert \widetilde{\varvec{\zeta }}-\varvec{\zeta }_0\Vert ^2=O_p(N_n/n)+O_p(n^{-1})=o_p(n^{-1/2})$ and $\Vert \widehat{\varvec{\gamma }}-{\widetilde{\varvec{\gamma }}}\Vert ^2=O_p(N_n/n)=o_p(n^{-1/2}).$ Define $A_n(\varvec{\zeta }_0,{\widetilde{g}})= n^{-1}\sum \limits _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\zeta }-G_n(\varvec{\zeta }_0,{\widetilde{g}})n^{-1}\sum _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\zeta }$ with $G_n(\varvec{\zeta }_0,{\widetilde{g}})=n^{-1}\sum _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\gamma }\Big \{n^{-1}\sum _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\gamma }\Big \}^{-1}$ and $H_n(\varvec{\zeta }_0,{\widetilde{g}})=N_n^{1/2}n^{-1}\sum _{i=1}^{n} \partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})/\partial \varvec{\gamma }$. By Lemma 7.1 and Condition (G), for sufficiently large n, we can conclude that $A_n(\varvec{\zeta }_0,{\widetilde{g}})$ and $H_n(\varvec{\zeta }_0,{\widetilde{g}})$ are nonsingular matrices. Let

  $$\begin{aligned} K_n(\varvec{\zeta }_0,{\widetilde{g}})= \begin{pmatrix} \{A_n(\varvec{\zeta }_0,{\widetilde{g}})\}^{-1/2}&{} \{A_n(\varvec{\zeta }_0,{\widetilde{g}})\}^{-1/2}G_n(\varvec{\zeta }_0,{\widetilde{g}}) \\ 0 &{} N_n^{1/2}\{H_n(\varvec{\zeta }_0,{\widetilde{g}})\}^{-1/2} \\ \end{pmatrix}, \end{aligned}$$

  then we have $K_n(\varvec{\zeta }_0,{\widetilde{g}})n^{-1}\sum _{i=1}^n {\textbf{U}}_{i}({\widehat{\varvec{\zeta }}},{\widehat{g}})=0$ and by some direct calculations,

  $$\begin{aligned} \begin{pmatrix} \widehat{\varvec{\zeta }}-\varvec{\zeta }_0\\ \widehat{\varvec{\gamma }}-{\widetilde{\varvec{\gamma }}} \end{pmatrix}&= \left( \begin{array}{cc} \{A_n(\varvec{\zeta }_0,{\widetilde{g}})\}^{-1}n^{-1}\sum _{i=1}^n\Big \{ G_n(\varvec{\zeta }_0,{\widetilde{g}}){\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})-{\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,{\widetilde{g}})\Big \}\\ n^{-1}\sum _{i=1}^{n}\Big \{\frac{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})}{\partial \varvec{\zeta }^\top }(\widehat{\varvec{\zeta }}-\varvec{\zeta }_0)-{\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,{\widetilde{g}})\Big \} \end{array} \right) \\&\quad +O_p(N_n/n). \end{aligned}$$

  By (7.20), Condition (F) and Condition (G), we have

  $$\begin{aligned}&\sqrt{n}(\widehat{\varvec{\zeta }}-\varvec{\zeta }_0)\nonumber \\&\quad =\{A(\varvec{\zeta }_0,g_0)+o_p(1)\}^{-1}\frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n} [\{G(\varvec{\zeta }_0,g_0)+o_p(1)\}{\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,g_0)\nonumber \\&\qquad -{\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0) ]+o_p(1)\nonumber \\&\quad =-\{A(\varvec{\zeta }_0,g_0)\}^{-1}\frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n} \{{\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)-G(\varvec{\zeta }_0,g_0){\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,g_0) \}+o_p(1), \end{aligned}$$

  (7.25)

  where $A(\varvec{\zeta }_0,g_0)=E\{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)/\partial \varvec{\zeta }\}-G(\varvec{\zeta }_0,g_0)E\{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0, g_0)/\partial \varvec{\zeta }\}$ and $G(\varvec{\zeta }_0,g_0)=E\{\partial {\textbf{U}}_{\varvec{\zeta },i}(\varvec{\zeta }_0,g_0)/\partial \varvec{\gamma }\}[E\{\partial {\textbf{U}}_{\varvec{\gamma },i}(\varvec{\zeta }_0,g_0)/\partial \varvec{\gamma }\}]^{-1}$. Applying the central limit theorem on the term of the right-hand side of (7.25), the asymptotic normality of the estimator of $\widehat{\varvec{\zeta }}$ can be established. $\square$