1 Introduction

Regression is by far the most widely used statistical methodology in empirical applications in several fields, ranging from economic and social sciences to life sciences. Even if plenty of variants have been proposed, encompassing parametric, semi- and non parametric approaches, conditional linear models retain their appeal for the ease interpretation and the availability of tools and strategies suitable to deal with different types of data and/or validity of theoretical assumptions. Today more than ever, in the era of big data, it is common practice to collect numerous variables to use as predictors of a response variable of interest. For instance, many of the customer satisfaction surveys conducted by businessess and industries collect numerous variables to predict how consumers perceive and evaluate the quality of a product/service. If, on the one hand, the use of numerous explanatory variables offers a more accurate view on the response variable, on the other engenders redundant information deriving from correlation among predictors. The collinearity among predictors is one of the main problems associated with multiple linear regression (MLR) [5, 45]. In particular, it affects least squares estimates, standard errors, computational accuracy, fitted values and predictions [19, 34]. Several are the methods generally used to diagnose collinearity. Among these, the condition index and the variance inflation factor [15]. Several are also the proposals to address the problem. They range from methods based on calculating various types of components (partial least squares regression (PLS) and principal component regression (PCR)) to a technique based on penalizing the solution using the L2 norm [24, 37]. The most well-known here is ridge regression [35]. Other examples are the more general Tikhonov regression [43] and the elastic net [50], which also penalizes the L1 norm (in addition to the L2 norm) to reduce the variables. In principle, any of these methods could be used since there is no consensus about which one is best in general: they are good in different situations.

Quantile regression (QR) extends least squares regression (LSR) beyond conditional mean. It fits conditional quantiles of the response variable with a general linear model that assumes no parametric form for the conditional distribution of the response [11, 17]. QR is a valuable tool when the conditions of linear regression are not met (i.e., linearity, homoscedasticity, independence, or normality) [29], as well as the interest is in modeling the effect of regressors at different locations of the response. This interest is present in several applications. In the decades since the introduction of quantile regression, the potential of this method has been appreciated more and more and in the most diverse fields of application (see [32] and [47] for a review of the research areas). In addition to the numerous applications in the economic framework that characterised the first years of the methodology’s dissemination ( [6, 16, 22]), contributions in social and behavioral sciences (among many [9, 12]) as well as in medicine and survival analysis ( [23]), consumer and customer satisfaction analysis [8, 10] are also widespread.

The contributions in the literature dealing with possible solutions to the problem of multicollinearity in QR focus, essentially, on variants of the ridge regression or the proposal of variable selection techniques. While the former [3, 49] shrink the coefficients, the latter introduces many different types of penalties to achieve a proper variable selection (among many, see [1, 28, 46]). The present paper faces the multicollinearity problem from a different perspective, where the whole set of variables is preserved but eliminating any redundancy that is unnecessary and detrimental to the estimation process. The use of a method of synthesising the original variables before proceeding to a quantile regression has been proposed by other authors but with different methods and aims. On the one hand, Fan et al. [13] combine Principal Component Analysis and QR with a different purpose as the authors propose the use of principal component factors as input variables for a stepwise cluster analysis prior to a QR. On the other hand, Fang et al. [14], Ando and Tsay (2011) [2] and Giglio et al. [18] use very different dimensionality reduction methods and in different contexts, respectively proper orthogonal decomposition for time series, quantile regression model with factor-augmented predictors for panel data and factor models for time series quantile regression.

The principal component regression (PCR) [39] inspires the present work to solve the problem of collinearity. It is used a lot for standard regression and is well understood theoretically. PCR is a transparent technique concerning the effects involved and easy to implement. An additional advantage of PCR is the graphical representation of the results. The representation of the regression coefficients on the principal components (loading plot) allows understanding which are the most critical variables in constructing the principal components and, therefore, in predicting the response variable. Furthermore, the representation of the scores (coordinates of the observations on the principal components) allows the detection of similarities and differences between the different statistical units and can be used for outlier detection [39]. PCR essentially consists of two steps, the first of which applies a PCA on the predictor matrix, while the second regresses the response variable on the first principal components (those that explain most of the variability). The present paper transfers the principles of PCR to the context of quantile regression giving life to a new method called quantile principal component regression (QPCR). The two approaches share the first step of the analysis, while they differ in the second as the QR is used in QPCR instead of the classic LSR to regress the response variable on the principal components. QPCR is simple to implement and can use the same graphical outputs as PCR. The primary purpose of the new method is to apply quantile regression even in contexts where the model’s predictors are strongly correlated with each other. To this end, the QPCR identifies components that summarise the information in the predictors. Like all other regression methods on latent components, the principle is to exploit the correlation structure between the predictors to precisely identify a few latent components that best summarise the set of predictors and leave aside the remaining components that would explain residual information. Unlike the other regression methods mentioned above, QPCR does not penalise the regression coefficients by selecting the observed variables. Instead, it exploits the correlations between these to identify new variables, synthesising all the observed variables that contribute to the construction of the components to different degrees. The role of each variable in the construction of the components lies in the loadings, generally displayed through appropriate graphical representations (loadings plots). On the other hand, the main components themselves can be represented by scatterplots that allow you to view the values of the statistical units on the new components (scores plots). A comparative study of different approaches will be presented in the case study to understand the different philosophies of QPCR compared to other treatment methods of multicollinearity. The two approaches are not competitors but follow different strategies with different relative results, to solve a common problem. QPCR is a good choice when the correlation structure between the variables assumes the existence of latent factors, which can be interpreted in terms of all the starting variables and used as new predictors in the regression model taken into account. The case study presented, based on the assessment of the quality of the service, represents an example of a context in which the QPCR is suitable: the set of starting predictors, highly correlated with each other, can be suitably synthesized into new variables, representing latent dimensions of observed data, and that can be effectively used to predict online purchases.

The paper is organized as follows. Section 2 offers an essential presentation of LSR and QR, discussing the problem of multicollinearity. Section 3 presents PCR, one of the best known and easiest to implement solutions to the problem. Furthermore, it presents QPCR as the extension of PCR to the context of QR. An in-depth evaluation of the effect of collinearity among predictors in QR with some insights on the use of PCR as a possible solution is addressed through a simulation study in Sect. 4. Section 5 concerns a case study on the application of QR in evaluating service quality in terms of consumer satisfaction buying online and in-store products. Finally, concluding remarks are offered in Sect. 6 along with a short discussion of the implications of these findings for future research.

2 Least squares regression and quantile regression: a short recap

Regression analysis is widely used for modelling the relationship between a single dependent variable (response) and one or more independent variables (regressors or predictors). In the following subsections, we focus on the linear model, briefly summarizing LSR and QR, limiting the treatment to the basic notation and aspects concerning collinearity.

2.1 Least squares regression

In formal notation, the MLR model can be expressed as:

$$\begin{aligned} {\mathbf {y}} = {\mathbf {X}}\varvec{\beta } + {\mathbf {e}}, \end{aligned}$$
(1)

where \({\mathbf {y}}\) is a \((n \times 1)\) vector of observations on the dependent variable, \({\mathbf {X}}\) is a \((n \times p)\) fixed matrix of observations on the independent variables, \(\varvec{\beta }\) is a \((p \times 1)\) vector of unknown regression coefficients, and \({\mathbf {e}}\) is a \((n \times 1)\) vector of errors assumed to be normally distributed with \({\mathbf {E}}({\mathbf {e}})={\mathbf {0}}\) and \({\mathbf {E}}(\mathbf {ee^\prime })=\sigma ^{2}{\mathbf {I}}_{n}\). In the following, without loss of generality, we assume that \({\mathbf {X}}\) and \({\mathbf {y}}\) are centered columnwise.

Least squares (LS) method is commonly used to estimate the regression coefficient \(\varvec{\beta }\). It minimizes the least squares loss function \(||{\varvec{y}} - {\mathbf {X}}\varvec{\beta }||^{2}\) whose closed-form solution provides the LS estimates:

$$\begin{aligned} \varvec{{\hat{\beta }}}= ({\mathbf {X}}^\prime {\mathbf {X}})^{-1} {\mathbf {X}}^\prime {\mathbf {y}}, \end{aligned}$$
(2)

when \({\mathbf {X}}^\prime {\mathbf {X}}\) is nonsingular. The covariance matrix of the LS estimator is:

$$\begin{aligned} cov(\varvec{{\hat{\beta }}})= \sigma ^{2}({\mathbf {X}}^\prime {\mathbf {X}})^{-1} \end{aligned}$$
(3)

and can be also formulated in terms of the singular value decomposition of the \({\mathbf {X}}^\prime {\mathbf {X}}\) matrix as:

$$\begin{aligned} cov(\varvec{{\hat{\beta }}})= \sigma ^{2}\sum _{a=1}^{A}{\mathbf {p}}_{a}(1/\lambda _{a}){\mathbf {p}}_{a}^\prime \end{aligned}$$
(4)

where the \({\mathbf {p}}_{a}\)s and \(\lambda _{a}\)s are the eigenvectors and the eigenvalues of \({\mathbf {X}}^\prime {\mathbf {X}}\), respectively.

The problem of collinearity concerns the case where there are linear or near-linear relationships among the predictors. In the case of exact linear relationships, i.e. if one predictor is an exact linear combination of some others, \({\mathbf {X}}^\prime {\mathbf {X}}\) becomes singular and no unique \(\varvec{{\hat{\beta }}}\) can be produced. If the predictors are nearly linearly dependent, \({\mathbf {X}}^\prime {\mathbf {X}}\) is nearly singular, and the estimation equation for the regression parameters is ill-conditioned. Therefore, parameter estimates \(\varvec{{\hat{\beta }}}\) will be unstable, as evident from Eq. (3): the variances of the regression coefficients become very large, which implies that the confidence intervals tend to be larger. Equation 4 suggests the same conclusion, but in terms of the eigenvalues of \({\mathbf {X}}^\prime {\mathbf {X}}\). If some eigenvalues are very small, as occurs in the presence of multicollinearity, the variances of the regression coefficients become very large.

Collinearity is relatively easy to detect by calculating the variance inflation factor (VIF) and the condition number (CN) [39]. The VIF is computable for each predictor \(\mathbf {x_j}\) (\(j=1, \ldots , J\)) as follows

$$\begin{aligned} VIF_{j}=\frac{1}{1-R^{2}_{j}} \end{aligned}$$

where \(R^{2}_{j}\) is the squared correlation coefficient obtained by predicting \(\mathbf {x_j}\) with the remaining explanatory variables. The VIF represents the factor of increase of the estimator’s variance due to the correlation between \(\mathbf {x_j}\) and the other explanatory variables. Multicollinearity is present if one of the \(R^{2}_{j}\) is close to 1. Generally, a VIF of 10 or above indicates that (multi) collinearity is a problem [20]. The condition number can be written as

$$\begin{aligned} CN=\left( \frac{{\hat{\lambda }}_1}{{\hat{\lambda }}_{J}}\right) ^{1/2} \end{aligned}$$

where \({\hat{\lambda }}_1\) and \({\hat{\lambda }}_{J}\) are respectively the largest and the smallest eigenvalue of the empirical covariance matrix of \({\mathbf {X}}\). An informal rule of thumb is that if the condition number is 15, multicollinearity is a concern, while multicollinearity is a severe concern if it is greater than 30 (these are just informal rules of thumb but have little theoretical basis).

2.2 Quantile regression

QR extends LSR replacing the classical estimate of the conditional mean (a single value) with estimates of conditional quantiles (several values). Therefore, it allows estimating the whole distribution of the conditional quantiles of the response variable. A typical QR model is formulated as:

$$\begin{aligned} Q_{\theta }(\hat{\mathbf{y }} \vert \mathbf{X })=\mathbf{X }{\hat{\beta }}(\theta ), \end{aligned}$$
(5)

where \(Q_{\theta }(. \vert .)\) is the conditional quantile function for the \(\theta \)-th conditional quantile with \(0< \theta <1\). QR provides separate models for each conditional quantile \(\theta \) of interest. Although it is theoretically possible to estimate an infinite number of quantiles, a finite number is numerically distinct, the so-called quantile process. QR does not pose any parametric assumption for the error (and hence response) distribution. In line with classical linear models, each \({\hat{\beta }}_{p}(\theta )\) coefficient represents the rate of change in the \(\theta \)-th conditional quantile of the dependent variable per unit change in the value of the p-th regressor \((p = 1, \ldots ,P)\), holding the others constant.

QR is a modified version of the \(L_1\) problem, the median regression, placing asymmetric weights on positive and negative residuals:

$$\begin{aligned} {\hat{\beta }}\left( \theta \right) =\underset{\beta (\theta )}{\mathrm {argmin}} ~\sum _{i=1}^n \rho _{\theta }\left( y_i-\mathbf{x }^{\top }_i\beta (\theta ) \right) \end{aligned}$$
(6)

where \(\rho _{\theta }(.)\) denotes the following asymmetric loss function:

$$\begin{aligned} \rho _{\theta }\left( y \right) = \left[ \theta - I(y< 0) \right] y = \left[ (1 - \theta ) I(y < 0) + \theta I(y > 0)\right] |y| \end{aligned}$$
(7)

Such loss function is a weighted sum of absolute deviations, where a \((1 - \theta )\) weight is assigned to the negative deviations and a \(\theta \) weight is instead used for the positive deviations. Therefore QR estimates of Eq. (6) can be formulated as:

$$\begin{aligned} {\hat{\beta }}\left( \theta \right) = \underset{\beta (\theta )}{\mathrm {argmin}} ~ \sum _{y_i < \mathbf{x }^{\top }_i\beta (\theta ) } (1-\theta ) \left| y_i- \mathbf{x }^{\top }_i\beta (\theta ) \right| + \sum _{y_i\ge \mathbf{x }^{\top }_i\beta (\theta ) } \theta \left| y_i-\mathbf{x }^{\top }_i\beta (\theta ) \right| \end{aligned}$$
(8)

QR allows the vector \({\hat{\beta }}\left( \theta \right) \) to variate on different \(\theta \), the median case (\(\theta \)=0.5) being equivalent to minimize the sum of absolute values of the residuals.

Asymptotic normality holds for the distribution of the estimators, where the form of the covariance matrix depends on the model assumptions [30, 31]. An alternative to asymptotic inference is provided by resampling methods [27] that do not require any assumption for the error distribution. Finally, the assessment of goodness of fit exploits the general idea leading to the typical \(R^{2}\) goodness of fit index in classical regression analysis. The most common goodness of fit index in the QR framework is called pseudo-\(R^{2}\) [33]. For an extensive discussion of QR methodological details, the reader is referred to the reference literature [11, 17, 29].

As the asymptotic distribution of the QR estimator depends on the inverse of the variance covariance matrix [29], the variance of the QR estimator increases with the degree of correlation among the predictors.

3 Principal component regression approach

3.1 Principal component regression

The basic idea of PCR is to find some linear combinations (components or factors) of the original variables and use them as regressors to predict \({\mathbf {y}}\). The identification of the main components takes place on the basis of dimensionality reduction techniques [24]. Specifically, principal components analysis (PCA) is applied to the matrix of predictors \({\mathbf {X}}\) in order to extract the A most dominating principal components.

The model structure for PCR is given by the following two equations:

$$\begin{aligned} {\mathbf {X}}= & {} {{\mathbf {T}}}{{\mathbf {P}}}^\prime + {\mathbf {E}} \\ {\mathbf {y}}= & {} {{\mathbf {T}}}{{\mathbf {q}}} + {\mathbf {f}} \nonumber \end{aligned}$$
(9)

where \({\mathbf {T}}\) is called scores matrix and collects the A dimensions responsible for the systematic variation in \({\mathbf {X}}\), \({\mathbf {P}}\) and \({\mathbf {q}}\) are called loadings and describe how the variables in \({\mathbf {T}}\) relates to the original variables in \({\mathbf {X}}\) and \({\mathbf {y}}\), respectively [39].

The estimated scores matrix \({\hat{\mathbf {T}}}\) of PCR is obtained by minimizing the loss function \( ||{\mathbf {X}} - {{\mathbf {T}}}{{\mathbf {P}}}||^{2}, \) whose solution is obtained through the singular value decomposition of \({\mathbf {X}}\). The estimated scores \({\hat{\mathbf {T}}}\) are then used in the regression equation in place of the original predictors:

$$\begin{aligned} {\mathbf {y}}={\hat{\mathbf {T}}q} + {\mathbf {f}}, \end{aligned}$$
(10)

where LSR is used to estimate the regression coefficients in \({\mathbf {q}}\), and \({\mathbf {f}}\) corresponds to the error term. Note that the PCR solution, i.e. the loadings \({\hat{\mathbf {P}}}\) and the regression coefficients \({\hat{\mathbf {q}}}\), can be combined to give the regression equation:

$$\begin{aligned} {\hat{y}}={\bar{y}} + \mathbf {X}{\hat{\mathbf {P}}}{\hat{\mathbf {q}}}, \end{aligned}$$
(11)

which can be interpreted in the same way as a classical LSR and where the intercept is equal to the mean \({\bar{y}}\) since the \({\mathbf {X}}\) matrix is centred.

If all the components are included in the regression (\(A = P\)), the resulting model is equivalent to the LSR model. It is worth highlighting that the variability of the estimates is larger for the last components, corresponding to the smaller eigenvalues. By considering only the first components, the ones associated with the larger eigenvalues, estimates are more stable. Equation (4) shows indeed that the directions with the smaller eigenvalues have a large impact on the variances if they are unstable, as shown in [38]. This is quite natural since they are dominated by noise. The variances of PCR estimates are the same as for LSR except that now the influence of the eigenvalues after component A is eliminated. This shows exactly that PCR gives more stable regression coefficients than LSR. For this reason, the PCR aims to use in the regression a reduced number of components that maximize the variability of \({\mathbf {X}}\), leaving aside those that include noise. PCR belongs to the class of regression estimators that are biased but can simultaneously greatly reduce any large variances for regression coefficient estimators caused by multicollinearity [25].

3.2 Quantile principal component regression

As anticipated in Sect. 1, the extension of the principal component regression to the context of the QR is straightforward. The extraction of the main components from the predictor matrix occurs in the same way. In contrast, the regression of the response variable on the extracted components uses the QR instead of the LSR.

The model structure for PCR is given by the following two equations:

$$\begin{aligned}&{\mathbf {X}}&= {{\mathbf {T}}}{{\mathbf {P}}}^\prime + {\mathbf {E}} \\&Q_{\theta }&(\hat{\mathbf{y }} \vert \mathbf{T })=\mathbf{T }{\hat{\beta }}(\theta ) \nonumber \end{aligned}$$
(12)

where \(Q_{\theta }(. \vert .)\) is the conditional quantile function for the \(\theta \)-th conditional quantile with \(0< \theta <1\).

It is worth noting that QPCR can produce the same numerical and graphical outputs as PCR, with the only difference being that the results will be specific for each selected theta.

4 On the effects of collinearity in QR: a simulation study

4.1 Description of the simulation plan

The simulation presented in this section exploits the concept of relevant subspace and relevant predictors. Relevant subspace essentially consists of the subspace of the predictors, space that is relevant for the variation in the response variable. The approach is based on principal components and exploits, in particular, the degree of dependence among the predictors on the basis of the eigenvalue structure of their covariance matrix. More specifically, the relevant components derive from a subset of the eigenvectors of the covariance matrix of the predictors. They allow obtaining a set of relevant predictors preserving all relevant information for the prediction of the response variable. The set of relevant predictor variables will have truly non-zero regression coefficients [21, 36].

The simulation study considers different degrees of correlation among predictors and different types of response with the aim to compare LSR and QR performance. We carried out the analysis using the software R [40] and the simrel package [41] for linear model data simulations. We considered a sample size of 100 observations and 3 relevant predictors. The last might seem a small number, but it is sufficient to illustrate the presence of multicollinearity in QR. Taking into account the small number of predictors, we set only one component relevant for prediction. Without loss of generality, the relevant component was set at the first position. Data were simulated so that the correspondent population model explain 70% of the variation in the response, i.e. setting the theoretical \(R^2\) equal to 0.7. Finally, we regulated the level of collinearity among predictors using a coefficient that control for the speed of decline in eigenvalues (i.e. variances) of the principal components. We denote this coefficient with \(\gamma \) in the following. The first eigenvalue was set equal to 1, and the subsequent decline according to an exponential model. We considered a grid of values for \(\gamma \) ranging from 0 to 5, using an increment of 0.5. In case of low values of \(\gamma \) we expect no or very low collinearity among predictors, while high collinearity should be present by incrementing \(\gamma \).

Table 1 Percentage of cumulated explained variance on the three principal components (columns) for the considered scenarios (different values of \(\gamma \) on the rows)
Full size table

As an example, Table 1 reports the percentage of cumulated explained variance for the three components (\(Comp_1\), \(Comp_2\) and \(Comp_3\) on the columns) using one random sample for each level of \(\gamma \) (rows). For each value of the \(\gamma \) grid, the standard errors of the classical linear regression and QR models were computed. We opted to compute LS standard errors using the bootstrap procedure in order to have a fair comparison with QR, where bootstrap is typically used. We carried out 1000 simulations for each value in the design grid. The illustrated simulation schema was replicated for different types for the following types of responses:

  • classical normal i.i.d. errors, and hence the response

  • normal heteroscedastic errors

  • skewness in the response (errors).

4.2 Main simulation results

In the presentation of the simulation results, we focus on discussing the effects of multicollinearity in QR. A comparison with what happens in LSR is still presented in case the relevant components method is adopted, namely when the PCs are used in place of the original regressors. Since we considered only three regressors for our illustrative purposes, we retain all the three components in PCR. The expected result is a different pattern in correspondence of the last component, where the largest variance associated with the noise should provide less stable estimates. In summary, the main objective is to explore the effect of multicollinearity in QR both when the original regressors are considered in the model and when PCs are used. Such results are compared with classical PCR for the different types of response considered.

Fig. 1
figure 1

Distributions of the standard errors of the first predictor (equivalent for the second predictor) in case of homoscedasticity and heteroscedasticity (rows) for LSR (first column) and QR (from the second to the last column, for the five considered quantiles). Colours refer to the results obtained using the original regressors (darker densities) or the principal components (lighter densities) in the model

Full size image

The distribution of the standard errors of the coefficients for the estimated models are summarized in Figs. 1, 2 and 3. The three figures display all the settings of the simulation design, and in particular the data generation scheme (homogeneous vs heterogeneous errors in Figs. 1 and 2, skewed errors in Fig. 3), the type of regressors included in the model (original regressors versus PCs), and the estimated model (classical LS versus QR for several quantiles). The representations are organized in the following way: the horizontal panels refer to the type of errors while the columns display the different estimated models. At each intersection two different situations are compared: the standard errors estimated when the original regressors are considered in the model (darker histograms) and the ones when PCs are used (lighter histograms). The different values of \(\gamma \) (from 0, no collinearity, to 5, highest collinearity) are depicted on the vertical axis, the values of the standard errors being represented on the horizontal axis. The results corresponding to the first two variables (X1 and X2), as well as the ones associated to the first two components are identical and therefore Fig. 1 expresses both the two coefficients (darker densities) and the two components (lighter densities). Figure 2 depicts instead the standard errors for the regressor X3 and the third PC.

Fig. 2
figure 2

Distributions of the standard errors of the third predictor in case of homoscedasticity and heteroscedasticity (rows) for LSR (first column) and QR (from the second column to the last column, for the five considered quantiles). Colours refer to the results obtained using the original regressors (darker densities) or the principal components (lighter densities) in the model

Full size image

From the analysis of the plots the following findings seem relevant:

  • when original regressors are used in the model, standard errors increase in value and variability as the collinearity increases. This is more marked in QR than in LSR. The effect is more pronounced in the extreme parts of the distribution (\(\theta =0.1\) and \(\theta =0.9\))

  • the previous consideration is amplified in the heteroscedastic case

  • when PCs are used in place of the original regressors, multicollinearity does not affect the variability of the estimates both in the homoscedastic and heteroscedastic case. This is true for all the values of \(\gamma \) regulating the level of collinearity among predictors

  • the distributions of the standard errors for X3 and the third PC (Fig. 2) coincide and the densities related to the two cases perfectly overlap

  • the variability of the estimators for X3 and the third PC is more pronounced than shown in Fig. 1, especially in the heteroscedastic case. This result was expected considering that the third component explains a residual part of the variability. In PCR, in fact, it is appropriate to use only a subset of components that explain a sufficient part of variability, or even the first component that is the most relevant

  • PCR estimator, even if biased, is a reduced variance estimator, as highlighted in Sect. 2

  • in the skewness scenario (Fig. 3), QR is less affected by the multicollinearity on the left side of the distribution (\(\theta =0.1\) and \(\theta =0.25\)) while standard errors increase in size and variability on the right side. It is worthy of notice that this scenario is quite different from the others: the range of the standard errors is much wider, as evident comparing the values on the horizontal axis in Fig. 3 with the values in Figs. 1 and 2. Using the PCs in place of the regressors, any multicollinearity does not affect the variability of the estimates.

Fig. 3
figure 3

Distributions of the standard errors of the three predictors (rows) in case of skewness for LSR (first column) and QR (from the second to the last column, for the five considered quantiles). Colours refer to the results obtained using the original regressors (darker densities) or the principal components (lighter densities) in the model

Full size image

5 A case study for the analysis of consumer purchasing behaviour of a multi-channel retailer

The aim of the study presented in this section is to describe the effects of the presence of multicollinearity on the results of LSR and QR through a practical case study. The empirical analysis will show that strong linear relationships among regressors provide unstable estimated regression coefficients and inadequate statistical measures. Dropping one or more of the highly collinear regressors could be a possible solution to the collinearity problem even if the improvement in the efficiency of the estimates not always balances the loss of information triggered from the deletion of some variables. Moreover, the omission of relevant regressor(s) from the model may result in a specification error. A different option, as described in Sect. 2, consists of eliminating only the redundant information in the data by identifying a subset of new variables through a PCA. The resulting PCs are indeed linear combinations of the original variables but orthogonal and therefore uncorrelated. The use of a regression on the PCs will lead to satisfactory results both for LSR and QR, allowing a reduction in the standard errors of the estimators and, therefore, showing the real and significant contribution of the regressors.

A completely different approach to deal with the problem of multicollinearity is the use of penalty methods such as LASSO regression [42]. The empirical analysis discussed in this paper is further refined by the results obtained by applying a penalty term to the regression model. The objective is not a comparison between the LASSO regression and the proposed quantile regression on principal components as the logic followed by the two approaches are completely different, although in both cases it leads to overcoming the multicollinearity problem. The results provided by the LASSO approach, however, make it possible to show empirically the different philosophies followed by the two approaches. In the first, principal component regression, the original space is reduced by identifying components that are linear combinations of all variables. Penalty term methods, on the other hand, are in effect variable selection techniques whereby they suggest a subset of the observed variables.

The empirical analysis is carried out on a data set regarding customers of a retail who offers products both online and in-store. Data have been simulated using the guidelines provided in [7] to reproduce a typical situation of customer relationship management where personal information of the customers are related to their purchase habits and to the evaluation of the quality of service/product. We aim to assess whether and to what extent the purchasing behaviour, the level of satisfaction with the seller and the personal characteristics of customers influence purchases made online and whether this impact changes according to the amount of money spent (for example, according to categories of customers who make low, medium or high amount purchases). The use of artificial data guarantees the transparency of the analysis process and allows the interested reader to replicate the procedure, in line with the standard of reproducible research [26]. In this section, the simulation process proposed by [7] has been completely pursued, limiting the analysis to consumers with at least one online purchase in the year. Data deals with 632 customers, which are supposed to represent a random sample from a company’s customer relationship management system.

The variables in the dataset are listed below, along with quick comments (labels in parentheses are used for tables and graphs):

  • Age (age): the distribution is quite symmetric and ranges from 48 to 50.

  • Credit score (credit.score): a typical measure that reflects the propensity of a customer to pay the credit back. This variable has been generated as a function of age, assuming that older customers have higher credit scores on average. For this reasons the shape of the distribution is very similar to age, centred on an average value of €725.

  • Distance from the store (distance.to.store): most of customers lives very close to the store and very few of them (less than 25% of the sample) very far. The variable is expressed in meters.

  • On line visits (online.visits), transactions (online.trans) and total spending (online.spend) during a year: online activity is rather limited both in terms of frequency and amounts spent. Half of the consumers make a maximum of 20 visits for a total of 20 transactions on the company website. The average amount spent is equal to €269, and very high amounts of expenditure are very limited.

  • Store transactions (store.trans) and total spending (store.spend) during a year: the attendance of the stores is more limited compared to the website both in terms of the transaction and purchase amounts. Also in this case, the distributions are rather asymmetrical.

  • Level of satisfaction with service (sat.service) and with the selection of products (sat.selection): the evaluation of the satisfaction, recorded through a 5-points Likert scale, shows a quite symmetric distribution with respect to the service while the group of customers providing a negative evaluation about the selection of products (below the central point 3) prevails.

Distributions and univariate statistics are reported in Figs. 4 and 5 and Table 2.

Fig. 4
figure 4

Distribution of the quantitative variables

Full size image
Fig. 5
figure 5

Distribution of the ordinal satisfaction variables

Full size image
Table 2 Central tendency statistics
Full size table
Fig. 6
figure 6

Scatterplot matrix of the variables related to the online behavior

Full size image
Fig. 7
figure 7

Scatterplot matrix of the variables related to the in store behavior

Full size image

Some remarks on the bivariate relationships are necessary before proceeding with the estimation of a model that involves the simultaneous analysis of all the variables. Figures 6 and 7 show the correlation coefficients and scatter plots (respectively above and below the main diagonal) for the two groups of variables with very high correlations and thus herald of multicollinearity problems.

The analysis of the VIF values (Table 3, second column) confirms that these strong correlations will also condition the joint analysis of all variables. The results of the LSR model but also of the QR for the median (Table 3, from the third column) obviously reveal a strange behaviour of the regressors in terms of rather high error standards. The effect seems even amplified in QR where only online.trans has a significant effect among the five variables related to online and in-store behaviour. The effect of the multicollinearity on the estimate of the conditioned median of the dependent variable is evident so that the analysis of the effects on more extreme parts of the distribution would lead to a predictable result. As it is known, regression results for more extreme \(\theta \) values often lead to higher error standards.

Using PCA and inserting PCs in place of the original regressors allows eliminating redundant information in the data. By choosing the first four PCs as a synthesis of the original variables, it is possible to maintain an interesting share of variability (76.14%) as well as respecting the criterion of eigenvalue one (Table 4). These PCs, orthogonal to each other, represent different aspects of the phenomenon. From the correlations between variables and PCs (Table 5), it is in fact possible to interpret the first PC (F1.store) as the one linked to consumers who prefer the shop for their purchases and transaction, the second to customers who prefer online sales (F2.online). The third PC, on the other hand, contrasts customers with respect to the level of satisfaction for the seller (F3.sat), while the fourth summarises the personal aspects of the consumer, age and credit score (F4.personal). It therefore contrasts mature customers, both in a personal and economic sense, with those who are younger and have less credit credibility.

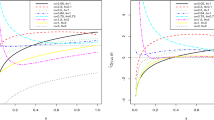
The four PCs can provide a valuable contribution to the explanation of expenses made online. Table 6 shows the results of LSR and QR for the median considering the four synthetic factors as regressors. It results that all the regressors provide significant contributions to the prediction of online.spend. In both models, the main impact is exerted by online visits and transactions (F2.online) followed, with a negative coefficient, by shopping behaviour at the stores. Median regression does not add interesting information to the results of classical LSR, but the estimation of QR for a denser grid of quantiles allows differentiating the impact of the regressors on the dependent variable. Figure 8 shows, for each regressor, the coefficient plot typically used in QR. The horizontal axis displays the different quantiles, and the vertical axis the values of regression coefficients estimated at different quantiles (from 0.01 to 0.99 with a step equal to 0.01). Moving from lower to higher quantiles, the sign of the coefficients does not change while the size changes, in some cases of relevant amount. Results limited to the average effect flattens the different effects that can occur when the amounts spent online vary. For example, for large online purchases, it is very important how the consumer behaves in terms of how she/he accesses the seller’s products (online or in-store). This means, for example, that being able to increase access to the site and also online transactions involves a greater impact among those who make very expensive online purchases than those who spend small amounts.

Table 3 VIF and OLS and median regression results (coefficients, standard errors and p-value)
Full size table
Table 4 Eigenvalues, percentage and cumulative percentage of variability
Full size table
Table 5 Correlations between variables and factors
Full size table
Table 6 OLS and median regression results (coefficients, standard errors, p-values)
Full size table
Fig. 8
figure 8

Quantile regression coefficients

Full size image
Fig. 9
figure 9

Results obtained by applying the LASSO approach to the median regression model

Full size image

The analysis of the data presented in this section now extends to a description of the results obtained by applying the LASSO approach to the median regression model presented in Table 3. It is known that the output and performance of a LASSO regression depends on a tuning parameter, named lambda: when lambda is small, the result is essentially the least squares estimate while as lambda increases, the method shrinks the coefficient estimates towards zero. Figure 9 shows the distribution of the p-values associated with the regressors of the median regression model obtained by considering a dense grid of lambdas (from 0.01 to 10 with step 0.01). It is interesting to note that the method highlights a predominant, indeed unique, role for the variable online.trans, which is the only one to have significant coefficients. In other words, this means that, regardless of the performance of the model, the results obtained lead to a complete loss of the information provided by the other regressors. The combined use of PCA-regression allows, on the other hand, to preserve part of the contribution of all regressors. In fact, the factors extracted by PCA represent a linear combination of all the initial regressors, albeit with different weights.

Table 7 provides results obtained estimating a cross-validated quantile regression with quantile equal to the median. The use of cross-validation to identify the best lambda is quite common in LASSO regression [48], and it has been extended in quantile regression setting by Wang et al. [44]. Results in Table 7 shows a very penalised model where just the regressor online.trans is significantly different from zero.

Table 7 Results by a cross validated quantile regression with quantile equal to the median
Full size table

6 Conclusion

This paper presents a thorough study of the effect of collinearity in QR using both artificial and empirical data.

Simulations results suggest different effects of collinearity in case of the different settings considered in the simulation design, and in particular several degrees of collinearity and different distributions of the response. Empirical findings show that as collinearity increases, standard errors in LS increase, but those in QR increase more. The larger increase is even more evident in the heteroscedastic case. In case PCR is adopted, the stability of the results was confirmed in the different scenarios. Multicollinearity is properly solved using as regressors only the components that maximize the variability. The effect of the collinearity is similar in LSR and QR from the case study on the evaluation of the quality of services. The case study on empirical data also shows how to estimate a quantile regression model appropriately when some explanatory variables correlate highly with each other. Therefore, the steps to follow in the analysis should be as follows:

  1. 1.

    Descriptive bivariate analysis to analyze the correlations between pairs of variables;

  2. 2.

    Use of traditional multicollinearity diagnostic methods, such as VIF and NC, to identify the predictors responsible for multicollinearity;

  3. 3.

    Implementation of the QPCR, first identifying the relevant principal components and then regressing the explanatory variable on them;

  4. 4.

    Analysis of the correlations between original variables and principal components (loadings) to trace the most relevant explanatory variables.

The main findings of the study is the relevance of collinearity also in QR and the use of PCR as a possible solution, as already well experienced in LSR. The opportunity of having more stable results even for the most extreme quantiles can be a really significant advantage considering the QR feature of modelling the tails of the distribution of the response. The present study focused on the effect of collinearity on standard errors. Future research will focus on the effect of collinearity also in terms of prediction ability, considering both in-sample and out of sample prediction and in terms of estimate bias. Moreover, a comparison between QR on the principal components and the use of penalized regression will be also explored.