Introduction

When the quality variable has a skewed distribution, it might be misleading to observe the process by using the Shewhart \(\bar{X}\) and R control charts. The usage of Shewhart control charts in skewed distributions causes an increase in type I risk (p) when the skewness increases because of the variability in population. For this reason, three methods which use the asymmetric control limits were considered as an alternative to the classical method [13]. The first one is the weighted variance (WV) method proposed by Choobineh and Ballard [6], which is based on the semivariance approximation of Choobineh and Branting [5]. They obtained the asymmetric control limits of \(\bar{X}\) and R charts for skewed distributions based on the standard deviation of sample means and ranges. Bai and Choi [2] also proposed a simple heuristic method of constructing \(\bar{X}\) and R charts by using the WV method. The second one is the weighted standard deviations (WSD) proposed by Chang and Bai [4] to obtain control limits by decomposing the standard deviation into two parts. The last one is a skewness correction (SC) method proposed by Chan and Cui [3] for constructing \(\bar{X}\) and R chart by taking into consideration the degree of skewness of the process distribution, with no assumptions on the distribution. Karagöz and Hamurkaroğlu [13] worked on \(\bar{X}\) and R control charts for skewed distributions which are Weibull, gamma and lognormal. Classical methods of estimating parameters of the distribution of quality characteristic may be affected by the presence of outliers. In order to overcome such situation, robust estimators, which are less affected by the extreme values or small departures from the model assumptions, are introduced in industrial application. Abu-Shawiesh [1] presented a simple approach to robust estimation of the process standard deviation based on a very robust scale estimator, namely, the median absolute deviation (MAD) from the sample median. The proposed method provides an alternative to the Shewhart S control chart. Schoonhove et al. [19] studied design schemes for the standard deviation control charts with estimated parameters. Different estimators of the standard deviation were considered, and the effect of the estimator on the performance of the control charts under non-normality was investigated.

Jensen et al. [12] conducted a literature survey of the effects of parameter estimation on control chart properties and identified several issues for future research. The effect of using robust or other alternative estimators has not been studied thoroughly. Most evaluations of performance have considered standard estimators based on the sample mean and standard deviation and have used the same estimators for both Phases I and II. However, in Phase I applications, it seems more appropriate to use an estimator that will be robust to outliers, step changes and other data anomalies. Examples of paper discussing robust estimation methods in Phase I control charts include [7, 16, 17, 25, 26]. One of Jensen et al. [12] their recommendations is to consider the effect of using these robust estimators on Phase II performance. By considering this recommendation, Schoonhove et al. [19] study the impact of these estimators on the Phase II performance of standard deviation control chart.

Recently works on control charts: Sukparungsee [23] studied the robustness of the asymmetric Tukey’s control chart for skew and non-skew distributions as Lognormal and Laplace distributions. The results found that the asymmetric performs better than symmetric Tukey’s control chart for both cases of skew and non-skew process observation. Sindhumol et al. [22] introduced a modification to trimmed standard deviation to increase its efficiency and it is used in controlling process dispersion. Authors constructed a Phase I control chart derived from standard deviation of trimmed mean, which is robust. Wei-Heng et al. [11] proposed a new control chart for monitoring the standard deviation of a lognormal process based on the methodologies studied in Tang and Yeh [24]. The fundamental assumption in deriving the approximate confidence intervals in Tang and Yeh [24] was that the variance of the log-transformed normal distribution is less than 1. If the variance is larger than 1, they further derived an approximate confidence interval and develop the control chart accordingly. The proposed chart was compared to the existing charts based on the average run length (ARL), where the run length is defined as the number of samples taken before the first out-of-control signal shows up on a control chart. Duclos and Pillet [8] proposed the use of a control chart (L chart) build with a minimum variance estimator whose performances have been compared to those of the average in term of variance and distribution shape. They studied this estimator in the case of data incoming from a Multi -generator process. Koyuncu and Karagöz [14] proposed to construct the mean control chart limits based on Shewhart, weighted variance and skewness correction methods using simple random sampling, ranked set sampling, median ranked set sampling and neoteric ranked set sampling designs. The performance of the proposed control charts based on neoteric ranked set sampling designs is compared with their counterparts in ranked set sampling, median ranked set sampling and simple random sampling by Monte Carlo simulation.

In this paper, we consider this recommendation to construct asymmetric control limits of R charts under non-normality and contamination. We propose to modify the Shewhart, WV and SC methods by using the interquartile range estimator of the standard deviation. And we called them modified Shewhart (MS), modified weighted variance (MWV) and modified skewness correction (MSC) methods, respectively. We study on the effect of the robust estimator on control chart performance under non-normality for moderate sample size (30 subgroups of 5–10). The considered standard estimator is interquartile range. The performance of the estimator is evaluated by assessing their root mean squared error (RMSE) under skewed distribution and in the presence of several types of contamination. Moreover, we derive factors of range control chart for each modified method. The modified robust methods are evaluated in terms of their type I risks and average run length and then compared with the modified Shewhart method. By using Monte Carlo simulation, the p and ARL values of proposed R control charts are compared based on classic and robust estimators. The performance of the proposed robust range charts is assessed when the Phases I and II data are uncontaminated and contaminated skewed distributed process. The Weibull, gamma and lognormal distributions are chosen since they can represent a wide variety of shapes from nearly symmetric to highly skewed. Khodabin and Ahmadabadi [10] was introduced the generalized gamma (GG) distribution that is a flexible distribution in statistical literature, and has exponential, gamma, and Weibull as subfamilies, and lognormal as a limiting distribution.

The remainder of the paper is structured as follows. The next section presents the design schemes and gives the methods. In the subsequent “Measuring estimator’s efficiency” section, the efficiency of measuring estimators is described and the control chart constants are given in “Determination of control charts constants” section. The performance of methods is evaluated in “The performance of the modified methods” section by considering simulation study. “Results” section evaluates the results of the study. Finally, a conclusion of this study is given in “Conclusion” section.

Skewed distributions, estimators and modified methods

The main interest of this section is to give all mathematical details by regarding the robust R control charts for skewed distributions. Firstly, the skewed distributions are discussed in “Skewed distributions” section. Secondly, the classic and robust estimators are given in “Classic and robust estimators” section. We propose to modify Shewhart, WV and SC methods by replacing the mean of the subgroup ranges with the mean of the subgroup interquartile ranges. And finally, the modified methods based on robust estimator for skewed distributions are given in “Modified methods” section.

Skewed distributions

The Weibull, gamma and lognormal distributions are chosen as skewed distributions since they can represent a wide variety of shapes from nearly symmetric to highly skewed.

  • The probability density function of the Weibull distribution is defined as

    $$\begin{aligned} f(x|\beta ,\lambda )=\beta \lambda ^\beta {x}^{\beta -1}\exp (-x\lambda )^\beta \end{aligned}$$

    for \(x>0\), where \(\beta\) is a shape parameter and \(\lambda\) is a scale parameter.

  • The probability density function of the gamma distribution is defined as

    $$\begin{aligned} f(x|\alpha ,\beta )=\frac{1}{\Gamma (\alpha )\beta ^\alpha }x^{\alpha -1}\exp \left( -\frac{x}{\beta }\right) \end{aligned}$$

    for \(x>0\), where \(\alpha\) is a shape parameter and \(\beta\) is a scale parameter.

  • The probability density function of the lognormal distribution is defined as

    $$\begin{aligned} f(x|\sigma ,\mu )=\frac{1}{x\sigma \sqrt{2\pi }}\exp \left( -\frac{({{\text{ln}}(x)-\mu })^2}{2\sigma ^2}\right) \end{aligned}$$

    for \(x>0\), where \(\sigma\) is a scale parameter and \(\mu\) is a location parameter.

Classic and robust estimators

The process is assumed to be in control (i.e., in Phase I) with given \(\hat{\sigma }\) . The process parameters \(\mu\) and \(\sigma\) are estimated from samples, and the resulting estimates are used to monitor the process in Phase II. We define \(\hat{\mu }\) and \(\hat{\sigma }\) as unbiased estimates of \(\mu\) and \(\sigma\), respectively, based on the number of sample k.

The first scale estimator is the mean of the sample range

$$\begin{aligned} \bar{R}= \frac{1}{k}\sum _{i=1}^{k}R_i \end{aligned}$$
(2.1)

where \(R_i\) is the range of the ith sample. An unbiased estimator of \(\sigma\) is \(\bar{R}/d_2(n)\). We also consider the mean of the sample interquartile ranges since the mean of the sample range is not robust against to outliers. The mean of the sample interquartile ranges (IQRs) is defined by

$$\begin{aligned} \bar{\text {IQR}}=\frac{1}{k}\sum _{i=1}^{k}{{\text {IQR}}_{i}} \end{aligned}$$
(2.2)

where IQR\(_{i}\) is the interquartile range of sample i

$$\begin{aligned} {\text {IQR}}_{i} = Q_{75,i}-Q_{25,i} \end{aligned}$$
(2.3)

where \(Q_{r,i}\) is the rth percentile of the values in sample i.

Modified methods

In this section, we construct the control limits of R control chart by considering modification in the Shewhart, WV and SC methods. The control limits are derived by assuming that the parameters of the process are unknown. What actually we do is to use simple robust estimator in these three models under the contaminated skewed process. These proposed models are called the MS, MWV and MS methods. When the control limits of MS are symmetric for normal distributed process, the control limits of MWV and MSC are asymmetric for the skewed distributed process.

The MS method

The conventional control charts when the distribution is normal are the Shewhart control charts. We first consider the Shewhart method proposed by Montgomery [15]. The Shewhart R control chart limits are given as follows:

$$\begin{aligned} {\text {UCL}}_{\mathrm{{Shewhart}}}&= {} \left( 1+\frac{3d_3}{d_2}\right) \bar{R}, \end{aligned}$$
(2.4)
$$\begin{aligned} {\text {LCL}}_{\mathrm{{Shewhart}}}&= {} \left( 1-\frac{3d_3}{d_2}\right) \bar{R} \end{aligned}$$
(2.5)

where \(d_2\) and \(d_3\) are constants that depend on the subgroup size n, and are calculated when the distribution is normal [15].

The MS R control chart limits are derived by replacing the range with the interquartile range as follows:

$$\begin{aligned} {\text {UCL}}_{\mathrm{{MS}}}&= {} \left( 1+\frac{3d_3^Q}{d_2^Q}\right) \bar{{\text {IQR}}}, \end{aligned}$$
(2.6)
$$\begin{aligned} {\text {LCL}}_{\mathrm{{MS}}}&= {} \left( 1-\frac{3d_3^Q}{d_2^Q}\right) \bar{{\text {IQR}}} \end{aligned}$$
(2.7)

where \(d_2^Q\) and \(d_3^Q\) are constants that depend on the subgroup size n, and are calculated when the distribution is skewed.

The MWV method

The WV method was proposed by Choobineh and Ballard [6]. The WV method decomposes the skewed distribution into two parts at its mean, and both parts are considered symmetric distributions which have the same mean and different standard deviation. In this method, \(\mu _{R}\) is normally estimated using the mean of the subgroup ranges \(\bar{R}\).

When the parameters of the process are unknown, the WV R control chart limits are defined by Bai and Choi [2] as follows:

$$\begin{aligned} {\text {UCL}}_{\mathrm{{WV}}}&= {} \bar{R}\left[ 1+3\frac{d_{3}^{*}}{d_{2}^{*}}\sqrt{2\hat{P}_{x}}\right] \end{aligned}$$
(2.8)
$$\begin{aligned} {\text {LCL}}_{\mathrm{{WV}}}&= {} \bar{R}\left[ 1-3\frac{d_{3}^{*}}{d_{2}^{*}}\sqrt{2\left( 1-\hat{P}_{x}\right) }\right] \end{aligned}$$
(2.9)

where \(d_{2}^{*}\) and \(d_{3}^{*}\) are the control chart constants for R chart based on WV. These constants which are defined as the mean and standard deviation of relative range \(\left( \frac{R}{\sigma }\right)\) have been obtained under the non-normality assumption. These values can be computed via numerical integration once the distribution is specified. In Eq. (2.9) \(P_{X}\) indicates the probability that can be estimated by using the number of observations less than or equal to

$$\begin{aligned} \bar{\bar{X}}: \hat{P}_{X}=\frac{\sum _{i=1}^k \sum _{j=1}^{n} \delta \left( \bar{\bar{X}}-X_{ij}\right) }{nk} \end{aligned}$$
(2.10)

where k and n are the number of samples and the number of observations in a subgroup, and \(\delta (X) =1\) for \(X\ge 0, 0\) otherwise. Usually, \(\mu _{x}\) is estimated by the grand mean of the subgroup means \(\bar{\bar{X}}\) and \(\mu _{R}\) is estimated by the mean of the subgroup ranges \(\bar{R}\) [2].

In this paper, we propose the MWV method in which the mean of the subgroup ranges is replaced by the mean of the subgroup interquartile ranges. If the parameters of the process are unknown, the MWV R control chart limits are given by

$$\begin{aligned} {\text {UCL}}_{\mathrm{{MWV}}}&= {} \bar{{\text {IQR}}}\left[ 1+3\frac{d_{3}^{Q}}{d_{2}^{Q }}\sqrt{2\hat{P}_{x}^Q}\right] \end{aligned}$$
(2.11)
$$\begin{aligned} {\text {LCL}}_{\mathrm{{MWV}}}&= {} \bar{{\text {IQR}}}\left[ 1-3\frac{d_{3}^{Q}}{d_{2}^{Q }}\sqrt{2\left( 1-\hat{P}_{x}^Q\right) }\right] \end{aligned}$$
(2.12)

where \(d_{2}^{Q }\) and \(d_{3}^{Q }\) are the control chart constants of MWV R control charts. These constants which are defined as the mean and standard deviation of interquartile range \(\left( \frac{{\text {IQR}}}{\sigma }\right)\) have been obtained under the non-normality assumption, see in “Measuring estimator’s efficiency” and “Determination of control charts constants” sections. In this paper, this constant based on classic and robust estimators is obtained via simulation for each skewed distribution, because of the difficulty in numerical integration. Equation (2.12) allows the probability to be estimated from

$$\begin{aligned} \hat{P}_{X}^Q=\frac{\sum _{i=1}^k \sum _{j=1}^{n} \delta \left( \bar{{\text {TM}}_\alpha }-X_{ij}\right) }{nk} \end{aligned}$$
(2.13)

where k and n are the number of samples and the number of observations in a subgroup, respectively, and \(\delta (X) =1\) for \(X\ge 0, 0\) otherwise. In Eq. (2.13), \(\bar{{\text {TM}}_\alpha }\) is the mean of the sample trimmed means, defined by

$$\begin{aligned} \bar{{\text {TM}}_\alpha }=\frac{1}{k}\sum _{i=1}^k{\bar{{\text {TM}}_{(v)_i}}} \end{aligned}$$
(2.14)

where TM\(_{(v)_i}\) denotes the vth ordered value of the sample trimmed means defined by

$$\begin{aligned} \bar{{\text {TM}}_{(v)_i}}=\frac{1}{n-2 \lceil n \alpha \rceil } \left[ \sum _{j=\lceil n\alpha \rceil + 1}^{n-\lceil n\alpha \rceil }{X_{(ij)}}\right] \end{aligned}$$
(2.15)

where \(\alpha\) denotes the percentage of samples to be trimmed and \(\lceil n \alpha \rceil\) denotes the ceiling function, i.e., the smallest integer not less than \(n\alpha\).

The MSC method

The last method being considered is the SC method proposed by Chan and Cui [3]. They proposed to construct the \(\bar{X}\) and R control charts limits for SC method under the skewed distributions. It’s asymmetric control limits are obtained by taking into consideration the degree of skewness estimated from subgroups and making no assumptions about distributions.

If the parameters of the process are unknown, the SC R control chart limits are defined by Chan and Cui [3] as follows:

$$\begin{aligned} {\text {UCL}}_{\mathrm{{SCR}}}&= {} \left[ 1+\left( 3+d_{4}^{*}\right) \frac{d_{3}^{*}}{d_{2}^{*}}\right] \bar{R} \end{aligned}$$
(2.16)
$$\begin{aligned} {\text {LCL}}_{\mathrm{{SCR}}}&= {} \left[ 1+\left( -3+d_{4}^{*}\right) \frac{d_{3}^{*}}{d_{2}^{*}}\right] ^{+}\bar{R} \end{aligned}$$
(2.17)

where \(d_{4}^{*}\) is the control chart constant that is obtained as follows:

$$\begin{aligned} d_{4}^{*}=\frac{\frac{4}{3}k_{3}(R)}{1+0.2k_{3}^{2}(R)} \end{aligned}$$
(2.18)

where \(k_{3}(R)\) is the skewness of the subgroup range R [3].

In this paper, we propose MSC method in which the mean of the subgroup ranges is replaced by the mean of the subgroup interquartile ranges. If the parameters of the process are unknown, the MSC R control chart limits are defined as follows:

$$\begin{aligned} {\text {UCL}}_{\mathrm{{MSCR}}}&= {} \left[ 1+\left( 3+d_{4}^{Q }\right) \frac{d_{3}^{Q}}{d_{2}^{Q}}\right] \bar{{\text {IQR}}} \end{aligned}$$
(2.19)
$$\begin{aligned} {\text {LCL}}_{\mathrm{{MSCR}}}&= {} \left[ 1+\left( -3+d_{4}^{Q}\right) \frac{d_{3}^{Q }}{d_{2}^{Q }}\right] ^{+}\bar{{\text {IQR}}} \end{aligned}$$
(2.20)

where \(d_{4}^{Q }\) are the control chart constant which is obtained for the MSC method as follows:

$$\begin{aligned} d_{4}^{Q }=\frac{\frac{4}{3}k_{3}({\text {IQR}})}{1+0.2k_{3}^{2}({\text {IQR}})} \end{aligned}$$
(2.21)

where \(k_{3}\) (IQR) is the skewness of the subgroup interquartile ranges.

Simulation study

The considered standard deviation estimator is interquartile range. The performance of the estimator is evaluated by assessing their RMSE under skewed distribution and in the presence of several types of contamination. The simulation studies evaluate the efficiency of measuring estimator in “Measuring estimator’s efficiency” section, the control chart constants in “Determination of control charts constants” section and the performance of modified methods in “The performance of the modified methods” section.

Measuring estimator’s efficiency

In this section, we evaluate the effect of outliers on the accuracy of the conventional and proposed robust estimators by means of a Monte Carlo simulation. \((M=50{,}000)\) simulation runs of 30 (\(k=30\)) subgroups each of size \(\hbox {n}=5,10\) are performed to generate data under the skewed distributions. The generated data are Weibull, lognormal and gamma distributions with different parameters as presented in Table 1. The process dispersion is estimated by both classic and robust methods. We consider four models in the case of no outliers and outliers like [9],

  • Model 1: The reference distribution parameters are selected with respect to skewness of distribution that is given in Table 1.

  • Model 2: The case of 10% replacement outliers coming from another Weibull distribution with a different scale parameter (\(\lambda _1=0.2\)) and a shape parameter \((\beta _1={0.2*\beta })\) , another lognormal distribution with a different location parameter (\(\mu _1=0.2\)) and a scale parameter \((\sigma _1=2*\sigma )\) and another gamma distribution with a different shape parameter (\(\alpha _1=2\alpha\)) and a scale parameter \((\beta _1=0.2)\).

  • Model 3: The case of 10% replacement outliers from a uniform distribution on [0, 20].

  • Model 4: The more extreme case of 10% of outliers placed at 50. We replace 10% of observations from the data with extreme values such as 50 to create a outliers in the data.

We thus allow that some observations come from a different skewed population, and in the last two models, we allow for the occurrence of gross errors.

Table 1 Values of the skewness and the parameters of distributions
Full size table

We run the simulation \(M=50{,}000\) times and generate \(k=30\) samples of size \(n=5,10\) according to different simulation schemes and compute the scale estimate \(\hat{\sigma }_j\) for each sample for \(j=1,\ldots ,M\). For each simulation setting and for estimators, we compute the RMSE of the scale estimator

$$\begin{aligned} {\text {RMSE}}_\sigma = \sqrt{\frac{1}{M}\sum _{j=1}^{M}(\hat{\sigma }_j-\sigma )^2}. \end{aligned}$$

where \(\hat{\sigma }_j\) is the robust estimation of the standart deviation \(\hat{\sigma }\).

Table 2 RMSE of the scale (\(\sigma\)) estimator under the skewed distributions for \(n = 5,10\)
Full size table

The results for Weibull, lognormal and gamma distributions are reported in Table 2. The conclusions from the study are as follows:

  1. (i)

    When there is no contamination for small sample size, the efficiency of the classic and robust estimators is more or less similar. However, for the large sample size, the robust estimator of scale performs better than the classic estimator when no contamination is present.

  2. (ii)

    Contamination by extreme outliers causes a large increase in the RMSE of the classical estimator, especially for large samples \(n=10\) and a much smaller increase in the RMSE of the robust alternative. The fact that the best performing estimator is robust one, when diffuse outlier disturbances is present for large sample sizes.

  3. (iii)

    For the scale estimation, the interquartile range estimator performs for large sample size better than the small sample size, especially in contamination by extreme outliers for all considered distributions.

  4. (iv)

    In the presence of outliers, the classic scale estimator has the highest RMSE of all skewed distributions.

  5. (v)

    For three skewed distributions, the robust scale estimator has a lower RMSE than the classical in all contaminated cases considered. So it is seen that the robust estimator is more efficient than the classic estimator.

Determination of control charts constants

The constants \(d_2, d_3\) and \(d_4\) are considered under non-normality to correct the control chart limits. The corrected constants are determined such that the expected value of the statistic divided by the constant is equal to the true value of \(\sigma\). The WV method constants \(d_{2}^{*}\) and \(d_{3}^{*}\) were calculated by taking the mean and standard deviation of range \(\left( \frac{R}{\sigma }\right)\), respectively. In this study, we consider the MS and MWV methods constants \(d_{2}^{Q }\) and \(d_{3}^{Q }\) which are calculated by taking the mean and standard deviation of interquartile range \(\left( \frac{{\text {IQR}}}{\sigma }\right)\), respectively. The SC method constant \(d_{4}^{*}\) is calculated by using Eq. (2.18). We consider the MSC method constant \(d_{4}^{Q }\) which is calculated by using Eq. (2.21).

In this paper, these constants based on the classic and robust estimators are obtain via simulation for each skewed distribution, because of the difficulty of numerical integration. These all constants are obtained for three skewed distributions via simulation. We obtain \(E(\bar{{\text {IQR}}})\) by simulation: we generate 100,000 times k samples of size n, compute IQR for each instance and take the average of the values. The results of the constants for the Shewhart, WV and SC methods are presented in Table 3 for \(k=30\) and \(n=5,10\). Moreover, the results of the constants for the MS, MWV and MSC methods are presented in Table 4 for \(k=30\) and \(n=5,10\).

Table 3 Values of constants for the skewed distributions
Full size table
Table 4 Values of robust constants for the skewed distributions
Full size table

The performance of the modified methods

When the parameters of the process are unknown, control charts can be applied in a two-phase procedure. In Phase I, control charts are used to define the in-control state of the process and to assess process stability for ensuring that the reference sample is representative of the process. The parameters of the process are estimated from Phase I sample, and control limits are estimated for using in Phase II. In Phase II, samples from the process are prospectively monitored for departures from the in-control state. The p indicates the probability of a subgroup range falling outside the control limits. The ARL is the number of points plotted within the control limits before one exceeds the limits. The ARL is the most common measure of control chart performance, and much of it is popularity is due to it is intuitively appealing and more widely applicable.

In the process control, the R, S and \(S^2\) control charts are widely used tools to monitor process variability. Let \(X_{ij}\) , \(i=1,2,3,\ldots\) and \(j=1,\ldots ,n\) denote independent random samples of size n taken in sequence on the process variable of interest; let \(\hat{\sigma }_i\) denote an estimate of the process standard deviation \(\sigma\) based on the ith sample. The control limits are

$$\begin{aligned} \hat{\text {UCL}}=U_n\hat{\sigma } \quad \quad \hat{\text {LCL}}=L_n\hat{\sigma } \end{aligned}$$

where \(U_n\) and \(L_n\) are chosen based on the skewness for this study so that the desired control chart limits are constructed when the process is in control. When the \(\hat{\sigma }_i\) falls with in the control limits, the process is called in control. Let \(E_i\) denote the event that the ith sample standard deviation is beyond the limits. Further, denote by \(P(Ei| \hat{\sigma })\) the conditional probability that is given for \(\hat{\sigma }\); the sample standard deviation \(\hat{\sigma _i}\) is beyond the control limits

$$\begin{aligned} P(Ei|\hat{\sigma })=P(\hat{\sigma _{i}} < {\text {LCL}} \quad or\quad \hat{\sigma _{i}} > {\text {UCL}}| \hat{\sigma } ) \end{aligned}$$
(3.1)

The RL as the run length is the number of subgroups until the first \(\hat{\sigma }_i\) falls beyond the limits. Given \(\hat{\sigma }\), when the \(E_s\) and \(E_t (s = t)\) are independent, and therefore, the distribution of the run length is geometric with parameter \(P(Ei|\hat{\sigma })\). The mean of the geometric distribution is given by 1 / p . Consequently, the conditional ARL is given by

$$\begin{aligned} E(RL| \hat{\sigma })= \frac{1}{P(Ei|\hat{\sigma })} \end{aligned}$$
(3.2)

When the standard deviation is estimated, the conditional runlength—the run length given an estiamte of \(\sigma\)—has a geometric distribution. However, the unconditional run length distribution the run length distribution averaged overall possible values of the estimated \(\sigma\)—is not geometric [20].

In contrast with the conditional RL distirbution, the marginal RL distribution takes into account the random variability introduced into the charting procedure through parameter estimation. It can be obtained by averaging the conditional RL distribution over all possible values of the parameter estimates. The unconditional p and unconditional average run length are given in [19] as, respectively

$$\begin{aligned} p&= {} E(P(Ei|\hat{\sigma })) \end{aligned}$$
(3.3)
$$\begin{aligned} {\text {ARL}}&= {} E(E({\text {RL}}| \hat{\sigma }))=E\left( \frac{1}{P(Ei|\hat{\sigma })}\right) . \end{aligned}$$
(3.4)

These expectations are simulated by generating 10,000 times k data samples of size n: numerous datasets are generated from the contaminated skewed distributions and computing for each data set the conditional value \((Ei|\hat{\sigma })\). By averaging these values, we obtain the unconditional values over the data sets. Note that for the calculation of the control limits in Phase I the process is considered to be in control [18].

In this section, we consider design schemes for the R control chart for non-contaminated and contaminated skewed distributed data. We use the mean and the trimmed mean estimators of mean and the range and the interquartile range estimators of the standard deviation for considered methods. To evaluate the control chart performance, we obtain p and ARL for moderate sample size (30 subgroups of 3–10) for each skewed distribution. Control charts can be applied in a two-stage procedure, when the parameters of a quality characteristic of the process are unknown. In Phase I, control charts are used to study a historical data set and determine the samples that are out of control. On the basis of the resulting reference sample, the process parameters are estimated and control limits are calculated for Phase II. In Phase II, control charts are used for real-time process monitoring [21].

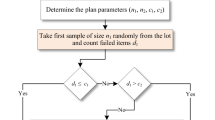
The simulation consists of two phases is run by using MATLAB R2013. The steps of each phase are described as follows.

Phase I:

  1. 1.a.

    Generate n i.i.d. Weibull \((\beta ,1)\), gamma \((\alpha ,1)\) and lognormal \((0,\sigma )\) varieties for \(n=3,5,7,10\).

  2. 1.b.

    Repeat step 1.a 30 times \(\left( k=30\right) .\)

  3. 1.c.

    By using classic estimators, compute the control limits for Shewhart, the WV and the SC methods. By using robust estimators, compute the control limits for the MS, the MWV and the MSC methods.

Phase II:

  1. 2.a.

    Generate n i.i.d. Weibull \((\beta ,1)\), gamma \((\alpha ,1)\) and lognormal \((0,\sigma )\) varieties using the procedure of step 1.a.

  2. 2.b.

    Repeat step 2.a 100 times (\(k=100\)).

  3. 2.c.

    Compute the sample statistics for R chart for the Shewhart, WV and SC methods. Compute the robust estimator interquartile range IQR for the MS, MWV and MSC methods.

  4. 2.d.

    Record whether or not the sample statistics calculated in step 2.c are within the control limits of step 1.c. for all methods.

  5. 2.e.

    Repeat steps 1.a through 2.d, 100.000 times and obtain p and ARL values for each method.

In the simulation study, we consider non-contaminated and contaminated data set in Phases I and II. We consider the \(20\%\) trimmed mean, which trims the six smallest and the six largest sample trimmed means when \(k=30\).

  • Non-contaminated case: The reference distribution parameters are selected with respect to skewness of distribution given in Table 1.

  • Contaminated case: The more extreme case of 10% of outliers placed at 50. We consider the contamination in Phases I and II.

The simulation results of p and ARL for the R control chart for non-contaminated data under skewed distributions are given in Tables 5 and 7. The results of p and ARL for the R control chart for contaminated Weibull, lognormal and gamma distrubuted data are given in Tables 8, 9 and 10, respectively.

Table 5 Results of p and ARL values for the R control chart under the skewed distributions for \(n=5,10\)
Full size table
Table 6 Results of p and ARL values for the R control chart under the contaminated skewed distributions for \(n=5,10\)
Full size table
Table 7 Results of p and ARL values for the modified R control chart under the skewed distributions for \(n=5, 10\)
Full size table
Table 8 Results of p and ARL values for the R control chart for contaminated Weibull distrubuted data for \(n=5,10\)
Full size table
Table 9 Results of p and ARL for the R control chart for contaminated lognormal distrubuted data for \(n=5,10\)
Full size table
Table 10 Results of p and ARL for the R control chart for contaminated gamma distrubuted data for \(n=5,10\)
Full size table

Results

In this section, the performance of design schemes is evaluated. When the process in control, it is expected that p is to be as low as possible and ARL is to be as high as possible. First we consider the design scheme where the process follows skewed distribution and the Phase I data are non-contaminated. Tables 5 and 7 present the p and the ARL values for the R control chart based on classic and robust estimators under the skewed distributions. The tables shows that :

  • The results for the uncontaminated case based on classic estimator are given in Table 5 as follows:

    When the distribution is approximately symmetric (\(k_3=0.5\)), then the p of SC, WV and Shewhart method are comparable, while the SC method has a noticeable smaller p values. When the skewness increases, the ARL values decrease for all design schemes while the ARL values of the Shewhart chart decrase too much and are quite lower than others. The ARL values based on Shewhart and WV methods are lower than the SC method. So the SC method performs better than the others, especially for skewness. According to the p and ARL values, there is no difference between the Weibull, gamma and lognormal distributions. It is seen from the results, in the case of skewness, the Shewhart charts does not perform well any more. So we can recommend to use asymmetric control charts based on WV and SC methods (see more details in [13]).

  • The results for the contaminated case based on classic estimator are given in Table 6 as follows:

    When we consider the contamination in the skewed distributed data, the WV and SC are effected so much from the outliers. So control charts based on WV and SC methods do not perform well any more. So we reccomend to use asymmetric control charts based on robust estimator.

  • The results for the uncontaminated case based on robust estimator are given in Table 7 as follows:

    As the skewness increases, the MWV method gives better results than the MS, MSC gives better results than the MS and WV. The MSC method works very well for all skewed distributions for small and large sample sizes for all skewed distributions, except gamma distribution for \(n=10\).

    When the skewed data are uncontaminated, the performance of the control charts based on WV and SC methods using classic estimators is comparable with the modified control charts based on MWV and MSC methods using robust estimators.

  • The results for the contaminated case based on robust estimator are given in Tables 8, 9 and 10 for Weibull, lognormal and gamma distributed data, respectively, as follows:

    The p values for MSC method for gamma distribution are increasing when the number of the sample size is increasing. So the modified models perform well for large size, except MSC for gamma distribution. MSC method has the lowest p values and the highest ARL values for all skewed distributions in all designs. So this modified method has the best performance in the case of contamination in Phases I and II for the skewed data .

When the simulation program is run for \(n=25\), the results are the same results as \(n=10\). So we can say that the results are same for large sample size.

We investigate the effect of non-normality on estimated limits under the contamination. The SC and MSC methods have the best performance for all design schemes, especially in the case of skewness.

Conclusion

Control charts are known to be effective tools for monitoring the quality of process and are applied in many industries. In this study, we consider the non-normality and the contamination for the R control charts. We propose to use the interquartile range estimator of the standard deviation to modify the methods. We study the effect of the estimator on control chart performance under non-normality for moderate sample size (30 subgroups of 5–10). To evaluate the control chart performance, we obtain p and ARL values of this control charts and the results used to compare the methods. We consider the design schemes where the Phase I and the Phase II data are non-contaminated and contaminated. The results are: The Shewhart chart has the worst performance for all design schemes, since the p values of the Shewhart chart are quite higher than others. As the skewness increases, the p values of the Shewhart chart increase too much and are effected by skewness. So the asymmetric control charts based on WV and SC methods can be used in the case of skewness. When the skewed data are uncontaminated, the performance of the control charts based on WV and SC methods using classic estimators is comparable with the modified control charts based on MWV and MSC methods using robust estimators. When there is no contamination, the SC and MSC methods work very well for all skewed distributions for small and large sample sizes for all skewed distributions. However, in the case of contamination, control charts based on WV and SC methods do not perform well any more. The MSC method has the lowest p values and the highest ARL values for all skewed distributions under contamination and so has the best performance. We reccomend to use asymmetric control charts based on MSC method for the skewed data in the case of contamination in Phases I and II.

As a future research, the proposed control chart can be extended using some other sampling schemes such as repetitive sampling, multiple dependent state sampling, ranked set sampling and neoteric rank set sampling.

As another future research, it is possible to consider other skewed distributions as heavy-tailed distributions.