Formation of highly nonlinear dust-acoustic solitary waves due to high-temperature electrons and ions

Abstract

The nonlinear propagation of dust-acoustic solitary waves (DASWs) in an unmagnetized dusty plasma consisting of two distinct temperature ions, two distinct temperature electrons and mobile dust fluid has been investigated by employing reductive perturbation method. It has been assumed that the two distinct temperature ions follow the Maxwell–Boltzmann distribution and nonthermal (Cairn’s) distribution separately while the two distinct temperature electrons follow the nonextensive (Tsallis) distribution and superthermal (Kappa) distribution separately. The system has been treated by deriving and solving a set of three highly nonlinear equations such as K-dV, modified K-dV and Gardner equations. It has been noted that the basic properties of the DASWs are significantly modified by the presence of the nonthermal ions, nonextensive electrons and superthermal electrons. The possible applications of this investigation in astrophysical, space and laboratory plasma systems have also been briefly addressed.

Introduction

The dusty plasma has become one of the prominent matters of studies during the last five decades because of its maximum presence in the universe. This is the most amazing and exciting matter of fact that more than ninety nine percent of the known universe is in the form of plasma and the remaining one percent or less which includes our earth is not in the form of plasma. No doubt, this statement stresses strongly the importance of studying the plasma and hence dusty plasma. A plasma with dust particles or grains is termed as dust in a plasma or dusty plasma. Dust grains can be billions times heavier than proton, and their sizes range from nanometers to micrometers [1]. During the early studies of dusty plasmas, it had been assumed that the temperature of the dusty plasma particles is finite and the distribution of the dusty plasma particles follows the well-known Maxwellian distribution (based on the Boltzmann–Gibbs distribution) due to thermodynamic equilibrium. Boltzmann–Gibbs (BG) distribution is the distribution which describes the properties of plasma particles when the system is in the thermal equilibrium. But the BG distribution is unable to describe the properties of many complex systems which are not in thermal equilibrium. However, Tsalli [2] proposed a generalized version of BG statistics, known as nonextensive statistical mechanics for describing and analyzing complex systems out of thermal equilibrium. However, Tsalli’s nonextensive statistical mechanics also known as nonextensive (q) distribution has been successfully applied by some authors [3,4,5] for a large number of complex (dusty) plasma systems. Cairns, Verheest, Hellberg [6, 7] and many others utilized the effect of nonthermality on the dust-acoustic solitary waves using the ion density as

$$\begin{aligned} n_i=n_{i0}\left[ 1+\beta \left( \frac{e\phi }{T_i}\right) + \beta \left( \frac{e\phi }{T_i}\right) ^2\right] \hbox{Exp}\left[ -\frac{e\phi }{T_i}\right] , \end{aligned}$$

(1)

where

$$\begin{aligned} \beta =\left( \frac{4\alpha }{1+3\alpha }\right) \end{aligned}$$

(2)

characterizes the nonthermal effect and $\alpha$ is the number of nonthermal ions. The density of electrons on the basis of the Tsalli’s nonextensive distribution can be given as

$$\begin{aligned} n_e=n_{e0}\left[ 1+(q-1)\frac{e\phi }{T_e}\right] ^{\frac{(q+1)}{2(q-1)}}, \end{aligned}$$

(3)

where q measures the strength and degree of nonextensivity of electrons having temperature $T_e$. It is evident that weakly coupled unmagnetized dusty plasma supports dust-acoustic (DA) mode [8]. The phase speed of such a (DA) mode is very much lower than electron or ion thermal speed. Consequently, the charged mobile dust grains can be regarded as immobile in comparison with electrons or ions. The dust-acoustic wave (DA mode) is extremely low phase velocity wave in which inertia comes from the dust mass and restoring force is provided by the pressure of the inertialess electrons and ions [8,9,10]

Many authors studied the dusty plasma theoretically as well as experimentally and found that the massive charged dust can modify the plasma systems generating the low-frequency dust-acoustic waves [9, 10]. The pure plasmas (electron-ion plasmas) are often contaminated by solid impurities like dust which are in general not neutral and become charged (either positively or negatively) [11] by absorbing positive ions or electrons [12,13,14,15]. Plasma can also contain a significant amount of neutral particles [16]. Ikezi [17, 18] first pointed out a simple electron-ion plasma with a few micron-sized negatively charged dust grains which undergo strongly coupled regime due to high charge density and low temperature. A number of authors demonstrated the Ikezi’s prediction by laboratory experiments [19,20,21] and simulation studies [22].

The kappa distribution for high energetic particles is convenient in analyzing the observational data which show a Maxwellian “core” at low energies and a power law-like tail at high energies [23]. Spacecraft and satellite observations revealed the fact the charged particles in astrophysical and space environments are very far from the thermodynamic equilibrium due to their extremely high temperature and low densities. These high energetic plasma particles follow the non-Maxwellian distribution like generalized Lorentzin distribution (kappa distribution) [24, 25]. The density of high energetic plasma particles like electrons following superthermal kappa distribution can be given by [26, 27]

$$\begin{aligned} n_e=n_{e0}\left[ 1-\frac{e\phi /T_e}{(\kappa -\frac{3}{2})} \right] ^{(-\kappa +1/2)}, \end{aligned}$$

(4)

where $\kappa$ is called the spectral index parameter, and if $\kappa \rightarrow \infty$, this distribution goes to Maxwellian distribution. In this manuscript, we have utilized two temperature ions following Maxwellian and nonthermal distributiions and two temperature electrons following nonextensive and superthermal kappa distributions separately and analyzed the model for dust-acoustic solitary waves. To the best of our knowledge, there is no any published work in which two temperature ions and two temperature electrons have been considered for treating the dust-acoustic solitary waves. In order to understand the variables and parameters easily, they have been tabulated. We have organized the manuscript as follows. The model equations are given in “Model equations” section. The construction and the solution of K-dV equation are performed in “Construction of K-dV equation” section. The derivation and the solution of the modified K-dV equation are given in “Modified K-dV equation” section. The construction and the solution of Gardner equation are performed in “Gardner equation” section. The numerical analysis has been made in “Numerical analysis” section. Finally, the findings and discussion are presented in “Discussion” section (Table 1).

Table 1 Meanings of important parameters and variables

Model equations

We would like to consider a collisionless unmagnetized dusty plasma containing Maxwellian ions, nonthermal ions, nonextensive electrons, superthermal electrons and negatively charged mobile dust fluid. Some authors [28,29,30] have studied these types of dusty plasmas theoretically while some others [31,32,33] have studied experimentally.

The restoring force and the inertia which are the preconditions for the formation of dust-acoustic waves come, respectively, from the electron or ion thermal pressure and the dust mass. Thus, the extremely low-frequency dust-acoustic waves are formed. The quasi-neutrality condition of the system, at equilibrium, can be given as $n_{ic0}+n_{ih0}=n_{ec0}+n_{eh0}+Z_dn_{d0}$, or in normalized form, $\mu _{ic}+\mu _{ih}=\mu _{ec}+\mu _{eh}+1$, where $Z_d$ is the number of electrons residing onto the dust grain surface; $n_{ec0}$, $n_{eh0}$, $n_{ic0}$, $n_{ih0}$ and $n_{d0}$ are, respectively, the equilibrium number densities of cold electrons (with temperature $T_{ec}$), hot electrons (with temperature $T_{eh}$), cold ions (with temperature $T_{ic}$), hot ions (with temperature $T_{ih}$) and dust; we also assume that $T_{eh}>T_{ec}>T_{ih}>T_{ic}$, and we call the electrons with temperature $T_{eh}$ as hot superthermal electrons, electrons with temperature $T_{ec}$ as cold nonextensive electrons, ions with temperature $T_{ih}$ as hot nonthermal ions, ions with temperature $T_{ic}$ as cold Maxwellian ions; $\mu _{ec}$, $\mu _{eh}$, $\mu _{ic}$ and $\mu _{ih}$ are respectively the equilibrium number density ratios of cold nonextensive electron to dust, hot superthermal electron to dust, cold Maxwellian ion to dust and hot nonthermal ion to dust. The dynamics of the system can be described by the normalized equations of the forms:

$$\begin{aligned}&\frac{\partial n_d}{\partial t}+\nabla \cdot (n_d\mathbf{u }_d)=0, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial u_d}{\partial t} + \left( \mathbf{u }_d\cdot \nabla \right) \mathbf{u }_d= \nabla \phi , \end{aligned}$$

(6)

$$\begin{aligned}\nabla ^2\phi &=-\rho \\ &=n_d+\mu _{ec}D^{\frac{\left( q+1\right) }{2\left( q-1\right) }}+\mu _{eh}E^{(-\kappa + \frac{1}{2})}-F-G, \end{aligned}$$

(7)

where

$$\begin{aligned} D= & {} \left\{ 1+\left( q-1\right) \sigma _{ec}\phi \right\} , \\ E= & {} \left\{ 1-\frac{\sigma _{eh}\phi }{\left( \kappa -\frac{3}{2}\right) }\right\} , \\ F= & {} \mu _{ic}e^{-\phi }, \\ G= & {} \mu _{ih}\left( 1+\beta \sigma _{ih}\phi +\beta \sigma _{ih}^2\phi ^2 \right) e^{-\sigma _{ih}\phi }, \end{aligned}$$

and $n_d$ is the dust number density normalized by its equilibrium value $n_{d0}$; $u_d$ is the dust fluid speed normalized by $C_{d}$; $\phi$ is the electrostatic wave potential normalized by $T_{ic}/e$. According to our assumption, $\mu _{ic}=n_{ic0}/(Z_dn_{d0})$, $\mu _{ih}=n_{ih0}/(Z_dn_{d0})$, $\mu _{ec}=n_{ec0}/(Z_dn_{d0})$, $\mu _{eh}=n_{eh0}/(Z_dn_{d0})$, $\sigma _{ih}=T_{ic}/T_{ih}$, $\sigma _{ec}=T_{ic}/T_{ec}$, $\sigma _{eh}=T_{ic}/T_{eh}$; $T_{ic}$, $T_{ih}$, $T_{ec}$ and $T_{eh}$ are, respectively, the temperatures of the cold Maxwellian ions, the hot nonthermal ions, the cold nonextensive electrons and the hot superthermal electrons in units of energy. The time variable t is normalized by $\omega _{pd}^{-1}=(m_{d}/4\pi Z_d^2 e^2n_{d0})^{1/2}$ and the space variable x is normalized by $\lambda _{Dm}=(T_{ic}/4\pi n_{d0}Z_de^2)^{1/2}$. The parameter $\kappa$ measures the slope of the energy spectrum of the superthermal particles that form the tail of the distribution function, called spectral index parameter.

Construction of K-dV equation

In order to construct the nonlinear Burger’s equation by utilizing the reductive perturbation method (ROPM), we must introduce the proper stretched coordinates. To study the electrostatic dust-acoustic shock waves in the dusty plasma system under consideration, we develop a nonlinear theory of dust-acoustic waves with small but finite amplitude which leads us to a scaling of the independent variables through the stretched coordinates [34,35,36]

$$\begin{aligned} \left. \begin{array}{l} \zeta =\epsilon ^{\frac{1}{2}}\left( x-V_Pt\right) ,\\ \tau =\epsilon ^{\frac{3}{2}}t, \end{array} \right\} \end{aligned}$$

(8)

where $V_p$ is the phase speed of the perturbation mode and $\epsilon$ is a small and dimensionless parameter ($0<\epsilon <1$) which measures the weakness of the dispersion. Now, the perturbed quantities $n_d$, $u_d$ and $\phi$ can be expanded in power series of $\epsilon$ as

$$\begin{aligned} \left. \begin{array}{l} n_d=1+\epsilon n_d^{(1)}+\epsilon ^{2}n_d^{(2)}+\epsilon ^{3}n_d^{(3)}+ \cdots ,\\ u_d=0+\epsilon u_d^{(1)}+\epsilon ^{2}u_d^{(2)}+\epsilon ^{3}u_d^{(3)}+\cdots ,\\ \rho =0+\epsilon \rho ^{(1)}+\epsilon ^2\rho ^{(2)}+\epsilon ^3\rho ^{(3)}+\cdots ,\\ \phi =0+\epsilon \phi ^{(1)}+\epsilon ^{2}\phi ^{(2)}+\epsilon ^{3}\phi ^{(3)}+\cdots . \end{array} \right\} \end{aligned}$$

(9)

Applying stretched coordinates (8) and perturbed quantities (9) into Eqs. (5)–(7), three equations are formed. Now, equating the coefficients of $\epsilon ^{\frac{3}{2}}$ from first two equations and the coefficient of $\epsilon$ from the third equation, one can find

$$\begin{aligned} u_d^{(1)}= & {} -\frac{\phi ^{(1)}}{V_p}, \end{aligned}$$

(10)

$$\begin{aligned} n_d^{(1)}= & {} -\frac{\phi ^{(1)}}{V_p^2}, \end{aligned}$$

(11)

$$\begin{aligned} V_p= & {} \left( \mu _{ic}+\mu _{ih}\sigma _{ih}P+\frac{1}{2}\mu _{ec}\sigma _{ec}Q+\mu _{eh}\sigma _{eh}R \right) ^{-\frac{1}{2}}, \end{aligned}$$

(12)

where

$$\begin{aligned} P= & {} (1-\beta ), \end{aligned}$$

(13)

$$\begin{aligned} Q= & {} (q+1), \end{aligned}$$

(14)

$$\begin{aligned} R= & {} \frac{\kappa -1/2}{\kappa -3/2}. \end{aligned}$$

(15)

Equation (10) indicates the linear dispersion relation for the low-frequency dust-acoustic solitary waves superimposed by Maxwellian and nonthermal ions, and nonextensive and superthermal electrons of high temperature. Now, equating the coefficients of $\epsilon ^{5/2}$ from first two Eqs. (5)–(6) and simplifying them, one can get

$$\begin{aligned} \frac{\partial n_d^{(2)}}{\partial \zeta }=\frac{3\phi ^{(1)}}{V_P^4}\frac{\partial \phi ^{(1)}}{\partial \zeta }-\frac{2}{V_P^3}\frac{\partial \phi ^{(1)}}{\partial \tau }-\frac{1}{V_P^2}\frac{\partial \phi ^{(2)}}{\partial \zeta }. \end{aligned}$$

(16)

Again, equating the coefficients of $\epsilon ^2$ from Eq. (7), differentiating it with respect to $\zeta$, utilizing Eqs. (10) and (16), rearranging and replacing $\phi ^{(1)}$ by $\phi$, we have an equation of the form:

$$\begin{aligned} \frac{\partial \phi }{\partial \tau }+A\phi \frac{\partial \phi }{\partial \zeta }+B\frac{\partial ^3 \phi }{\partial \zeta ^3}, \end{aligned}$$

(17)

where

$$\begin{aligned} A&= B\left[\mu _{ic}+\frac{2\mu _{eh}\sigma _{eh}^2(-\kappa +1/2) (\kappa +1/2)}{(\kappa -3/2)^2}\right.\\ &\left.\quad- \frac{1}{4}\mu _{ec}\sigma _{ec}^2(q+1)(3-q)-2\mu _{ih} (\beta \sigma _{ih}-1) -\frac{3}{V_P^4}\right], \end{aligned}$$

(18)

$$\begin{aligned} B= & {} \frac{V_P^3}{2}, \end{aligned}$$

(19)

where A and B are, respectively, the nonlinear and dispersion coefficients. Equation (17) is the nonlinear K-dV equation. Equation (17) is known as the K-dV equation.

Solution of K-dV equation

The localized stationary solution of K-dV Eq. (17) is given as

$$\begin{aligned} \phi =\phi _m \hbox{sech}^{2} \left[ \frac{\zeta }{\Delta _1}\right] , \end{aligned}$$

(20)

where $\phi _m=3U_0/A$ is the amplitude, $\Delta _1=\sqrt{4B/U_0}$ is the width and $U_0$ is the static velocity of the K-dV soliton.

Modified K-dV equation

We carefully observe that the nonlinear K-dV equation does not give satisfactory result when the nonlinear coefficient $A\rightarrow 0$ at the critical value of the spectral index parameter $\kappa =\kappa _c=1.4983$. In such a situation, higher-order nonlinear equation is needed to describe the situation at $A\rightarrow 0$. This higher-order nonlinear equation is constructed by equating the higher-order coefficients of $\epsilon$. Now we proceed to form the higher-order nonlinear equation, i.e., modified K-dV equation. The stretched coordinates we require to introduce for modified K-dV equation are

$$\begin{aligned} \left. \begin{array}{l} \zeta =\epsilon \left( x-V_Pt\right) ,\\ \tau =\epsilon ^3t, \end{array} \right\} \end{aligned}$$

(21)

where $V_P$ is the phase velocity of the perturbed mode and $\epsilon$ is the small and dimensionless parameter ($0<\epsilon <1$) as mentioned before. Substituting (9) and (21) in Eqs. (5)–(7), equating the coefficients of $\epsilon ^3$ from first two equations and equating the coefficients of $\epsilon ^2$ from the last equation, and then, simplifying, one can show that

$$\begin{aligned} \rho ^{(2)}=\frac{1}{2}A\psi ^2, \end{aligned}$$

(22)

where

$$\begin{aligned} A&= \mu _{ic}+\mu _{ih}\sigma _{ih}^2-\frac{\mu _{ec} \sigma _{ec}^2(q+1)(3-q)}{4} \\ &\quad-\frac{\mu _{eh}\sigma _{eh}^2(\kappa ^2-1/4)}{(\kappa -3/2)^2}- \frac{3}{V_P^4}\cdot \end{aligned}$$

(23)

Now, equating the coefficients of $\epsilon ^4$ from first two equations, equating the coefficients of $\epsilon ^3$ from the last equation and differentiating it with respect to $\zeta$ and finally simplifying these three equations, we have the desired modified K-dV equation of the form

$$\begin{aligned} \frac{\partial \psi }{\partial \tau }+A_1A_2\psi ^2 \frac{\partial \psi }{\partial \zeta } +A_1\frac{\partial ^3\psi }{\partial \zeta ^3}=0, \end{aligned}$$

(24)

where

$$\begin{aligned} A_1=B=\frac{V_P^3}{2} \end{aligned}$$

(25)

and

$$\begin{aligned} A_2&= \frac{15}{2V_P^6}-\frac{\mu _{ic}}{2}-\mu _{ih}\sigma _{ih}^3(3\beta /2+1/2) \\ &\quad-\frac{1}{16}\mu _{ec}\sigma _{ec}^3(q+1)(3-q)(5-3q) \\ &\quad-\frac{\mu _{ih}\sigma _{ih}^3(\kappa ^2-1/4)(\kappa +3/2)}{2(\kappa -3/2)^3}\cdot \end{aligned}$$

(26)

are, respectively, known as the dispersion and nonlinear coefficients.

Solution of modified K-dV Equation

The steady-state localized solution of modified K-dV (mK-dV) equation can be shown to be

$$\begin{aligned} \psi =\psi _m \hbox{sech}\left[ \frac{\zeta }{\Delta _2}\right] , \end{aligned}$$

(27)

where the amplitude $\psi _m$ and the width $\Delta _2$ are, respectively, given as $\psi _m=\sqrt{6U_0/A_1A_2}$ and $\Delta _2=\psi _m \sqrt{A_2/6}$.

Gardner equation

Now we wish to derive the most nonlinear equation, i.e., the Gardner equation. Equating the coefficients of $\epsilon ^4$ from first two equations, simplifying, equating the coefficients of $\epsilon ^3$ from the last equation and differentiating it with respect to $\zeta$, involving it with the previous two, one can find the equation

$$\begin{aligned} \frac{\partial ^3\psi }{\partial \zeta ^3}=-\frac{2}{V_P^3}- A_2\psi ^2\frac{\partial \psi }{\partial \zeta }. \end{aligned}$$

(28)

Again, equating the coefficients of $\epsilon ^2$ from the Poisson’s equation using the term $\epsilon ^2\rho ^{(2)}=\frac{1}{2}SC\epsilon ^3\psi ^2$, we have

$$\begin{aligned} \frac{\partial ^2\psi }{\partial \zeta ^2}=\frac{1}{2}SC\epsilon ^3\psi ^2-\rho ^{(3)}. \end{aligned}$$

(29)

Differentiating it with respect to $\zeta$, using the value of $\rho ^{(3)}$ and using other relevant equations, we ultimately reach an equation of the form

$$\begin{aligned} \frac{\partial \psi }{\partial \tau }+A_1SC\psi \frac{\partial \psi }{\partial \zeta }+ A_1A_2\psi ^2\frac{\partial \psi }{\partial \zeta }+A_1 \frac{\partial ^3\psi }{\partial \zeta ^3}=0. \end{aligned}$$

(30)

Equation (30) is a highly nonlinear equation and known as Gardner nonlinear equation.

Solution of Gardner equation

It is not easy to solve the Gardner equation. One way to solve the Gardner equation is to use a transformation relation as $\xi =\zeta -U_0t$ in steady-state condition. Using this transformation relation, Gardner Eq. (30) can be expressed as

$$\begin{aligned} \frac{1}{2}\left[ \frac{\mathrm{d}\psi }{\mathrm{d}\xi }\right] ^2+V(\psi )=0, \end{aligned}$$

(31)

where $V(\psi )$ is the pseudo-potential and it is the function of amplitude $\psi _{m1,2}$, the steady-state velocity $U_0$ of the solitary waves, the dispersion coefficient $A_1$, the nonlinear coefficient $A_2$, etc. The pseudo-potential can now be expressed as

$$\begin{aligned} V(\psi )=\frac{1}{12}A_2\psi ^4+\frac{1}{6}CS\psi ^3-\frac{U_0}{2A_1}\psi ^2, \end{aligned}$$

(32)

where the parameters $A_1$ and $U_0$ are positive. Imposing the boundary conditions

$$\begin{aligned}{}[V(\psi )]_{\psi =0}=0 \quad {\text {and}}\quad \left[ \frac{\mathrm{d}V(\psi )}{\mathrm{d}\psi }\right] _{\psi =0}=0, \end{aligned}$$

on Eq. (32), one can show that

$$\begin{aligned} \left[ \frac{\mathrm{d}^2V(\psi )}{\mathrm{d}\psi ^2}\right] _{\psi =0}<0. \end{aligned}$$

(33)

Using these conditions on Eq. (32), we can solve the equation

$$\begin{aligned} \frac{1}{12}A_2\psi _m^2+\frac{1}{6}CS\psi _m-\frac{U_0}{2A_1}=0. \end{aligned}$$

(34)

Explicitly, Eq. (34) is a quadratic equation and it has two roots. Comparing Eq. (34) with standard quadratic equation

$$\begin{aligned} ax^2+bx+c=0, \end{aligned}$$

the two solutions of this equation can be written as

$$\begin{aligned} \psi _m=-\frac{C S}{A_2}\left( 1\mp \sqrt{1+\frac{6A_2U_0}{A_1C^2 S^2}}\right) \end{aligned}$$

(35)

or separately,

$$\begin{aligned} \psi _{m1}=\psi _0\left( 1-\sqrt{1+\frac{U_0}{V_0}}\right) , \end{aligned}$$

(36)

and

$$\begin{aligned} \psi _{m2}=\psi _0\left( 1+\sqrt{1+\frac{U_0}{V_0}}\right) , \end{aligned}$$

(37)

where $\psi _0=-CS/A_2$ is the amplitude and $V_0=6A_2/(A_1C^2S^2).$ The solitary solution of the quadratic Eq. (31), also called as an “energy integral” of an oscillating particle with unit mass, with pseudo-position $\psi$, with pseudo-time $\zeta$ and pseudo-speed $d\psi /d\zeta$, can now be given as

$$\begin{aligned} \psi =\left[ \frac{1}{\psi _{m2}}-\left( \frac{1}{\psi _{m2}}-\frac{1}{\psi _{m1}}\right) \cosh ^2 \left( \frac{\zeta }{\Delta _3}\right) \right] ^{-1}, \end{aligned}$$

(38)

where $\Delta _3=2/\left( \sqrt{A_2\psi _{m1}\psi _{m2}/6}\right)$ is the width of the Gardner solitary waves.

Numerical analysis

In order to express the results of this investigation numerically and graphically, we have assumed that the temperature of the hot electrons is ten times greater than the temperature of cold electrons, temperature of cold electrons is ten times greater than the temperature of hot ions, and the temperature of the hot ions is ten times greater than the temperature of cold ions. That is, by our assumptions, $T_{eh}>10T_{ec}$; $T_{ec}>10T_{ih}$; $T_{ih}>10T_{ic}$ or, $T_{eh}>10T_{ec}$; $>100T_{ih}$; $>1000T_{ic}$. The temperature ratio of cold ions to hot ions has been designated as $\sigma _{ih}$, the temperature ratio of cold ions to cold electrons has been designated as $\sigma _{ec}$, and the temperature ratio of cold ions to hot electrons has been designated as $\sigma _{eh}$. So, by our assumptions, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$ and $\sigma _{ec}=0.001$. It is notable from K-dV Eq. (17) that it does not give any significant result corresponding to the nonlinear coefficient $A\rightarrow 0$. Solution (20) of K-dV Eq. (17) will give finite amplitude solitary waves if the static velocity $U_0>0$ and the condition $\phi >(<)0$ is maintained. We have calculated the critical value for the current model of the dusty plasma by arbitrarily choosing the spectral index parameter $\kappa$ to have a desired parametric solution of highly nonlinear Gardner equation. We have used the typical vales for the parameters as $\mu _{ic}=0.8$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, $\beta =0.5$, $q=1.49$ for evaluating the critical value corresponding to the nonlinear coefficient $A=0$. Using these values of the parameters and applying the condition $A=0$, we get two critical values for the spectral index parameter as $\kappa _c=1.49828$ (Approx) and $\kappa _c=1.49829$ (Approx). Depending on these critical values of the spectral index parameter and using the typical values of the other parameters at the condition $A_{\kappa =\kappa _c}=0$, we have also evaluated the C value for the system and these are $C=0.0000319999$ (when $\kappa _c=1.49828$) and $C=-0.0000319999$ (when $\kappa _c=1.49829$). We have plotted the variation of the amplitude of DASWs with the spectral index parameter on the basis of the solution of the K-dV equation in Fig. 3. We have also shown the variation of the amplitude of DASWs with the spectral index parameter on the basis of the solution of mK-dV equation in Fig. 5. If we compare these two Figs. 3 and 5, we note that mK-dV solitary waves or mK-dV solitons exist for the larger value of the spectral index parameter $\kappa$ than the K-dV solitary waves or K-dV solitons. It is justified because mK-dV equation is more nonlinear than the K-dV equation. We have drawn the variation of the amplitude of the DASWs with the spectral index parameter $\kappa$ on the basis of the solution of Gardner Eq. (32) in Figs. 7 and 8. In Fig. 7, we have used the positive value of C, and thus, we get the positive potential Gardner solitary waves or Gardner solitons, whereas we have utilized the negative value of C in Fig. 8 and we get the negative potential Gardner solitary waves or Gardner solitons.

We see from Eq. (18) that the nonlinear coefficient A is the function of a set of parameters such as $\sigma _{ih}$, $\sigma _{ec}$, $\mu _{ih}$, $\mu _{ec}$, $\kappa$ and $\beta$. We have used a set of standard values of the parameters like many authors.

In Fig. 1, we have plotted the variation of the phase velocity $V_P$ of DASWs with the nonthermal parameter $\beta$ and the different values of the nonextensive parameter q. It is clear from this figure that if the value of the nonthermal parameter $\beta$ increases, the phase velocity increases almost linearly for a long range of the value of the nonthermal parameter $\beta$. The phase velocity decreases smoothly at the increase in the nonextensive parameter q which can be seen from the blue ($q=0.7$), the green ($q=1.1$) and the red ($q=1.49$) curves in Fig. 1.

Fig. 1

(color figure online) Variation of phase velocity $V_P$ of DASWs with nonthermal parameter $\beta$ and the different values of the nonextensive parameter q. For blue, green and red curves, the values of q are, respectively, $q=0.70$, $q=1.10$ and $q=1.49$. For other parameters, we have chosen $\mu _{ic}=0.8$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, and $\kappa =1.4983$

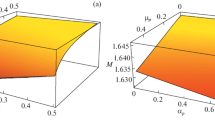
In Fig. 2, we have shown the variation of the phase velocity of the DASWs with the spectral index parameter $\kappa$ and the different values of the cold ion number density parameter $\mu _{ic}$. The phase velocity of DASWs increases at first, almost linearly with the spectral index parameter $\kappa$, and then, it increases sharply and exponentially with the increase in the spectral index parameter $\kappa$. The phase velocity decreases abruptly with a small increase in the cold ion number density parameter $\mu _{ic}$ which can be seen from the blue, the green and the red curves in Fig. 2.

Fig. 2

(color figure online) Variation of phase velocity $V_P$ of DASWs with spectral index parameter $\kappa$ and the different values of the cold ion number density parameter $\mu _{ic}$. For blue, green and red curves, the values of $\mu _{ic}$ are, respectively, $\mu _{ic}=0.75$, $\mu _{ic}=0.7505$ and $\mu _{ic}=0.751$. For other parameters, we have chosen $\beta =0.5$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, and $q=1.49$

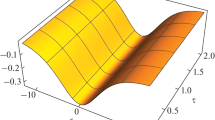
Figure 3 shows the variation of the amplitude of the DASWs (obtained from the solution of the nonlinear K-dV equation) with the position coordinate $\xi$ and the spectral index parameter $\kappa$. The amplitude of the DASWs remains almost constant with the increase in the spectral index parameter $\kappa$ for a long range of the value of the spectral index parameter. When the spectral index parameter reaches its critical value, i.e., when $\kappa =\kappa _c=1.4983$ corresponding to $A\rightarrow 0$, the breakdown of ROPM occurs due to the infinitely large amplitude of DASWs (not shown in figure).

Fig. 3

(color figure online) Variation of the amplitude $\psi$ of DASWs with position coordinate $\xi$ and the spectral index parameter $\kappa$. For other parameters, we have chosen $\beta =0.5$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, $q=1.49$ and $U_0=0.01$

Figure 4 shows the variation of the amplitude of the DASWs (obtained from the solution of the nonlinear K-dV equation) with the position coordinate $\xi$ and the nonthermal parameter $\beta$. The amplitude of the DASWs decreases slightly with the increase in the nonthermal parameter $\beta$ up to a certain value of the nonthermal parameter.

Fig. 4

(color figure online) Variation of the amplitude $\psi$ of DASWs with position coordinate $\xi$ and the nonthermal parameter $\beta$. For other parameters, we have chosen $\kappa =1.4$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, $q=1.49$ and $U_0=0.01$

In Fig. 5, we have plotted the variation of the amplitude of the DASWs (obtained from the solution of the modified K-dV equation) with the position coordinate $\xi$ and the spectral index parameter $\kappa$. The amplitude of the DASWs remains almost constant with the increase in the spectral index parameter $\kappa$ for value near to the critical value of the spectral index parameter. If the value of the $\kappa$ is further increased, the breakdown of ROPM occurs again due to the infinitely large-amplitude DASWs.

Fig. 5

(color figure online) Variation of the amplitude $\psi$ of DASWs (on the basis of the solution of modified K-dV equation) with position coordinate $\xi$ and the spectral index parameter $\kappa$. For other parameters, we have chosen $\beta =0.5$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, $q=1.49$ and $U_0=0.01$

In Fig. 6, we have depicted the variation of the amplitude of the DASWs (obtained from the solution of the modified K-dV equation) with the position coordinate $\xi$ and the nonthermal parameter $\beta$. The amplitude of the DASWs remains almost constant with the increase in the nonthermal parameter $\beta$ for a wide range of the value of the nonthermal parameter.

Fig. 6

(color figure online) Variation of the amplitude $\psi$ of DASWs (on the basis of the solution of modified K-dV equation) with position coordinate $\xi$ and the nonthermal parameter $\beta$. For other parameters, we have chosen $\kappa =1.45$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, $q=1.49$, $U_0=0.01$, $S=1$ and $C=0.000032$

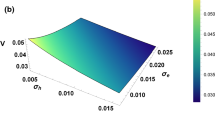
Figure 7 shows the variation of the (negative) amplitude DASWs (on the basis of the solution of Gardner equation) with position coordinate $\xi$ and the spectral index parameter $\kappa$. It is observed from this figure that amplitude of the DASWs remains constant with the increase in the spectral index parameter for a long range of the value of the spectral index parameter $\kappa$. It can be noted from this figure that the increase in the value of $\kappa$ up to its critical value ($\kappa =\kappa _c=1.4983$) does not affect the amplitude of the DASWs. In other words, solitary waves or Gardner solitons exist at the critical value of the spectral index parameter. That means, no breakdown of ROPM occurs at the critical value of the spectral index parameter ($\kappa =\kappa _c=1.4983$) corresponding to $A\rightarrow 0$. So, Gardner solitons exist for this model of dusty plasmas.

Fig. 7

(color figure online) Variation of the (negative) amplitude DASWs (on the basis of the solution of Gardner equation) with position coordinate $\xi$ and the spectral index parameter $\kappa$. For other parameters, we have chosen $\beta =0.5$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, $q=1.49$, $U_0=0.01$, $S=1$ and $C=-0.000032$

Figure 8 shows the variation of the (positive) amplitude DASWs (on the basis of the solution of Gardner equation) with position coordinate $\xi$ and the spectral index parameter $\kappa$. It is notable from this figure that the amplitude of the DASWs remains constant up to the critical value of the spectral index parameter. Gardner solitons exist at the critical value of the spectral index parameter (i.e., at $\kappa =\kappa _c=1.4983$) corresponding to nonlinear coefficient $A\rightarrow 0$.

Fig. 8

(color figure online) Variation of the (positive) amplitude DASWs (on the basis of the solution of Gardner equation) with position coordinate $\xi$ and the spectral index parameter $\kappa$. For other parameters, we have chosen $\beta =0.5$, $\mu _{ih}=0.6$, $\mu _{ec}=0.3$, $\mu _{eh}=0.1$, $\sigma _{ih}=0.1$, $\sigma _{ec}=0.01$, $\sigma _{eh}=0.001$, $q=1.49$, $U_0=0.01$, $S=1$ and $C=0.000032$

Discussion

In this article, we have carried out an investigation on the dust-acoustic solitary waves in an unmagnetized dusty plasma consisting of two temperature ions (nonthermal Cairn’s distributed ions and Maxwell–Boltzmann distributed ions), two temperature electrons (superthermally distributed electrons and nonextensively distributed electrons) and negatively charged mobile dust fluid. By employing reductive perturbation method (ROPM), we have constructed a set of three highly nonlinear equations (K-dV equation, modified K-dV equation and Gardner equation) and solved these equations under steady-state conditions. The results of this investigation have been treated and explained both graphically and numerically. In this current model of dusty plasmas, we have observed that the solitary waves or solitons exist, particularly K-dV solitons exist very far below the critical value of the spectral index parameter ($\kappa _c=1.4983$), modified K-dV solitons exist far below (not very far), and Gardner solitons exist at and around the critical value of the spectral index parameter ($\kappa _c=1.4983$). The basic properties of the dust-acoustic solitary waves are found to be modified strongly by the changes of the nonthermal, nonextensive and superthermal effects of ions and electrons. However, the important results of this investigation are pointed out as

(I) :

Dust-acoustic solitary waves exist on the basis of the solutions of the K-dV, modified K-dV and Gardner equations for the current model of dusty plasmas.

(II) :

K-dV solitons exist far below the critical value of the spectral index parameter ($\kappa _c$) corresponding to $A\rightarrow 0$.

(III) :

The amplitude of the K-dV solitons slightly decreases with the increase in the nonthermal parameter $\beta$ (Fig. 4), and the amplitude remains constant with the increase in the spectral index parameter $\kappa$ (Fig. 3).

(IV) :

At the critical of the spectral index parameter, i.e., at $\kappa =\kappa _c$, the breakdown of the ROPM occurs due to the infinitely large-amplitude solitary waves corresponding to $A\rightarrow 0$.

(V) :

No K-dV solitons are available near and at the critical value of the spectral index parameter ($\kappa =\kappa _c$).

(VI) :

Modified K-dV (mK-dV) solitons exist near the critical value of the spectral index parameter ($\kappa =\kappa _c$).

(VII) :

The amplitude of the modified K-dV solitons remains nearly constant with the increase in the spectral index parameter $\kappa$ (Fig. 5) and the nonthermal parameter $\beta$ (Fig. 6).

(VIII) :

Both negative and positive amplitude Gardner solitons exist at the critical value of the spectral index parameter ($\kappa =\kappa _c$).

(IX) :

No breakdown of ROPM occurs for higher-order nonlinear Gardner equation corresponding to $A\rightarrow 0$ and Gardmer solitons exist for the current model of dusty plasmas.

(X) :

The amplitude of negative and positive amplitude DASWs remains constant with the increase in the spectral index parameter $\kappa$ (Figs. 7 and 8).

We have carefully noted that both positive and negative polarity K-dV, mK-dV and Gardner solitary waves or solitons exist for this multitemperature dusty plasma model. The fundamental properties of the dust-acoustic solitary waves such as amplitude, width and polarity are seen to be strongly modified by the presence of the two temperature ions (Maxwellian and nonthermal ions), two temperature electrons (nonextensive and superthermal electrons) and negatively charged mobile dust. It can be inferred that the results of this investigation should be useful for treating the nonlinear features of localized electrostatic disturbances in both astrophysical plasma systems such as the edges of the AKR (auroral kilometric radiation) source regions [37], the noctilucent cloud region in the Earth’s atmosphere [38], the solar neutrino deficit problems, the self-gravitating polytropic systems, the peculiar velocity distribution of galaxy clusters, Saturn’s rings, cometary environments and the laboratory plasma systems such as the radio frequency discharge plasma [39], hot turbulent thermonuclear plasma [40], dissipative optical lattices [4], thermoluminescence dosimetry and the dating of archeological and geological minerals [3]. We, therefore, propose to perform a laboratory experiment which would be able to identify such special features of DASWs found in our present investigation.