Introduction

Dielectric barrier discharges (DBDs) can be used for generating of low-temperature plasma under atmospheric pressure. As compared to the other types of gas discharge, the simplicity in the configuration and absence of the vacuum system of the DBD are obvious advantages for consideration of industrial applications. DBDs are used in many industrial applications, such as ozone generation [1, 2], decontamination [3, 4], lighting especially of UV light generation by means of DBD excimer lamps [5, 6], the manufacture of plasma display cells [7], modification and surface treatment [8,9,10,11] and semiconductor manufacturing. This type of discharge can be produced when at least one of the electrodes is covered by a dielectric layer, such as glass, quartz or ceramics. An alternating voltage or a repetitively pulsed power source can be used to power the DBD cell. The function of the dielectric layer between the electrodes is to prevent the formation of arc discharge and to limit the current discharge.

A space gap of a few mm is commonly recommended in this case. In order to generate the plasma, the minimum peak-to-peak applied voltage must be higher than the breakdown voltage of the gas.

At atmospheric pressure, we distinguish two forms of discharge:

  • The homogeneous discharge more precisely in glow mode, the physical parameters of this type of discharges can be controlled in space and in time which makes it possible to treat the surface more uniformly.

  • Otherwise, the parameters of the filamentary discharge are random and difficult to control. The filamentary and the homogeneous modes can often be readily distinguished with the human eye, because the homogeneous discharge forms are uniformly distributed over the electrode area, whereas the filamentary discharge consists of spatially divided filaments [12].

Due to small discharge geometries (the gap between electrodes generally does not exceed a few millimeters), the understanding of discharge physics is rather difficult, and numerical modeling is therefore an important tool for plasma discharge diagnostics.

DBD modeling can be classified into physical modeling and electrical modeling. Electrical modeling is the modeling by constructing an electrical circuit to characterize the overall discharge behavior of the DBD. The electrical modeling can be used to predict the external quantities such as external current and voltage [13,14,15,16]. On the other hand, the physical modeling is based on theoretical model such as the ionization and fluid models. The physical modeling is commonly used to predict the interaction phenomena between the electrons, ions, molecules and metastables states in the discharge [17].

In the case of a glow discharge where the radial structure of the plasma parameters is homogeneous over the entire volume, the 1D model is rather advisable and has the great advantage of reducing the computation time unlike the two-dimensional model.

With regard to the discharge characteristics of DBD, numerical work shows that homogeneous DBD in helium at atmospheric pressure has two different discharge modes:

  • The glow mode and the Townsend mode. Homogeneous DBD in glow mode has discrete discharge structures similar to DC glow discharges at low pressures. On the other hand, the DBD in Townsend mode has no quasi-neutral region but a positively charged space region, the electric field is not significantly altered in the discharge region, and the current density and electron density are relatively small compared to those of the glow mode [18, 19].

In this paper and in the order of 1 atm of pressure, we developed a 1D fluid model of a glow DBD in helium with a certain level of nitrogen impurities, taking into account the most significant chemical reactions. In fact, the amount of nitrogen added in helium is very small (~ 100 ppm), but its effect on the discharge behavior is very important, which has not been discussed in previous work in 2013 and 2016 for researchers in the same context in the laboratory group of electrical discharge and their applications in Oran. Algeria [20, 21]. The goal therefore is the study of the spatiotemporal evolution of the discharge parameters in a plane and parallel dielectric barrier configuration by means of numerical simulation. By the use of the finites differences method, this is adapted to the numerical processing of the model equations (already used in our preceding works [22,23,24]). The parametric behavior of the discharge is analyzed according to the optimization of the external parameters such as the width of the discharge gap, the thickness of the dielectrics, amplitude and frequency of the external voltage.

The paper is organized as follows: after a general introduction, Sect. 2 describes the DBD geometry. Fluid model descriptions, numerical procedure, simulation parameters and initial–boundary conditions are introduced in Sects. 3, 4, 5 and 6, respectively. Section 7 is devoted to interpretation of the results. The influence of the impurity rate on the discharge physical parameters is presented in Section 8.1. Section 8.2 is dedicated to the effect of impurity on the electrical properties of the discharge, and Sect. 9 summarizes the main conclusions and final remarks.

DBD geometry

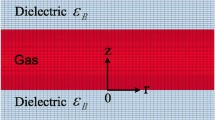
A schema of the DBD reactor considered in this numerical work is depicted in Fig. 1. In this DBD modeling, it is assumed that the discharge region is filled with He-plasma distributed uniformly along the planes parallel to the electrode surface, which enables a 1-D approach to be used for the description of theoretical formulation. The numerical simulation treats the parallel-plate DBD reactor with double dielectric barriers of a = 0.1 cm in thickness and are separated by a plasma region of which gap distance d is 0.5 cm. The relative permittivity of the dielectric barrier material is εr= 10.

Fig. 1
figure 1

Schema a parallel-plate DBD reactor with double dielectric barriers

Full size image

Fluid model descriptions

A self-consistent fluid model is used for the description of low-temperature plasma generated by a DBD at atmospheric pressure, based on a set of balance equations derived from the Boltzmann transport equation. The one-dimensional description considering the axial component x of the plasma, only, assumes in a first approach that the main characteristics of the discharge are not influenced by radial effects.

The Poisson equation for the electric field and the equations of continuity and momentum for all the considered species are solved in a self-consistent way [25]. The resolution of our system of equations is to couple the Poisson equation for the electric field to the transport equations for all species of particles taken into account in our model (Table 1).

Table 1 List of chemical reactions considered for a He–N2 discharge and their rate coefficients [17, 26]
Full size table

The momentum equations are simplified by using the drift–diffusion flux approximation. The governing equations for discharge are [27,28,29]:

  • For electrons:

    $$ \frac{{\partial n_{\mathrm{e}} (x,t)}}{\partial t} + \frac{\partial }{\partial x}\varGamma_{\mathrm{e}} {(}x,t{) } = S_{\mathrm{e}} (x,t ) $$
    (1)

  • For positives ions:

    $$ \frac{{\partial n_{\mathrm{p}} (x,t)}}{\partial t} + \frac{\partial }{\partial x}\varGamma_{\mathrm{p}} (x,t) = S_{\mathrm{p}} (x,t) $$
    (2)

  • For the excited particles (helium metastables state):

    $$ \frac{{\partial n_{\mathrm{m}} (x,t)}}{\partial t} + \frac{\partial }{\partial x}\varGamma_{\mathrm{m}} (x,t) \, = \, G_{\mathrm{m}} (x,t) \, - \, L_{\mathrm{m}} (x,t) $$
    (3)

    ne(x, t), np(x, t) and nm(x, t) are electron, positive ion number and excited particles densities, respectively. Γe(x, t), Γp(x, t) and Γm(x, t) are their flux. The flux densities for electrons, ions and excited particles have the form:

    $$ \varGamma_{\mathrm{e}} (x,t) = - \mu_{\mathrm{e}} n_{\mathrm{e}} (x,t)E(x,t) - \frac{\partial }{\partial x}(D_{\mathrm{e}} n_{\mathrm{e}} (x,t)) $$
    (4)
    $$ \varGamma_{p} (x,t) = \mu_{\mathrm{p}} n_{\mathrm{p}} (x,t)E(x,t) - \frac{\partial }{\partial x}(D_{\mathrm{p}} n_{\mathrm{p}} (x,t)) $$
    (5)
    $$ \varGamma_{\mathrm{m}} (x,t) = - \frac{\partial }{\partial x}\left( {D_{\mathrm{m}} n_{\mathrm{m}} (x,t)} \right) $$
    (6)

    E(x, t) is the electric field, µe and µp are the mobility’s of particles, and De, Dp, Dm are diffusion coefficients for each type of particle.

The source terms Se(x, t) and Sp(x, t) for electrons and ions are given by Radu and Bartnikas [17, 26] and [30]:

$$ \begin{aligned} S_{\mathrm{e}} (x,t) & = S_{\mathrm{p}} (x,t) = \alpha_{\mathrm{ionis}} (x,t)N\mu_{\mathrm{e}} n_{\mathrm{e}} (x,t)E(x,t) \\ & \quad + k_{\mathrm{em}} (x,t)n_{\mathrm{e}} (x,t)n_{\mathrm{m}} (x,t) + k_{\mathrm{pm}} n_{\mathrm{m}} (x,t)N_{\mathrm{imp}} \\ \end{aligned} $$
(7)

The generation term Gm(x, t) and loss term Lm(x, t) for helium metastables atoms adoptees in our model according the works of Radu and Bartnikas are:

$$ G_{\mathrm{m}} (x,t) \, = \alpha_{\mathrm{ex}} (x,t)N\mu_{\mathrm{e}} n_{\mathrm{e}} (x,t) E(x,t) $$
(8)
$$ \begin{aligned} L_{\mathrm{m}} (x,t) & = k_{\mathrm{em}} n_{\mathrm{e}} (x,t)n_{\mathrm{m}} (x,t) + k_{\mathrm{pm}} n_{\mathrm{m}} (x,t)N_{\mathrm{imp}} \\ & \quad + k_{\mathrm{rm}} n_{\mathrm{m}} (x,t) + k_{{ 2 {\text{m}}}} n_{\mathrm{m}} (x,t)N^{2} \\ \end{aligned} $$
(9)

For the calculation of electric potential, Poisson’s equation must be included in the model:

$$ \frac{{\partial^{2} }}{{\partial x^{2} }}V(x,t) = - \frac{q}{{\varepsilon_{0} }}\left( {n_{\mathrm{p}} (x,t) - n_{\mathrm{e}} (x,t)} \right) $$
(10)

q = 1602 × 10−19 C is the elementary charge.

ε0= 8854 × 10−14 F/cm is the free space permittivity.

The electric field is the negative gradient of the electric potential:

$$ E(x,t) = - \frac{\partial }{\partial x}V(x,t) $$
(11)

The electrical properties, i.e., the applied voltage, the gas voltage and the discharge current, are represented according to the following equations:

$$ V_{\mathrm{app}} (t) = V_{\mathrm{m}} \sin \left( {2\pi f \times t} \right) $$
(12)

Knowing that Vm is the amplitudes and f is the frequency of the applied voltage.

$$ V_{\mathrm{g}} (t) = V_{\mathrm{app}} (t) - V_{\mathrm{sd}} (t) = V_{\mathrm{app}} (t) - \frac{1}{{C_{\mathrm{sd}} }}\int\limits_{{t_{0} }}^{t} {I_{\mathrm{d}} (x,t)}\, {\text{d}}t $$
(13)

Note that:

$$ I_{\mathrm{d}} (x,t) = \left| q \right| \cdot S\int\limits_{{t_{0} }}^{t} {\int\limits_{0}^{d} {\left[ {\varGamma_{\mathrm{e}} (x,t) - \varGamma_{\mathrm{p}} (x,t)} \right]} {\text{ d}}x\,{\text{d}}t} $$
(14)

With Vsd (t) is the voltage of the solid dielectrics and Csd its capacitance, S is the area of the electrode.

Numerical procedure

Equations. (1), (2), (3) and (10) are partial differential equations, and the numerical procedure based on finite difference method with an implicit scheme of time [31] is used in their discretization (Fig. 2).

Fig. 2
figure 2

Gird for 1-D finite difference scheme

Full size image

The inter-electrode space is divided into N + 1 equal spatial intervals in x direction, where i = 0 is the boundary point at the left position and i = N + 1 is the boundary point at the right position, Δx the spacial steps along the x axis and Δt being the time step; superscripts k and k + 1 refer to time tk and tk+1, respectively (tk+1= tk+ Δt). Knowing that k =1 means the initial time and k = N is the final time.

After discretization, Eqs. (1) and (2) have the form:

$$ \frac{{n_{i}^{e,k + 1} - n_{i}^{e,k} }}{{{\Delta} t}} + \frac{{\varGamma_{{i + \frac{1}{2}}}^{e,k + 1} - \varGamma_{{i - \frac{1}{2}}}^{e,k + 1} }}{{{\Delta} x}} = S_{i}^{e,k} $$
(15)
$$ \frac{{n_{i}^{p,k + 1} - n_{i}^{p,k} }}{{{\Delta} t}} + \frac{{\varGamma_{{i + \frac{1}{2}}}^{p,k + 1} - \varGamma_{{i - \frac{1}{2}}}^{p,k + 1} }}{{{\Delta} x}} = S_{i}^{p,k} $$
(16)

The 1-D numerical processing of the excited particles equation and Poisson equation Eqs. (3) and (10) according to the centered finite difference method is given as follows:

$$ \frac{{n_{i}^{m,k + 1} - n_{i}^{m,k} }}{{{{\Delta} }t}} - D_{m} \frac{{n_{i + 1}^{m,k + 1} - 2n_{i}^{m,k + 1} + n_{i - 1}^{m,k + 1} }}{{{{\Delta} }x^{2} }} = G_{i}^{m,k} - L_{i}^{m,k} $$
(17)
$$ \frac{{V_{i + 1}^{k + 1} - 2V_{i}^{k + 1} + V_{i - 1}^{k + 1} }}{{{{\Delta} }x^{2} }} = - \frac{q}{{\varepsilon_{0} }}\left( {n_{i}^{p,k} - n_{i}^{e,k} } \right) $$
(18)
$$ E_{{i + \frac{1}{2}}}^{k + 1} = - \left( {\frac{{V_{i + 1}^{k + 1} - V_{i}^{k + 1} }}{{{{\Delta} }x}}} \right),E_{{i - \frac{1}{2}}}^{k + 1} = - \left( {\frac{{V_{i}^{k + 1} - V_{i - 1}^{k + 1} }}{{{{\Delta} }x}}} \right) $$
(19)

The superscripts e, p, m in Eqs. (15), (16) and (17) represent the species of electrons, positive ions and metastables state.

After implementation of exponential form for fluxes of electron and ion densities (Scheme of Scharfetter and Gummel) [32], the relations (4) and (5) become:

For flux of electron:

$$ \varGamma_{{i + \frac{1}{2}}}^{e,k + 1} = \frac{1}{{{{\Delta} }x}}\left[ {n_{i}^{e,k + 1} D_{i}^{e,k + 1} \exp \left( {Z_{1} } \right) - n_{i + 1}^{e,k + 1} D_{i + 1}^{e,k + 1} } \right].\frac{{Z_{1} }}{{\exp \left( {Z_{1} } \right) - 1}} $$
(20)
$$ \varGamma_{{i + \frac{1}{2}}}^{p,k + 1} = \frac{1}{{{\Delta} x}}\left[ {n_{i}^{p,k + 1} D_{i}^{p,k + 1} \exp \left( {Z_{1} } \right) - n_{i + 1}^{p,k + 1} D_{i + 1}^{p,k + 1} } \right].\frac{{Z_{1} }}{{\exp \left( {Z_{1} } \right) - 1}} $$
(21)

where

$$ Z_{1} = \left( { - \frac{{\mu_{i + 1}^{e,k + 1} + \mu_{i}^{e,k + 1} }}{{D_{i + 1}^{e,k + 1} + D_{i}^{e,k + 1} }}} \right)\left( {V_{i + 1}^{k + 1} - V_{i}^{k + 1} } \right), $$
$$ Z_{2} = \left( { - \frac{{\mu_{i}^{e,k + 1} + \mu_{i - 1}^{e,k + 1} }}{{D_{i}^{e,k + 1} + D_{i - 1}^{e,k + 1} }}} \right)\left( {V_{i}^{k + 1} - V_{i - 1}^{k + 1} } \right). $$

Flux for ion density has the same form like flux for electron density.

By inserting the relations (19), (20) and (21) into Eqs. (15), (16), we get:

$$ \begin{aligned} &\Delta tA_{1} n_{i + 1}^{e,k + 1} + \left( {\Delta x +\Delta tA_{2} } \right)n_{i}^{e,k + 1} +\Delta tA_{3} n_{i - 1}^{e,k + 1} \\ & \quad = xn_{i}^{e,k} +\Delta x\Delta t\alpha_{ionis}^{k} N\mu_{e} n_{i}^{e,k} E_{i}^{k} \\ & \quad \quad+\Delta x\Delta tk_{em}^{k} n_{i}^{e,k} n_{i}^{m,k} +\Delta x\Delta tk_{pm} n_{i}^{m,k} N_{imp} \\ \end{aligned} $$
(22)
$$ \begin{aligned} &\Delta tB_{1} n_{i + 1}^{p,k + 1} + \left( {\Delta x +\Delta tB_{2} } \right)n_{i}^{p,k + 1} +\Delta tB_{3} n_{i - 1}^{p,k + 1} \\ & \quad =\Delta xn_{i}^{p,k} +\Delta x\Delta t\alpha_{\mathrm{ionis}}^{\text{k}} N\mu_{e} n_{i}^{e,k} E_{i}^{k} \\ & \quad \quad +\Delta x\Delta tk_{em}^{k} n_{i}^{e,k} n_{i}^{m,k} +\Delta x\Delta tk_{pm} n_{i}^{m,k} N_{imp} \\ \end{aligned} $$
(23)

where

$$ A_{1} = \frac{{ - Z_{1} \left( {\frac{1}{{\Delta x}}} \right)D_{i + 1}^{e,k + 1} }}{{\exp (Z_{1} ) - 1}}, $$
$$ A_{2} = \frac{{Z_{1} \left( {\frac{1}{{\Delta x}}} \right)D_{i}^{e,k + 1} }}{{\exp (Z_{1} ) - 1}} \cdot \exp (Z_{1} ) + \frac{{Z_{2} \left( {\frac{1}{{\Delta x}}} \right)D_{i}^{e,k + 1} }}{{\exp (Z_{2} ) - 1}}, $$
$$ A_{3} = \frac{{ - Z_{2} \left( {\frac{1}{{\Delta x}}} \right)D_{i - 1}^{e,k + 1} }}{{\exp (Z_{2} ) - 1}} \cdot \exp (Z_{2} ). $$

The coefficients B1, B2, B3 for ions have the same form as A1, A2, A3 for electrons.

After arranging, the equation for excited particles (17) and Poisson’s Eq. (18) take the form:

$$ \begin{aligned} & -\Delta tD_{m} n_{i + 1}^{m,k + 1} + \left( {\Delta x^{2} + 2\Delta tD_{m} } \right)n_{i}^{m,k + 1} -\Delta tD_{m} n_{i - 1}^{m,k + 1} \\ & \quad =\Delta x^{2} n_{i}^{m,k} +\Delta t\Delta x^{2} \alpha_{ex}^{k} N\mu_{e} n_{i}^{e,k} E_{i}^{k} -\Delta t\Delta x^{2} k_{em}^{k} n_{i}^{e,k} n_{i}^{m,k} \\ & \quad \quad -\Delta t\Delta x^{2} k_{pm} n_{i}^{m,k} N_{imp} -\Delta t\Delta x^{2} k_{rm} n_{i}^{m,k} -\Delta t\Delta x^{2} k_{2m} n_{i}^{m,k} N_{{}}^{2} \\ \end{aligned} $$
(24)
$$ V_{i + 1}^{k + 1} - 2V_{i}^{k + 1} + V_{i - 1}^{k + 1} = -\Delta x^{2} \frac{q}{{\varepsilon_{0} }}\left( {n_{i}^{p,k} - n_{i}^{e,k} } \right) $$
(25)

The iteration procedure for equations of the electrical properties in the points of the grid (Fig. 2) is presented as follows:

$$ V_{\mathrm{app}}^{k} = V_{M} \sin \left( {2\pi f \times t^{k} } \right) $$
(26)
$$ V_{\mathrm{g}}^{k} = V_{\mathrm{app}}^{k} - V_{\mathrm{sd}}^{k} = V_{\mathrm{app}}^{k} - \frac{1}{{C_{\mathrm{sd}} }}\left[ \sum\limits_{k = 1}^{k = N} {I_{d_{{i + \frac{1}{2},i - \frac{1}{2}}}^{k}}}\Delta t \right] $$
(27)

with

$$ I_{d_{{i + \frac{1}{2}}}^{k}} = \left| q \right| \cdot S\left[ {\sum\limits_{k = 1}^{k = N} {\sum\limits_{i = 0}^{i = N + 1} {\left( {\varGamma_{{i + \frac{1}{2}}}^{e,k} - \varGamma_{{i + \frac{1}{2}}}^{p,k} } \right)} }\Delta x\Delta t} \right] $$
(28)
$$ I_{d_{{i - \frac{1}{2}}}^{k}} = \left| q \right| \cdot S\left[ {\sum\limits_{k = 1}^{k = N} {\sum\limits_{i = 0}^{i = N + 1} {\left( {\varGamma_{{i - \frac{1}{2}}}^{e,k} - \varGamma_{{i - \frac{1}{2}}}^{p,k} } \right)} }\Delta x\Delta t} \right] $$
(29)

Equations (22), (23), (24) and (25) are the system of linear equations which are solved by Thomas’s algorithm. Details will be given in literature [33, 34].

Simulation parameters

All constants and coefficients necessary to carry out the calculations have been taken from the work on atmospheric pressure helium discharges presented by Radu and Bartnikas [17, 26]:

The electron diffusion coefficient is a function of electric field given by the relationships:

$$ \left\{ {\begin{array}{*{20}l} {D_{\mathrm{e}} (x,t) = 5,43 \times 10^{3} \left( {\frac{{\left| {E(x,t)} \right|}}{3040}} \right){\text{ cm/s }}} \hfill & \quad {\text{ if}}\; E \le 3040\;{\text{V}}/{\text{cm}} \hfill \\ {D_{\mathrm{e}} (x,t) = 5,43 \times 10^{3} \;{\text{cm}}^{2} /{\text{s }}} \hfill & \quad {\text{if}}\; E > 3040\, {\text{V/cm}} \hfill \\ \end{array} } \right. $$

The ionization coefficient and the excitation coefficients are, respectively, represented in function of electric field by the relationships:

$$ \left\{ \begin{array}{ll} N\alpha_{\mathrm{ionis}} (x,t) = 0 &\quad {\text{for}}\;\, E \le 2280\;{\text{V/cm}} \hfill \\ N\alpha_{\mathrm{ionis}} (x,t) = 9.32 \times 10^{ - 5} \left( {\left| {E(x,t)} \right| - 2280} \right)^{1.5} {\text{cm}}^{ - 1} &\quad {\text{ for}}\,\;E > 2280\;{\text{V/cm }} \hfill \\ \end{array} \right. $$

and

$$ \left\{ \begin{array}{ll} N\alpha_{\mathrm{ex}} (x,t) = 0 &\quad {\text{ for}}\,\, E\;\; \le 2280 \;{\text{V/cm}} \hfill \\ N\alpha_{\mathrm{ex}} (x,t) = 1.54 \times \left( {\left| {E(x,t)} \right| - 2280} \right)^{0.6} {\text{cm}}^{ - 1} &\quad {\text{for}}\,\,E > 2280\;{\text{V/cm}} \hfill \\ \end{array} \right. $$

The stepwise ionization coefficient is defined as:

$$ \left\{ \begin{array}{ll} k_{\mathrm{em}} (x,t) = 0 { }&\quad {\text{for}} \;\;E \le 380 \,{\text{V/cm}} \hfill \\ k_{\mathrm{em}} (x,t) = 3.03 \times 10^{ - 9} \left( {\left| {E(x,t)} \right| - 380} \right)^{0.4} {\text{ cm}}^{3} / {\text{s}}&\quad {\text{for}}\;\;E > 380\; {\text{V/cm}} \hfill \\ \end{array} \right. $$

Table 2 gathers the simulation parameters which are necessary in our modeling.

Table 2 Definition of constants and coefficients for simulation
Full size table

Boundary and initial conditions

Because the discharge under study is a DBD, the effect of the dielectrics covering the electrodes needs to be taken into account in the model. On the interface between the dielectric and the plasma, the influence of charge accumulation on the dielectric material σ is considered using Gauss’s law:

$$ \varepsilon_{\mathrm{Diel}} \overrightarrow {E}_{{_{\mathrm{Diel}} }} \cdot \overrightarrow {u}_{\mathrm{n}} - \varepsilon_{\mathrm{gas}} \overrightarrow {E}_{\mathrm{gas}} \cdot \overrightarrow {u}_{\mathrm{n}} = \sigma $$

It is the boundary conditions for the electric field in Poisson’s equation, where EDiel and Egas are the electric field inside the dielectric and in the gas discharge, respectively, un is the unit vector pointing normal to the wall, where the charge accumulation takes place [35]. σ is the surface charge density on the dielectric, calculated from the charged particle flux directed to the surface at cathode and anode, respectively, by:

$$ \frac{{\partial \left. {\sigma \left( t \right)} \right|_{\mathrm{Cath}} }}{\partial t} = \left| q \right|\left( {\varGamma_{\mathrm{p}} (1 + \gamma_{ \sec } )} \right) $$
$$ \frac{{\partial \left. {\sigma \left( t \right)} \right|_{\mathrm{Anod}} }}{\partial t} = \left| q \right|\left( {\varGamma_{\mathrm{p}} - \varGamma_{\mathrm{e}} } \right) $$

The boundary values of electric potential at the two electrodes are:

At the left electrode: V = VApp

At the right electrode: V =0 V.

The boundary values of space density and flux particles at cathode are:

$$ \varGamma_{\mathrm{e}} = - \gamma_{\sec} \varGamma_{\mathrm{p}} ,\nabla n_{\mathrm{p}} = 0,\nabla n_{\mathrm{m}} = 0 $$

At anode:

$$ \nabla n_{\mathrm{p}} = \nabla n_{\mathrm{e}} = \nabla n_{\mathrm{m}} = 0 $$

As an initial condition for the simulation, electrons, ions, metastables state and surface charge are uniformly distributed in the discharge gap with an initial density [36, 37]:

$$ \begin{aligned} &n_{\mathrm{e}} (t = 0) = n_{\mathrm{p}} (t = 0) = 10^{6} ({\text{cm}}^{ - 3} ) \hfill \\ & n_{\mathrm{m}} (t = 0) = 10^{9} ({\text{cm}}^{ - 3} ) \hfill \\ &\sigma (t = 0) = 10^{ - 8} ({\text{C/cm}}^{2} ) \hfill \\ \end{aligned} $$

Results and discussion

The DBD simulation conditions in He–N2 mixture with a rate of N2 is 100 ppm at atmospheric pressure are considered as follows: the discharge gap is d =0.5 cm, the amplitude Vm of the voltage source is 1.3 kV, while the frequency is fixed at 10 kHz. The dielectric thickness is a = 0.1 cm. The time step is 10−9 s.

The value of gas capacitance and equivalent capacitance of two dielectric barriers were calculated, respectively, according to these equations [38]:

$$ C_{\mathrm{g}} = \frac{{\varepsilon_{0} \cdot S}}{d} = 2.22\;{\text{pF}} $$
$$ C_{\mathrm{sd}} = \frac{{\varepsilon_{0} \varepsilon_{\mathrm{r}} \cdot S}}{2a} = 4 7. 2\;{\text{ pF}} $$

The profiles of the applied voltage VApp (t), the gas voltage Vg (t) and the discharge current Id (t) during one cycle of applied voltage are illustrated in Fig. 3.

Fig. 3
figure 3

Time variation of the calculated values of applied voltage VApp(t), gas voltage Vg(t) and discharge current Id(t) during one cycle of applied voltage

Full size image

The duration of the discharge is about 5 μs (time interval t2 − t1) for the positive half cycle of the applied voltage, in this time interval, there is a sudden increase in the current from 1 to a maximum of 32.1 mA for the positive peak of the Id, in the negative alternation of Vapp, the discharge current keeps its behavior but in the sign (−) and the peak value of the negative peak reaches 33 mA, and the profile of the discharge current remains exactly the same from one cycle to another, i.e., it has the same periodicity as the external voltage. In our case, this behavior of the discharge current shows that there is only one breakdown per half cycle of the applied voltage, and this is the most important feature of the glow regime of DBD under atmospheric pressure.

For the temporal variation of the gas voltage Vg during one period of Vapp: the voltage Vg increases from 705.3 V at time t = 0 s to 1.2 kV for t = 9 μs, which corresponds at the instant just before the first discharge appears. A value of 1.2 kV of voltage sufficient to maintain the breakdown of the gas, the fall of Vg after the moment of the peak of the current causes the extinction of the discharge and during the next half cycle of Vapp, a new negative voltage Vg will trigger the ignition of the second discharge and so on for the cycles Following, the profile of the gas voltage during the time interval of the discharge follows the profile of the discharge current.

Therefore, at each half cycle of the discharge, the accumulation of charges in the inner layers of the dielectric barriers generates an opposite voltage called dielectric voltage Vsd which in turn reduces the voltage Vg and causes the extinction of the discharge avoiding the formation of the electric arc and consequently the generation of cold plasma.

When the calculation of the electric field is directly proportional to the electron and ion densities, we have chosen to represent the characteristics of the discharge for the helium–nitrogen impurities at atmospheric pressure in only one figure.

Figure 4 shows the numerical results of the spatial distribution of the electric field as well as the electron and ion densities obtained at the time when the discharge current is maximal (at t =10 µs).

Fig. 4
figure 4

Spatial distributions of electric field, electron density and ion density at the maximum of the discharge current. The cathode is on the left side and the anode on the right side

Full size image

The discharge characteristics have similarities to those appeared in the dc glow discharge at low pressure, and they are distinguished by four discharge regions featuring the typical glow mode.

First, a cathode fall region exists where the electric field drops drastically from a maximum value of about 16.5 kV/cm to nearly zero because of large positive space charges near the cathode; in this region the density of ions reaches a maximum value of 4.7 × 1011 cm−3 and a maximum of 3.6 × 1011 cm−3 for the electrons. Thickness of the cathode fall is about 0.29 mm. At the cathode, the ions are the majority with respect to the electrons, because the electrons leave this region quickly under the effect of drift in the presence of a strong electric field and leaving behind them a quantity of the positive ions. Near the cathode, the electron density is small but never zeros (ne ≈ 2 × 107 cm−3) because the cathode region is the source of electron generation by the secondary emission process, which is taken into account in our modeling.

The second region that corresponds to negative glow extends to 0.73 mm in thickness, where the electron and ion densities are equal and the electric field remains low. Then, the electric field increases and the electron and ion densities are very close: it is the Faraday dark space. Its thickness is of the order of 1.4 mm. In this zone, a small negative space charge is formed.

The 4th observed zone occupies the most space: it is the positive column, a region of electrically neutral plasma. Its width is 2.58 mm, and the electric field is constant. The value of this field is relatively low and close to 2 kV/cm. The electron and ion densities are equal; with a density is approximately 2 × 1010 cm−3. In this region, the mobility of the electrons is reduced because of their interaction with the ions.

In our case, the helium metastables are included in the model; the spatial distribution of the density of these excited particles at the moment when the discharge current is maximal is shown in Fig. 5

Fig. 5
figure 5

Spatial distribution of the Helium metastables density at the moment when the discharge current is maximal

Full size image

The distribution profile of the metastables density is very similar to the profiles of the electron and ion densities; with a maximum density calculated in the region of cathode fall is reached 6.3 × 1011 cm−3, it is constant in the area of the positive column and its value is about 1.2 × 1011 cm−3.

In terms of validation, our numerical simulation results of the discharge parameters were very similar to the results of the work in the same context, namely the result of literature [39,40,41,42,43,44].

In this paragraph, we present a study on the kinetics of electrons and ions in helium in a glow discharge at atmospheric pressure.

The mobility of electrons and ions characterizes the speed with which an electron or ion can move through a medium, when driven by an electric field, while we find that the neutral and excited metastables particles tend to diffuse by the influence of the diffusion coefficient since their mobility is null.

When an electric field E is applied, electrons and ions respond by moving with a mean velocity called drift velocity.

The drift velocity is a parameter defined by the product of the mobility and the electric field Wi= sµiE, with µi is the mobility of the particles of type i and s is a parameter which is 1 for the positive ions and − 1 for the electrons, the drift velocity closely depends on the value of the electric field.

Figure 6 shows the variation of electron drift velocity We and ion drift velocity Wp as a function of the electric field at an impurity rate of 100 ppm of N2. The electron and ion drift velocities vary linearly with the electric field, the electrons move with a much greater velocity than ions under the effect of the electric field, drift velocities reach up to 3.4 × 107 cm/s for electrons and 4.8 × 105 cm/s for the positive ions when the electric field is maximum, the electrons are about 71 times faster than the positive ions, this is due to the fact that the electrons are very light because of the difference in mass between them and the ions, they quickly acquired kinetic energy in the presence of an intense electric field which is responsible for their very fast movement, while the very heavy ions remain almost immobile compared to the electrons.

Fig. 6
figure 6

Evolution of the electron and ion drift velocity as a function of the electric field

Full size image

Influence of the impurity rate

Impurity effect on physical properties

In this part of work, we have varied the concentration rate of nitrogen as an impurity present in the gas with rates, respectively, 150 ppm, 100 ppm, 70 ppm, 50 ppm and 10 ppm; under the same previous conditions of the discharge, we will study the influence of the impurity rate on the evolution of charged and excited particles, as well as the spatial distribution of the electric field at the time when the discharge current is maximal.

Figures 7 and 8 show, respectively, the spatial evolution of the electron and ion densities for different impurity rates. These figures clearly show that the densities of electrons and ions increase with increase in impurity rates, for example at 150 ppm of nitrogen impurities, a peak of about 7 × 1011 cm−3 for electron density and 8 × 1011 cm−3 for ions in the cathode fall region. A growth in the generation of charged particles almost two times compared to 100 ppm and more than seven times compared to 50 ppm, this increase in densities continues in Faraday dark space and positive column zones. This increase at the level of the charged particles is due to the penning effect, as an indication, the percentage of the presence of the N2 molecules in gas promotes the generation of the electrons in more and consequently of the positive ions He+ following the reaction of ionization penning:

$$ {\text{He}}^{*} \, + \,{\text{N}}_{2} \, \to \,{\text{He}}\, + \,{\text{N}}_{2}^{ + } \, + \,{\text{e}}. $$
Fig. 7
figure 7

Spatial distribution of the electron densities for various nitrogen impurities level

Full size image
Fig. 8
figure 8

Spatial distribution of the ion densities for various nitrogen impurities level

Full size image

For 150 ppm, 100 ppm, 70 ppm and 50 ppm, the discharge keeps its glow regime and at a rate less than or equal to 10 ppm, the densities of electron and ion are very low, and its profiles do not correspond to glow mode of the discharge at atmospheric pressure. Note that this difference in discharge behavior at ≤ 10 ppm is attributed to the fact that the contribution of the Penning effect to electron production is lower when the nitrogen concentration is decreased. The loss of electrons by recombination becomes predominant and is no longer compensated by the electronic production by the process of ionization and direct excitation.

The influence of impurity rates on the spatial distribution of the electric field (Fig. 9) appears mainly in the regions of cathode fall and positive column. At 100 and 150 ppm, there is a contraction in the area of the cathode fall (< 0.3 mm), while the area of the positive column widens (> 2.5 cm). The electric field is very intense near the cathode due to the high space charge in the area of the cathode fall, low and constant in the positive column. On the other hand, at 70 and 50 ppm of N2 the positive column decreases and the length of the cathode fall increases.

Fig. 9
figure 9

Spatial distribution of the electric field for various nitrogen impurities level

Full size image

At a rate = 10 ppm, the electric field is very weak and no distinct zone of the glow discharge appears.

Contrary to what is observed in Figs. 7 and 8, Fig. 10 shows that the densities of metastables increase when the concentration of N2 molecules in the gas is decreased, and a density peak close to 2.5 × 1012 cm−3 is observed for 10 ppm, which is almost 13 times larger than the maximum density recorded at 150 ppm; this shows that the effect of Penning ionization at high impurity levels dominates the other processes in terms of generation and loss of metastables and accelerates the rate of its destruction.

Fig. 10
figure 10

Spatial distribution of the metastables densities for various nitrogen impurities level

Full size image

Figure 11a–d, respectively, shows the effect of the N2 impurity at concentrations of 150 ppm, 100 ppm, 50 ppm and in the case of without impurity on the evolution of drift velocities of electrons and ions. The variations of the drift velocities are very different in all cases between electrons and positive ions. They increase gradually with the increase in the electric field values in the case of concentrations of 150 ppm, 100 ppm and 50 ppm. At a maximum electric field of 17.4 kV/cm, they reach a maximum value estimated at 4 × 107 cm/s for We and 5.6 × 105 cm/s for Wp at a concentration of 150 ppm and do not exceed a maximum of 1.8 × 107 cm/s and 2.7 × 105 cm/s for We and Wp, respectively, at a concentration of 50 ppm. At case without impurity, We and Wp are very slow and constant because the electric field is weak and almost invariable and their maximum values do not exceed 4.4 × 106 cm/s for the electrons and 6.3 × 104 cm/s for ions. As an indication, We and Wp in the case of 150 ppm are about 9 times larger than We and Wp in the case of without impurity. This confirms the apparent effect of the N2 impurity concentration in the gas on the electrically charged particle drift velocities, since the high concentrations of impurities increase the electric field values as previously demonstrated in (Figs. 7 and 8), which increases the velocity of plasma species because of its strong coupling to the electric field.

Fig. 11
figure 11

Evolution of the electron and ion drift velocity for various nitrogen impurities level and without impurity

Full size image

Impurity effect on electrical properties

Let us discuss in this part the influence of the N2 concentration on the electrical properties of the discharge, in particular the gas voltage, i.e., the discharge voltage and the discharge current. We chose to plot the results for a three different levels of nitrogen impurities: 150 ppm, 100 ppm and without impurity (0 ppm).

The sinusoidal applied voltage is imposed by the external supply of the discharge at an amplitude is fixed at 1.3 kV. In Fig. 12, a remarkable influence of the nitrogen impurities is observed on the time profile of the discharge voltages. For the positive half cycle of the applied voltage, the onset discharge voltage is 810 V at 150 ppm which is higher than the onset voltage of the discharge for 100 ppm (~ 705 V), while it does not exceed 117 V in the case of without impurities; then, they increase steeply up to a maximum value of 1436 V for 150 ppm and 1115 V at 100 ppm which correspond to the moment of the first breakdown of the gas and the ignition of the discharge, but the voltage in the case of without impurities remains very low (~ 195 V) and much lower than the voltage of the breakdown of the gas, which never leads to the appearance of the discharge. For the next half cycle of the applied voltage, the same process is repeated for the values and forms of the voltages but with an opposite sign.

Fig. 12
figure 12

Impurity influence on the temporal variation of the gas voltage

Full size image

Therefore, the effect of increase in the impurity concentration is directly proportional to the increase in the discharge voltages, which in turn accelerates the appearance of the discharge.

The results obtained confirm that the absence of impurities in the gas does not lead to any discharge (Fig. 13).

Fig. 13
figure 13

Influence of impurity on the temporal variation of the discharge current

Full size image

The influence of the impurities is manifested on the positive and negative peaks of the discharge current; for example, a value of (44.3 mA and − 49.1 mA), respectively, for + and − peaks recorded at 150 ppm of nitrogen and (32 mA and − 33.2 mA) recorded per 100 ppm of N2, On the other hand, a zero current is observed for the whole of time in the case without impurities due to the impossibility to reach the minimum value of the breakdown voltage in this case.

The increase in current intensity is due to the abundance of electrons and positive ions (electric charge carriers), whenever the concentration of impurities is large (demonstrated results in Figs. 7 and 8). The increase in the concentration of impurities somewhat accelerates the onset of the first discharge and reduces its duration.

Conclusions and final remarks

A 1-D fluid simulation of homogeneous dielectric barrier discharge at atmospheric pressure in He–N2 mixture has been developed in a parallel-plate geometry, while adopting the assumption of the approximation of the local electric field.

Due to the rapid evolution of physical phenomena in the plasma and the strong coupling between the particle transport equations and the Poisson’s equation, we must adopt a very adequate computation time step. These calculations were made possible in a reasonable computation time using a very efficient implicit numerical scheme ‘unconditionally stable’ of the finite difference method for the momentum and momentum transfer equations.

The simulation results for the variation of the discharge current well reflect the behavior of a glow discharge (presence a single peak of current per half period) and a spatial structure of the electric field; electron and ion density are similar to that for an ordinary DC glow discharge a low pressure is formed during the breakdown. This confirms that the uniform DBD in atmospheric helium is a glow type discharge.

At atmospheric pressure condition, glow discharge can be stable and dependent on the external parameters of discharge, i.e., the amplitude and frequency of external voltage, width of the discharge gap and thickness of the dielectric barriers. The values of these external parameters have been mentioned in the “Results and discussion” section.

Our model indicates that Penning ionization of nitrogen impurities by helium metastables plays a major role; it is the dominant ionization mechanism in the discharge which strongly exceeds direct ionization, direct excitation and stepwise ionization. The effect of increasing the level of impurities is evident in increasing the velocity of the charged particles, in the discharge current peaks and the discharge voltage.

Without the addition of nitrogen impurities, no gas breakdown occurred and the simulation gave no results. As well, this type of ionization can occur at low electric field levels, which helps to maintain the discharge under these conditions and to produce more charged particles. We therefore conclude that Penning ionization is a necessary mechanism for obtaining a glow discharge at atmospheric pressure.