Abstract
We introduce a new class of stochastic partial differential equations (SPDEs) with seed bank modeling the spread of a beneficial allele in a spatial population where individuals may switch between an active and a dormant state. Incorporating dormancy and the resulting seed bank leads to a two-type coupled system of equations with migration between both states. We first discuss existence and uniqueness of seed bank SPDEs and provide an equivalent delay representation that allows a clear interpretation of the age structure in the seed bank component. The delay representation will also be crucial in the proofs. Further, we show that the seed bank SPDEs give rise to an interesting class of “on/off”-moment duals. In particular, in the special case of the F-KPP Equation with seed bank, the moment dual is given by an “on/off-branching Brownian motion”. This system differs from a classical branching Brownian motion in the sense that independently for all individuals, motion and branching may be “switched off” for an exponential amount of time after which they get “switched on” again. On/off branching Brownian motion shows qualitatively different behaviour to classical branching Brownian motion and is an interesting object for study in itself. Here, as an application of our duality, we show that the spread of a beneficial allele, which in the classical F-KPP Equation, started from a Heaviside intial condition, evolves as a pulled traveling wave with speed \(\sqrt{2}\), is slowed down significantly in the corresponding seed bank F-KPP model. In fact, by computing bounds on the position of the rightmost particle in the dual on/off branching Brownian motion, we obtain an upper bound for the speed of propagation of the beneficial allele given by \(\sqrt{\sqrt{5}-1}\approx 1.111\) under unit switching rates. This shows that seed banks will indeed slow down fitness waves and preserve genetic variability, in line with intuitive reasoning from population genetics and ecology.
Similar content being viewed by others
1 Introduction and main results
1.1 Motivation
One of the most fundamental models in spatial population genetics and ecology, describing the spread of a beneficial allele subject to directional selection, was introduced by Fisher in [14]. Denoting by \(p(t,x)\in [0,1]\) the frequency of the advantageous allele at time \(t\ge 0\) and spatial position \(x \in \mathbb {R}\), and assuming diffusive migration of individuals (described by the Laplacian), Fisher considered the partial differential equation
The same system was independently investigated around the same time by Kolmogorov, Petrovsky, and Piscounov in [25], and thus the above PDE is now commonly known (and abbreviated) as F-KPP Equation, see e.g. [9] for a recent overview. It is well known that there exists a so called travelling wave solution with speed \(\sqrt{2}\) meaning that there exists a function w such that
solves (1.1). Much finer results about the asymptotic behaviour of the wave-speed and the shape of the function w are known (see e.g. [10, 26, 32]), and the F-KPP Equation and its extensions with different noise terms are still an active field of research (see e.g. [24, 30]). A very interesting feature of the F-KPP Equation and a main reason for the amenability of its analysis is given by the fact that the solution to (1.1) is dual to branching Brownian motion (BBM), as was shown by McKean [29] (and earlier by Ikeda, Nagasawa and Watanabe [18]). Indeed, starting in a (reversed) Heaviside initial condition given by \(p(0,\cdot ):= \mathbf{1}_{]-\infty , 0]}\), we have the probabilistic representation
where \((R_t)_ {t\ge 0}\) is the position of the rightmost particle of a (binary) branching Brownian motion with branching rate 1, started with a single particle in 0. Bramson [11] then also showed that the rightmost particle of this system thus governs the asymptotic wave-speed of the original equation via the equality
Since the days of Fisher, mathematical modeling in population genetics has expanded rapidly, and many additional “evolutionary forces” have been incorporated into the above model. For example, one may include mutations between alleles and a “Wright-Fisher noise” as a result of random reproduction, leading to the system
Here \(m_1\ge 0\) and \(m_2\ge 0\) are the mutation rates to and from the beneficial allele, \(s\ge 0\) denotes the strength of the selective advantage of the beneficial allele, \(\nu \ge 0\) governs the variance of the reproductive mechanism and \(W=(W(t,x))_{t \ge 0, x \in \mathbb {R}}\) denotes a Gaussian white noise process. The Wright-Fisher noise term is the standard null-model of population genetics, in the non-spatial setting corresponding to an ancestry governed by the Kingman-coalescent [23]. A justification for its use in population genetics can be found in [30].
From a biological point of view one may think of a one-dimensional habitat modeled by \(\mathbb {R}\) on which two types (or species) compete for limited resources. The Heaviside initial condition (induced perhaps by some initial spatial barrier separating the two interacting types) admits a detailed analysis of the impact of the selective advantage of the beneficial type on its propagation in space (see e.g. [35]).
Recently, an additional evolutionary mechanism has drawn considerable attention in population genetics. Indeed, dormancy, and, as a result, seed banks, are both ubiquitous in microbial species as well as crucial for an understanding of their evolution and ecology (see e.g. [28, 36]). Corresponding discrete-space population genetic models have recently been studied in [15] and non-spatial models, where dormancy and resuscitation are modeled in the form of classical migration between an active and an inactive state, have been derived and investigated in [6] and [7] (these papers also provide biological background and motivation). There, the population follows a two-dimensional “seed bank diffusion”, given by the system of SDEs
where p describes the frequency of the allele under consideration in the active population, and q its frequency in the dormant population. The constants \(c,c'>0\) represent the switching rates between the active and dormant states, respectively, and \((B(t))_{t\ge 0}\) is a standard Brownian motion. Though reminiscent of Wright’s two island model (cf. [5]), the system above exhibits quite unique features. For example, it is dual to an “on/off”-coalescent (instead of the Kingman coalescent), in which lines may be turned on and off with independent exponential rates given by c and \(c'\). Lines which are turned off are prevented from coalescences. Note that this structure also appears in the context of meta-population models from ecology, see [27]. It can be shown that this new “seed bank coalescent” does not come down from infinity and exhibits qualitatively prolonged times to the most recent common ancestor [7]. A further interesting feature is that the above system exhibits a long-term memory, which can be well understood in a delay SDE reformulation obtained in ([5, Prop. 1.4]). Assume starting frequencies \(p_0=x\in [0,1], q_0=y \in [0,1]\) and for simplicity \(c=c'=1\). Then, the solution to (1.6) is a.s. equal to the unique strong solution of the stochastic delay differential equations
with the same initial condition. The result rests on the fact that there is no noise in the second component and can be proved by a integration-by-parts argument. The second component is now just a deterministic function of the first.
It appears natural to incorporate the above seed bank components into a F-KPP framework in order to analyse the combined effects of seed banks, space and directional selection. We will thus investigate systems of type
where \(c,c'\ge 0\) are the switching rates between active and dormant states, \(s\ge 0\) is the selection parameter, \(\nu \ge 0\) the reproduction parameter and \(m_1,m_2 \ge 0\) are the mutation parameters. One may view this as a continuous stepping stone model (cf. [33]) with seed bank. Due to technical reasons, which will become clear in Sect. 3, it is actually advantageous for us to consider in the following the process
satisfying the system
instead. We expect to see the on/off mechanism of (1.6) emerge also in the dual of the above system. In particular, in the F-KPP Equation with seed bank (setting \(s=1\) for simplicity) given by
we expect to obtain an “on/off branching Brownian motion” with switching rates \(c,c'\) and branching rate 1 as a moment dual. Further, we aim to derive a delay representation for the above SPDE and hope to get at least partial information about the wave speed of a potential traveling wave solution. Intuition from ecology suggests that the spread of the beneficial allele should be slowed down due to the presence of a seed bank. However, we also expect new technical problems, since the second component v(t, x) comes without the Laplacian, so that all initial roughness of \(v_0\) will be retained for all times, preventing jointly continuous solutions.
1.2 Main results
In this section, we summarize the main results of this paper. We begin by showing that our Equation (1.7) is well-defined, i.e. we establish weak existence, uniqueness and boundedness of solutions. This is done via the following theorems:
Theorem 1.1
The SPDE given by Eq. (1.7) for \(s,c,c',m_1,m_2, \nu \ge 0\) with initial conditions \((u_0,v_0) \in B(\mathbb {R},[0,1]) \times B(\mathbb {R},[0,1])\) has a weak solution (u, v) (in the sense of Definition 2.3 below) with paths taking values in \(C(]0,\infty [,C(\mathbb {R},[0,1])) \times C([0,\infty [, B(\mathbb {R},[0,1]))\).
Here, for Banach spaces X and Y we denoted by B(X, Y) the space of bounded, measurable functions on X taking values in Y and by C(X, Y) the space of continuous functions on X taking values in Y. We usually suppress the dependence on the image space whenever our functions are real-valued and equip both spaces with the topology of locally uniform convergence.
Theorem 1.2
Under the conditions of Theorem 1.1, the SPDE (1.7) exhibits uniqueness in law on \(C(]0,\infty [,C(\mathbb {R},[0,1])) \times C([0,\infty [, B(\mathbb {R},[0,1]))\).
Note that it turns out that the absence of a Laplacian in the second equation in (1.7) gives rise to technical difficulties regarding existence and uniqueness. However, as in the seed bank diffusion case, a reformulation as a stochastic partial delay differential equation is possible allowing one to tackle these issues. To our knowledge, this is a new application of a delay representation in this context, and a detailed explanation of this approach can be found in Sect. 2.
Proposition 1.3
The Eq. (1.7) is equivalent to the Stochastic Partial Delay Differential Equation (SPDDE)
in the sense that under the same initial conditions solutions of (1.7) are also solutions of (1.9) and vice versa.
Remark 1.4
Proposition 1.3 gives rise to an elegant interpretation of the delay term. It shows that the type of any “infinitesimal” resuscitated individual is determined by the active population present an exponentially distributed time ago (with a cutoff at time 0), which the individual spent dormant in the seed bank (cf. Proposition 1.4. in [5]).
Another major tool needed for deriving the uniqueness result is the powerful duality technique, i.e. we prove a moment duality with an “on/off branching coalescing Brownian motion” (with killing) which as in [3] we define slightly informally as follows. For a rigorous construction, we refer the reader to the killing and repasting procedure of Ikeda, Nagasawa and Watanabe (cf. [16,17,18]) or [2]. Note also that the introduction of the on/off-mechanism will lead, as in the on/off-coalescent case in [7], to an extension of the state space allowing each particle to carry an active or dormant marker.
Definition 1.5
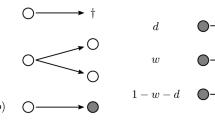
We denote by \(M=(M_t)_{t \ge 0}\) an on/off branching coalescing Brownian motion with killing taking values in \(\bigcup _{k \in \mathbb {N}_0} \left( \mathbb {R}\times \lbrace {\varvec{a}},{\varvec{d}}\rbrace \right) ^k\) starting at \(M_0= ((x_1,\sigma _1), \ldots , (x_n,\sigma _n ))\in \left( \mathbb {R}\times \lbrace {\varvec{a}}, {\varvec{d}}\rbrace \right) ^n\) for some \(n \in \mathbb {N}\). Here the marker \({\varvec{a}}\) (resp. \({\varvec{d}}\)) means that the corresponding particle is active (resp. dormant). The process evolves according to the following rules:
-
Active particles, i.e. particles with the marker \({\varvec{a}}\), move in \(\mathbb {R}\) according to independent Brownian motions, die at rate \(m_2\) and branch into two active particles at rate s.
-
Pairs of active particles coalesce according to the following mechanism:
-
We define for each pair of particles labelled \((\alpha , \beta )\) their intersection local time \(L^{\alpha , \beta }=(L^{\alpha , \beta }_t)_{t \ge 0}\) as the local time of \(M^\alpha -M^\beta \) at 0 which we assume to only increase whenever both particles carry the marker \({\varvec{a}}\).
-
Whenever the intersection local time exceeds the value of an independent exponential clock with rate \(\nu /2\), the two involved particles coalesce into a single particle.
-
-
Independently, each active particle switches to a dormant state at rate c by switching its marker from \({\varvec{a}}\) to \({\varvec{d}}\).
-
Dormant particles do not move, branch, die or coalesce.
-
Independently, each dormant particle switches to an active state at rate \(c'\) by switching its marker from \({\varvec{d}}\) to \({\varvec{a}}\).
Moreover, denote by \(I=(I_t)_{t\ge 0}\) and \(J=(J_t)_{t \ge 0}\) the (time dependent) index set of active and dormant particles of M, respectively, and let \(N_t\) be the random number of particles at time \(t\ge 0\) so that \(M_t=(M^1_t, \ldots , M^{N_t}_t)\). For example, if for \(t\ge 0\) we have
then
Remark 1.6
For future use we highlight the following special cases of the process M. They admit the same mechanisms as described in Definition 1.5 except for those where we set the rate to 0:
-
\(m_1=m_2=0\): M is called an on/off branching coalescing Brownian motion (without killing) or on/off BCBM.
-
\(m_1=m_2=\nu =0\): M is called an on/off branching Brownian motion (without killing) or on/off BBM (Fig. 1).
-
\(m_1=m_2=s=0\): M is called an on/off coalescing Brownian motion (without killing) or on/off CBM.
-
\(m_1=m_2=\nu =s=0\): M is called an on/off Brownian motion (without killing) or on/off BM.
We have the following moment duality for the process M of Definition 1.5 which uniquely determines the law of the solution of the system (1.7).
Theorem 1.7
Let (u, v) be a solution to the system (1.7) with initial conditions \(u_0,v_0 \in B (\mathbb {R},[0,1])\). Then we have for any initial state \(M_0 =((x_1, \sigma _1), \ldots , (x_n, \sigma _n)) \in \left( \mathbb {R}\times \lbrace {\varvec{a}}, {\varvec{d}} \rbrace \right) ^n\), \(n\in \mathbb {N}\), and for any \(t \ge 0\)
Finally, as an application of the preceding results we consider the special case without mutation and noise. This is the F-KPP Equation with seed bank, i.e. Equation (1.8). In this scenario the duality relation takes the following form.
Corollary 1.8
Let (u, v) be the solution to Equation (1.8) with initial condition \(u_0=v_0=\mathbbm {1}_{[0,\infty [}\). Then the dual process M is an on/off BBM (see Remark 1.6). Moreover, if we start M from a single active particle, the duality relation is given by
Using this duality and a first moment bound, we can show that the propagation speed of the beneficial allele is significantly reduced to at least \(\sqrt{\sqrt{5}-1}\approx 1.11\) compared to the previous speed of \(\sqrt{2}\) in the case of the classical F-KPP Eq. (1.1).
Theorem 1.9
For \(s=c=c'= 1\), \(u_0=v_0=\mathbbm {1}_{[0,\infty [}\) and any \(\lambda \ge \sqrt{\sqrt{5}-1}\) we have that
A more general statement highlighting the exact dependence of the upper bound on the switching parameters c and \(c'\) is given later in Proposition 4.3.
1.3 Outline of paper
In Sect. 2, we first state results concerning (weak) existence of solutions of our class of SPDEs from (1.7) and then prove the equivalent characterization of solutions in terms of the delay representation (1.9). In Sect. 3, we establish uniqueness (in law) of the solutions to (1.7) and show duality to on/off BCBM with killing. Then, in Sect. 4, we investigate the special case of the F-KPP Equation with dormancy and show that the beneficial allele spreads at reduced speed in comparison with the corresponding classical F-KPP Equation (when started in Heaviside initial conditions). Finally, in Sect. 5 we provide outlines for the proofs of the results from Sect. 2.
2 Weak existence for a class of stochastic partial differential equations
In this section we provide a proof for Theorem 1.1. We begin by establishing strong existence and uniqueness for general systems of SPDEs with Lipschitz coefficients and use these results to obtain weak existence for systems with non-Lipschitz diffusion coefficients under some additional regularity assumptions. Finally, we show that Equation (1.7) fits into the previously established framework. In order to increase the readability of this section, we postpone the rather technical yet standard proofs of most theorems to Sect. 5.
We begin with the definition of the white noise process which is crucial to the introduction of SPDEs.
Definition 2.1
A (space-time) white noise W on \(\mathbb {R}\times [0,\infty [\) is a zero-mean Gaussian process indexed by Borel subsets of \(\mathbb {R}\times [0,\infty [\) with finite measure such that
where \(\lambda \) denotes the Lebesgue measure on \(\mathbb {R}\times [0,\infty [\). If a set \(A \in \mathcal {B}(\mathbb {R}\times [0,\infty [)\) is of the form \(A=C\times [0,t]\) with \(C \in \mathcal {B}(\mathbb {R})\) we write \(W_t(C)=W(A)\).
We are now in a position to introduce the general setting of this section.
Definition 2.2
Denote by
and
measurable maps. Then we consider the system of SPDEs
with bounded initial conditions \(u_0,v_0\in B(\mathbb {R})\), where W is a 1-dimensional white noise process.
The equation is to be interpreted in the usual analytically weak sense (cf. [34]), as follows:
Definition 2.3
Let \(u_0,v_0 \in B(\mathbb {R})\) and consider a random field \((u,v) = (u(t,x),v(t,x))_{t\ge 0, x\in \mathbb {R}}\).
-
We say that \(((u,v),W,\Omega , \mathcal {F},(\mathcal {F}_t)_{t \ge 0} , \mathbb {P})\) is a weak solution (in the stochastic sense) to Equation (2.1) with initial conditions \((u_0,v_0)\) if for each \(\phi \in C^\infty _c (\mathbb {R})\), almost surely it holds for all \(t\ge 0\) and \(y\in \mathbb {R}\) that
$$\begin{aligned} \int _\mathbb {R}u(t,x) \phi (x) \, \text {d}x&= \int _\mathbb {R}u_0(x) \phi (x) \, \text {d}x + \int _0^t \int _\mathbb {R}u(s,x) \frac{\Delta }{2} \phi (x) \, \text {d}x \, \text {d}s\nonumber \\&\quad + \int _0^t \int _\mathbb {R}b(s,x,u(s,x),v(s,x)) \phi (x) \, \text {d}x \,\text {d}s \nonumber \\&\quad + \int _0^t\int _\mathbb {R}\sigma (s,x,u(s,x), v(s,x)) \phi (x) \, W(\text {d}s, \text {d}x), \end{aligned}$$(2.2)$$\begin{aligned} v(t,y)&= v_0(y) + \int _0^t \tilde{b}(s,y,u(s,y),v(s,y)) \, \text {d}s \end{aligned}$$(2.3)and both (u, v) and W are adapted to \((\mathcal {F}_t)_{t \ge 0}\). We usually suppress the dependence of weak solutions on the underlying probability space and white noise process.
-
We say that (u, v) is a strong solution (in the stochastic sense) to Eq. (2.1) if on some given probability space \((\Omega , \mathcal {F}, \mathbb {P})\) with some white noise process W, the process (u, v) is adapted to the canonical filtration \((\mathcal {F}_t)_{t \ge 0}\) of W and for each \(\phi \in C^\infty _c (\mathbb {R})\) satisfies almost surely (2.2)-(2.3) for all \(t \ge 0\) and \(y\in \mathbb {R}\).
-
For \(p\ge 2\), we say that a solution (u, v) is \(L^p\)-bounded if
$$\begin{aligned} \Vert (u,v)\Vert _{T,p}{:}{=}\sup _{0\le t\le T} \sup _{x \in \mathbb {R}} \mathbb {E}\left[ \left( \vert u(t,x) \vert +\vert v(t,x) \vert \right) ^p\right] ^{1/p} < \infty \end{aligned}$$for each \(T>0\).
The solutions (u, v) we construct will have paths in \(C(]0,\infty [,C(\mathbb {R}))\times C([0,\infty [,B_{\text {loc}}(\mathbb {R}))\). Here, we denote by \(C(\mathbb {R})\) resp. \(B_{\text {loc}}(\mathbb {R})\) the space of continuous resp. locally bounded measurable functions on \(\mathbb {R}\). The spaces are endowed with the topology of locally uniform convergence. Note that for the random field u, this means equivalently that u is jointly continuous on \(]0,\infty [\times \mathbb {R}\). Since we allow for non-continuous (e.g. Heaviside) initial conditions \(u_0\) and \(v_0\), we have to restrict the path space for u by excluding \(t=0\). For the same reason and due to the absence of the Laplacian in (2.3), we cannot expect continuity of v in the spatial variable y.
We start by establishing, for solutions with the above path properties, an equivalent mild representation involving the Gaussian heat kernel
which is the fundamental solution of the classical heat equation.
Proposition 2.4
Let \(u_0,v_0 \in B(\mathbb {R}) \) and assume that for all \(T>0\), the linear growth condition
holds for every \((t,x,u,v)\in [0,T]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R}\).
Let (u, v) be an adapted and \(L^2\)-bounded process with paths taking values in \(C(]0,\infty [, C(\mathbb {R}))\times C([0,\infty [, B_{\mathrm {loc}}(\mathbb {R}))\). Then (u, v) is a solution of Equation (2.1) in the sense of Definition 2.3 iff (u, v) satisfies the following Stochastic Integral Equation (SIE): For each \(t>0\) and \(y\in \mathbb {R}\), almost surely it holds
and almost surely Eq. (2.3) holds for all \(t\ge 0\) and \(y\in \mathbb {R}\).
Using the mild formulation of the equation, the next step is to show strong existence and uniqueness by a standard Picard iteration scheme. For this we need to impose the usual Lipschitz assumptions.
Theorem 2.5
Assume that for all \(T>0\), we have the linear growth condition (2.4) and the following Lipschitz condition:
for every \((t,x) \in [0,T]\times \mathbb {R}\) and \((u,v),({\tilde{u}}, {\tilde{v}}) \in \mathbb {R}^2\).
Then for \(u_0, v_0\in B(\mathbb {R})\), Eq. (2.1) has a unique strong \(L^2\)-bounded solution (u, v) with paths taking values in \(C(]0,\infty [,C(\mathbb {R}))\times C([0,\infty [,B_{\mathrm {loc}}(\mathbb {R}))\). Moreover, this solution is \(L^p\)-bounded for each \(p\ge 2\).
Remark 2.6
Although the paths of u are not continuous at \(t=0\) for non-continuous initial conditions \(u_0\), Step 2 in the proof of Theorem 2.5 will in fact show that the process
has always paths in \(C([0,\infty [,C(\mathbb {R}))\) and thus, in particular, is locally bounded in \((t,x)\in [0,\infty [\times \mathbb {R}\).
Our next goal is to establish conditions under which we can ensure that the solutions to our SPDE stay in [0, 1].
Theorem 2.7
Assume that the conditions of Theorem 2.5 are satisfied. In addition, suppose that b and \({\tilde{b}}\) are even Lipschitz continuous jointlyFootnote 1 in (x, u, v) and satisfy the inequalities
Finally, assume that \(\sigma \) is a function of (t, x, u) alone, Lipschitz continuous jointly in (x, u) and satisfies
For initial conditions \(u_0,v_0 \in B(\mathbb {R}, [0,1])\), let \((u,v)\in C(]0,\infty [,C(\mathbb {R}))\times C([0,\infty [,B_{\mathrm {loc}}(\mathbb {R}))\) be the unique strong \(L^2\)-bounded solution to Eq. (2.1) from Theorem 2.5. Then we have
In particular, almost surely the solution has paths taking values in \(C(]0,\infty [, C(\mathbb {R},[0,1]))\times C([0,\infty [, B(\mathbb {R},[0,1]))\), where the spaces are endowed with the topology of locally uniform convergence.
Remark 2.8
By the same approximation procedure as in the proof of Theorem 2.9 below, it is possible to relax the condition in Theorem 2.7 that \(b, {\tilde{b}}\) resp. \(\sigma \) are Lipschitz continuous jointly in (x, u, v) resp. (x, u) and to require merely joint continuity and the Lipschitz condition (2.6).
In order to extend Theorem 2.7 to non-Lipschitz diffusion coefficients \(\sigma \), we need to impose an additional assumption on our SPDE in what follows. For given \(u\in C(]0,\infty [\times \mathbb {R},[0,1])\) and fixed \(y \in \mathbb {R}\), we consider Eq. (2.3) as an ordinary integral equation in \(v(\cdot , y)\). We then assume in effect that the unique solution v is a deterministic functional of u and \(v_0\), in the sense of (2.9) below. We are then in a position to prove:
Theorem 2.9
Assume that \( b,{\tilde{b}} \) and \(\sigma \) satisfy the following:
-
(i)
We have that \(b, {\tilde{b}} :\mathbb {R}^2 \rightarrow \mathbb {R}\) are Lipschitz-continuous functions of (u, v) alone and satisfy the inequalities in (2.7).
-
(ii)
We have that \(\sigma :\mathbb {R}\rightarrow \mathbb {R}\) is a continuous (not necessarily Lipschitz) function of u alone which satisfies the conditions in (2.8) and a linear growth bound
$$\begin{aligned} |\sigma (u)| \le K (1+|u|) \end{aligned}$$for all \(u \in \mathbb {R}\) and some \(K>0\).
-
(iii)
We assume that there exist continuous functionals
$$\begin{aligned} F&:C(]0,\infty [\times \mathbb {R},[0,1]) \rightarrow C([0,\infty [ \times \mathbb {R}, [0,1]), \\ H&:[0,\infty [ \times B(\mathbb {R}, [0,1])\rightarrow B(\mathbb {R},[0,1]) \end{aligned}$$such that for each given \(u \in C(]0,\infty [\times \mathbb {R},[0,1])\), \(v_0 \in B(\mathbb {R},[0,1])\) and \(y\in \mathbb {R}\), the unique solution \(v(\cdot ,y)\) to Eq. (2.3) has the following representation:
$$\begin{aligned} v(t,y)&= F(u)(t,y) + H(t,v_0)(y),\qquad t\ge 0. \end{aligned}$$(2.9)
Then for given initial conditions \(u_0,v_0\in B(\mathbb {R},[0,1])\) there exists a white noise process W and a corresponding filtered probability space such that Eq. (2.1) has a weak solution (u, v) with paths in \(C(]0,\infty [, C(\mathbb {R},[0,1]))\times C([0,\infty [, B(\mathbb {R},[0,1]))\) almost surely.
Remark 2.10
Note that we have to impose the condition (2.9) that v is a deterministic functional of u (and \(v_0)\) in order to reduce our coupled system of equations (2.1) to an equation in u only. This is due to the fact that the methods we employ for tightness require Polish spaces and \(B(\mathbb {R},[0,1])\) (the state space of v) is not separable.
Our next goal is to show that our specific model, i.e. the SPDE (1.7) fits into the framework of the preceding theorems. To this end, we first prove Proposition 1.3, which allows us to represent our system of SPDEs as a single Stochastic Partial Delay Differential Equation (SPDDE).
Proof of Proposition 1.3
For given \(u\in C(]0,\infty [\times \mathbb {R},[0,1])\) and \(v_0\in B(\mathbb {R},[0,1])\), we consider for each fixed \(x\in \mathbb {R}\) the second component of the system (1.7) as an integral equation in \(v(\cdot ,x)\), i.e.
Then by an application of the variation of constants formula we get for all \(x\in \mathbb {R}\) that
One may verify this through a simple application of the integration by parts formula. To see this we calculate as follows for each \(x \in \mathbb {R}\):
Rearranging we obtain (2.10), which we note is just the integral form of the second equation in (1.9). Now it is easy to see that \((u,v)\in C(]0,\infty [,C(\mathbb {R},[0,1]))\times C([0,\infty [,B(\mathbb {R},[0,1]))\) is a solution of (1.7) in the sense of Definition 2.3 iff it is a solution of the SPDDE (1.9). \(\square \)
We are finally in a position to provide the following:
Proof of Theorem 1.1
Consider the SPDE given by
Then we note that
satisfy all assumptions of Theorem 2.9. Moreover, (2.10) shows that (2.9) holds with
Thus, all conditions of Theorem 2.9 are fulfilled and we have existence of a \([0,1]^2\)-valued weak solution (u, v) with paths in \( C(]0,\infty [,C(\mathbb {R},[0,1]))\times C([0,\infty [,B(\mathbb {R},[0,1]))\) almost surely. This means in turn that we may get rid of the indicator functions and hence (u, v) solves Eq. (1.7). \(\square \)
Remark 2.11
Note that the preceding results become only notationally harder to prove if we consider larger systems of equations of the following form:
Let \(d,{\tilde{d}},r \in \mathbb {N}\) and denote by
and
measurable maps. Then we may consider the system of SPDEs
where \(W=(W_k)_{k=1, \ldots , r}\) is a collection of independent 1-dimensional space-time white noise processes.
Written component-wise, (2.11) means
for \(i\in \lbrace 1, \ldots , d \rbrace \) and \(j\in \lbrace 1, \ldots ,{\tilde{d}} \rbrace \).
3 Uniqueness in law and duality
In this section we aim to establish a moment duality which in particular will yield uniqueness in law for Equation (1.7). We follow the approach of Athreya and Tribe in [3]. Now recall that on the one hand it is a well-known result by Shiga (cf. [33]) that the SPDE without seedbank given by
satisfies a moment duality with a branching coalescing Brownian motion with killing \({\tilde{M}}\) and mutation compensator given by
where \({\tilde{I}}_t\) is the index set of particles that are alive at time \(t\ge 0\). On the other hand, in the seed bank diffusion case given by Eq. (1.6) it has been established that the dual process is an “on/off” version of a (Kingman-)coalescent (cf. [6]).
In lieu of this we have defined a combination of all the previous mechanisms by allowing the movement of the particles of Shiga’s dual process to also be subject to an additional “on/off” mechanism as in the on/off coalescent case in Definition 1.5. Recall that we denote by \(M=(M_t)_{t \ge 0}\) an on/off BCBM with killing and that \(I_t\) and \(J_t\) are the index sets of active and dormant particles, respectively, at time \(t \ge 0\).
Remark 3.1
In the discrete setting the proof of duality can usually be reduced to a simple generator calculation using the arguments in [13, pages 188–190]. However, due to the involvement of the collision local time stemming from the coalescence mechanism in the dual process, the generator of the dual process can only be defined formally. Hence, we use a regularization procedure to still be able to use the main ideas from [13].
Proof of Theorem 1.7
Consider for \(\epsilon >0\) the Gaussian heat kernel \(\rho _\epsilon (x)= G(\epsilon , x,0) =\frac{1}{\sqrt{2 \pi \epsilon }}\exp \left( -\frac{x^2}{2\epsilon } \right) \) and set
and note that \(u_\epsilon (t , \cdot )\) is smooth for each \(t \ge 0\). Then by Definition 2.3\(u_\epsilon \) satisfies the integral equation
where \(b_\epsilon (u,s,x){:}{=} \int _\mathbb {R}(1-u(s,y))u(s,y) \rho _\epsilon (x-y) \, \text {d}y \). Note that the above two quantities \(u_\epsilon \) and \(v_\epsilon \) are semimartingales. Thus, taking \(n,m \in \mathbb {N}\) and choosing arbitrary points \(x_1, \ldots , x_n \in \mathbb {R}\) and \(y_1 , \ldots , y_m \in \mathbb {R}\) we see by an application of Itô’s formula to the \(C^2\) map
that after taking expectations
where \(\sigma (x)=\sqrt{ x(1-x)}\). Now, we replace the \(x_i\) and \(y_j\) by an independent version of our dual process taken at a time \(r\ge 0\) and multiply by the independent quantity \(K(r):=e^{-m_1 \int _0^r |I_s| \, \text {d}s}\). This gives
Further, since we have the following integrable upper bound
we may use Fubini’s theorem and similar bounds (which are possibly independent of \(\epsilon \)) for the remaining quantities to justify that the terms in (3.2) are finite. Note that this also allows for applications of the dominated convergence theorem later on.
On the other hand, for any \(C^2\)-functions h, g we see by adding and substracting the compensators of the jumps
where we recall from Definition 1.5 that \(L^{\beta ,\delta }\) is the local time of \(M^\beta -M^\delta \) at 0 whenever both particles are active. By the integration by parts formula we then see including the factor K(t)
Further, note that that for each \(\epsilon >0\) and \(r\ge 0\) the maps \(u_\epsilon (r,\cdot ),\, v_\epsilon (r, \cdot )\) are bounded and smooth as they originate from mollifying with the heat kernel. Thus, replacing h and g with the independent quantities \(u_\epsilon (r,\cdot )\) and \(v_\epsilon (r,\cdot )\) we have
Finally, define
Then we may follow the idea from [13] and calculate for \(t\ge 0\) by substituting with our previously calculated quantities
Now, again by Fubini’s theorem, taking the limit as \(\epsilon \rightarrow 0\) we see that all the quantities except (3.6) and (3.7) vanish. Note that we used properties of mollifications (since u is continuous we have convergence everywhere) and the dominated convergence theorem to justify this. Moreover, the use of Lemma 3.2 allows us to argue that the same is true for the remaining two terms. By the (left-)continuity of the the processes u, v, M in r we finally see that after differentiation
as desired. \(\square \)
Lemma 3.2
In the setting of Theorem 1.7 we have
as \(\epsilon \rightarrow 0\).
Proof of Lemma 3.2
We adapt and elaborate the proof of [3]. Consider for each \(m \in \mathbb {N}\) the time of the m-th birth \(\tau _m\). Assume for now that we may restrict ourselves to \([0, \tau _m]\). Now, we argue pathwise in \(\omega \). Set for \(\beta , \delta \in \lbrace 1, \ldots , m \rbrace \) after a change of variables
Here, we set
Now, by a modification of Tanaka’s occupation time formula (cf. [3]) we see thatFootnote 2
The goal for now is to replace \(L^{\beta , \delta }_{r,x}\) by the local time at 0 and get rid of the dependence of Z on z and \(\epsilon \). To do so we first use the triangle inequality to see that
First, note that \(r \mapsto Z^{\beta ,\delta ,\epsilon }_r(z)\) is piece-wise continuous and uniformly bounded for each \(z \in \mathbb {R}\) and that \(z \mapsto Z^{\beta ,\delta }_r(z)\) is continuous at 0 uniformly in \(r \le t\) and \(\epsilon >0\). Hence, for any \(\eta >0\) there exists some \(\zeta >0\) such that
whenever \(|z|<\zeta \) uniformly in r and \(\epsilon \). Using that \(L_{r,x}\) is uniformly bounded in \(r\in [0,t],x\in \mathbb {R}\) by Barlow and Yor’s local time inequalities from [4] we obtain for all \(\epsilon >0\)
for some constant \(C>0\). Moreover, noting in addition that \(Z^{\beta , \delta , \epsilon }\) is bounded uniformly in \(r, \epsilon \) and z we have for the remaining part of the integral
as \(\epsilon \rightarrow 0\). Hence, we obtain that the entire term in Equation (3.8) vanishes as \(\epsilon \rightarrow 0\).
For the term (3.9) we set for \(\varphi \in \lbrace 1,\ldots , m\rbrace \) and \(\varphi \ne \beta , \delta \)
By the same argument as for the term (3.8) we see that as \(\epsilon \rightarrow 0\) that
Iterating through the finitely many \(u_\epsilon \) and \(v_\epsilon \) terms we indeed obtain that the entire term (3.9) vanishes as \(\epsilon \rightarrow 0\).
For the last term we take a Riemann sum approximation of \(Z_r^{\beta , \delta }\), i.e. taking a sequence of partitions of [0, t] given by \(0= t_0 \le \cdots \le t_n =t \) with mesh size \(\Delta _n \rightarrow 0\) as \(n \rightarrow \infty \) we consider
Recall that we may choose the partition in a way such that
uniformly in \(r \in [0,t]\) as \(n \rightarrow \infty \). Thus, since on a set with probability one we have \(\sup _{x \in \mathbb {R}} L^{\beta , \delta }_{s,x} < \infty \) for each \(s \in [0,t]\) we may deduce that uniformly in \(x \in \mathbb {R}\) using the piece-wise continuity of \(r \mapsto Z_r^{\beta , \delta }\) we have
Next, we see by the triangle inequality again that
holds true. Now for any \(\eta >0\) choose n large enough such that
for all \(x \in \mathbb {R}\). Then choose \(\epsilon >0\) small enough to get
using the mollifying property of the heat kernel. This finally yields that indeed as \(\epsilon \rightarrow 0\) we have that the term (3.10) also vanishes. Combining the above we obtain path-wise in \(\omega \) that as \(\epsilon \rightarrow 0\)
It now suffices to justify the exchange of limit and expectation. For this we invoke the dominated convergence theorem. In order to find a dominating function we calculate as follows:
for some constant \(C>0\). Then again using the fact that \(\sup _{x \in \mathbb {R}}L^{\beta , \delta }_{t,x}\) is integrable the proof is concluded.
It remains to justify the restriction to the interval \([0,\tau _m]\) in the preceding argument. To do so we modify our dual process such that it stops branching, coalescing and dying at time \(\tau _m\) but may perform independent on/off Brownian motions up until time t, i.e. we set for all particles \(\alpha \) whenever they exist at time \(\tau _m\)
where \((B^\alpha _t)_{t\ge 0}\) is an independent on/off Brownian motion started from the state of \(M_{\tau _m}^\alpha \) (which is also independent of the on/off Brownian motions needed for the other particles). We denote by \({\bar{L}}_t, {\bar{I}}_t, {\bar{J}}_t, {\bar{K}}_t\) the quantities corresponding to the modified dual process \((\bar{M}_t)_{t\ge 0}\). We may then repeat the proof of Theorem 1.7. Moreover, the preceding calculations from this Lemma then show that
as \(\epsilon \rightarrow 0\). Note however that since the modified dual process neither branches, dies nor coalesces after time \(\tau _m\) we must add the indicator \(\mathbbm {1}_{\lbrace s \le \tau _m\rbrace }\) to the quantities (3.3), (3.5) and (3.7) so that the duality relation for the modified process becomes
The second term may be bounded for some \(C>0\) by
which vanishes since \(\mathbbm {1}_{\lbrace s \ge \tau _m\rbrace } \rightarrow 0\) as \(m \rightarrow \infty \) almost surely and \(\vert {\bar{I}}_s \vert \) can be dominated by a Yule process with rate s uniformly in m. A similar calculation yields the same conclusion for the third term. For the first term we have the bound
Now, since there is no more branching, coalescence and death after time \(\tau _m\) the expected intersection local time per pair of particles after time \(\tau _m\) is dominated by the expected local time of a single standard Brownian motion at 0 up until time \(\sqrt{2}t\) which we denote by L. Hence, denoting by \((\mathcal {G}_t)_{t \ge 0}\) the natural filtration of the dual process we even have that the first term is bounded by
This quantity also vanishes as \(m \rightarrow \infty \). Thus, we obtain that the right hand side of Eq. (3.13) converges to 0 as \(m \rightarrow \infty \). For the left hand side note that the modified dual converges to the original dual process as \(m \rightarrow \infty \) and invoke the dominated convergence theorem. \(\square \)
As a corollary, the moment duality of Theorem 1.7 allows us to infer uniqueness in law for the SPDE (1.7). Note that the underlying arguments are standard but some care is needed due to the fact that we allow for non-continuous initial conditions.
Proof of Theorem 1.2
Recall that if (u, v) is a solution of the system (1.7) with initial conditions \(v_0,u_0 \in B(\mathbb {R},[0,1])\), then
have paths taking values in \(C([0,\infty [,C(\mathbb {R}))\), see Remark 2.6 and (2.10). Now, by Theorem 1.7 the law of the dual process uniquely determines the mixed moments of
and hence, by uniqueness in the Hausdorff moment problem, also the joint distribution of the above quantity for each fixed \(t\ge 0\) and arbitrarily chosen \(x_1,y_1,\ldots ,x_n,y_n \in \mathbb {R}\), \(n\in \mathbb {N}\). Since the cylindrical \(\sigma \)-algebra on \(C(\mathbb {R})\) coincides with the Borel-\(\sigma \)-algebra w.r.t. the topology of locally uniform convergence, this shows that the distribution of \((\tilde{u}(t,\cdot ),{\tilde{v}}(t,\cdot ))\) on \(C(\mathbb {R})^2\) is uniquely determined for each fixed \(t\ge 0\). In order to extend this to the finite-dimensional distributions, one can use the martingale problem corresponding to the weak formulation of the equation. Using the well-known fact that uniqueness of the one-dimensional time marginals in a martingale problem implies uniqueness of the finite-dimensional time marginals, we then obtain that the distribution of \(({\tilde{u}},{\tilde{v}})\) on \(C([0,\infty [,C(\mathbb {R}))^2\) is uniquely determined. Finally, this implies that also the distribution of \(( u, v)=({\tilde{u}}+{\hat{u}}_0,{\tilde{v}}+{\hat{v}}_0)\) on \(C\left( ]0,\infty [,C(\mathbb {R},[0,1])\right) \times C\left( [0,\infty [,B(\mathbb {R},[0,1])\right) \) is uniquely determined. \(\square \)
4 An application to the F-KPP Equation with seed bank
We are interested in applying the previously established results to the F-KPP Equation with seed bank, i.e. the system:
with \(p_0=q_0 =\mathbbm {1}_{] -\infty ,0]}\). This means that in our original equation we set \(m_1=m_2=\nu =0,s=1\) and return to the setting \(p =1-u\). We do this to make the results of this section more easily comparable with the literature concerning the original F-KPP Equation and avoid confusion (see e.g. [14, 29]). This also implies that the dual process is now “merely” an on/off branching Brownian motion. Note that here the selection term is always positive for p, implying that it corresponds to the beneficial type.
Recall for the case of the classical F-KPP Equation that, since we start off with a Heaviside initial condition concentrated on the negative half axis, the wave speed \(\sqrt{2}\) also becomes the asymptotic speed at which the beneficial allele “invades” the positive half axis.
In this section, we consider the question to what extent the introduction of the seed bank influences the invasion speed of the beneficial allele.
We begin by proposing a formal definition of the invasion speed.
Definition 4.1
In the setting of Eq. (4.1), with Heaviside initial conditions, we call \(\xi \ge 0\) the asymptotic invasion speed of the beneficial allele if
In the case of the classical F-KPP Equation, we have \(\xi =\sqrt{2}\). Intuitively, one would expect this speed to be reduced in the presence of a seed bank. In order to investigate this, we aim to employ the duality technique established in the preceding section. Recall, that in the setting of Corollary 1.8 the duality is given by
where \((M_t)_{t\ge 0}\) is an on/off branching Brownian motion, \(I_t,J_t\) are the corresponding index sets of active and dormant particles at time \(t\ge 0\), respectively, and \(\mathbb {P}_{(x,{\varvec{a}})}\) is the probability measure under which the on/off BBM is started from a single active particle at \(x\in \mathbb {R}\). This clearly resembles the duality from the classical FKPP Equation given by
where \(( {\tilde{B}}_t)_{t\ge 0}\) is a simple branching Brownian motion.
Proof of Corollary 1.8
For initial values \((x_1,\ldots , x_n) \in \mathbb {R}^n\) and \((y_1, \ldots , y_m) \in \mathbb {R}^m\), we have by Theorem 1.7 that
Plugging in our specific initial conditions and using that the solution (p, q) is deterministic, we see
\(\square \)
Next, we turn to establishing an upper bound on the invasion speed of the beneficial allele. Writing \(K_t{:}{=} I_t \cup J_t\) for \(t \ge 0\) and denoting by \(B=(B_t)_{t \ge 0}\) an on/off BM without branching, we have
where we have used the following simple many-to-one lemma:
Lemma 4.2
For any \(t\ge 0\) and any non-negative measurable function \(F:\mathbb {R}\rightarrow \mathbb {R}\) we have
where B is an on/off Brownian motion under \(\mathbb {P}_{(x,\sigma )}\) starting in a single particle with initial state \(\sigma \in \lbrace {\varvec{a}}, {\varvec{d}} \rbrace \) and initial position \( x \in \mathbb {R}\).
Proof
Using that the number of particles is independent of the movement of the active particles, we get
This proves the result. \(\square \)
Now, we first compute \(\mathbb {E}_{(0, {\varvec{a}})}\left[ \,|K_t|\right] \). Note, that \((|I_t|, |J_t|)_{t \ge 0}\) is a continuous time discrete state space Markov chain on \(\mathbb {N}_0 \times \mathbb {N}_0\) with the following transition rates:
For the expectations we then get the following system of ODE’s for \(x=x(t)=\mathbb {E}_{(0, {\varvec{a}})}\left[ \,|I_t| \right] \) and \(y=y(t)=\mathbb {E}_{(0, {\varvec{a}})}\left[ \,|J_t| \right] \) (cf. [1, V.7] )
With the initial condition \((x(0),y(0))=(1,0)\) we obtain the following closed form solution:
abbreviating \(a:=(c-1)^2 +2cc' + (c')^2 +2c'\). Finally, we aim to control \(\mathbb {P}_{(0,{\varvec{a}})}(B_t >\lambda t)\). To this end, we recall the well known tail bound for the normal distribution given by
for \(x \ge 0\). To employ this, note first that \(\mathbb {P}_{(0,{\varvec{a}})}(B_t> \lambda t )\) is equivalent to
where \(X_t\) is the amount of time the on/off Brownian path \((B_t)_{t \ge 0}\) is switched off until time \(t\ge 0\) and \({\tilde{B}} =(\tilde{B}_t)_{t \ge 0}\) is a standard Brownian motion started at 0. By independence, we then have
Then, using Eq. (4.2), we get for \(s<t\)
Thus, we may complete our calculation in the following manner:
as \(t \rightarrow \infty \) for \(\lambda ^2 \ge -c'-c+\sqrt{a}+1\). Now, an application of the duality from Corollary 1.8 shows that we have proved the following result:
Proposition 4.3
In the case of the F-KPP Equation with seed bank (4.1), we have for the asymptotic invasion speed from Definition 4.1 that
where \(a=(c-1)^2 +2cc' +(c')^2 +2c'\).
Proof
This follows directly from the above calculations together with the fact that
by the duality from Corollary 1.8. \(\square \)
This shows that indeed the invasion speed for \(c=c'=1\) is slowed down from \(\sqrt{2}\) to (at least) \(\sqrt{\sqrt{5}-1} \approx 1.111\).
Remark 4.4
The calculations leading to Prop. 4.3 suggest that in the case \(c=c'=s=1\) we have, almost surely, the upper bound
where \({\tilde{\lambda }}=\sqrt{\sqrt{5}-1}\) and \(R_t\) denotes the position of the rightmost particle of the on/off BBM at time \(t \ge 0\). At first glance, judging from simulations (cf. Fig. 2), this upper bound does not seem unreasonable. However, note that the value of our bound for \({\tilde{\lambda }}\) is entirely specified by the expected number of particles, as we may use the same tail bounds for \(\mathbb {P}(B_t > \lambda t)\) and \(\mathbb {P}(M_t >\lambda t)\). This indicates that the bound is not tight – in contrast to the case of the classical BBM. Indeed, using martingale methods which are beyond the scope of this paper, it has subsequently been established in [8] that one actually has
where \(\lambda ^*\approx 0.99 < {\tilde{\lambda }} \).
Remark 4.5
Note that for the boundary case \(c=c'\rightarrow 0\) we recover the upper bound \(\sqrt{2}\) from the classical F-KPP Equation. For \(c,c' \rightarrow \infty \), the upper bound becomes \(\sqrt{1}\) showing that instantaneous mixing with the dormant population leads to a slow down from the classical F-KPP Equation corresponding to a doubled effective population size. On the level of the dual process this could be interpreted as essentially halving diffusivity and branching rate.
5 Proofs for section 2
Proof of Proposition 2.4
The proof is standard and follows along the lines of [34, Thm. 2.1] which is why we only provide a rough outline.
Suppose that for each fixed \((t,y)\in \,]0,\infty [\times \mathbb {R}\), Equation (2.5) is satisfied almost surely. Then using the linear growth bound and \(L^2\)-boundedness, a simple Fubini argument shows that almost surely Eq. (2.5) is satisfied for almost all \((t,y)\in \,]0,\infty [\times \mathbb {R}\). Thus given \(\phi \in C_c^\infty (\mathbb {R})\), we can plug (2.5) (with s in place of t) into \(\int _0^t\langle u(s,\cdot ),\Delta \phi \rangle \,\text {d}s\). Then a straightforward but tedious calculation using Fubini’s theorem for Walsh’s stochastic integral (cf. Theorem 5.30 in [22]) shows that Eq. (2.2) holds almost surely for each fixed \(t\ge 0\). Since both sides are continuous in \(t\ge 0\), (2.2) holds for all \(t\ge 0\), almost surely. Thus (u, v) is also a solution to (2.1) in the sense of Definition 2.3.
Conversely, suppose that for each \(\phi \in C_c^\infty (\mathbb {R})\), Eq. (2.2) holds for all \(t\ge 0\), almost surely.
Step 1: Defining
and
one can show that Eq. (2.2) also holds for each \(\psi \in C^2_{\text {rap}}(\mathbb {R})\). Step 2: For \(T>0\), define \(C^{(1,2)}_{T,\text {rap}}\) as the space of all functions \(f:[0,T[\times \mathbb {R}\rightarrow \mathbb {R}\) such that \( t\mapsto f(t,\cdot )\) is a continuous \(C^2_{\text {rap}}\)-valued function and \(t\mapsto \partial _tf(t,\cdot )\) is a continuous \(C_{\text {rap}}\)-valued function of \(t\in [0,T[\). Then one can show that for each \(\phi \in C^{(1,2)}_{T,\text {rap}}\), we have that an integration-by-parts like equation holds, i.e. for all fixed \( t\in [0,T[\) we have almost surely
Step 3: Fix \(T>0\), \(y\in \mathbb {R}\) and define the time-reversed heat kernel \(\phi _{T}^y(t,x):=G(T-t,x,y)\) for \( t\in [0,T[\) and \(x\in \mathbb {R}\). Then we have \(\phi _{T}^y\in C^{(1,2)}_{T,\text {rap}}\), and plugging it into (5.1) in place of \(\phi \) and using that the heat kernel solves the heat equation, we obtain the required result upon taking the limit as \(t\uparrow T\). \(\square \)
Proof of Theorem 2.5
The proof follows along the lines of [34, Thm. 2.2] and only has to be adapted to the two component case.
Step 1: Fix \(p\ge 2\). Define \(u_1(t,y){:}{=}\langle u_0, G(t,\cdot , y) \rangle \) and \(v_1(t,y){:}{=} v_0(y)\) for all \((t,y) \in [0,\infty [\,\times \mathbb {R}\) and inductively
for all \(n\in \mathbb {N}\). Then one can use the linear growth bound (2.4) to obtain that this defines a sequence such that for every \(n \in \mathbb {N}\) and \(T>0\)
Similarly, using the Lipschitz condition (2.6) instead of the linear growth bound one can obtain that for all \(n \in \mathbb {N}\) and \(t\in [0,T]\)
Applying Hölders inequality for some \( q>1\) with conjugate \(\frac{q}{q-1}\in \, ]1,2[\), we get
for all \(n \in \mathbb {N}\), \(t\in [0,T]\), \(T>0\). By a version of Gronwall’s lemma (see e.g. [22, Lemma 6.5]), this implies
Thus \((u_{n}(t,y), v_{n}(t,y))_{n\in \mathbb {N}}\) is a Cauchy sequence in \(L^p\) for each fixed \(t\ge 0\) and \(y \in \mathbb {R}\), and we can define a predictable random field \((u(t,y),v(t,y))_{t\ge 0,y\in \mathbb {R}}\) as the corresponding limit in \(L^p\). Clearly we have
as \(n \rightarrow \infty \) for all \(T>0\), and (u, v) satisfies Equation (2.5) and (2.3) almost surely for each fixed \(t\ge 0\) and \(y\in \mathbb {R}\). Up to now, \(p\ge 2\) was fixed, but since convergence in \(L^{p'}\) implies convergence in \(L^p\) for \(p'>p\), (u, v) is actually \(L^p\)-bounded for all \(p\ge 2\) in the sense of Definition 2.3.
Step 2: We argue that u constructed in Step 1 has a modification \({\tilde{u}}\) with paths in \(C(]0,\infty [,C(\mathbb {R}))\), which is equivalent to the random field \({\tilde{u}}\) being jointly continuous in \((t,x)\in \ ]0,\infty [\, \times \mathbb {R}\).
Consider first the stochastic integral part
Then for each \(p\ge 1\) and \( t,r\in [0, T]\), using the Burkholder-Davis-Gundy and Jensen inequalities as well as the linear growth bound and \(L^{2p}\)-boundedness of (u, v) from Step 1, we obtain that
Here, for the last inequality we have also used that by the calculation in the proof of [22, Theorem 6.7] we have
Next, consider the term
for \(t \ge 0, y\in \mathbb {R}\). Let \(0\le r<t\le T\). To obtain similar estimates as for X we first split the difference into two terms:
By Jensen’s inequality, the linear growth bound and \(L^{2p}\)-boundedness of (u, v), we have for the first term on the right hand side that
For the second term we proceed analogously, using in addition [31, Lemma 5.2] (choose \(\beta =\frac{1}{2}\) and \(\lambda '=0\) there), to obtain
for all \(0\le r<t\le T\). Combining the above, we have shown for \(Z:=X+Y\) that
for all \(t,r\in [0,T]\), \(y,z\in \mathbb {R}\) and \(p\ge 1\). Choosing \(p>4\), we see that indeed the conditions of Kolmogorov’s continuity theorem (see e.g. [20, Thm. 3.23]) are satisfied. Hence, Z has a modification jointly continuous in \((t,x)\in [0,\infty [\times \mathbb {R}\).
Now observing that
is continuous on \(]0,\infty [\times \mathbb {R}\), we are done. Note however that we cannot extend this to \(t=0\) if the initial condition \(u_0\) is non-continuous.
Step 3: Let us write \({\tilde{u}}\) for the continuous modification of u from Step 2. Given this \({\tilde{u}}\) we consider path-wise in \(\omega \) for each \(y \in \mathbb {R}\) the integral equation
Since \((s,{\tilde{v}})\mapsto {\tilde{b}}(s,y,{\tilde{u}}(s,y),{\tilde{v}})\) is locally bounded, the Lipschitz condition (2.6) implies that (5.3) has a unique solution \({\tilde{v}}(\cdot ,y)\). Note that since \({\tilde{v}}\) is defined path-wise, almost surely it satisfies (5.3) for all \(t\ge 0\) and \(y\in \mathbb {R}\). In order to see that \({\tilde{v}}\) has paths taking values in \(C([0,\infty [,B_{\mathrm {loc}}(\mathbb {R}))\), it suffices to show that it is locally bounded in \((t,y)\in [0,\infty [\times \mathbb {R}\), which follows from the linear growth bound by a simple Gronwall argument.
Now using the Lipschitz condition again, it is easy to see that \({\tilde{v}}\) is a modification of v constructed in Step 1 and that for each fixed \(t>0\) and \(y\in \mathbb {R}\), \(({\tilde{u}},\tilde{v})\) satisfies Eq. (2.5) almost surely. By Proposition 2.4 we conclude that \(({\tilde{u}}, {\tilde{v}})\) is a solution of Eq. (2.1) in the sense of Definition 2.3.
Step 4: It remains to show uniqueness: Let \((u,v), (h,k)\in C(]0,\infty [,C(\mathbb {R}))\times C([0,\infty [,B_{\mathrm {loc}}(\mathbb {R}))\) be two \(L^2\)-bounded (strong) solutions to Eq. (2.1) in the sense of Definition 2.3 with the same initial conditions \(u_0,v_0\in B(\mathbb {R})\). Then using Proposition 2.4 we notice that for each fixed \(t>0\) and \(y\in \mathbb {R}\) we have almost surely
By the same argument as in Step 1, we obtain using the Lipschitz condition (2.6) that for each \(T>0\) and some constant \(C_{T}\)
for all \(t\in [0,T]\). Thus, by Gronwall’s Lemma we get
and hence
for each fixed \((t,x) \in [0,\infty [ \times \mathbb {R}\). By continuity of u and h we then obtain that
By assumption, v and k satisfy
and
for all \(t\ge 0\) and \(x\in \mathbb {R}\), almost surely. Then due to Equation (5.4) we have on a set with probability one that for every \(x \in \mathbb {R}\) the maps \(v(\cdot , x)\) and \(k(\cdot , x)\) solve the same integral equation (with given \(u=h\)) and hence coincide by uniqueness of solutions on \([0,\infty [\). Thus, we actually obtain
\(\square \)
Proof of Theorem 2.7
The proof is inspired by the proof of [34, Thm. 2.3] and [12, Thm. 1.1]. Step 1: We consider a regularized noise given by
where we set \(\rho _\epsilon (x)=G(\epsilon ,x,0)\) for all \(x \in \mathbb {R}\). Note that \(W_\epsilon ^x(t)\) is a local martingale with quadratic variation \(\frac{1}{\sqrt{4 \epsilon }}t\) and is hence a constant multiple of a standard Brownian motion. This allows us to consider the following SDE
where we set
For this equation we use the following facts which can also be proven by the usual Picard iteration schemes:
Proposition 5.1
Equation (5.5) has a unique (not necessarily continuous in the space variable due to the initial conditions) solution under the assumption that \(b, {\tilde{b}}\) and \(\sigma \) are Lipschitz in (x, u, v). Moreover, this solution also satisfies the following SIE:
where we set \(G_\epsilon (t,x,y) = e^{-t/\epsilon } \sum _{n=0}^\infty \frac{(t/\epsilon )^n}{n!}G(n\epsilon ,x,y) = e^{-t/\epsilon }\delta _x+R_\epsilon (t,x,y)\).
Then we may proceed as in the standard proof of comparison results (cf. [19]). Note that by our assumptions and the Lipschitz condition we have that
Thus, approximating and localizing as in the one dimensional case [19, Chapter VI Theorem 1.1]Footnote 3 we see that using (5.7)
where \((x)^-=\mathbbm {1}_{\lbrace x\le 0\rbrace }|x|\) for \(x \in \mathbb {R}\). Hence, we have
An application of Gronwall’s LemmaFootnote 4 will now yield that for all \((t,x) \in [0,\infty [\times \mathbb {R}\)
By an application of Itô’s formula to \((1-u_\epsilon (t,x),1-v_\epsilon (t,x))\) and using (5.8) instead of (5.7) we can proceed analogously to see that indeed for all \((t,x) \in [0,\infty [\times \mathbb {R}\)
Step 2: We approximate (u, v) by \((u_\epsilon ,v_\epsilon )\). Note first that we have
where the first two statements can be shown using the boundedeness of the inital condition, Lemma 5.2 (1) below and Gronwall’s Lemma. Then using the SIE representation of our solutions given by
and Eq. (5.6) we get by subtracting the corresponding terms
where we also used Fubini’s theorem for Walsh’s integral (cf. Theorem 5.30 in [22]). In order to proceed we recall the following elementary bounds from [34, Lemma 6.6] and [12, Appendix].
Lemma 5.2
For \(R_\epsilon \) as in Proposition 5.1 we have the following:
-
(1)
It holds for all \(t>0\) and \(x \in \mathbb {R}\) that
$$\begin{aligned} \int _\mathbb {R}R_\epsilon (t,x,y)^2 \, \text {d}y \le \sqrt{\frac{3}{8\pi }} \frac{1}{\sqrt{t}}. \end{aligned}$$ -
(2)
There exist constants \(\delta ,D >0\) such that
$$\begin{aligned} \int _\mathbb {R}|R_\epsilon (t,x,y)-G(t,x,y)| \, \text {d}y \le e^{-t/\epsilon } + D (\epsilon /t)^{1/3} \end{aligned}$$for all \(\epsilon >0\) such that \(0<\epsilon /t \le \delta \) and \(t\ge 0, x\in \mathbb {R}\).
-
(3)
For all \(t\ge 0\) and \(x \in \mathbb {R}\) we have
$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \int _0^t \int _\mathbb {R}(R_\epsilon (s,x,y)-G(s,x,y))^2 \, \text {d}s \, \text {d}y =0. \end{aligned}$$ -
(4)
We have for all \(x,y \in \mathbb {R}\) and \(t\in [0,T]\), \(T>0\) that
$$\begin{aligned} \mathbb {E}\left[ \,|u(t,x)-u(t,y)|^2\right] \le C_{T,u_0} (t^{-1/2} |x-y|+ |x-y|). \end{aligned}$$
Proof
The proof of statements (1), (2) and (3) can be found in the Appendix of [12].
For (4), we write
with Z as in Step 2 of the proof of Theorem 2.5. Then we note that by (5.2) (with \(p=1\)) and by [31, Lemma 5.2] (using \(\beta =1/2\) and \(\lambda '=0\) there) we get
for all \(0\le t\le T\) and \(x,y\in \mathbb {R}\), which gives the desired result. \(\square \)
Using Lemma 5.2 it is now possible to show in the spirit of [12, Theorem 1.1], by considering each of the terms in Eq. (5.10) individually, that
for each \(T>0\). Hence, we obtain that for all \((t,x) \in [0,\infty [\times \mathbb {R}\)
Since u is jointly continuous on \(]0,\infty [\times \mathbb {R}\), this of course implies
To obtain the same result for v note that by assumption and Eq. (5.7), almost surely it holds for all \(t\ge 0\) and \(x\in \mathbb {R}\) that
Since \(v_0(\cdot )\ge 0\), by comparing path-wise to the solution of the ODE
which is the constant zero function, we obtain path-wise for every \(x \in \mathbb {R}\) that \(v(\cdot ,x) \ge 0\) on \([0,\infty [\). Hence,
Repeating the argument for \(1-v\) and using (5.8) gives then finally
as desired. \(\square \)
Proof of Theorem 2.9
Take a sequence of Lipschitz continuous functions \((\sigma _n)_{n \in \mathbb {N}}\) each satisfying (2.8) such that \(\sigma _n \rightarrow \sigma \) uniformly on compacts as \(n \rightarrow \infty \) and
for all \(u \in \mathbb {R}\) and \(n\in \mathbb {N}\). Then the maps \(b,{\tilde{b}}\) and \(\sigma _n\) satisfy the conditions of Theorems 2.5 and 2.7Footnote 5 for all \(n \in \mathbb {N}\), thus Eq. (2.1) with coefficients \((b,{\tilde{b}},\sigma _n)\) and initial conditions \(u_0,v_0\in B(\mathbb {R},[0,1])\) has a unique strong solution \((u_n,v_n)\) with paths in \(C\left( ]0,\infty [,C(\mathbb {R},[0,1])\right) \times C\left( [0,\infty [,B(\mathbb {R},[0,1])\right) \). Now, making use of assumption (2.9) to replace \(v_n\) in Eq. (2.2) by the corresponding quantity, we have that for each \(\phi \in C^\infty _c (\mathbb {R})\), almost surely it holds for all \(t\ge 0\)
Note that this is now an equation of \(u_n \in C(]0,\infty [\times \mathbb {R},[0,1])\) alone! In order to proceed, we reformulate this as the corresponding martingale problem: For each \(\phi \in C^\infty _c (\mathbb {R})\), the process
is a continuous martingale with quadratic variation
We say that \( u_n\) solves \(MP(\sigma _n^2,b)\).
Now recall from Step 2 of the proof of Theorem 2.5 that
is jointly continuous on \([0,\infty [\times \mathbb {R}\), thus \(Z_n\) takes values in \(C([0,\infty [\times \mathbb {R},[-1,1])\). Moreover, by the same calculation as there we see that (5.2) holds for \(Z_n\) in place of Z (this is where we need Equation (5.11)). Hence, it follows from the Kolmogorov Chentsov Theorem [20, Corollary 16.9] that the sequence \((Z_n)_{n \in \mathbb {N}}\) is tight in \(C([0, \infty [\times \mathbb {R},[-1,1])\) with the topology of locally uniform convergence. Extracting a convergent subsequence, which we continue to denote \((Z_n)_{n\in \mathbb {N}}\), we obtain the existence of a weak limit point \(Z \in C([0, \infty [\times \mathbb {R},[-1,1])\). Note that in order to apply the Kolmogorov Chentsov Theorem, we had to subtract the problematic quantity \({\hat{u}}_0\) which is not continuous at \(t=0\). But since \({\hat{u}}_0\) is deterministic, it follows that also \(u_n=Z_n+{\hat{u}}_0\rightarrow Z+{\hat{u}}_0{=}{:}u\) weakly in \(B([0,\infty [\times \mathbb {R})\) as \(n\rightarrow \infty \). Then clearly u is almost surely [0, 1]-valued and continuous on \(]0,\infty [\times \mathbb {R}\), thus \(u\in C(]0,\infty [\times \mathbb {R},[0,1])\).
Now, using the continuous mapping theorem as in the proof of [20, Thm. 21.9] we see that u actually solves the martingale problem \(MP(\sigma ^2,b)\), i.e. for each \(\phi \in C_c^\infty (\mathbb {R})\) the process
is a continuous martingale with quadratic variation
Then [21, Thm. III-7] gives us the existence of a white noise process W on some filtered probability space such that
hence u solves the SPDE
But again note that by (2.9)
is the unique solution to the integral equation (given u)
Thus, (u, v) is a weak solution to Eq. (2.1). \(\square \)
Notes
This is stronger than the Lipschitz condition (2.6) which only requires that the bound holds in (u, v).
Here we split the integral into the random time intervals on which both \(M^\delta \) and \(M^\beta \) are active and then apply Tanaka’s formula. Moreover, note that the intersection local time of two on/off Brownian motions can always be dominated by the local time of two corresponding standard Brownian motions. This will also allow for applications of the local time inequalities by Barlow and Yor later in the proof.
This is where we need the additional condition (2.8) on \(\sigma \).
Note that the bounded initial condition ensures via Picard iteration that \(\mathbb {E}[(u_\epsilon (t,x))^- +(v_\epsilon (t,x))^-]\) is bounded.
Note that in this context, the assumed Lipschitz continuity implies the linear growth bound (2.4) for b, \({\tilde{b}}\).
References
Athreya, K.B., Ney, P.E.: Branching Processes. Springer-Verlag, New York-Heidelberg (1972) (Die Grundlehren der mathematischen Wissenschaften, Band 196)
Athreya, S.: Probability and Semilinear Partial Differential Equations. Ph.D. dissertation, Univ. Washington (1998)
Athreya, S., Tribe, R.: Uniqueness for a class of one-dimensional stochastic PDEs using moment duality. Ann. Probab. 28(4), 1711–1734 (2000)
Barlow, M.T., Yor, M.: (semi-) martingale inequalities and local times. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 55(3), 237–254 (1981)
Blath, J., Buzzoni, E., González Casanova, A., Wilke-Berenguer, M.: Structural properties of the seed bank and the two island diffusion. J. Math. Biol. 79(1):369–392 (2019)
Blath, J., González Casanova, A., Eldon, B., Kurt, N., Wilke-Berenguer, M.: Genetic variability under the seedbank coalescent. Genetics 200(3), 921–934 (2015)
Blath, J., González Casanova, A., Kurt, N., Wilke-Berenguer, M.: A new coalescent for seed-bank models. Ann. Appl. Probab. 26(2), 857–891 (2016)
Blath, J., Jacobi, D., Nie, F.: How the interplay of dormancy and selection affects the wave of advance of an advantageous gene. ArXiv e-prints (2021)
Bovier, A.: Gaussian processes on trees: from spin glasses to branching brownian motion. Cambridge Studies in Advanced Mathematics. Cambridge University Press (2016)
Bramson, M.: Convergence of solutions of the Kolmogorov equation to travelling waves. Mem. Am. Math. Soc. 44(285), iv+190 (1983)
Bramson, M.D.: Maximal displacement of branching Brownian motion. Comm. Pure Appl. Math. 31(5), 531–581 (1978)
Chen, L., Kim, K.: On comparison principle and strict positivity of solutions to the nonlinear stochastic fractional heat equations. Ann. Inst. H. Poincaré Probab. Statist. 53(1), 358–388, 02 (2017)
Ethier, S., Kurtz, T.: Markov processes. Wiley Series in Probability and Mathematical Statistics: Probability and Mathematical Statistics. John Wiley & Sons, Inc., New York (1986) (Characterization and convergence)
Fisher, R.A.: The Wave of Advance of an Advantageous Gene. Ann, Eugenics (1937)
Greven, A., den Hollander, F., Oomen, M.: Spatial populations with seed-bank: well-posedness, duality and equilibrium. arXiv e-prints, arXiv:2004.14137 (2020)
Ikeda, N., Nagasawa, M., Watanabe, S.: Branching Markov processes. I. J. Math. Kyoto Univ. 8, 233–278 (1968)
Ikeda, N., Nagasawa, M., Watanabe, S.: Branching Markov processes. II. J. Math. Kyoto Univ. 8, 365–410 (1968)
Ikeda, N., Nagasawa, M., Watanabe, S.: Branching Markov processes. III. J. Math. Kyoto Univ. 9, 95–160 (1969)
Ikeda, N., Watanabe, S.: Stochastic differential equations and diffusion processes. In: North-Holland Mathematical Library, vol. 24, 2nd edn. North-Holland Publishing Co., Amsterdam; Kodansha, Ltd., Tokyo (1989)
Kallenberg, O.: Foundations of modern probability. In: Probability and its Applications (New York), 2nd edn. Springer-Verlag, New York (2002)
Karoui, N.E., Méléard, S.: Martingale measures and stochastic calculus. Probab. Theory Related Fields 84(1), 83–101 (1990)
Khoshnevisan, D.: A primer on stochastic partial differential equations. In: A Minicourse on Stochastic Partial Differential Equations, volume 1962 of Lecture Notes in Math., pp 1–38. Springer, Berlin (2009)
Kingman, J.F.C.: The coalescent. Stochastic Process. Appl. 13(3), 235–248 (1982)
Kliem, S.: Travelling wave solutions to the KPP equation with branching noise arising from initial conditions with compact support. Stochastic Process. Appl. 127(2), 385–418 (2017)
Kolmogorov, A., Petrovsky, N., Piscounov, N.: Etude de l’ équation de la diffusion avec croissance de la quantité de matière et son application à un problème biologique. Moscow Univ. Math. Bull. 1(1), 1–25 (1937)
Lalley, S.P., Sellke, T.: A conditional limit theorem for the frontier of a branching Brownian motion. Ann. Probab. 15(3), 1052–1061 (1987)
Lambert, A., Ma, C.: The coalescent in peripatric metapopulations. J. Appl. Probab. 52(2), 538–557 (2015)
Lennon, J., Jones, S.: Microbial seed banks: the ecological and evolutionary implications of dormancy. Nat. Rev. Microbiol. 9, 119–130, 02 (2011)
McKean, H.P.: Application of Brownian motion to the equation of Kolmogorov-Petrovskii-Piskunov. Comm. Pure Appl. Math. 28(3), 323–331 (1975)
Mueller, C., Mytnik, L., Ryzhik, L.: The speed of a random front for stochastic reaction-diffusion equations with strong noise. arXiv e-prints, arXiv:1903.03645 (2019)
Mytnik, L., Perkins, E., Sturm, A.: On pathwise uniqueness for stochastic heat equations with non-Lipschitz coefficients. Ann. Probab. 34(5), 1910–1959 (2006)
Roberts, M.I.: A simple path to asymptotics for the frontier of a branching Brownian motion. Ann. Probab. 41(5), 3518–3541 (2013)
Shiga, T.: Stepping stone models in population genetics and population dynamics. In: Stochastic Processes in Physics and Engineering (Bielefeld, 1986), volume 42 of Math. Appl., pp. 345–355. Reidel, Dordrecht (1988)
Shiga, T.: Two contrasting properties of solutions for one-dimensional stochastic partial differential equations. Can. J. Math. 46(2), 415–437 (1994)
Shigesada, N., Kawasaki, K.: Biological Invasions: Theory and Practice. Oxford University Press, UK (1997)
Shoemaker, W.R., Lennon, J.T.: Evolution with a seed bank: the population genetic consequences of microbial dormancy. Evol. Appl. 11(1), 60–75 (2017)
Acknowledgements
The authors gratefully acknowledge support from the DFG Priority Program 1590 “Probabilistic Structures in Evolution”. The third author gratefully acknowledges support from the Berlin Mathematical School (BMS).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Blath, J., Hammer, M. & Nie, F. The stochastic Fisher-KPP Equation with seed bank and on/off branching coalescing Brownian motion. Stoch PDE: Anal Comp 11, 773–818 (2023). https://doi.org/10.1007/s40072-022-00245-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40072-022-00245-x