Abundant exact solutions and interaction phenomena of the (2 + 1)-dimensional YTSF equation

Abstract

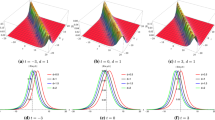
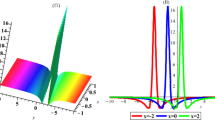
In this paper, we study abundant exact solutions including the lump and interaction solutions to the (2 + 1)-dimensional Yu–Toda–Sasa–Fukuyama equation. With symbolic computation, lump solutions and the interaction solutions are generated directly based on the Hirota bilinear formulation. Analyticity and well-definedness is guaranteed through some conditions posed on the parameters. With special choices of the involved parameters, the interaction phenomena are simulated and discussed. We find the lump moves from one hump to the other hump of the two-soliton, while the lump separates from the hump of the one-soliton.

Appendices

Appendix A

For simplicity, we consider three cases with $a_{1}=0$, $a_{2}=0$ or $a_{10}=0$, respectively:

Case 1

$$\begin{aligned} \Bigg \{&a_{1}=a_{1}, a_{2}=0, a_{3}=-\frac{3(a_{1}^2+a_{5}^2)a_{9}^2}{4a_{1}}, a_{4}=a_{4}, a_{5}=a_{5}, a_{6}=\varepsilon \frac{(a_{1}^2+a_{5}^2)a_{9}}{a_{1}},\\&a_{7}=\frac{3a_{5}a_{9}^2(a_{1}^2+a_{5}^2)}{4a_{1}^2}, a_{8}=a_{8}, a_{9}=a_{9}, a_{10}=\varepsilon \frac{a_{5}a_{9}^2}{a_{1}}, a_{11}=-\frac{a_{9}^3(a_{1}^2-3\,a_{5}^2)}{4a_{1}^2},\\&a_{12}=a_{12}, a_{13}=\frac{4\,a_{1}^2+8\,a_{1}^2a_{5}^2+4\,a_{5}^4+a_{9}^4}{4a_{9}^2(a_{1}^2+a_{5}^2)}\Bigg \}, \end{aligned}$$

Case 2

$$\begin{aligned} \Bigg \{&a_{1}=0, a_{2}=\varepsilon \,a_{5}a_{9}, a_{3}=\varepsilon \,\frac{3}{2}\,a_{6}a_{9}, a_{4}=a_{4}, a_{5}=a_{5}, a_{6}=a_{6},\\&a_{7}=-\frac{3(a_{5}^2a_{9}^2-a_{6}^2)}{4a_{5}}, a_{8}=a_{8}, a_{9}=a_{9},a_{10}=\frac{a_{6}a_{9}}{a_{5}},\\&a_{11}=-\frac{a_{9}(a_{5}^2a_{9}^2-3\,a_{6}^2)}{4a_{5}^2}, a_{12}=a_{12},a_{13}=\frac{4\,a_{5}^4+a_{9}^4}{4a_{5}^2a_{9}^2}\Bigg \}, \end{aligned}$$

Case 3

$$\begin{aligned} \Bigg \{&a_{1}=a_{1}, a_{2}=\varepsilon \,a_{5}a_{9}, a_{3}=-\frac{3}{4}\,a_{1}a_{9}^2, a_{4}=a_{4}, a_{5}=a_{5}, \\&a_{6}=-\varepsilon a_{1}a_{9}, a_{7}=-\frac{3}{4}\,a_{5}a_{9}^2, a_{8}=a_{8}, a_{9}=a_{9}, a_{10}=0, \\&a_{11}=-\frac{1}{4}\,a_{9}^3, a_{12}=a_{12}, a_{13}=\frac{4\,a_{1}^4+8\,a_{1}^2a_{5}^2 +4\,a_{5}^4+a_{9}^4}{4a_{9}^2(a_{1}^2+a_{5}^2)}\Bigg \}, \end{aligned}$$

where $\varepsilon =\pm 1$. Actually, these three sets of solutions contain six cases corresponding to different values of $\varepsilon$.

Appendix B

Case 1

$$\begin{aligned} \Bigg \{&a_{1}=a_{1}, a_{2}=\frac{a_{5}k_{1}^2+a_{1}k_{2}}{k_{1}}, a_{3}=-\frac{3}{4}\,\frac{a_{1}k_{1}^4-2\,a_{5}k_{1}^2k_{2}-a_{1}k_{2}^2}{k_{1}^2}, a_{4}=a_{4}, a_{5}=a_{5}, \\&a_{6}=-\frac{a_{1}k_{1}^2-a_{5}k_{2}}{k_{1}}, a_{7}=-\frac{3}{4}\,\frac{a_{5}k_{1}^4+2\,a_{1}k_{1}^2k_{2}-a_{5}k_{2}^2}{k_{1}^2},\\&a_{8}=a_{8}, a_{9}=\frac{a_{1}^2+a_{5}^2}{k_{1}^2},k_{1}=k_{1}, k_{2}=k_{2}, k_{3}=-\frac{k_{1}^4-3\,k_{2}^2}{4k_{1}}\Bigg \}, \end{aligned}$$

Case 2

$$\begin{aligned} \Bigg \{&a_{1}=0, a_{2}=\varepsilon a_{5}k_{1}, a_{3}=\varepsilon \frac{3}{2}\,a_{6}k_{1}, a_{4}=a_{4}, a_{5}=a_{5}, a_{6}=a_{6},\\&a_{7}=-\frac{3}{4}\,\frac{a_{5}^2k_{1}^2-a_{6}^2}{a_{5}}, a_{8}=a_{8}, a_{9}=\frac{a_{5}^2}{k_{1}^2}, \\&k_{1}=k_{1}, k_{2}=\frac{a_{6}k_{1}}{a_{5}}, k_{3}=-\frac{k_{1}(a_{5}^2k_{1}^2-3\,a_{6}^2)}{4a_{5}^2}\Bigg \}, \end{aligned}$$

Case 3

$$\begin{aligned} \Bigg \{&a_{1}=a_{1}, a_{2}=\frac{-a_{5}k_{1}^2+a_{1}k_{2}}{k_{1}}, a_{3}=-\frac{3}{4}\,\frac{a_{1}k_{1}^4+2\,a_{5}k_{1}^2k_{2}-a_{1}k_{2}^2}{k_{1}^2}, a_{4}=a_{4}, a_{5}=a_{5},\\&a_{6}=\frac{a_{1}k_{1}^2+a_{5}k_{2}}{k_{1}}, a_{7}=\frac{3}{4}\,\frac{-a_{5}k_{1}^4+2\,a_{1}k_{1}^2k_{2}+a_{5}k_{2}^2}{k_{1}^2}, \\&a_{8}=a_{8}, a_{9}=\frac{a_{1}^2+a_{5}^2}{k_{1}^2},k_{1}=k_{1}, k_{2}=k_{2}, k_{3}=-\frac{k_{1}^4-3\,k_{2}^2}{4k_{1}}\Bigg \}, \end{aligned}$$

where $\varepsilon =\pm 1$.