High-fidelity modeling approaches for the analysis of reinforced structures using one-, two- and three-dimensional elements

Abstract

The present paper proposes a method for analyzing reinforced thin-walled structures based on high-order one-, two- and three-dimensional finite elements (FE). Refined finite elements are developed in the domain of the Carrera unified formulation (CUF). The node-dependent kinematic approach (NDK), which allows to connect in an easy manner elements with incompatible kinematics, has been used to connect elements with different dimensions without the need of ad hoc connection techniques. The formulation ensures the continuity of the displacement at the interface preventing the onset of singularities that lead to inaccurate results when beam, plate and solid elements have to be coupled to solve complex structures. The effectiveness of the present method has been confirmed by comparing the results with those from literature and with those obtained using commercial finite element codes. Static and free-vibration analyses of reinforced panels have been carried out to demonstrate the capabilities of the present models. The results show that the limits of classical structural models can be easily overcome using the present approach, and at the same time, a quasi three-dimensional solution can be obtained with a large computational cost saving.

1 Introduction

Reinforced thin-walled structures are largely used when a high strength-to-weight ratio is required. Finite element models (FEM) are widely used to design complex reinforced structures. The finite element models allow each structural component to be discretized into a finite number of elementary elements. One- (beams/rods), two- (plates/shells) and three-dimensional (solids) elements can be used for the design of complex structures. Beam elements are suitable for the analysis of slender bodies, e.g., stringers, while two-dimensional elements are adopted for thin-walled components, e.g., plates. The kinematic assumption behind the formulation of beam and plate elements are usually based on classical models. One-dimensional elements are based on Euler–Bernoulli [1] or Timoshenko [2] theories. Two-dimensional finite elements are generally based on the assumptions of Kirchoff–Love [3, 4], Reissener [5] and Mindlin [6]. When the assumptions of one- and two-dimensional models are not respected, three-dimensional elements can be used to directly solve the equation of elasticity in their complete formulation, as shown by [7]. The accuracy of the FE models depends on the number of elements used to discretize the domain and on their kinematic assumptions. The use of refined mesh can led to a more accurate solution of the problem, but cannot overcome the limitations due to the kinematic assumption used by the model, e.g., a beam model based on the Euler–Bernoulli theory cannot predict the shear stress whatever mesh is used. To avoid limitations introduced by the kinematic model, the use of three-dimensional models is obviously the best choice and lead to accurate results but can require huge computational costs, especially when thin-walled structures are considered.

Many numerical models have been proposed for the analysis of reinforced panels. When the reinforcements are equally spaced, an equivalent orthotropic homogeneous panel of constant thickness can be obtained by smearing out the stiffness property of the ribs over the plate, as proposed by Olivie et al. [8]. This approach evaluates the contribution of each component locally, then superimposed onto the global properties of the panel. In this case, the results do not provide detailed information about the behavior of each component of the structure. Deb et al. [9] and Civan et al. [10] proposed a method able to consider separately plate and ribs considering both the unknown interface forces, due to the coupling between the components and the direct loads. The interface forces, unlike direct loads, are unknown, and as a result, they must be computed iteratively to satisfy the compatibility between the components. This method does not include the effect of torsion or shear transfer from the ribs to the plate. More detailed models have been presented by [11] and [12], which introduced some ad hoc finite element models that are able to deal with reinforced structures. Recently, Alaimo et al. [13] introduced a strategy for the modelization of thin-walled reinforced structures by considering each structural component, e.g., skin, flange and web, as layers of the plate structure. When classical FE models are adopted, 1D-, 2D- and 3D-dimensional elements are mixed together to provide accurate results with an acceptable number of degrees of freedom (DOFs). The coupling between these different elements is a challenging problem, since classical FEM models approximate the kinematics using three displacements and three rotations at each node and the nodes usually are not placed on physical surfaces. Appropriate coupling techniques should be introduced to ensure an accurate solution. The coupling between elements characterized by different kinematics becomes more complex when refined formulations are used, because the assumption of three displacements and three rotations in each node is not verified. Hoseini et al. [14] proposed a method to joining full three-dimensional finite element with 1D finite element using the variation asymptotic method [15, 16] to find the interaction between the solid and the beam parts.

The limitations introduced by classical structural models can be overcome by refining the kinematic model, as proposed by Carrera et al. [17] in the review of advanced beam models. Cavallo et al. [18] and Carrera et al. [19] have shown various approaches used to study reinforced structures by means of refined beam elements. The Carrera unified formulation (CUF), first proposed in 1995 [20] and developed in [21, 22], provides a unified approach able to derive variable kinematic models. One-, two- and three-dimensional theories are expressed in terms of a few fundamental nuclei, $FN_{s}$, the structures of which do not formally depend on the assumptions (type of functions or order) that have been used to describe the displacement field over the cross section and through the thickness for the 1D and 2D elements, respectively. The use of Lagrange multipliers to connect beam models has been shown by Carrera et al. [23]. In 2013, Carrera and Zappino [24] proposed for the first time a case of study where elements with different kinematics have been connected without the use of an ad hoc techniques. Carrera and Zappino [25, 26] later presented a general approach to build variable kinematic models, including 1D, 2D and 3D elements, for the free-vibration analysis of complex structures. The introduction of the node-dependent kinematic (NDK) approach presented by Carrera and Zappino [27, 28], and recently extended for the global–local analysis of smart structures by the same authors [29], can be used to switch between models with different kinematics without the need of any ad hoc formulation or compatibility equations.

The present paper aims to explore the use on these advanced numerical techniques to investigate the static and dynamic response of reinforced panels. Multidimensional models and variable kinematic approaches will be used to provide a high-fidelity description of the model and to provide an accurate solution with a general reduction of the computational costs with respect to full three-dimensional solutions. The paper is organized as follows. Section 2 describes the CUF models applied to beam, plate and solid elements. Section 3 is devoted to the description of the coupling method between one-, two- and three-dimensional models including the NDK approach. The results are presented in Sect. 4, where the present model is assessed with experimental and reference solutions. The final considerations and conclusions are reported in the last section.

2 One-, two- and three-dimensional models

The general and unified approach proposed by Carrera et al. in [30] allows the matrices of one-, two- and three-dimensional finite element models to be derived in a unified manner regardless of the kinematic model.

The generic three-dimensional displacement field can be written as:

$$\begin{aligned} {\textbf {u}}={\textbf {u}}(x,y,z). \end{aligned}$$

(1)

The vector ${\textbf {u}}(x,y,z)$ contains the three displacement components in the case of the mechanical problem. When the geometry allows one of the dimensions to be considered negligible, the problem can be reduced to a two-dimensional problem. This is the case of plate/shell elements, where the through-the-thickness dimension, z, is negligible if compared to the other two. For the two-dimensional problem, Eq. 1 becomes:

$$\begin{aligned} {\textbf {u}}={\textbf {u}}_{\tau }(x,y)F^{1D}_{\tau }(z),\qquad \tau =1\ldots M, \end{aligned}$$

(2)

where $F^{1D}_{\tau }$ represents a generic function expansion used to approximate the displacement field through the thickness. M is the number of terms in the expansion.

In the case in which two dimensions, e.g., x and z, can be considered negligible with respect the third one, e.g., y-direction, Eq. 1 takes the following form:

$$\begin{aligned} {\textbf {u}}={\textbf {u}}_{\tau }(y)F^{2D}_{\tau }(x,z),\qquad \tau =1\ldots M, \end{aligned}$$

(3)

where $F^{2D}_{\tau }$ represents the function expansion used to approximate the solution over the cross section of the beam model, and M is the number of terms in the expansion.

$F^{1D}_{\tau }$ and $F^{2D}_{\tau }$ functions can be assumed a priori whether the problem is 1D or 2D and their choice denotes the kinematic pf of the structural model considered for the analyses.$u_{\tau }$ represents the unknown of the structural problem. The FE approach can be used to solve the problem through the discretization of the domain in a finite number of elements on which the solution is approximated using the shape functions, $N_i$. The generic displacement field can be represented as follows:

$$\begin{aligned} {\textbf {u}}={\textbf {u}}_{i\tau } N_i F_{\tau }, \qquad \tau =1\ldots M; \qquad i=1\ldots N_n, \end{aligned}$$

(4)

where i stands for the FE model. The index $\tau$ comes from the kinematics used in the structural model approximation. $N_n$ is the number of nodes in the finite element. ${\textbf {u}}_{i \tau }$ is the coefficient of expansion and is also the unknown factor of the problem.

Equation 4 can be adopted for all the structural models, since only the choice of $N_i$ and $F_{\tau }$ makes the difference:

$$\begin{aligned} 3D\longrightarrow {\textbf {u}}=&{\textbf {u}}_{i} N_i^{3D}(x,y,z)\;\cdot \; 1 \nonumber \\ 2D\longrightarrow {\textbf {u}}=&{\textbf {u}}_{i\tau } N_i^{2D}(x,y) F_{\tau }^{1D}(z)\nonumber \\ 1D\longrightarrow {\textbf {u}}=&{\textbf {u}}_{i\tau } N_i^{1D}(y)\; F_{\tau }^{2D}(x,z). \end{aligned}$$

(5)

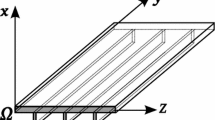
Figure 1 shows how the same structure can be modeled using one- and two-dimensional models. For the 1D model, $N_i^{1D}$ and $F_{\tau }^{2D}$ are the FEM shape functions along the y-axis (A 2-node beam element, B2) and the expansion used over the beam cross section (Lagrange expansion function with 4-nodes, LE4), respectively. For the 2D model, $N_i^{2D}$ and $F_{\tau }^{1D}$ are the FEM shape functions on the middle yz-plane (Lagrange expansion function with 9-nodes, LE9) and the expansion used thorough the thickness (a linear Lagrange expansion), respectively. More details can be found in the work of Zappino et al. [31].

Fig. 1

Example of one- and two-dimensional modeling approaches for a simple structure

2.1 Node-dependent kinematic (NDK) modeling approach

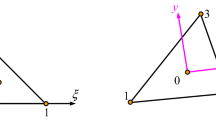
The use of higher-order models is mandatory when the problem features do not respect the assumption of the classical theories. In this case, the solution can be improved by the refinement of the kinematics, but, as a drawback, the computational costs can dramatically increase. This makes the refined kinematics model suitable for analysis of local areas. The new class of node-dependent kinematic (NDK) elements that have already been discussed in the work of Zappino et al. [31] for one-dimensional models and in [32] for the plate case are introduced in this work to increase the model accuracy only in the area where it is required. To explain in a simple manner the NDK approach, a two-node 1D element is considered in Fig. 2.

Fig. 2

A two-node one-dimensional element with node-dependent kinematics

The displacement functions at node 1 can be written as:

$$\begin{aligned} {\textbf {u}}^{1}={\textbf {u}}_{1 \tau } F_{\tau }^{1}, \qquad \tau =1\ldots M^{1}. \end{aligned}$$

(6)

Meanwhile, the displacements at the second node read:

$$\begin{aligned} {\textbf {u}}^{2}={\textbf {u}}_{2 \tau } F_{\tau }^{2}, \qquad \tau =1\ldots M^{2}. \end{aligned}$$

(7)

The cross-sectional expansions, $F_{\tau }^{1}$ and $F_{\tau }^{2}$, can be chosen arbitrarily at each node. If the same expansion is used in each FE node, it can be considered as a uniform kinematic model. In contrast, the NDK approach allows the kinematics to be different in each node as required by the problem. The three-dimensional displacement field referred to the whole element is:

$$\begin{aligned} {\textbf {u}}={\textbf {u}}_{1\tau } N_1 F_{\tau }^1 + {\textbf {u}}_{2\tau } N_2 F_{\tau }^2, \qquad \tau =1\ldots M^i. \end{aligned}$$

(8)

The three components of the displacement field in each node are smeared by the FE shape functions along the beam length, and this ensures a smooth transition between the displacement fields of the two nodes. This approach allows the displacement field to be continuous at each point. This approach can be easily included in the CUF formulation and extended to any order beam and plate models. The generic displacement field can be written as:

$$\begin{aligned} {\textbf {u}}={\textbf {u}}_{i\tau } N_i(y) F_{\tau }^i(x,z), \qquad \tau =1\ldots M^i; \qquad i=1\ldots N_n, \end{aligned}$$

(9)

where the index i included into the notation states that the function expansion $F_{\tau }^i(x,z)$ is not a property of the element, but of the ith nodes, while the index i in the $M^i$ shows that the number of terms in the expansion, M, can be different at each node.

2.2 Governing equations of NDK FE models

The governing equations can be derived by applying the principle of virtual displacement (PVD). Consider the energy of the system:

$$\begin{aligned} \delta L_{int} = \int _{V} \delta \varepsilon ^T \sigma dV = \delta L_{ext}, \end{aligned}$$

(10)

where V is the volume of the integration domain, $\delta L_{int}$ is the internal energy and $\delta L_{ext}$ is the external work. In the case of free-vibration problems, $\delta L_{ext}=0$. $\varepsilon$ and $\sigma$ are the strain and stress vectors. By considering the geometrical relations, the constitutive equations, end the generic displacement field, the internal work can be written as:

$$\begin{aligned} \delta L_{int} = \delta q_{js} \int _V N_j F^j_{s} D^T C D F^i_{\tau } N_i dV q_{i \tau }. \end{aligned}$$

(11)

In a compact form, the above expression can be written as:

$$\begin{aligned} \delta L_{int} = \delta q^T_{j s} k_{ij \tau s} q_{i \tau }, \end{aligned}$$

(12)

where $k_{ij \tau s}$ is the generalized stiffness matrix expressed in the form of ’fundamental nucleus’:

$$\begin{aligned} {\textbf {k}}_{ij \tau s} = \int _V N_j F^j_{s} {\textbf {D}}^T {\textbf {C}} {\textbf {D}} F^i_{\tau } N_i dV. \end{aligned}$$

(13)

In the case of a mechanical problem, the fundamental nucleus of the mechanical stiffness matrix $,{\textbf {k}}_{ij \tau s}$, is a $3 \times 3$ matrix. The explicit formulation of the fundamental nuclei has been presented by [30] and [31].

3 Approaches for the high-fidelity modeling of reinforced structures

This section presents the approach used to connect 1D, 2D and 3D CUF models to ensure the displacement continuity at the interfaces between two different elements when reinforced structures are analyzed.

Fig. 3

Reinforced structure example

When a reinforced structure is considered, see Fig. 3, panels and stringers can be modeled using different types of elements depending on the desired accuracy and computational costs. Models made with solid elements are very accurate, but a large number of degrees of freedom (DOF) may be required, that is, high computational costs have to be expected. Beam elements, 1D, can be used to analyze slender parts of a structure, while plate/shell elements are commonly used for panels.

The use of refined beam models allows one-dimensional elements to be used for both panels and reinforcements. In this case, since the same kinematic is used in the whole structure, at the panel/stringers interface, the continuity of the displacements is guaranteed. When 1D CUF elements are used for both panel and stringer, the y-axis is the beam axis and the cross section contains panels and stringers profiles, as shown in Fig. 4.

Fig. 4

One-dimensional modeling approach for a reinforced structure

Figure 4 shows a reinforced structure modeled using only 1D refined models. Nine-point Lagrange expansion functions (LE9) are used on the cross section, while on the beam axis, the FEM approximation adopted considers a three-node beam element B3 (quadratic functions). When 2D and 1D elements are used for plate and stringer, respectively, the interface between the two different elements could show the discontinuity of the displacements since different kinematic models are adopted. The use of displacement-based kinematic models, for both plate and beam, allows the plate/beam interface to be modeled avoiding displacement discontinuity end ensuring a high-fidelity representation of the geometry.

3.1 Mixed one-/two-dimensional models

Figure 5 shows the case on which the 2D refined CUF elements are used for panels and the 1Delements are adopted for the stringers.

Fig. 5

Modeling approach for a reinforced structure using one- and two-dimensional models

Two-dimensional elements are represented as the median surface of the element and an expansion through the thickness defines the geometry of the panel. There are three expansion functions that can be taken through thickness, linear function with two nodes, quadratic functions with three nodes and cubic functions with four nodes.

3.2 Mixed one-/two- and three-dimensional models

A rigorous connection between plate and beam can be obtained using a solid element at the interface. In other cases, solid elements can be adopted in a limited area of the structure to study static and dynamic behavior in detail. Extensive use of solid elements is not recommended, because the number of degrees of freedom increases rapidly as well as the calculation costs. Figure 6 shows the details of the coupling of 3D, 2D and 1D elements.

Fig. 6

Modeling approach for a reinforced structure using one-, two- and three-dimensional models

4 Model verification

The aim of this section is to verify the effectiveness of the proposed method. At fist, a reinforced panel is considered to verify the accuracy of the present models, and the results are compared with many references presented in the literature. After that, two reinforced panel have been studied to show the computational advantages introduced by the present approach in terms of computational cost reduction. Both dynamic and static analyses have been carried out.

4.1 Numerical assessment: eccentrically stiffened panel

A reinforced plate with two longitudinal stiffeners, see in Fig. 7, is considered as the first example to assess the present models. Experimental and theoretical results for the same geometry were presented by [33] in 1977. The FE model presented in ([33])uses triangular elements for the plate, while the stiffeners were modeled by refined beam elements able to include bending and torsion. The same structure has been studied in [34] using a semi-analytical solution of the state-vector equation theory. The algebraic equation of plate and stiffeners are derived separately. Later on, the equations of plate and stiffeners are coupled ensuring the compatibility of displacements and stresses at the interface between the structural elements. The transverse shear deformation and the rotary inertia are also considered in the model, and the thickness of plate and the height of stiffeners are not restricted. The clamped plate is made with an aluminum alloy with a Young’s modulus of 68.7 GPa, $\nu$ = 0.29 and $\rho$ = 2823 $kg/m^{3}$, as reported in [35].

Fig. 7

Geometry of the metallic plate with two longitudinal stiffeners

The models presented in this paper have been used to investigate the dynamic response of the present structure. Two different modeling approaches have been used. The first model is a one-dimensional model in which the cress section kinematic is approximated using nine-point Lagrange elements (LE9), see Fig. 8). The cross section of the stringers is modeled using 2-LE9 elements. Along the beam axis, the y-axis, eight B3 beam elements are adopted. The second model is made by coupling two- and one-dimensional elements; in particular, 2D elements for the plate and 1D elements for the stringers. The mesh used is shown in Fig. 9. The upper plate uses $8\times 12$ elements in each panel between the stringers. The stringers are modeled using one-dimensional elements and are modeled as in the full one-dimensional model. The second modeling approach uses two different expansions for the plate elements, as shown in Fig. 9. The kinematic of the elements in blue can be approximated using a Taylor or a Lagrange expansion. When a quadratic Lagrange expansion is considered, the model is called $2D-1D_{LE}$. When a Taylor expansion is considered, the models are called $2D-1D_{LE \& TE-N}$, where N represents the order of the Taylor expansion. As an example, a model called $2D-1D_{LE \& TE-2}$ uses a second-order Taylor expansion for the plate elements, the NDK approach is used to have a smooth transition to the Lagrange kinematic in the elements at the interface with the stringers. The use of a Lagrange expansion in these areas makes the joining with the beam elements easier.

Fig. 8

Details of the cross-sectional mesh of the one-dimensional model

Fig. 9

Details of the one-/two-dimensional model. The blue elements are those where the kinematics has been changed using the NDK approach

Table 1 reports the first natural frequency of the structure evaluated using different modeling approach. The experimental and numerical references are reported in the first four lines. The proposed 1D and $2D-1D$ models provide a good accuracy in the evaluation of the dynamic response of the structure. Both constant and node-dependent kinematic models are able to reproduce the experimental results.

Table 1 Natural frequencies for eccentrically stiffened clamped plate with double stiffeners, Hz

Figure 10 shows the first four modal shapes of the considered structure

Fig. 10

Bending and shell-like mode shape evaluated using the $2D-1D_{LE}$ model

4.2 Free-vibration analysis of square reinforced panel

The geometrical features of the considered structure are shown in Fig. 11. The material used for the analysis has the following properties: Young’s modulus, E, of 75 GPa, Poisson’s ratio, $\nu$, equal to 0.3, and the material density, $\rho ,$ equal to 2700 $kg/m^{3}$.The panel is clamped at $y=0$ m and $y=0.5$ m, which means that all the displacements of the nodes placed in the end sections have been forced to be zero.

Fig. 11

Geometry and reference system of the reinforced square panel

A variable kinematic model based on one-/two-dimensional elements is considered. The stringers cross section is discretized using two LE9 elements, as in the previous case. On the $y-axis$, 12 quadratic beam elements (B3) are adopted.

Fig. 12

LE & TE-N model description. The blue panels are those where NDK strategy has been used to impose a Taylor based model at the nodes

Six plate elements are used between two stringers, while only one plate element is used at the interface with the beam elements. Twelve elements are used along the panel length. As for the previous assessment, the NDK approach has been used to change the kinematic in some areas of the plate, and the blue elements in Fig. 12 are those where Taylor or Lagrange expansion are used. Model $2D-1D_{LE}$ uses a uniform kinematic model, based on a quadratic Lagrange expansion, on the panel. When a Taylor-based model is used in some areas, see Fig. 12, the nomenclature $2D-1D_{LE \& TE-N}$ is used, where N denotes the order of the Taylor expansion.

Three models, developed using the commercial code FEMAP, have been used to compare the results. The reference solution is a refined solid model, called $3D^{REF}$. A coarse 3D model, $3D_{FEMAP}$, is proposed to have a solid model with a number of DOFs comparable with the present approach. Finally, a classical two-dimensional model called $2D_{FEMAP}$ has been considered.

Figure 13 shows the first ten modal shapes of the LE model, where global and local deformations can be noticed. Mode 8 shows a very complex shell-like shape that require accurate kinematic model to be detected. Classical bending model is shown in Fig. 13a. Figure 13g shows local modes at the stringer level.

Fig. 13

The first ten modes evaluated using the $2D-1D_{LE}$ model

Table 2 shows the first ten frequencies for all the models considered, and the second row reports the degrees of freedom required by each approach

Table 2 The first ten frequencies evaluated using different models

Results reported in Table 2show the accuracy of the present modeling approach in the analysis of the free vibrations of the reinforced panel. A coarse 3D model, as well as a classical plate model, leads to inaccurate results compared with the reference solution, and the results show errors up to $6\%$ in the value of the first ten natural frequencies. All the models based on the present theory provide an accuracy comparable with the refined solid model. In this case, the error is always lower than $1\%$ except for the fifth frequency of the model $2D-1D_{LE \& TE2}$, where it is slightly higher. The use of refined kinematic model led to a considerable reduction in the computational cost, and the present model uses only the $13\%$ of the DOFs used by the refined solid model.

Figure 14 compares the evolution of the first ten frequencies for the model $2D-1D_{LE \& TE2}$ with respect to the classical models considered. It is clear that the coarse FEM model overestimates the values of the natural frequencies, while the two-dimensional model derived with FEMAP underestimates the stiffness of the structure, that is, lower frequency values are detected.

Fig. 14

Evolution of the firsts ten natural frequencies evaluated using different numerical approaches

4.3 Static analysis of a square reinforced panel

This section investigates the static response of a thin-walled stiffened panel reinforced with three longitudinal stringers. The cross section is shown in Fig. 16. The panel is clamped in $y=0$ and in $y=2$, as for the previous case this means that all the displacements of the nodes placed in the end sections have been forced to be zero.

The geometry of the structure is shown in Fig. 17, where the edges a and b are both equal to 2 m.

The panel is subjected to a point load, F, which is applied at point (C) with magnitude of 20000 N, as shown in Fig. 17. As a reference solution, the refined 3D model, $FEM_{3D-REF}$, proposed in [37] is considered. Figure 15 shows the $FEM_{3D-REF}$ model analyzed using the commercial Nastran with 724299 DOFs. A second coarse solid model, $FEM_{3D}$, with 14325 DOFs has been considered.

Fig. 15

3D refined model (724299 DOFs) presented in [37]

Figure 17 shows the points on which the vertical displacement is evaluated on the panel. A, B, C, D, E, $A'$, $B'$, $D'$, $E'$ geometric coordinates are proposed in Table 3.

Fig. 16

Cross section geometrical properties

Fig. 17

Thin-walled reinforced panel under a static load

Table 3 Coordinates of the points where the displacements are evaluated

The present one-/two-dimensional model (see. Fig. 18) considers for the beam elements two nine-point Lagrange elements (LE9) for the beam cross section and 12 quadratic (B3) beam elements on the $y-axis$. For the plate, six elements are used between the stringers and two 2D elements for the free edge near the outer stringers.

As shown in Fig. 18, various combinations of LE and TE expansion functions are considered for the plate and in particular the kinematic of the blue area has been changed. As mentioned in the previous section, the present models are called $2D-1D_{LE \& TE-N}$, where N represents the order of Taylor expansion. The model with only Lagrange kinematic is named $2D-1D_{LE}$

Fig. 18

$2D-1D_{LE \& TE-N}$ model with Taylor expansion function on the nodes of the blue panels

Table 4 shows the vertical displacement in some points of the structures (see Fig. 17). Although the $3D_ {FEMAP}$ model has more DOFs than the present models, the synergistic use of one- and two-dimensional elements led to a remarkable accuracy, much higher than that provided by the coarse solid model. Figure 19 shows the behavior of the displacement field evaluated in the selected points.

Table 4 Vertical displacement for various FEM models (displacement $\times$ $10^{-3}$ [m])

Fig. 19

Displacement field in the zy and xz-plane for the panel proposed in Fig. 18

A stress analysis is carried out in four points through the thickness of the central stringers ($\alpha$, $\beta$, $\gamma$, $\delta$, see Fig. 16b). $\sigma _{yy}$ is evaluated through the thickness of the central stringer for $x=\dfrac{a}{2}$ and $y=\dfrac{b}{2}$. Table 5 reports the stress values evaluated with different models. Also in the analysis of the stress field, the present approach provides an accuracy comparable with the refined solid model with a small fraction of the computational cost. Some discrepancy could be reduced with further refinements of the model. Figure 20a shows the $\sigma _{yy}$ distribution through the thickness of the structure. The results show that the use of the preset approach leads to results closer to the refined reference solution with respect to a coarse 3D model. These results point out the limits of solid elements in the analysis of thin-walled structures, where, to ensure a high-fidelity solution, a huge computational cost is required.

Table 5 $\sigma _{yy}$ for various FEM models expressed in [MPa]

Fig. 20

Stiffened plate: stress field through the thickness

5 Dynamic and static analysis-reinforced sandwich panel

This section extends the use of the present approach to a laminated reinforced structure. The static and dynamic analysis of an eccentrically stiffened laminated plate with four T-type stiffeners and clamped at edges (see Fig. 21 is presented. Since the panel is clamped, the displacements along the four edges are forced to be zero, both in the panel edges and in the stringers’ ends. The geometry of the structure has been proposed by [34].

The plate has a sandwich layout with two external thin orthotropic layers and an inner core. The three layers have the material properties of the aragonite crystals (as proposed in [38, 39]) with the following stiffness ratio: C22/C11 = 0.543103, C12/C11 = 0.23319, C23/C11 = 0.098276, C13/C11 = 0.010776, C33/C11 = 0.530172, C44/C11 = 0.26681, C55/C11 = 0.159914, C66/C11 = 0.262931. In the present work, C11$^{f}$ has been assumed to be 150 GPa and $\rho ^{f}$ = 1600 kg/m3 for the two outer layers, while the core has C11$^{c}$=C11$^{f}$/2 and $\rho ^{c}$=$\rho ^{f}$/2. The material properties of stiffeners are the same as those of the outer layers.

Fig. 21

Eccentrically stiffened laminated plate with four T-type stiffeners and clamped at the edges

Fig. 22

CUF model composed of 3D, 2D and 1D elements

The CUF model is obtained by using solid, plate and beam elements as shown in Fig. 22. In particular, solid (3D) elements are used to connect stringers and plates to provide a high-fidelity description of the area. The panel is modeled using plate elements (2D).

The stringers are discretized using beam (1D) elements, nine-points Lagrange elements are used on the cross section and three-node beam elements are used along the y-axis.

Different FE models, derived using FEMAP®, are used to compare the results for the free-vibration and static analysis. A refined solid model, called $3D_{FEMAP} refined model$, is used as a reference solution. This model is made using only 3D elements for all the components of the plate and stringers (see Fig. 23a). Figure 23b shows the subdivision between the core and the outer layers.

Fig. 23

$3D_{FEMAP}$ refined model from FEMAP® commercial code

Figure 24 shows the second solid model, derived using FEMAP®, called $3D_{FEMAP} Model$. The $3D_{FEMAP} model$ has a number of DOFs comparable with those of the $3D-2D_{LE}-1D$ model.

Fig. 24

$3D_{FEMAP}$ model from FEMAP® commercial code

Figures 25 and 26 show the FEMAP® refined models made using only 2D elements for both plate and stringers and 2D elements for plates and 1D elements for stringers, respectively.

Fig. 25

$2D_{FEMAP}$ model from FEMAP® commercial code

Fig. 26

$2D-1D_{FEMAP}$ model from FEMAP® commercial code

5.1 Free-vibration analysis

The free-vibration analysis is presented in this section. The first four frequencies proposed in the work by [34] are considered. Table 6 presents the first natural frequencies evaluated with all the models considered.

Table 6 First 4 modes of the eccentrically stiffened laminated plate with four T type stiffeners (see. Fig.21)

The comparison between the the results by [34] and those from the present models demonstrate the efficiency of the CUF models; in fact, a higher accuracy is reached with a reduction in the computational costs. When CUF model are considered, four different kinematic setups have been taken into account. The first model is based on a full layerwise approach, while the other three models use different Taylor expansions thought the thickness of the panels. In Fig. 22, the blue areas are those where a Taylor model has been used with a consequent reduction in the computational costs, the DOFs of the $3D-2D_{LE \& TE1}-1D$ model are reduced by 15% with respect to those of the $3D-2D_{LE}-1D$ model.

The results from the present approach are comparable with those from the $3D_{FEMAP}Refined$ model in terms of accuracy, but can be achieved using 13$\%$ of the degrees of freedom. The large advantages of the present approach are in the prediction of mode 4, see Fig. 27, where the modal shape in characterized by a local deformation of the stiffeners. This mode can be predicted only by a refined 3D model, while the use of a full 2D approach, model ${2D}_{FEMAP}$, leads to a large error. Since the mode involves mainly the stringers, it cannot be detected by the $3D-2D_{LE}-1D$ model.

Fig. 27

The first four modes evaluated with different FEM models. Mode 4 is not found by model ${2D-1D}_{FEMAP}$

5.2 Static analysis

This section presents the static analysis of the panel shown in Fig. 21. The structure is subjected to a uniform pressure distributed on the top of the panel as shown in Fig. 28.

Fig. 28

Clamped reinforced panel subjected to a uniform pressure of 1000 Pa

5.2.1 Displacement analysis

Figure 29 shows the panel deformed under the pressure of 1000 Pa applied on the top. Figure 22) shows the whole model where the NDK approach is applied in the nodes of the 2D elements far from the bonding areas of the stiffeners.

Fig. 29

Deformation of the $3D-2D_{LE \& TE1}-1D$ CUF model under the pressure load of 1000 Pa

The displacement analysis is computed on the points proposed in Fig. 30 located on the top of the panel with the coordinates shown in Table 7.

Fig. 30

Thin-walled reinforced panel under a uniform pressure. Points used for the evaluation of the displacement field

Table 7 Coordinates of the points where the results have been evaluated

Table 8 Displacement evaluated on the points proposed in Table 7, ( × $10^{-7}$ m)

Table 8 highlights the capability of the present models in the prediction of the displacement field of the complex reinforced structure analyzed. The $2D_{FEMAP}$ and ${2D-1D}_{FEMAP}$ models allow the DOFs to be reduced compared to the $3D_{FEMAP}$ refined model, but led to errors that range from 5% to 9%. The results obtained using the CUF models ensure a high accuracy with a strong reduction of the computational cost, and the use of the NDK approach can be used to provide an even higher reduction of the computational cost using a poor kinematic model in the panels. Despite the use of TE1 on the nodes of the plates, the $3D-2D_{LE \& TE1}-1D$ model is able to provide a solution very close to the reference model by using only the 13$\%$ of the DOFs. The computational advantages of the NDK approach are limited for the present geometry, but can have a strong impact when large-scale structures are considered and the panels areas are predominant.

5.2.2 Stress analysis

The tensile, $\sigma _{yy}$, and the shear, $\sigma _{xy}$, stresses are investigated. The stresses have been evaluated through the thickness in the point (x = 1.005, y = 0.795).

Figures 31 and 32 show the behavior of the $\sigma _{yy}$ through the thickness of the panel and the stringer, respectively. The stress distributions obtained using the present approach can reproduce the results of the refined solid model ensuring a strong reduction of the computational cost. The same can be said for the stress distribution in the stringer. The coarse two- and three-dimensional models are not able to predict the accurate stress field, while the present approach ensures a solution comparable with the refined solid model.

The accuracy of the present approach and the limits of classical models are even more clear when the shear stress is considered. Figures 33 and 34 show the behavior of $\sigma _{xy}$ through the thickness of the panel and of the stringer. The present approach confirms the capability to provide a 3D solution comparable with the refined solid model, while the classical approaches show a wide discrepancy with reference results.

Fig. 31

Behavior of $\sigma _{yy}$ through the panel evaluated using the considered FE models

Fig. 32

Behavior of $\sigma _{yy}$ through the stringer evaluated using the considered FE models

Fig. 33

Behavior of $\sigma _{xy}$ through the panel evaluated using the considered FE models

Fig. 34

Behavior of $\sigma _{xy}$ through the stringer evaluated using the considered FE models

Tables 9 and 10 show the values of $\sigma _{yy}$ and $\sigma _{xy}$ at different points through the thickness.

Table 9 Values of the $\sigma _{yy}$, [Pa], at different points through-the-thickness of the reinforced panel

Table 10 Values of the $\sigma _{xy}$, [Pa], at different points through-the-thickness of the reinforced panel

The stress results highlight the accuracy of the present CUF models. As observed for the displacement, the present models can provide a high level of accuracy if compared with the $3D_{\text {FEMAP}}$ Refined Model, with a fraction of the computational costs. The layerwise model, $3D-2D_{LE}-1D$, is the more accurate in the analysis of normal stress. The introduction of an NDK approach has a small impact of the results, especially when high-order Taylor models are used, $3D-2D_{LE \& TE3}-1D$.

The same conclusion can be drawn when the shear is considered, see Table 10. The present model is by far more accurate than the other models considered and provide results comparable with the $3D_{\text {FEMAP}}$ Refined Model. The use of classical approaches, e.g., $2D_{\text {FEMAP}}$ or $2D-1D_{FEMAP}$, led to inaccurate results and should not be considered for such kind of analysis.

6 Conclusion

In this paper, a multidimensional model for the analysis of reinforced structures has been presented. One-, two- and three-dimensional elements have been used to have a high-fidelity modeling of the structure. Different kinematic models have been used since the approach has been developed in the framework of the Carrera unified formation. The use of a node-dependent approach has led to a general reduction of the computational costs limiting the use of refined models only in the areas where they are required.

The results obtained by combining three-, two- and one-dimensional models have been compared with experimental results, semi-analytical solution or with finite element solutions from a commercial tool. Static and dynamic (free-vibration) analyses have been carried out. The following conclusions state:

• the present multidimensional model can be used to develop high-fidelity models of reinforced structure, leading to accurate results also in the areas where different structural elements are joined;

• the Carrera unified formulation can be used to arbitrarily refine the models leading to quasi-3D results;

• the node-dependent kinematic approach leads to a reduction in the computational cost, since accurate models are used only where necessary;

• the synergistic use of multidimensional NDK models leads to a continuous displacement field even at the interface between different elements or structural components.

In conclusion, the present paper demonstrates that the use of appropriate kinematic approximation leads to accurate results without the need of expensive solid models. The high-fidelity modeling approach presented in this paper overcame the limitations of classical FE models based on beam and plate elements and offers an excellent compromise between computational cost and accuracy.