Interpolation of Precipitation Extremes on a Large Domain Toward IDF Curve Construction at Unmonitored Locations

Abstract

An intensity–duration–frequency (IDF) curve describes the relationship between rainfall intensity and duration for a given return period and location. Such curves are obtained through frequency analysis of rainfall data and commonly used in infrastructure design, flood protection, water management, and urban drainage systems. However, they are typically available only in sparse locations. Data for other sites must be interpolated as the need arises. This paper describes how extreme precipitation of several durations can be interpolated to compute IDF curves on a large, sparse domain. In the absence of local data, a reconstruction of the historical meteorology is used as a covariate for interpolating extreme precipitation characteristics. This covariate is included in a hierarchical Bayesian spatial model for extreme precipitations. This model is especially well suited for a covariate gridded structure, thereby enabling fast and precise computations. As an illustration, the methodology is used to construct IDF curves over Eastern Canada. An extensive cross-validation study shows that at locations where data are available, the proposed method generally improves on the current practice of Environment and Climate Change Canada which relies on a moment-based fit of the Gumbel extreme-value distribution.

1 Introduction

Reliable estimates of the frequency and magnitude of extreme rainfall events are essential for designing flood protection, water management, and urban drainage infrastructures such as dams, reservoirs, and sewer systems. When sufficient data are available at a given gauging station, extreme-value analysis techniques can be used to produce an estimate Q of the T-year return level of rainfall accumulation, usually expressed in millimeters (mm), during a period of D hours (h). To facilitate comparisons between durations, the accumulation Q is typically converted to an hourly rate $I = Q/D$.

In hydrology and engineering, estimates of the intensity I of short-duration (5 min–24 h) rainfall extremes are commonly used for the construction of intensity–duration–frequency (IDF) curves, which summarize the relationship observed at a given location between duration D and mean intensity I of precipitation events characterized by the same return period T; see, e.g., Koutsoyiannis et al. (1998) for a review.

Fig. 1

IDF curves for the Pierre Elliott Trudeau International Airport in Montréal, QC. Source: Environment and Climate Change Canada (ECCC)

1.1 IDF Curves

To illustrate the concept, Fig. 1 displays a log–log plot of six IDF curves derived from data collected at the Pierre Elliott Trudeau International Airport in Montréal, QC. This chart, released by Environment and Climate Change Canada (ECCC) in 2019, is based on pluviometric data recorded every 5 min using tipping bucket rain gauges at this site, which was operational from 1943 to 2014, inclusively.

For each of nine durations identified on the x-axis, six crosses mark the estimated quantiles of the rain intensity distribution corresponding to a return period of 2, 5, 10, 25, 50, and 100 years, respectively. For example, this chart suggests that a $D = 30$ min rainfall of $I = 84$ mm/h occurs on average once every $T = 100$ years. In other words, an accumulation of precipitation in excess of $Q = 42$ mm per half-hour is expected to occur on average once in a hundred years.

As interpolation at intermediate durations is often necessary in practice, six regression lines are superimposed in Fig. 1, each of which is based on the nine points corresponding to a given return period. This choice of model is based on the stylized fact that, for short-duration events, the relationship between I and D can be represented adequately by a power law, viz.

$$\begin{aligned} I = A \times D^B, \end{aligned}$$

(1)

where B is the slope of the line on the log scale and A measures the intensity of a rain event of unit duration (Sherman 1931; Koutsoyiannis et al. 1998). The regression line is intended as a visual guide only. Confidence bands for each regression line on the log–log scale are also available (not shown).

1.2 Methodological Issues

The predictive accuracy of an IDF curve depends critically on a set of assumptions, most importantly the stationarity of the series of historical extreme rainfall observations, and the statistical reliability of the quantile estimates Q from which the intensity values I are obtained at any given gauging station. In their study of Canadian short-duration extreme rainfall, Shephard et al. (2014) concluded to a general lack of a detectable trend signal, at the 5% significance level, at any monitored site; however, they could identify upward and downward patterns at some regional levels.

As for quantile estimation at its gauging stations, ECCC currently computes the accumulation of precipitation over all periods of length D, and the annual maximum is recorded. A Gumbel extreme-value distribution is then fitted to the series of annual maxima using the method of moments, and an estimate of Q is provided by the upper quantile of level 1/T of this fitted distribution (Hogg et al. 2015). A similar approach is used in various countries, even though the appropriateness of Gumbel’s distribution in extreme rainfall modeling has been questioned; see, e.g., Koutsoyiannis (2003).

Beyond the reliance of ECCC on Gumbel’s model, the sparsity of the Canadian meteorological station network is a major limitation which has long been identified by the Canadian Standards Association; see, e.g., CSA (2012). While 596 weather stations have been operated in Canada for periods extending from 10 to more than 80 years, most of them are located in the southern part of the country, where the population is concentrated.

Figure 2 shows the distribution of the stations located east of the Ontario–Manitoba border. When predictions are needed at northern latitudes, where many dams, reservoirs, and power transformation sites are located, the nearest meteorological station can sometimes be quite far. In such cases, current engineer practice—often enforced by law, as in the province of Québec—relies on data from the closest gauging station.

1.3 Objectives and Plan of the Paper

This paper has a threefold objective:

• (a) to propose a more flexible and realistic choice than Gumbel’s extreme-value distribution for the estimation of high quantiles of short-duration rainfall events at gauging stations throughout Eastern Canada;

• (b) to describe an efficient computational strategy for spatial interpolation and temporal extrapolation throughout the domain while taking into account regional weather patterns;

• (c) to present an extensive comparison showing the benefits of the proposed approach versus the engineering standard of using the IDF curve at the closest monitored location, wherever it may be.

Fig. 2

Distribution of ECCC weather stations in Eastern Canada. The color associated with each station reflects the magnitude (in mm/h) of the 20-year return level of a 30-min rainfall, based on a Gumbel distribution

However, the traditional two-step approach of building IDF curves based on Eq. (1) is not questioned. For ways to resolve inconsistencies that may arise from estimating high quantiles separately at each duration, see, e.g., Koutsoyiannis et al. (1998), Lehmann et al. (2016) or Ulrich et al. (2020).

To enhance the flexibility and realism of extreme rainfall modeling and estimation for any given duration and location, it is proposed here to model annual rainfall maxima through a Generalized Extreme-Value (GEV) distribution with location $\mu \in {\mathbb {R}}$, scale $\sigma \in (0, \infty )$, and shape parameter $\xi \in {\mathbb {R}}$. Its distribution function is given, for all $y \in {\mathbb {R}}$, by

$$\begin{aligned} \Pr (Y \le y) = \left\{ \begin{array}{ll} \exp [ - \exp \{ - (y - \mu )/\sigma \}] &{} \text{ if } \xi = 0, \\ \exp \left[ -\left\{ 1 + \xi (y - \mu )/\sigma ) \right\} _+^{-1/\xi } \right] &{} \text{ if } \xi \ne 0, \end{array} \right. \end{aligned}$$

(2)

where $x_+ = \max (0, x)$ for any $x \in {\mathbb {R}}$. From the Fisher–Tippett–Gnedenko theorem, this class of distributions includes all possible limits of properly normalized maxima of a sequence of independent and identically distributed observations, including Gumbel’s model corresponding to $\xi = 0$.

The parameters of the GEV distribution can all vary with duration and site but to take into account both the local and global nature of precipitations, as well as possible trends over time, the location $\mu$ and scale $\sigma$ at any given site are also modeled as a function of orography and mean precipitation. Based on evidence described later in this paper, the shape parameter $\xi$ is assumed constant across the spatial domain for a given duration. This assumption, which is fairly common in the literature, increases the reliability of this parameter estimate and avoids unidentifiability issues.

To secure values of the covariates throughout the spatial domain, information about the relief is derived from the Elevation Application Programming Interface from Natural Resources Canada and a run of the 5th generation of the Canadian Regional Climate Model (Martynov et al. 2013; Šeparović et al. 2013) is averaged over the period 1981–2014. The results, which reproduce past climatology and daily precipitation data, are available on a fine grid throughout the Canadian landmass. The use of such a synthetic covariate for extreme rainfall modeling and interpolation is not new per se but constitutes a major advance over ECCC’s current approach.

The model proposed in Sect. 3 enables information sharing across locations without the need to delineate homogeneous areas through a regional frequency analysis before quantiles at a given site can be estimated. The errors are governed by an isotropic Gaussian random field so that the variability at any given site is more largely influenced by sites which are nearby than by sites which are distant.

To ensure that uncertainty is quantified in a coherent manner, inference is conducted in a Bayesian framework. As argued by Davison et al. (2012), Sebille et al. (2017) and Cao and Li (2019), Bayesian hierarchical models are well suited for interpolation of marginal characteristics such as return levels. Moreover, missing values and non-concomitant record periods of different stations can be readily handled. According to these authors, Bayesian hierarchical models also tend to be more robust than competing approaches based, e.g., on extreme-value copulas or max-stable processes. For descriptions of these other modeling strategies, see Joe (1994), Schlather (2002), Cooley et al. (2007), Reich and Shaby (2012), and references therein.

The use of Bayesian modeling to estimate extreme precipitation is not new; see, e.g., Rohrbeck and Tawn (2021). Bayesian modeling of extreme precipitation simulated from a climate model has also been considered, e.g., by Jalbert et al. (2017), Reich and Shaby (2019), and Sharkey and Winter (2019). The model proposed here is different from those because it focuses on interpolating the observed precipitation at sites without observations by relating the simulated extreme to the observed extreme precipitation.

One limitation of Bayesian hierarchical models is that they are not designed to generate stationary max-stable spatial random fields of extreme precipitation. However, this is not considered to be an issue in the present context, considering that IDF curves are used on a site-by-site basis in applications. Moreover, given the paper’s focus on the interpolation of annual maximum precipitation accumulations over a large spatial domain, the inter-duration dependence present in IDF curve construction is not addressed.

For recent work on inter-duration dependence using max-stable processes, see, e.g., Le et al. (2016) and Tyralis and Langousis (2019). See also Lehmann et al. (2016) for a Bayesian approach for linking the GEV parameters at the data level between durations. Finally, for an alternative way of deriving quantile estimates at an ungauged site by pooling information from monitored sites with similar characteristics via quantile regression, see Ouali and Cannon (2018) and references therein.

The ECCC data used here, which are public, are described in Sect. 2. Section 3 details the construction of the Bayesian hierarchical model and its interpretation. As shown in Sect. 4, this model not only allows for interpolation at ungauged locations but also improves estimation at most monitored sites. Further comparisons are made in Sect. 5, where supporting evidence for some model assumptions is presented. Challenges surrounding the construction of consistent IDF curves are mentioned in Sect. 6, where conclusions and avenues for future research can also be found.

An Appendix provides a short overview of the computational approach and points to a GitHub site where documented Julia code and the data are stored so that all results presented herein can be reproduced easily.

2 Data

Various sources of pluviometric data are available in Canada. The most abundant and reliable source is Environment and Climate Change Canada (ECCC), whose data are publicly available and fulfill the quality standards set by the World Meteorological Organization. In contrast, it is not unusual to find blatant errors in data collected by weather stations operated by state utilities or the private sector such as Hydro-Québec or Rio Tinto.

Figure 2 shows ECCC’s network of weather stations in Eastern Canada. The number of sites at which data are available varies slightly, e.g., from 329 to 336 for the 30 min and 24 h duration, respectively. At each site, precipitations (in mm) are recorded every 5 min and are available for a period ranging from 10 to 81 years. The oldest gauging station, located in the capital, Ottawa, collected data from 1905 to 2011, with significant interruptions, e.g., from 1908 to 1934 and from 1939 to 1953. The annual maxima for the nine durations specified on the x-axis of Fig. 1 are available directly at

https://climate.weather.gc.ca/prods_servs/engineering_e.html.

Fig. 3

Mean daily precipitation (in mm) from the Canadian Regional Climate Model CRCM5 driven by the Era-Interim reanalysis, averaged from 1981 to 2014

For each station and duration, the stationarity of the series of maxima was checked using the standard Mann–Kendall test at the 5% nominal level. For each duration, the proportion of stations for which the null hypothesis of absence of a monotonic trend was rejected hovered around 5%. Given the amount of data currently available, the overall stationarity assumption appears to be sensible for all durations. These results are consistent with those of Shephard et al. (2014) and Ouali and Cannon (2018).

As is commonly known, the main factors which influence precipitation are orography (elevation) and local weather conditions. Preliminary analyses revealed that elevation above sea level (in meters, m) is indeed an important predictor, and hence it was retained for modeling purposes.

To emulate local weather conditions, one possibility would be to extract variables from a reanalysis such as ERA5, the fifth generation of the atmospheric reanalyses of the global climate released by the European Centre for Medium-Range Weather Forecasts. See

http://climate.copernicus.eu/products/climate-reanalysis

ERA5 combines vast amounts of observations into global estimates using advanced model and data assimilation systems but the $30 \times 30 \text{ km}^2$ resolution of this reconstruction was deemed too coarse for the purpose at hand.

As an alternative, it was decided to rely on a run of the 5th generation of the Canadian Regional Climate Model (CRCM5) driven by the Era-Interim reanalysis (Martynov et al. 2013; Šeparović et al. 2013). The data, which were generated for the Northeastern part of North America and archived at 3-h intervals (Bresson et al. 2017), are available on a regular lattice with 90, 000 grid cells, each of which corresponds to a $12 \times 12 \text{ km}^2$ parcel.

Analogously to Geirsson et al. (2015), the average daily precipitation over the period 1981–2014 was used as the spatial covariate. A heat map of this variable is shown in Fig. 3. Once this variable was incorporated into the model, standard geophysical variables such as latitude, longitude, surface roughness, slope, aspect, and shortest distance from coast line were found to be insignificant, as they were already accounted for in the CRCM5.

3 Statistical Model

A Bayesian hierarchical approach is proposed to interpolate extreme precipitation for any specific duration. It is then applied independently to each and every duration. At the data level, maxima are assumed to follow a GEV distribution, as described in Sect. 3.1. At the second level of the hierarchy, considered in Sect. 3.2, the GEV parameters are assumed to vary as a function of spatial covariates, which represent fixed effects, and a latent Gaussian field modeling residual deviations that may be spatially correlated. An interpretation of the model is given in Sect. 3.3 and the selected priors for the parameters are specified in Sect. 3.4.

3.1 Data Level

As mentioned in Sect. 2, the covariates that were selected for the analysis are elevation and weather conditions through a run of the CRCM5. However, the latter are not available everywhere in the domain but rather on a high-resolution, regular lattice. It was thus resolved to define the model on the same fine grid, in contrast to the common approach which consists of interpolating the gridded covariates; see, e.g., Dyrrdal et al. (2015) and Geirsson et al. (2015). In addition to ensuring a simple correspondence between the covariates and the return levels of extreme precipitation, this proposal yields substantial computational benefits, as described in Sect. 4.1.

To justify defining the model on the same grid as the CRCM5 data, one must assume that within a grid cell, the extreme precipitations are governed by the same GEV distribution and hence lead to a unique return level. This assumption does not appear to be unduly restrictive, given the high grid resolution of $12 \times 12 \text{ km}^2$. Data-based evidence in support of this simplification is provided in Sect. 5.2.

Let ${\mathcal {V}}$ be the set of grid cells covering Eastern Canada; the size of this set is $|{\mathcal {V}}| = 48{,}694$. Further let ${\mathcal {S}} \subset {\mathcal {V}}$ be the subset of grid cells containing at least one meteorological station, e.g., $|{\mathcal {S}}| = 310$ or $|{\mathcal {S}}| = 315$ for the 30 min and 24 h duration, respectively. Indeed, some grid points contain more than one station. In such cases, the series of maxima from the station with the longest record was selected; when relevant, maxima of non-overlapping years recorded at the other stations within the same grid cell were added.

While the above procedure ignores the relation between concurrent maxima for different stations within the same grid cell, this issue is negligible because of the small number of cases involved. As the overlapping series of maxima are also very short (5–10 points), multivariate extreme-value modeling of these concurrent maxima was not considered worthwhile.

For grid element $i \in {\mathcal {S}}$ where data are available, let $\varvec{Y}_i = (Y_{i1},\ldots ,Y_{i n_i})$ be the series of the $n_i$ annual maxima, which can be assumed to be mutually independent and identically distributed in view of the stationarity of the precipitation series. From the classical Fisher–Tippett theorem, as described, e.g., by Coles (2001), the common marginal distribution of these maxima is well approximated by a Generalized Extreme-Value (GEV) distribution of the form (2) with location parameter $\mu _i \in {\mathbb {R}}$, scale parameter $\sigma _i \in (0, \infty )$, and shape parameter $\xi \in {\mathbb {R}}$, assumed constant across the spatial domain.

Evidence in support of a common shape parameter $\xi$ is presented in Sect. 5.4. This assumption makes it possible to obtain a reliable estimation of this critical parameter and circumvents the identifiability issues that can occur when all GEV parameters are spatially varying. If $\xi < 0$, then $Y_{ij}$ has a Weibull distribution which is bounded above, i.e., $Y_{ij} < \mu _{i}-\sigma _{i}/\xi$ with probability 1 for every $j \in \{ 1, \ldots , n_i \}$. When $\xi = 0$, the distribution of $Y_{ij}$ is Gumbel and its right tail decays exponentially. If $\xi > 0$, then $Y_{ij}$ has a Fréchet distribution and its right tail decays only polynomially.

3.2 Spatial Model

Let $\varvec{x}$ be the design matrix of covariates defined on the complete set ${\mathcal {V}}$ of grid cells. It is assumed that for each site $i \in {\mathcal {V}}$ with (column) vector ${\varvec{x}}_i$ of covariate values,

$$\begin{aligned} \mu _i = \varvec{x}_i^\top \varvec{\beta }_\mu + U_i, \quad \phi _i = \ln (\sigma _i) = \varvec{x}_i^\top \varvec{\beta }_\phi + V_i, \end{aligned}$$

(3)

where $\varvec{\beta }_\mu$ and $\varvec{\beta }_\phi$ are regression coefficients while $U_i$ and $V_i$ are independent spatial effects defined on the complete set of grid cells. This choice is consistent with evidence that $\mu _i$ is proportional to the mean annual precipitation at site i (Benestad et al. 2012; Geirsson et al. 2015). Because extreme precipitation data are often such that the scale parameter is proportional to the location parameter, one could also have used $\ln (\varvec{x})$ as an explanatory variable for $\ln (\sigma _i)$ but in the present context, this made no substantial difference in terms of prediction.

In Model (3), the error between the overall regression and the true value is assumed to be spatially dependent. The GEV parameters of a given grid cell are therefore influenced by the regression residuals of its neighbors.

That the model was defined on a grid has the added benefit that the spatial effect can be captured by a Gaussian Markov random field (GMRF). Such models have a consistent set of conditional distributions that are both jointly (and conditionally) Gaussian with a sparse precision matrix; see, e.g., Rue and Held (2005). These models are also computationally convenient because the Markov property implies that at any site $i \in {\mathcal {V}}$, the conditional distributions of $\mu _i$ and $\sigma _i$ only depend on the neighboring sites.

Because the precision matrix of GMRFs must be positive definite, the range of site-to-site marginal correlations is limited (Besag and Kooperberg 1995). As these bounds were too narrow for the high-resolution grid considered here, it was necessary to resort to intrinsic Gaussian Markov random fields (iGMRFs). The latter models have an improper joint distribution because the corresponding precision matrix is not of full rank, but this feature is not problematic as long as the posterior distribution is proper.

The class of iGMRFs scales a pre-defined structure matrix W for the graph configuration; see Rue and Held (2005). The improper joint distribution is given by

$$\begin{aligned} f_{(\varvec{U}|\kappa _u)}(\varvec{u}) \propto \kappa _u^{(m-r)/2} \exp {\big (} - \kappa _u \varvec{u}^\top W \varvec{u}/2 {\big )}, \end{aligned}$$

where $\kappa _u$ is the precision parameter, $m = {\text {Card}}({\mathcal {V}})$ is the total number of grid cells, and r corresponds to the rank deficiency of the structure matrix W. Taking a constant precision parameter $\kappa _u$ amounts to assuming that the spatial dependence is invariant across the spatial domain, i.e., the dependence between two grid cells does not depend on their location but only on their relative position.

In iGMRFs, the coarseness of the field is controlled by both the precision parameter $\kappa _u$ and the dependence pattern of the structure matrix, which specifies the number of neighbors and their weights. For each $i \in {\mathcal {V}}$, the conditional distribution of $U_i$ given all the other grid cells is given by

$$\begin{aligned} f_{ ( U_i | \varvec{U}_{-i} = \varvec{u}_{-i} ) }(u_i) = {\mathcal {N}} \big [ u_i \mid {\bar{u}}_i , 1/(\kappa _u W_{ii} ) \big ] , \end{aligned}$$

where ${\mathcal {N}}(u \mid \nu , \phi ^2)$ denotes the Gaussian density with mean $\nu$ and variance $\phi ^2$ evaluated at u, and where

$$\begin{aligned} {\bar{u}}_i = - \displaystyle \frac{1}{W_{ii}}\displaystyle \sum _{j\ne i}W_{ij}u_j. \end{aligned}$$

A similar expression holds for $V_i$.

In the present context, two pre-defined matrix structures W were considered which correspond to the first- and second-order iGMRF. In the first-order iGMRF, the precision matrix has rank deficiency 1 while for the second-order iGMRF, the rank deficiency is 3.

Second-order iGMRFs are much smoother than first-order iGMRFs. It is also shown by Rue and Held (2005) that

• (a) the first-order iGRMF is invariant to the inclusion of an overall constant and the second-order iGMRF is invariant to that of a plane;

• (b) first-order iGMRFs approximate the two-dimensional Brownian motion while second-order iGMRFs approximate the thin plate spline.

In comparing first- and second-order iGMRFs, Paciorek (2013) found that the former are preferable for capturing small-scale variation while the latter are more apt at describing large-scale variation.

In the final analysis, a first-order iGRMF was selected on the basis of the predictive power revealed through the cross-validation study described in Sect. 4. Therefore, it can be safely assumed that the synthetic covariate removes the large-scale variation and that the first-order iGMRF suitably models the small-scale residuals between the covariates and the parameters.

3.3 Model Interpretation

For any grid point $i\in {\mathcal {S}}$, i.e., containing a meteorological station, the conditional distribution of the location parameter is given by

$$\begin{aligned} f_{\left( \mu _i | - \right) }(\mu _i) \propto \displaystyle \prod _{j=1}^{n_i} \mathcal {GEV} (y_{ij}\ \mid \mu _i, e^{\phi _i},\xi ) \times {\mathcal {N}}\left[ \mu _i \mid {\bar{\mu }}_i, (\kappa _u W_{ii})^{-1} \right] \end{aligned}$$

while the conditional distribution of the scale parameter is given by

$$\begin{aligned} f_{\left( \phi _i | - \right) }(\phi _i) \propto \displaystyle \prod _{j=1}^{n_i} \mathcal {GEV} (y_{ij} \mid \mu _i, e^{\phi _i}, \xi ) \times {\mathcal {N}}\left[ \phi _i \mid {\bar{\phi }}_i, (\kappa _v W_{ii}) ^{-1} \right] , \end{aligned}$$

where $n_i$ is a number of observations available at grid point i, and where

$$\begin{aligned} {\bar{\mu }}_i = {\varvec{x}}_i^\top {\varvec{\beta }}_\mu - \displaystyle \frac{1}{W_{ii}} \sum _{j \ne i}W_{ij} u_j, \quad {\bar{\phi }}_i = {\varvec{x}}_i^\top {\varvec{\beta }}_\phi - \frac{1}{W_{ii}} \sum _{j \ne i}W_{ij} v_j. \end{aligned}$$

See Sect. 5.3 for some discussion concerning the conditional independence assumption. In the expression for $f_{ (\mu _i|- )}$, the first factor is the likelihood while the second represents the spatial prior for $\mu _i$. The Bayesian estimate is thus a compromise between the spatial information and the local features imparted by the data. A similar interpretation holds for $f_{ (\phi _i|- )}$.

In the spatial prior distribution for $\mu _i$, the marginal mean $\varvec{x}_i^\top \varvec{\beta }_\mu$ is corrected by the error surrounding grid point i. For example, if the linear relationship $\varvec{x}_i^\top \varvec{\beta }_\mu$ overestimates $\mu _i$ for the region around grid point i, then $u_i = \varvec{x}_i^\top \varvec{\beta }_\mu - \mu _i$ is negative to account for the regional effect in the regression.

Similar approaches were adopted by Dyrrdal et al. (2015) and Geirsson et al. (2015) but they used a continuous Gaussian model even though their explanatory variables lay on a grid in the latent layer. In contrast to Geirsson et al. (2015), an unstructured error term was not added here to the latent layer as the Gaussian Markov random field was deemed flexible enough to model the error between the covariates and the GEV parameters. In modeling the simulated precipitation maxima by a climate model, Cooley and Sain (2010) did include an unstructured random error in a Gaussian Markov random field at the process layer, but their approach was not developed for interpolation of extreme characteristics.

3.4 Prior and Hyperprior Distributions

Relatively vague proper prior gamma distributions were assigned to the hyperparameters $\kappa _u$ and $\kappa _v$, viz.

$$\begin{aligned} f_{\kappa _u}(\kappa _u) = {\mathcal {G}} (\kappa _u \mid 1,1/100 ),\quad f_{\kappa _v}(\kappa _v) = {\mathcal {G}} (\kappa _v \mid 1,1/100 ), \end{aligned}$$

where ${\mathcal {G}}(\cdot |\alpha ,\beta )$ denotes the Gamma density with mean $\alpha /\beta$ and variance $\alpha /\beta ^2$. Note, however, that the posterior is relatively insensitive to this prior choice given the large number of grid cells.

For the GEV shape parameter $\xi$, the Beta prior proposed by Martins and Stedinger (2000) was adopted, viz.

$$\begin{aligned} f_{\xi }(\xi ) = {\mathcal {B}} (\xi + .5 \mid 6, 9 ). \end{aligned}$$

In this prior, which is commonly used for precipitation data, the shape parameter $\xi$ is restricted to the interval $[-0.5, 0.5]$. A constant improper prior would also be adequate. However, the posterior distribution is not sensitive to this choice either, given the large number of combined stations to estimate this parameter.

For the regression parameters $\varvec{\beta }_\mu$ and $\varvec{\beta }_\phi$, constant improper distributions were used as hyperpriors, viz.

$$\begin{aligned} f_{\varvec{\beta }_\mu } ({\varvec{\beta }}_\mu ) \propto 1, \quad f_{\varvec{\beta }_\phi } (\varvec{\beta }_\phi ) \propto 1. \end{aligned}$$

While informative or vaguely hyperpriors would also be possible, the posterior distribution is once again insensitive to this choice because of the large number of stations that were combined to estimate these parameters.

4 Main Results

The model was implemented in Julia. The code is available on the public repository GitHub with a copy of the data and detailed documentation, as described in the Appendix.

4.1 Computational Details

An overview of the computational approach is given in the Appendix. As stated there, a posterior sample of size 10, 000 for the parameters of the model was obtained via Gibbs sampling with 215, 000 iterations, including a warm-up of size 15, 000 and 95% thinning of the rest.

The time needed to generate a sample from the posterior distribution is short considering the large number of grid cells: it takes about 10 min to perform 100, 000 MCMC iterations on a personal laptop (Intel Core i7, 2.7 GHz). The gridded structure facilitates the use of Gaussian Markov random fields, which yields substantial computational benefits. Thanks to the conditional independence assumption, the parameters of half the grid points can be updated simultaneously (i.e., in parallel) in the MCMC procedure.

In the first-order Gaussian Markov random field, a point, knowing its four neighbors in the cardinal directions, is independent of the other points. The conditionally independent points can be updated in a single step in the Gibbs sampling scheme, as first described by Besag (1974) and used, e.g., by Jalbert et al. (2017) to reduce the computation time in a latent variable model. No additional feature (e.g., an integrated Laplace approximation) is needed to speed up the algorithm. Moreover, very efficient routines for sampling a GMRF or evaluating the density are available.

Fig. 4

Trace of the shape parameter $\xi$ for the first 500 iterations of the Gibbs sampling algorithm after warm-up

Figure 4 shows the trace of the shape parameter $\xi$ for the first 500 iterations of the Gibbs sampling algorithm after warm-up. Traces for all other components of the vector $(\varvec{\mu },\varvec{\phi }, \xi , \varvec{\beta }_\mu ,\varvec{\beta }_\phi ,\kappa _u,\kappa _v)$ with $\varvec{\mu }= (\mu _i : i \in {\mathcal {V}})$ and $\varvec{\phi }= (\phi _i : i \in {\mathcal {V}})$ show similar stationary behavior.

The 10, 000 observations in the posterior sample allow for the computation of credibility intervals for any return level and are the source of the credibility bands appearing in the QQ-plots of Figs. 8 and 9 in Sect. 4.2.

The diagnostic of Gelman and Rubin (1992) and Brooks and Gelman (1998) was computed for the model parameters $\beta _\mu$, $\beta _\phi$, $\kappa _\mu$, $\kappa _\phi$, $\xi$, $\mu _i$, and $\phi _i$ at all grid cells $i \in S$ containing a station. As a rule of thumb, convergence is rejected if the 97.5th centile of the potential scale reduction factor is greater than 1.2. In the present case, this never occurred. The maximum value was 1.152 and it corresponds to the log-scale factor of Station $i = 122$ (Quaqtaq, QC). According to this diagnostic, the chain reaches its stationary state after approximately 1000 iterations.

The diagnostic of Raftery and Lewis (1992a, 1992b) was also run. It assesses the number of autocorrelated samples required to estimate a specified parameter quantile $\theta _q$ of order q with a given accuracy r, viz. $\Pr (\theta _q - r< {\hat{\theta }}_q < \theta _q + r) = 0.95$, where ${{\hat{\theta }}}_q$ is the estimate of $\theta _q$. The diagnostic for each model parameter was computed using $q = 0.025$ and $r = 0.005$.

In the absence of autocorrelation, only 3746 iterations would be needed to reach the set precision for all parameters. With strong autocorrelation, however, this is not enough. In particular for $\kappa _u$ and $\kappa _v$, about a million iterations are needed to reach the desired precision. For the other parameters, the required number of iterations hovers around 100, 000. Since interest centers not on $\kappa _u$ and $\kappa _v$ but rather on the GEV parameters at each grid cell, it can be argued that 215, 000 iterations suffice for the purpose at hand.

4.2 Comparisons With the Nearest-Neighbor Approach

It is clear from Fig. 4 that the shape parameter is strictly positive in all cases. Therefore, a two-sided credible interval would exclude the case $\xi = 0$. This is in sharp contrast to the current modeling strategy of ECCC which, as described in Sect. 1.2, assumes independent Gumbel extreme-value distributions and hence $\xi = 0$ at all stations.

The computational efficiency of the code resulting from the discretization of the latent field on the same lattice as the covariate makes it feasible to compare the proposed approach with alternative imputation methods through various diagnostic tools based on cross-validation.

In the absence of a local IDF curve, the engineering standard in many Canadian jurisdictions consists of relying on the nearest station, as this is deemed to be the station whose characteristics are most likely to resemble that of the site of interest. In Québec, for instance, this is the standard imposed by the Ministère de l’Environnement et de la Lutte contre les changements climatiques to ensure the legal compliance of stormwater management systems as per Section 22 of Order in Council 871–2020, August 19, 2020; see Gouvernement du Québec (2020).

For each given duration, the quality of the probabilistic forecasts of extreme precipitations was assessed using a leave-one-out cross-validation at each of the grid cells in ${\mathcal {S}}$ containing at least one station. For each $i \in {\mathcal {S}}$, let $(\mu _{-ik}, \sigma _{-ik}, \xi _{-ik})$ denote the GEV parameters at iteration k of the MCMC procedure without using the data in grid cell i. A Monte Carlo estimate of ${{\hat{F}}}_i$ which encompasses parameter uncertainty was obtained by averaging the GEV distributions with parameters $(\mu _{ik}, \sigma _{ik}, \xi _{ik})$ with $k \in \{ 1, \ldots , 10{,}000 \}$. The index i on the shape parameter accounts for the possibility that its value changes when the observations from Station i are discarded.

The quality of the predictive distribution ${{\hat{F}}}_i$ can then be assessed with a Cramér–von Mises statistic measuring the (squared) distance between the predictive distribution ${{\hat{F}}}_{ik}$ for grid cell i at MCMC iteration k and the empirical distribution function $F_i$ of the maxima recorded at grid cell i, viz.

$$\begin{aligned} \displaystyle {{{\hat{\omega }}}}_{ik} = \int \big | \hat{F}_{ik}(y) - F_i(y) \big |^2 \, \hbox {d}F_i (y). \end{aligned}$$

A mean score ${{\hat{\omega }}}_i$ is then obtained by averaging over all iterates.

The $L_2$ distance associated with the Cramér–von Mises statistic was preferred here to the $L_1$ distance corresponding to the Kolmogorov–Smirnov analog, as the former is widely known to be more powerful than the latter. The use of Anderson–Darling or other statistics emphasizing goodness of fit in the tails was also deemed unnecessary as the distributions of interest already pertain to annual precipitation maxima.

The coefficient ${{\hat{\omega }}}_i$ is a squared distance between the two distributions: the smaller it is, the better is the fit between them. For comparison with the current nearest-neighbor approach based on the ECCC curves, one can also compute, for each $i \in {\mathcal {S}}$,

$$\begin{aligned} \displaystyle {{\bar{\omega }}}_i = \int \big | {{{\bar{F}}}}_i (y) - F_i (y) \big |^2 \, \hbox {d} F_i (y), \end{aligned}$$

i.e., the squared distance between $F_i$ and the (Gumbel) IDF curve ${{{\bar{F}}}}_i$ for the meteorological station which is closest to location i. The ratios

$$\begin{aligned} \displaystyle {{\bar{\Delta }}}_i = ({{\bar{\omega }}}_i - {{{\hat{\omega }}}}_i)/{{\bar{\omega }}}_i, \quad {{{\hat{\Delta }}}}_i = ({{{\hat{\omega }}}}_i - {{\bar{\omega }}}_i)/{{{\hat{\omega }}}}_i \end{aligned}$$

give measures of the relative performance of the two methods.

The proposed method is preferable to the standard whenever ${{\bar{\Delta }}}_i > 0$ or ${{{\hat{\Delta }}}}_i < 0$. In ${{\bar{\Delta }}}_i$, the size of the improvement is taken with respect to the current approach, and hence limited above by 1. In ${{{\hat{\Delta }}}}_i$, the reference point is the new method, so that one can better assess the relative loss induced by the use of the current nearest-neighbor approach favored by ECCC.

Table 1 reports, for each duration, the proportion of the grid cells for which ${{\bar{\Delta }}}_i > 0$ and the median of the set $\{100 \times {{\bar{\Delta }}}_i: i \in {\mathcal {S}} \}$. The proportion of stations at which the proposed method improves over the current practice hovers around 75%. The median distance to the empirical distribution function $F_i$ of the maxima at grid cell i is also cut in half.

Additional insight into the performance of the proposed method is provided by Fig. 5, which pertains to a 30-min duration. The plot shows the values of ${{\bar{\Delta }}}_i$ (left) and ${{{\hat{\Delta }}}}_i$ (right) for $i \in {\mathcal {S}}$ as a function of the distance (in km) as the crow flies between Station i and the closest neighboring station, whose data were used in computing ${{\bar{\omega }}}_i$. In both graphs, about 75% of the points are red; they correspond to stations where the proposed method performs better than the nearest-neighbor imputation approach.

Table 1 For each given duration, the table gives the percentage of values of ${{\bar{\Delta }}}_i$ which are strictly positive and the median of the set $\{100 \times {{\bar{\Delta }}}_i: i \in {\mathcal {S}}\}$

Fig. 5

Values of ${{\bar{\Delta }}}_i$ (left) or ${{{\hat{\Delta }}}}_i$ (right) for $i \in {\mathcal {S}}$ as a function of the $\log _{10}$ distance from Station i to its closest neighbor for a 30-min duration. The red dots indicate the stations where the proposed method performs better than the nearest-neighbor method and the blue dots indicate the opposite

Note the widely different scales of the two graphs in Fig. 5: while negative values of ${{\bar{\Delta }}}_i$ range from 0 to $-12$, negative values of ${{{\hat{\Delta }}}}_i$ range from 0 to $-180$. Thus, when the proposed approach does worse than the ECCC nearest-neighbor approach, i.e., the deterioration ${\bar{\Delta }}_i \in (-12, 0)$ is generally small, while the gain $- {\hat{\Delta _i}} \in (0, 180)$ accrued over the current method is often quite large. There is thus an order of magnitude more to gain in favoring the proposed approach over ECCC’s nearest-neighbor technique.

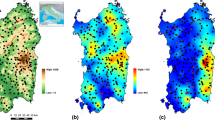
Figures 6 and 7 show the values of ${{\bar{\Delta }}}_i$ for $i \in {\mathcal {S}}$ for a 30-min and 24-h duration, respectively. About 75% of dots are red; they represent grid cells where an improvement over the current methodology occurred. The blue dots are those where the current methodology led to a smaller value of ${{\bar{\Delta }}}_i$.

In Figs. 6 and 7, the blue dots are widely scattered and occur mostly in areas with multiple meteorological stations. The new approach can be seen to perform very well overall, especially where stations are few and far between. In some cases, it improves the interpolation for one duration but worsens the other. To solve this issue, one would need to model inter-duration dependence. Happily, there is no station at which the new method worsens the interpolation for all durations.

Fig. 6

Values of ${{\bar{\Delta }}}_i$ for $i \in {\mathcal {S}}$ for a 30-min duration

Fig. 7

Values of ${{\bar{\Delta }}}_i$ for $i \in {\mathcal {S}}$ for a 24-h duration

Fig. 8

QQ-plot of $F_i$ versus ${{{\bar{F}}}}_i$ (left) or versus ${{\hat{F}}}_i$ (right) for a 30-min duration at grid cell 271, Charlottetown Station, Prince Edward Island

Fig. 9

QQ-plot of $F_i$ versus ${{{\bar{F}}}}_i$ (left) or versus ${{\hat{F}}}_i$ (right) for a 30-min duration at grid cell 243, Lac Témiscamingue Dam Station, Québec-Ontario border

Fig. 10

IDF curve for the International Airport in Montréal, QC, based on the proposed model and data from all grid cells except the airport

Fig. 11

Spatial variation over all grid cells of the model’s estimate of the 25-year return level intensity (in mm/h) for a 30-min duration

As a complement of information, the QQ-plots in Figs. 8 and 9 show the fit of ${{{\bar{F}}}}_i$ (left) and ${{\hat{F}}}_i$ (right) for a 30-min duration at two grid cells corresponding to the smallest and largest values of ${{\bar{\Delta }}}_i$, respectively.

Additional evidence in favor of the new approach is given by Fig. 10, which shows IDF curves for the Pierre Elliott Trudeau International Airport in Montréal, QC, based on the proposed model and data from all grid cells except the airport. In comparison with Fig. 1, which is the current reference for this location, one can see that information pooling across locations yields estimates of high quantiles, and hence IDF curves, that are quite consistent across durations.

Finally, Fig. 11 shows the 25-year return levels for all grid points in the spatial domain. At most grid cells, no data are available but when there are, they dominate when they are inconsistent with the covariate, as captured by a dot effect on the map. It is also obvious from this map that the bias between the observations and the covariate is smoothly interpolated in the surrounding grid cells until it disappears once the station effect vanishes.

5 Additional Model Comparisons and Validation

This section reports additional proof of the good performance of the new model, as well as evidence in support of some of its underlying assumptions.

5.1 Comparison With Other Models

The current approach used by ECCC is simplistic in the sense that the GEV shape parameter is taken to be zero. Therefore, the superior performance of the proposed model may not come as a surprise. As additional evidence in favor of the proposal, the new methodology was thus compared to two more sophisticated approaches involving

• I. a GEV distribution independent at each site;

• II. a GEV distribution at each site, but with a common and unknown $\xi$.

Model I and Model II were implemented. Because there are very few observations for some of the stations, the constraint $\xi _i \in (-0.5, 0.5)$ was imposed for the shape parameter at every site $i \in {\mathcal {S}}$ in Model I to ensure that the maximum likelihood procedure converges.

Judging from the Bayesian Information Criterion (BIC), Model II with a common unknown shape parameter is preferable to Model I with a free shape parameter at each station. For the 24 h duration for instance, the BIC for Model II is $-37{,}944$ against $-36{,}708$ for Model I. The common shape parameter estimate is ${{{\hat{\xi }}}}_{\mathrm{ML}} = 0.0856$, which suggests heavy-tailedness. With the proposed spatial model, the common shape parameter estimate is lower, ${{\hat{\xi }}} = 0.0788$, but the 95% credible interval (0.0597, 0.0981) includes ${\hat{\xi }}_\mathrm{ML}$.

Although Model II with an unknown common shape parameter provides a better fit than the Gumbel distribution, naive interpolation at a given site by taking the GEV parameters of the nearest station is worse than the approach using the Gumbel model. In 54% of the stations in the cross-validation analysis, the method using the GEV distribution with ${{\hat{\xi }}}_{\mathrm{ML}}$ increases the Cramér–von Mises distance compared to the Gumbel model, suggesting an erosion in the fit between the interpolated model and the data.

A possible explanation for this phenomenon is that the naive interpolation method taking the parameters of the nearest station is inadequate over such a large territory, no matter what model is used. When the observation network is dense, this method can be advantageous, e.g., in densely populated regions, but a genuine spatial model is otherwise required.

The proposed spatial model was also compared to a Bayesian hierarchical model without the iGMRF component accounting for the error between the covariate and the weather stations. The assumption was that the spatial covariate could be sufficiently informative to carry all the spatial information. This model assuming independent errors at the process level increases the Cramér–von Mises criterion for 50.2% of the stations. It is nevertheless a relatively good model even if the improvement is on half of the stations. Indeed, the size of each improvement is important: the difference between ${\hat{\omega _i}}$ and ${\bar{\omega }}_i$ is large for many stations. The model is easy to interpret and quick to fit. However, the spatial model with the iGMRF term remains preferable.

5.2 Extreme-Value Homogeneity Within a Grid Cell

The proposed model assumes constant GEV parameters within each $12 \times 12 \text{ km}^2$ grid cell. This assumption was checked independently for all durations and grid cells having more than one station. For the 30-min duration, there are eight grid cells with two stations, five with three stations, and one with four stations. In each case, a model based on a single GEV distribution for the pooled annual maxima of all stations in the grid cell was compared with a model using different sets of GEV parameters per station. For all durations and grid cells, the model with a single GEV distribution was favored by the BIC, in support of the homogeneity assumption.

One drawback of assuming that the GEV parameters are the same for precipitation inside a $12 \times 12$ $\hbox {km}^2$ is that the parameters are then discontinuous at the edges. In the present case, the transition turned out to be quite smooth compared to the Thiessen polygon interpolation method currently used at ECCC, which can induce abrupt changes at the edges. While the use of a continuous model in the latent layer would fix this issue, it would lead to a major loss in computational efficiency. Additionally, the gridded covariate would have to be interpolated, too.

5.3 Conditional Independence Assumption

The proposed model also assumes conditional independence at the data level. This assumption can be violated when for example a single intense rain event affects several weather stations. While this may not unduly affect point estimates of marginal return levels as shown by, e.g., Davison et al. (2012), it can still have a strong effect on the associated credible intervals.

In a frequentist framework, Smith (1990) used a misspecified likelihood to tackle spatial dependence. He assumed that the maximum likelihood estimator $\hat{\varvec{\theta }}$ of the parameter vector $\varvec{\theta }$ is asymptotically Gaussian, viz.

$$\begin{aligned} \displaystyle \hat{\varvec{\theta }} \approx {\mathcal {N}}\left( \varvec{\theta }, \frac{1}{n} \, H^{-1}VH^{-1} \right) , \end{aligned}$$

where n is the number of observations and $H^{-1}VH^{-1}$ is the modified covariance matrix under model misspecification. Here,

$$\begin{aligned} \displaystyle H = {\text {E}} \left\{ -\frac{\partial ^2}{\partial \varvec{\theta }^2} \ln f_{(\varvec{Y}|\varvec{\theta })}(\varvec{y}) \right\} \end{aligned}$$

is the information matrix and V to the covariance matrix

$$\begin{aligned} \displaystyle V = {\text {cov}} \left\{ \frac{\partial }{\partial \varvec{\theta }} \ln f_{(\varvec{Y}|\varvec{\theta })}(\varvec{y}) \right\} . \end{aligned}$$

Under independence, $H = V$ and the asymptotic variance of maximum likelihood estimators is recovered. In the dependent case, the point estimates remain the same but the sample variance is larger. A similar approach was used by Fawcett and Walshaw (2007) for temporal dependence.

In a Bayesian framework, Ribatet et al. (2012) proposed to inflate the posterior variance under the misspecification of conditional independence by raising the misspecified likelihood $f_{(\varvec{Y}|\varvec{\theta })}(\varvec{y})$ to the power $k \in (0, 1]$. The parameter estimates are unchanged but the posterior variance increases by 1/k. The same authors proposed a method to estimate k using the eigenvalues of the matrix $H^{-1}V$. Sharkey and Winter (2019) used a similar approach for modeling the spatio-temporal dependence. They found that the standard deviation of parameter estimates increases by up to 20% compared with their misspecified spatial model.

In the present framework, the approach of Ribatet et al. (2012) or Sharkey and Winter (2019) could be adapted to relax the conditional independence assumption and obtain a more accurate posterior distribution variance. However, this would affect the computational efficiency of the model. Also, when it comes to IDF curves, the marginal estimates are the quantities of interest to engineers, who use safety factors anyway. It is nevertheless important to stress that the credibility intervals derived from the proposed approach are likely shorter than they should be.

5.4 Spatially Invariant Shape Parameter Assumption

A third important ingredient of the proposed approach is the assumption that for a given duration, the shape parameter of the GEV distribution does not vary across space. To assess the plausibility of this condition, an attempt was made to model $\xi$ using an iGMRF component with an informative prior to avoid unreasonable shape parameter values. Unfortunately, it proved impossible to fit this model as such, perhaps due to identifiability issues.

As an alternative, an exploratory analysis was conducted in which maximum likelihood estimates of the shape parameter were obtained independently at each station. These estimates did not exhibit any sign of spatial correlation. While this finding is not surprising in view of the large uncertainty on this parameter, it is consistent with the assumption that the shape parameter is spatially invariant.

6 Conclusion

In this paper, a Bayesian hierarchical model was proposed for interpolating GEV parameters in a large spatial domain. Although its implementation was described in a Canadian pluviometric context, it could easily be adapted to other regions and variables, given that the spatial model is formulated in terms of departures from fixed effects derived from a climate reconstruction.

While the general approach used is not new per se, the context to which it is applied is definitely novel, and an application to such a large domain does not seem to have been attempted before. In Québec, the model’s excellent performance, coupled with the availability of open-source Julia code which is easily understandable and well documented, has recently led to its adoption by Hydro-Québec and the Ministère de l’Environnement et de la Lutte contre les changements climatiques as a new engineering standard.

The key features of the approach described herein are as follows:

• (a) the discretization of the latent Gaussian field on the same lattice as the covariate to enable efficient and precise computation;

• (b) the avoidance of an unstructured error term through a first-order iGMRF which allows for random deviations from the expected level;

• (c) a quality assessment of spatial interpolations via cross-validation.

In the cross-validation framework, the new approach improves the quantile prediction for a vast majority of stations. Enhancement on current practice in 100% of cases would clearly be desirable but it is an unreasonable expectation. The chances are approximately 3 to 1 that the proposed method provides a better estimate that the old one, and that the improvements are large; in contrast, the deterioration is small when it occurs. Overall, the new approach marks a substantial advance over current ECCC practice.

In future work, two of the assumptions of the modeling approach presented here could possibly be relaxed.

First, improper, and hence marginally uninformative, priors were chosen for the location and log-scale parameters $\varvec{\mu }$ and $\varvec{\phi }$. Given the wealth of data available, it did not seem worthwhile to try and elicit more specific prior distributions that could account, e.g., for dependence between these two spatial priors. Such dependence is incorporated into the posterior distribution via the likelihood, on which the posterior distribution is largely based. In other applications, however, it might be beneficial to introduce prior dependence between the GEV parameters, e.g., as done by Cooley and Sain (2010).

Second, it was assumed that the marginal GEV distributions share the same shape parameter, $\xi$. This common assumption avoids unidentifiability issues (Davison et al. 2012). Here, $\xi$ was estimated from data, which already represents a vast improvement over the current methodology employed by Environment and Climate Change Canada, which fixes $\xi = 0$.

By allowing $\xi$ to depend on covariates, one might possibly alleviate the identifiability issue. This option was considered, e.g., by Dyrrdal et al. (2015), Geirsson et al. (2015), and Lehmann et al. (2016) for the analysis of extreme rainfall in Norway, Iceland, and Australia, respectively. In all cases, however, the assumption that $\xi$ is spatially invariant could not be rejected. Therefore, the benefits of such an extension are likely to be limited.

Finally, one aspect of this work that could definitely be improved pertains to the construction of IDF curves per se, based on the high-quantile estimates derived from the model for different durations. First, as already mentioned in the Introduction, the linear relation (1) between intensity and duration on the logarithmic scale was not questioned. While it did seem to provide a good fit, as portrayed in Fig. 10, more complex relations could be envisaged. Specifically, Koutsoyiannis et al. (1998) showed that all commonly observed empirical relations can be expressed in the form

$$\begin{aligned} I = A \times (D^\nu + \theta )^B, \end{aligned}$$

(4)

where $\theta \in [0, \infty )$ and $\nu B \le -1$.

Second, and more importantly, given that GEV distributions were fitted separately for a certain number of durations, a potential problem is that the estimated return level curves might not be consistent with each other. For example, if the shape parameter $\xi$ is estimated to be larger for shorter durations, then the corresponding return level curves might cross each other as the return period increases, thereby leading to inconsistent results.

While these consistency issues did not occur for the durations and return periods considered in this particular analysis, they might arise in other contexts. Different ways of dealing with the problem were considered, e.g., by Lehmann et al. (2016) and Ulrich et al. (2020). For example, the latter proposed to incorporate relation (4) as a constraint in the model. However, their work assumes that the shape parameter is constant over all durations, whereas it varied between 0.0198 and 0.1105 for the ECCC data. Fitting regression curves simultaneously with order constraints would be another way of dealing with the issue. This may be the object of future work.

Appendix: Technical details

This appendix describes, in broad terms, the computational strategy used to fit the model and interpolate at unmonitored locations. It provides guidance for the Julia code which is available on the public repository GitHub with a copy of the data and detailed documentation; see

https://github.com/jojal5/Publications/tree/master/JalbertGenestPerreault2022

All the results obtained herein can easily be reproduced with this code.

Available for modeling are the values of the two covariates at 48, 694 grid points and, for each of the nine durations provided by Environment and Climate Change Canada, the vectors of maxima at the grid cells $i \in {\mathcal {S}}$ where the agency has meteorological stations.

The first step is to sample from the posterior joint distribution of the vector $(\mu , \phi , \xi , \beta _\mu , \beta _\phi , \kappa _u, \kappa _v)$, where $\mu = (\mu _i: i \in {\mathcal {S}})$ and $\phi = (\phi _i: i \in {\mathcal {S}})$, $\xi$, $\beta _\mu$, $\beta _\phi \in {\mathbb {R}}$, and $\kappa _u, \kappa _v \in (0, \infty )$. This is done through Gibbs sampling with 215, 000 iterations, the first 15, 000 of which are discarded as the warm-up. To reduce autocorrelation in the MCMC sample, only every 20th iteration is retained. The resulting length of the posterior sample is thus 10, 000.

Let $\bar{{\mathcal {S}}} = {\mathcal {V}} \setminus {\mathcal {S}}$ be the set of grid cells containing no meteorological station. To determine the spatial effect at grid cells $i \in \bar{{\mathcal {S}}}$, one proceeds conditionally on the realized values of spatial effects $(U_i = u_i: i \in {\mathcal {S}})$ defined in Eq. (3).

Let $Q_{\bar{{\mathcal {S}}},{\mathcal {S}}} = \kappa _u W_{\bar{{\mathcal {S}}}, {\mathcal {S}}}$ and $Q_{\bar{{\mathcal {S}}},\bar{{\mathcal {S}}}} = \kappa _u W_{\bar{{\mathcal {S}}},\bar{{\mathcal {S}}}}$, where

$$\begin{aligned} \displaystyle W_{\bar{{\mathcal {S}}},{\mathcal {S}}} = (W_{ij} : i \in \bar{{\mathcal {S}}}, j \in {\mathcal {S}}) , \quad W_{\bar{{\mathcal {S}}},\bar{{\mathcal {S}}}} = (W_{ij} : i \in \bar{{\mathcal {S}}}, j \in \bar{{\mathcal {S}}}). \end{aligned}$$

Sampling from the distribution

$$\begin{aligned} \displaystyle f_{(\varvec{U}_{\bar{{\mathcal {S}}}} | \varvec{U}_{{\mathcal {S}}} = \varvec{u}_{{\mathcal {S}}} )}(\varvec{u_{\bar{{\mathcal {S}}}}}) = {\mathcal {N}} {\Big [} \varvec{u}_{\bar{{\mathcal {S}}}} \mid -Q_{\bar{{\mathcal {S}}},\bar{{\mathcal {S}}}}^{-1} Q_{\bar{{\mathcal {S}}},{\mathcal {S}}} \varvec{u}_{{\mathcal {S}}} \, , \, Q_{\bar{{\mathcal {S}}},\bar{{\mathcal {S}}}}^{-1} {\Big ]} \end{aligned}$$

can be achieved efficiently using the algorithm provided in Appendix B of Rue and Held (2005). This algorithm relies on the notion of sparse precision matrix. Details of the implementation are given in the Julia code.