A Class of Multivariate Power Skew Symmetric Distributions: Properties and Inference for the Power-Parameter

Abstract

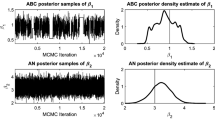
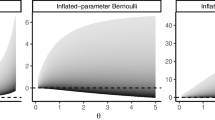
Let SPd be the class of all multivariate sign and permutation invariant densities and SPD be the corresponding class of distribution functions. The class of all distributions corresponding to a positive power of the members of SPD is called the Power Skew Symmetric class of distributions and it is denoted by PSS. We consider the problem of inference associated with the nonnegative power, in the PSS class, with a member of SPD as a nuisance parameter. As the structural forms of the members of PSS are not known, one can’t directly use the sufficiency, invariance, or likelihood function. Hence by using certain properties of the SPD and the PSS classes, we identify maximal statistics whose distributions depend only on the power but not on the members of SPD. We then use the concept of minimal dimensionality for retaining the information about the parameter of interest. We use the minimax criterion, which leads to a statistic having Binomial distribution depending only on the parameter of interest. Hence inferences about the parameter of interest can be carried out using the standard methods for the binomial model. A simulation study indicates that the proposed estimator of the power parameter is asymptotically normal and is insensitive to the nuisance parameter. The proposed method is implemented for the analysis of a data set.

Appendix:

Proof Proof of Theorem 4.1.

For any finite positive integer k and r = 0,1, ...,k, let $P\left (r,\ k\right )$ denote the probability of a quadrant with exactly r positive coordinates. Since variables are exchangeable, it is enough to show that

$$ \begin{array}{@{}rcl@{}} P\left( r,\ k\right)&=&Prob\left\{X_{1}\le 0,{..,X}_{k-r}\le 0,X_{k-r+1}>0,...,\ X_{k}>0\right\}\\ &=&{\left\{\frac{1}{2^{\alpha }}\right\}}^{k-r}{(1-\frac{1}{2^{\alpha }})}^{r},\ \ 0\le \ r\le k. \end{array} $$

We shall use the method of induction and a recurrence relation. For any k ≥ 1 we have $P\left (0,\ k\right )=P\left \{\mathbf {X}\le 0\right \}=G\left (0\right ){=\left \{F(0)\right \}}^{\alpha }={\left \{\frac {1}{2^{k}}\right \}}^{\alpha }={\left \{\frac {1}{2^{\alpha }}\right \}}^{k}$, that is

$$ P\left( 0,\ k\right)={\left\{\frac{1}{2^{\alpha }}\right\}}^{k}, k=1, 2, ... $$

(5)

Let k = 1. Here X is a real random variable and from the above, $P\left (0,\ 1\right )=\frac {1}{2^{\alpha }}$ hence $P\left (1,\ 1\right )=1-$ $P\left \{X\le 0\right \}=1-$ $\frac {1}{2^{\alpha }}$. Thus result is true for 0 ≤ r ≤ k = 1.

For k = 2, since X₁,X₂ are exchangeable, the two quadrants {x₁ ≤ 0, x₂ > 0} and $\left \{x_{1}>0,{\ x}_{2}\le 0\right \}$ have equal probabilities and we have $P\left (0,\ 2\right )={\left \{\frac {1}{2^{\alpha }}\right \}}^{2}$. Now

$$ \begin{array}{@{}rcl@{}} P\left( 1,\ 2\right)&=& P\left\{X_{1}\le 0,{\ X}_{2}>0\right\}=\ \ P\left\{X_{1}\le 0\right\}-P\left\{X_{1}\le 0,{\ X}_{2}\le 0\right\}\\ &=&P\left( 0,\ 1\right)-P\left( 0,\ 2\right) =\frac{1}{2^{\alpha }}-{\left\{\frac{1}{2^{\alpha }}\right\}}^{2}={\left\{\frac{1}{2}\right\}}^{\alpha }\left( 1-\ {\left\{\frac{1}{2}\right\}}^{\alpha }\ \right). \\ P\left( 2,\ 2\right)&=&P\left\{X_{1}>0,{\ X}_{2}>0\right\} =P\left\{{\ X}_{2}>0\right\}-P\left\{X_{1}\le 0,{\ X}_{2}>0\right\}\\ &=& P\left( 1,\ 1\right)-P\left( 1,2\right)\\ &=& 1- \frac{1}{2^{\alpha }}-{\left\{\frac{1}{2}\right\}}^{\alpha }\left( 1-\ {\left\{\frac{1}{2}\right\}}^{\alpha }\ \right)={\left( 1-{\left\{\frac{1}{2}\right\}}^{\alpha }\right)}^{2}. \end{array} $$

Thus the result is true for k ≤ 2, r ≤ k. Suppose that the result is true for k ≤ t − 1, 0 ≤ r ≤ k. Let $\mathbf {X}=\left (X_{1},\ {\ X}_{,\ \ 2},{{\dots } ,X}_{t}\right ). {\!}^{\prime }\sim G_{t;\ F,\ \alpha }\ \in PSSD(t),$ then we know that every l (≤ t) dimensional marginal distribution of X is a member of PSSD(l). That is $\mathbf {X}^{\left (1\right )}=\left (X_{1},\ {\ X}_{2},{\dots , ,X}_{t-1}\right )^{\prime }$ and $\mathbf {X}^{\left (2\right )}=$ X_t are respectively members of PSS(t − 1) and that of PSS(1). We have $P\left (0,t\right )={\left \{\frac {1}{2^{\alpha }}\right \}}^{t}$ and $P\left (1,t\right )=$ $P\left \{X_{1}\le 0,\ {..,\ X}_{t-1}\le 0,\ \ X_{t}>0\right \} =\ \mathrm {\ }P\left \{X_{1}\le 0,\ {..,\ X}_{t-1}\le 0\right \}-Prob\left \{X_{1}\le 0,\ {..,\ X}_{t}\le 0,\right \}=P\left (0,\ \ t-1\right ) -\mathrm {P}\left (0,\ t\right ) ={\left \{\frac {1}{2^{\alpha }}\right \}}^{t-i}-{\left \{\frac {1}{2^{\alpha }}\right \}}^{t} ={\left \{\frac {1}{2^{\alpha }}\right \}}^{t-1}{(1-\frac {1}{2^{\alpha }})}$.

Suppose, by now we know $P\left (i,t\right )$ for i = 0,1,2,,,r − 1 and $P\left (i,j\right )$ for0 ≤ i ≤ j ≤ t -1. Consider

$$ \begin{array}{@{}rcl@{}} P\left( r,t\right)&=&P\left\{X_{1}\le 0,\ {..,\ X}_{t-r}\le 0,X_{t-r+1}>0,..,\ X_{t}>0\right\}\\ &=& P\left\{X_{1}\le 0,\ {..,\ X}_{t-r}\le 0,X_{t-r+2}>0,..,\ X_{t}>0\right\}\\ &&-P\left\{X_{1}\le 0,\ {..,\ X}_{t-r+1}\le 0,X_{t-r+2}>0,..,\ X_{t}>0\right\}. \end{array} $$

Since marginal distributions are members of PSS classes of appropriate dimensions, retaining the same value of α, from the above we have the recurrence relation

$$P\left( r,t\right)\mathrm{=}P\left( r-1,t-1\right)-P\left( r-1,t\right).$$

That is $P\left (r,t\right ) ={\left \{\frac {1}{2^{\alpha }}\right \}}^{t-r}{\left (1-\frac {1}{2^{\alpha }}\right )}^{r-1}-{\left \{\frac {1}{2^{\alpha }}\right \}}^{t-r+1}{\left (1-\frac {1}{2^{\alpha }}\right )}^{r-1}$$={\left \{\frac {1}{2^{\alpha }}\right \}}^{t-r}$ ${(1-\frac {1}{2^{\alpha }})}^{r}$.

Hence the theorem.□

Proof Proof of Lemma 5.3.

For k = 2, let $C_{1}=\{\left (y_{1},\ y_{2}\right ):y_{1}\ \le 0<y_{2}\ \le {-y}_{1}\}$ and $C_{2}=\{\left (y_{1},\ y_{2}\right ):y_{1}\ \le 0<y_{2} >{-y}_{1}\}$ be the two disjoint non empty cones in ${\mathcal {C}}^{(2)}$ which are subsets of the quadrant $Q=\{\left (y_{1},\ y_{2}\right ):y_{1}\ \le 0<y_{2}\ \}$. Now $P\left \{\ C_{2}\ \right \}={\int \limits }^{0}_{-\infty }{\int \limits }^{\infty }_{-y_{1}}\ d F^{\alpha }\ \left (y_{1},\ y_{2}\right )$. By substituting y₁ = − z₂ and y₂ = − z₁, HCode $P\left \{\ C_{2}\ \right \}={\int \limits }^{\infty }_{0} {\int \limits }^{z_{2}}_{-\infty }\ d F^{\alpha }\ \left ({-z}_{2},\ {-z}_{1}\right )$. By changing the orders of integrations we have $P\left \{\ C_{2}\ \right \}= {\int \limits }^{0}_{-\infty }{\int \limits }^{{-z}_{1}}_{0}\ d F^{\alpha }\ \left ({-z}_{1},\ {-z}_{2}\right ), \ P$ $\left \{\ C_{1}\ \right \}= {\int \limits }^{0}_{-\infty }{\int \limits }^{{-z}_{1}}_{0}\ d {F}^{\alpha }\ \left (z_{1},\ z_{2}\right )$.

Hence $P\left \{ C_{2}\right \}- P\left \{ C_{1}\ \right \}={\int \limits }^{0}_{-\infty }{\int \limits }^{{-z}_{1}}_{0}\ d [{ F}^{\alpha }\ \left ({-z}_{1},\ {-z}_{2}\right )-{F}^{\alpha }\ \left (z_{1},\ z_{2}\right )]$.

But in the domain of the above integration, we have z₁ ≤ 0 < z₂ ≤−z₁, and hence the point $\left (-z_{1},\ {-z}_{2}\right )$ is coordinate-wise larger than the point $\left (z_{1},\ z_{2}\right )$. Thus

$$ {H\left( z_{1}, z_{2}\right)={F}^{\alpha} \left( {-z}_{1}, {-z}_{2}\right)-F}^{\alpha} \left( z_{1}, z_{2}\right)\ge 0 $$

and inequality is strict on a set of positive Lebesgue measure. Thus difference $P\left \{\ C_{2}\ \right \}$-$\ P\left \{\ C_{1}\ \right \}$ depends on both α and F. But as the sum $P\left \{\ C_{2}\ \right \}$ +$P\left \{\ C_{1}\ \right \}$ is only a function of α, and hence both $P\left \{\ C_{2}\ \right \}$ and$\ P\left \{\ C_{1}\ \right \}$ depend on both α and F. □

The following results are used in Section 7.

Lemma A.1.

Let f, F be the density and the distribution functions of standard normal variate. Then function $m\left (x \right )=1 + \left \lbrack \frac {\text {xF}\left (x \right )}{f\left (x \right )} \right \rbrack$ is strictly increasing and $\lim _{x \rightarrow - \infty }{m(x)} = 0$, $\lim _{x \rightarrow \infty }{m(x)} = \infty$.

Proof.

Consider $m^{\prime }(x) = \frac {F\left (x \right )}{f\left (x \right )} + x\{ 1 - \frac {F\left (x \right )f^{\prime }\left (x \right )}{f\left (x \right )f\left (x \right )}\} = \frac {F\left (x \right )}{f\left (x \right )} + x\{ 1 + x\frac {F\left (x \right )}{f\left (x \right )}\} = \frac {F\left (x \right )}{f\left (x \right )}\left \{ 1 + x^{2} \right \} + x$. Hence $m^{\prime }\left (x \right ) > 0$ for x > 0.

Now forx < 0, we have

$$ \begin{array}{@{}rcl@{}} \frac{1}{x^{2}}{\int}_{- \infty}^{x}{e^{{- u}^{2}/2}du > \ }{\int}_{- \infty}^{x}{\frac{1}{u^{2}}e^{{- u}^{2}/2}du = \frac{- 1}{u}e^{{- u}^{2}/2}\ }|_{- \infty}^{x} - {\int}_{- \infty}^{x}{e^{{- u}^{2}/2}\text{du\ }}\\ = \frac{- 1}{x}e^{{- x}^{2}/2} - {\int}_{- \infty}^{x}{e^{{- u}^{2}/2}\text{du\ }}. \end{array} $$

That is, $(1 + \frac {1}{x^{2}}){\int \limits }_{- \infty }^{x}{e^{{- u}^{2}/2}du > \ }\frac {- 1}{x}e^{{- x}^{2}/2},$ implies that

$$ \left( 1 + x^{2} \right)F\left( x \right) + xf\left( x \right) > 0 $$

(6)

and hence ${ \ m}^{\prime }(x)$ > 0. Hence $m\left (x \right )$ is strictly increasing.

It is easy to check that $\lim _{x \rightarrow \infty }{m(x)} = \infty$.

Further for x < 0, from Eq. 6 we have $\frac {\left (1 + x^{2} \right )F\left (x \right )}{xf\left (x \right )} < - 1$. Now

$$ \begin{array}{@{}rcl@{}} \lim_{x \rightarrow - \infty}\frac{\left( 1 + x^{2} \right)F\left( x \right)}{xf\left( x \right)} &=& \lim_{x \rightarrow - \infty}\frac{\text{xF}\left( x \right)}{f\left( x \right)} = \lim_{x \rightarrow - \infty}\frac{F\left( x \right)}{f\left( x \right)/x} \\&=& \lim_{x \rightarrow - \infty}\frac{f\left( x \right)}{\frac{f^{\prime}(x)}{x} - f(x)/x^{2}}\\ &=& \lim_{x \rightarrow - \infty}\frac{f\left( x \right)}{- f(x) - f(x)/x^{2}}= \lim_{x \rightarrow - \infty}\frac{- x^{2}}{x^{2} + 1} = - 1. \end{array} $$

Thus $\lim _{x \rightarrow - \infty }{m(x)}= \lim _{x \rightarrow - \infty } \{1 + \left \lbrack \frac {x F(x))}{f(x)} \right \rbrack = 0$.

Hence the Lemma. □

Lemma A.2.

If $f\left (x \right ) = \frac {1}{\sqrt {2\pi }}e^{- x^{2}/2}$ then the density function g(x,α) is unimodal and the mode is the unique solution of $1 + \left \lbrack \frac {\text {xF}\left (x \right )}{f\left (x \right )} \right \rbrack$ = α.

Proof.

If $f\left (x \right ) = \frac {1}{\sqrt {2\pi }}e^{- x^{2}/2}$ then we have

$$ \begin{array}{@{}rcl@{}} g^{\prime}(x,\ \alpha)& =& \alpha\{\left( \alpha - 1 \right)\left( F\left( x \right) \right)^{\alpha - 2}f(x)f\left( x \right) - \left( F\left( x \right) \right)^{\alpha - 1}xf(x)\}\\ &=& \alpha\left( F\left( x \right) \right)^{\alpha - 2}f\left( x \right)\{\left( \alpha - 1 \right)f(x) - xF\left( x \right)\}\\ &=& \alpha\left( F\left( x \right) \right)^{\alpha - 2}f\left( x \right)f\left( x \right)\left\{ \alpha - \left( 1 + \left\lbrack \frac{\text{xF}\left( x \right)}{f\left( x \right)} \right\rbrack \right) \right\}\\ &=& \alpha\left( F\left( x \right) \right)^{\alpha - 2}f\left( x \right)f(x)\{\alpha - m\left( x \right)\}. \end{array} $$

Hence from the Lemma A.1, for any α > o, the function $g^{\prime }\left (x, \alpha \right )$ changes the sign only once, that too from positive to negative. That is g(x,α) is increasing for x < m₀(α) and decreasing for x > m₀(α). Hence the Lemma. □