HEOSAT: a mean elements orbit propagator program for highly elliptical orbits

Abstract

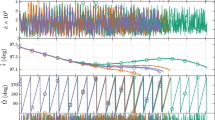
The algorithms used in the construction of a semi-analytical propagator for the long-term propagation of highly elliptical orbits (HEO) are described. The software propagates mean elements and include the main gravitational and non-gravitational effects that may affect common HEO orbits, as, for instance, geostationary transfer orbits or Molniya orbits. Comparisons with numerical integration show that it provides good results even in extreme orbital configurations, as the case of SymbolX.

Appendices

Appendix A: Some useful partial derivatives in elliptic motion

When dealing with automatic manipulation of literal expressions, it results practical to limit the symbolic algebra to the basic arithmetic operations, to wit, addition, subtraction, multiplication and division—integer powers being a particular case of multiplication. However, square roots and trigonometric functions appear naturally in the formulation of the perturbation in canonical variables. To avoid dealing explicitly with square roots, it is wise to be equipped with a battery of partial derivatives that ease handling and simplifying symbolic expressions.

Since our perturbation approach relies on the use of Delaunay and polar-nodal canonical variables, the partial derivatives of the classical Keplerian variables $(a,e,I,\Omega ,\omega ,M)$, standing for semi-major axis, eccentricity, inclination, right ascension of the ascending node, argument of the periapsis and mean anomaly, respectively, as well as the usual functions of the Keplerian variables

• the mean motion $n=\sqrt{\mu /a^3}$,

• the parameter (or semilatus rectum) $p=a\,(1-e^2)$,

• the eccentricity function $\eta =\sqrt{1-e^2}$,

• the cosine of the inclination $c=\cos {I}$,

• the sine of the inclination $s=\sqrt{1-c^2}$,

• the eccentric anomaly u, given by $M=u-e\sin {u}$,

• the true anomaly f, given by $(1-e)\tan \frac{1}{2}f=\eta \tan \frac{1}{2}u$,

• the radial distance $r=a\,(1-e\cos {u})=p/(1+e\cos {f})$,

• the radial velocity $R=a\,n\,(a/r)\,e\sin {u}=a\,n\,(e/\eta )\sin {f}$,

• the argument of the latitude $\theta =f+\omega$,

• the projections of the eccentricity vector in the orbital frame: $k=e\cos {f}=-1+p/r$, and $q=e\sin {f}=R\,\eta /(n\,a)$,

are provided both in the Delaunay chart $(\ell ,g,h,L,G,H)$ and in the polar-nodal chart $(r,\theta ,\nu ,R,\Theta ,N)$.

We found convenient to express all the partial derivatives by means of the Keplerian functions:

$$\begin{aligned} p,n,e,\eta ,k,q,s,c \end{aligned}$$

from whose definition it is obtained

$$\begin{aligned} L &= n\,p^2/\eta ^4 \\ G &= L\,\eta =n\,p^2/\eta ^3=\Theta \\ H &= G\,c=n\,p^2\,c/\eta ^3=N \\ R &= n\,p\,q/\eta ^3 \\ r &= p/(1+k) \end{aligned}$$

Recall also that, from the ellipse geometry, the following relations apply, cf. Eq. (34),

$$\begin{aligned} \sin {f}=(a/r)\eta \sin {u}, \quad \cos {f}=(a/r)(\cos {u}-e). \end{aligned}$$

Finally, it is worth to mention that the use of logarithmic derivatives is helpful in finding the differentials that eased the computation of the partial derivatives. Note that only non-vanishing derivatives are presented.

1.1 A.1: With respect to Delaunay variables

1.1.1 A.1.1: Orbital elements and related functions

• Semi-major axis a:

  $$\begin{aligned} \frac{\mathrm {d}a}{\mathrm {d}L}=2\frac{L}{\mu } = 2\frac{\eta ^2}{n\,p} \end{aligned}$$

  (56)

• Mean motion n:

  $$\begin{aligned} \frac{\mathrm {d}n}{\mathrm {d}L} = -3\frac{\eta ^4}{p^2} \end{aligned}$$

  (57)

• Parameter p:

  $$\begin{aligned} \frac{\mathrm {d}p}{\mathrm {d}G}= 2\frac{G}{\mu } =2\frac{\eta ^3}{n\,p} \end{aligned}$$

  (58)

• Eccentricity function $\eta$:

  $$\begin{aligned} \frac{\mathrm {d}\eta }{\mathrm {d}L}= & \eta \left( -\frac{1}{L}\right) = -\frac{\eta ^5}{n\,p^2} \end{aligned}$$

  (59)
  $$\begin{aligned} \frac{\mathrm {d}\eta }{\mathrm {d}G}= & \eta \left( \frac{1}{G}\right) = \frac{\eta ^4}{n\,p^2} \end{aligned}$$

  (60)

• Eccentricity e:

  $$\begin{aligned} \frac{\mathrm {d}e}{\mathrm {d}L}= & \frac{\eta ^2}{e}\,\frac{1}{L} = \frac{\eta ^6}{e\,n\,p^2} \end{aligned}$$

  (61)
  $$\begin{aligned} \frac{\mathrm {d}e}{\mathrm {d}G}= & -\frac{\eta ^2}{e}\,\frac{1}{G} =-\frac{\eta ^5}{e\,n\,p^2} \end{aligned}$$

  (62)

• Cosine of inclination c:

  $$\begin{aligned} \frac{\mathrm {d}c}{\mathrm {d}G} = -\frac{c}{G}=-c\,\frac{\eta ^3}{n\,p^2} \end{aligned}$$

  (63)
  $$\begin{aligned} \frac{\mathrm {d}c}{\mathrm {d}H} = \frac{c}{H}=\frac{1}{G}=\frac{\eta ^3}{n\,p^2} \end{aligned}$$

  (64)

• Sine of inclination s:

  $$\begin{aligned} \frac{\mathrm {d}s}{\mathrm {d}G} = \frac{c^2}{s}\,\frac{\eta ^3}{n\,p^2} \end{aligned}$$

  (65)
  $$\begin{aligned} \frac{\mathrm {d}s}{\mathrm {d}H} = -\frac{c}{s}\,\frac{\eta ^3}{n\,p^2} \end{aligned}$$

  (66)

• Eccentric anomaly u:

  $$\begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}\ell } = \frac{p}{r\,\eta ^2}=\frac{1+k}{\eta ^2} \end{aligned}$$

  (67)
  $$\begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}L} = \frac{R\,\eta ^8}{e^2\,n^2\,p^3}= \frac{q\,\eta ^5}{e^2\,n\,p^2} \end{aligned}$$

  (68)
  $$\begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}G} = -\frac{R\,\eta ^7}{e^2\,n^2\,p^3}=-\frac{q\,\eta ^4}{e^2\,n\,p^2} \end{aligned}$$

  (69)

1.1.2 A.1.2: Polar-nodal variables and related functions

• Radial distance r:

  $$\begin{aligned} \frac{\mathrm {d}r}{\mathrm {d}\ell } = \frac{R}{n}=\frac{p\,q}{\eta ^3} \end{aligned}$$

  (70)
  $$\begin{aligned} \frac{\mathrm {d}r}{\mathrm {d}L} = \frac{\eta ^4}{e^2\,n}\left( \frac{2 e^2 r}{p^2}+\frac{1}{p}-\frac{1}{r}\right) =\frac{\eta ^4}{n\,p}\left( \frac{2}{1+k}-\frac{k}{e^2}\right) \end{aligned}$$

  (71)
  $$\begin{aligned} \frac{\mathrm {d}r}{\mathrm {d}G} = \frac{\eta ^3}{e^2\,n}\left( \frac{1}{r}-\frac{1}{p}\right) =\frac{\eta ^3\,k}{e^2\,n\,p} \end{aligned}$$

  (72)

• Radial velocity R:

  $$\begin{aligned} \frac{\mathrm {d}R}{\mathrm {d}\ell } = \frac{p\,n}{\eta ^6}\frac{p^2}{r^2}\left( \frac{p}{r}-1\right) =\frac{p\,n}{\eta ^6}\,k\,(1+k)^2 \end{aligned}$$

  (73)
  $$\begin{aligned} \frac{\mathrm {d}R}{\mathrm {d}L} = \eta ^4\,\frac{R}{n\,r^2}\left( \frac{1}{e^2}-\frac{r^2}{p^2}\right) =\eta \,\frac{q}{p}\left[ \frac{(1+k)^2}{e^2}-1\right] \end{aligned}$$

  (74)
  $$\begin{aligned} \frac{\mathrm {d}R}{\mathrm {d}G} = -\frac{\eta ^3}{e^2}\,\frac{R}{n\,r^2}=-\frac{(1+k)^2}{e^2}\,\frac{q}{p} \end{aligned}$$

  (75)

• True anomaly f:

  $$\begin{aligned} \frac{\mathrm {d}f}{\mathrm {d}\ell } = \frac{\eta \,r}{a\,n\,(p-r)}\,\frac{\mathrm {d}R}{\mathrm {d}\ell }=\frac{p^2}{r^2\,\eta ^3}=\frac{(1+k)^2}{\eta ^3} \end{aligned}$$

  (76)
  $$\begin{aligned} \frac{\mathrm {d}f}{\mathrm {d}L} = \frac{R\,\eta ^7}{e^2\,n^2\,p^2}\left( \frac{1}{p}+\frac{1}{r}\right) =\frac{q\,\eta ^4}{e^2\,n\,p^2}\,(2+k)\end{aligned}$$

  (77)
  $$\begin{aligned} \frac{\mathrm {d}f}{\mathrm {d}G} = -\frac{R\,\eta ^6}{e^2\,n^2\,p^2}\left( \frac{1}{p}+\frac{1}{r}\right) =-\frac{q\,\eta ^3}{e^2\,n\,p^2}\,(2+k) \end{aligned}$$

  (78)

• Argument of the latitude $\theta$:

  $$\begin{aligned} \frac{\mathrm {d}\theta }{\mathrm {d}\ell } = \frac{\mathrm {d}f}{\mathrm {d}\ell }\end{aligned}$$

  (79)
  $$\begin{aligned} \frac{\mathrm {d}\theta }{\mathrm {d}g} = 1\end{aligned}$$

  (80)
  $$\begin{aligned} \frac{\mathrm {d}\theta }{\mathrm {d}L} = \frac{\mathrm {d}f}{\mathrm {d}L}\end{aligned}$$

  (81)
  $$\begin{aligned} \frac{\mathrm {d}\theta }{\mathrm {d}G} = \frac{\mathrm {d}f}{\mathrm {d}G} \end{aligned}$$

  (82)

• Modulus of the angular momentum $\Theta$:

  $$\begin{aligned} \frac{\mathrm {d}\Theta }{\mathrm {d}G} = 1 \end{aligned}$$

  (83)

• Argument of the node $\nu$:

  $$\begin{aligned} \frac{\mathrm {d}\nu }{\mathrm {d}h} = 1 \end{aligned}$$

  (84)

• Polar component of the angular momentum N:

  $$\begin{aligned} \frac{\mathrm {d}N}{\mathrm {d}H} = 1 \end{aligned}$$

  (85)

• Eccentricity vector k:

  $$\begin{aligned} \frac{\mathrm {d}k}{\mathrm {d}\ell } = -\frac{p\,R}{r^2\,n}=-\frac{q}{\eta ^3}(1+k)^2 \end{aligned}$$

  (86)
  $$\begin{aligned} \frac{\mathrm {d}k}{\mathrm {d}L} = \frac{\eta ^4}{n\,r^2}\left( \frac{k}{e^2}-\frac{2}{k+1}\right) \end{aligned}$$

  (87)
  $$\begin{aligned} \frac{\mathrm {d}k}{\mathrm {d}G} = -\frac{\eta ^3}{n\,r^2}\left( \frac{k}{e^2}-\frac{2}{k+1}\right) \end{aligned}$$

  (88)

• Eccentricity vector q:

  $$\begin{aligned} \frac{\mathrm {d}q}{\mathrm {d}\ell } = \frac{1}{\eta ^3}\frac{p^2}{r^2}\left( \frac{p}{r}-1\right) =\frac{k}{\eta ^3}\frac{p^2}{r^2}=\frac{k}{\eta ^3}\,(1+k)^2 \end{aligned}$$

  (89)
  $$\begin{aligned} \frac{\mathrm {d}q}{\mathrm {d}L} = \frac{q\,\eta ^4}{n\,r^2}\left( \frac{1}{e^2}-\frac{r^2}{p^2}\right) =\frac{q\,\eta ^4}{n\,p^2}\left[ \frac{(1+k)^2}{e^2}-1\right] \end{aligned}$$

  (90)
  $$\begin{aligned} \frac{\mathrm {d}q}{\mathrm {d}G} = -\frac{q\,\eta ^3}{n\,r^2}\left( \frac{1}{e^2}-\frac{r^2}{p^2}\right) =-\frac{q\,\eta ^3}{n\,p^2}\left[ \frac{(1+k)^2}{e^2}-1\right] \end{aligned}$$

  (91)

1.2 A.2: With respect to polar-nodal variables

1.2.1 A.2.1: Delaunay variables

• Delaunay action L:

  $$\begin{aligned} \frac{\mathrm {d}L}{\mathrm {d}r} = -\frac{\Theta }{p}\,\frac{k}{\eta ^3}\,(1+k)^2 =-np\,\frac{k}{\eta ^6}\,(1+k)^2\end{aligned}$$

  (92)
  $$\begin{aligned} \frac{\mathrm {d}L}{\mathrm {d}R} = \frac{\Theta }{n}\,\frac{q}{p} = p\frac{q}{\eta ^3} \end{aligned}$$

  (93)
  $$\begin{aligned} \frac{\mathrm {d}L}{\mathrm {d}\Theta } = \frac{p^2}{\eta ^3\,r^2} = \frac{(1+k)^2}{\eta ^3} \end{aligned}$$

  (94)

• Modulus of the angular momentum $\Theta$:

  $$\begin{aligned} \frac{\mathrm {d}G}{\mathrm {d}\Theta } = 1 \end{aligned}$$

  (95)

• Polar component of the angular momentum N:

  $$\begin{aligned} \frac{\mathrm {d}H}{\mathrm {d}N} = 1 \end{aligned}$$

  (96)

• Mean anomaly $\ell$:

  $$\begin{aligned} \frac{\mathrm {d}\ell }{\mathrm {d}r} = \eta \,\frac{q}{r}\left( \frac{1+k}{e^2}-\frac{1}{1+k}\right) \end{aligned}$$

  (97)
  $$\begin{aligned} \frac{\mathrm {d}\ell }{\mathrm {d}R} = \eta \,\frac{q}{R}\left( \frac{k}{e^2}-\frac{2}{1+k}\right) \end{aligned}$$

  (98)
  $$\begin{aligned} \frac{\mathrm {d}\ell }{\mathrm {d}\Theta }= -\eta \,\frac{q}{\Theta }\,\frac{2+k}{e^2} \end{aligned}$$

  (99)

• Argument of the perigee g:

  $$\begin{aligned} \frac{\mathrm {d}g}{\mathrm {d}r}= -\frac{q}{r}\,\frac{1+k}{e^2} \end{aligned}$$

  (100)
  $$\begin{aligned} \frac{\mathrm {d}g}{\mathrm {d}\theta } = 1 \end{aligned}$$

  (101)
  $$\begin{aligned} \frac{\mathrm {d}g}{\mathrm {d}R} = -\frac{q}{R}\,\frac{k}{e^2} \end{aligned}$$

  (102)
  $$\begin{aligned} \frac{\mathrm {d}g}{\mathrm {d}\Theta } = \frac{q}{\Theta }\,\frac{2+k}{e^2} \end{aligned}$$

  (103)

• Right ascension of the ascending node h:

  $$\begin{aligned} \frac{\mathrm {d}h}{\mathrm {d}\nu } = 1 \end{aligned}$$

  (104)

1.2.2 A.2.2: Orbital elements and related functions

• Parameter p:

  $$\begin{aligned} \frac{\mathrm {d}p}{\mathrm {d}\Theta } &= 2\frac{p}{\Theta }=2\frac{\eta ^3}{n\,p} \end{aligned}$$

  (105)

• Eccentricity vector k:

  $$\begin{aligned} \frac{\mathrm {d}k}{\mathrm {d}r} = -\frac{p}{r^2}=-\frac{(1+k)^2}{p} \end{aligned}$$

  (106)
  $$\begin{aligned} \frac{\mathrm {d}k}{\mathrm {d}\Theta } = \frac{2p}{r\,\Theta }=\frac{2q}{r\,R} =\frac{2(1+k)\,\eta ^3}{n\,p^2} \end{aligned}$$

  (107)

• Eccentricity vector q:

  $$\begin{aligned} \frac{\mathrm {d}q}{\mathrm {d}R} = \frac{q}{R}=\frac{p}{\Theta } =\frac{\eta ^3}{n\,p} \end{aligned}$$

  (108)
  $$\begin{aligned} \frac{\mathrm {d}q}{\mathrm {d}\Theta } = \frac{q}{\Theta }=\frac{q^2}{R\,p} =\frac{q\,\eta ^3}{n\,p^2} \end{aligned}$$

  (109)

• Eccentricity e:

  $$\begin{aligned} \frac{\mathrm {d}e}{\mathrm {d}r} = -\frac{k}{e}\,\frac{p}{r^2} =-\frac{k}{e}\,\frac{(1+k)^2}{p} \end{aligned}$$

  (110)
  $$\begin{aligned} \frac{\mathrm {d}e}{\mathrm {d}R} = \frac{q^2}{e\,R} =\frac{q\,\eta ^3}{e\,n\,p} \end{aligned}$$

  (111)
  $$\begin{aligned} \frac{\mathrm {d}e}{\mathrm {d}\Theta }= \eta ^3\frac{2k(1+k)+q^2}{e\,n\,p^2} \end{aligned}$$

  (112)

• Eccentricity function $\eta$:

  $$\begin{aligned} \frac{\mathrm {d}\eta }{\mathrm {d}r} = \frac{k}{\eta }\,\frac{p}{r^2} =\frac{k}{\eta }\,\frac{(1+k)^2}{p} \end{aligned}$$

  (113)
  $$\begin{aligned} \frac{\mathrm {d}\eta }{\mathrm {d}R} = -\frac{q^2}{\eta \,R} =-\frac{q\,\eta ^2}{n\,p} \end{aligned}$$

  (114)
  $$\begin{aligned} \frac{\mathrm {d}\eta }{\mathrm {d}\Theta } = -\eta ^2\frac{2k\,(1+k)+q^2}{n\,p^2} \end{aligned}$$

  (115)

• Semi-major axis a:

  $$\begin{aligned} \frac{\mathrm {d}a}{\mathrm {d}r} = -2\frac{k}{\eta ^4}\,(1+k)^2 \end{aligned}$$

  (116)
  $$\begin{aligned} \frac{\mathrm {d}a}{\mathrm {d}R}= 2\frac{p\,q^2}{R\,\eta ^4}=2\frac{q}{n\,\eta } \end{aligned}$$

  (117)
  $$\begin{aligned} \frac{\mathrm {d}a}{\mathrm {d}\Theta }= 2\frac{p^3}{\eta ^4\,\Theta \,r^2} =2\frac{(1+k)^2}{n\,p\,\eta } \end{aligned}$$

  (118)

• Mean motion n:

  $$\begin{aligned} \frac{\mathrm {d}n}{\mathrm {d}r} = \frac{3n\,k}{\eta ^2}\,\frac{(1+k)^2}{p} \end{aligned}$$

  (119)
  $$\begin{aligned} \frac{\mathrm {d}n}{\mathrm {d}R} = -\frac{3n\,q^2}{R\,\eta ^2}=-3\frac{q\,\eta }{p} \end{aligned}$$

  (120)
  $$\begin{aligned} \frac{\mathrm {d}n}{\mathrm {d}\Theta } = -\frac{3n\,p^2}{\eta ^2\,\Theta \,r^2} =-\frac{3\eta }{r^2} \end{aligned}$$

  (121)

• True anomaly f:

  $$\begin{aligned} \frac{\mathrm {d}f}{\mathrm {d}r} = \frac{q}{r}\,\frac{1+k}{e^2} \end{aligned}$$

  (122)
  $$\begin{aligned} \frac{\mathrm {d}f}{\mathrm {d}R} = \frac{q}{R}\,\frac{k}{e^2}\end{aligned}$$

  (123)
  $$\begin{aligned} \frac{\mathrm {d}f}{\mathrm {d}\Theta } = -\frac{q}{\Theta }\,\frac{2+k}{e^2} \end{aligned}$$

  (124)

• Eccentric anomaly u:

  $$\begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}r} = \frac{\eta }{pq}\left[ 1+\frac{e^2-k}{e^2}\frac{k}{\eta ^2}\,(1+k)\right] (1+k)\end{aligned}$$

  (125)
  $$\begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}R} = \frac{a\,n}{R}\left( -\frac{r-a}{r}\,\frac{\mathrm {d}e}{e\mathrm {d}R}-\frac{\mathrm {d}a}{a\mathrm {d}R}\right) \end{aligned}$$

  (126)
  $$\begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}\Theta } = \frac{a\,n}{R}\left( -\frac{r-a}{r}\,\frac{\mathrm {d}e}{e\mathrm {d}\Theta }-\frac{\mathrm {d}a}{a\mathrm {d}\Theta }\right) \end{aligned}$$

  (127)

• Equation of the center $\phi$:

  $$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}r} = \frac{q}{r}\left( \frac{1+k}{1+\eta }+\frac{\eta }{1+k}\right) \end{aligned}$$

  (128)
  $$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}R} = \frac{q}{R}\left( \frac{k}{1+\eta }+\frac{2\eta }{1+k}\right) \end{aligned}$$

  (129)
  $$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}\Theta } = -\frac{q}{\Theta }\,\frac{2+k}{1+\eta } \end{aligned}$$

  (130)

• Cosine of inclination c:

  $$\begin{aligned} \frac{\mathrm {d}c}{\mathrm {d}\Theta } = -\frac{c}{\Theta } =-\frac{c\,q}{R\,p} = -\frac{c\,\eta ^3}{n\,p^2} \end{aligned}$$

  (131)
  $$\begin{aligned} \frac{\mathrm {d}c}{\mathrm {d}N} = \frac{1}{\Theta } =\frac{q}{R\,p} =\frac{\eta ^3}{n\,p^2} \end{aligned}$$

  (132)

• Sine of inclination s:

  $$\begin{aligned} \frac{\mathrm {d}s}{\mathrm {d}\Theta } = \frac{c^2\,\eta ^3}{s\,n\,p^2} \end{aligned}$$

  (133)
  $$\begin{aligned} \frac{\mathrm {d}s}{\mathrm {d}N} = -\frac{c\,\eta ^3}{s\,n\,p^2} \end{aligned}$$

  (134)

Appendix B: Tables of coefficients

The coefficients of the trigonometric series used by HEOSAT are provided in following tables

Table 1 Eccentricity polynomials $Q_{m,k+m\bmod 2}$ in Eq. (27); $Q_{m,m-2}=1$, $Q_{m,m-4}=2m-6+3e^2$ and $Q_{6,0}=8 + 40 e^2 + 15 e^4$

Table 2 Even inclination polynomials $B_{2m,2k}$ in Eq. (27)

Table 3 Odd inclination polynomials $B_{2m+1,2k+1}$ in Eq. (27).

Table 4 Eccentricity polynomials $A_{m,j}$ in Eq. (38)

Table 5 Inclination polynomials $P_{m,j,l}$ in Eq. (38) ($\chi =c{\pm }\, 1$)

Table 6 Inclination polynomials $P_{5,j,l}$ in Eq. (38) ($\chi =c{\pm }\, 1$)

Table 7 Inclination polynomials $P_{6,j,l}$ in Eq. (38) ($\chi =c{\pm }\, 1$)

Table 8 Third-body direction polynomials in Eq. (38); $u\equiv {u}^\star$, $v\equiv {v}^\star$, $w\equiv {w}^\star$