Impact of heat and mass transport on Rayleigh–Taylor instability of Walter’s B viscoelastic fluid layer

Abstract

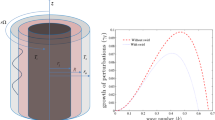
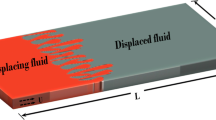
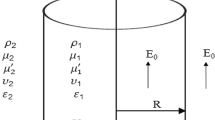
The behavior of viscous fluid-Walter’s B viscoelastic fluid interface in a planar configuration is investigated through an irrotational flow theory. The interface is transferring heat and mass from one fluid phase to the other. The viscoelastic fluid lies above the viscous fluid, and therefore, the interface is accepting the Rayleigh–Taylor instability. The linear stability theory is employed, and an explicit relationship between perturbation’s growth and wavenumber is established. The implicit stability criterion is achieved and analyzed numerically through the Newton–Raphson numerical scheme. The nature of the interface is examined for various non-dimensional parameters such as Atwood number, Weber number, Froude number, Reynolds number, etc. by means of stability plots. The results are discussed for the various values of gravitational acceleration through the variation of the Froude number. The instability is postponed if the interface experiences more heat transfer. Additionally, compared to the Walter's B fluid interface, the Newtonian fluid interface has proven to be more stable.

Appendices

Appendix A

The equation $y=\Upsilon (x,t)$ represents the interface position in the perturbed state and hence, the interface equation $f(x,y,t)=y-\Upsilon (x,t)=0$. Then the mass transfer Eq. (6) can be written as

$$\begin{array}{l}{\rho }_{w}\left(\frac{\partial f}{\partial t}+{V}_{w}\cdot \nabla f\right)={\rho }_{v}\left(\frac{\partial f}{\partial t}+{V}_{v}\cdot \nabla f\right)\\ \Rightarrow {\rho }_{w}\left(-\frac{\partial \Upsilon }{\partial t}+\left({{u}^{^{\prime}}}_{w},{{v}^{^{\prime}}}_{w}\right)\cdot \left(-\frac{\partial \Upsilon }{\partial x},1\right)\right)={\rho }_{v}\left(-\frac{\partial \Upsilon }{\partial t}+\left({{u}^{^{\prime}}}_{v},{{v}^{^{\prime}}}_{v}\right)\cdot \left(-\frac{\partial \Upsilon }{\partial x},1\right)\right)\\ \Rightarrow {\rho }_{w}\left(-\frac{\partial \Upsilon }{\partial t}-{{u}^{^{\prime}}}_{w}\frac{\partial \Upsilon }{\partial x}+{{v}^{^{\prime}}}_{w}\right)={\rho }_{v}\left(-\frac{\partial \Upsilon }{\partial t}-{{u}^{^{\prime}}}_{v}\frac{\partial \Upsilon }{\partial x}+{{v}^{^{\prime}}}_{v}\right).\end{array}$$

(A.1)

Retaining linear terms only, one can get Eq. (12) as

$${\rho }_{w}\left(-\frac{\partial \Upsilon }{\partial t}+{{v}^{^{\prime}}}_{w}\right)={\rho }_{v}\left(-\frac{\partial \Upsilon }{\partial t}+{{v}^{^{\prime}}}_{v}\right).$$

(A.2)

Appendix B

Equation (7) is given as

$$L{\rho }_{w}\left(\frac{\partial f}{\partial t}+\varvec{V}_{w}\cdot \nabla f\right)=H(y)=\frac{{\kappa }_{w}({T}_{w}-T)}{{h}_{w}-y}-\frac{{\kappa }_{v}(T-{T}_{v})}{{h}_{v}+y}$$

(B.1)

The interface in basic and perturbed states can be given as $y=0$, and $y=\Upsilon (x,t)$. In the perturbed state, the net heat flux is given as $H(y=\Upsilon )$, and expanding this term about $y=0$ through Taylor’s series expansion, we have

$$H(\Upsilon )=H(0)+\Upsilon {H}^{^{\prime}}(0)+\frac{{\Upsilon }^{2}}{2!}{H}^{^{\prime\prime} }(0)+..............$$

(B.2)

As in the basic state, the net heat flux is zero because the interface is taken in saturation state, and therefore,

$$H(0)=0\Rightarrow \frac{{\kappa }_{w}({T}_{w}-T)}{{h}_{w}}=\frac{{\kappa }_{v}(T-{T}_{v})}{{h}_{v}}=G$$

(B.3)

Hence, equation (B.1) becomes

$$\begin{array}{l}L{\rho }_{w}\left(\frac{\partial f}{\partial t}+\varvec{V}_{w}\cdot \nabla f\right)=H(y)=\frac{{\kappa }_{w}({T}_{w}-T)}{{h}_{w}-y}-\frac{{\kappa }_{v}(T-{T}_{v})}{{h}_{v}+y}\\ \Rightarrow L{\rho }_{w}\left(-\frac{\partial \Upsilon }{\partial t}+\left({{u}^{^{\prime}}}_{w},{{v}^{^{\prime}}}_{w}\right)\cdot \left(-\frac{\partial \Upsilon }{\partial x},1\right)\right)=\Upsilon {H}^{^{\prime}}(0)+\frac{{\Upsilon }^{2}}{2!}{H}^{^{\prime\prime} }(0)+..............\\ \Rightarrow L{\rho }_{w}\left(-\frac{\partial \Upsilon }{\partial t}-{{u}^{^{\prime}}}_{w}\frac{\partial \Upsilon }{\partial x}+{{v}^{^{\prime}}}_{w}\right)=\Upsilon {H}^{^{\prime}}(0)+\frac{{\Upsilon }^{2}}{2!}{H}^{^{\prime\prime} }(0)+..............\end{array}$$

(B.4)

Retaining only linear terms, one can get the Eq. (13) as

$$\begin{array}{l}L{\rho }_{w}\left(-\frac{\partial \Upsilon }{\partial t}+{{v}^{^{\prime}}}_{w}\right)=\Upsilon {H}^{^{\prime}}(0)\\ \Rightarrow {\rho }_{w}\left(-\frac{\partial \Upsilon }{\partial t}+{{v}^{^{\prime}}}_{w}\right)=\alpha \Upsilon ;\alpha =\frac{{H}^{^{\prime}}(0)}{L}\end{array}$$

(B.5)

Here ${H}^{^{\prime}}(0)={\left[{H}^{^{\prime}}(\Upsilon )\right]}_{\Upsilon =0}$ can be obtained as follows;

$$\begin{array}{l}H(\Upsilon )=\frac{{\kappa }_{w}({T}_{w}-T)}{{h}_{w}-\Upsilon }-\frac{{\kappa }_{v}(T-{T}_{v})}{{h}_{v}+\Upsilon }\Rightarrow {H}^{^{\prime}}(\Upsilon )=\frac{{\kappa }_{w}({T}_{w}-T)}{{\left({h}_{w}-\Upsilon \right)}^{2}}+\frac{{\kappa }_{v}(T-{T}_{v})}{{\left({h}_{v}+\Upsilon \right)}^{2}}\\ \Rightarrow {\left[{H}^{^{\prime}}(\Upsilon )\right]}_{\Upsilon =0}=\frac{{\kappa }_{w}({T}_{w}-T)}{{h}_{w}^{2}}+\frac{{\kappa }_{v}(T-{T}_{v})}{{h}_{v}^{2}}=G\left(\frac{1}{{h}_{w}}+\frac{1}{{h}_{v}}\right).\end{array}$$

(B.6)

Appendix C

The perturbed flow is considered as irrotational and therefore, ${\varvec{V}^{^{\prime}}}_{w}=\nabla {{\varphi }^{^{\prime}}}_{w},\varvec{V}_{v}=\nabla {{\varphi }^{^{\prime}}}_{v}$. The velocity components can be expressed as $({{u}^{^{\prime}}}_{w},{{v}^{^{\prime}}}_{w})=\left(\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial x},\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial y}\right)$, $({{u}^{^{\prime}}}_{v},{{v}^{^{\prime}}}_{v})=\left(\frac{\partial {{\varphi }^{^{\prime}}}_{v}}{\partial x},\frac{\partial {{\varphi }^{^{\prime}}}_{v}}{\partial y}\right)$. The momentum equations in Eq. (10) can be expressed in the irrotational flow as

$$\left.\begin{array}{ll}\text{X - momentum equation} &:{\rho }_{w}\left(\frac{\partial }{\partial t}\left(\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial x}\right)\right)=-\frac{\partial {{p}^{^{\prime}}}_{w}}{\partial x}\\ \text{Y - momentum equation} & :{\rho }_{w}\left(\frac{\partial }{\partial t}\left(\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial y}\right)\right)=-\frac{\partial {{p}^{^{\prime}}}_{w}}{\partial y}-{\rho }_{w}g\end{array}\right\}$$

(C.1)

Then, we obtain

$$\begin{array}{l}d{{p}^{^{\prime}}}_{w}=\frac{\partial {{p}^{^{\prime}}}_{w}}{\partial x}dx+\frac{\partial {{p}^{^{\prime}}}_{w}}{\partial y}dy\\ \Rightarrow d{{p}^{^{\prime}}}_{w}=-{\rho }_{w}\left(\frac{\partial }{\partial x}\left(\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial t}\right)\right)dx-{\rho }_{w}\left(\frac{\partial }{\partial y}\left(\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial t}\right)\right)dy-{\rho }_{w}gdy\\ \Rightarrow d{{p}^{^{\prime}}}_{w}=-{\rho }_{w}d\left(\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial t}\right)-{\rho }_{w}gdy\end{array}$$

(C.2)

Further, after integrating this equation, we can obtain.

$${{p}^{^{\prime}}}_{w}=-{\rho }_{w}\left(\frac{\partial {{\varphi }^{{^{\prime}}}}_{w}}{\partial t}\right)-{\rho }_{w}gy+{C}_{1}$$

(C.3)

In a similar fashion, we can obtain

$${{p}^{^{\prime}}}_{v}=-{\rho }_{v}\left(\frac{\partial {{\varphi }^{^{\prime}}}_{w}}{\partial t}\right)-{\rho }_{v}gy+{C}_{2}$$

(C.4)

In the basic state, the pressure was the same in both phases, and therefore, C₁ = C₂ and these constants will cancel out as we take the pressure difference. Hence, the gravitational acceleration will be included through pressure terms.