Reducing degradation and age of items in imperfect repair modeling

Abstract

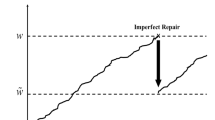
We develop new models for imperfect repair and the corresponding generalized renewal processes for stochastic description of repairable items that fail when their degradation reaches the specified deterministic or random threshold. The discussion is based on the recently suggested notion of a random virtual age and is applied to monotone processes of degradation with independent increments. Imperfect repair reduces degradation of an item on failure to some intermediate level. However, for the nonhomogeneous processes, the corresponding age reduction, which sets back the ‘clock’ of the process, is also performed. Some relevant stochastic comparisons are obtained. It is shown that the cycles of the corresponding generalized imperfect renewal process are stochastically decreasing/increasing depending on the monotonicity properties of the failure rate that describes the random failure threshold of an item.

Appendix

We first need some definitions and preliminary lemmas on multivariate stochastic orders.

Definition A1

Let ${\mathbf{X}}{ = (}X_{1} ,X_{2} ,\ldots,X_{n} )$ and ${\mathbf{Y}}{ = (}Y_{1} ,Y_{2} ,\ldots,Y_{n} )$ be two $n$-dimensional random vectors such that

$$ P({\mathbf{X}} \in U) \le P({\mathbf{Y}} \in U),\,{\text{for all upper sets}}\,U \subseteq {\mathbf{R}}^{n} . $$

Then, ${\mathbf{X}}$ is said to be smaller than ${\mathbf{Y}}$ in the usual stochastic order, denoted by ${\mathbf{X}} \le_{st} {\mathbf{Y}}$.

Lemma A1

(Shaked and Shanthikumar 2007) Let ${\mathbf{X}}{ = (}X_{1} ,X_{2} ,\ldots,X_{n} )$ and ${\mathbf{Y}}{ = (}Y_{1} ,Y_{2} ,\ldots,Y_{n} )$ be two $n$-dimensional random vectors. If

$$ X_{1} \le_{st} Y_{1} $$

and, for $i = 2,3,\ldots,n$

$(X_{i} |X_{1} = x_{1} ,X_{2} = x_{2} ,\ldots,X_{i - 1} = x_{i - 1} ) \le_{st} (Y_{i} |Y_{1} = y_{1} ,Y_{2} = y_{2} ,\ldots,Y_{i - 1} = y_{i - 1} )$ whenever $x_{j} \le y_{j}$, $j = 1,2,\ldots,i - 1$, then ${\mathbf{X}} \le_{st} {\mathbf{Y}}$.

Lemma A2

(Shaked and Shanthikumar 2007) Let ${\mathbf{X}}{ = (}X_{1} ,X_{2} ,\ldots,X_{n} )$ and ${\mathbf{Y}}{ = (}Y_{1} ,Y_{2} ,\ldots,Y_{n} )$ be two $n$ -dimensional random vectors. If ${\mathbf{X}} \le_{st} {\mathbf{Y}}$ and ${\mathbf{g}}$ : ${\mathbf{R}}^{n} \to {\mathbf{R}}^{k}$ is any $k$-dimensional increasing (decreasing) function, for any integer $k$, then the $k$-dimensional vectors ${\mathbf{g}}({\mathbf{X}})$ and ${\mathbf{g}}({\mathbf{Y}})$ satisfy ${\mathbf{g}}({\mathbf{X}}) \le_{st} ( \ge_{st} ){\mathbf{g}}({\mathbf{Y}})$ .

Theorem A1

Suppose that the distribution $G(x)$ is DFR, i.e., $\lambda_{L} (x)$ is decreasing in $x$ . Then,

$$ L_{1} \le_{st} L_{2} \le_{st} L_{3} \le_{st} \ldots. $$

Proof

First, we show $L_{1} <_{st} L_{2}$. Observe that

$$ P(L_{1} > w) = \overline{G}(w) = \exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (x){\rm d}x } \right\}, $$

whereas

$$ P(L_{2} > w|L_{1} = w_{1} ) = \overline{G}(w|qw_{1} ) = \exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (qw_{1} + x){\rm d}x}\right\} , $$

and $P(L_{2} > w) = E[P(L_{2} > w|L_{1} )]$. When $\lambda_{L} (x)$ is decreasing,

$$ P(L_{1} > w) \le P(L_{2} > w|L_{1} = w_{1} ),\,{\text{for }}\,{\text{all }}\,{\text{realization }}\,{\text{of}}\,w_{1} > 0,\,{\text{for all}}\,w > 0. $$

(A1)

This implies that $P(L_{1} > w) \le E[P(L_{2} > w|L_{1} )] = P(L_{2} > w)$, for all $w > 0$.

Observe that

$$ P(L_{3} > w|L_{1} = w_{1} ,L_{2} = w_{2} ) = \overline{G}(w|q(qw_{1} + w_{2} )) =\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q(qw_{1} + w_{2} ) + x){\rm d}x}\right\} . $$

Thus, $P(L_{3} > w|L_{1} = w_{1} ,L_{2} ) =\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{2} w_{1} + qL_{2} + x){\rm d}x}\right\} \ge\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (qL_{2} + x){\rm d}x }\right\}$, and

$$\begin{aligned}& P(L_{3} > w|L_{1} = w_{1} ) = E_{{(L_{2} |L_{1} = w_{1} )}} [P(L_{3} > w|L_{1} = w_{1} ,L_{2} )] \\ &\qquad\ge E_{{(L_{2} |L_{1} = w_{1} )}} \left[\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (qL_{2} + x){\rm d}x}\right\} \right ].\end{aligned} $$

On the other hand, $P(L_{2} > w) = E\left[\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (qL_{1} + x){\rm d}x }\right\} \right]$. As $L_{1} \le_{st} (L_{2} |L_{1} = w_{1} )$, for all realization of $w_{1} > 0$, due to Lemma 1-(i),(ii),

$$ P(L_{3} > w|L_{1} = w_{1} ) \ge E_{{(L_{2} |L_{1} = w_{1} )}} \left[\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (qL_{2} + x){\rm d}x}\right\} \right] $$

$\ge E\left[\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (qL_{1} + x){\rm d}x}\right\} \right] = P(L_{2} > w)$, for all realization of $w_{1} > 0$, for all $w > 0$,

which implies that $P(L_{3} > w) \ge P(L_{2} > w)$, for all $w > 0$.

In general, for $n = 3,4,\ldots$,

$$ \begin{aligned} & P(L_{n} > w|L_{1} = w_{1} ,L_{2} = w_{2} ,\ldots,L_{n - 1} = w_{n - 1} ) \\ &\quad = \exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{n - 1} w_{1} + q^{n - 2} w_{2} + \cdots + qw_{n - 1} + x){\rm d}x}\right\}\end{aligned} $$

and

$$ \begin{aligned} & P(L_{n + 1} > w|L_{1} = w_{1} ,L_{2} = w_{2} ,\ldots,L_{n} = w_{n} ) \\ &\quad =\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{n} w_{1} + q^{n - 1} w_{2} + \cdots + qw_{n} + x){\rm d}x}\right\} . \end{aligned} $$

Thus,

$$ P(L_{n} > w) = E_{{(L_{1} ,L_{2} \ldots,L_{n - 1} )}} \left[\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{n - 1} L_{1} + q^{n - 2} L_{2} + \cdots + qL_{n - 1} + x){\rm d}x}\right\} \right ] $$

and

$$ \begin{aligned} & P(L_{n + 1} > w|L_{1} \\ & \quad = w_{1} ) = E_{{(L_{2} ,L_{3} \ldots,L_{n} |L_{1} = w_{1} )}} [P(L_{n + 1} > w|L_{1} = w_{1} ,L_{2} ,L_{3} ,\ldots,L_{n} )] \\ &\quad \ge E_{{(L_{2} ,L_{3} \ldots,L_{n} |L_{1} = w_{1} )}} \left[\exp\left \{ - \int\limits_{0}^{w} {\lambda_{L} (q^{n - 1} L_{2} + \cdots + q^{2} L_{n - 1} + qL_{n} + x){\rm d}x}\right\} \right]. \\ \end{aligned} $$

Now we stochastically compare $(L_{1} ,L_{2} ,\ldots,L_{n - 1} )$ with $(L_{2} ,L_{3} ,\ldots,L_{n} |L_{1} = w_{1} )$. From (A1),

$$ L_{1} \le_{st} (L_{2} |L_{1} = w_{1} ). $$

Also,

$$ \begin{aligned} P(L_{i} > w|L_{1} & = w_{1} ,L_{2} = w_{2} ,\ldots,L_{i - 1} = w_{i - 1} ) \\ & =\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{i - 1} w_{1} + q^{i - 2} w_{2} + \cdots + qw_{i - 1} + x){\rm d}x}\right\} , \\ \end{aligned} $$

whereas

$$ \begin{aligned} P(V_{i} & > w|L_{1} = w_{1} ,V_{1} = v_{1} ,V_{2} = v_{2} ,\ldots,V_{i - 1} = v_{i - 1} ) \\ & =\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{i} w_{1} + q^{i - 1} v_{1} + \cdots + qv_{i - 1} + x){\rm d}x}\right\} , \\ \end{aligned} $$

where $V_{j} = L_{j + 1}$, $j = 1,2,\ldots$. Then, we have

$$ \begin{aligned} &\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{i - 1} w_{1} + q^{i - 2} w_{2} + \cdots + qw_{i - 1} + x){\rm d}x}\right\} \\ &\quad \le\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{i} w_{1} + q^{i - 1} v_{1} + \cdots + qv_{i - 1} + x){\rm d}x}\right\} , \end{aligned} $$

for all $w > 0$, whenever $w_{j} \le v_{j}$, $j = 1,2,\ldots,i - 1$, which implies that

$$\begin{aligned} & (L_{i} |L_{1} = w_{1} ,L_{2} = w_{2} ,\ldots,L_{i - 1} = w_{i - 1} ) \\ &\quad \le_{st} (V_{i} |L_{1} = w_{1} ,V_{1} = v_{1} ,V_{2} = v_{2} ,\ldots,V_{i - 1} = v_{i - 1} ), \end{aligned} $$

(A2)

whenever $w_{j} \le v_{j}$, $j = 1,2,\ldots,i - 1$. Inequality (A2) holds for all $i = 2,\ldots,n - 1$. Thus, by Lemma A1, $(L_{1} ,L_{2} ,\ldots,L_{n - 1} ) \le_{st} (V_{1} ,V_{2} ,\ldots,V_{n - 1} |L_{1} = w_{1} )$ and thus

$$ (L_{1} ,L_{2} ,\ldots,L_{n - 1} ) \le_{st} (L_{2} ,L_{3} ,\ldots,L_{n} |L_{1} = w_{1} ). $$

(A3)

Observe that

$$ h(w_{1} ,w_{2} ,\ldots,w_{n - 1} ) =\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{n - 1} w_{1} + q^{n - 2} w_{2} + \ldots + qw_{n - 1} + x){\rm d}x}\right\} $$

is an increasing function of $(w_{1} ,w_{2} ,\ldots,w_{n - 1} )$. Then, from (A3) and Lemma A3,

$$ \begin{aligned} P(L_{n} > w) & = E_{{(L_{1} ,L_{2} \ldots,L_{n - 1} )}} \left[ {\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{n - 1} L_{1} + q^{n - 2} L_{2} + \ldots + qL_{n - 1} + x){\rm d}x}\right\} } \right] \\ & \le E_{{(L_{2} ,L_{3} \ldots,L_{n} |L_{1} = w_{1} )}} \left[\exp \left\{ - \int\limits_{0}^{w} {\lambda_{L} (q^{n - 1} L_{2} + \cdots + q^{2} L_{n - 1} + qL_{n} + x){\rm d}x}\right\} \right] \\ &\le P(L_{n + 1} > w|L_{1} = w_{1} ), \\ \end{aligned} $$

for all realization of $w_{1} > 0$, for all $w > 0$. This again implies that

$$ P(L_{n} > w) \le P(L_{n + 1} > w),\,{\text{ for }}\,{\text{all}}\,w > 0. $$

Therefore, we have shown that $P(L_{n} > w) \le P(L_{n + 1} > w)$, for all $n = 1,2,\ldots$

■

Theorem A2

Suppose that the distribution $G(x)$ is DFR, i.e., $\lambda_{L} (x)$ is decreasing in $x$ . Then,

$$ Z_{1} \le_{st} Z_{2} \le_{st} Z_{3} \le_{st} \ldots. $$

Proof

It is obvious that $Z_{1} \le_{st} Z_{2}$. In the proof of Theorem A1, we have shown that

$$ (L_{1} ,L_{2} , \ldots ,L_{n} ) \le_{st} (L_{2} ,L_{3} , \ldots ,L_{n + 1} |L_{1} = w_{1} ). $$

Furthermore,

$$ h(w_{1} ,w_{2} ,\ldots,w_{n - 1} ) = q^{n - 1} w_{1} + q^{n - 2} w_{2} + \cdots + q^{{}} w_{n - 1} $$

is an increasing function of $(w_{1} ,w_{2} ,\ldots,w_{n - 1} )$. Then, from Lemma A2,

$$ \begin{aligned}&q^{n-1}L_1+ q^{n-2}L_2+\cdots+qL_{n-1}\le_{st} (q^{n-1}L_2+q^{n-2}L_3+\cdots+qL_n|L_1=w_1 )\\ &\quad\le_{st} (q^{n}w_1+q^{n-1}L_2+q^{n-2}L_3+\cdots+qL_n|L_1=w_1 )\end{aligned}$$

which implies that $Z_{n} \le_{st} (Z_{n + 1} |L_{1} = w_{1} )$, for all realizations of $w_{1}$. Therefore, we have

$$ Z_{n} \le_{st} Z_{n + 1} ,\,n = 1,2,\ldots $$

■