On sums of dependent random lifetimes under the time-transformed exponential model

Abstract

For a given pair of random lifetimes whose dependence is described by a time-transformed exponential model, we provide analytical expressions for the distribution of their sum. These expressions are obtained by using a representation of the joint distribution in terms of bivariate distortions, which is an alternative approach to the classical copula representation. Since this approach allows one to obtain conditional distributions and their inverses in simple form, then it is also shown how it can be used to predict the value of the sum from the value of one of the variables (or vice versa) by using quantile regression techniques.

1 Introduction

Let ${\mathbf {X}}=(X_1,X_2)$ be a pair of dependent lifetimes. The vector ${\mathbf {X}}$ is said to be described by a time-transformed exponential model (shortly, TTE model) if its joint survival function ${\bar{\mathbf {F}}}(x_1,x_2)=\Pr (X_1>x_1,X_2>x_2)$ can be written as

$$\begin{aligned} {\bar{\mathbf {F}}}(x_1,x_2)={\bar{G}}(R_1(x_1)+R_2(x_2)), \ x_1,x_2 \ge 0, \end{aligned}$$

(1.1)

for a suitable one-dimensional, continuous, convex and strictly decreasing survival function $\bar{G}$ and two suitable continuous and strictly increasing functions $R_i:[0,+\infty )\rightarrow [0,+\infty )$ such that $R_i(0)=0$ and $\lim _{x\rightarrow \infty }R_i(x)=\infty$, for $i=1,2$. Clearly, the marginal survival functions for the lifetimes $X_i$ are given by $\bar{F}_i(x_i)=\bar{G}(R_i(x_i))$, $x_i \ge 0$, $i=1,2$.

TTE models have been considered in the literature as an appropriate manner to describe bivariate lifetimes (see, e.g., Bassan and Spizzichino (2005), Mulero et al. (2010), Navarro and Mulero (2020) and references therein). Their main characteristic is that they “separate", in a sense, aging of single lifetimes through the functions $R_i$, and dependence properties through $\bar{G}$, being the corresponding survival copula a transformation of ${\bar{G}}$ only (see Eq. (2.2) below and the references above for definition of the copula). This model is of interest in a variety of fields of application, given that it is equivalent to the random frailty model, which assumes that the two lifetimes are conditionally independent given a random parameter that represents the risk due to a common environment. The well-known proportional hazard rate Cox model, where the proportional factor is not fixed but random, is an example. In this case, the different choices for the function $\bar{G}$ are obtained just by changing the distribution of the random risk parameter. This dependence model is also equivalent to consider the wide family of strict Archimedean survival copulas. Moreover, it contains the model recently proposed in Genest and Kolev (2021) and the Schur constant model.

For a number of applicative purposes, one can be interested in the sum $S=X_1+X_2$. This happens, for example, in considering the total lifetime in stand-by systems, where a component is replaced by a new one under the same environmental stress after its failure, or in insurance theory, where the sum of two dependent claims, due to common risks, may be evaluated. In this case, because of the dependence between $X_1$ and $X_2$, the classical convolution cannot be applied to determine the distribution of S, and C-convolutions (whose definition is recalled in the next section) must be used instead. But in some cases, like for the one considered here, the integrals appearing in formulas for C-convolutions are not easy to be solved, especially when a simple expression of the copula is not available.

The aim of this paper is to provide an alternative tool to deal with the sum $S=X_1+X_2$ that can be used when the joint distribution of ${\mathbf {X}}$ is defined as in Eq. (1.1). This approach is based on a different representation for the survival function of ${\mathbf {X}}$, which makes use of the distortion representations of multivariate distributions recently introduced in Navarro et al. (2022), whose definition is provided in the next section. The advantage of this approach is twofold. On the one hand, it is particularly useful when the inverse of ${\bar{G}}$ is not available in closed form, thus also ${\widehat{C}}$. On the other hand, it provides simple representations of the conditional distribution of S given one of the $X_i$, and of its inverse, so that one can use it to predict the value of the sum from the value of one of the variables (or vice versa) by using quantile regression techniques. The purpose of this paper is to describe such an approach.

The rest of the paper is structured as follows. Basic definitions, notations and some preliminary results are introduced in Sect. 2. The main results for the representation of the distribution of the sum S under model (1.1) are provided in Sect. 3, while the expressions for predictions and examples of their application are presented in Sects. 4 and 5, respectively.

Throughout the paper the notions increasing and decreasing are used in a wide sense, that is, they mean non-decreasing and non-increasing, respectively, and we say that f is increasing (decreasing) if $f({\mathbf {x}})\le f({\mathbf {y}})$ for all ${\mathbf {x}}\le {\mathbf {y}}$ (where this last inequality means that for every ith component of the vectors one has $x_i\le y_i$). Also, if f is a real-valued function in more than one variable, then $\partial _i f$ denotes the partial derivative of f with respect to its ith variable. Analogously, $\partial _{i,j} f=\partial _i \partial _j f$ and so on. Whenever we use a partial derivative we are tacitly assuming that it exists.

2 Notation and preliminary results

To simplify the notation we just consider here the bivariate case; the extension to the n-dimensional case is straightforward.

Thus, let ${\mathbf {X}}=(X_1,X_2)$ be a random vector with two possibly dependent nonnegative random variables having an absolutely continuous joint distribution function ${\mathbf {F}}$ and marginal distributions $F_1$ and $F_2$. Let ${\mathbf {f}}$ be the joint probability density function (PDF) of $(X_1,X_2)$ and let $f_1$ and $f_2$ be the PDFs of $X_1$ and $X_2$, respectively. Then it is well known (see, e.g., Nelsen 2006) that, from Sklar’s Theorem, there exists a unique absolutely continuous copula C such that ${\mathbf {F}}$ can be written as

$$\begin{aligned} {\mathbf {F}}(x_1,x_2)=\Pr (X_1\le x_1,X_2\le x_2)=C(F_1(x_1), F_2(x_2)) \end{aligned}$$

(2.1)

for all $x_1,x_2$. The copula of a random vector (which is the joint distribution of a vector having univariate marginal distributions) entirely describes the dependence between the components of the vector, as extensively pointed out in the monograph Nelsen (2006) (see also Navarro et al. (2021)), for a recent survey on how to describe different dependence notions of a random vector in terms of the properties of the corresponding copula).

As a consequence of (2.1), the PDF function of $(X_1,X_2)$ can be expressed as

$$\begin{aligned} {\mathbf {f}}(x_1,x_2)=f_1(x_1)f_2(x_2)c(F_1(x_1), F_2(x_2)), \end{aligned}$$

where $c:=\partial _{1,2}C$ is the PDF of the copula C. A similar representation holds for the joint survival function

$$\begin{aligned} {\bar{\mathbf {F}}}(x_1,x_2)=\Pr (X_1>x_1,X_2>x_2)={\widehat{C}}({\bar{F}}_1(x_1),{\bar{F}}_2(x_2)) \end{aligned}$$

for all $x_1,x_2$, where ${\bar{F}}_1(x_1)=\Pr (X_1>x_1)$ and ${\bar{F}}_2(x_2)=\Pr (X_2>x_2)$ are the marginal survival functions and ${\widehat{C}}$ is another suitable copula, called survival copula. We observe that from a mathematical viewpoint, both the connecting copula C and the survival copula ${\widehat{C}}$ can be used to describe the dependence structure of $(X_1,X_2)$.

In the particular case of TTE models, i.e., when the joint survival function ${\bar{\mathbf {F}}}$ is defined as in Eq. (1.1), then the corresponding survival copula ${\widehat{C}}$ is defined as

$$\begin{aligned} {\widehat{C}}(u_1,u_2)={\bar{G}}({\bar{G}}^{-1}(u_1)+{\bar{G}}^{-1}(u_2)) \ \end{aligned}$$

(2.2)

for all $u_1,u_2 \in [0,1]^2$, which is a strict bivariate Archimedean copula [see, e.g., McNeil and Nešlehová (2009), Nelson (2006, p. 112)]. This wide model contains many families of copulas [(see Nelson (2006, p. 117)], thus it is a very general dependence model. The inverse function ${\bar{G}}^{-1}$ is called the additive generator of the copula.

Given a vector $(X_1,X_2)$, consider now the sum $S=X_1+X_2$. When $X_1$ and $X_2$ are dependent then one can calculate the survival function of S by means of the C-convolution, i.e., as

$$\begin{aligned} \bar{F}_S(s)=\Pr (S>s)= \int _{-\infty }^{\infty } f_1(x)\ \partial _{1}{\widehat{C}}({\bar{F}}_1(x),{\bar{F}}_2(s-x))dx, \ s\in {\mathbb {R}}, \end{aligned}$$

(2.3)

where ${\bar{F}}_1$ and ${\bar{F}}_2$ are the marginal survival functions of $X_1$ and $X_2$, respectively, $f_1$ is the density function of $X_1$ (assuming its existence) and ${\widehat{C}}$ is the survival copula of the vector $\mathbf {{\mathbf {X}}}$. This expression, obtained in Cherubini et al. (2011), is a key tool in our results (see, also Cherubini et al. (2016) and Navarro and Sarabia (2020), for additional examples of C-convolutions).

Note that the integral appearing in Eq. (2.3) cannot be solved analytically in many cases, especially when the expression of ${\widehat{C}}$ is complicate, or, as an extreme case, when its expression is not available. This is the case, for example, of a copula defined as in (2.2) when the inverse ${\bar{G}}^{-1}$ cannot be expressed in closed form. In this case an alternative approach for the computation of the survival function of S must be considered. The alternative approach suggested here is based on the representation of ${\bar{\mathbf {F}}}$ through the distortion representations of multivariate distributions introduced in the recent paper (Navarro et al. 2022).

For it first recall that a function $d:[0,1]\rightarrow [0,1]$ is said to be a distortion function if it is continuous, increasing and satisfies $d(0)=0$ and $d(1)=1$. If G is a distribution function, we say that F is a distorted distribution from G if there exists a distortion function d such that $F(x)=d(G(x))$ for all x, and similarly for the survival functions. This kind of representations were introduced in the theory of decision under risk (see, e.g., Wang (1996); Yaari (1987)) and they were also applied in the fields of coherent systems, order statistics and conditional distributions (see, e.g., Navarro et al. (2013) and Navarro and Sordo (2018), and the references therein).

These representations were further extended to the multivariate case in Navarro et al. (2022). According to what is defined there, and restricting to the bivariate case, a function $D:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ is a bivariate distortion if it is a continuous 2-dimensional distribution with support included in $[0,1]^2$, and a bivariate distribution function ${\mathbf {F}}$ is a distortion of the univariate distribution functions $H_1$ and $H_2$ if there exists a bivariate distortion D such that

$$\begin{aligned} {\mathbf {F}}(x_1,x_2)=D(H_1(x_1),H_2(x_2)) \end{aligned}$$

(2.4)

for all $x_1,x_2$. This representation is similar to the copula representation, but here $H_1$ and $H_2$ are not necessarily the marginal distributions of ${\mathbf {X}}$ and D is not necessarily a copula. Actually, in some situations, we can choose a common univariate distribution $H=H_1=H_2$. Some examples will be provided later (see also Navarro (2021); Navarro et al. (2022)). Moreover, if D has uniform univariate marginal distributions over the interval (0, 1), then D is a copula, $H_1$ and $H_2$ are the marginal distributions and (2.4) is the same as the copula representation (2.1) (but only in this case).

The main properties of the model given in (2.4) were provided in Navarro et al. (2022) and they are very similar to that of copulas. For example, if D is a distortion function, then the right-hand side of (2.4) defines a proper multivariate distribution function for any univariate distribution functions $H_1$ and $H_2$. Moreover, a similar representation holds for the joint survival function, that is, one can write

$$\begin{aligned} {\bar{\mathbf {F}}}(x_1,x_2)={\widehat{D}}({\bar{H}}_1(x_1),{\bar{H}}_2(x_2)), \end{aligned}$$

(2.5)

where ${\bar{\mathbf {F}}}(x_1,x_2)=\Pr (X_1>x_1,X_2>x_2)$, ${\bar{H}}_i=1-H_i$ for $i=1,2$, and ${\widehat{D}}$ is another suitable distortion function.

For the TTE model note that, defining

$$\begin{aligned} {\bar{H}}_i(x_i)=\exp (-R_i(x_i)), \ i=1,2, \end{aligned}$$

(2.6)

one has

$$\begin{aligned} {\bar{\mathbf {F}}}(x_1,x_2)={\bar{G}}(R_1(x_1)+R_2(x_2)) ={\widehat{D}}({\bar{H}}_1(x_1),{\bar{H}}_2(x_2)) \end{aligned}$$

for all $x_1,x_2 \ge 0$, where

$$\begin{aligned} {\widehat{D}}(u,v)={\bar{G}}(-\ln (uv)), \ \ {u,v \in (0,1]} \end{aligned}$$

(2.7)

and ${\widehat{D}}(u,v)=0$ for $u=0$ or $v=0$. The function ${\widehat{D}}$ satisfies the property to be a bivariate distortion if ${\bar{G}}$ satisfies the properties mentioned above, i.e., when ${\bar{G}}$ is an absolutely continuous strictly decreasing and strictly convex function in $[0,\infty )$ with ${\bar{G}}(0)=1$ and ${\bar{G}}(\infty )=0$. Note that if we add ${\bar{G}}(t)=1$ for $t<0$, then ${\bar{G}}$ is the survival function of a nonnegative random variable. Also note that ${\bar{H}}_1$ and ${\bar{H}}_2$ are two arbitrary survival functions satisfying ${\bar{H}}_1(0)={\bar{H}}_2(0)=1$. Thus, a representation through bivariate distortions as in (2.4) holds for the TTE model, with ${\widehat{D}}$ defined as in (2.7). Even more, note that our model can be used to extend the TTE model by considering also reliability functions ${\bar{H}}_1$ and ${\bar{H}}_2$ with bounded support. In particular, if we choose ${\bar{H}}_1(x)={\bar{H}}_2(x)=1-x$ for $x\in [0,1]$, then $(X_1,X_2)$ has support $[0,1]^2$ and the joint distribution of $(1-X_1,1-X_2)$ is ${\hat{D}}$. However, in any case, the support of the reliability function ${\bar{G}}$ should be $(0,\infty )$.

It must be pointed out that with this representation the marginal survival functions ${\bar{F}}_i, i=1,2,$ are not explicitly displayed, but can be obtained as

$$\begin{aligned} {\bar{F}}_i(x_i)={\bar{G}}(-\ln {\bar{H}}_i(x_i))={\widehat{D}}({\bar{H}}_i(x_i),1)={\widetilde{d}}({\bar{H}}_i(x_i)), \ \ x_i \ge 0, \end{aligned}$$

where ${\widetilde{d}}(u)={\bar{G}}(-\ln u)$ for $u \in (0,1]$ and ${\widetilde{d}}(0)=0$. Note that ${\widetilde{d}}$ is a univariate distortion function. Finally, note that the representation through the multivariate distortion (2.7) and the univariate survivals (2.6) is a copula representation if and only if ${\widehat{D}}(u,1)=u,$ that is, ${\bar{G}}(-\ln (u))=u$ for $0\le u\le 1$. This property leads to ${\bar{G}}(x)=\exp (-x)$ for $x\ge 0$ and ${\widehat{D}}(u,v)=uv$ for $u,v\in [0,1]$ which is the product copula that represents the independence case. For other (non-exponential) survival functions ${\bar{G}}$, we obtain models with dependent variables, whose dependence is described by ${\bar{G}}$ (i.e., by the Archimedean survival copula obtained from ${\bar{G}}$ given in (2.2)).

As an interesting particular case, this dependence model includes the one recently proposed by Genest and Kolev (2021) for nonnegative random variables, which is characterized by the joint survival function

$$\begin{aligned} {\bar{\mathbf {F}}}(x_1,x_2)={\bar{G}} (\alpha x_1+\beta x_2) \end{aligned}$$

(2.8)

for $x_1,x_2\ge 0$, where $\alpha ,\beta >0$ are two positive scale parameters and ${\bar{G}}$ satisfies the above mentioned properties [see Proposition 3.1 in Genest and Kolev (2021)]. This model that from now on will be referred as GK-model [where the letters G and K refer to the initials of the authors of reference Genest and Kolev (2021)]. This model is an extension of the well-known Schur-constant model which is obtained when $\alpha =\beta$ (see Caramellino and Spizzichino (1994), and references therein). Properties of the Schur-constant model and of the corresponding sum $X_1+X_2$ are studied also in Pellerey and Navarro (2021). The GK-model represents distributions satisfying the so-called law of uniform seniority of dependent lives (see Genest and Kolev 2021). It must be observed that the marginal survival functions are ${\bar{F}}_1(x_1)={\bar{G}}(\alpha x_1)$ and ${\bar{F}}_2(x_2)={\bar{G}}(\beta x_2)$ for $x_1,x_2\ge 0$, and both of them belong to the scale parameter model defined by ${\bar{G}}$. Actually, this model is obtained by the distortion of univariate exponential distributions, i.e., (2.8) holds if and only if

$$\begin{aligned} {\bar{\mathbf {F}}}(x_1,x_2)={\widehat{D}}({\bar{H}}_1(x_1),{\bar{H}}_2(x_2) ) \end{aligned}$$

for all $x_1,x_2\ge 0$, where ${\bar{H}}_1(x_1)=\exp (-\alpha x_1)$, ${\bar{H}}_2(x_2)=\exp (-\beta x_2)$ and ${\widehat{D}}$ is defined as in Eq. (2.7).

3 Joint and conditional distributions of the sum

In this section we use the distortion representation (2.5), with the bivariate distortion ${\widehat{D}}$ defined as in (2.7), to study the sum $S=X_1+X_2$ under the dependence model defined in the preceding section. As a consequence, we also obtain analogous properties for the GK-model, i.e., the generalization (2.8) of the Schur-constant model.

Proposition 3.1

If (2.5) and (2.7) hold for $(X_1,X_2)$ and $S=X_1+X_2$, then the joint PDF of $(X_1, S)$ is

$$\begin{aligned} {\mathbf {g}}(x,s)=r_1(x)r_2(s-x) {\bar{G}}''\left( -\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x)\right) \end{aligned}$$

(3.1)

for $0\le x\le s$ (zero elsewhere), where $r_i=(-\ln {\bar{H}}_i)'$ is the hazard rate function of ${\bar{H}}_i$ for $i=1,2$.

Proof

From (2.5), the joint PDF of $(X_1,X_2)$ is

$$\begin{aligned} {\mathbf {f}}(x_1,x_2)=h_1(x_1)h_2(x_2){\widehat{d}}({\bar{H}}_1(x_1),{\bar{H}}_2(x_2)) \end{aligned}$$

for $x_1,x_2\ge 0$, where $h_i=-{\bar{H}}_i'$ and ${\widehat{d}}=\partial _{1,2}{\widehat{D}}$. Then the joint PDF of $(X_1,S)$ is

$$\begin{aligned} {\mathbf {g}}(x,s)={\mathbf {f}}(x,s-x)=h_1(x)h_2(s-x){\widehat{d}}({\bar{H}}_1(x),{\bar{H}}_2(s-x)) \end{aligned}$$

for $0\le x\le s$. The PDF of our specific distortion function ${\widehat{D}}$ is

$$\begin{aligned} {\widehat{d}}(u,v)=\frac{1}{uv} {\bar{G}}''(-\ln (uv)) \end{aligned}$$

and

$$\begin{aligned} {\mathbf {g}}(x,s)=\frac{h_1(x)h_2(s-x)}{{\bar{H}}_1(x){\bar{H}}_2(s-x)} {\bar{G}}''\left( -\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x)\right) \end{aligned}$$

for $0\le x\le s$, which concludes the proof. $\square$

Remark 1

In particular, for the GK-model in (2.8), that is, with exponential survival functions $H_1$ and $H_2$ with shape parameters (hazard rates) $\alpha$ and $\beta$, the PDF reduces to

$$\begin{aligned} {\mathbf {g}}(x,s)=\alpha \beta {\bar{G}}''( (\alpha -\beta )x+\beta s ) \end{aligned}$$

for $0\le x\le s$ (zero elsewhere). Therefore, its joint distribution function is

$$\begin{aligned} {\mathbf {G}}(x,s)&=-\int _0^x \int _y^s \alpha \beta G''( (\alpha -\beta )y+\beta t )dtdy\\&= \int _0^x \alpha G'( \alpha y )dy-\int _0^x \alpha G'( (\alpha -\beta )y+\beta s )dy \end{aligned}$$

where $G=1-{\bar{G}}$. To solve this integral we consider two cases. If $\alpha =\beta$, then

$$\begin{aligned} {\mathbf {G}}(x,s)&= G(\alpha x)-\alpha x G'( \alpha s ), \end{aligned}$$

(3.2)

while if $\alpha \ne \beta$, then

$$\begin{aligned} {\mathbf {G}}(x,s)&=G(\alpha x)-\frac{\alpha }{\alpha -\beta } G ((\alpha -\beta )x+\beta s )+ \frac{\alpha }{\alpha -\beta } G(\beta s ) \end{aligned}$$

(3.3)

for $0\le x\le s$. In both cases, (3.2) and (3.3) can be represented as distorted distributions from G by replacing x with $G^{-1}(G(x))$ and s with $G^{-1}(G(s))$.

In particular, as an immediate consequence one can obtain the distribution of the sum (C-convolution) for the GK-model as

$$\begin{aligned} F_S(s)=\lim _{x\rightarrow \infty }{\mathbf {G}}(x,s)={\mathbf {G}}(s,s). \end{aligned}$$

If $\alpha =\beta$, then

$$\begin{aligned} F_S(s)= G(\alpha s)-\alpha s G'( \alpha s ), \end{aligned}$$

or if $\alpha \ne \beta$, then

$$\begin{aligned} F_S(s)= \frac{\alpha }{\alpha -\beta } G(\beta s )-\frac{\beta }{\alpha -\beta } G (\alpha s ) \end{aligned}$$

for $s\ge 0$. Note that the second expression is a negative mixture (i.e., a linear combination with a negative weight) of the distribution functions of $X_1$ and $X_2$ with PDF

$$\begin{aligned} f_S(s)=\frac{\alpha \beta }{\beta -\alpha } \left[ g (\alpha s )-g(\beta s )\right] \end{aligned}$$

(3.4)

for $s\ge 0$, where $g=G'$. In the first case, one gets

$$\begin{aligned} f_S(s)= -\alpha ^2 s G'' (\alpha s) \end{aligned}$$

(3.5)

for $s\ge 0$, which is the expression in Remark 2.7 of Caramellino and Spizzichino (1994) (i.e., for the Schur-constant model).

The joint survival function of $(X_1, S)$ under the model defined by (2.5) and (2.7) is obtained in the following proposition. Unfortunately, an explicit expression cannot be provided in general, but it is available in some cases, or easily available numerically (see the examples in the next sections).

Proposition 3.2

If (2.5) and (2.7) hold for $(X_1,X_2)$ and $S=X_1+X_2$, then the joint survival function of $(X_1, S)$ is

$$\begin{aligned} {\bar{\mathbf {G}}}(x,s)={\bar{G}}(-\ln {\bar{H}}_1(s) )+\int _x^s r_1(y) g\left( -\ln {\bar{H}}_1(y)-\ln {\bar{H}}_2(s-y)\right) dy \end{aligned}$$

for $0\le x\le s$, where $g=-{\bar{G}}'$ is the PDF of ${\bar{G}}$ and $r_i=(-\ln {\bar{H}}_i)'$ is the hazard rate function of ${\bar{H}}_i$ for $i=1,2$.

Proof

From Eq. (3.1) for the PDF of $(X_1, S)$ we get

$$\begin{aligned} {\bar{\mathbf {G}}}(x,s)&=\int _x^s \int _s^\infty {\mathbf {g}}(y,t) dtdy+ \int _s^\infty \int _y^\infty {\mathbf {g}}(y,t)dtdy\\&=\int _x^s \int _s^\infty r_1(y)r_2(t-y) {\bar{G}}''(-\ln {\bar{H}}_1(y)-\ln {\bar{H}}_2(t-y))dtdy\\&\quad +\int _s^\infty \int _y^\infty r_1(y)r_2(t-y) {\bar{G}}''(-\ln {\bar{H}}_1(y)-\ln {\bar{H}}_2(t-y))dt dy\\&=-\int _x^s r_1(y) {\bar{G}}'(-\ln {\bar{H}}_1(y)-\ln {\bar{H}}_2(s-y))dy -\int _s^\infty r_1(y) {\bar{G}}'(-\ln {\bar{H}}_1(y))dy\\&={\bar{G}}(-\ln {\bar{H}}_1(s) )+\int _x^s r_1(y) g(-\ln {\bar{H}}_1(y)-\ln {\bar{H}}_2(s-y))dy, \end{aligned}$$

which concludes the proof. $\square$

Therefore, the survival function of S can be obtained as

$$\begin{aligned} {\bar{F}}_S(s)={\bar{\mathbf {G}}}(0,s)= & {} {\bar{G}}(-\ln {\bar{H}}_1(s) )\nonumber \\&+\int _0^s r_1(y)g\left( -\ln {\bar{H}}_1(y)-\ln {\bar{H}}_2(s-y)\right) dy \end{aligned}$$

(3.6)

and its PDF as $f_S(s)=- \partial _2 {\bar{\mathbf {G}}}(0,s), \ s \ge 0$.

To get the explicit expression for ${\bar{F}}_S$ we need to explicate ${\bar{G}}$ and/or ${\bar{H}}_i$ and to solve this integral, eventually numerically. For example, if ${\bar{H}}_i(x)=\exp (-x)$ for $x\ge 0$ and $i=1,2$, then

$$\begin{aligned} {\bar{F}}_S(s)={\bar{\mathbf {G}}}(0,s)={\bar{G}}(s)+\int _0^s g(y+s-y)dy={\bar{G}}(s)+ sg(s) \end{aligned}$$

and $f_S(s)=sg'(s)$ for $s\ge 0$ which is the expression in Remark 2.7 of Caramellino and Spizzichino (1994) for the Schur-constant model.

4 Predictions

The aim of this section is to show how to predict the value of the sum $S=X_1+X_2$ from $X_1=x$ or vice versa by making use of the results in the previous section. To this purpose we need the conditional distribution of $(S\mid X_1=x)$ in the TTE dependence model, that is obtained in the following proposition.

Proposition 4.1

If (2.5) and (2.7) hold for $(X_1,X_2)$ and $S=X_1+X_2$, then the PDF of $( S\mid X_1=x)$ is

$$\begin{aligned} f_{S\mid X_1}(s\mid x)=-r_2(s-x)\frac{ g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))}{g(-\ln {\bar{H}}_1(x))} \end{aligned}$$

and its distribution function is

$$\begin{aligned} F_{S\mid X_1}(s\mid x) =1-\frac{ g(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))}{g(-\ln {\bar{H}}_1(x))} \end{aligned}$$

(4.1)

for $0\le x\le s$, where $g=-{\bar{G}}'$ and $r_2=(-\ln {\bar{H}}_2)'$ is the hazard rate function of ${\bar{H}}_2$.

Proof

From (3.1), the PDF of $(X_1,S)$ is

$$\begin{aligned} {\mathbf {g}}(x,s)=-r_1(x)r_2(s-x) g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x)) \end{aligned}$$

for $0\le x\le s$. Moreover, the first marginal survival function is

$$\begin{aligned} {\bar{F}}_1(x)=\Pr (X_1>x)={\mathbf {G}}(x,0)={\bar{G}}(-\ln {\bar{H}}_1(x)) \end{aligned}$$

and its PDF is $f_1(x)=r_1(x)g(-\ln {\bar{H}}_1(x))$, for $x\ge 0$.

Hence, the PDF of $(S\mid X_1=x)$ for $x\ge 0$ such that $f_1(x)>0$ can be obtained as

$$\begin{aligned} f_{S\mid X_1}(s\mid x)=\frac{{\mathbf {g}}(x,s)}{f_1(x)}=-r_2(s-x)\frac{ g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))}{g(-\ln {\bar{H}}_1(x))} \end{aligned}$$

for $s\ge x$ (zero elsewhere).

Then the associated distribution function is

$$\begin{aligned} F_{S\mid X_1}(s\mid x)&=\int _{x}^s f_{S\mid X_1}(t\mid x)dt\\&=-\int _{x}^s r_2(t-x)\frac{ g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(t-x))}{g(-\ln {\bar{H}}_1(x))}dt\\&=\left[ -\frac{ g(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(t-x))}{g(-\ln {\bar{H}}_1(x))}\right] _{t=x}^s\\&=1-\frac{ g(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))}{g(-\ln {\bar{H}}_1(x))} \end{aligned}$$

for $s\ge x\ge 0$ and we conclude the proof. $\square$

Hence, the conditional survival function is

$$\begin{aligned} {\bar{F}}_{S\mid X_1}(s\mid x) =\frac{ g(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))}{g(-\ln {\bar{H}}_1(x))} \end{aligned}$$

Clearly, this is a distortion representation from ${\bar{H}}_2(s-x)$, since

$$\begin{aligned} {\bar{F}}_{S\mid X_1}(s\mid x)=d_{S\mid X_1}({\bar{H}}_2(s-x)\mid {\bar{H}}_1(x)) \end{aligned}$$

for $s\ge x>0$, where

$$\begin{aligned} d_{S\mid X_1}(v\mid u)=\frac{ g(-\ln uv) }{g(-\ln u)} \end{aligned}$$

for $v\in [0,1]$ is a distortion function for all $0<u<1$.

Note that the inverse function of $\bar{F}_{S\mid X_1}$ can be obtained from the inverse functions of g and ${\bar{H}}_2$ as

$$\begin{aligned} {{{\bar{F}}}^{-1}_{S\mid X_1}(q\mid x) =x+{\bar{H}}_2^{-1} \left( \frac{\exp \left( -g^{-1}\left( qg(-\ln {\bar{H}}_1(x))\right) \right) }{{\bar{H}}_1(x)}\right) } \end{aligned}$$

(4.2)

for $0<q<1$. The inverse function of ${F}_{S\mid X_1}$ can be obtained in a similar way.

One can thus predict S from $X_1=x$ by using the quantile (or median) regression curve

$$\begin{aligned} m_{S\mid X_1}(x):= \bar{F}_{S\mid X_1}^{-1}(0.5\mid x). \end{aligned}$$

Moreover, one can compute the centered p confidence bands for these predictions as

$$\begin{aligned} I_p(x):=\left[ \bar{F}_{S\mid X_1}^{-1}\left( 0.5+0.5p\mid x\right) ,\bar{F}_{S\mid X_1}^{-1}\left( 0.5-0.5p\mid x\right) \right] . \end{aligned}$$

For example, the p $=$ 90% centered confidence band for S is

$$\begin{aligned} I_{0.9}(x):=\left[ \bar{F}_{S\mid X_1}^{-1}(0.95\mid x), \bar{F}_{S\mid X_1}^{-1}( 0.05\mid x) \right] . \end{aligned}$$

Such an interval is computed below in some illustrative examples.

Remark 2

In particular, for the GK-model in (2.8) we get

$$\begin{aligned} {{\bar{F}}}_{S\mid X_1}(s\mid x) =\frac{ g(\alpha x+\beta (s-x))}{g(\alpha x)}=\frac{ g((\alpha -\beta )x+\beta s)}{g(\alpha x)} \end{aligned}$$

(4.3)

and

$$\begin{aligned} {\bar{F}}^{-1}_{S\mid X_1}(q\mid x)=\frac{\beta -\alpha }{\beta } x+ \frac{1}{\beta } g^{-1}\left( qg(\alpha x) \right) \end{aligned}$$

(4.4)

for $s\ge x\ge 0$ and $0<q<1$. Note that these expressions hold both for $\alpha = \beta$ and for $\alpha \ne \beta$.

The other conditional distribution can be obtained in a similar manner. However, it is more difficult to get an explicit expression since we need the PDF $f_S$ of S. It is stated in the following proposition.

Proposition 4.2

If (2.5) and (2.7) hold for $(X_1,X_2)$ and $S=X_1+X_2$, then the PDF of $( X_1\mid S=s)$ is

$$\begin{aligned} {f}_{X_1\mid S}(x\mid s)=-\frac{r_1(x)r_2(s-x) g'\left( -\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x)\right) }{f_S(s)} \end{aligned}$$

and its distribution function is

$$\begin{aligned} {F}_{X_1\mid S}(x\mid s)=-\int _{0}^x \frac{r_1(t)r_2(s-t) g'\left( -\ln {\bar{H}}_1(t)-\ln {\bar{H}}_2(s-t)\right) }{f_S(s)}dt \end{aligned}$$

(4.5)

for $0\le x\le s$, where $g=-{\bar{G}}'$ and $r_i=(-\ln {\bar{H}}_i)'$ is the hazard rate function of ${\bar{H}}_i$ for $i=1,2$, and

$$\begin{aligned} f_S(s)=-\int _0^s r_1(x)r_2(s-x) g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))dx. \end{aligned}$$

(4.6)

Proof

From (3.1), the PDF of $(X_1,S)$ is

$$\begin{aligned} {\mathbf {g}}(x,s)=-r_1(x)r_2(s-x) g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x)) \end{aligned}$$

for $0\le x\le s$. Its second marginal survival function was obtained in (3.6). It can also be obtained as in (4.6).

Hence, the conditional PDF of $(X_1\mid S=s)$ is

$$\begin{aligned} {f}_{S\mid X_1}(x\mid s)=\frac{{\mathbf {g}}(x,s)}{f_S(s)}=-\frac{r_1(x)r_2(s-x) g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))}{f_S(s)}. \end{aligned}$$

Then the associated distribution function is the one given in (4.5) for $0\le x\le s$ and the assertion is proved. $\square$

In particular, for the GK-model we have the following explicit expressions.

Proposition 4.3

If (2.8) holds for $(X_1,X_2)$ and $S=X_1+X_2$, then the distribution function of $( X_1\mid S=s)$ is

$$\begin{aligned} {F}_{X_1\mid S}(x\mid s)=\frac{x}{s} \end{aligned}$$

(4.7)

when $\alpha =\beta$ and

$$\begin{aligned} {F}_{X_1\mid S}(x\mid s)=\frac{g((\alpha -\beta )x+\beta s)-g(\beta s)}{ g(\alpha s)-g(\beta s)} \end{aligned}$$

(4.8)

when $\alpha \ne \beta$, for $0\le x\le s$, where $g=-{\bar{G}}'$ and $\alpha ,\beta >0$ are the scale parameters in (2.8).

Proof

From the preceding proposition we have

$$\begin{aligned} {\mathbf {g}}(x,s)=-r_1(x)r_2(s-x) g'(-\ln {\bar{H}}_1(x)-\ln {\bar{H}}_2(s-x))= -\alpha \beta g'((\alpha -\beta )x+\beta s) \end{aligned}$$

for $0\le x\le s$ (zero elsewhere). Its second marginal PDF function $f_S$ was obtained in (3.5) ($\alpha =\beta$) and in (3.4) ($\alpha \ne \beta$).

In the first case we get

$$\begin{aligned} {f}_{X_1\mid S}(x\mid s)=\frac{{\mathbf {g}}(x,s)}{f_S(s)} =\frac{-\alpha ^2g'(\alpha s)}{ -\alpha ^2sg'(\alpha s)}=\frac{1}{s} \end{aligned}$$

and in the second

$$\begin{aligned} {f}_{X_1\mid S}(x\mid s)=\frac{{\mathbf {g}}(x,s)}{f_S(s)} =(\alpha -\beta ) \frac{g'((\alpha -\beta )x+\beta s)}{ g(\alpha s)-g(\beta s)} \end{aligned}$$

for $0\le x\le s$.

Then the associated distribution functions are

$$\begin{aligned} {F}_{X_1\mid S}(x\mid s)&=\int _{0}^x \frac{1}{s} dt=\frac{x}{s} \end{aligned}$$

(in the first case) and

$$\begin{aligned} {F}_{X_1\mid S}(x\mid s)&=\int _{0}^x (\alpha -\beta ) \frac{g'((\alpha -\beta )t+\beta s)}{ g(\alpha s)-g(\beta s)}dt\\&=\left[ \frac{g'((\alpha -\beta )t+\beta s)}{ g(\alpha s)-g(\beta s)}\right] _{t=0}^x\\&= \frac{g((\alpha -\beta )x+\beta s)-g(\beta s)}{ g(\alpha s)-g(\beta s)} \end{aligned}$$

(in the second case) for $0\le x\le s$. $\square$

Note that the expression (4.7) was obtained previously in Proposition 2.3 of Caramellino and Spizzichino (1994) for the Schur-constant model, which is equivalent to (2.8) with $\alpha =\beta$.

As in the preceding case, equations (4.7) and (4.8) can be used to obtain quantile regression curves to predict $X_1$ from S. An illustrative example is given in the following section. In both cases, they can be represented as distorted distributions from G by replacing x with $G^{-1}(G(x))$ and s with $G^{-1}(G(s))$.

In the first case ($\alpha =\beta$), the inverse function is ${F}^{-1}_{X_1\mid S}(q\mid s)=qs$ for $0<q<1$ and the trivial median regression curve is $m_{X_1\mid S}(s)=s/2$ (which in this case coincides with the classic mean regression curve ${\mathbb {E}}(X\mid S=s)$).

In the second case ($\alpha \ne \beta$), we get

$$\begin{aligned} {F}^{-1}_{X_1\mid S}(q\mid s)=\frac{\beta }{\beta -\alpha }s+\frac{1}{\alpha -\beta } g^{-1}\left( q g(\alpha s)+(1-q)g(\beta s)\right) \end{aligned}$$

(4.9)

for $0<q<1$ and $s>0$. Then the median regression curve is

$$\begin{aligned} m_{X_1\mid S}(s)=\frac{\beta }{\beta -\alpha }s+\frac{1}{\alpha -\beta } g^{-1}\left( \frac{1}{2} g(\alpha s)+\frac{1}{2}g(\beta s)\right) . \end{aligned}$$

The confidence bands can be obtained in a similar manner from (4.9) (see Example 2).

5 Examples

In this section we provide some examples to illustrate the theoretical findings described in previous sections. In the first one we consider the sum of two dependent random variables satisfying the GK-model proposed in Genest and Kolev (2021), i.e., the model (2.8).

Example 1

Let us assume that $(X_1,X_2)$ satisfies (2.8) for $\alpha \ne \beta$ and ${\bar{G}}(x)=(1+x)^{-\gamma }$ for $x\ge 0$ (Pareto type II survival function) and $\gamma >0$. This model is equivalent to consider an Archimedean Clayton survival copula with $\theta =1/\gamma$ [see (4.2.1) in Nelson (Nelsen (2006), p. 116)] and Pareto type II marginals. Then, from (3.3), the joint distribution function of $(X_1,S)$ is

$$\begin{aligned} {\mathbf {G}}(x,s)&= G(\alpha x)-\frac{\alpha }{\alpha -\beta } G ((\alpha -\beta )x+\beta s )+ \frac{\alpha }{\alpha -\beta } G(\beta s )\\&=1-\left( 1+\alpha x\right) ^{-\gamma }+\frac{\alpha }{\alpha -\beta }\left( 1+(\alpha -\beta )x+\beta s\right) ^{-\gamma } -\frac{\alpha }{\alpha -\beta } \left( 1+\beta s\right) ^{-\gamma } \end{aligned}$$

for $0\le x\le s$. Hence, the distribution function $F_S$ of S (i.e., the C-convolution) is

$$\begin{aligned} F_S(s)={\mathbf {G}}(s,s)=1+\frac{\beta }{\alpha -\beta } (1+\alpha s)^{-\gamma } -\frac{\alpha }{\alpha -\beta } (1+\beta s)^{-\gamma } \end{aligned}$$

for $s\ge 0$. Its PDF is

$$\begin{aligned} f_S(s)=\frac{\alpha \beta \gamma }{\alpha -\beta } (1+\beta s)^{-\gamma -1}-\frac{\alpha \beta \gamma }{\alpha -\beta } (1+\alpha s)^{-\gamma -1} \end{aligned}$$

for $s\ge 0$. The distribution of S is a negative mixture of two Pareto type II distributions; thus, its hazard rate goes to zero when $s\rightarrow \infty$ (which is the limit of the hazard rates of the members of the C-convolution). They are plotted in Fig. 1 (right) jointly with the associated PDF functions (left) for $\gamma =\alpha =2$ and $\beta =1$. Note that the hazard rates of $X_1$ and $X_2$ are decreasing while the one of S is not monotone, showing that the increasing failure rate (IFR) class is not preserved by the sum of dependent random variables. Some preservation properties can be seen in Navarro and Pellerey (2021).

If we want to predict $X_1$ from $S=s$, we need the conditional distribution obtained from (4.8) as

$$\begin{aligned} F_{X_1\mid S}(x\mid s)&=\frac{g((\alpha -\beta )x+\beta s)-g(\beta s)}{ g(\alpha s)-g(\beta s)}\\&=\frac{(1+(\alpha -\beta )x+\beta s)^{-\gamma -1}-(1+\beta s)^{-\gamma -1}}{ (1+\alpha s)^{-\gamma -1}-(1+\beta s)^{-\gamma -1}} \end{aligned}$$

for $0\le x\le s$. Its inverse function is then

$$\begin{aligned} F^{-1}_{X_1\mid S}(q\mid s)= \frac{-1-\beta s+ \left( q(1+\alpha s)^{-\gamma -1}+(1-q) (1+\beta s)^{-\gamma -1}\right) ^{-1/(\gamma +1)}}{\alpha -\beta } \end{aligned}$$

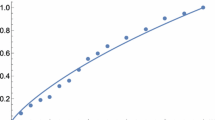
for $0<q<1$. The median regression curve is obtained by replacing q with 1/2. It is plotted in Fig. 2, jointly with a sample from $(X_1,S)$ and the associated 50% and 90% centered confidence bands. We also include there the parametric (top) and nonparametric (bottom) estimations for these curves (dashed lines). Here, nonparametric means that we use the linear quantile regression procedure in R (see Koenker (2005); Koenker and Bassett (1978)).

Fig. 1

Probability density (left) and hazard rate (right) functions for $X_1$ (red), $X_2$ (green) and $S=X_1+X_2$ (blue) under the dependence model (2.8) with Pareto type II marginals studied in Example 1

Fig. 2

Scatterplot of a simulated sample from $(S,X_1)$ in Example 1 jointly with the exact median regression curve (continuous red lines) and the exact 50% and 90% confidence bands (continuous blue lines). The dashed lines represent the estimated curves when the model is known and the parameters are estimated (top) and when the model is unknown and we use a nonparametric linear quantile regression estimators (bottom) from these data

To estimate the parameters in the model from the sample we use the Kendall’s tau coefficient of the pair $(X_1,X_2)$, which is given by

$$\begin{aligned} \tau =\frac{\theta }{2+\theta }=\frac{1}{1+2\gamma } \end{aligned}$$

[see Nelson (2006, p. 163)]. Therefore, $\gamma$ can estimated by

$$\begin{aligned} {\widehat{\gamma }}= \frac{1-{\widehat{\tau }}}{2{\widehat{\tau }}}=\frac{1-0.158}{2\cdot 0.158}=2.664557, \end{aligned}$$

where ${\widehat{\tau }}$ is the estimator of the Kendall’s tau. Then, to estimate $\alpha$ and $\beta$, we recall that ${\mathbb {E}}(X_1)=1/(\alpha (\gamma -1))$ and ${\mathbb {E}}(X_2)=1/(\beta (\gamma -1))$, obtaining

$$\begin{aligned} {\widehat{\alpha }}=\frac{1}{({\widehat{\gamma }}-1 ){\bar{X}}_1 }=\frac{1}{1.664557\cdot 0.3880776}=1.548042 \end{aligned}$$

and

$$\begin{aligned} {\widehat{\beta }}=\frac{1}{({\widehat{\gamma }}-1 ){\bar{X}}_2 }=\frac{1}{1.664557\cdot 0.8674393}=0.6925677. \end{aligned}$$

For the nonparametric linear estimators of the quantile regression curves, we use the R library quantreg (see Koenker (2005); Koenker and Bassett (1978); Navarro (2020)). The estimated median regression line to estimate $X_1$ from S obtained from our sample is

$$\begin{aligned} {\widehat{m}}_{X_1\mid S}(s)=0.09752378 +0.17721635 s. \end{aligned}$$

The procedure to predict S from $X_1$ is analogous.

In the second example we consider the more general TTE dependence model; in this case we show how to predict S from $X_1$.

Example 2

Let $(X_1,X_2)$ have joint survival function defined as in (2.5), where ${\widehat{D}}$ is given in (2.7). Thus, we can use the expressions obtained in Sect. 4, (4.1) and (4.2), to predict S from $X_1$.

For example, we can choose

$$\begin{aligned} {\bar{G}}(x)={\bar{H}}_1(x)={\bar{H}}_2(x)=c\ (1-\Phi (1+x))=c\ \Phi (-1-x)) \end{aligned}$$

for $x\ge 0$, where $\Phi$ is the standard normal distribution and $c=1/\Phi (-1)=6.302974$ (i.e., G is a truncated normal distribution). Hence, $g(x)=c\ \phi (1+x)$ where $\phi =\Phi '$ is the PDF of a standard normal distribution. Note that, in this case, the corresponding Archimedean copula (that we could call Gaussian Archimedean copula) does not have an explicit expression (since it depends on ${\bar{G}}$ and on ${\bar{G}}^{-1}$). Thus, this is a practical example where the distortion representation can be used as a proper alternative.

Under the previous assumptions, the inverse functions are

$$\begin{aligned} {\bar{G}}^{-1}(x)=-1-\Phi ^{-1}\left( \frac{x}{c}\right) \end{aligned}$$

and

$$\begin{aligned} g^{-1}(x)=-1+\left( 2\ln c-\ln (2\pi )-2\ln x \right) ^{1/2}. \end{aligned}$$

By using these expressions we compute ${{\bar{F}}}^{-1}_{S\mid X_1}$ as in (4.2), obtaining the quantile regression curve plotted in Fig. 3 (top). The same figure also includes a sample of $n=100$ points from $(X_1,S)$ and the exact centered 50% and 90% (blue) confidence bands. Moreover, it shows the plot of the nonparametric linear quantile estimate (dashed lines) obtained from this sample.

As we know that $X_1<S$, we could also provide bottom 50% and 90% confidence bands obtained as $\left[ x,{{\bar{F}}}^{-1}_{S\mid X_1}(0.5\mid x)\right]$ and $\left[ x,{{\bar{F}}}^{-1}_{S\mid X_1}(0.1\mid x)\right]$, respectively. They are plotted in Fig. 3 (bottom). In this case, the median regression curve is also the upper limit for the 50% confidence band. In our sample we obtain 10 data above the upper (exact) limit and 46 above the median regression curve (i.e., 54 data in the exact bottom 50% confidence band). The estimated median regression line obtained from our sample is

$$\begin{aligned} {\widehat{m}}_{S\mid X_1}(x)=0.3159734 +0.7284655x \end{aligned}$$

for $x\ge 0$.

Fig. 3

Scatterplot of a simulated sample from $(X_1,S)$ in Example 2 jointly with the median regression curve (red) and the centered (top) or bottom (bottom) 50% and 90% confidence bands (blue). The dashed lines represent the estimated values when we use a linear quantile regression estimator

In the next example we show a case of model (2.8) that cannot be represented with an explicit Archimedean copula, thus for which the distortion representations consists in a useful alternative tool. In fact, in this example ${\bar{G}}$ is convex and an explicit expression for its inverse is not available. For this model we compute the explicit expressions for the C-convolution and the two conditional survival functions.

Example 3

Let us consider (2.8) with $\alpha \ne \beta$ and the survival function

$$\begin{aligned} {\bar{G}}(x)=\frac{2+x}{2} e^{-x} \end{aligned}$$

for $x\ge 0$. Its PDF is

$$\begin{aligned} g(x)=\frac{1+x}{2} e^{-x} \end{aligned}$$

for $x\ge 0$, that is, a translated Gamma (Erlang) distribution. The joint survival function of $(X_1,X_2)$ is

$$\begin{aligned} {\bar{\mathbf {F}}}(x_1,x_2)={\bar{G}}(\alpha x_1+\beta x_2)= \frac{2+\alpha x_1+\beta x_2}{2} \exp (-\alpha x_1-\beta x_2) \end{aligned}$$

for $x_1,x_2\ge 0$. The marginals also follow translated Gamma distributions.

The joint distribution of $(X_1,S)$ can be obtained from (3.3). From this expression, the survival function of S (C-convolution) is

$$\begin{aligned} {\bar{F}}_S(s)&=\frac{\alpha }{\alpha -\beta } {\bar{G}}(\beta s )- \frac{\beta }{\alpha -\beta } {\bar{G}} (\alpha s )\\&=\frac{\alpha }{\alpha -\beta }e^{-\beta s}- \frac{\beta }{\alpha -\beta } e^{-\alpha s} + \frac{\alpha \beta s}{2(\alpha -\beta )}\left( e^{-\beta s}-e^{-\alpha s}\right) \end{aligned}$$

for $s\ge 0$. Note that it is a negative mixture of two translated Gamma distributions.

The conditional survival function of $(S\mid X_1=x)$ can be obtained from (4.3) as

$$\begin{aligned} {\bar{F}}_{S\mid X_1}(s\mid x)=\frac{g((\alpha -\beta )x+\beta s)}{g(\alpha x)}=\frac{1+ (\alpha -\beta )x+\beta s}{1+\alpha x}e^{-\beta (s-x)} \end{aligned}$$

for $s\ge x$. Analogously, from (4.8), the conditional survival function of $(X_1\mid S=s)$ is

$$\begin{aligned} {\bar{F}}_{X_1\mid S}(x\mid s)= & {} \frac{g(\alpha s)-g((\alpha -\beta )x+\beta s)}{g(\alpha s)-g(\beta s)}\nonumber \\= & {} \frac{1+\alpha s -(1+(\alpha -\beta )x+\beta s)e^{(\alpha -\beta )(s-x)}}{1+\alpha s-(1+\beta s)e^{(\alpha -\beta )s}} \end{aligned}$$

for $0\le x\le s$.

In Fig. 4 we plot the probability density (left) and hazard rate (right) functions of $X_1$ (red), $X_2$ (green) and S (blue) when $\alpha =2$ and $\beta =1$. Note that both marginals are IFR and the same holds for S. Also note that the limiting behavior of the hazard rate of S coincides with that of the best component in the sum ($X_2$). This is according with the results on mixtures obtained in Lemma 3.3 of Navarro and Shaked (2006) (or Lemma 4.6 in Navarro and Sarabia (2020)) and that in Theorem 1 of Block et al. (2015) on usual convolutions.

Fig. 4

Probability density (left) and hazard rate (right) functions for $X_1$ (red), $X_2$ (green) and $S=X_1+X_2$ (blue) under the dependence model (2.8) with translated gamma marginals studied in Example 3. The dashed lines represent the limiting behavior

In the last example we show a case dealing with the GK model (2.8) where the inverse of the conditional distribution function $F_{X_1\mid S}$ of $(X_1\mid S)$ cannot be obtained in a closed form. Then we need to use numerical methods (or implicit function plots). Moreover, it also shows that the quantile (median) regression curve $m_{X_1\mid S}(s)=F^{-1}_{X_1\mid S}(0.5\mid s)$ is not always increasing.

Example 4

Let us consider the model (2.8) with a survival copula in the family of Gumbel–Barnett copulas [see (4.2.9) in Nelson (2006, p. 116]. In this case, the additive generator of the copula is ${\bar{G}}^{-1}(x)=\ln (1-\theta \ln x)$ for $x\in (0,1]$ and $\theta \in (0,1]$. These copulas are strict Archimedean copulas and the independence (product) copula is obtained for $\theta \rightarrow 0$. Hence,

$$\begin{aligned} {\bar{G}}(x)= \exp \left( \frac{1}{\theta }- \frac{1}{\theta }e^x \right) \end{aligned}$$

and

$$\begin{aligned} g(x)=\frac{1}{\theta }\exp \left( x+\frac{1}{\theta }- \frac{1}{\theta }e^x \right) \end{aligned}$$

for $x\ge 0$. Note that the inverse of g does not have an explicit form, thus one cannot use (4.9) to compute the quantile functions of $(X_1\mid S)$. The same happens in (4.4) for the quantile functions of $(S\mid X_1)$.

However, it is possible to plot the level curves of the conditional distribution function by using (4.8), obtaining

$$\begin{aligned} {F}_{X_1\mid S}(x\mid s)=\frac{g((\alpha -\beta )x+\beta s)-g(\beta s)}{ g(\alpha s)-g(\beta s)} \end{aligned}$$

(5.1)

when $\alpha \ne \beta$. For example, if we choose $\alpha =3$, $\beta =1$ and $\theta =1$ in (5.1), we get

$$\begin{aligned} {F}_{X_1\mid S}(x\mid s)=\frac{g(2x+ s)-g(s)}{ g(3s)-g(s)} =\frac{\exp \left( 2x+s+ 1 - e^{2x+s} \right) -\exp \left( s+ 1 - e^{s} \right) }{\exp \left( 3s+ 1 - e^{3s} \right) -\exp \left( s+ 1 - e^{s} \right) } \end{aligned}$$

for $0\le x\le s$. These level curves are plotted in Fig. 5 (left) for $q=0.05,0.25,0.5,0.75$,0.95. Note that the median regression curve $m_{X_1\mid S}(s)=F^{-1}_{X_1\mid S}(0.5\mid s)$ (red line, left) is first increasing and then decreasing. To explain this surprising fact we plot ${F}_{X_1\mid S}(x\mid s)$ in Fig. 5 (right) for different values of s, where one can observe that these distribution functions are not ordered in s, that is, $(X_1\mid S=s)$ is not stochastically increasing in s. Here the greater values for $X_1$ are obtained when $S\approx 0.6$ (green line). Also note that ${\mathbb {E}}(X_2)=3{\mathbb {E}}(X_1)$ and that $X_1$ and $X_2$ are negatively correlated. Therefore, the greater values of S are mainly obtained from the greater values of $X_2$ and the smaller values of $X_1$. For that reasons $m_{X_1\mid S}$ is decreasing at the end.

Also note that

$$\begin{aligned} {\mathbb {C}}ov(X_1,S)={\mathbb {V}}ar(X_1)+{\mathbb {C}}ov(X_1,X_2)={\mathbb {V}}ar(X_1)+{\mathbb {E}}(X_1X_2)-{\mathbb {E}}(X_1){\mathbb {E}}(X_2). \end{aligned}$$

Therefore, ${\mathbb {C}}ov(X_1,S)\ge 0$ when ${\mathbb {C}}ov(X_1,X_2)\ge 0$ and, in particular, when $X_1$ and $X_2$ are independent. However, the covariance ${\mathbb {C}}ov(X_1,S)$ will be negative if ${\mathbb {V}}ar(X_1)<-{\mathbb {C}}ov(X_1,X_2)$. In our case, the marginal reliability functions of $X_1$ and $X_2$ are ${\bar{F}}_1(t)={\bar{G}}(3t)$ and ${\bar{F}}_2(t)={\bar{G}}(t)$, respectively. Their means are ${\mathbb {E}}(X_1)=0.198782$ and ${\mathbb {E}}(X_2)=0.596347$, their variances ${\mathbb {V}}ar(X_1)=0.019589$ and ${\mathbb {V}}ar(X_2)=0.176301$ and their covariance ${\mathbb {C}}ov(X_1,X_2)=-0.029889$. Hence

$$\begin{aligned} {\mathbb {C}}ov(X_1,S)={\mathbb {V}}ar(X_1)+{\mathbb {C}}ov(X_1,X_2)=0.019589-0.029889=-0.010299<0. \end{aligned}$$

Fig. 5

Median regression curve (red) and quantile regression curves (blue) for $q=0.05,0.25,0.75,0.95$ (left) for $(S,X_1)$ in Example 4. Conditional distribution functions $F_{X_1\mid S}(x\mid s)$ for $s=0.2$ (red), 0.4 (blue), 0.6 (green), 0.8 (orange), 1 (black) and 2 (purple). The black line in the left plot represents the line $X_1=S$

6 Conclusions

We formulated the TTE dependence model by using a distortion representation based on a specific fixed distortion function ${\widehat{D}}$. This representation is useful to compute the joint distribution of $X_1$ and the sum $S=X_1+X_2$, as well as to provide expressions for the survival function of S and the conditional distributions of S given $X_1$ or $X_1$ given S. They can be used also to predict one value from the other by using quantile regression. Some examples illustrate these facts, showing that sometimes the classical copula approach cannot be applied.

This paper is a first step on applications of distortion representations for the TTE dependence model. Thus, there are several tasks for future research. The main one could be to get explicit models by choosing appropriate functions ${\bar{G}}$, ${\bar{H}}_1$ and ${\bar{H}}_2$, to study their main properties and how they fit to real data sets, allowing for the use of the prediction techniques developed here for these data sets. Other interesting questions deal with dependence models for which the multivariate distortion function ${\widehat{D}}$ differs from the one in Eq. (2.7), or how to get explicit expressions for the multivariate case.