Where to find needles in a haystack?

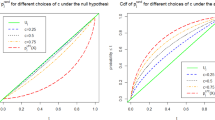
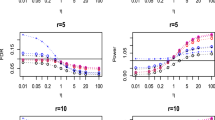
Abstract

In many existing methods of multiple comparison, one starts with either Fisher’s p value or the local fdr. One commonly used p value, defined as the tail probability exceeding the observed test statistic under the null distribution, fails to use information from the distribution under the alternative hypothesis. The targeted region of signals could be wrong when the likelihood ratio is not monotone. The oracle local fdr based approaches could be optimal because they use the probability density functions of the test statistic under both the null and alternative hypotheses. However, the data-driven version could be problematic because of the difficulty and challenge of probability density function estimation. In this paper, we propose a new method, Cdf and Local fdr Assisted multiple Testing method (CLAT), which is optimal for cases when the p value based methods are optimal and for some other cases when p value based methods are not. Additionally, CLAT only relies on the empirical distribution function which quickly converges to the oracle one. Both the simulations and real data analysis demonstrate the superior performance of the CLAT method. Furthermore, the computation is instantaneous based on a novel algorithm and is scalable to large data sets.

Appendix

1.1 Proof of Theorem 1

(a) Theorem 2.2 and its proof in He et al. (2015), the optimal rejection set $\mathbb {S}_F(q)$ is given as

$$\begin{aligned} \mathbb {S}_F(q) = \{x: \varLambda (x)>c\}, \end{aligned}$$

where c is chosen as the minimum value such that mfdr is less than or equal to q.

When $\varLambda$ is monotone increasing, then $\mathbb {S}_F(q) = (c', \infty )$. This agrees with the $\mathbb {I}_{BH}(q)$ and $\mathbb {I}_F(q)$ defined in Eq. (8).

(b) When $\mathbb {S}_F(q)$ is a finite interval, by the definition, $\mathbb {I}_F(q) = \mathbb {S}_F(q)$. Since the right end point of the interval $\mathbb {I}_F(q)$ is $\infty$, it is not optimal. $\square$

1.2 Proof of Theorem 2

For any interval $\mathbb {I}_i=[a,b]$, let $s(a,b)=(1-\pi _1)\int _a^b\hbox {d}F_0(x)-q\int _a^b\hbox {d}F(x)$. Then

$$\begin{aligned} \frac{\partial s}{\partial b}=(1-q)(1-\pi _1)f_0(b)\left( 1-\frac{\varLambda (b)}{q'}\right) >0. \end{aligned}$$

Consequently, for any fixed a, s(a, b) is increasing with respect to b. Since $s(a, a)=0$, therefore, $s(a, b)>0, \forall b>a$. This implies that $(1-\pi _1)\int _{\mathbb {I}_i}\hbox {d}F_0(x)> q\int _{\mathbb {I}_i}\hbox {d}F(x)$, for all $i=1,2,\ldots$. As a result,

$$\begin{aligned} (1-\pi _1)\int _{\mathbb {U}}\hbox {d}F_0(x)> q\int _{\mathbb {U}}\hbox {d}F(x), \end{aligned}$$

which completes the proof. $\square$

1.3 Proof of Theorem 3

Let $s(a,b)=(1-\pi _1)\int _a^b \hbox {d}F_0(x) - q\int _a^b \hbox {d}F(x)$. Consider $a=c_1$. Then $s(c_1,c_1)=0$. According to the proof of Theorem 2, $\frac{\partial s}{\partial b}<0, \forall b\in [c_1,c_2]$. This implies that $s(c_1,c_2)<0$ and consequently $[c_1,c_2]\subset \mathbb {S}_F(q)$. $\square$

1.4 Proof of Theorem 4

Define the function $s(a)=(1-\pi _1) \int _a^\infty \hbox {d}F_0(x) - q\int _a^\infty \hbox {d}F(x)$. Then

$$\begin{aligned} s'(a) = -(1-\pi _1)f_0(a) + \pi _1 f(a) = q\pi _1 f_0(a) (\varLambda (a)-q'). \end{aligned}$$

Let c be the value such that $\varLambda (c)=q'$. When $a\ge c$, $s'(a)>0$, implying that s(a) is increasing with respect to a. Since $s(\infty )=0$, therefore $s(c)<0$. Consequently, $\mathbb {I}_{F}(q)$ contains $[c,\infty )$. $\square$

1.5 Proof of Theorem 5

According to the definition of s(a, b) and $c_1, c_2$, we know that

$$\begin{aligned} \frac{\partial s}{\partial b}=(1-q)(1-\pi _1)f_0(b)\left( 1-\frac{1}{q'}\varLambda (b)\right) \left\{ \begin{array}{ll}>0, &{} \text {if}\, b<c_1,\\<0, &{} \text {if}\, c_1<b<c_2,\\>0, &{} \text {if}\, b>c_2.\end{array}\right. \end{aligned}$$

Consequently, for any fixed a, s(a, b) increases when $b<c_1$ or $b>c_2$ and decreases when $c_1<b<c_2$. Similarly,

$$\begin{aligned} \frac{\partial s}{\partial a}=(1-q)(1-\pi _1)f_0(a)\left( \frac{1}{q'}\varLambda (a)-1\right) \left\{ \begin{array}{ll}<0, &{} \text {if}\, a<c_1,\\>0, &{} \text {if}\, c_1<a<c_2,\\ <0, &{} \text {if}\, b>c_2.\end{array}\right. \end{aligned}$$

For any fixed b, s(a, b) decreases when $a<c_1$ or $a>c_2$ and inreases when $c_1<a<c_2$. To demonstrate this pattern, we plot various curves of s(a, b) in Fig. 11.

Fig. 11

Curve of the function of s(a, b). In the left panel, b is a fixed constant and we plot s(a, b) as a function of a. In the right panel, we plot it as a function of b with a being fixed as a constant

Since g(a) attains the maximum at $a_0$, according to Theorem 3, $a_0<c_1$ and $b_{a_0}(F)>c_2$. Consequently, $(1-\pi _1)f_0(a_0)-qF'(a_0)>0$, and $(1-\pi _1)f_0(b_{a_0}(F))-qF'(b_{a_0}(F))>0$. Therefore, the function $b_a(F)$ is a monotone increasing function of a at a small neighborhood of $a_0$. For a sufficiently small constant L independent of n, there exists a neighborhood $A'$ of $b_{a_0}(F)$ such that $f_0(x)-qF'(x)>L$, $\forall x\in A'\cup b^{-1}_{A'}(F)$ where $b^{-1}_{A'}(F)=\{a: b_a(F)\in A'\}$. Let $A=[a_1,a_2]=b^{-1}_{A'}(F)$ where $a_1<a_0<a_2<c_1$. The proof of Theorem 5 requires the following lemmas.

Lemma 1

Let $F_n$ be the empirical distribution function, then $\forall a$, if $b_a(F)=+\infty$ or $b_a(F)<+\infty$ and $F'(b_a(F))-\frac{1}{q}f_0(b_a(F))\ne 0$, then

$$\begin{aligned} b_a(F_n)\rightarrow b_a(F), \text {and}\quad g_n(a)\rightarrow g(a). \end{aligned}$$

If $F'(b_a(F))-\frac{1}{q}f_0(b_a(F))=0$, then $\limsup g_n(a)\le g(a)$.

Lemma 2

There exists a sub-interval $\mathbb {B}=[b_1,b_2]$ of $\mathbb {A}=[a_1,a_2]$, such that for all $a\in \mathbb {B}$, $|b_a(F_n)-b_a(F)|\le C\epsilon$ provided that $||F_n-F||<\epsilon$.

Lemma 3

The function $g_n(a)$ can not achieve the maximum at $\mathbb {B}^c$.

Lemma 4

For any $a\in \mathbb {B}$, $|g_n(a)-g(a)|<C\epsilon$.

Proof of Theorem 5

Assume that $g_n(a)$ attains the maximum at $a=a_n$, then according to Lemma 3, $a_n\in \mathbb {B}$. According to Lemma 4,

$$\begin{aligned} g_n(a_n)-g(a_0)= g_n(a_n)-g_n(a_0)+g_n(a_0)-g(a_0)>-C\epsilon . \end{aligned}$$

Since $g(a_n)-g(a_0)<0$, $g_n(a_n)-g(a_0)=g_n(a_n)-g(a_n)+g(a_n)-g(a_0) <C\epsilon$. In other words, $|g_n(a_n)-g(a_0)|<C\epsilon .$ Further, DKW’s inequality guarantees that $P(\sup _x|F_n(x)-F(x)|>\epsilon )\le 2e^{-2n\epsilon ^2}$. Consequently,

$$\begin{aligned} P(|g_n(a_n)-g(a_0)|>C\epsilon )\le 2e^{-2n\epsilon ^2}. \end{aligned}$$

Next, we will prove that $\limsup _{n\rightarrow \infty } m\textsc {fdr}\le q$. According to the definition of $a_n$,

$$\begin{aligned} \frac{ (1-\pi _1)\int _{a_n}^{b_{a_n}(F_n)} \hbox {d}F_0 }{ g_n(a_n) } = \frac{ (1-\pi _1)\int _{a_n}^{b_{a_n}(F_n)} \hbox {d}F_0 }{ \int _{a_n}^{b_{a_n}(F_n)}\hbox {d}F_n }\le q. \end{aligned}$$

The mfdr can be written as

$$\begin{aligned} m\textsc {fdr}=\frac{ ( 1-\pi _1 )\int _{a_n}^{b_{a_n}(F_n)}\hbox {d}F_0 }{ \int _{a_n}^{b_{a_n}(F_n)}\hbox {d}F}=\frac{ (1-\pi _1)\int _{a_n}^{b_{a_n}(F_n)}\hbox {d}F_0 }{g(a_n)}. \end{aligned}$$

Note that $|g_n(a_n)-g(a_n)|\le |g_n(a_n)-g(a_0)|+|g(a_n)-g(a_0)|\rightarrow 0$ and $g(a_n)\rightarrow g(a_0)>0$. Consequently,

$$\begin{aligned} \limsup _{n\rightarrow \infty } m\textsc {fdr}=\limsup _{n\rightarrow \infty } \frac{ (1-\pi _1)\int _{a_n}^{b_{a_n}(F_n)}\hbox {d}F_0 }{g_n(a_n)}\frac{g_n(a_n)}{g(a_n)}\le q. \end{aligned}$$

$\square$

Proof of Lemma 1

Since $F_n$ is the empirical cdf, DKW’s inequality guarantees that $\forall \epsilon >0$, with high probability $F(x)-\epsilon \le F_n \le F(x)+\epsilon ,\forall x.$ Consider the function

$$\begin{aligned} F_U(x)=\left\{ \begin{array}{ll} F(x)+\epsilon &{} \forall x>a \\ F(x)-\epsilon &{} \forall x\le a\end{array}\right. \end{aligned}$$

Then by the definition of $b_a(F_n)$ and $F_U$,

$$\begin{aligned} \frac{1}{q}\le \frac{F_n(b_a(F_n))-F_n(a)}{(1-\pi _1)(F_0(b_a(F_n))-F_0(a))}\le \frac{F_U(b_a(F_n))-F_U(a)}{(1-\pi _1)(F_0(b_a(F_n))-F_0(a))}. \end{aligned}$$

Consequently, $b_a(F_n)\le b_a(F_U)$. Similarly define

$$\begin{aligned} F_L(x)=\left\{ \begin{array}{ll} F(x)-\epsilon &{} \forall x>a \\ F(x)+\epsilon &{} \forall x\le a\end{array}\right. \end{aligned}$$

Then one can similarly show that $b_a(F_L)\le b_a(F_n)$. As a result, $b_a(F_L)\le b_a(F_n)\le b_a(F_U).$ If $(1-\pi _1)f_0(b_a(F))-qF'(b_a(F))\ne 0$ and $b_a(F)<\infty$, then the curve s(a, b) is strictly increasing at a neighbourhood of $b_a(F)$. Consequently, there exists a neighbourhood N of $b_a(F)$ such that $b_a(F_U)$ and $b_a(F_L)$ fall in this neighbourhood N. Consequently, $b_a(F_n)\rightarrow b_a(F).$ If $b_a(F)=+\infty$, then $b_a(F_L)\rightarrow \infty$, implying $b_a(F_n)\rightarrow b_a(F)$. Furthermore,

$$\begin{aligned}&|g_n(a)-g(a)|=|F_n(b_a(F_n))-F_n(a)-F(b_a(F))+F(a)|\\\le & {} |F_n(b_{a}(F_n))-F(b_a(F_n))|+|F(b_a(F_n)-F(b_a(F))|+|F_n(a)-F(a)|\\\le & {} 2\epsilon +|F(b_a(F_n)-F(b_a(F))| \rightarrow 0. \end{aligned}$$

If $(1-\pi _1)f_0(b_a(F))-qF'(b_a(F))=0$, then there exists an neighborhood C of $b_a(F)$ such that $s(a,x)>\delta > 0, \forall x\in C^c\cap [b_a(F), +\infty )$. Then $b_a(F_n)$ is bounded by $b_a(F_U)$ which converges to $b_a(F)$. Consequently,

$$\begin{aligned} \limsup g_n(a)\le g(a). \end{aligned}$$

$\square$

Proof of Lemma 2

Let $\mathbb {B}=[b_1,b_2]$ be a sub-interval of $\mathbb {A}=[a_1,a_2]$ that contains $a_0$ such that $b_{\mathbb {B}}(F)\subset b_{\mathbb {A}}(F)$. For any $a\in \mathbb {B}$, let $\varDelta = s(a, b_{a_2}(F)) >0$. Since $s(a, b_{a_2}(F))$ is a continuous function of a and $\mathbb {B}$ is a closed interval, one can find a common lower bound $\varDelta$ such that $s(a, b_{a_2}(F))>\varDelta , \forall a\in \mathbb {B}$. Since $\frac{\partial s(a, t)}{\partial t}>0$, $\forall t>b_{a_2}(F)$, $s(a, t)>\varDelta$ for all $a\in \mathbb {B}$ and $t>b_{a_2}(F)$. The definition of $b_a(F_n)$ indicates that

$$\begin{aligned} (1-\pi _1)( F_0(b_a(F_n))-F_0(a) ) -q ( F_n(b_a(F_n))-F_n(a) )\le 0. \end{aligned}$$

This leads to

$$\begin{aligned} ( 1-\pi _1) (F_0(b_a(F_n))- F_0(a)) - q (F(b_a(F_n))-F(a)) \le 2q\epsilon <\varDelta . \end{aligned}$$

Therefore $b_a(F_n)<b_{a_2}(F)$.

Next, we will show that $b_a(F_n)> b_{a_1}(F)$. According to the definition of $b_a(F)$, $s(a, b_a(F))=0$ and

$$\begin{aligned} \frac{\partial s(a,t)}{\partial t}|_{t=b_a(F)}=(1-\pi _1)f_0(b_a(F))-qF'(b_a(F))>0. \end{aligned}$$

We can find $t_0<b_a(F), t_0 > b_{a_1}(F)$, such that

$$\begin{aligned} (1-\pi _1)(F_0(t_0)-F_0(a))-q(F(t_0)-F(a))=-\varDelta <0 \end{aligned}$$

Therefore for sufficiently small $\epsilon$,

$$\begin{aligned} (1-\pi _1)(F_0(t_0)-F_0(a))-q(F_n(t_0)-F_n(a))<-\varDelta +2\epsilon <0 \end{aligned}$$

which implies that $b_a(F_n)>t_0> b_{a_1}(F)$. Consequently, $b_a(F_n)\in b_A(F)$.

Next, we will prove that $|b_a(F_n)-b_a(F)|\le L\epsilon .$ Indeed, since $(1-\pi _1)(F_0(b_a(F_n))-F_0(a))-q(F_n(b_a(F_n))-F_n(a))\le 0$ and

$$\begin{aligned} (1-\pi _1)(F_0(b_a(F))-F_0(a))-q(F(b_a(F))-F(a))=0, \end{aligned}$$

(14)

then

$$\begin{aligned}&q(F_n(b_a(F_n))-F(b_a(F)))-(1-\pi _1)(F_0(b_a(F_n))\\&\qquad -F_0(b_a(F)))\ge q(F_n(a)-F(a)). \end{aligned}$$

As a result,

$$\begin{aligned}&q(F(b_a(F_n))-F(b_a(F)))-(1-\pi _1)(F_0(b_a(F_n))-F_0(b_a(F)))\nonumber \\&\quad \ge (F_n(a)-F(a))+q(F(b_a(F_n))-F_n(b_a(F_n)))\ge -2q\epsilon . \end{aligned}$$

(15)

By the definition of $b_a(F_n)$, $(1-\pi _1)(F_0(b_a(F_n)^+) - F_0(a))-q(F_n( b_a(F_n)^+) - F_n(a))>0$. With (14), we know that

$$\begin{aligned}&q(F( b_a(F_n)^+) - F(b_a(F) ))- (1-\pi _1) ( F_0(b_a(F_n)^+)-F_0(b_a(F))) \\&\quad< q( F_n(a)-F(a))+ q (F(b_a(F_n)^+)- F_n(b_a(F_n)^+)) <2q\epsilon . \end{aligned}$$

When we take the limit in the previous formula and combine it with (15), we see that

$$\begin{aligned} | q(F(b_a(F_n))-F(b_a(F)))-(1-\pi _1)(F_0(b_a(F_n))-F_0(b_a(F))) | < 2q\epsilon . \end{aligned}$$

Therefore

$$\begin{aligned} |(b_a(F_n)-b_a(F))(qF'(\xi )-(1-\pi _1)f_0(\xi ))|\le 2q\epsilon . \end{aligned}$$

Since $b_a(F), b_a(F_n)\in b_{\mathbb {A}}(F)$, $|qF'(\xi )-f_0(\xi )|>L$, we conclude that $|b_a(F_n)-b_a(F)|\le C\epsilon$ for some constant C. $\square$

Proof of Lemma 3

Firstly, we will show that there exists a positive constant $\varDelta$ such that $g(a_1)-g(a_0)<-\varDelta$, $\forall a_1\notin \mathbb {B}$.

Since

$$\begin{aligned} s(-\infty ,c_2)=\int _{-\infty }^{c_2}(1-\pi _1)\hbox {d}F_0(x)-q\int _{-\infty }^{c_2}\hbox {d}F(x)>q\pi _1(q'\int _{-\infty }^{c_2}f_0-1)>0, \end{aligned}$$

and $s(a,c_2)$ decreases when $a<c_2$ and increases when $c_1<a<c_2$. Combining this with the fact that $s(c_2,c_2)=0$, one knows that there exists a unique $a^*<c_1$ such that $s(a^*,c_2)=0$. Let $\mathbb {I}=\{[a,b]: s(a,b)\le 0\}$ and

$$\begin{aligned} \mathbb {L}=\{a: \text {there exists}\,b>a\, \text {such that}\, [a,b]\in \mathbb {I}\}. \end{aligned}$$

First, we prove that $\mathbb {L}=[a^*,c_2)$. Indeed if $a'>c_2$, then for any $b>a'>c_2$, $s(a',b)>s(a',a')=0.$ Iff $a'<a^*<c_1$, then $s(a',b)>s(a^*,b)\ge 0, \forall b>a^*$. Consequently $\mathbb {L}\subset [a^*,c_2)$. On the other hand, for any $a^*\le a \le c_2$, $s(a,c_2)\le s(a^*,c_2)=0$, implying that $[a^*, c_2)\subset \mathbb {L}$. Consequently, $\mathbb {L}=[a^*,c_2)$.

Note that when $c_1<a\le c_2$, $g(a)<g(c_1)$. We thus only need to consider $\mathbb {L}'=[a^*,c_1]$. The function $g: \mathbb {L}'\rightarrow [0,1]$ is a continuous function and g(a) attains the maximal at a unique point $a=a_0$. Therefore, we can find a positive constant $\varDelta$ such that

$$\begin{aligned} g(a_1)-g(a_0)<-\varDelta , \forall a_1\in B^c. \end{aligned}$$

For any $a_1\in B^c$, if $a_1$ satisfies $f_0(b_{a_1}(F))-qF'(b_{a_1}(F))=0$, Lemma 1 implies that $\limsup _{n\rightarrow \infty } g_n(a_1)\le g(a_1)<g(a_0)-\varDelta$. The fact that $g_n(a_0)\rightarrow g(a_0)$ implies that $g_n(a_1)<g_n(a_0)$ for sufficiently large n.

If $(1-\pi _1)f_0(b_{a_1}(F))- qF'(b_{a_1}(F))\ne 0$, then

$$\begin{aligned}&g_n(a_1)-g_n(a_0)=g_n(a_1)-g(a_1)+g(a_1)-g(a_0)+g(a_0)-g_n(a_0) \\< & {} -\varDelta +g_n(a_1)-g(a_1)+g(a_0)-g_n(a_0). \end{aligned}$$

According to Lemma 1, $g_n(a_1)\rightarrow g(a_1), g_n(a_0)\rightarrow g(a)$, then $g_n(a_1)<g_n(a_0)$. Consequently, $g_n$ attains the maximum in $\mathbb {B}$. $\square$

Proof of Lemma 4

$$\begin{aligned}&|g_n(a)-g(a)| =|F_n(b_a(F_n))-F_n(a)-F(b_a(F))+F(a)|\\&\quad =|F_n(b_a(F_n))-F(b_a(F_n))+ F(b_a(F_n))-F(b_a(F))-(F_n(a)-F(a))|\\&\quad \le 2\epsilon +|F(b_a(F_n))-F(b_a(F))|\le 2\epsilon +|b_a(F_n)-b_a(F)||F'(\xi )|. \end{aligned}$$

According to Lemma 2, $b_a(F_n)-b_a(F)=O(\epsilon )$, consequently, $|g_n(a)-g(a)|\le C\epsilon .$ $\square$

1.6 EM algorithm

In this section, we outline the steps of EM algorithm. Let $X_1,X_2,\ldots ,X_n$ be the test statistic. We fit the following model

$$\begin{aligned} X_i{\mathop {\sim }\limits ^{\mathrm {iid}}}(1-\pi _1)\phi (x) + \pi _1\sum _{l=1}^L p_l\frac{1}{\sigma _l}\phi \left( \frac{x-\mu _l}{\sigma _l}\right) . \end{aligned}$$

The parameters to be estimated are $\pi _1$, $p_l$, $\mu _l$, and $\sigma _l^2$, for $l=1,2,\ldots , L$.